Linear Transformation
Table of Contents
1. 齐次坐标(射影坐标)
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry, as Cartesian coordinates are used in Euclidean geometry.

Figure 1: 两条铁轨在地平线处相交(图片摘自:http://www.songho.ca/math/homogeneous/homogeneous.html)
我们知道,欧拉平面中两条平行线不会相交,然而在投影空间里却不是这样。如图 1 所示,两条铁轨的间距随着视线变远而减小,直至在地平线处(无限远点)相交。
在齐次坐标系中,用 N+1 个分量来描述 N 维坐标。比如,对于 3 维笛卡尔坐标 \((X,Y,Z)\) ,其对应的齐次坐标为 4 维的,记为 \((x, y, z, w)\) ,两者对应关系为:
\[\begin{cases}
X = x/w \\
Y = y/w \\
Z = z/w \\
\end{cases}\]
如果 \(w=1\) ,则笛卡尔坐标到齐次坐标的转换非常简单 \((X,Y,Z) \to (X,Y,Z,1)\) 。
1.1. 缩放不变性(Scale Invariant)
齐次坐标中的点 \((1, 2, 3), (2, 4, 6), (4, 8, 12), \cdots, (1a, 2a, 3a)\) 映射到笛卡尔坐标中,为同一点 \((1/3, 2/3)\) 。 即这些点具有尺度不变性(Scale Invariant),是“齐性的”,这就是齐次坐标名字的由来。
1.2. 表示无穷远处的点
在笛卡尔坐标中的一个二维点 \((1,2)\) 可以在齐次坐标中表示为 \((1,2,1)\) ,如果这个点朝东北方向移向无穷远处,其欧式坐标没有太多意义会为 \((\infty, \infty)\) ,而齐次坐标变为 \((1,2,0)\) 。所以在齐次坐标下不需要 \(\infty\) 就可以表示无限远处的点。
2. 二维线性变换
可以用 \(2 \times 2\) 矩阵来表示二维线性变换(如缩放,旋转、切变等)。
\[\left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} a_{11}x + a_{12} y \\ a_{21}x + a_{22}y \end{array} \right]\]
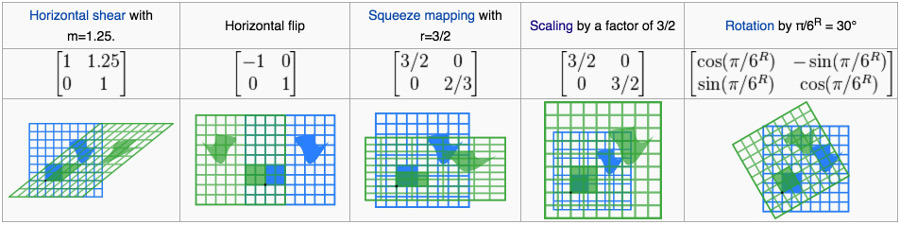
Figure 2: 二维线性变换实例(蓝色为变换前图形,绿色为变换后图形,中心坐标用黑点表示)
2.1. 二维线性变换组合
对物体的变换常常不只一种。例如,先用矩阵 \(\mathbf{S}\) 缩放,然后再用 \(\mathbf{R}\) 进行旋转。对于二维向量 \(v_1\) ,可以用两步实现:
\[v_2 = \mathbf{S} v_1, \; v_3 = \mathbf{R} v_2\]
也可用另外一种方式表示:
\[v_3 = \mathbf{R}(\mathbf{S}v_1) = (\mathbf{RS})v_1\]
换句话说,两个矩阵的变换效果可以用一个矩阵实现,该矩阵等于原来两个矩阵的积。
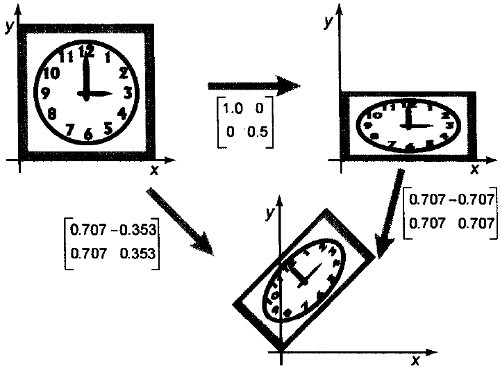
Figure 3: 按顺序使用两个变换矩阵(先在垂直方向上压缩 1/2,然后旋转 45 度),效果与一次使用两矩阵之积一样
参考:计算机图形学(第 2 版, 高春晓等译),6.1.5 二维变换组合
2.2. 二维线性变换分解(“旋转、缩放、再旋转”的乘积)
任何二维变换矩阵都可以分解成“旋转、缩放、再旋转”三个矩阵的乘积,其中缩放矩阵中的元素可能含有负号(也就是可能包含反射)。
利用矩阵的奇异值分解可以实现这个分解过程。
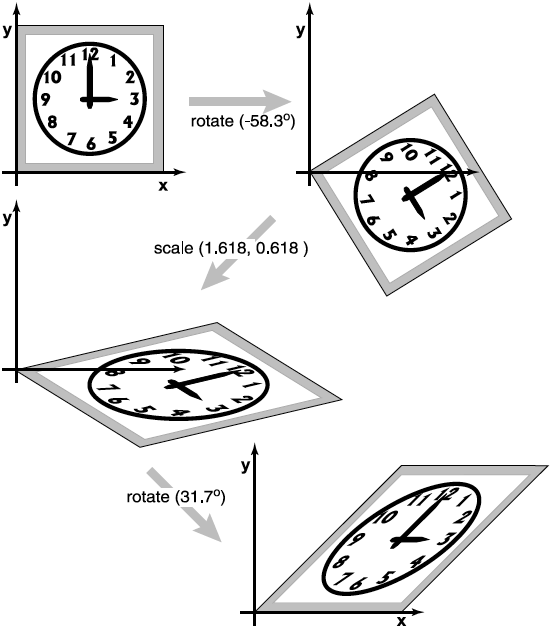
Figure 4: 切变矩阵的奇异值分解(分解为旋转、缩放、再旋转)
上面切变矩阵的分解可以通过下面的矩阵运算来验证。
\[\begin{aligned}
\left( \begin{array}{cc}
1 & 1 \\
0 & 1 \\
\end{array} \right)
& =
\left( \begin{array}{cc}
0.8507 & -0.5257 \\
0.5257 & 0.8507 \\
\end{array} \right) \left( \begin{array}{cc}
1.618 & 0 \\
0 & 0.618 \\
\end{array} \right) \left( \begin{array}{cc}
0.5257 & 0.8507 \\
-0.8507 & 0.5257 \\
\end{array} \right) \\
& = rotate(31.7^{\circ}) scale(1.618, 0.618) rotate(-58.3^{\circ})
\end{aligned}\]
参考:计算机图形学(第 2 版, 高春晓等译),6.1.6 二维变换分解
2.3. 二维线性变换(齐次坐标形式)
如果采用齐次坐标,二维变换的矩阵形式为:
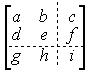
Figure 5: 二维变换的变换矩阵(采用齐次坐标)
这个变换矩阵的每一个元素都有特殊含义。 其中 \(\left[ \begin{array}{cc} a & b \\ d & e \end{array} \right]\) 可以对图形进行缩放、旋转、对称等变换; \(\left[ \begin{array}{c} c \\ f \end{array} \right]\) 是对图形进行平移变换; \(\left[ \begin{array}{cc} g & h \end{array} \right]\) 是对图形作投影变换; \(\left[ i \right]\) 是对图形整体进行缩放变换。
参考:http://netclass.csu.edu.cn/NCourse/hep089/Chapter6/CG_Txt_6_011.htm
2.3.1. 平移变换
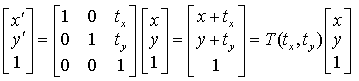
Figure 6: 平移变换
2.3.2. 缩放变换
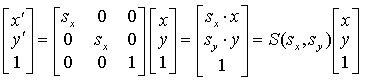
Figure 7: 缩放变换
2.3.3. 旋转变换
二维图形绕原点旋转 \(\theta\) 角(逆时针方向取正值)的变换如下:
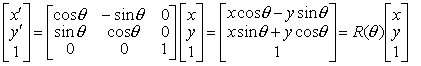
Figure 8: 旋转变换
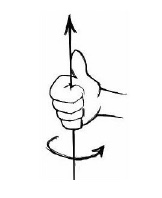
3. 右手坐标系(Right-handed coordinate system)
4. 三维线性变换
三维变换是对二维变换的扩展。例如,三维空间中沿笛卡尔坐标轴的缩放可表示为:
\[scale(s_x, s_y, s_z) = \left( \begin{array}{ccc} s_x & 0 & 0 \\
0 & s_y & 0 \\
0 & 0 & s_z
\end{array}
\right)\]
4.1. 平移、缩放等变换
如果采用齐次坐标,三维几何变换的矩阵是一个 4 阶方阵,其形式为:
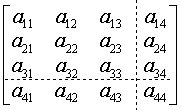
Figure 11: 三维变换的变换矩阵(采用齐次坐标)
上面变换矩阵中,每一个元素都有特殊含义。 其中 \(\left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right]\) 可以对图形进行缩放、旋转、对称等变换; \(\left[ \begin{array}{c} a_{14} \\ a_{24} \\ a_{34} \end{array} \right]\) 是对图形进行平移变换; \(\left[ \begin{array}{ccc} a_{41} & a_{42} & a_{43} \end{array} \right]\) 是对图形作投影变换; \(\left[ a_{44} \right]\) 是对图形整体进行缩放变换。
参考:http://netclass.csu.edu.cn/NCourse/hep089/Chapter6/CG_Txt_6_012.htm
4.1.1. 三维平移变换
参照二维平移变换,容易得到三维平移变换矩阵:
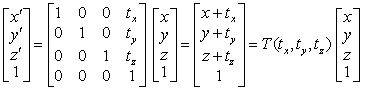
Figure 12: 三维平移变换
4.1.2. 三维缩放变换
直接考虑相对于参考点 \((x_f, y_f, z_f)\) 的缩放变换,其步骤为:
(1) 将平移到坐标原点处;
(2) 进行缩放变换;
(3) 将参考点 \((x_f, y_f, z_f)\) 移回原来位置。
则相对于参考点 (xf,yf,zf)(xf,yf,zf) 的三维缩放变换对应变换矩阵为:
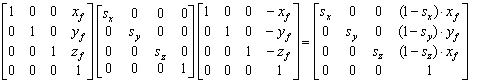
Figure 13: 三维缩放变换矩阵
4.2. 绕坐标轴的旋转
三维空间中,旋转变换比二维情况要复杂一些,因为旋转轴更多了。现在只考虑绕 \(x,y,z\) 轴旋转的简单情况。
参考:
https://www.siggraph.org/education/materials/HyperGraph/modeling/mod_tran/3drota.htm
http://www.cs.brandeis.edu/~cs155/Lecture_07_6.pdf
4.2.1. 绕 z 轴旋转
绕 z 轴旋转时,只有 x,y 轴坐标会变化。
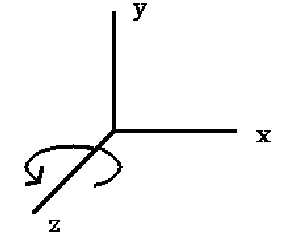
Figure 14: 绕 z 轴旋转
对应的坐标映射关系为:
\[\begin{cases}
x' = x \cos \theta - y \sin \theta \\
y' = x \sin \theta + y \cos \theta \\
z' = z
\end{cases}\]
从而有:
\[\left( \begin{array}{c} x' \\ y' \\ z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc}
\cos \theta & -\sin \theta & 0 & 0 \\
\sin \theta & \cos \theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 1 & 1 \\
\end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)\]
4.2.2. 绕 x 轴旋转
绕 x 轴旋转时,只有 y,z 轴坐标会变化。
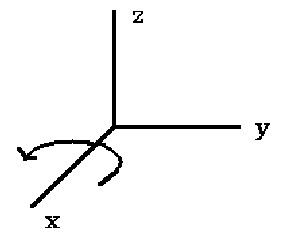
Figure 15: 绕 x 轴旋转
对应的坐标映射关系为:
\[\begin{cases}
y' = y \cos \theta - z \sin \theta \\
z' = y \sin \theta + z \cos \theta \\
x' = x
\end{cases}\]
从而有:
\[\left( \begin{array}{c} x' \\ y' \\ z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & \cos \theta & -\sin \theta & 0 \\
0 & \sin \theta & \cos \theta & 0 \\
0 & 0 & 0 & 1 \\
\end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)\]
4.2.3. 绕 y 轴旋转
绕 y 轴旋转时,只有 z,x 轴坐标会变化。
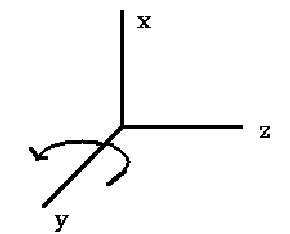
Figure 16: 绕 y 轴旋转
对应的坐标映射关系为:
\[\begin{cases}
z' = z \cos \theta - x \sin \theta \\
x' = z \sin \theta + z \cos \theta \\
y' = y
\end{cases}\]
从而有:
\[\left( \begin{array}{c} x' \\ y' \\ z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc}
\cos \theta & 0 & \sin \theta & 0 \\
0 & 1 & 0 & 0 \\
-\sin \theta & 0 & \cos \theta & 0 \\
0 & 0 & 0 & 1 \\
\end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)\]
4.3. 绕任意轴的旋转
设旋转轴 AB 由任意一点 \(A(x_a, y_a, z_a)\) 及其方向数 \((a, b, c)\) 定义,空间一点 \(P(x_p, y_p, z_p)\) 绕 AB 轴旋转 \(\theta\) 角到 \(P'(x'_p, y'_p, z'_p)\) ,则:
\[\left( \begin{array}{c} x'_p \\ y'_p \\ z'_p \\ 1 \end{array} \right) = R_{ab}(\theta) \left( \begin{array}{c} x_p \\ y_p \\ z_p \\ 1 \end{array} \right)\]
可以通过下列步骤来实现 P 点的旋转:
(1) 将 A 点移到坐标原点。
(2) 使 AB 分别绕 X 轴、Y轴旋转适当角度与 Z 轴重合。
(3) 将 AB 绕 Z 轴旋转 \(\theta\) 角。
(4) 作上述变换的逆操作,使 AB 回到原来位置。
所以, \(R_{ab}(\theta) = T^{-1}(x_a, y_a, z_a) R_x^{-1}(\alpha) R_y^{-1}(\beta) R_z(\theta) R_y(\beta) R_x(\alpha) T(x_a, y_a, z_a)\) 。其中, \(\alpha, \beta\) 分别是 AB 在 YOZ 平面与 XOZ 平面的投影与 Z 轴的夹角。 \(T,R\) 是相应的平移变换矩阵和绕坐标轴旋转变换矩阵。
参考:http://netclass.csu.edu.cn/NCourse/hep089/Chapter6/CG_Txt_6_012.htm
4.4. Yaw, Pitch, Roll
在航空领域中,常常用 Yaw, Pitch, Roll 来表示旋转方向。
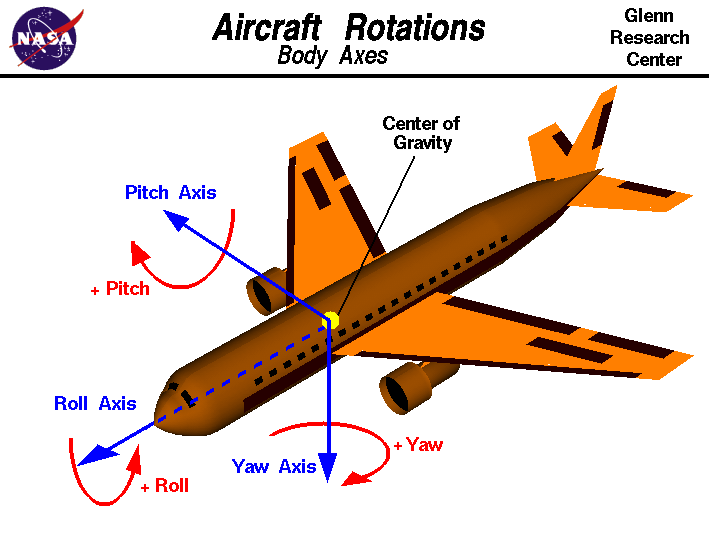
Figure 17: Yaw, Pitch, Roll 及其“正方向”
Yaw:航向;Pitch:俯仰;Roll:横滚。 如图 18, 19, 20 所示。

Figure 18: Yaw 图示(gif 动画)

Figure 19: Pitch 图示(gif 动画)

Figure 20: Roll 图示(gif 动画)
图片摘自:
https://www.grc.nasa.gov/www/k-12/airplane/rotations.html
http://www.grc.nasa.gov/WWW/K-12/airplane/bga.html
http://www.grc.nasa.gov/WWW/K-12/airplane/pitch.html
http://www.grc.nasa.gov/WWW/K-12/airplane/yaw.html
4.5. 用 Quaternion 表示三维旋转
四元数(Quaternions)是由爱尔兰数学家哈密顿(William Rowan Hamilton, 1805-1865)在 1843 年发明的数学概念。
四元数是超复数。我们知道,复数是实数加上虚数单位 \(i\) 组成,其中 \(i^2 = 1\) 。类似地,四元数是实数加上三个虚数单位 \(i,j,k\) 组成,其中 \(i^2 = j^2 = k^2 = ijk = -1\) 。四元数可以表示为 \(Q(q_0, q_1, q_2, q_3) = q_0 + q_1 i + q_2 j + q_3 k\) ,其中 \(q_0,q_1,q_2,q_3\) 都是实数,四元数的大小为 \(\Vert Q \Vert = q_0^2 + q_1^2 + q_2^2 + q_3^2\) ,如果 \(\Vert Q \Vert = 1\) 则四元数又称为规范化四元数。
用四元数 \(Q(q_0, q_1, q_2, q_3)\) 可以表示 3 维空间中物体绕着某个轴旋转,其公式如下:
\[\begin{cases} q_0 = \cos(\theta/2) \\
q_1 = \sin(\theta/2) \cos(\phi_x) \\
q_2 = \sin(\theta/2) \cos(\phi_y) \\
q_3 = \sin(\theta/2) \cos(\phi_z) \end{cases}\]
其中, \(\cos(\phi_x), \cos(\phi_y), \cos(\phi_z)\) 表示定位旋转轴的方向余弦, \(\theta\) 表示旋转的角度。
根据 欧拉旋转定理 ,任何两个坐标系的相对定向,可以由一组四个数字来设定;其中三个数字是方向余弦,用来设定特征矢量(固定轴旋轴);第四个数字是绕着固定轴旋转的角值。这就是用四元数表示 3 维旋转的原理。
和使用矩阵表示旋转相比,使用四元数表示旋转更加高效,占用的空间更小,也更便于插值。
参考:
Principles of Robot Motion: Theory, Algorithms, and Implementation. Appendix E.4 Quaternions
https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation