Abstract Algebra

1. 抽象代数简介
- 1.1. 什么是群、环、域（简单总结）
2. 群
3. 环
4. 域
5. 参考

1. 抽象代数简介

抽象代数（Abstract algebra）又称近世代数（Modern algebra），它作为数学的一门学科，主要研究对象是代数结构，比如群、环、域、格等。

19 世纪 30 年代，在寻找五次方程求解方法的过程中，法国青年数学家伽罗瓦（E. Galois）提出了群的概念， 证明了五次以上的方程式没有公式解 。伽罗瓦彻底地解决了这个在长达 200 多年的时间使不少数学家伤透脑筋的问题。伽罗瓦是超越时代的天才，不仅仅是因为他在方程求解上的贡献，还因为他所发现的结果，他的奇特思想和巧妙方法，发展成为一门新学科——抽象代数学。伽罗瓦群论还给出了判断几何图形能否用直尺和圆规作图的一般判别法，圆满解决了三等分任意角或倍立方体的问题都是不可解的。一般称 伽罗瓦为抽象代数学的创始人。

1.1. 什么是群、环、域（简单总结）

代数系统（又称代数结构）是抽象代数研究的主要对象。什么是代数系统呢？ 代数系统是包含运算的集合。 典型的代数系统有群、环、域。

简单地说：

群（Group）就是一个集合 $G$ ，在其中可进行一种运算及其逆运算；
环（Ring）就是定义有加法（及其逆运算减法）、乘法运算的集合，对加法为 Abel 群（即满足交换律），对乘法为半群（即只满足封闭性和结合律），且乘法对加法有分配律；
域（Field）就是一个内有加、减、乘、除法的集合。确切言之，域就是一个环且其非零元集是乘法 Abel 群。

2. 群

2.1. 集合基本知识

2.1.1. 映射、满射、单射、双射

设 $A$ 和 $B$ 是两个非空集合，如果存在一个法则 $f$ ，使得对 $A$ 中的每个元素 $a$ ，按法则 $f$ ，在 $B$ 中有唯一确定的元素 $b$ 与之对应，则称 $f$ 为从 $A$ 到 $B$ 的映射，记作： $f : A \to B$ 或者 $A \overset{f}{⟶} B$ 。而“ $f$ 把 $a$ 映射成 $f (a)$ ”这件事可记为： $a \mapsto f (a)$ 。其中， $b$ 称为元素 $a$ 在映射 $f$ 下的 象（Image） ， $a$ 称为 $b$ 关于映射 $f$ 的 原象（Preimage） 。集合 A 中所有元素的象的集合称为映射 $f$ 的值域，记作 $f (A)$ 。

如果 $A$ 中不同的元素被 $f$ 映射成 $B$ 中的不同元素（即有 $a, a^{'} \in A, a \neq a^{'} \Rightarrow f (a) \neq f (a^{'})$ ），则 $f$ 叫做“单射”（Injection）。如果 $B$ 中每个元素均是 $A$ 中某个元素在映射 $f$ 下的象（即有 $f (A) = B$ ），则 $f$ 叫做“满射”（Surjection）。如果 $f : A \to B$ 既是单射又是满射，则 $f$ 叫做“双射”（Bijection），也可以称为一一映射或一一对应。

单射、满射、双射和一般映射如图 1 所示。

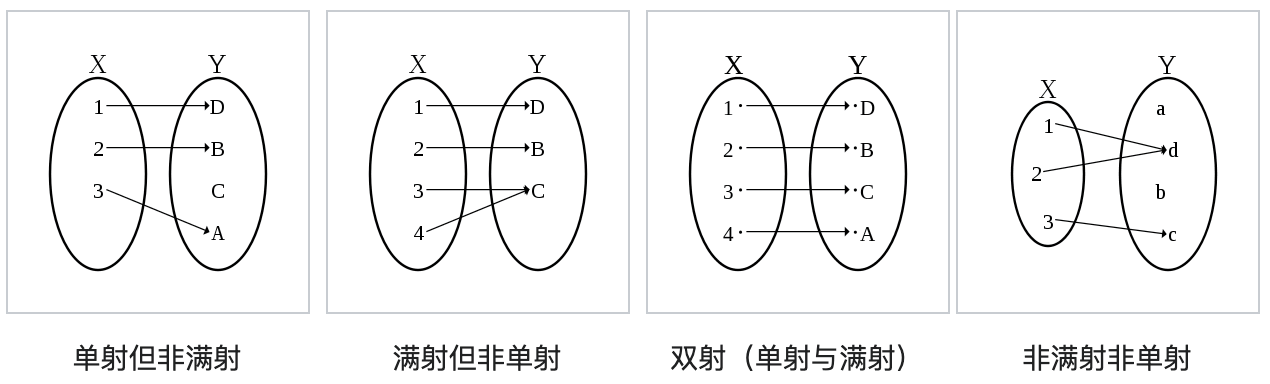
Figure 1: 单射、满射、双射和一般映射

单射的例子： $\exp : R \to R : x \mapsto e^{x}$
满射的例子： $R \to [- 1, 1] : x \mapsto \sin (x)$
双射的例子： $\exp : R \to R^{+} : x \mapsto e^{x}$
一般映射的例子： $R \to R : x \mapsto \sin (x)$

参考：https://zh.wikipedia.org/wiki/%E5%8D%95%E5%B0%84%E3%80%81%E5%8F%8C%E5%B0%84%E4%B8%8E%E6%BB%A1%E5%B0%84

2.1.2. 置换（Permutation）

一个集合的置换（Permutation）是指该集合到自身的双射（Bijection）。

2.1.3. 直积（笛卡尔积）

设 $A$ 和 $B$ 都是集合，我们把集合： $A \times B = {(a, b) ∣ a \in A, b \in B}$ 叫做 $A$ 和 $B$ 的 笛卡尔积（Cartesian Product），又称为直积（Direct product）。

2.1.4. 运算及其结合律、交换律

设 $A$ 是集合，从 $A \times A$ 到 $A$ 的映射： $f : A \times A \to A$ 叫做 集合 $A$ 上的一个（二元）运算 。我们经常把集合 $A$ 上的运算表示为 $∙$ ，即对于 $a, b \in A$ ， $f (a, b)$ 写为 $a ∙ b$ ，或者更简单地写为 $a b$ 。

如果运算 $∙$ 对任意 $a, b, c \in A$ 都有： $a ∙ (b ∙ c) = (a ∙ b) ∙ c$ 则称运算 $∙$ 满足 结合律 。

如果运算 $∙$ 对任意 $a, b \in A$ 都有： $a ∙ b = b ∙ a$ 则称运算 $∙$ 满足 交换律 。

2.2. 群的定义

代数结构（algebraic structure，又称代数系统）是指装备了一个以上的运算的非空集合。 群是满足一定条件的代数结构。

在介绍群之前，先介绍“半群”、“幺元素”、“逆元素”等概念：

半群定义：集合 $S$ 和 $S$ 上一个满足结合律的二元运算 $∙$ 所形成的代数结构叫做半群（Semigroup）。
幺元素定义：设 $S$ 是半群，元素 $e \in S$ 叫做半群 $S$ 的幺元素，如果满足对每个 $x \in S, x ∙ e = e ∙ x = x$ 。 具有幺元素的半群叫做含幺半群（Monoid），或幺半群。
逆元素定义：设 $S$ 是含幺半群（幺元素记为 $e$ ），元素 $y \in S$ 叫做元素 $x \in S$ 的逆元素，如果满足 $x ∙ y = y ∙ x = e$ 。 $x$ 的逆元素可记为 $x^{- 1}$ 。

群可以这样定义： 如果半群 $G$ 有幺元素，并且每个元素均可逆，则 $G$ 叫做群。

下面介绍群的另外一种定义方式。一个集合 $A$ 加上集合上一个二元运算 $∙$ 的代数结构，可记为 $(A, ∙)$ ，那么我们称 $G = (A, ∙)$ 为群（Group），当且仅当集合和运算满足以下几个条件：
(1) 封闭性（Closure）： $\forall a_{1}, a_{2} \in A, a_{1} ∙ a_{2} \in A$
(2) 结合律（Associativity）： $\forall a_{1}, a_{2}, a_{3} \in A, (a_{1} ∙ a_{2}) ∙ a_{3} = a_{1} ∙ (a_{2} ∙ a_{3})$
(3) 具有幺元素（Identity element，也称单位元）： $\exists e \in A, s . t . \forall a \in A, e ∙ a = a ∙ e = a$
(4) 都有逆元素（Inverse element）： $\forall a \in A, \exists a^{- 1} \in A, s . t . a ∙ a^{- 1} = e$

说明：如果仅满足(1)封闭性和(2)结合律，则 $G$ 就是“半群”。

2.2.1. 交换群（阿贝尔群）

如果群中的二元运算 $∙$ 还满足交换律，即：
(5) 交换律（Commutativity）： $\forall a_{1}, a_{2}, a_{1} ∙ a_{2} = a_{2} ∙ a_{1}$
则这个群又叫做交换群(Commutative Group)，或阿贝尔群（Abelian Group）。

2.2.2. 群的阶（集合中元素的个数）

设 $(G, ∙)$ 为群。若集合 $G$ 中元素个数有限，则称 $(G, ∙)$ 为“有限群”，否则叫“无限群”。

若有限群 $(G, ∙)$ 中有 $n$ 个元素，则称为 $n$ 阶群， $n = | G |$ 叫做有限群 $G$ 的阶。

2.2.3. 群的例子

设 $M$ 为非负整数全体， $(M, +)$ 是含幺半群，幺元素为数 0。但它不是群，因为 $M$ 中除数 0 外，其它元素没有逆元素，不满足群的定义。

$Z, Q, R, C$ 对于加法均是阿贝尔群，分别叫做“整数加法群”，“有理数加法群”，“实数加法群”，“复数加法群”。

2.2.3.1. Additive group of integer modulo $n$ (记为 $Z_{n}$ or $Z / n Z$ )

设集合 $N = {0, 1, 2, \dots, n - 1}$ ，定义 $N$ 上的运算 $+_{n}$ 如下：
$\forall x, y \in N, x +_{n} y = x + y (\mod n) 注：即为 x+y 除以 n 的余数$
容易验证 $(N, +_{n})$ 是群：因为它满足封闭性，结合律，且具有幺元素（幺元素为 0），每个元素都有逆元素（0 的逆元为 0，其它元素 $x, x \neq 0$ 的逆元为 $n - x$ ）。

注：上面介绍的群 $(N, +_{n})$ 称为 Additive group of integer modulo $n$ ，往往记为 $Z_{n}$ 或者 $Z / n Z$ 。

2.2.3.2. Multiplicative group of integers modulo $n$ (记为 $Z_{n}^{⋆}$ or $(Z / n Z)^{⋆}$ )

设集合 $N$ 是由集合 ${0, 1, 2, \dots, n - 1}$ 中和 $n$ 互质（最大公因数为 1）的数组成的，定义 $N$ 上的运算 $\times_{n}$ 如下：
$\forall x, y \in N, x \times_{n} y = x y (\mod n) 注：即为 x 乘 y 除以 n 的余数$
下面我们将证明 $(N, \times_{n})$ 是一个群。考察群定义的 4 个要求，容易验证它满足封闭性，结合律，且具有幺元素（幺元素为 1），难点在于如何判断它的每个元素是否都有逆元素。即对于任意 $a \in N$ ，是否存在 $x \in N$ 满足： $a x = 1 (\mod n)$ 呢？这个问题等价于 $a x + n y = 1$ 是否有解，答案是肯定的。这是因为 $g c d (a, n) = 1$ ，从而由裴蜀定理（又称贝祖定理， Bézout's identity）知一定存在整数 $x, y$ 满足： $a x + n y = 1$ 。

注 1：贝祖定理是指“两数的最大公约数可以用两数的整数倍相加来表示”，如：12 和 42 的最大公因数是 6，则方程 $12 x + 42 y = 6$ 有解。事实上有 $12 \times (- 3) + 42 \times 1 = 6$ 及 $12 \times 4 + 42 \times (- 1) = 6$ 。特别地，方程 $a x + b y = 1$ 有解当且仅当整数 $a$ 和 $b$ 互质。
注 2：贝祖定理描述的只是“存在逆元素”，具体如何求解逆元素可参考“扩展欧几里得算法（Extended Euclidean algorithm）”。

上面介绍的群 $(N, \times_{n})$ 称为 Multiplicative group of integers modulo $n$ ，记为 $Z_{n}^{⋆}$ 或者 $(Z_{n})^{\times}$ 或者 $(Z / n Z)^{\times}$ 或者 $(Z_{n})^{⋆}$ 或者 $(Z / n Z)^{⋆}$ 。

一般把 $Z_{n}^{⋆}$ 的元素个数记为 $φ (n)$ ，它可以由 Euler's totient 函数来计算。

表 1 是 $Z_{n}^{⋆}$ 的一些例子。

Table 1: $Z_{n}^{⋆}$ 的一些例子
$Z_{n}^{⋆}$	Elements	$φ (n)$
$Z_{5}^{⋆}$	1, 2, 3, 4	4
$Z_{6}^{⋆}$	1, 5	2
$Z_{7}^{⋆}$	1, 2, 3, 4, 5, 6	6
$Z_{8}^{⋆}$	1, 3, 5, 7	4
$Z_{9}^{⋆}$	1, 2, 4, 5, 7, 8	6
$Z_{10}^{⋆}$	1, 3, 7, 9	4
$Z_{11}^{⋆}$	1, 2, 3, 4, 5, 6, 7, 8, 9, 10	10
$Z_{12}^{⋆}$	1, 5, 7, 11	4
$Z_{13}^{⋆}$	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12

显然，当 $n$ 为素数时， $Z_{n}^{⋆}$ 的元素是从 $1$ 到 $n - 1$ ，此时 $φ (n) = n - 1$ 。

Euler's totient 函数 $φ (n)$ 有个性质： 当 $p, q$ 互素时， $φ (p q) = φ (p) φ (q)$ 。 比如， $2, 5$ 都是素数（显然它们互素），所以有 $φ (10) = φ (2) φ (5) = (2 - 1) (5 - 1) = 4$ ，这在表 1 中得到验证。

参考：
https://en.wikipedia.org/wiki/Multiplicative_group_of_integers_modulo_n

2.2.4. 群元素的阶（“与单位元的距离”）

如果我们说在群里，单位元 $e$ （即幺元）由于它的惟一性显得有些特别的话，那么其他的元素也有一些特殊的性质，其中之一就是与单位元的“距离”。

设 $(G, ∙)$ 是群，且 $a \in G$ ，我们把满足： $\underset{i 个 a 重复群运算}{\underset{⏟}{a ∙ a ∙ \dots a}} = e$ 的最小正整数 $i$ 称为 元素 $a$ 的阶，记为 $o r d (a)$ 。 如果这样的整数 $i$ 不存在，则称元素 $a$ 是无限阶元。

例：求群 $Z_{12}$ 中各个元素的阶。
解：因为 $0 \equiv 0 (\mod 12)$ ，所以 $o r d (0) = 1$ ；
因为 $\underset{12}{\underset{⏟}{1 + 1 + \dots 1}} = 12 \equiv 0 (\mod 12)$ ，所以 $o r d (1) = 12$ ；
因为 $\underset{6}{\underset{⏟}{2 + 2 + \dots 2}} = 12 \equiv 0 (\mod 12)$ ，所以 $o r d (2) = 6$ ；
因为 $3 + 3 + 3 + 3 = 12 \equiv 0 (\mod 12)$ ，所以 $o r d (3) = 4$ ；
因为 $4 + 4 + 4 = 12 \equiv 0 (\mod 12)$ ，所以 $o r d (4) = 3$ ；
因为 $\underset{12}{\underset{⏟}{5 + 5 + \dots 5}} = 60 \equiv 0 (\mod 12)$ ，所以 $o r d (5) = 12$ ；
因为 $6 + 6 = 12 \equiv 0 (\mod 12)$ ，所以 $o r d (6) = 2$ ；
因为 $\underset{12}{\underset{⏟}{7 + 7 + \dots 7}} = 84 \equiv 0 (\mod 12)$ ，所以 $o r d (7) = 12$ ；
因为 $8 + 8 + 8 = 24 \equiv 0 (\mod 12)$ ，所以 $o r d (8) = 3$ ；
因为 $9 + 9 + 9 + 9 = 36 \equiv 0 (\mod 12)$ ，所以 $o r d (9) = 4$ ；
因为 $\underset{6}{\underset{⏟}{10 + 10 + \dots 10}} = 60 \equiv 0 (\mod 12)$ ，所以 $o r d (10) = 6$ ；
因为 $\underset{12}{\underset{⏟}{11 + 11 + \dots 11}} = 132 \equiv 0 (\mod 12)$ ，所以 $o r d (11) = 12$ ；

2.2.4.1. 群的阶和群元素的阶之间的关系

设 $G$ 是一个有限群， $a \in G$ 为任意元素，则群的阶 $| G |$ 可以被 $o r d (a)$ 整除。

这个结论是节 2.3.3 中介绍的拉格朗日定理的一个推论。它的证明思路：元素自乘，形成循环子群，元素的阶就是相应循环子群的阶；由拉格朗日定理知，子群（当然也包含这里的循环子群）的阶必然能够整除群的阶，即元素的阶必然能够整除群的阶。证毕！

2.2.5. 群同态（Homomorphism）、群同构（Isomorphism）

设 $(G, ∙)$ 和 $(G^{'}, *)$ 是两个群，如果映射 $f : G \to G^{'}$ 满足： $f (a ∙ b) = f (a) * f (b), \forall a, b \in G$ 有时直接简记为 $f (a b) = f (a) f (b), \forall a, b \in G$ 则称映射 $f : G \to G^{'}$ 是群 $G$ 到群 $G^{'}$ 的同态（Homomorphism）。

此外，若 $f$ 又为单射或满射，则分别叫单同态或满同态。如果同态 $f$ 是一一对应，则称是群 $G$ 到群 $G^{'}$ 的同构（Isomorphism）。这时，称群 $G$ 和 $G^{'}$ 是同构的，记为： $G ≅ G^{'}$ 或者 $G \tilde{\to} G^{'}$ 。

彼此同构的群具有完全相同的群结构。在群论中， 同构的群认为本质上是同个群，我们更主要的是研究本质不同的群之间的联系，所以，同态是群论中更重要的研究手段。

2.2.5.1. 群同构实例

定义映射 $f (x) = e^{x}$ ，则群 $(R, +) ≅ (R^{+}, \times)$ 。

2.3. 子群和陪集分解

设 $(G, ∙)$ 为群， $A$ 为 $G$ 的子集。如果 $(A, ∙)$ 也是群，则称 $A$ 为 $G$ 的子群（Subgroup），表示成 $A \leq G$ 。此外，若 $A \neq G$ ，则称 $A$ 为 $G$ 的真子群（Proper Subgroup），表示成 $A < G$ 。

任何群 $G$ 都有两个子群（“仅包含幺元素的群”和“群 $G$ 本身”），我们称这两个子群为平凡子群（Trivial Subgroup）。

2.3.1. 子群的例子

例子 1：对每个非负整数 $n$ ， $n Z = {n a ∣ a \in Z}$ 是整数加法群的子群。

例子 2：求群 $Z_{4}$ （其定义参见节 2.2.3.1 ）的子群。
解：集合 ${0, 1, 2, 3}$ 的所有的非空子集如下：
${0}, {1}, {2}, {3}, {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 3}, {2, 3}, {0, 1, 2}, {0, 1, 3}, {0, 2, 3}, {1, 2, 3}, {0, 1, 2, 3}$
此时仅有三个子集：
${0}, {0, 2}, {0, 1, 2, 3}$

关于运算 $+_{4}$ 满足群定义的 4 个要求：
（1）封闭性：运算 $+_{4}$ 关于集合 ${0}, {0, 2}, {0, 1, 2, 3}$ 是封闭的；
（2）结合律：这是显然的；
（3）幺元素存在：对集合 ${0}, {0, 2}, {0, 1, 2, 3}$ 都有幺元素“0”存在；
（4）每个元素的逆元素存在：对集合 ${0}$ ，有： $0^{- 1} = 0$ ；对集合 ${0, 2}$ ，有： $0^{- 1} = 0, 2^{- 1} = 2$ ；对集合 ${0, 1, 2, 3}$ ，有： $0^{- 1} = 0, 1^{- 1} = 3, 2^{- 1} = 2, 3^{- 1} = 1$

从而知： $({0}, +_{4}), ({0, 2}, +_{4}), ({0, 1, 2, 3}, +_{4})$ 是 $Z_{4}$ 的子群，其中子群 $({0}, +_{4}), ({0, 1, 2, 3}, +_{4})$ 为 $Z_{4}$ 的平凡子群。

例子 3：和上一个例子类似。可知群 $Z_{12}$ 的子群有： $({0}, +_{12})$ , $({0, 6}, +_{12})$ , $({0, 4, 8}, +_{12})$ , $({0, 3, 6, 9}, +_{12})$ , $({0, 2, 4, 6, 8, 10}, +_{12})$ , $({0, 1, 2, 3, \dots, 10, 11}, +_{12})$

2.3.2. 陪集分解

设 $(G, ∙)$ 为群， $A$ 为 $G$ 的子群，而 $g$ 是 $G$ 中元素，则集合 $g ∙ A ≜ {g ∙ a ∣ a \in A}$ 是 $A$ 在 $G$ 中的左陪集（Left Cosets），称 $g$ 是左陪集 $g ∙ A$ 中的代表元素。类似地，集合 $A ∙ g ≜ {a ∙ g ∣ a \in A}$ 是 $A$ 在 $G$ 中的右陪集（Right Cosets）。

下面介绍如何计算左陪集。前面介绍过 $({0, 2}, +_{4})$ 是群 $Z_{4}$ 的子群，记这个子群为 $A$ ，则 $A$ 在 $Z_{4}$ 中的左陪集有： $\begin{array}{r} 0 +_{4} A = {0 +_{4} 0, 0 +_{4} 2} = {0, 2} \\ 1 +_{4} A = {1 +_{4} 0, 1 +_{4} 2} = {1, 3} \\ 2 +_{4} A = {2 +_{4} 0, 2 +_{4} 2} = {2, 0} \\ 3 +_{4} A = {3 +_{4} 0, 3 +_{4} 2} = {3, 1} \end{array}$ 集合是不关心元素顺序的，所以 $A$ 在 $Z_{4}$ 中的左陪集有两个，分别是 ${0, 2}, {1, 3}$ 。 $A$ 在 $G$ 中的左陪集（或右陪集）个数记为 $[G : A]$ 。

可以用 $A$ 在 $G$ 中的左陪集（或右陪集）对 $G$ 进行分解，这种分解会满足两个性质：

每个陪集的元素个数相等；
不同陪集中的元素不会重合。

下面表示了 $G$ 的左陪集分解：
$G = ⋃_{g \in G} g ∙ A$

类似地， $G$ 的右陪集分解：
$G = ⋃_{g \in G} A ∙ g$

2.3.3. 拉格朗日定理（子群的阶一定是有限群的阶的因数）

拉格朗日定理（Lagrange's theorem）：设 $G$ 为有限群， $A \leq G$ （即 $A$ 是 $G$ 的子群），则 $| A |$ 是 $| G |$ 的因数，满足： $| G | = | A | \cdot [G : A]$ 其中 $[G : A]$ 是 $A$ 在 $G$ 中的左陪集（或右陪集）个数。

拉格朗日定理是群论中简单而有用的定理。例如：一个 6 阶群只能有 1，2，3，6 阶子群，不能有 4 阶或 5 阶子群。

2.4. 循环群

设 $G$ 是乘法群（即带有乘法运算），若存在一个元素 $g \in G$ ，使得任意元素 $a \in G$ 都可以写为 $a = g^{i}$ （其中 $i \in Z$ ）的形式（即 任意元素 $a$ 可由 $g$ 重复多次群运算而得到 ），则称 $G$ 为循环群（Cyclic Group），记为 $G = ⟨ g ⟩$ ，并称 $g$ 为该循环群的一个生成元（Generating Element）。循环群 $G$ 可能有多个生成元，所有生成元的集合称为 $G$ 的生成集（Generating Set）。

除乘法群外，类似地，在加法运算的情况下，循环群可定义为 $⟨ g ⟩ = {i g}$ （其中 $i \in Z$ ）。

循环群最简单的例子是“整数加法群”，它由元素 1 或 -1 生成。

2.4.1. 循环群的例子

如 $Z_{5}$ （参见节 2.2.3.1）是循环群，这个群有元素 ${0, 1, 2, 3, 4}$ ，其中元素 $1, 2, 3, 4$ 都是它的生成元。下面验证一下生成元 $1$ $\begin{aligned} 1 & = 1 mod 5 \\ 1 + 1 & = 2 mod 5 \\ 1 + 1 + 1 & = 3 mod 5 \\ 1 + 1 + 1 + 1 & = 4 mod 5 \\ 1 + 1 + 1 + 1 + 1 & = 0 mod 5 \end{aligned}$ 可见群 $Z_{5}$ 中每个元素都可由 $1$ 生成。下面验证一下生成元 $2$ $\begin{aligned} 2 & = 2 mod 5 \\ 2 + 2 & = 4 mod 5 \\ 2 + 2 + 2 & = 1 mod 5 \\ 2 + 2 + 2 + 2 & = 3 mod 5 \\ 2 + 2 + 2 + 2 + 2 & = 0 mod 5 \end{aligned}$ 可见群 $Z_{5}$ 中每个元素都可由 $2$ 生成。下面验证一下生成元 $3$ $\begin{aligned} 3 & = 3 mod 5 \\ 3 + 3 & = 1 mod 5 \\ 3 + 3 + 3 & = 4 mod 5 \\ 3 + 3 + 3 + 3 & = 2 mod 5 \\ 3 + 3 + 3 + 3 + 3 & = 0 mod 5 \end{aligned}$ 可见群 $Z_{5}$ 中每个元素都可由 $3$ 生成。下面验证一下生成元 $4$ $\begin{aligned} 4 & = 4 mod 5 \\ 4 + 4 & = 3 mod 5 \\ 4 + 4 + 4 & = 2 mod 5 \\ 4 + 4 + 4 + 4 & = 1 mod 5 \\ 4 + 4 + 4 + 4 + 4 & = 0 mod 5 \end{aligned}$ 可见群 $Z_{5}$ 中每个元素都可由 $4$ 生成。不过， $Z_{5}$ 中的幺元素（单位元） $0$ 显然不是生成元。

再举一个循环群的例子： $(Z_{5})^{⋆}$ （参见节 2.2.3.2），这个群有元素 ${1, 2, 3, 4}$ 它们可以由 $2$ 生成： $\begin{aligned} 2^{1} & = 2 mod 5 \\ 2^{2} & = 4 mod 5 \\ 2^{3} & = 3 mod 5 \\ 2^{4} & = 1 mod 5 \end{aligned}$ 可见群 $(Z_{5})^{⋆}$ 中每个元素都可由 $2$ 生成。

我们看一个不是循环群的例子： $(Z_{12})^{⋆}$ （参见节 2.2.3.2），这个群有元素 ${1, 5, 7, 11}$ 。显然幺元素 $1$ 不是生成元，我们看看另外三个元素是不是生成元： $\begin{aligned} 5^{1} & = 5 mod 12 \\ 5^{2} = 25 & = 1 mod 12 \\ 5^{3} = 125 & = 5 mod 12 \\ \dots \\ 7^{1} & = 7 mod 12 \\ 7^{2} = 49 & = 1 mod 12 \\ 7^{3} = 343 & = 7 mod 12 \\ \dots \\ 11^{1} & = 11 mod 12 \\ 11^{2} = 121 & = 1 mod 12 \\ 11^{3} = 1331 & = 11 mod 12 \\ \dots \end{aligned}$ 可见 $5, 7, 11$ 都无法生成出 $(Z_{12})^{⋆}$ 的所有元素，从而 $(Z_{12})^{⋆}$ 没有生成元，显然不可能是循环群。

2.4.2. 循环群性质

由循环群可以推导出很多有用的结论，如（证明略）：

循环群的每一个子群均为循环群。
$G$ 为循环群，则对于 $| G |$ 的每一个正因子 $d$ ， $G$ 恰好包含一个 $d$ 阶子群。
$G$ 为循环群，则对于 $| G |$ 的每一个正因子 $d$ ， $G$ 包含 $φ (d)$ 个 $d$ 阶元（注：这里 $φ (n)$ 表示 Euler's totient function，即小于 $n$ 且与 $n$ 互素的正整数的个数）。

例： $Z_{12}$ （参见 2.2.3.1 ）是循环群，因为任意元素都可以由元素 1 重复多次群运算 $+_{12}$ 而得到。 $| G | = 12$ ，它的正因子有：1,2,3,4,6,12。从而，由上面的结论 2 有：
$Z_{12}$ 包含一个 1 阶子群（为 ${0}$ ）；
$Z_{12}$ 包含一个 2 阶子群（为 ${0, 6}$ ）；
$Z_{12}$ 包含一个 3 阶子群（为 ${0, 4, 8}$ ）；
$Z_{12}$ 包含一个 4 阶子群（为 ${0, 3, 6, 9}$ ）；
$Z_{12}$ 包含一个 6 阶子群（为 ${0, 2, 4, 6, 8, 10}$ ）；
$Z_{12}$ 包含一个 12 阶子群（为 ${0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}$ ）。
由上面的结论 3 有（节 2.2.4 中介绍了 $Z_{12}$ 中各个元素的阶，可以去那里验证一下）：
$Z_{12}$ 包含 1 阶元 $φ (1) = 1$ 个（为 0）；
$Z_{12}$ 包含 2 阶元 $φ (2) = 1$ 个（为 6）；
$Z_{12}$ 包含 3 阶元 $φ (3) = 2$ 个（为 4 和 8）；
$Z_{12}$ 包含 4 阶元 $φ (4) = 2$ 个（为 3 和 9）；
$Z_{12}$ 包含 6 阶元 $φ (6) = 2$ 个（为 2 和 10）；
$Z_{12}$ 包含 12 阶元 $φ (12) = 4$ 个（为 1、5、7 和 11）。

2.4.2.1. 素阶群都是循环群，且非单位元都是生成元

如果群 $G$ 的阶为素数（往往记为 $p$ ），则群 $G$ 一定是循环群，而且群 $G$ 中任意非单位元都是生成元。

证明：设 $a \in G$ 为任意非单位元，由 2.2.4.1 节中的结论有： $o r d (a)$ 可以被 $| G | = p$ 整除，而 $p$ 是素数，从而 $o r d (a) = 1$ 或者 $o r d (a) = p$ 。又由于 $a$ 不是单位元，所以 $o r d (a) \neq 1$ ，从而 $o r d (a) = p$ 。所以它生成的 $G$ 的循环子群的阶也是 $p$ ，从而等于整个群 $G$ ，所以 $G$ 等于它的任一非单位元生成的循环群。证毕。

比如， $Z_{5}$ 是一个素阶群（它的元素个数为 5，而 5 为素数），它是循环群，且任意非单位元都是生成元，在节 2.4.1 中有详细的验证过程。

2.4.3. 循环子群

设 $G$ 为群，则 $G$ 中每个元素 $a$ 生成的循环群 $⟨ a ⟩$ ，都称为 $G$ 的循环子群（Cyclic Subgroup）。

2.5. 正规子群、商群和同态定理

2.5.1. 正规子群

设 $(G, ∙)$ 为群， $N$ 为 $G$ 的子群，而 $g$ 是 $G$ 中元素，记 $g N = {g ∙ n ∣ n \in N}, N g = {n ∙ g ∣ n \in N}$ ，这个记号在节 2.3.2 中也使用过。

设 $N$ 是 $G$ 的子群，如果对于每个 $g \in G$ ，都有 $g N = N g$ ，则说 $N$ 是 $G$ 的正规子群（Normal Subgroup），记为 $N ◃ G$ 。

正规子群还有一些彼此等价的定义，如：

$g n g^{- 1} \in N$ 对于所有 $g \in G, n \in N$ 都成立；
$G$ 对于 $N$ 的每个左陪集都是右陪集。

阿贝尔群（或交换群）的所有子群都是它的正规子群，因为显然有 $g N = N g$ 。 不是阿贝尔群，但全部子群都是正规子群的群叫做哈密尔顿群（Hamiltonian group）。

2.5.1.1. 正规子群实例

假设群 $G$ 是 Dihedral group of order 6，它的 6 个元素可以表示为 ${I, a, a^{2}, b, a b, a^{2} b}$ ，这个群上定义了乘法运算，且有关系 $a^{3} = b^{2} = I$ 和 $b a = a^{- 1} b$ ，它的乘法运算如表 2 所示，摘自 https://en.wikipedia.org/wiki/Coset#First_example 。

Table 2: Multiplication Table
$*$	$I$	$a$	$a^{2}$	$b$	$a b$	$a^{2} b$
$I$	$I$	$a$	$a^{2}$	$b$	$a b$	$a^{2} b$
$a$	$a$	$a^{2}$	$I$	$a b$	$a^{2} b$	$b$
$a^{2}$	$a^{2}$	$I$	$a$	$a^{2} b$	$b$	$a b$
$b$	$b$	$a^{2} b$	$a b$	$I$	$a$	$a^{2}$
$a b$	$a b$	$b$	$a^{2} b$	$a$	$a^{2}$	$I$
$a^{2} b$	$a^{2} b$	$a b$	$b$	$a^{2}$	$I$	$a$

${I, a, a^{2}}$ 是 $G$ 的子群，这个子群在 $G$ 中的左陪集有两个，为 ${I, a, a^{2}}$ 和 ${b, b a, b a^{2}}$ ，它的右陪集也有两个，为 ${I, a, a^{2}}$ 和 ${b, a b, a^{2} b} = {b, b a^{2}, b a}$ 。可见，它的左陪集都是右陪集，所以 子群 ${I, a, a^{2}}$ 是 $G$ 的正规子群。

我们看一个是子群但不是正规子群的例子。还是前面介绍的例子， ${I, b}$ 是 $G$ 的子群，记为 $T$ ，这个子群在 $G$ 中的左陪集有三个 $\begin{aligned} I T & = T = {I, b} \\ a T & = {a, a b} \\ a^{2} T & = {a^{2}, a^{2} b} \end{aligned}$ 这个子群在 $G$ 中的右陪集也有三个 $\begin{aligned} T I & = T = {I, b} \\ T a & = {a, b a} = {a, a^{2} b} \\ T a^{2} & = {a^{2}, b a^{2}} = {a^{2}, a b} \end{aligned}$ 但除了 ${I, b}$ 既是左陪集又是右陪集外，其它两个左陪集并不是右陪集，所以子群 ${I, b}$ 不是正规子群。

2.5.2. 商群（因子群）

在随后的讨论中，我们将使用在 $G$ 的子集上的二元运算：如果给出 $G$ 的两个子集 $S$ 和 $T$ ，我们定义它们的乘积为 $S T = {s t : \forall s \in S, t \in T}$ 。这个运算是符合结合律的，并有单位元为单元素集合 ${e}$ ，这里的 $e$ 是 $G$ 的单位元。因此， $G$ 的所有子集的集合形成了在这个运算下的幺半群。

凭借这个运算我们可以首先解释商群是什么？ 群 $G$ 的商群是 $G$ 的一个划分，而它在上面这个乘积运算下是群。

设 $N$ 是群 $G$ 的正规子群。我们定义 商群 $G / N$ 是 $N$ 在 $G$ 中的所有左陪集的集合，就是说 $G / N = {g N : g \in G}$ 。 因为 $N$ 的正规性， $N$ 在 $G$ 中的左陪集和右陪集是相等的，所以 $G / N$ 也可以定义为 $N$ 在 $G$ 中所有的右陪集的集合。

群 $Z_{n}$ 有个正规子群 $(N = {0, 3}, +_{6})$ ，则商群（ $N$ 在 $G$ 中的所有左陪集的集合）为 $G / N = {g +_{6} N : g \in G} = {0 +_{6} N, 1 +_{6} N, 2 +_{6} N} = {{0, 3}, {1, 4}, {2, 5}}$ 可见群 $G$ 的商群是 $G$ 的一个划分。

2.5.3. 群同态定理（群同构定理）

群同态定理也称群同构定理（参考：https://en.wikipedia.org/wiki/Isomorphism_theorems ），在泛代数领域有广泛的应用。

2.5.3.1. Kernal 和 Image

节 2.2.5 中介绍了群同态的定义。

下面介绍一下 Kernel 和 Image 的概念。假设映射 $f : G \to H$ 是从 $G$ 到 $H$ 的同态映射。那么 $f$ 的 Kernal 和 Image 分别定义为： $\begin{aligned} Ker f & = {g \in G : f (g) = e_{H}} \\ Im f & = {f (g) : g \in G} \end{aligned}$

图 2 演示了 $Ker f$ 的含义。

Figure 2: $Ker f$

2.5.3.2. 同态基本定理

定理 1（同态基本定理）：设 $G$ 和 $H$ 都是群， $f : G \to H$ 是同态映射，则有：

$Ker f$ 是 $G$ 的正规子群；
$Im f$ 是 $H$ 的子群；
$G / Ker f$ 和 $Im f$ 在映射 $μ (g H) = f (g)$ 下同构，即 $G / Ker f ≅ Im f$ 。

由同态基本定理的第 3 点可知，有两个途径可以从 $G$ 到 $Im f$ ，如图 3 所示。

Figure 3: 有两个途径可以从 $G$ 到 $Im f$

2.5.3.3. 同态基本定理实例

下面介绍同态基本定理实例，例子摘自：https://www.math.uci.edu/~ndonalds/math120a/7homo.pdf

设 $f (x) = 4 x (\mod 20)$ ，易知 $f : Z_{10} \to Z_{20}$ 是同态映射，则： $\begin{aligned} Ker f & = {x \in Z_{10} : 4 x = 0 (\mod 20)} = {0, 5} \\ Im f & = {4 x (\mod 20) : x \in Z_{10}} = {0, 4, 8, 12, 16} \end{aligned}$

容易验证同态基本定理的前 2 条结论： $Ker f$ 是 $Z_{10}$ 的正规子群， $Im f$ 是 $Z_{20}$ 的子群。

第 3 条结论是说商群 $Z_{10} / Ker f = {{0, 5}, {1, 6}, {2, 7}, {3, 8}, {4, 9}}$ 和 $Im f$ 同构。因为存在同态映射： $μ : Z_{10} / Ker f \to Im f : (\begin{matrix} {0, 5} \\ {1, 6} \\ {2, 7} \\ {3, 8} \\ {4, 9} \end{matrix}) \mapsto (\begin{matrix} 0 \\ 4 \\ 8 \\ 12 \\ 16 \end{matrix}) i.e. μ (x + Ker f) = 4 x (\mod 20)$

2.5.3.4. 另外几个同态定理

除同态基本定理，还有几个同态定理，这里不介绍，可参考：https://en.wikipedia.org/wiki/Isomorphism_theorems

2.6. 正交群 O(n)、特殊正交群 SO(n)

实数域上所有 $n$ 维正交矩阵组成的集合，对于矩阵的乘法可构成一个群，称为正交群（Orthogonal Group），记作 $O (n)$ 。特别地，对应行列式为 1 或者-1 的所有 $n$ 维正交矩阵组成的集合，对于矩阵乘法也可构成一个群，称它为特殊正交群（Special Orthogonal Group），记作 $S O (n)$ 。特殊正交群又称为旋转群（Rotation Group），因为在 2 维（记为 $S O (2)$ ）或 3 维（记为 $S O (3)$ ）情况下，它的元素可以用来表示物体的旋转。

参考：
https://en.wikipedia.org/wiki/Orthogonal_group
https://en.wikipedia.org/wiki/Rotation_group_SO(3)

2.6.1. 特殊欧氏群 SE(n)

我们可以把 刚体的“平移”和“旋转”两种运动记在一个矩阵中 ，这个 $(n + 1) \times (n + 1)$ 矩阵有下面形式：
${(\begin{matrix} R & v \\ 0 & 1 \end{matrix}) | R \in S O (n) and v \in R^{n}}$
上面矩阵组成的集合对于矩阵乘法构成的群称为特殊欧氏群（Special Euclidean group），记为 $S E (n)$ 。

参考：
https://en.wikipedia.org/wiki/Euclidean_group
http://planning.cs.uiuc.edu/node147.html

2.7. 群的应用

参考：
Teacher package: Group theory
Why is group theory important?

3. 环

环（Ring）是一个集合 $R$ 和 $R$ 上两个二元运算（通常表示成加法 $+$ 和乘法 $∙$ ）组成的代数结构 $(R, +, ∙)$ ，并且满足以下三个条件：
(1) $(R, +)$ 是阿贝尔群，这个群的单位元称为零元素，记为 0。
(2) $(R, ∙)$ 是半群。这意味着 $R$ 中乘法运算满足结合律。
(3) 加法和乘法满足分配律。即对任意的 $a, b, c \in R$ ，有： $a ∙ (b + c) = a ∙ b + a ∙ c, (b + c) ∙ a = b ∙ a + c ∙ a$ .

注记：如果只是前两个条件，那么 $R$ 不过是具有阿贝尔群 $(R, +)$ 和乘法半群 $(R, ∙)$ 两个彼此孤立的代数结构。正是条件(3)将两个运算用分配律联系在一起，从而形成新的代数结构——环。

如果环 $R$ 满足条件：
(4) 对所有 $a, b \in R$ 有 $a ∙ b = b ∙ a$ 。
则称 $R$ 为“交换环”。这里“交换”二字是表明 $R$ 中乘法满足交换律（因为环中加法永远规定有交换律）。

如果环 $R$ 还满足：
(5) 存在元素 $1 \in R$ ，使得对每个元素 $a \in R$ ，都有 $1 ∙ a = a ∙ 1 = a$ ，则称 $R$ 为“含幺环”，元素 1 叫做环 $R$ 的幺元素。

下面介绍一下“零因子”的概念：环 $R$ 中非零元素 $a$ 叫做 $R$ 中的左零因子，是指存在非零元素 $b \in R$ ，使得 $a ∙ b = 0$ 。类似地，若 $b ∙ a = 0$ ，则 $a$ 叫环 $R$ 的右零因子。如果 $a$ 同时是左零因子和右零因子，则 $a$ 叫做环 $R$ 的零因子。若 $R$ 中没有非零的零因子，则称 $R$ 为“无零因子环”。此定义等价于以下任何一条：

$R ∖ {0}$ 对乘法形成半群；
$R ∖ {0}$ 对乘法封闭；
$R$ 中非零元素的乘积非 0。

3.1. 各种特殊的环

表 3 总结了各种特殊的环。

Table 3: 各种特殊的环
	非零元素对乘法运算封闭	乘法运算存在单位元	乘法运算存在逆元	乘法运算满足交换律
交换环				✓
含幺环		✓
无零因子环	✓
整环（Integral Domain）	✓	✓		✓
除环（Division Ring），也称为体（Skew Field）	✓	✓	✓
域	✓	✓	✓	✓

3.2. 特征（Characteristic）

设 $R$ 为环，如果存在正整数 $m$ ，使得对每个 $r \in R$ 均有 $\underset{m times}{\underset{⏟}{r + r + \dots + r}} = 0$ ，我们把满足此条件的最小正整数 $m$ 称为环 $R$ 的特征。如果不存在这样的正整数 $m$ ，便称环 $R$ 的特征是零。

3.3. 环的直积

设有两个环 $R, S$ ，我们在集合 $R$ 和 $S$ 的笛卡尔积 $R \times S = {(r, s) ∣ r \in R, s \in S}$ 上定义如下两种运算：

$(r_{1}, s_{1}) + (r_{2}, s_{2}) = (r_{1} + r_{2}, s_{1} + s_{2})$
$(r_{1}, s_{1}) \cdot (r_{2}, s_{2}) = (r_{1} \cdot r_{2}, s_{1} \cdot s_{2})$

可以验证 $(R \times S, +, \cdot)$ 也构成环，我们称其为环 $R$ 和 $S$ 的直积。

3.4. 子环

设 $S$ 是环 $R$ 的子集合。如果 $S$ 本身对于环 $R$ 中的运算也是环，则称 $S$ 是 $R$ 的“子环”。如果 $S$ 对于 $R$ 中运算是体或域，则 $S$ 叫做 $R$ 的子体或子域。

3.5. 理想和商环（剩余类环）

环论中理想的概念相当于群论中的正规子群。大家知道，正规子群的引入是为了构作商群，类似地，设 $S$ 是环 $R$ 的子环，则 $S$ 是阿贝尔加法群 $R$ 的子群，于是有加法商群 $R / S$ 。我们希望在 $R / S$ 上自然地定义乘法，使得 $R / S$ 为环。所谓“自然”定义乘法，即是希望 $\overset{―}{a} ∙ \overset{―}{b} = \overset{―}{a b}$ 。这里遇到两个问题：首先, 这个乘法是否可以定义，即是否不依赖陪集代表元的选取？其次， $R / S$ 对于加法 $\overset{―}{a} + \overset{―}{b} = \overset{―}{a + b}$ 和乘法 $\overset{―}{a} ∙ \overset{―}{b} = \overset{―}{a b}$ 是否形成环？下面引理表明，为了做到这些，需要对子环加上进一步的条件。

引理：设 $S$ 是环 $R$ 的子环。为了使加法商群 $R / S$ 对于乘法 $\overset{―}{a} ∙ \overset{―}{b} = \overset{―}{a b}$ 是环, 其充要条件是 $S$ 满足要求：对于每个 $r \in R$ 和 $a \in S$ ，有 $r a \in S$ 和 $a r \in S$ 。

定义：满足上述引理中条件的子环 $S$ 叫做环 $R$ 的理想（Ideal）。设 $A$ 是环 $R$ 的理想，根据上述引理，集合 $R / A$ 对于自然定义的加法和乘法形成环，叫做 $R$ 对于理想 $A$ 的商环（Quotient Ring），也称为因子环（Factor Ring），剩余类环（Residue Class Ring）。

每个环 $R$ 至少有两个理想：一个是由一个零元素组成的理想，称为零理想，这时商环就是 $R$ 本身（或说同构于 $R$ ）；另一个是由 $R$ 本身组成的理想，这时商环是零环。除这两个理想以外的其他理想称为真理想（Proper Ideal）。

如果用更直白的话来表述， 理想就是环 $R$ 中的一个运算封闭的子集 $I$ ，它即便乘上 $I$ 外面的元素，得到的结果也仍然在 $I$ 中。 例如 $Z$ 的子集 $n Z$ ，也就是所有 $n$ 的倍数组成的子集，它显然满足理想的定义，因为 $n$ 的倍数不论乘上多少，结果仍然是 $n$ 的倍数。

3.5.1. 主理想

设 $I$ 是交换环 $R$ 的理想，如果存在 $x \in R$ 使得 $I = R x$ ，则 $I$ 被称为交换环的“主理想”（Principal Ideal）。

从主理想的定义中可知， 主理想就是“可由一个元素生成的理想”。

比如， $Z$ 的每个理想都是主理想。事实上 $Z$ 是主理想整环（后文将介绍）。

3.5.2. 主理想整环

如果一个整环（整环定义参见节 3.1）的理想都是主理想，则该整环称为“主理想整环”（Principal Ideal Domain，简称 PID）。

所有的域（Field）都是主理想整环。

3.5.3. 素理想

环 $R$ 的理想 $P$ 如果满足下面两个条件，则称 $P$ 为“素理想”：

$P \neq R$
对于任意 $a \in R, b \in R$ ，如果 $a b \in P$ ，那么 $a$ 或者 $b$ 至少有一个属于 $P$ ，即满足 $a \in P$ 或者 $b \in P$

整数环 $Z$ 的理想均有形式 $n Z (n \geq 0)$ 。由于 $Z$ 是整环，从而零理想 $(0)$ 为素理想。当 $n \geq 2$ 时， $n Z$ 为素理想 $⟺$ $Z / n Z$ 为整环 $⟺$ $n$ 为素数，这就表明整数环 $Z$ 的全部素理想由 $p Z$ （ $p$ 为素数）和零理想 $(0)$ 组成。即 素理想和素数概念基本上是一致的。

3.6. 环同态和环同构

环同态是指两个环 $R$ 与 $S$ 之间的映射 $f$ 保持两个环的加法与乘法运算。更加精确地，如果 $R$ 和 $S$ 是环，则环同态是一个函数 $f : R \to S$ ，使得：

$f (a + b) = f (a) + f (b)$ ，对于 $R$ 内的所有 $a$ 和 $b$ ；
$f (a b) = f (a) f (b)$ ，对于 $R$ 内的所有 $a$ 和 $b$ 。

3.6.1. 单同态（又称嵌入）、满同态、同构

如果环同态 $f$ 是单射，则 $f$ 叫“单同态”，单同态 $f$ 也称为环 $R$ 到环 $S$ 中的嵌入（Embedding）。如果环同态 $f$ 是满射，则 $f$ 叫“满同态”。如果环同态 $f$ 是一一映射，则 $f$ 叫“同构”（Isomorphism），记为 $R ≅ S$ 或者 $R \tilde{\to} S$ 。

3.6.2. 环同构定理

环论中的同构定理和群论中的同构定理（节 2.5.3）很相似。将群同构基本定理中的“群”换为“环”，“子群”换为“子环”，“正规子群”换为“理想”，“商群”换为“商环”就得到环的同构基本定理。

4. 域

域（Field）是一个集合 $F$ 和 $F$ 上两个二元运算（通常表示成加法 $+$ 和乘法 $∙$ ）组成的代数结构 $(F, +, ∙)$ ，并且满足以下几个条件（没特别说明时假设 $a, b, c$ 是 $F$ 中任意元素）：
(1) 加法和乘法具有结合性。即 $a + (b + c) = (a + b) + c, a ∙ (b ∙ c) = (a ∙ b) ∙ c$
(2) 加法和乘法满足交换律。即 $a + b = b + a, a ∙ b = b ∙ a$
(3) 加法和乘法都有幺元素，并且这两个运算下的幺元素不相同，分别记为 0 和 1。即 $a + 0 = a, a ∙ 1 = a$
(4) 所有元素的加法运算具有逆元素， $a$ 的加法逆元素记为 $- a$ 。即 $a + (- a) = 0$
(5) 除加法幺元素 0 外的所有元素的乘法运算具有逆元素， $a$ 的乘法逆元素记为 $a^{- 1}$ 或者 $\frac{1}{a}$ 。即 $a ∙ a^{- 1} = 1, a \neq 0$
(6) 加法和乘法满足分配律。即 $a ∙ (b + c) = a ∙ b + a ∙ c, (b + c) ∙ a = b ∙ a + c ∙ a$

注：域还有其它等价的定义形式，如在集合上定义加减乘除 4 种运算。显然， 域是一种特殊的环。

有限群、子群、群的阶等概念可以直接推广到环和域。

在通常的加法和乘法运算下， $Q, R, C$ 都是域。注意， $Z$ 不是域，比如 2 对于乘法运算没有逆元素（因为 $\frac{1}{2}$ 并不在 $Z$ 中）。

4.1. 有限域 $GF (n)$

如果域中元素个数有限，则称为有限域（Finite field，也称为 Galois Field）。阶（即元素的个数）为 $n$ 的有限域一般记为 $GF (n)$ ，GF 是 Galois Field 的缩写。

图 4 是有限域的例子，它含有 4 个元素。如果只包含两个元素 $O, I$ ，即红色部分 $({O, I}, +, ∙)$ 也是域，它是最小的域。

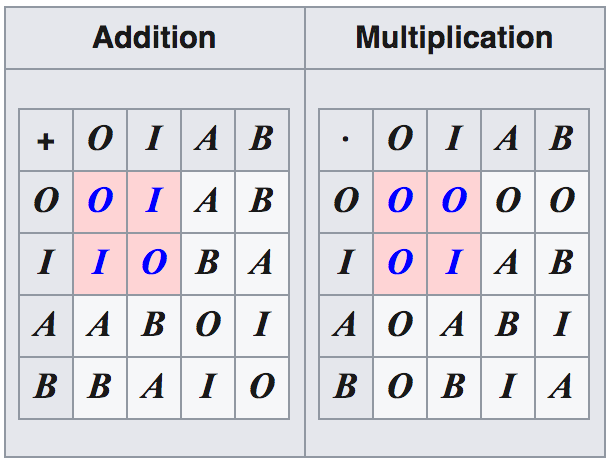
Figure 4: 具有 4 个元素的域

4.1.1. 有限域的阶是素数的幂，特征是素数

定理： 有限域的阶（即元素的个数）一定是一个素数的幂（即可表示为 $p^{k}$ 的形式，其中， $p$ 为素数， $k$ 为正整数）。 并且，素数 $p$ 就是有限域的“特征”（即对每个元素 $a$ 均有 $\underset{p times}{\underset{⏟}{a + a + \dots + a}} = 0$ ，特征的定义参考节 3.2 ）。

4.2. 有限素域 $GF (p)$

前面介绍过有限域的阶一定是一个素数的幂（可表示为 $p^{n}$ 的形式），这一节介绍当 $n = 1$ 时的特殊情况。

采用下面的定义可以构造出一个素域 $GF (p)$ ：
1、集合为 ${0, 1, 2, \dots, p - 1}$ ，其中 $p$ 为素数；
2、加法运算为“模 $p$ 加法”运算 $+_{p}$ （这个记号可参考节 2.2.3.1 ）；
3、乘法运算为“模 $p$ 乘法”运算 $\times_{p}$ （这个记号可参考节 2.2.3.2 ）；
4、加法幺元素为 0，乘法幺元素为 1；
5、任意元素 $a$ 的加法逆元素由 $a + (- a) = 0 (\mod p)$ 给出（注：可求出加法逆元 $- a$ 为 $p - a$ ）；
6、任意非零元素 $a$ 的乘法逆元素由 $a \times a^{- 1} = 1 (\mod p)$ 给出（注：可由“扩展欧几里得算法”求出乘法逆元 $a^{- 1}$ ）。
基于上面定义，容易验证它满足域的所有条件。

有限素域 $GF (p)$ 有时也记为 $F_{p}$ 。

4.2.1. 实例： $GF (7)$

图 5 （摘自 Cryptography and Network Security - Principles and Practice, 6th Edition）演示了 $GF (7)$ 的两种运算及在这两种运算下的逆元素。

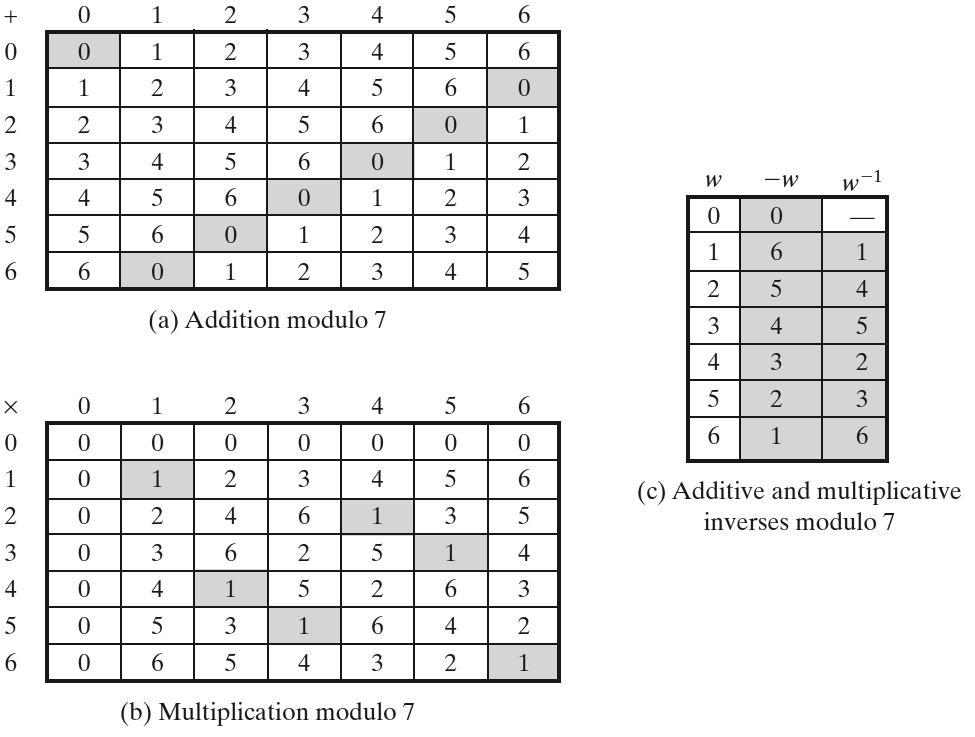
Figure 5: $GF (7)$

4.3. 有限域 $GF (2^{n})$

前面介绍过有限域的阶一定是一个素数的幂（可表示为 $p^{k}$ 的形式），这一节介绍当 $p = 2$ 时的特殊情况。

我们可以采用前一节构造素域 $GF (p)$ 的思路来构造 $GF (2^{n})$ 吗？即定义集合元素为小于 $2^{n}$ 的非负整数，定义加法运算为“模 $2^{n}$ 加法”运算，定义乘法运算为“模 $2^{n}$ 乘法”运算。答案是当 $n > 1$ 时（当 $n = 1$ 时，显然就是上一节的特殊情况），不能！因为这样的定义不能满足域的所有条件。

为了构造有限域 $GF (2^{n})$ ，我们将：
1、使用不同的符号表示域内的元素（后面会介绍，其元素是多项式）；
2、使用不同的规则定义域的加法运算和乘法运算。

构造 $GF (2^{n})$ 会涉及“多项式运算”。这里不详细介绍，仅给出 $GF (2^{3})$ 的一个例子。

为了构造 $GF (2^{3})$ ，我们需要选择一个 3 次既约多项式（Irreducible Polynomial）。只有两个满足条件的多项式： $x^{3} + x^{2} + 1$ 和 $x^{3} + x + 1$ 。这里我们仅考虑选择 $x^{3} + x + 1$ 为既约多项式时如何构造 $GF (2^{3})$ ，具体构造如图 6 所示。在这个 $GF (2^{3})$ 中，域元素集合是多项式集合 ${0, 1, x, x + 1, x^{2}, x^{2} + 1, x^{2} + x, x^{2} + x + 1}$ （也可以表示为 ${000, 001, 010, 011, 100, 101, 110, 111}$ ），加法运算是模 $x^{3} + x + 1$ 的多项式加法，乘法运算是模 $x^{3} + x + 1$ 的多项式乘法。

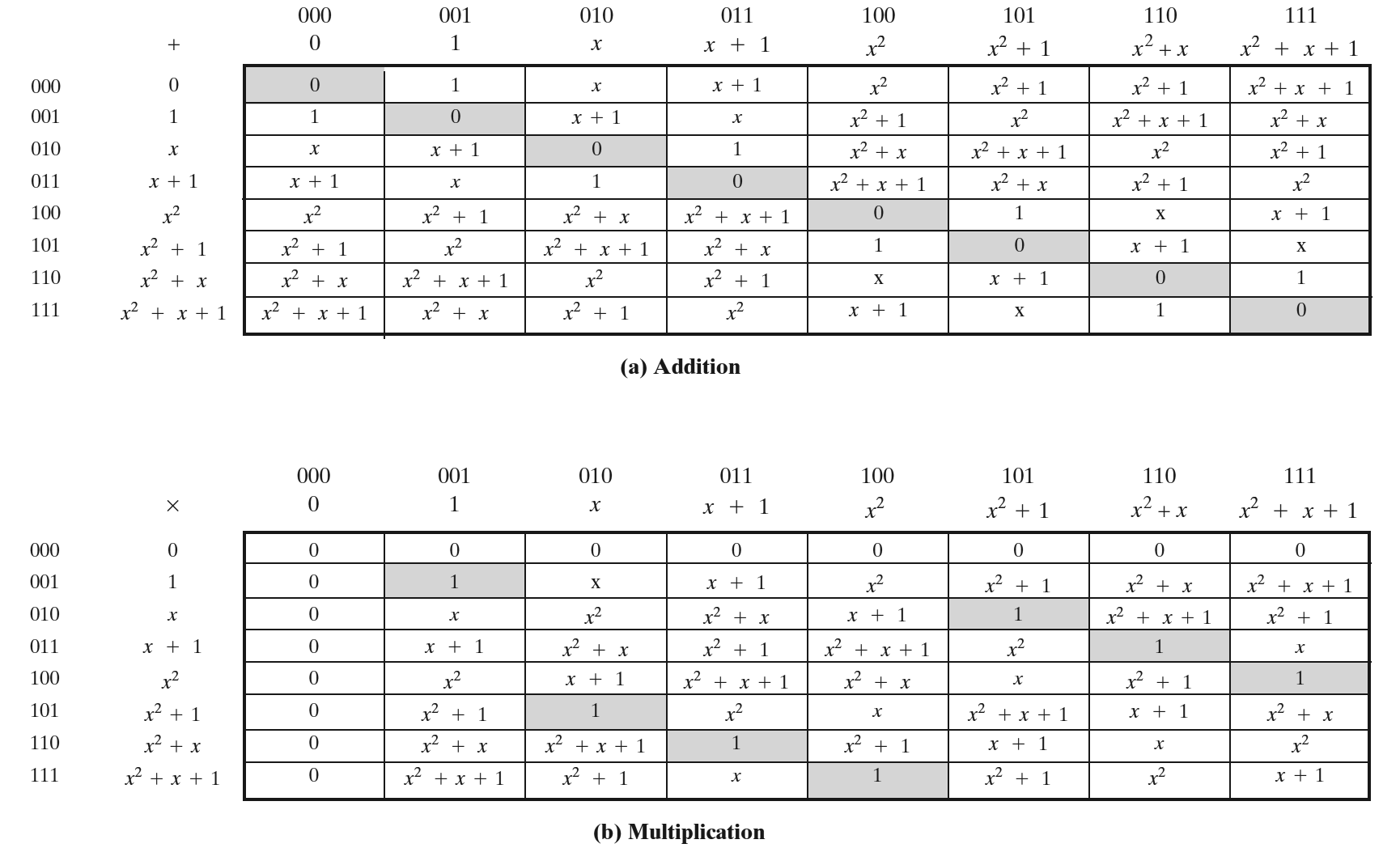
Figure 6: $GF (2^{3})$ 实例：以 $x^{3} + x + 1$ 为模的多项式运算

参考：Cryptography and Network Security, 6th Edition, Chapter 4 Basic Concepts in Number Theory and Finite Fields

4.4. 域的扩张（Field Extensions）

如果域 $K$ 是域 $F$ 的子域，则 $F$ 称为 $K$ 的扩张域，而 $K$ 称域扩张的“基域”，这样一对域通常记为 $F / K$ （这个记号可读为“F over K”），有的书籍也记为 $K \subseteq F$ 或者 $K \subset F$ 。

每个域扩张中，“扩域”可以看作是以“基域”为系数域的向量空间。 设有域扩张 $F / K$ ，将 $F$ 中元素看作向量， $K$ 中元素看作系数，可以定义 $F$ 中的域加法运算作为向量的加法运算，同时可以定义 $K$ 中元素作为系数与 $F$ 中元素的数乘运算。 向量空间的维数称为域扩张的次数或度数，一般记作 $[F : K]$ 。 次数为 1 的扩张，扩域和基域同构，称为“平凡扩张”；次数有限的域扩张称为“有限扩张”；否则称为“无限扩张”。

复数域 $C$ （如图 7 所示）是实数域 $R$ 的扩域，实数到复数的域扩张次数 $[C : R] = 2$ ，因为 $C$ 可以看作是以 ${1, i}$ 为基的向量空间。

Figure 7: Complex Number

域 $Q (\sqrt{2}) ≜ {a + b \sqrt{2} ∣ a, b \in Q}$ 是有理数域 $Q$ 的一个扩域，扩张次数 $[Q (\sqrt{2}) : Q] = 2$ ，因为 ${1, \sqrt{2}}$ 可作为一个基。

域 $Q (\sqrt{2}, \sqrt{3}) ≜ {a + b \sqrt{3} ∣ a, b \in Q (\sqrt{2})} = {a + b \sqrt{2} + c \sqrt{3} + d \sqrt{6} ∣ a, b, c, d \in Q}$ 是有理数域 $Q$ 的一个扩域，扩张次数 $[Q (\sqrt{2}, \sqrt{3}) : Q] = 4$ ，因为 ${1, \sqrt{2}, \sqrt{3}, \sqrt{6}}$ 可作为一个基。

5. 参考

本文主要参考：近世代数引论（第 3 版, 冯克勤等著）