Cryptographic Accumulator
Table of Contents
1. Accumulator 简介
密码学累加器(Accumulator)是这样一种算法: 它能够高效地证明某个元素是否在一个集合中,且不会在过程中暴露集合中的成员。
累加器可以描述为:首先将一个集合 \(X=\{x_1, x_2, \cdots, x_n \}\) 中的所有元素保存到累加器 \(acc_X\) 中,然后计算元素 \(x_i \in X\) 的证据(或称 Commitment) \(w_i\) ,最后利用证据 \(w_i\) 和累加器值 \(acc_X\) 来证明元素 \(x_i\) 存在于集合 \(X\) 中。显然, Merkle Tree 可以当作是一种简单的 Accumulator。
2. RSA Accumulator
Accumulator 这个概念是 Josh Benaloh 和 Michael de Mare 于 1993 年在论文 One-way Accumulators: A Decentralized Alternative to Digital Signatures (Extended Abstract) 中提出的,作者在该论文中提出了一种 RSA Accumulator。
下面介绍 RSA Accumulator 的主要过程。
- Setup 过程:选择大素数 \(g\) 作为后面指数运算的底数,随机选择大素数 \(p,q\) ,计算 \(N=p\cdot q\)
- 加入元素到 Accumulator 过程。假设 Accumulator 中需要保存集合 \(X=\{x_1, x_2, \cdots, x_n \}\) 所有元素,设 \(e_i = H(x_i)\) 是 \(x_i\) 的一种素数表达(即 \(e_i\) 是素数)。 \[acc_X = g^{e_1 \cdot e_2 \cdots e_n} \pmod N = g^{\prod_{i \in [n]}e_i} \pmod N\] 要证明 \(x_i\) 存在于 Accumulator 中需要一个 witness,这个 witness 为: \[w_i = g^{e_1 \cdot e_2 \cdots e_{i-1} \cdot e_{i+1} \cdots e_n} \pmod N = g^{\prod_{j \in [n] \setminus \{i\}}e_j} \pmod N\]
- 证明元素 \(x_i\) 存在于 Accumulator 过程。如果式子 \[acc_X \stackrel{?}{=} w_i^{e_i} \pmod N\] 成立,则可证明 \(x_i\) 在 Accumulator 中。
2.1. RSA Accumulator 实例
下面通过实例演示一下 Alice 往 Accumulator 中加入元素 \(X=\{x_1,x_2,x_3\}=\{3, 5, 11\}\) (注:由于这里的元素本身就是素数,下面省略了把元素转换为某种素数表达的过程) ,并向 Bob 证明元素 \(x_1,x_2,x_3\) 确实存在于 Accumulator 中。
首先确定好参数 \(g, p, q\) ,一旦计算完 \(N=p\cdot q\) ,就丢弃掉 \(p,q\) ,这是一个 Trusted Setup 步骤。也就是说,需要一个可信任的第三方来完成这个 Setup 步骤, \(p,q\) 不能让 Alice 知道,否则 Alice 可能构造一些假的 witness。因为 RSA Accumulator 是基于 Strong RSA assumption ,如果 \(p,q\) 泄露了,就不满足 Strong RSA assumption 的前提了,构造假 witness 会变得可行。
Alice 进行下面计算:
- 往 Accumulator 加入 \(3\) 时,计算 \(root_1 = g^3 \pmod N\) ,
- 再往 Accumulator 加入 \(5\) 时,计算 \(root_2 = root_1^5 \pmod N = g^{3 \times 5} \pmod N\) ,
- 再往 Accumulator 加入 \(11\) 时,计算 \(root_3 = root_2^{11} \pmod N = g^{3 \times 5 \times 11} \pmod N\) ,
最终得到的 \(acc_X = root_3 = g^{3 \times 5 \times 11} \pmod N\)
Alice 还要计算每个元素的 witness: \[\begin{aligned} w_1 &= g^{ x_2 \times x_3} \pmod N = g^{ 5 \times 11} \pmod N \\
w_2 &= g^{ x_1 \times x_3} \pmod N = g^{ 3 \times 11} \pmod N \\
w_3 &= g^{ x_1 \times x_2} \pmod N = g^{ 3 \times 5} \pmod N \end{aligned}\]
Bob 验证 \[acc_X \stackrel{?}{=} w_i^{x_i}\] 是否成立,如果成立则说明 \(x_i\) 在这个 Accumulator 中,比如,如果 \(acc_X = w_1^{x_1}\) 成立则说明 \(x_1\) 在 Accumulator 中。
注:计算所有元素的 witness 是比较耗时间的,时间复杂度为 \(O(n^2)\) ,Dan Boneh 等在论文 Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains 中提出一种名为 RootFactor 的分治算法可以把时间复杂度降低为 \(O(n \log n)\) 。
2.2. Unknown Order Group
RSA Accumulator 加入元素的运算是在整数模 \(N\) 乘法群 \((\mathbb{Z}/N\mathbb{Z})^*\) 上的运算。这个群的 Order 为 Euler's totient function \(\phi(n)=(p-1)(q-1)\) ,由于 \(p,q\) 生成后就会被弃掉,所以没人知道 \(\phi(n)=(p-1)(q-1)\) 是多少(除非有办法把合数 \(N\) 重新分解为两个素数的乘积,但分解大整数是个数学难题,目前没有有效算法)。RSA Accumulator 中所谓的 Unknown Order Group 就是指整数模 \(N\) 乘法群 \((\mathbb{Z}/N\mathbb{Z})^*\) 。
2.3. 为什么把元素转换为素数
前面提到过,加入元素到 RSA Accumulator 中前,要先把元素转换为它的素数表达。因为,如果加入到 RSA Accumulator 中的元素不是素数,则攻击者可以伪造元素的 witness,这个元素不在 RSA Accumulator 中,但它的 witness 却可以通过校验,下面进行举例说明。
假设 Accumulator 中直接保存了 \(X=\{5,6,11\}\) (注:这其中的元素 \(6\) 并不是素数),即 \[acc_X = g^{5 \times 6 \times 11} \pmod N = g^{330} \pmod N\] 那么攻击者可以提供一个假证明 \[w=g^{110} \pmod N\] 来证明元素 \(3\) 存在于 Accumulator 中。因为验证者计算 \[acc_X = \left(g^{110}\right)^3 \pmod N\] 会确实成立的。但事实上 \(3\) 并不存在于 Accumulator 中,这样攻击者成功地欺骗了验证者。
2.4. 证明元素不存在于 Accumulator 中(Non-Membership)
2007 年,Jiangtao Li 等在论文 Universal Accumulators with Efficient Nonmembership Proofs 中提出了证明某元素不存在于某 Accumulator 中的方法。
给定 RSA Accumulator \(acc_X\) 其中加入了集合 \(S\) 的所有元素,元素 \(x\) 不属于 Accumulator 的 witness 的计算如下:
- \(s^{*} \leftarrow \prod_{s \in S}s\)
- \(a,b \leftarrow Bezout(x, s^*)\)
- \(d \leftarrow g^a\)
则 \(x\) 不属于 Accumulator 的 witness 就是二元组 \(\{d, b\}\)
有了 witness,证明 \(x\) 不属于 Accumulator 的过程如下,检测 \[d^x acc_X^b \stackrel{?}{=} g\] 是否成立,如果成立则 \(x\) 不属于 Accumulator。
为什么这种方法可以证明 \(x\) 不属于 \(S\) 呢?背后的原理是对于任何 \(x \notin S\) , \(gcd(x, \prod_{s \in S}s)=1\) 一定成立,从而由 Bézout's identity 可知, \(a \times x + b \times \prod_{s \in S}s = 1\) 一定有解,这里把它的解做为了 \(x \notin S\) 的证据。
2.4.1. Non-Membership 实例
假设 Accumulator \(acc_X\) 中加入了元素 \(S = \{3,5,11\}\) ,有 \(acc_X = g^{3\times5\times11} \pmod N = g^{165} \pmod N\)
现在要证明 \(7\) 不存在于 \(acc_X\) 中,它的 witness 计算如下:
- \(s^{*} \leftarrow \prod_{s \in S}s = 3 \times 5 \times 11 = 165\)
- 计算 Bezout 系数,即求解 \(a \times 7 + b \times 165 = 1\) ,具体方法是 Extended Euclidean algorithm ,这里不详细介绍,直接给出结果 \(a=-47, b=2\)
- witness 为 \(\{d, b\} = \{g^{-47}, 2\}\)
验证者校验 \(d^x acc_X^b \stackrel{?}{=} g\) 是否成立,即校验 \(\left(g^{-47}\right)^7 \times \left(g^{165}\right)^2 = g\) 是否成立,容易验证它确实成立,所以元素 \(7\) 不存在于 \(acc_X\) 中。
3. Merkle Tree Accumulator
前面提到过,Merkle Tree 可以当作 Accumulator。
下面以真实的应用场景介绍一下 Merkle Tree 如何作为 Accumulator。
在以太坊区块链中,经常有 DApp 项目方给他的用户空投(AirDrop)代币。如果直接在链上向用户地址中转移代币,则当用户多时 DApp 项目方会要付出昂贵的交易手续费。一般项目方采用的办法是:把代币保存在智能合约中,用户需要调用智能合约中的方法来领取代币,这产生的交易手续费是由用户支付的。
现在的问题是:智能合约如何知道用户具有领取资格呢?显然基于 Gas 考虑,以及智能合约最大字节数的限制(EIP 170 限制了合约不能超过 24KB) ,不能直接把全部有资格的用户的地址列表保存在智能合约中用于资格校验。
下面介绍一种基于 Merkle Tree 的空投方案:
- 把有资格的用户的地址作为 Merkle Tree 的叶子节点,生成一个 Merkle Tree;
- 智能合约中只保存 Merkle Tree 的 Root Hash(即图 1 中的 Top Hash);
- 当用户调用智能合约中的方法来领取空投代币时,先去 DApp 项目方的后端服务器获得一个可以证明用户地址存在于 Merkle Tree 中的 witness(即一系列 Hash 值,它们是树的一些中间节点)。用户得到 witness 后,把它提交给合约,如果合约校验用户地址确实存在于 Merkle Tree 中(具体方法是先计算 Address 4 的哈希 Hash 1-1,然后利用 witness 中包含的 Hash 1-0 计算出 Hash 1,最后利用 witness 中包含的 Hash 0 计算出 Top Hash,如果计算得到的 Top Hash 和合约中保存的值一样,则通过校验),则给用户地址转移代币。
如图 1 所示。
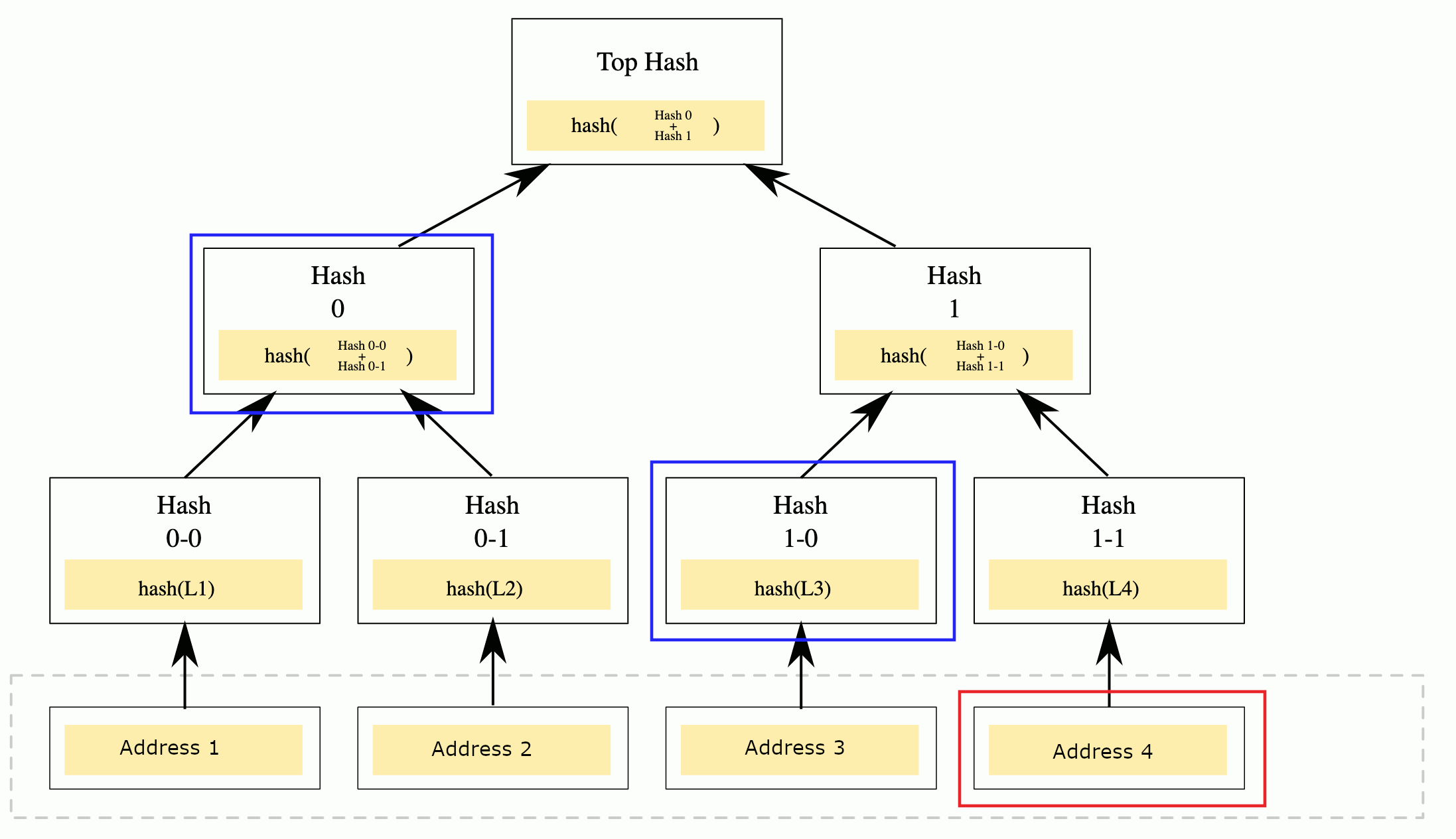
Figure 1: 蓝色方框中的哈希时可以作为 Address 4 存在于 Merkle Tree 中的 witness
利用 Merkle Tree 向用户空投代币的智能合约相关代码可参考:https://etherscan.io/address/0x08c7676680F187A31241E83e6d44C03A98AdaB05#code