Data Structure for Strings

1. Motivation
2. Tries（前缀树）
3. Suffix Trees
4. Suffix Arrays

1. Motivation

当我们把数据保存到二叉树，红黑树等数据结构中时，往往会对数据中 key 的大小进行多次比较，显然 key 的大小比较应该越快越好。当 key 是数字时这不是问题，但当 key 是字符串（不是数字）时，我们需要给 key 的比较定义一个规则（比如按“字典序”），不过，“基于字典序的字符串大小比较”显然没有“数字大小比较”高效。而且，字符串按字典序排序后，相邻的字符串并不会意味着它们会更相似，这使得排序后按范围查找部分数据的意义变得不是很大。

后文介绍的数据结构能够更高效地处理“字符串”相关问题。比如， Tries 支持比二叉树（或红黑树）更快的查找操作。而相对于哈希表，Tries 有可比拟的查找速度，且还支持一些“有序”的操作，如它能快速地查找 key 以“abc”开头的所有数据。

参考：Advanced Data Structures, by Peter Brass, 2008, Chapter 8. Data Structures for Strings

2. Tries（前缀树）

Tries were first described by René de la Briandais in 1959. The term trie (comes from retrieval) was coined two years later by Edward Fredkin.
Tries 又称为“前缀树（Prefix tree）”，它的核心思想是“空间换时间”。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

图 1 是 Trie 的一个例子。

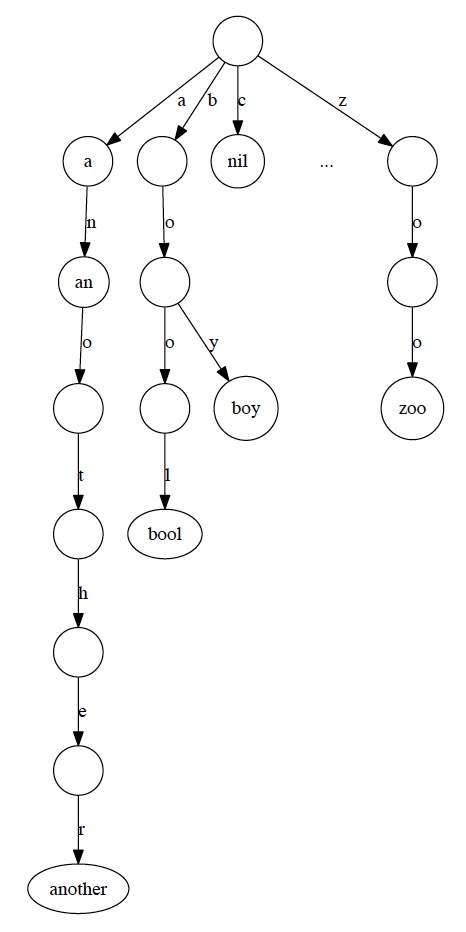
Figure 1: Trie 的例子（包含 a、an、another、bool、boy 和 zoo 共 6 个 key）

Tries 中有两种结点：一种是分支结点，一种是数据元素结点（常用一个标记来区分这两种结点）。图 1 中结点为空的结点是分支结点，而结点中有字母（nil 除外）的结点是数据元素结点。

参考：
Algorithms, 4th(Robert Sedgewick and Kevin Wayne), 5.2 Tries

2.1. Tries 分析和实现

Tries 的插入（Insert）、删除（Delete）和查找（Find）比较简单，用一个一重循环即可。
结点中儿子的指向，一般有三种方法：
(1) 对每个结点开一个字母集大小的数组（指针数组），对应的下标是儿子所表示的字母（0-25 个下标分别表示 26 个字母），内容是儿子结点的指针（为 NULL 时表示不含对应的字母）；
(2) 对每个结点上挂一个链表，按一定顺序记录每个儿子是谁；
(3) 使用左儿子右兄弟表示法记录这棵树。
这三种方法，各有特点。第一种易实现，但实际的空间要求较大；第二种，较易实现，空间要求相对较小，但比较费时；第三种，空间要求最小，但相对费时且不易编写。

下面我们采用第一种方法，Trie 树的结点表示如下：

struct Trie_node
{
    bool isStr;            //记录此处是否构成一个串（即是否是数据元素结点）
    Trie_node *next[26];   //指针数组，指向各个子树的指针，下标0-25分别代表26字符
};

一个插入了 abc、d、da、dda 四个字符串的 Trie 树如图 2 所示。

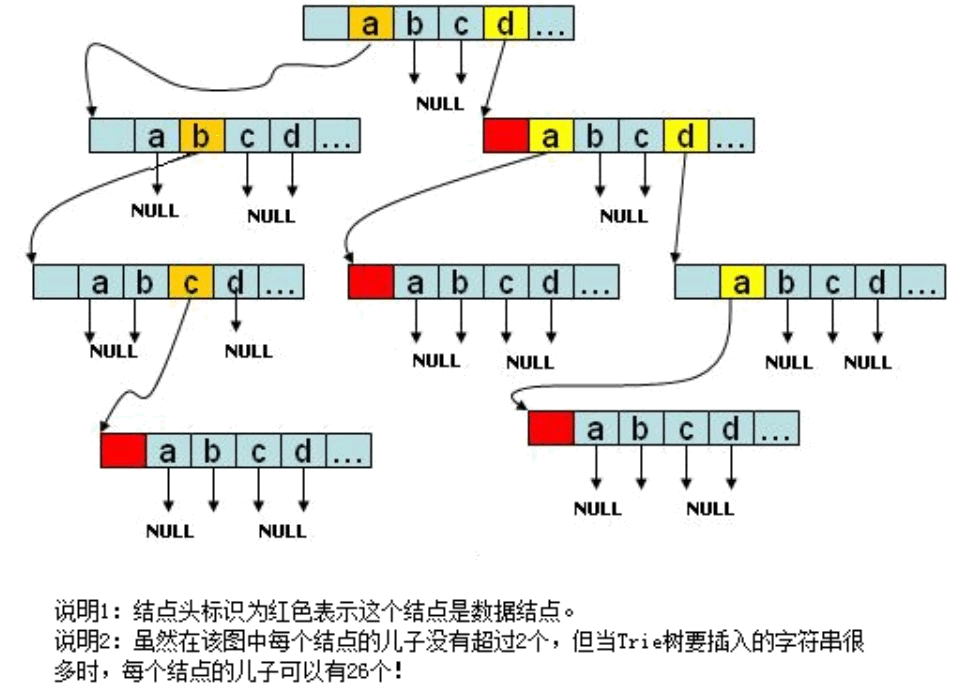
Figure 2: 插入了 abc、d、da、dda 四个字符串的 Trie 树

2.1.1. Tries 的简单实现

下面是 Trie 的 C++实现：

//Trie树的C++实现（插入、删除和查找）
//下面代码来源于http://www.cnblogs.com/cherish_yimi/archive/2009/10/12/1581666.html

#include<iostream>
#include<cstring>
using std::cout;
using std::endl;

const int branchNum = 26;

struct Trie_node {
    bool isStr;                   //记录此处是否构成一个串（即是否是数据元素结点）
    Trie_node *next[branchNum];   //指针数组，指向各个子树的指针，下标0-25分别代表26字符
    Trie_node():isStr(false) {    //构造函数里初始化数组为NULL
        memset(next, 0, sizeof(next));
    }
};

class Trie {
public:
    Trie();
    void insert(const char* word);
    bool search(const char* word);
    void deleteTrie(Trie_node *root);
private:
    Trie_node* root;
};

Trie::Trie() {
    root = new Trie_node();
}

void Trie::insert(const char* word) {
    Trie_node *location = root;
    while(*word) {
        if(location->next[*word-'a'] == NULL) {   //不存在则建立
            Trie_node *tmp = new Trie_node();
            location->next[*word-'a'] = tmp;
        }
        location = location->next[*word-'a'];     //每插入一步，相当于有一个新串经过，指针要向下移动
        word++;
    }
    location->isStr = true;                       //到达尾部，标记为数据元素结点
}

bool Trie::search(const char *word) {
    Trie_node *location = root;
    while(*word && location) {
        location = location->next[*word-'a'];
        word++;
    }
    return(location!=NULL && location->isStr);
}

void Trie::deleteTrie(Trie_node *root) {
    for(int i = 0; i < branchNum; i++) {
        if(root->next[i] != NULL) {
            deleteTrie(root->next[i]);
        }
    }
    delete root;
}

int main() {
    Trie t;
    t.insert("a");
    t.insert("abandon");
    t.insert("abandoned");
    t.insert("abashed");
    if(t.search("abashed")) {
        cout<<"find key abashed"<<endl;
    }
    return 0;
}

2.1.2. Tries 的时间复杂度

Tries 的插入（Insert）、删除（Delete）和查找（Find）的时间复杂度都为 \(O(n)\) ，其中 \(n\) 为 key 的长度。

2.1.3. Tries 的高级实现(Double-Array Trie)

双数组 Trie 结构由日本研究学者于 1989 年提出（发表于论文“An Efficient Digital Search Algorithm by Using a Double-Array Structure”）。该结构有效结合了数字搜索树（Digital Search Tree）检索时间高效的特点和链式表示的 Trie 空间结构紧凑的特点。在双数组 Trie 中所有键中包含的字符之间的联系都是通过简单的数学加法运算来表示，不仅提高了检索速度，而且省去了链式表示的结构中大量使用的指针，节省了存储空间。

参考：
An Implementation of Double-Array Trie: http://linux.thai.net/~thep/datrie/datrie.html

2.2. Tries 应用

2.2.1. 单词自动补齐

用户使用电子词典时，一般不用完整地输入单词，输入部分单词后，相同前缀的单词会自动列出。这可以通过 Trie 来实现。如图 3 所示。

Figure 3: Tries 应用：电子词典单词自动补齐

2.2.2. AC 自动机

AC 自动机(Aho-Corasick automation)于 1975 年产生于贝尔实验室，是著名的多模匹配算法之一。比如，给出 n 个单词，再给出一段文章，让你找出有多少个单词在文章里出现过。AC 自动机利用 Trie 作为其数据结构。

2.3. Tries 相对 Hash 的优点

Tries 可以作为 Hash 表的替代器，它的查找性能和 Hash 表相当，但 Tries 还能提供和 key 的顺序相关的操作。 A trie implements an ordered map while a hash table cannot!

2.4. Binary Trie (Bitwise Trie, A digital search tree)

尽管 Trie 中数据的 key 往往为字符串，但不一定要求这样。下面介绍的 Binary Trie 的 key 的类型是整数。

Binary Trie（又称为 Bitwise Trie）是⼀种特殊的⼆叉树，它的 key 是整数，每个 key 存放的位置由它的全部⼆进制位来决定。0表⽰在左侧分支，⽽1 表⽰在右侧分支。

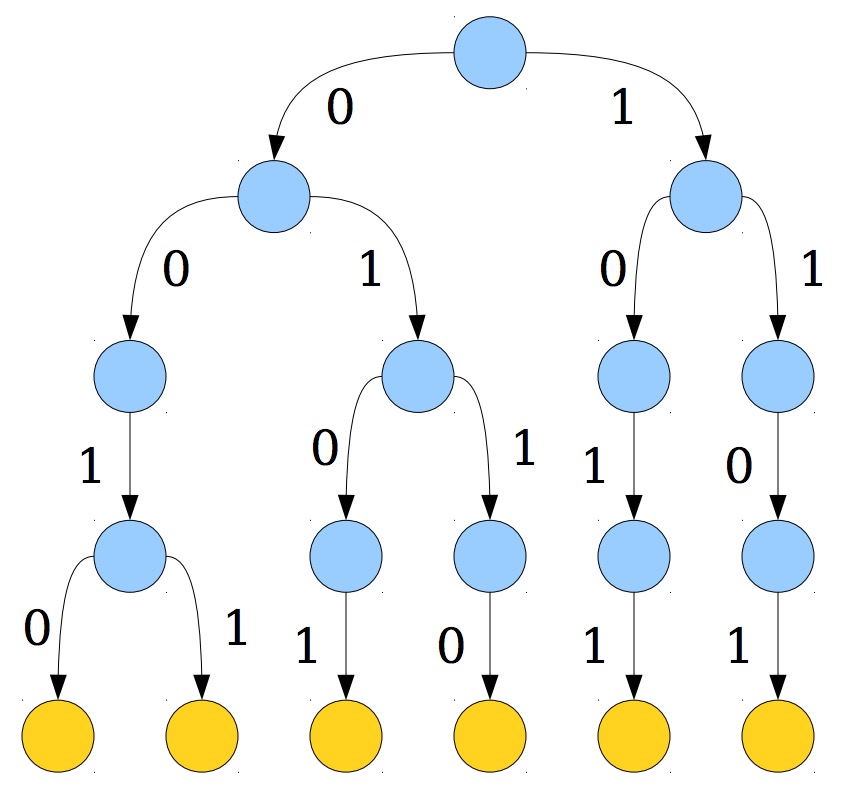
Figure 4: Example of Bitwise Trie

图 4 所示的 Bitwise Trie 保存着整数 2（二进制为 0010）, 3（二进制为 0011）, 5（二进制为 0101）, 6（二进制为 0110）, 11（二进制为 1011）, 13（二进制为 1101）。图片摘自http://web.stanford.edu/class/archive/cs/cs166/cs166.1166/lectures/15/Small15.pdf

参考：《Fundamentals of Data Structures in C, 数据结构基础(C 语言版)(第 2 版)》12.1 节数字查找树

2.4.1. X-fast trie and Y-fast trie

X-fast trie 和 Y-fast trie 是 Bitwise Trie 的变种，关于它们的说明可参考：x-Fast and y-Fast Tries

2.5. Compressed Tries (Patricia)

Trie 的空间利⽤率很低，为了提⾼空间利⽤率，可以将⼀连串“独⽣⼦⼥”压缩为⼀个节点。Patricia 就是这样的数据结构（Patricia 是“Practical algorithm to retrieve information coded in alphanumeric”的⾸字母缩写）。

图 1 所示的 Trie 经过压缩后，可以得到图 5 所示 Patricia。

Figure 5: Compressed Tries (Patricia)，保存着 a、an、another、bool、boy 和 zoo 共 6 个 key

2.6. Radix Tree（基数树）

Radix Tree（基数树）与 Trie 树的思想有点类似， 我们可以把 Trie 树看为一个基为 26 的基数树。

“基数树”一般用于长整数到对象的映射，而 Trie 树一般用于字符串到对象的映射。

2.6.1. 基数树应用

Linux 内核中有对基数树的实现，参考 radix-tree.c 。

Redis 中也大量地使用了基数树：

Radix trees are extensively used inside Redis. The new Stream data type is completely backed by radix trees, also Redis Cluster tracks keys using a radix tree and so forth.

3. Suffix Trees

后缀树（Suffix tree）是一种数据结构，能快速地解决很多关于字符串的问题。

后缀树的概念最早由 Weiner 于 1973 年提出，后来由 McCreight 在 1976 年简化了后缀树的构造算法（从右向左构造后缀树），Ukkonen 在 1995 年给出了第一个从左向右的 on-line 构造算法。

3.1. 后缀树定义

字符串 S 的后缀树就是串 S 非空后缀的压缩 Trie 树。即：后缀树就是一个压缩后的 Trie 树，存储了某个字符串的所有非空后缀。

例如，字符串 S=peeper 的非空后缀有 peeper、eeper、eper、per、er、r。因此字符串 peeper 的后缀树是数据元素为 peeper、eeper、eper、per、er、r 构造的压缩 Trie 树，如图 6 所示。

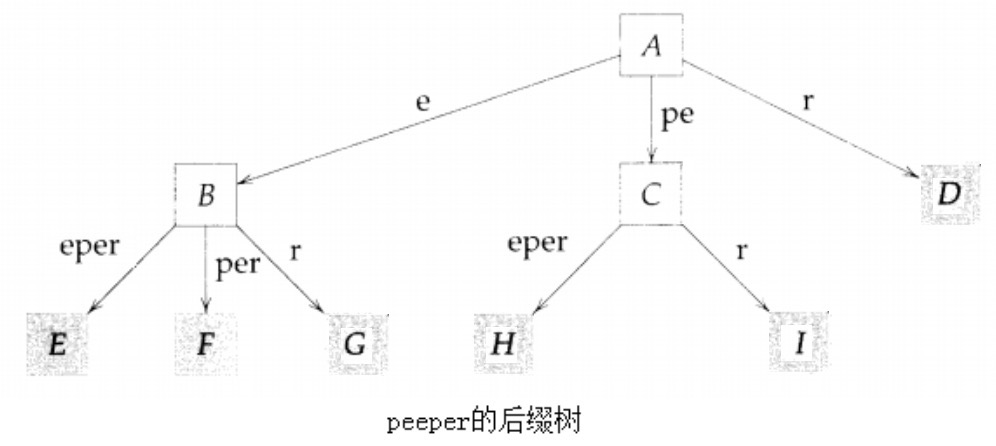
Figure 6: 字符串 peeper 的后缀树

在后缀树中，往往在数据元素结点上存放该后缀在串中出现的下标值，如图 7 所示。

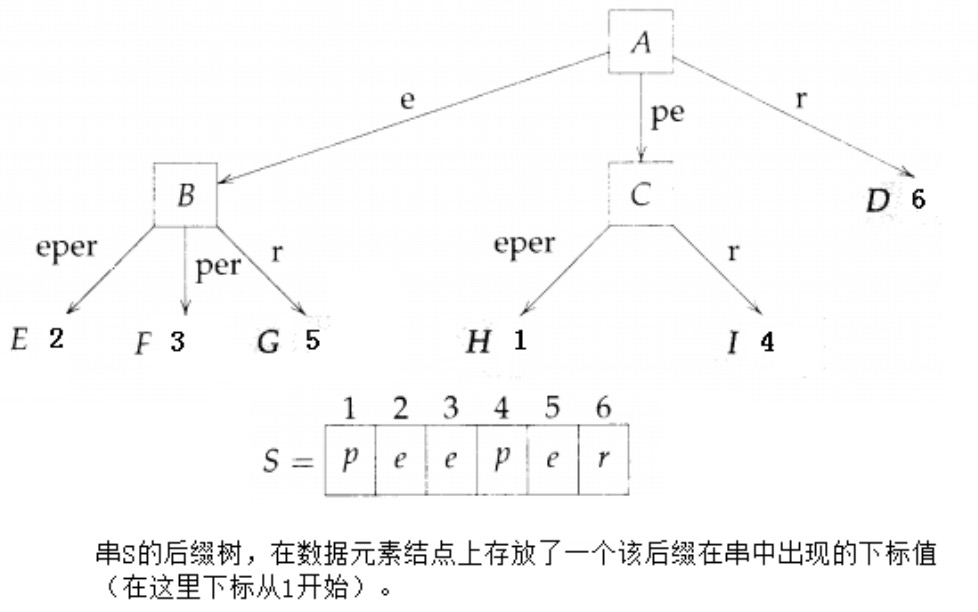
Figure 7: 字符串 peeper 的后缀树（标记了下标）

参考：《Fundamentals of Data Structures in C, 数据结构基础(C 语言版)(第 2 版)》12.4 节后缀树

3.1.1. 广义后缀树（Generalized Suffix Tree）

前面讲的后缀树只能存储“一个”单词的所有后缀，而 广义后缀树能存储任意“多个”单词的所有后缀。
我们需要增加记号来区分不同单词的后缀。

3.2. 后缀树的构造

人们提出了很多后缀树算法，其时间和空间复杂度是线性的，后缀树的建立时间与被索引的字符串的长度成正比，在后缀树上进行字符串匹配查找时需要的时间与待查找的字符串的长度成正比。 Weiner 的算法、McCreight 的 McC 算法和 UkKonen 算法是三种经典的后缀树构造算法，它们都在线性时间内完成长度为 n 的字符串的后缀树的建立。 虽然 Weiner 的算法是最早提出的线性时间算法，但该算法使用了较多的存储空间；而 McC 算法使用了后缀链接等技术使算法的时间复杂度减少到线性，与其它两种算法相比 McC 算法更高效，使用的存储空间更少；对于 UkKonen 算法也使用了后缀链接技术，其最大特点在于它是在线算法(On-line)，也就是说算法的任何阶段都生成当前子串的后缀树。

3.3. 后缀树的应用

后缀树的应用比较广泛。

下面是后缀树的一些应用：
(1) 从目标串 T 中判断是否包含模式串 P（其时间复杂度接近 KMP 算法）；
(2) 从目标串 T 中查找最长的重复子串；
(3) 从目标串 T1 和 T2 中查找最长公共子串；
(4) Ziv-Lampel 无损压缩算法；
(5) 从目标串 T 中查找最长的回文子串。

3.3.1. 查找字符串

问题描述：查找一个字符串 S 是否包含了另一个字符串 T。
分析：如果 S 包含 T，那么 T 必定是 S 的某个后缀的前缀。因为 S 的后缀树包含了所有的后缀，因此只需对 S 的后缀树使用和 Trie 树相同的查找方法即可。

3.3.2. 统计子字符串出现次数

问题描述：统计字符串 S 中出现子字符串 T 的次数。
分析：每出现一次 T，必定对应着一个不同的后缀，而这所有的后缀又都有着共同的前缀 T。因此这些后缀在 S 的后缀树中必定属于某一棵子树。这棵子树的叶子数便等于 T 在 S 中出现的次数。

3.3.3. 最长重复子串(Longest Repeated Substring)

问题描述：找出 S 中最长的重复子串。例如“Ask not what your country can do for you, but what you can do for your country”中最长的重复子串是“can do for you”。
分析：定义节点的“字符深度”为当前节点到后缀树根节点所经过的字符串总长。遍历后缀树，找出具有最大字符深度的非叶节点，则从根节点到该非叶节点所经过的字符串即为所求。如图 8 所示。

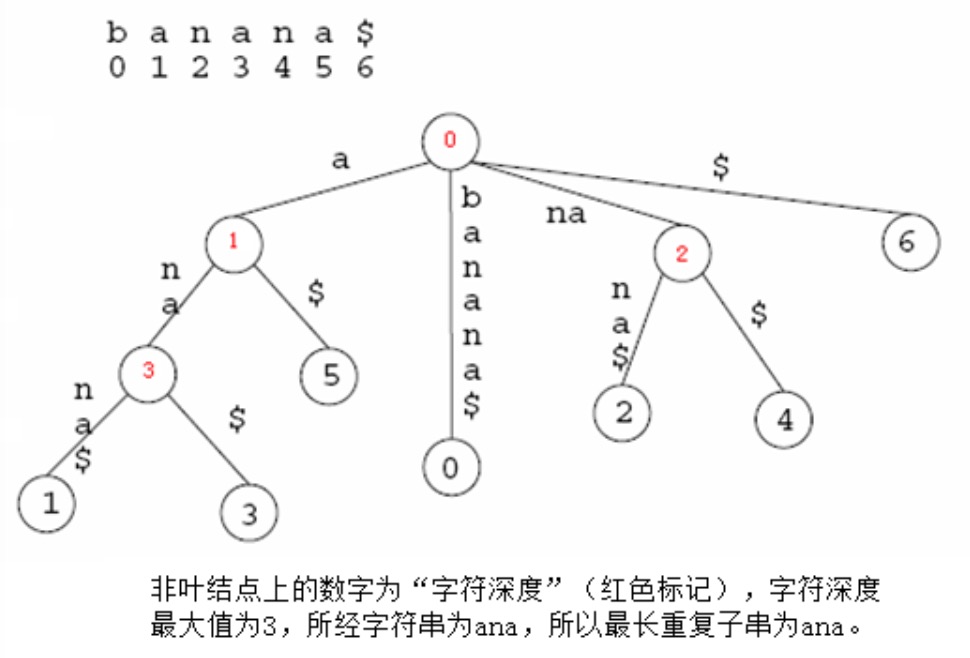
Figure 8: 用后缀树求解 banana 的最长重复子串

为了更清楚地表示出后缀，我们在字符串末尾添加一个特殊字符作为结束标记，在这里我们使用\(。因此 banana 的所有后缀就可以表示为：banana\)、anana\(、nana\)、ana\(、na\)、a\(、\)。

参考：https://en.wikipedia.org/wiki/Longest_repeated_substring_problem

4. Suffix Arrays

后缀数组(Suffix Arrays)于1990年提出，是一个通过对字符串的所有后缀经过排序后得到的数组。此数据结构被运用于全文索引、数据压缩算法、以及生物信息学。 后缀数组可作为对后缀树的一种替代，它更加简单以及节省空间。

参考：https://en.wikipedia.org/wiki/Suffix_array