Data Structure
Table of Contents
- 1. 数据结构简介
- 2. Asymptotic Notation(渐近记号)
- 3. 基本数据结构(链表、栈、队列)
- 4. Binary Trees and Binary Search Trees
- 5. Balanced Search Trees
- 6. Priority Queue(Heap)
- 7. Hash Table
- 8. Disjoint-Set(Union–Find)
1. 数据结构简介
In computer science, a data structure is a particular way of organizing data in a computer so that it can be used efficiently.
经典的数据结构参考书籍:
Data Structures and Algorithm Analysis in C, 2nd Edition by Mark A. Weiss
Data Structures, Algorithms, and Applications in C++, 2nd Edition by Sartaj Sahni
Handbook of Data Structures and Applications, by Dinesh P. Mehta and Sartaj Sahni
2. Asymptotic Notation(渐近记号)
在计算机科学中,常用渐近记号来表示算法的时间复杂度,如表 1 所示。
| Notation | Name | 含义 |
|---|---|---|
| \(O\) | Big O | 上界 |
| \(\Omega\) | Big Omega | 下界 |
| \(\Theta\) | Big Theta | 准确界 |
| \(o\) | Small O | 非渐近准确上界 |
| \(\omega\) | Small Theta | 非渐近准确下界 |
上界记号 Big O 的定义为: 如果存在正常数 \(c\) 和 \(n_0\) 使得当 \(N \ge n_0\) 时 \(T(N) \le cf(N)\) ,则记为 \(T(N) = O(f(N))\) 。其它渐近记号的定义与此类似。记号 \(o\) 和 \(\omega\) 在计算机科学中使用比较少。
3. 基本数据结构(链表、栈、队列)
3.1. Linked Lists
3.1.1. Singly Linked Lists
单向链表,这是最简单的链表。每个结点有个 next 指针,指向下一个结点。
单向链表基本操作:
//在实现单向链表时,删除第一个结点可能导致链表的位置变化了(可以采用复制第二个结点的数据域到第一个结点,再删除第二个结点的方式来变相删除第一个结点)。
//更方便的办法是在第一个结点前增加head结点,它的数据域没有含义。
//下面是含有head结点的实现。
#include<stdio.h>
#include<stdlib.h>
typedef struct node
{
int data;
struct node *next;
}Node;
/* 带头链表,头结点数据域没有含义。 */
Node *create()
{
Node *head = malloc(sizeof(Node));
if (head == NULL) {
printf("error when malloc");
return NULL;
}
head->next = NULL;
return head;
}
/* 返回含keyData的结点,如果有多个则返回第一个,没找到则返回NULL */
Node *find(Node *head, int keyData)
{
Node *node = head->next;
while( node != NULL && node->data != keyData){
node = node->next;
}
return node;
}
/* 在keyData结点后面插入一个结点,如果keyData结点不存在,则插入到表头。 */
void insert(Node *head, int keyData, int data)
{
Node *newNode = malloc(sizeof(Node));
if (newNode == NULL) {
printf("error when malloc");
return;
}
newNode->data = data;
Node *keyNode = find(head, keyData);
if (keyNode == NULL) { //没找到就插入到表头。
newNode->next = head->next;
head->next = newNode;
} else {
newNode->next = keyNode->next;
keyNode->next = newNode;
}
}
/* 带头结点链表的反转 */
void reverse(Node *head)
{
if (head == NULL) { return; }
Node *pNode = head->next;
Node *pPrev = NULL;
while (pNode != NULL) {
Node *pNext = pNode->next;
head->next = pNode;
pNode->next = pPrev;
pPrev = pNode;
pNode = pNext;
}
}
void print(Node *head){
Node *node = head->next;
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
/* 如果keyData在链表中有多个,则删除第1个;
如果keyData不在链表中,则什么也不做。*/
void delete(Node *head, int keyData)
{
Node *p1 = head;
/* 先找到含有keyData结点的前一个结点,保存到p1中。 */
while(p1->next != NULL && p1->next->data != keyData) {
p1 = p1->next;
}
if (p1->next != NULL) { // 如果p1不是最后结点,即链表中存在keyData结点。
Node *node = p1->next;
p1->next = node->next;
free(node);
}
}
/* 删除整个链表(删除带表头结点的列表,一般指删除除头结点外的所有结点);
当提到销毁列表时,才指删除包括表头结点在内的所有结点。*/
void deleteList(Node *head)
{
Node *p = head->next;
head->next = NULL;
while(p != NULL) {
Node *tmp = p->next; //删掉当前结点前,备份下一个结点。
free(p);
p = tmp;
}
}
int main()
{
Node *head = create();
insert(head, 1, 2); //结点1不存在,所以会在表头插入结点2
insert(head, 2, 3); //在结点2后插入结点3
insert(head, 3, 4);
insert(head, 2, 8); //在结点2后插入结点8
print(head); //会打印出:2 8 3 4
}
3.1.2. Doubly Linked Lists
如果我们需要快速的反向遍历链表,则双向链表是很好的选择。
双向链表在基本链表的基础上增加了指向前一个结点的指针。
3.1.3. Circular Lists
循环链表如下所示:
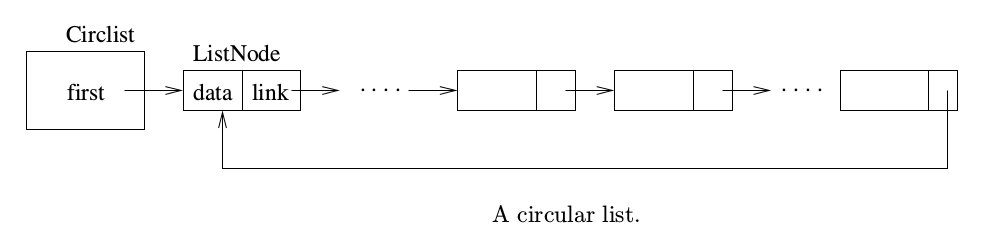
Figure 1: 循环链表
参考:Handbook of Data Structures and Applications, Dinesh P. Mehta and Sartaj Sahni, 2005
3.1.4. Doubly Linked Circular Lists
双向循环链表
3.2. Stacks
数据结构栈是只允许在一端插入和删除的线性表。其特点是后进先出(LIFO)。
3.2.1. 栈的数组实现
用数组实现栈的唯一缺陷是需要提前声明一个数组的大小。但一般来说栈中的元素不会太多。 所以栈的数组实现比较流行。
栈的数组实现如下:
//栈的数组实现(C++)。
//注:类中有指针成员,所以有浅拷贝和深拷贝的问题(但这里没考虑)。
#include<cstdlib>
using std::rand;
#include<iostream>
using std::cerr;
using std::cout;
using std::endl;
template<typename T>
class Stack
{
public:
Stack(int MaxStackTop=10);
~Stack(){delete[] stack;}
bool isEmpty()const{return -1==TopOfStack;}
bool isFull()const{return TopOfStack== Capacity;}
void Push(const T& value);
T Top()const; //返回栈顶元素。
void Pop(); //栈顶元素出栈。
private:
T *stack; //堆栈元素的数组。
int TopOfStack; //栈顶,数组下标,元素个数减1。
int Capacity;
};
template<typename T>
Stack<T>::Stack(int MaxStackTop)
{
Capacity = MaxStackTop;
stack = new T[MaxStackTop];
TopOfStack = -1; //不要初始化为0,因为前面约定为元素个数减1。
}
template<typename T>
void Stack<T>::Push(const T& value)
{
if(!isFull())
stack[++TopOfStack]= value;
else
cerr<<"Full Stack!";
}
template<typename T>
T Stack<T>::Top()const
{
if(!isEmpty())
return stack[TopOfStack];
else {
cerr<<"Empty Stack!";
return 0;//为避免编译警告,栈为空,弹出元素时将返回0。
}
}
template<typename T>
void Stack<T>::Pop()
{
if(!isFull())
TopOfStack--;
else
cerr<<"Empty Stack!";
}
//测试栈
int main()
{
int N = 20;
Stack<int> a(N);
cout<<"元素依次入栈"<<endl;
for(int i=0; i < N; i++) {
int tmp = rand()%100;
cout<<tmp<<" ";
a.Push(tmp);
}
cout<<endl<<"元素依次出栈"<<endl;
for(int i=0; i < N; i++) {
cout<<a.Top()<<" ";
a.Pop();
}
return 0;
}
3.2.2. 链表实现
栈的链表实现简单且直接,在此省略。
3.3. Queues
队列是只允许在一端(叫做队头 front)删除,在另一端(叫做队尾 rear)插入的线性表。其特点是先进先出(FIFO)。
3.3.1. 队列的数组实现
如果简单地用数组实现队列,则队列的 front 和 rear 可能很快就到达数组尾部了,为解决这个问题,常常用循环数组(Circular Buffer)实现队列,叫做循环队列(Circular Queue)。
循环队列的图示如下:
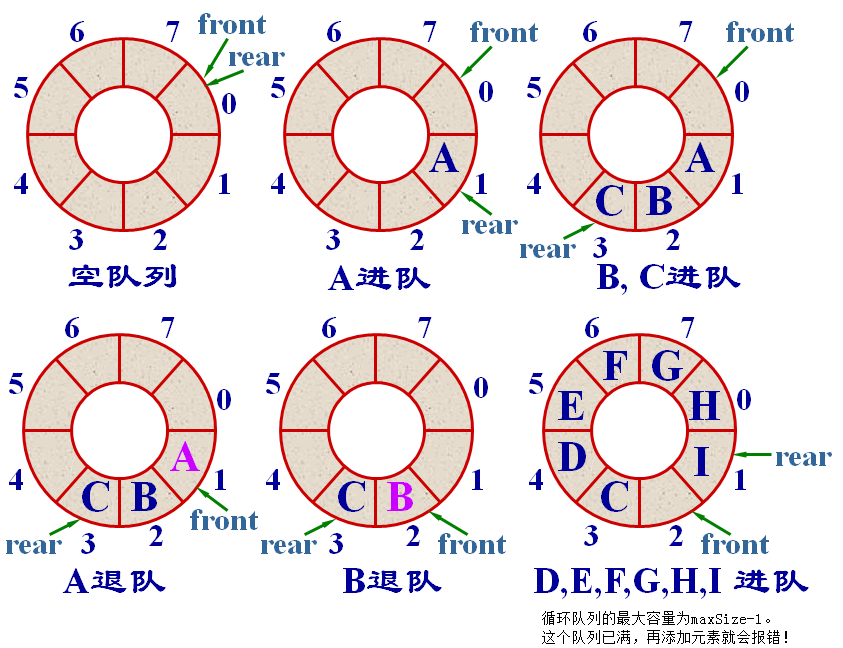
Figure 2: 循环队列
为了便于队空和队满能很好区分,我们不允许队列填满(允许填满的话,队空和队满的条件都为 front==rear,无法区分这两种情况了)!
循环队列的最大容量为 maxSize-1。
3.3.1.1. 循环队列的实现
实现循环队列的关键细节如下:
队头指针进1:front = (front+1) % maxSize; 队尾指针进1:rear = (rear+1) % maxSize; 队空条件:front == rear; 队满条件:(rear+1) % maxSize == front; 队列元素个数:(rear-front+maxSize) % maxSize;
其具体实现可参考《数据结构、算法与应用——C++语言描述》6.2 节。
3.3.1.2. 使循环队列的容量变为 maxSize
循环队列的最大容量为 maxSize-1,如何使循环队列的容量变为 maxSize?
一种可能的办法是增加一个整数变量 counter,初始化为 0,每次向队列中增加一个新项时,counter 就增 1;每次从队列中移动一项时,counter 就减 1。
队空,队满的测试条件改为测试 counter 的值为 0 或 maxSize。
参考:《操作系统概念(第六版),西尔伯查茨》7.1 节。
3.3.2. 队列的链表实现
队列的链表实现简单直接,在此省略。
3.4. Double-Ended Queues
双端队列,它可以在首尾两端进行插入和删除操作,可看作是更通用的 Stacks 或 Queues。
4. Binary Trees and Binary Search Trees
“二叉树”是指每个结点最多两个子结点的树。如果对于二叉树的每个结点 X,它的左子树中的所有关键字值小于 X 的关键字值,而它的右子树中的所有关键字值大于 X 的关键字值,那么这样的二叉树称为“二叉查找树”(或二叉搜索树)。
4.1. 二叉树两种表现形式(leaf trees and node trees)
二叉查找树常用来保存对象,每个对象都有个 key 用来标记对象。
二叉查找树有下面两种表现形式:
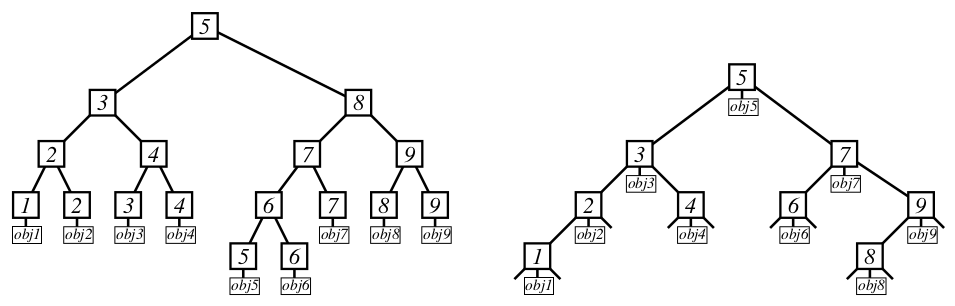
Figure 3: leaf trees and node trees
在第一种形式(leaf trees)的形状更加有规则,其所有的对象保存在叶子结点中。但在描述二叉查找树的书籍中,使用第二种形式(node trees)的更多,这是由于描述简单情况时 key 往往就是对象本身,如果采用第一种形式树中每个 key 都有两份,看起来不自然。本文的实现也采用第二种形式。
Model 2 became the preferred textbook-version, since in most textbooks the distinction between object and its key is not made: the key is the object. Then it becomes unnatural to duplicate the key in the tree structure. But in all real applications, the distinction between key and object is quite important, one almost never wishes to keep track of just a set of numbers, the numbers are normally associated with some further information, which is often much larger than the key itself.
In some literature, where this distinction is made, trees of model 1 are called leaf trees and trees of model 2 are called node trees.
摘自 Advanced Data Structures, by Peter Brass, 2008
4.2. 二叉树的遍历
一般来说,遍历二叉树有三种基本方式:
(1) 先序遍历:先访问节点,再访问左子树,最后访问右子树;
(2) 中序遍历:先访问左子树,再访问节点,最后访问右子树;
(3) 后序遍历:先访问左子树,再访问右子树,最后访问节点。
有两种基本实现手段:一是递归(隐式使用栈);二是迭代(显式地使用栈)。
这两种实现手段都要求 \(O(n)\) 空间。Morris 发明了一种空间要求仅为 \(O(1)\) 的遍历算法(称为 Morris 遍历),这种方法采用了线索二叉树(Threaded binary tree)的思路,可参考:http://www.cnblogs.com/AnnieKim/archive/2013/06/15/MorrisTraversal.html
4.2.1. 二叉树遍历的迭代实现(借助栈)
二叉树三种基本遍历方式的递归实现简单直接,不介绍。这里介绍它们的迭代实现。
4.2.1.1. 先序遍历的迭代版本
借助栈,可以方便地实现二叉树先序遍历的迭代版本。
// 二叉树先序遍历的迭代版本
vector<int> preorderTraversal(TreeNode *root) {
vector<int> result;
stack<TreeNode *> s;
if (root != nullptr)
s.push(root);
while (!s.empty()) {
TreeNode *p = s.top();
result.push_back(p->val);
s.pop();
if (p->right != nullptr) // 右孩子先压栈
s.push(p->right);
if (p->left != nullptr)
s.push(p->left);
}
return result;
}
4.2.1.2. 中序遍历的迭代版本
二叉树中序遍历的迭代版本(比先序遍历迭代版本稍微复杂些)的基本思路:
- 若其左孩子不为空,则将 P 入栈并将 P 的左孩子置为当前的 P,然后对当前结点 P 再进行相同的处理;
- 若其左孩子为空,则取栈顶元素并进行出栈操作,访问该栈顶结点,然后将当前的 P 置为栈顶结点的右孩子;
- 直到 P 为 NULL 并且栈为空则遍历结束。
// 二叉树中序遍历的迭代版本
vector<int> inorderTraversal(TreeNode *root) {
vector<int> result;
stack<TreeNode *> s;
TreeNode *p = root;
while (!s.empty() || p != nullptr) {
if (p != nullptr) {
s.push(p);
p = p->left;
} else {
p = s.top();
result.push_back(p->val);
s.pop();
p = p->right;
}
}
return result;
}
4.2.1.3. 后序遍历的迭代版本
二叉树后序遍历的迭代版本分析如下。考虑二叉树:
1
/ \
2 3
/ \ / \
4 7 5 6
上面二叉树的后序遍历为“4 7 2 5 6 3 1”。其前序遍历(root-left-right)为“1 2 4 7 3 5 6”,如果我们修改前序遍历的顺序为“root-right-left”,则“变种的前序遍历”为“1 3 6 5 2 7 4”,这其实就是后序遍历的“逆序序列”。基于这个思路,我们可以通过修改前序遍历的相关代码得到二叉树后序遍历的迭代版本。
// 二叉树后序遍历的迭代版本
vector<int> preorderTraversal(TreeNode *root) {
vector<int> result;
stack<TreeNode *> s;
if (root != nullptr)
s.push(root);
while (!s.empty()) {
TreeNode *p = s.top();
result.push_back(p->val);
s.pop();
if (p->left != nullptr) // 与前序遍历的不同处之:左孩子先压栈
s.push(p->left);
if (p->right != nullptr)
s.push(p->right);
}
reverse(result.begin(),result.end()); // 与前序遍历的不同处之:多了个栈的逆序操作
return result;
}
说明:尽管 STL 中 stack 提供了 reverse 操作,但它并不是栈的基本操作。如果栈不支持逆序操作,我们可以用两个栈来实现上面的思路,这称为“双栈法”。
// 二叉树后序遍历的迭代版本(双栈法)
vector<int> preorderTraversal(TreeNode *root) {
vector<int> result;
stack<TreeNode *> s1, s2;
if (root != nullptr)
s1.push(root);
while (!s1.empty()) {
TreeNode *p = s1.top();
s1.pop();
s2.push(p);
if (p->left != nullptr)
s1.push(p->left);
if (p->right != nullptr)
s1.push(p->right);
}
while (!s2.empty()) {
result.push_back(s2.top()->val);
s2.pop();
}
return result;
}
4.3. 二叉查找树实现
二叉查找树实现如下:
// 二叉查找树的实现
#include<stdio.h>
#include<stdlib.h>
typedef struct tnode
{
int Element;
struct tnode *Left;
struct tnode *Right;
}TNode;
TNode *Insert( int X, TNode *T )
{
if( T == NULL ) {
/* Create and return a one-node tree */
T = malloc( sizeof( TNode ) );
if( T == NULL )
printf( "Out of space!!!" );
else {
T->Element = X;
T->Left = T->Right = NULL;
}
} else if( X < T->Element ) {
T->Left = Insert( X, T->Left );
} else if( X > T->Element )
T->Right = Insert( X, T->Right );
/* Else X is in the tree already; we'll do nothing */
return T; /* Do not forget this line!! */
}
TNode *Find( int X, TNode *T )
{
if( T == NULL )
return NULL;
if( X < T->Element )
return Find( X, T->Left );
else if( X > T->Element )
return Find( X, T->Right );
else
return T;
}
TNode *FindMin( TNode *T )
{
if( T == NULL )
return NULL;
else if( T->Left == NULL )
return T;
else
return FindMin( T->Left );
}
/* 采用替换右子树的最小结点。 */
TNode *Delete( int X, TNode *T )
{
TNode *TmpCell;
if( T == NULL ) {
printf( "Element not found" );
return NULL;
}
if( X < T->Element ) /* Go left */
T->Left = Delete( X, T->Left );
else if( X > T->Element ) /* Go right */
T->Right = Delete( X, T->Right );
else { /* Found element to be deleted */
if( T->Left && T->Right ) { /* Two children */
/* Replace with smallest in right subtree */
TmpCell = FindMin( T->Right );
T->Element = TmpCell->Element;
T->Right = Delete( T->Element, T->Right );
} else { /* One or zero children */
TmpCell = T;
if( T->Left == NULL ) /* Also handles 0 children */
T = T->Right;
else if( T->Right == NULL )
T = T->Left;
free( TmpCell );
}
}
return T;
}
Delete 操作的两种方式:
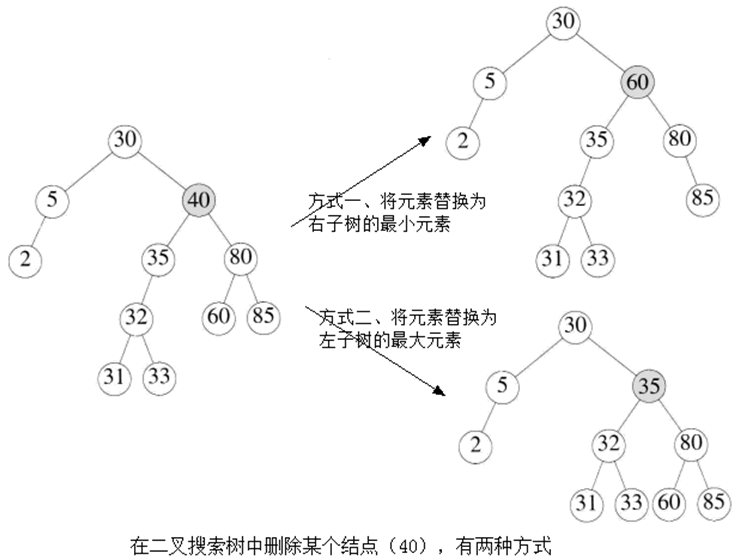
Figure 4: 二叉查找树中进行 Delete 操作的两种方式
注 1:这种删除操作的效率并不高,因为它沿该树进行两趟搜索以查找和删除右了树的最小元素(或左子树的最大元素)。
注 2:上面实现的 Delete 采用的是替换右子树的最小结点。很多次这样的操作过后,会使树的左子树比右子树深度深。如果采用的是替换左子树的最大结点,则可能会使树的右子树比左子树深度深。
4.4. 二叉查找树的 Merge 操作
思路:
- Flatten trees into sorted lists.
- Merge sorted lists.
- Create tree out of merged list.
参考:
http://stackoverflow.com/questions/1008513/how-to-merge-two-bsts-efficiently
4.5. Tournament Tree(竞赛树)
竞赛树可解决下面问题:
Given a team of N players. How many minimum games are required to find second best player?
参考:
http://www.geeksforgeeks.org/tournament-tree-and-binary-heap/
http://www.cise.ufl.edu/~sahni/cop3530/slides/lec252.pdf
Data Structures, Algorithms, and Applications in C++(Sartaj Sahni), Chapter 10.
5. Balanced Search Trees
二叉查找树是基础性的数据结构,本节介绍一些改进版的二叉查找树,它们具有更好的查询效率。 常使用这些改进的二叉查找树构建一些更为抽象的数据结构,如 Set、Multiset、Associative Array(Map)等等。
5.1. AVL Trees
AVL 树是每个节点的左子树和右子树的高度最多差 1 的二叉树。
它是 1962 年俄国的两个数学家 G.M.Adelson-Velsky 和 E.M.Landis 发明的(AV 代表 Adelson-Velsky,而 L 代表 Landis)。
5.1.1. 最小 AVL 树的高度和节点数关系
所谓最小 AVL 树,是指高度一定时其节点数最少的 AVL 树。
定义只有一个根节点的树的高度为 1(有的书上定义这种情况的高度为 0)。
图 5 是高度为 10 的最小的 AVL 树(143 个结点)。
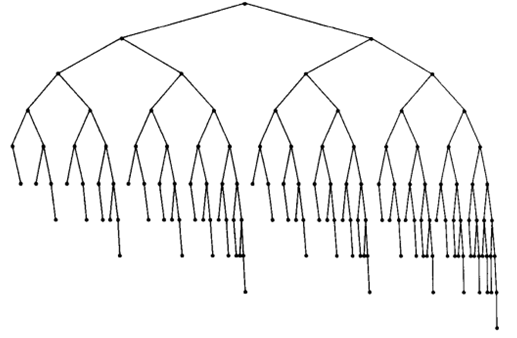
Figure 5: 高度为 10 的最小的 AVL 树(143 个结点)
它的左子树是高度为 8 的最小 AVL 树,右子树是高度为 9 的最小 AVL 树。
定义高度为 h 的最小 AVL 树的结点个数为 \(N(h)\) ,则显然有:
\[N(h) = N(h-1) + N(h-2) + 1, N(0) = 0, N(1) = 1\]
这与斐波纳契数: \(F(h) = F(h-1) + F(h-2), F(0) = 0, F(1) = 1\) ,非常地相似。
容易用归纳法证明: \(N(h) = F(h+2) - 1, h≥0\)
再利用斐波纳契数的性质可以得到:
\[h < 1.44 \log_{2} (n+2) - 0.328\]
其推导过程可参考《计算机程序设计艺术——第 3 卷排序与查找(第 2 版)》第 6.2.3 节。
由结论 \(h < 1.44 \log_{2} (n+2) - 0.328\) 容易得到:\(n>2^{\frac{h+0.328}{1.44}}-2\)
我们用它来验证一下高度为 10 的最小 AVL 的结点数:\(2^{\frac{10+0.328}{1.44}}-2 = 142.23\) ,所以 n 为 143,与前面图中所示一致。
5.1.1.1. 满二叉树/完全二叉树高度和节点数关系
满二叉树(Full Binary Tree)如下图所示:
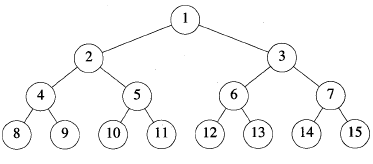
Figure 6: 高度为 4 的满二叉树
由归纳法容易得到,高度为 h 的满二叉树的节点数为: \(n=2^{h}-1\) ,所以有: \(h = \log_{2} (n+1)\)
还有一个概念是完全二叉树(complete binary tree),它不一定是满的。
完全二叉树满足两个条件: 先填充上层节点再填下层节点!先填充左孩子再填充右孩子!
显然,完全二叉树高度和节点数的关系为: \(h >= \log_{2} (n+1)\)
5.1.2. AVL 树的插入分析
参考:《数据结构与算法分析——C 语言描述(原书第 2 版)》4.4 节。
简单地往 AVL 树中插入一个节点,可能导致插入后的树不满足 AVL 性质(不再平衡)。
插入后,只有那些从插入点到根节点的路径上的节点的平衡可能被改变,这是由于只有这些节点的子树可能发生变化。当我们沿着这条路径上行到根并更新平衡信息时,我们可以找到一个节点,它的新平衡破坏了 AVL 条件。
假设 a 是从插入节点到根的路径上第一个不平衡的节点。那么 a 节点的两个子树的高度差为 2,这有四种情况:
情形 1. 对 a 的左儿子的左子树进行了一次插入;
情形 2. 对 a 的左儿子的右子树进行了一次插入;
情形 3. 对 a 的右儿子的左子树进行了一次插入;
情形 4. 对 a 的右儿子的右子树进行了一次插入。
情形 1 和情形 4 是关于 a 点镜像对称,情形 2 和情形 3 是关于 a 点镜像对称。
5.1.2.1. Single Rotation
情形 1 和情形 4 可以通过单旋转实现重新平衡。
假设 k2 是从插入节点到根的路径上第一个不平衡的节点。
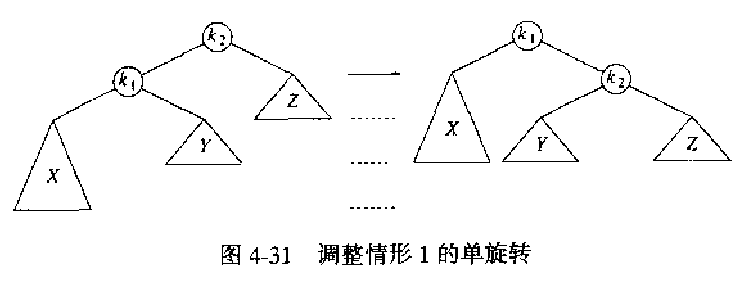
Figure 7: 调整情形 1 的单旋转
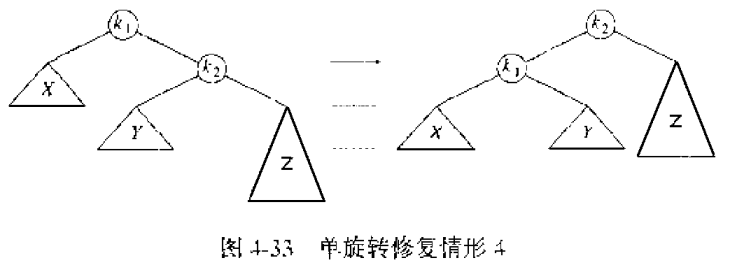
Figure 8: 调整情形 4 的单旋转
5.1.2.2. Double Rotation
一次单旋转并不能重新平衡情形 2 和情形 3。
下图所示在旋转后还是没有平衡。
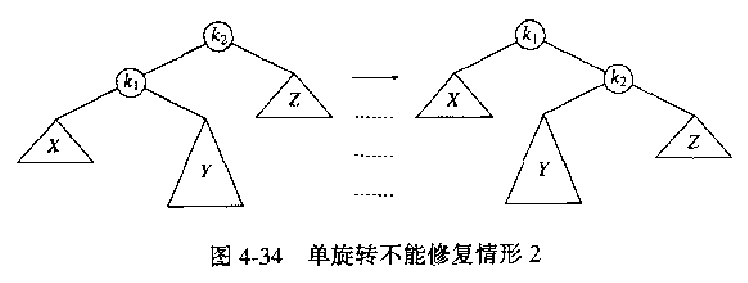
Figure 9: 单旋转不能修复情形 2
情形 2 和情形 3 需要通过双旋转实现重新平衡。
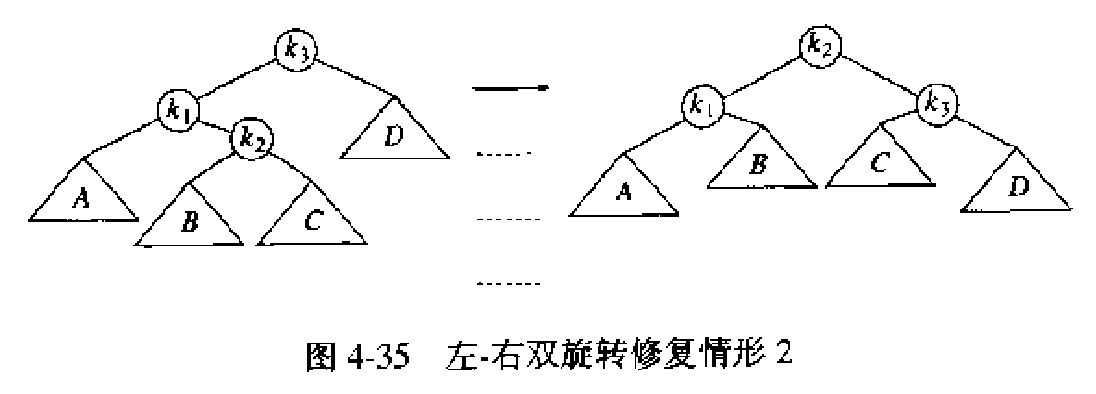
Figure 10: 双旋转修复情形 2
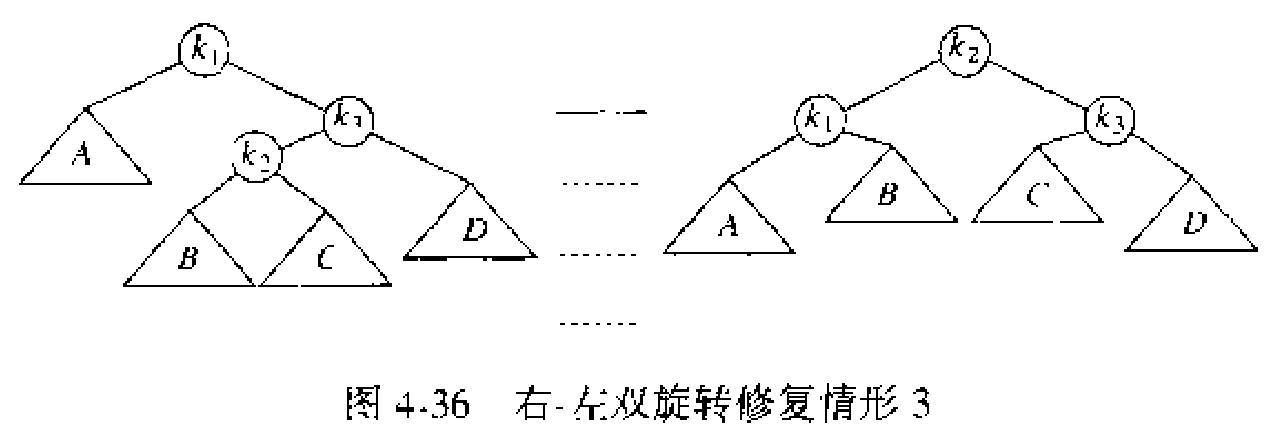
Figure 11: 双旋转修复情形 3
5.1.2.3. 用两次单旋转实现双旋转
双旋转可以用再次单旋转实现,当然效率没有直接实现双旋转快,只是编程简单些。
以修复情形 2 的双旋转为例:
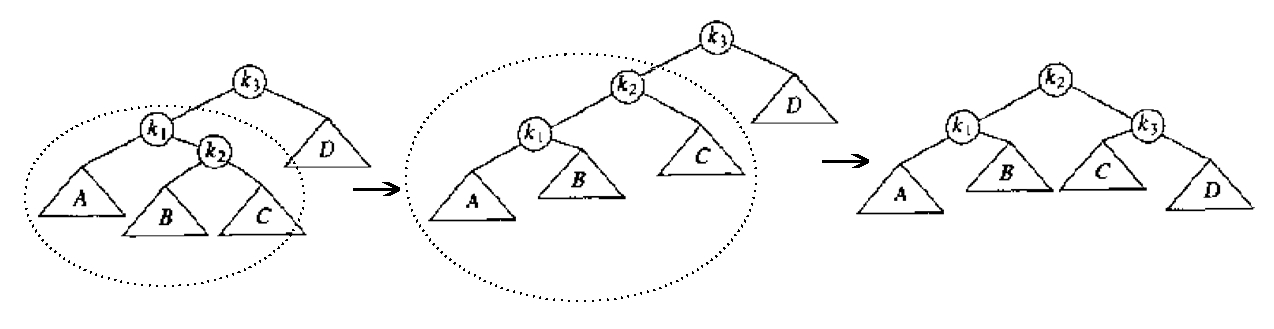
Figure 12: 用两次单旋转修复情形 2
5.1.3. AVL 插入的实现
参考:《数据结构与算法分析——C 语言描述(原书第 2 版)》4.4 节。
#include <stdlib.h>
#include<stdio.h>
typedef int ElementType;
struct AvlNode
{
ElementType Element;
struct AvlNode *Left;
struct AvlNode *Right;
int Height;
};
typedef struct AvlNode *AvlTree;
int Height( AvlTree P )
{
if( P == NULL )
return -1;
else
return P->Height;
}
int Max( int Lhs, int Rhs )
{
return Lhs > Rhs ? Lhs : Rhs;
}
/* This function can be called only if K2 has a left child */
/* Perform a rotate between a node (K2) and its left child */
/* Update heights, then return new root */
AvlTree SingleRotateWithLeft( AvlTree K2 )
{
AvlTree K1;
K1 = K2->Left;
K2->Left = K1->Right;
K1->Right = K2;
K2->Height = Max( Height( K2->Left ), Height( K2->Right ) ) + 1;
K1->Height = Max( Height( K1->Left ), K2->Height ) + 1;
return K1; /* New root */
}
/* This function can be called only if K1 has a right child */
/* Perform a rotate between a node (K1) and its right child */
/* Update heights, then return new root */
AvlTree SingleRotateWithRight( AvlTree K1 )
{
AvlTree K2;
K2 = K1->Right;
K1->Right = K2->Left;
K2->Left = K1;
K1->Height = Max( Height( K1->Left ), Height( K1->Right ) ) + 1;
K2->Height = Max( Height( K2->Right ), K1->Height ) + 1;
return K2; /* New root */
}
/* This function can be called only if K3 has a left */
/* child and K3's left child has a right child */
/* Do the left-right double rotation */
/* Update heights, then return new root */
AvlTree DoubleRotateWithLeft( AvlTree K3 )
{
/* Rotate between K1 and K2 */
K3->Left = SingleRotateWithRight( K3->Left );
/* Rotate between K3 and K2 */
return SingleRotateWithLeft( K3 );
}
/* This function can be called only if K1 has a right */
/* child and K1's right child has a left child */
/* Do the right-left double rotation */
/* Update heights, then return new root */
AvlTree DoubleRotateWithRight( AvlTree K1 )
{
/* Rotate between K3 and K2 */
K1->Right = SingleRotateWithLeft( K1->Right );
/* Rotate between K1 and K2 */
return SingleRotateWithRight( K1 );
}
AvlTree Insert( ElementType X, AvlTree T )
{
if( T == NULL ) {
/* Create and return a one-node tree */
T = malloc( sizeof( struct AvlNode ) );
if( T == NULL )
//FatalError( "Out of space!!!" );
printf("Out of space!!!" );
else {
T->Element = X; T->Height = 0;
T->Left = T->Right = NULL;
}
}
else if( X < T->Element ) {
T->Left = Insert( X, T->Left );
if( Height( T->Left ) - Height( T->Right ) == 2 )
if( X < T->Left->Element )
T = SingleRotateWithLeft( T );
else
T = DoubleRotateWithLeft( T );
}
else if( X > T->Element ) {
T->Right = Insert( X, T->Right );
if( Height( T->Right ) - Height( T->Left ) == 2 )
if( X > T->Right->Element )
T = SingleRotateWithRight( T );
else
T = DoubleRotateWithRight( T );
}
/* Else X is in the tree already; we'll do nothing */
T->Height = Max( Height( T->Left ), Height( T->Right ) ) + 1;
return T;
}
直接实现双旋转(不用两次单旋转)
摘自:《数据结构与算法分析——C 语言描述(原书第 2 版)》习题 4.22。
/* This function can be called only if K3 has a left */
/* child and K3's left child has a right child */
/* Do the left-right double rotation */
/* Update heights, then return new root */
AvlTree DoubleRotateWithLeft( AvlTree K3 )
{
AvlTree K1, K2;
K1 = K3->Left;
K2 = K1->Right;
K1->Right = K2->Left;
K3->Left = K2->Right;
K2->Left = K1;
K2->Right = K3;
K1->Height = Max( Height(K1->Left), Height(K1->Right) ) + 1;
K3->Height = Max( Height(K3->Left), Height(K3->Right) ) + 1;
K2->Height = Max( K1->Height, K3->Height ) + 1;
return K2;
}
5.1.4. AVL 删除分析
AVL 树的删除操作相对比较复杂,这里不进行介绍。如果删除操作比较少,可以采用惰性删除策略。
5.2. Splay Trees
A splay tree is a self-adjusting binary search tree with the additional property that recently accessed elements are quick to access again.
5.2.1. 3 种旋转
伸展树的基本思想是,当一个节点被访问后,它要经过一系列旋转被放到根处(如果节点不存在,和访问节点最接近的节点被放在根处)。
伸展树定义了 3 种旋转(注意:各还有一个对称情况未示出):
情形 1(zig case):如果访问节点 X 的父节点是根(没有祖父节点),进行如图 13 所示旋转(AVL 单旋转)。

Figure 13: zig case (Splay Trees)
情形 2(zig-zag case):如果访问节点 X 有祖父节点,且 X 和父节点 P 和祖父节点 G 是之字形,则进行如图 14 所示旋转(AVL 双旋转)。
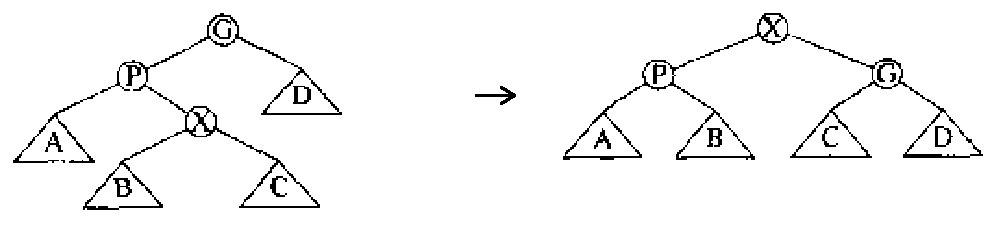
Figure 14: zig-zag case (Splay Trees)
情形 3(zig-zig case):如果访问节点 X 有祖父节点,且 X 和父节点 P 和祖父节点 G 是一字形,则进行如图 15 所示旋转(可称作一字形旋转)。
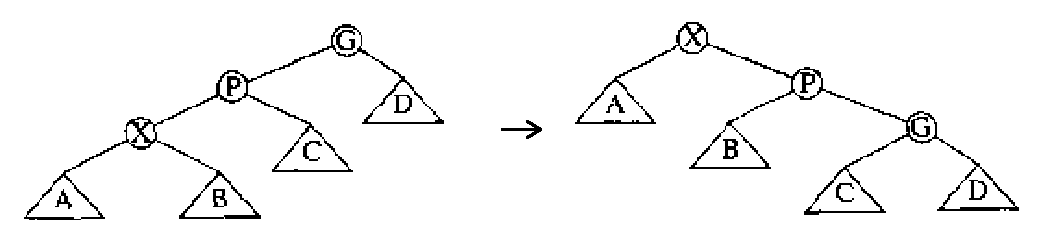
Figure 15: zig-zig case (Splay Trees)
情形 2 和情形 3 可能多次进行,直到把访问节点推向树根。
注:zig 表示‘/’,zag 表示‘\’。
5.2.2. 伸展树的说明
要保证当一个节点被访问后,它要被放到树根处的方法有很多,如多次采用 AVL 单旋转就可以把访问节点推向树根,但是这种方法确不能保证 \(O(logN)\) 的摊还时间界!可参考:《数据结构与算法分析——C 语言描述(原书第 2 版)》4.5.1 节。
伸展树的摊还时间界为 \(O(logN)\) 。它的证明比较麻烦。其证明可参考:《数据结构与算法分析——C 语言描述(原书第 2 版)》11.5 节。
伸展树基于这样一个事实:对于二叉查找树来说,每次操作最坏情形时间 \(O(N)\) 并不坏,只要它相对不常发生就行。如果特定操作可以有最坏时间界 \(O(N)\) ,而我们仍然要求一个 \(O(logN)\) 的摊还时间,那么只要一个节点被访问,它就必须被移动。否则,一旦我们发现一个深层的节点访问花费 \(O(N)\) ,我们就有可能不断对它进行访问操作,那么 \(M\) 次访问将花费 \(O(MN)\) 的时间。
伸展树有个优点是不需要记录用于平衡树的冗余信息。
伸展树还有个特点:被访问频率高的那些节点经常处于靠近树根的位置,访问它们会更快!所以它是一种 Self-adjusting data structures。
伸展操作在将访问节点移动到根处的同时,还能把访问路径上的大部分节点的深度大致减少一半(某些浅节点最多向下推后两层)。
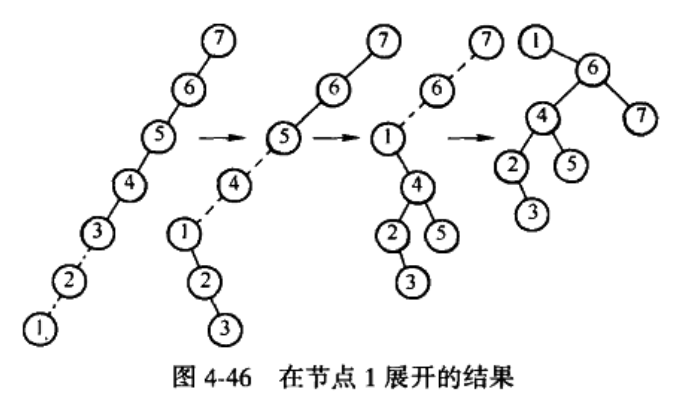
Figure 16: 伸展树在移动节点到根处的同时能减少其它节点的深度
前面定义的 Splay tree 又称为 Bottom-up 伸展树。
直接实现需 Bottom-up 伸展树要从根沿树往下的一次遍历(查找),以及从底向上的一次遍历(Splay)。这可能通过保存一些父指针来完成,或者通过将访问路径存在一个栈中来完成。但两种方法都需要大量的开销,且需要处理很多特殊的情况。
用父指针的实现可参考:http://www.cnblogs.com/vamei/archive/2013/03/24/2976545.html
用栈的实现可参考:Advanced Data Structures, by Peter Brass, 2008. Section 3.8
下文将介绍一个伸展树的变种,它的实现更简单。
5.2.3. Top-down splay tree
在自顶向下的伸展树中,我们沿着树向下(每次下降两个节点)搜索某个节点 X 时,将搜索路径上的其它节点及其子树移走(移走的策略下面将介绍),构建两个临时树左树和右树:左树保存着小于 X 的节点;右树保存着大于 X 的节点。没有被移走的节点及其子树构成中树。最后,在查找到节点后,将三棵树重新组合为一个树(以中树的根作为新树的根)。
移走的策略如下:
每次下降两个节点时,只有两种情况(省略对称的情况):一字形和之字形。
情况一(zig-zig,一字形)的策略,先旋转后再移到右树:
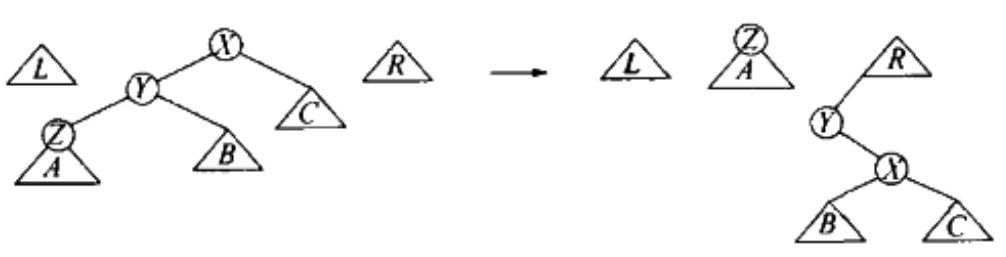
Figure 17: zig-zig (Top-down splay tree)
情况二(zig-zag,之字形)的策略,无旋转,分别移到左右树:
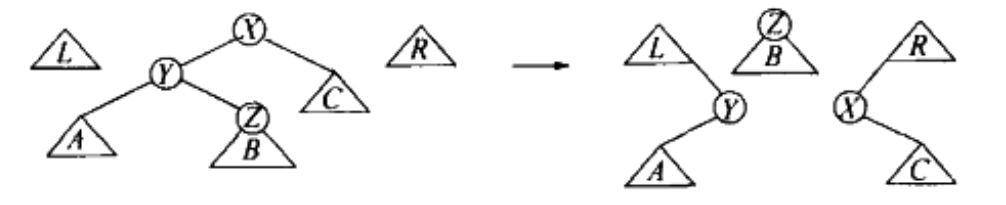
Figure 18: zig-zag (Top-down splay tree)
当然,还有下面情况:不够下降两个节点就已找到搜索节点或已经下降到叶节点。
情况三(zig,只下降一个节点),无旋转,移到右树:
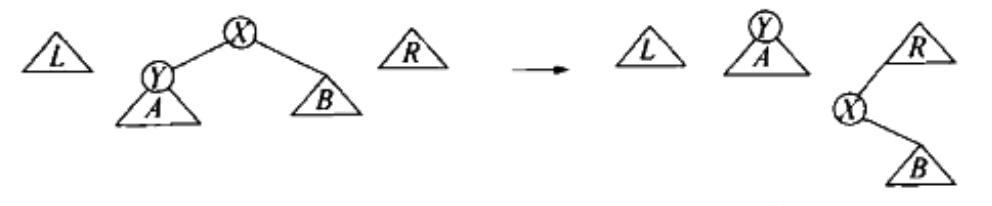
Figure 19: zig (Top-down splay tree)
三棵树重新组合为一个树的过程:
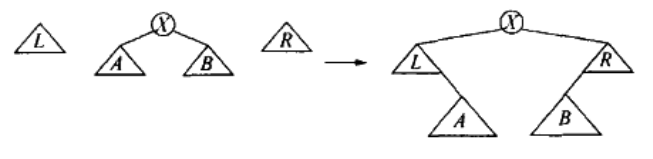
Figure 20: reassembling (Top-down splay tree)
说明:
对情况二可以通过应用两次情况三的策略来达到相同的结果。所以可以认为只有两种情况:情况一和情况三。
总结:实现自顶向下伸展树时,每次下降两个节点,当发现 zig-zig 或 zag-zag 时,需要先旋转,其它情况直接移到左树或右树即可!
5.2.4. Top-down splay tree 说明
对情况一(zig-zig)应用两次情况三(zig)的策略会得到:
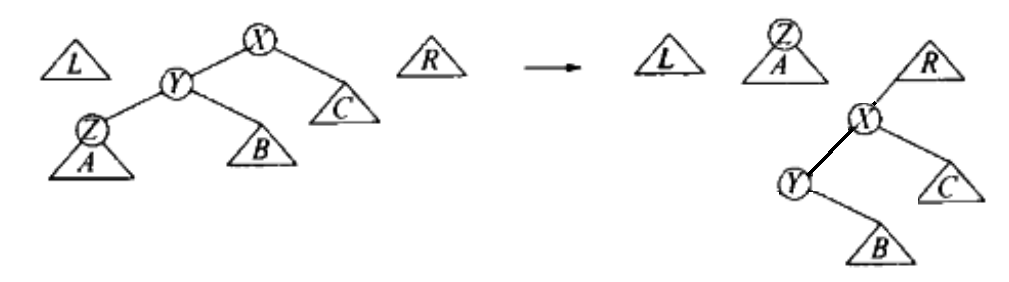
Figure 21: 两次应用情况三的策略来处理 zig-zig
上面的结果和情况一策略得到的结果不同。
为什么我们不选择“两次应用情况三的策略来处理 zig-zig”呢,它在编程实现时只有一种情况会更简单。
之所以不采用这个策略,是因为它无法保证摊还时间界。
其证明比较复杂,我们从简单的实例来说明“两次应用情况三的策略来处理 zig-zig”比情况一的策略差(不利于降低树的高度)。在下面树中查看节点 1 的过程:
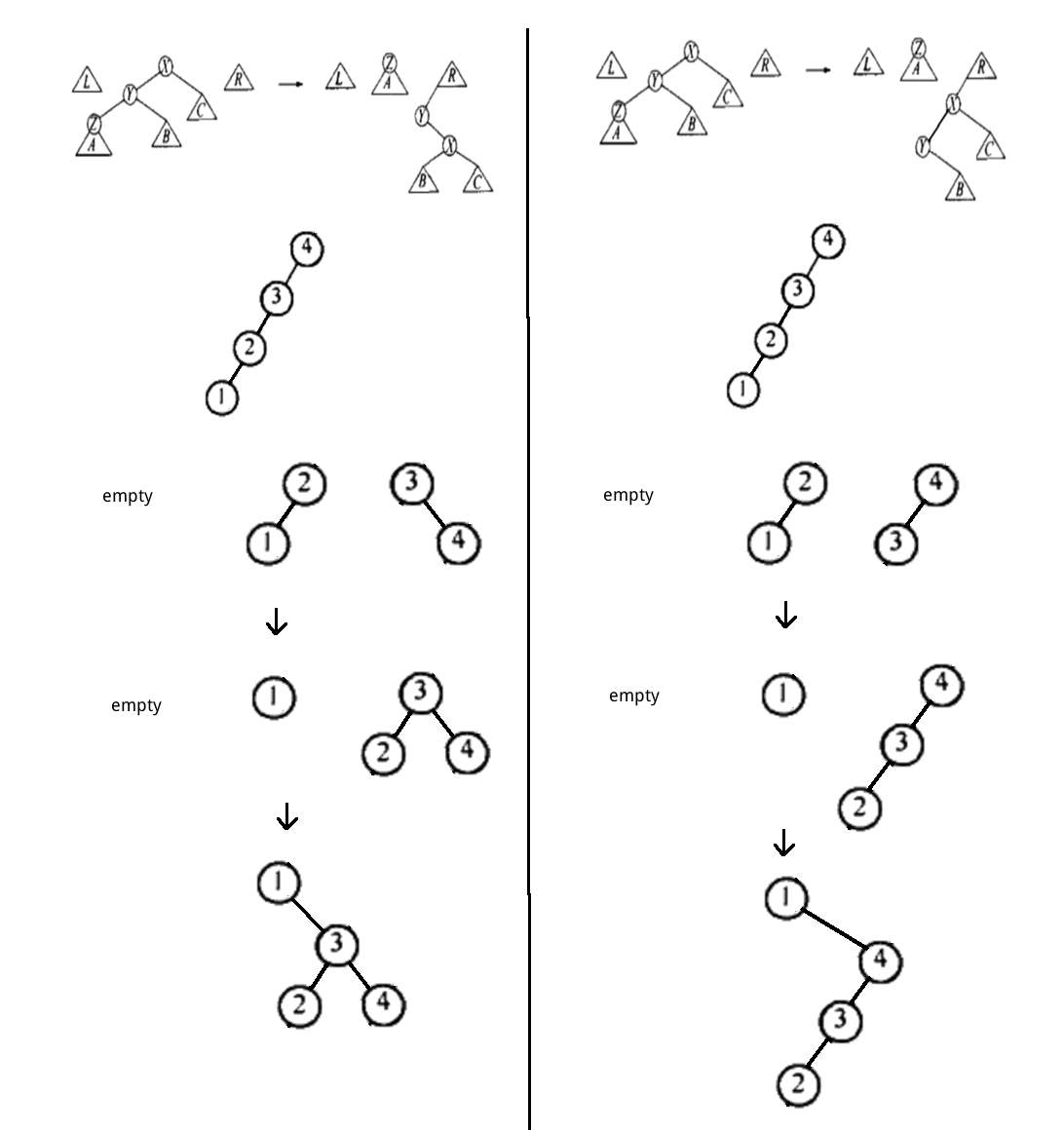
Figure 22: 处理 zig-zig 的两种方法(左过方法更好)
在上面的实例中,右边是“两次应用情况三的策略来处理 zig-zig”。左边是直接用情况一的策略,要求旋转后再移到右树,这使得右树的左子树为空,由于下次移动节点到右树时总是移到左子树,所以有得于整个右树的高度更低,最后得到的树的高度也更低。
5.2.5. Top-down 和 bottom-up splay trees 的区别
Top-down splay trees 和 bottom-up splay trees 的形状可能不一样!它们的摊还时间界都是 \(O(logN)\) 。 参考《数据结构与算法分析——C 语言描述(原书第 2 版)》习题 12.1
Top-down splay trees are another way of implementing splay trees. Both the trees coincide if the node being searched is at an even depth , but if the item being searched is at an odd depth, then the top-down and bottom-up trees may differ.
参考:Handbook of Data Structures and Applications, Dinesh P. Mehta and Sartaj Sahni, 2005, section 12.9.
5.2.6. Top-down splay tree 实现
参考:http://www.cnblogs.com/UnGeek/archive/2013/04/10/3013333.html
//refers to:http://www.link.cs.cmu.edu/link/ftp-site/splaying/top-down-splay.c
/*
An implementation of top-down splaying
D. Sleator <sleator@cs.cmu.edu>
March 1992
*/
#include <stdlib.h>
#include <stdio.h>
int size; /* number of nodes in the tree */
/* Not actually needed for any of the operations */
typedef struct tree_node Tree;
struct tree_node
{
Tree * left, * right;
int item;
};
//在splay的实现中,在最后重新组装前,N.left和N.right分别指着右树和左树的根。
//在for循环中,l,r并不是指着左树和右树根,它们分别指着左树的最大节点和右树的最小节点。
Tree * splay (int i, Tree * t)
{
/* Simple top down splay, not requiring i to be in the tree t. */
Tree N, *l, *r, *y;
if (t == NULL)
return t;
N.left = N.right = NULL;
l = r = &N;
for (;;) {
if (i < t->item) {
if (t->left == NULL) {
break;
}
if (i < t->left->item) { /* zig-zig case */
y = t->left; /* rotate right */
t->left = y->right;
y->right = t;
t = y;
if (t->left == NULL) {
break;
}
}
r->left = t; /* link right */
r = t;
t = t->left;
} else if (i > t->item) {
if (t->right == NULL) {
break;
}
if (i > t->right->item) { /* zag-zag case */
y = t->right; /* rotate left */
t->right = y->left;
y->left = t;
t = y;
if (t->right == NULL) {
break;
}
}
l->right = t; /* link left */
l = t;
t = t->right;
} else {
break;
}
}
l->right = t->left; /* assemble */
r->left = t->right;
t->left = N.right;
t->right = N.left;
return t;
}
Tree * insert(int i, Tree * t)
{
/* Insert i into the tree t, unless it's already there. */
/* Return a pointer to the resulting tree. */
Tree * new;
new = (Tree *) malloc (sizeof (Tree));
if (new == NULL) {
printf("Ran out of space\n");
exit(1);
}
new->item = i;
if (t == NULL) {
new->left = new->right = NULL;
size = 1;
return new;
}
t = splay(i,t);
if (i < t->item) {
new->left = t->left;
new->right = t;
t->left = NULL;
size ++;
return new;
} else if (i > t->item) {
new->right = t->right;
new->left = t;
t->right = NULL;
size++;
return new;
} else {
/* We get here if it's already in the tree */
free(new);
return t;
}
}
Tree * delete(int i, Tree * t)
{
/* Deletes i from the tree if it's there. */
/* Return a pointer to the resulting tree. */
Tree * x;
if (t==NULL) {
return NULL;
}
t = splay(i,t);
if (i == t->item) { /* found it */
if (t->left == NULL) {
x = t->right;
} else {
x = splay(i, t->left);
x->right = t->right;
}
size--;
free(t);
return x;
}
return t; /* It wasn't there */
}
int main(int argv, char *argc[])
{
/* A sample use of these functions. Start with the empty tree, */
/* insert some stuff into it, and then delete it */
Tree * root;
int i;
root = NULL; /* the empty tree */
size = 0;
for (i = 0; i < 1024; i++) {
root = insert((541*i) & (1023), root);
}
printf("size = %d\n", size);
for (i = 0; i < 1024; i++) {
root = delete((541*i) & (1023), root);
}
printf("size = %d\n", size);
}
上面的实现没有 find 函数,其实 find 就是 splay,只是 splay 在失败后返回最接近的节点。
5.3. Red-Black Trees
红黑树是二叉搜索树,它的每个节点要么是红色,要么是黑色,同时具有下列性质:
- 根节点是黑色;
- 没有两个连续的红色节点;
- 对每个节点,从该节点到其子孙节点的所有路径上包含相同数目的黑节点。
注:为什么取个红黑树的名字?
The color "red" was chosen because it was the best-looking color produced by the color laser printer available to the authors while working at Xerox PARC.
红黑树还有另外一种表示形式——颜色标记在链接(指针)上。
如下图,用细线表示黑色链接,用粗线表示红色链接。
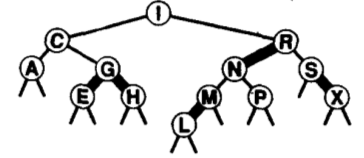
Figure 23: 红黑树的另一种表示形式——颜色标记在链接(指针)上
这种表达方式和用节点颜色是一致的:父指针的颜色对应当前节点的颜色。
注:红黑树的定义一般采用结点颜色形式的定义,指针颜色这种形式的定义也经常出现在名著中,如:Robert Sedgewick 的《C 算法(第一卷基础、数据结构、排序和搜索)(第三版)》13.4 节和 Sartaj Sahni 的《数据结构、算法与应用——C++语言描述》11.3 节。
5.3.1. 自底向上插入分析
把一个新节点作为树叶插入到一个非空的红黑树中,如果新节点涂成黑色,则一定会违反性质 3,因为它将会生成一条更长的黑节点的路径。
所以,新插入的节点如果不是根节点,我们把它涂成红色。显然,这可能违反性质 2,我们通过颜色的改变和树的旋转来使其重新满足红黑树的性质。
如果父节点是黑色,则插入一个红色节点不会违反性质 2,插入完成。
如果父节点是红色(那么祖父节点必然是黑色),我们分情况来讨论(两个圈的节点为红色节点,G:祖父节点,P:父节点,S:叔节点,X:插入节点):
情况一(简单):叔节点为黑色,插入节点、父节点、祖父节点为一字形(对称情况未示出)。
通过下面的旋转和改变颜色可恢复红黑树的性质:
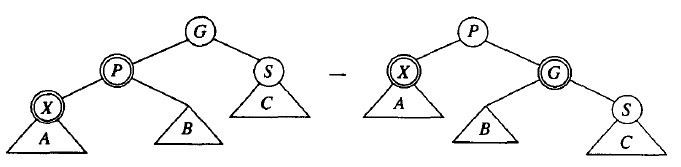
Figure 24: 红黑树旋转和变色(叔节点为黑色,插入节点、父节点、祖父节点为一字形)
情况二(简单):叔节点为黑色,插入节点、父节点、祖父节点为之字形(对称情况未示出)。
通过下面的旋转和改变颜色可恢复红黑树的性质:
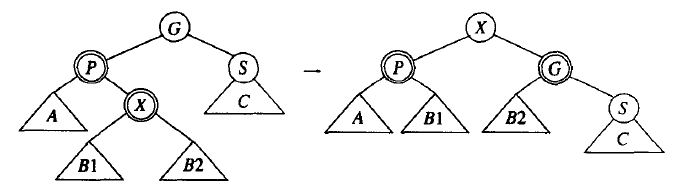
Figure 25: 红黑树旋转和变色(叔节点为黑色,插入节点、父节点、祖父节点为之字形)
情况三(复杂):叔节点为红色(无需区分插入节点、父节点、祖父节点为一字形还是之字形,调整都是一样的)。
通过只改变颜色,可以同时满足性质 2 和性质 3,但它把祖父节点的颜色改成了红色,这样如果曾祖也是红色,那么这个调整的过程并没有结束,还得朝着根的方向上滤,直到不再有两个相连的红色节点或者到达根处为止。
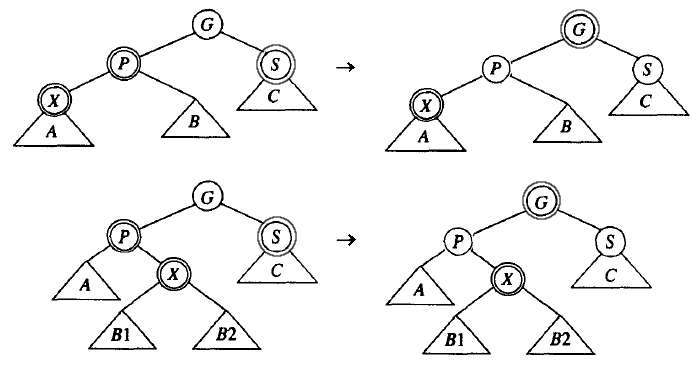
Figure 26: 红黑树变色(叔节点为红色)
注:何必还需要上滤这么麻烦呢,因为这种情况下,无法在不改变祖父节点的颜色前提下,通过旋转和改变颜色同时满足性质 2 和性质 3,一旦改变祖父节点的颜色就可能破坏“没有两个连续的红色节点”的性质,所以需要上滤。
5.3.2. 红黑树删除分析
略
5.3.3. 红黑树实现
略
5.3.4. 2-3-4 树
2-3-4 树是多叉树,它有三种结点类型:
2-node:1 个关键字,2个孩子;
3-node:2 个关键字,3个孩子;
4-node:3 个关键字,4个孩子。
下图是 2-3-4 树(我们说 2-3-4 树一般就是指 2-3-4 搜索树)的一个例子:
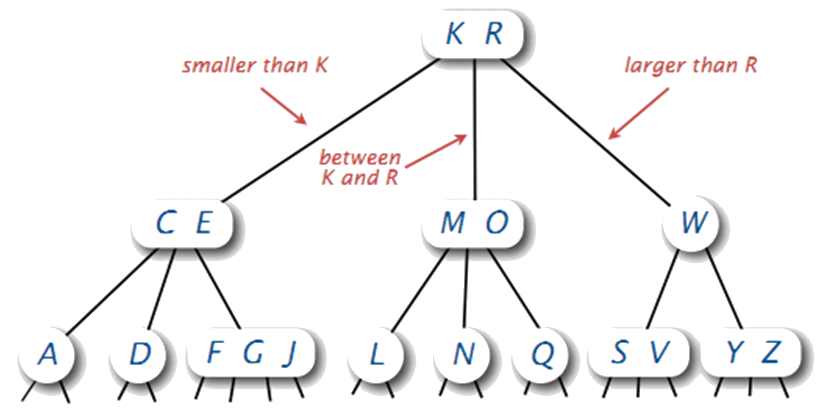
Figure 27: 2-3-4 搜索树实例
参考:C算法(第一卷 基础、数据结构、排序和搜索)(第三版)(Robert Sedgewick 著)
5.3.5. 2-3-4 树的插入分析(Bottom-up solution)
新节点一般插入到叶子节点中,先找到插入位置。
如果它是一个 2-node,把它转换为 3-node,加入新节点;
如果它是一个 3-node,把它转换为 4-node,加入新节点;
如果它是一个 4-node,则先把 4-node 分解为 2 个 2-node,将中间关键字上传到节点的父亲,剩下的 2 个关键字分别是 2 个 2-node 的关键字(现在可以直接插入了)。但如果节点父亲也是一个 4-node,它无法容纳上传的节点,则还需要一直往上分解。
下图演示在图中 2-3-4 树中插入节点 H 的过程:
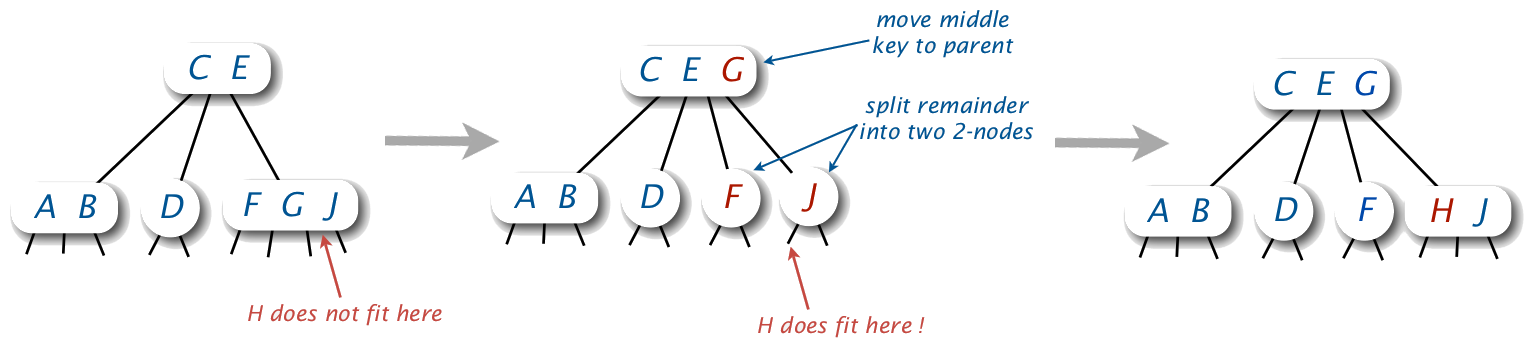
Figure 28: 2-3-4 树中插入节点的实例
5.3.6. 2-3-4 树的插入分析(Top-down solution)
在寻找插入位置的路径(Top-down 过程)上,发现有 4-node 就提前把它分解。这样,最后找到的插入位置不会是 4-node,路径上也不会出现连续两个 4-node。
伪代码如下:
// fantasy code
private void insert(Key key, Val val)
{
Node x = root;
while (x.getTheCorrectChild(key) != null)
{
x = x.getTheCorrectChild(key);
if (x.is4Node()) x.split();
}
if (x.is2Node()) x.make3Node(key, val);
else if (x.is3Node()) x.make4Node(key, val);
return x;
}
5.3.7. 红黑树是 2-3-4 树的二叉树表现形式
2-3-4 树的实现比较麻烦,需要维护不同类型的结点等。如果能统一节点就好了。
红黑树其实是 2-3-4 树的二叉树表现形式。它按如下方式把 3-node 和 4-node 统一为 2-node,其中内部链接用红色表示:

Figure 29: 红黑树是 2-3-4 树的二叉树表现形式(3-node 和 4-node 统一为 2-node)
红黑树结合 2-3-4 树和二叉树两者的优点:二叉搜索树的简单搜索过程,2-3-4 搜索树的简单插入平衡过程。
红黑树性能比较好的原因就在于对树重新平衡的工作量比较少: 只有当 4-node 时(叔节点为红色)需要采取平衡措施。
5.3.8. 红黑树变种:左斜红黑树(Left-leaning red-black tree)
Sedgewick 教授(他也是红黑树的发明人之一)在 2008 年发明了实现起来相对简单的左斜红黑树。
左斜红黑树简化了 red-black tree 的实现,代码相对变得简洁。
所谓 Left-leaning red-black tree 就是统一 2-3-4 树中 3-结点的两种转换形式为左斜形式:
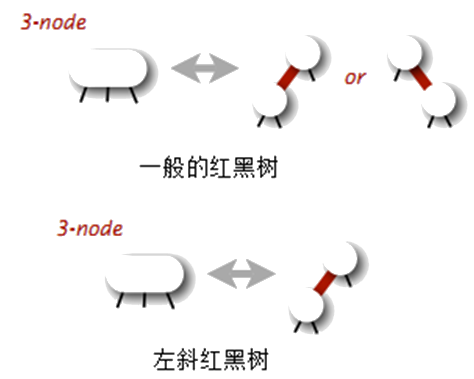
Figure 30: 左斜红黑树统一了 2-3-4 树中 3-结点的两种转换形式
显然,2-3-4 树到左斜红黑树的转换是唯一的,如下面例子:

Figure 31: 2-3-4 树可唯一地转换为左斜红黑树
参考:
http://en.wikipedia.org/wiki/Left-leaning_red%E2%80%93black_tree
http://www.cs.princeton.edu/~rs/talks/LLRB/LLRB.pdf
http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf
但也有专家认为左倾红黑树的实现没简单多少,性能不如红黑树。详情可参考:Left-Leaning Red-Black Trees Considered Harmful
5.4. AA Trees (a variation of the Red-Black tree)
AA trees are a variation of the red-black tree, a form of binary search tree which supports efficient addition and deletion of entries. Unlike red-black trees, red nodes on an AA tree can only be added as a right subchild. In other words, no red node can be a left sub-child.
AA 树在红黑树上增加了下面限制:红色结点只能出现在右孩子中。因此它没有两个孩子都是红节点的情况(4-node),所以它模拟是的 2-3 树,而不是 2-3-4 树。
AA 树是用其发明者名字(Arne Andersson)命名的。
下图是一个 AA 树实例,水平向右的孩子为红节点。
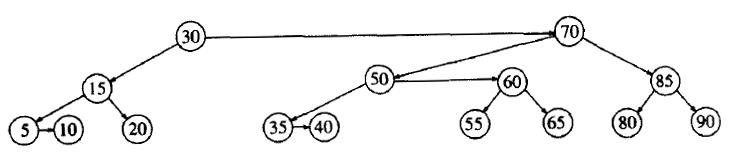
Figure 32: AA 树实例(水平向右的孩子为红节点)
AA 树采用 level 值来记录红黑树中黑节点高度,因此 level 满足下面性质:
- 每个叶子节点的 level 是 1。
- 每个左孩子的 level 是其父节点 level 值减 1。
- 每个右孩子的 level 和其父节点的 level 相等或是其父节点的 level 减 1。
- 每个 level 大于 1 的节点有两个孩子。

Figure 33: AA 树用 level 值记录红黑树中黑节点高度
参考:
http://user.it.uu.se/~arnea/ps/simp.pdf
http://www.blogjava.net/DLevin/archive/2013/10/27/405683.html
《数据结构与算法分析——C 语言描述(原书第 2 版)》12.4 节
5.4.1. AA 树插入分析
和红黑树一样,在 AA-Tree 插入时也只能插入红节点,即只能水平方向插入,但是这时会出现 2 种禁止出现的情况:
情况 1:出现向左的水平方向链,这是 AA 树中规定的;
情况 2:出现连续向右的水平方向链,即在红黑树中不能出现连续 2 个红节点。
在上面的 AA 树实例中插入节点 2、23、45。插入节点 2 出现了向左的水平方向链,插入节点 45 出现了连续向右的水平方向链。插入节点 23 没有出现禁止情况,插入完成。

Figure 34: 在 AA 树实例中插入节点导致禁止情况的出现
对于两种禁止出现的情况,可以通过单旋转来解决:通过右旋转(skew)消除左水平链接,而通过左旋转(split)消除连续的右水平链接。分别把这两个过程称为 skew 和 split。
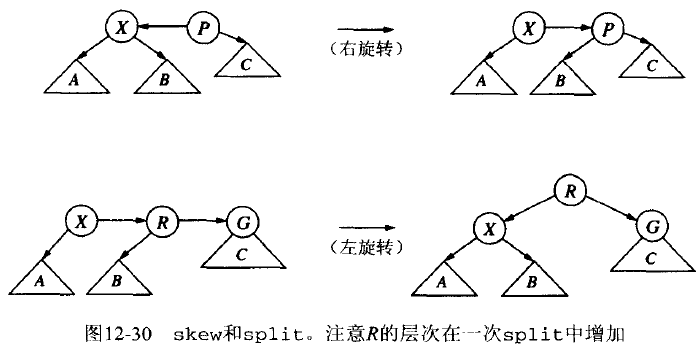
Figure 35: AA 树的 skew 和 split 示意图
注意:一次 skew 可除去一个左水平链接,但可能会创建连续的右水平链接,因此要先执行 skew,然后再执行 split。在 split 后,中间节点 R 的 level 会增加,会引起 X 的原父节点的问题,这可通过上滤 skew/split 方法来解决。如果使用递归算法,那么这可以自动地完成。
5.4.2. AA 树插入实例
下面将演示将节点 45 插入到上面 AA 树实例中产生了连续右水平链,使其重新平衡的过程。
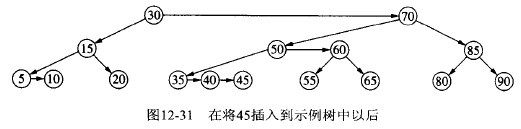
Figure 36: AA 树中插入节点 45 后,再平衡过程(1)
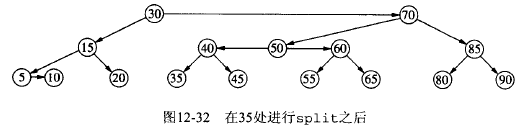
Figure 37: AA 树中插入节点 45 后,再平衡过程(2)
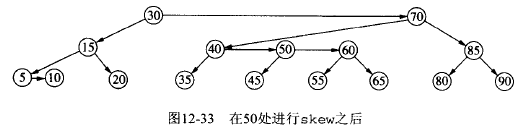
Figure 38: AA 树中插入节点 45 后,再平衡过程(3)
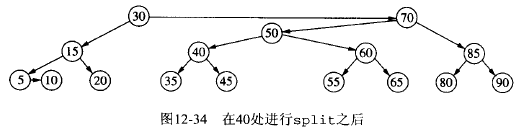
Figure 39: AA 树中插入节点 45 后,再平衡过程(4)
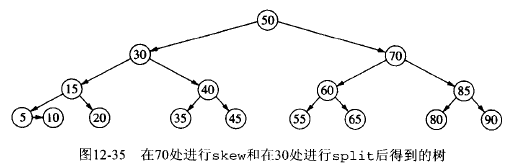
Figure 40: AA 树中插入节点 45 后,再平衡过程(5)
5.4.3. AA 树插入实现
摘自:《数据结构与算法分析——C 语言描述(原书第 2 版)》12.4 节
#include <stdlib.h>
#include <stdio.h>
struct AANode;
typedef struct AANode *Position;
typedef struct AANode *AATree;
struct AANode
{
int Element;
AATree Left;
AATree Right;
int Level;
};
Position NullNode = NULL; /* Needs more initialization */
AATree
Initialize( void )
{
if( NullNode == NULL ) {
NullNode = malloc( sizeof( struct AANode ) );
if( NullNode == NULL )
printf( "Out of space!!!" );
NullNode->Left = NullNode->Right = NullNode;
//上面这种使用哨兵节点的技巧可以简化程序,不用检测空节点;
//这种技巧在实现红黑树时也常用。
NullNode->Level = 0;
}
return NullNode;
}
static Position
SingleRotateWithLeft( Position K2 )
{
Position K1;
K1 = K2->Left;
K2->Left = K1->Right;
K1->Right = K2;
return K1; /* New root */
}
static Position
SingleRotateWithRight( Position K1 )
{
Position K2;
K2 = K1->Right;
K1->Right = K2->Left;
K2->Left = K1;
return K2; /* New root */
}
/* If T's left child is on the same level as T, */
/* perform a rotation */
AATree
Skew( AATree T )
{
if( T->Left->Level == T->Level )
T = SingleRotateWithLeft( T );
return T;
}
/* If T's rightmost grandchild is on the same level, */
/* rotate right child up */
AATree
Split( AATree T )
{
if( T->Right->Right->Level == T->Level ) { //有哨兵节点,不用担心为空
T = SingleRotateWithRight( T );
T->Level++;
}
return T;
}
AATree
Insert( int Item, AATree T )
{
if( T == NullNode ) {
/* Create and return a one-node tree */
T = malloc( sizeof( struct AANode ) );
if( T == NULL )
printf( "Out of space!!!" );
else {
T->Element = Item;
T->Level = 1;
T->Left = T->Right = NullNode;
}
}
else {
if( Item < T->Element )
T->Left = Insert( Item, T->Left );
else if( Item > T->Element )
T->Right = Insert( Item, T->Right );
/* Otherwise it's a duplicate; do nothing */
}
T = Skew( T );
T = Split( T );
return T;
}
void Print(AATree T)
{
if (T != NullNode) {
Print(T->Left);
printf("%d, %d\n", T->Element, T->Level);
Print(T->Right);
}
}
int main(int argv, char *argc[])
{
NullNode = Initialize();
AATree root = NullNode;
int i;
for (i = 0; i < 1024; i++) {
root = Insert((541*i) & (1023), root);
}
Print(root);
}
5.4.4. AA 树删除分析
和在普通的二叉搜索树中删除一样,在 AA 树中删除一个节点,实际删除的总是树叶节点。如果待删除节点是树叶,则直接删除;如果待删除节点不是树叶,则删除它的右孩子的最小节点(由 AA 树性质可以知道右孩子的最小节点的 level 一定为 1,所以对它的删除操作不用递归地进行,可直接删除,但要注意它可能还有红孩子)。
上面的删除操作可能会破坏 AA 树的性质,我们在删除节点到根节点的路径上的每个节点进行再平衡操作:
- 先检测是否需要平衡(检测左孩子和右孩子的 level 值和自己是否相差超过 1)。
- 如果需要平衡,把自己的 level 减 1。
- 如果自己的右节点是红孩子,则把右节点的 level 也减 1。
- 进行 skew 操作消除左水平链接。
- 进行 split 操作消除连续右水平链接。
注意:一次 skew 操作可能无法消除同一层的所有左水平链接,应该进行多次 skew;一次 split 操作可能无法消除同一层的所有连续右水平链接,应该进行多次 split。具体需要几次操作后文将介绍。
5.4.5. AA 树删除实例(无需平衡)
在最开始介绍的 AA 树实例中删除节点 30。
第一步,找到待删节点(DeletePtr),和实际会被删除的节点(LastPtr)。
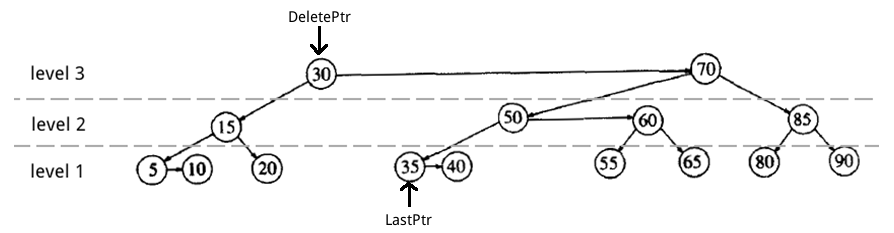
Figure 41: AA 树中删除节点 30(找到待删节点和实际会被删除的节点)
第二步,删除节点。操作如下:把 LastPtr 节点中的 key 复制到 DeletePtr 节点中;删除 LastPtr 节点;用 LastPtr 的右孩子代替原 LastPtr 位置。
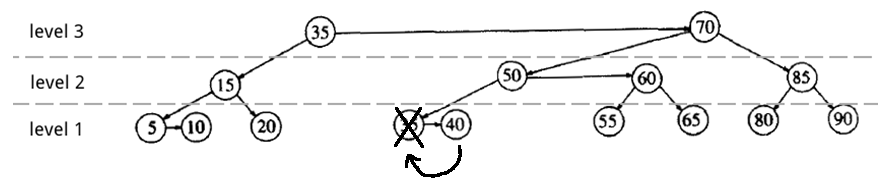
Figure 42: AA 树中删除节点 30(删除节点)
最后,检测删除节点到根的路径上是否要重新平衡。这个例子中不需要。
5.4.6. AA 树删除实例(仅降低 level 值,无需 skew 和 split 操作)
在最开始介绍的 AA 树实例中删除节点 50。
第一步,找到待删节点(DeletePtr),和实际会被删除的节点(LastPtr)。
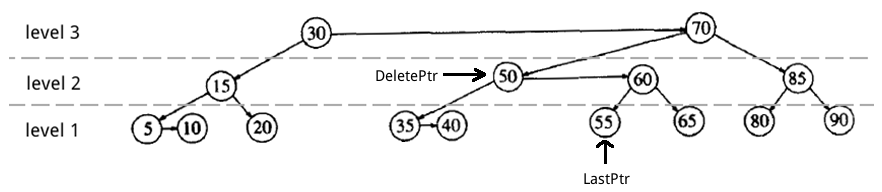
Figure 43: AA 树中删除节点 50(找到待删节点和实际会被删除的节点)
第二步,删除节点。操作如下:把 LastPtr 节点中的 key 复制到 DeletePtr 节点中;删除 LastPtr 节点;用 LastPtr 的右孩子代替原 LastPtr 位置。

Figure 44: AA 树中删除节点 50(删除节点)
最后,检测删除节点到根的路径上是否要重新平衡。发现节点 60 的 level 值和它左孩子的 level 值相差超过 1。我们把节点 60 的 level 值降低 1。

Figure 45: AA 树中删除节点 50(检测删除节点到根的路径上是否要重新平衡)
5.4.7. AA 树删除实例(降低 level 值,2次 skew 和 1 次 split 操作)
在最开始介绍的 AA 树实例中删除节点 15。
和前面类似地做完第一步和第二步操作后,得到:

Figure 46: AA 树中删除节点 15(检测删除节点到根的路径上是否要重新平衡)
检测删除节点到根的路径上是否要重新平衡。发现节点 20 的 level 值和它右孩子的 level 值相差超过 1。我们把节点 20 的 level 值降低 1。
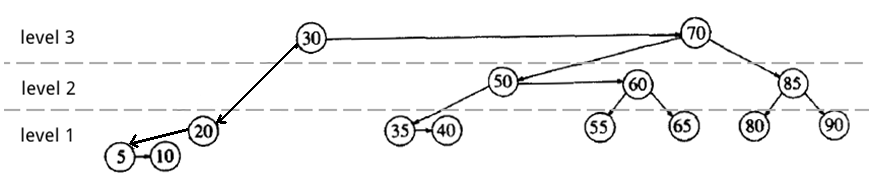
Figure 47: AA 树中删除节点 15(降低 level 值)
重新平衡还不能结束,因为结点 20 中出现了左水平链接。需要进行 skew 操作。
进行 T = Skew(T); 操作后得到下图:
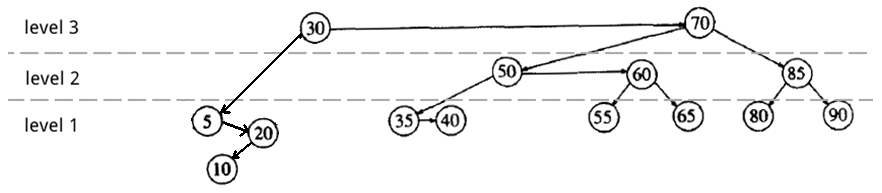
Figure 48: AA 树中删除节点 15(进行 skew 操作)
还是有左水平链接,再进行 skew 操作。
进行 T->Right = Skew(T->Right); 操作后得到下图:
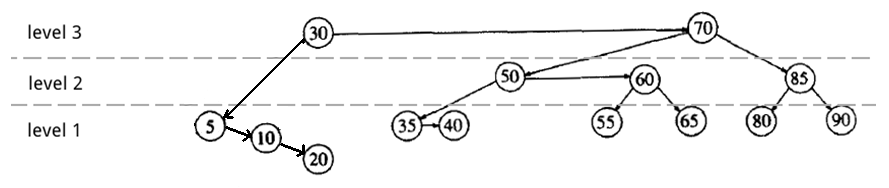
Figure 49: AA 树中删除节点 15(再进行 skew 操作)
但出现了连续右水平链接,我们进行 split 操作。
进行 T = Split(T); 操作后得到下图:

Figure 50: AA 树中删除节点 15(进行 split 操作)
注:在上面平衡过程中,我们一共进行了 2 次 skew 操作来消除左水平链接,1次 split 操作来消除连续右水平链接。
5.4.8. AA 树删除实例(2次 skew 和 2 次 split 操作)
再看一个实例:在下面 AA 树中删除节点 1。
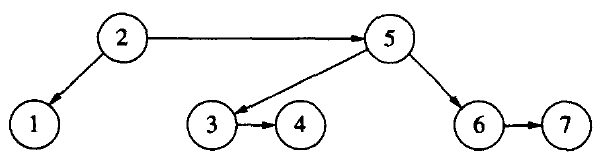
Figure 51: AA 树中删除节点 1
其删除的详细过程如下:
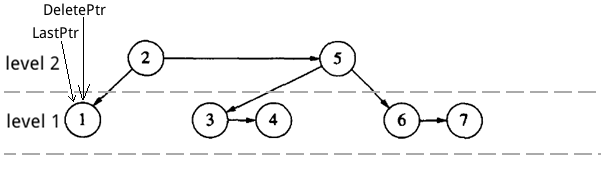
Figure 52: AA 树中删除节点 1(找到待删节点和实际会被删除的节点)
删除节点 1,把节点 2 及节点 2 的红孩子 level 值减一。所有节点的 level 变成了 1。
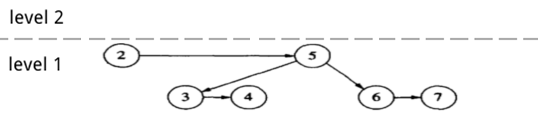
Figure 53: AA 树中删除节点 1(删除节点 1,把节点 2 及节点 2 的红孩子 level 值减一)
发现节点 5 有左水平链接,进行 skew 操作。
进行 T->Right = Skew(T->Right); 操作后得到下图:
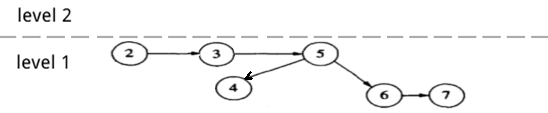
Figure 54: AA 树中删除节点 1(进行 skew 操作)
发现节点 5 还有左水平链接,再进行 skew 操作:
进行 T->Right->Right = Skew(T->Right->Right); 操作后得到下图:

Figure 55: AA 树中删除节点 1(再进行 skew 操作)
发现连续的右水平链接,进行 split 操作:
进行 T = Split(T); 操作后得到下图:

Figure 56: AA 树中删除节点 1(进行 split 操作)
还发现连续的右水平链接,进行 split 操作:
进行 T->Right = Split(T->Right); 操作后得到下图:

Figure 57: AA 树中删除节点 1(再进行 split 操作)
至此,删除操作完成。
在删除过程中进行了 2 次 skew 操作和 2 次 split 操作。
2 次 skew 操作:
T->Right = Skew(T->Right); //先对自己的右孩子skew。
T->Right->Right = Skew(T->Right->Right);
2 次 split 操作:
T = Split(T);
T->Right = Split(T->Right);
上节例子中重新平衡过程进行了 2 次 skew 操作和 1 次 split 操作。但它的 2 次 skew 和本节中的 2 次 skew 却不同,它分别是:
T = Skew(T); //先对自己skew。
T->Right = Skew(T->Right);
总结:
我们可以检测不同的情况,分别处理。
也可以省略检测,每次做 3 次 skew 操作和 2 次 split 操作,这则能覆盖所有情况(在一个具体情况下,最多只有 2 次 skew 有效)。
3 次 skew 操作:
T = Skew(T);
T->Right = Skew(T->Right);
T->Right->Right = Skew(T->Right->Right);
2 次 split 操作:
T = Split(T);
T->Right = Split(T->Right);
5.4.9. AA 树删除实现
摘自:《数据结构与算法分析——C 语言描述(原书第 2 版)》12.4 节
//DeletePtr和LastPtr可看作全局的,它们最后分别指向期待被删除的节点和实际上被删除的节点(它们可能指向同一个节点)。
AATree
Remove( int Item, AATree T )
{
static Position DeletePtr, LastPtr;
if( T != NullNode ) {
/* Step 1: Search down tree */
/* set LastPtr and DeletePtr */
LastPtr = T;
if( Item < T->Element )
T->Left = Remove( Item, T->Left );
else {
DeletePtr = T;
T->Right = Remove( Item, T->Right );
}
/* Step 2: At the bottom of the tree we remove it */
/* if it is present */
if( T == LastPtr ) {
if( DeletePtr != NullNode &&
Item == DeletePtr->Element )
{
DeletePtr->Element = T->Element;
DeletePtr = NullNode;
T = T->Right;
free( LastPtr );
}
}
/* Step 3: On the way back, we are not at the bottom; */
/* we rebalance */
else if( T->Left->Level < T->Level - 1 ||
T->Right->Level < T->Level - 1 ) {
T->Level = T->Level – 1;
if( T->Right->Level > T->Level )
T->Right->Level = T->Level;
T = Skew( T );
T->Right = Skew( T->Right );
T->Right->Right = Skew( T->Right->Right );
T = Split( T );
T->Right = Split( T->Right );
}
}
return T;
}
5.4.10. AA 树删除实例
关于 AA 树删除,再看一个复杂的例子。
该实例摘自 AA 树发明人 Arne Andersson 的原始论文:http://user.it.uu.se/~arnea/ps/simp.pdf
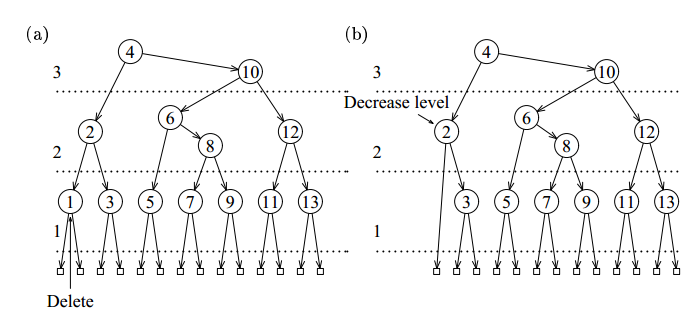
Figure 58: AA tree - Example of deletion (1).
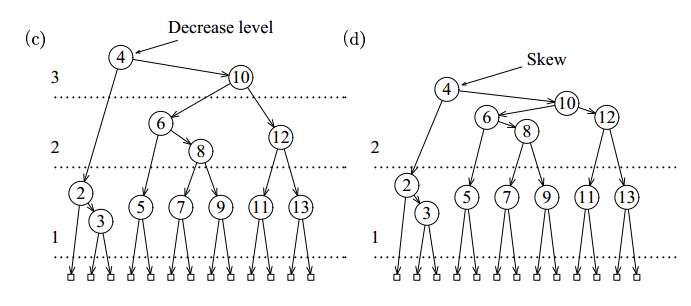
Figure 59: AA tree - Example of deletion (2).
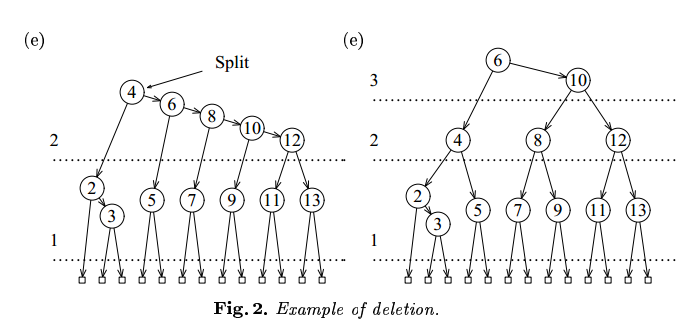
Figure 60: AA tree - Example of deletion (3).
5.5. Treap Trees (Randomized Data Structures)
The treap was first described by Cecilia R. Aragon and Raimund Seidel in 1989; its name is a portmanteau of tree and heap.
Treap 这个名字来自 tree 和 heap 的组合。
Treap 很简单,不用画图就可以描述它。
Treap 在普通二叉搜索树节点中增加了一个 Priority 域,每次插入节点时选择一个随机值作为 Priority 值。每个节点的 Priority 值满足堆序性:每个节点的 Priority 值大于等于它父节点的 Priority 值。
参考:
《数据结构与算法分析——C 语言描述(原书第 2 版)》12.5 节
5.5.1. Treap 的插入和删除分析
Treap 树的插入操作较简单,新节点作为树叶插入后,将它沿着 Treap 树向上旋转直到它的 Priority 值满足堆序性质为止。
Treap 树的删除操作可以这样进行:找到需要被删除的节点后,想办法把它旋转到树叶上,一旦发现它在树叶上,就可以直接删除了。
5.5.2. Treap 的实现
#include <stdlib.h>
#include <stdio.h>
struct TreapNode;
typedef struct TreapNode *Position;
typedef struct TreapNode *Treap;
typedef int ElementType;
#define Infinity 32767
struct TreapNode
{
ElementType Element;
Treap Left;
Treap Right;
int Priority;
};
Position NullNode = NULL; /* Needs initialization */
Treap
Initialize( void )
{
if( NullNode == NULL ) {
NullNode = malloc( sizeof( struct TreapNode ) );
if( NullNode == NULL )
printf( "Out of space!!!" );
NullNode->Left = NullNode->Right = NullNode;
NullNode->Priority = Infinity;
}
return NullNode;
}
int
Random( void )
{
return rand() % Infinity; //Use ANSI C random number generator for simplicity
}
static Position
SingleRotateWithLeft( Position K2 )
{
Position K1;
K1 = K2->Left;
K2->Left = K1->Right;
K1->Right = K2;
return K1; /* New root */
}
static Position
SingleRotateWithRight( Position K1 )
{
Position K2;
K2 = K1->Right;
K1->Right = K2->Left;
K2->Left = K1;
return K2; /* New root */
}
Treap
Insert( ElementType Item, Treap T )
{
if( T == NullNode ) {
/* Create and return a one-node tree */
T = malloc( sizeof( struct TreapNode ) );
if( T == NULL )
printf( "Out of space!!!" );
else {
T->Element = Item;
T->Priority = Random(); //新插入节点使用随机值作为Priority
T->Left = T->Right = NullNode;
}
} else if( Item < T->Element ) {
T->Left = Insert( Item, T->Left );
if( T->Left->Priority < T->Priority )
T = SingleRotateWithLeft( T );
} else if( Item > T->Element ) {
T->Right = Insert( Item, T->Right );
if( T->Right->Priority < T->Priority )
T = SingleRotateWithRight( T );
}
/* Otherwise it's a duplicate; do nothing */
return T;
}
Treap
Remove( ElementType Item, Treap T )
{
if( T != NullNode ) {
if( Item < T->Element )
T->Left = Remove( Item, T->Left );
else if( Item > T->Element )
T->Right = Remove( Item, T->Right );
else {
/* Match found */
if( T->Left->Priority < T->Right->Priority )
T = SingleRotateWithLeft( T );
else
T = SingleRotateWithRight( T );
if( T != NullNode ) /* Continue on down */
T = Remove( Item, T );
else {
/* At a leaf */
free( T->Left );
T->Left = NullNode;
}
}
}
return T;
}
Treap
MakeEmpty( Treap T )
{
if( T != NullNode ) {
MakeEmpty( T->Left );
MakeEmpty( T->Right );
free( T );
}
return NullNode;
}
void
PrintTree( Treap T )
{
if( T != NullNode ) {
PrintTree( T->Left );
printf( "%d ", T->Element );
PrintTree( T->Right );
}
}
int main(int argv, char *argc[])
{
NullNode = Initialize();
Treap root = NullNode;
int i;
for (i = 0; i < 1024; i++) {
root = Insert((541*i) & (1023), root);
}
printf("\nPrint after Insert:\n");
PrintTree(root);
for (i = 0; i < 1024; i++) {
root = Remove((541*i) & (1023), root);
}
printf("\nPrint after Remove:\n");
PrintTree(root);
}
5.6. Skip Lists (Randomized Data Structures)
Skip list is a data structure that allows fast search within an ordered sequence of elements. Fast search is made possible by maintaining a linked hierarchy of subsequences, each skipping over fewer elements.
Skip lists are a probabilistic data structure that seem likely to supplant balanced trees as the implementation method of choice for many applications. Skip list algorithms have the same asymptotic expected time bounds as balanced trees and are simpler, faster and use less space.
跳跃表是一种随机化数据结构,它的时间性能和平衡二叉树一样,可用来代替平衡二叉树。
跳跃表随机选择新插入节点的 level 值。

Figure 61: 跳跃表实例
参考:
http://www.cl.cam.ac.uk/teaching/2005/Algorithms/skiplists.pdf
5.6.1. 跳跃表实现
代码摘自:Data Structures,Algorithms,and Applications in C++(Sartaj Sahni)
// skipNode.h (C++) node type used in skip lists
// node with a next and element field; element is a pair<const K, E>
// next is a 1D array of pointers
#ifndef skipNode_
#define skipNode_
using namespace std;
template <class K, class E>
struct skipNode
{
typedef pair<const K, E> pairType;
pairType element;
skipNode<K,E> **next; // 1D array of pointers
skipNode(const pairType& thePair, int size)
:element(thePair){next = new skipNode<K,E>* [size];}
};
#endif
// skipList.h (C++) skip list data structure, implements dictionary
#ifndef skipList_
#define skipList_
#include <iostream>
#include <math.h>
#include <stdlib.h> // rand() RAND_MAX
#include <sstream>
#include <string>
#include "skipNode.h"
using namespace std;
template<class K, class E>
class skipList
{
public:
skipList(K, int maxPairs = 10000, float prob = 0.5);
~skipList();
bool empty() const {return dSize == 0;}
int size() const {return dSize;}
pair<const K, E>* find(const K&) const;
void erase(const K&);
void insert(const pair<const K, E>&);
void output(ostream& out) const;
protected:
float cutOff; // used to decide level number
int level() const; // generate a random level number
int levels; // max current nonempty chain
int dSize; // number of pairs in dictionary
int maxLevel; // max permissible chain level
K tailKey; // a large key
skipNode<K,E>* search(const K&) const; // search saving last nodes seen
skipNode<K,E>* headerNode; // header node pointer
skipNode<K,E>* tailNode; // tail node pointer
skipNode<K,E>** last; // last[i] = last node seen on level i
};
template<class K, class E>
skipList<K,E>::skipList(K largeKey, int maxPairs, float prob)
{// Constructor for skip lists with keys smaller than largeKey and
// size at most maxPairs. 0 < prob < 1.
cutOff = prob * RAND_MAX;
maxLevel = (int) ceil(logf((float) maxPairs) / logf(1/prob)) - 1;
levels = 0; // initial number of levels
dSize = 0;
tailKey = largeKey;
// create header & tail nodes and last array
pair<K,E> tailPair;
tailPair.first = tailKey;
headerNode = new skipNode<K,E> (tailPair, maxLevel + 1);
tailNode = new skipNode<K,E> (tailPair, 0);
last = new skipNode<K,E> *[maxLevel+1];
// header points to tail at all levels as lists are empty
for (int i = 0; i <= maxLevel; i++)
headerNode->next[i] = tailNode;
}
template<class K, class E>
skipList<K,E>::~skipList()
{// Delete all nodes and array last.
skipNode<K,E> *nextNode;
// delete all nodes by following level 0 chain
while (headerNode != tailNode) {
nextNode = headerNode->next[0];
delete headerNode;
headerNode = nextNode;
}
delete tailNode;
delete [] last;
}
template<class K, class E>
pair<const K,E>* skipList<K,E>::find(const K& theKey) const
{// Return pointer to matching pair.
// Return NULL if no matching pair.
if (theKey >= tailKey)
return NULL; // no matching pair possible
// position beforeNode just before possible node with theKey
skipNode<K,E>* beforeNode = headerNode;
for (int i = levels; i >= 0; i--) // go down levels
// follow level i pointers
while (beforeNode->next[i]->element.first < theKey)
beforeNode = beforeNode->next[i];
// check if next node has theKey
if (beforeNode->next[0]->element.first == theKey)
return &beforeNode->next[0]->element;
return NULL; // no matching pair
}
template<class K, class E>
int skipList<K,E>::level() const
{// Return a random level number <= maxLevel.
// 注:可以简化随机level值的生成,根本不需要cutOff
int lev = 0;
while (rand() <= cutOff)
lev++;
return (lev <= maxLevel) ? lev : maxLevel;
}
template<class K, class E>
skipNode<K,E>* skipList<K,E>::search(const K& theKey) const
{// Search for theKey saving last nodes seen at each
// level in the array last
// Return node that might contain theKey.
// position beforeNode just before possible node with theKey
skipNode<K,E>* beforeNode = headerNode;
for (int i = levels; i >= 0; i--) {
while (beforeNode->next[i]->element.first < theKey)
beforeNode = beforeNode->next[i];
last[i] = beforeNode; // last level i node seen
}
return beforeNode->next[0];
}
template<class K, class E>
void skipList<K,E>::insert(const pair<const K, E>& thePair)
{// Insert thePair into the dictionary. Overwrite existing
// pair, if any, with same key.
if (thePair.first >= tailKey) {// key too large
// TODO: throw exception
return;
}
// see if pair with theKey already present
skipNode<K,E>* theNode = search(thePair.first);
if (theNode->element.first == thePair.first) {
// update theNode->element.second
theNode->element.second = thePair.second;
return;
}
// not present, determine level for new node
int theLevel = level(); // level of new node
// fix theLevel to be <= levels + 1
if (theLevel > levels) {
theLevel = ++levels;
last[theLevel] = headerNode;
}
// get and insert new node just after theNode
skipNode<K,E>* newNode = new skipNode<K,E>(thePair, theLevel + 1);
for (int i = 0; i <= theLevel; i++) {
// insert into level i chain
newNode->next[i] = last[i]->next[i];
last[i]->next[i] = newNode;
}
dSize++;
return;
}
template<class K, class E>
void skipList<K,E>::erase(const K& theKey)
{// Delete the pair, if any, whose key equals theKey.
if (theKey >= tailKey) // too large
return;
// see if matching pair present
skipNode<K,E>* theNode = search(theKey);
if (theNode->element.first != theKey) // not present
return;
// delete node from skip list
for (int i = 0; i <= levels &&
last[i]->next[i] == theNode; i++)
last[i]->next[i] = theNode->next[i];
// update levels
while (levels > 0 && headerNode->next[levels] == tailNode)
levels--;
delete theNode;
dSize--;
}
template<class K, class E>
void skipList<K,E>::output(ostream& out) const
{// Insert the dictionary pairs into the stream out.
// follow level 0 chain
for (skipNode<K,E>* currentNode = headerNode->next[0];
currentNode != tailNode;
currentNode = currentNode->next[0])
out << currentNode->element.first << " "
<< currentNode->element.second << " ";
}
// overload <<
template <class K, class E>
ostream& operator<<(ostream& out, const skipList<K,E>& x)
{x.output(out); return out;}
#endif
测试代码:
// test skip list class
#include <iostream>
#include "skipList.h"
using namespace std;
int main()
{
skipList<int, int> z(1000);
pair<int, int> p;
// test insert
p.first = 2; p.second = 10;
z.insert(p);
p.first = 10; p.second = 50;
z.insert(p);
p.first = 6; p.second = 30;
z.insert(p);
p.first = 8; p.second = 40;
z.insert(p);
p.first = 1; p.second = 5;
z.insert(p);
p.first = 12; p.second = 60;
z.insert(p);
cout << "The dictionary is " << z << endl;
cout << "Its size is " << z.size() << endl;
// test find
cout << "Element associated with 1 is " << z.find(1)->second << endl;
cout << "Element associated with 6 is " << z.find(6)->second << endl;
cout << "Element associated with 12 is " << z.find(12)->second << endl;
// test erase
z.erase(1);
z.erase(2);
z.erase(6);
z.erase(12);
cout << "Deleted 1, 2, 6, 12" << endl;
cout << "The dictionary is " << z << endl;
cout << "Its size is " << z.size() << endl;
}
/* This test code would output following:
The dictionary is 1 5 2 10 6 30 8 40 10 50 12 60
Its size is 6
Element associated with 1 is 5
Element associated with 6 is 30
Element associated with 12 is 60
Deleted 1, 2, 6, 12
The dictionary is 8 40 10 50
Its size is 2
*/
5.6.2. 跳跃表的应用
List of applications and frameworks that use skip lists:
- Cyrus IMAP server offers a "skiplist" backend DB implementation.
- Lucene uses skip lists to search delta-encoded posting lists in logarithmic time.
- QMap (up to Qt 4) template class of Qt that provides a dictionary.
- Redis, an ANSI-C open-source persistent key/value store for Posix systems, uses skip lists in its implementation of ordered sets.
- nessDB, a very fast key-value embedded Database Storage Engine (Using log-structured-merge (LSM) trees), uses skip lists for its memtable.
- skipdb is an open-source database format using ordered key/value pairs.
- ConcurrentSkipListSet and ConcurrentSkipListMap in the Java 1.6 API.
- leveldb, a fast key-value storage library written at Google that provides an ordered mapping from string keys to string values
- Skip lists are used for efficient statistical computations of running medians (also known as moving medians).
参考:http://en.wikipedia.org/wiki/Skip_list
A variant of skip lists is used in the HP-UX operating system kernel’s process management structures.
参考 HP-UX process management white paper, version 1.3, 1997.
5.6.3. Skip Lists vs. Binary Search Trees
跳跃表更适合应用于并行算法中。
参考:http://stackoverflow.com/questions/256511/skip-list-vs-binary-tree
5.7. Scapegoat Tree
一般的平衡二叉树像 AVL,红黑树,Splay Trees,都是通过旋转节点让两侧保持大小一致。但替罪羊树,不是通过旋转节点来保持平衡。
不旋转节点的平衡树还有 B 树,他们保持平衡的方法是分裂提升节点。这样太复杂了, 替罪羊树用了一种非常暴力的方式,直接将树重构成一个完美二叉树, 对已排序的序列很容易实现每次重构的复杂度 \(O(N)\) ,由于并非每次添加或删除都会重构,添加或删除操作的平摊复杂度为 \(O(log_{2}N)\) ,查找操作的最坏时间复杂度为 \(O(log_{2}N)\) 。
参考:
http://www.freopen.com/?p=10637
http://en.wikipedia.org/wiki/Scapegoat_tree
6. Priority Queue(Heap)
Priority Queue 是能有效支持 Insert,DeleteMin 这两种基本操作的数据结构(这里只讨论“最小堆”,如果是“最大堆”则对应的删除操作为 DeleteMax)。
有很多方法可以实现 Priority Queue,如:
| Insert | DeleteMin | |
|---|---|---|
| 链表 | \(O(1)\) | \(O(N)\) |
| 有序链表 | \(O(N)\) | \(O(1)\) |
| 二叉查找树 | \(O(log_{2}N)\) | \(O(log_{2}N)\) |
注:上面描述的二叉查找树时间界是平均运行时间界。如果使用平衡二叉查找树,可以得到最坏情形的时间界为 \(O(log_{2}N)\) 的实现,但用平衡二叉查找树实现 Priority Queue 有些大材小用,它支持很多并不需要的操作(如 Find,Delete)。
我们在后文将介绍二叉堆,它的 Insert,DeleteMin 操作最坏情形的时间界为 \(O(log_{2}N)\) 。
虽然二叉堆和平衡二叉查找树实现 Priority Queue 的最坏时间界是一样的,但二叉堆显然更快,它直接用数组实现,没有平衡二叉树的旋转操作。
6.1. Binary Heap(二叉堆)
二叉堆是实现 Priority Queue 最常用的方式。
它有两个性质,即结构性质和堆序性质。
结构性质:二叉堆是完全二叉树(complete binary tree)。
堆序性质:父节点的关键字小于等于孩子的关键字。
由于完全二叉树很有规律,我们可以直接用数组表示:对于数组中任意位置 i 上的元素,其左儿子在位置 2i 上,右儿子在位置 2i + 1 中,它的父亲则在位置 floor(i/2)上。
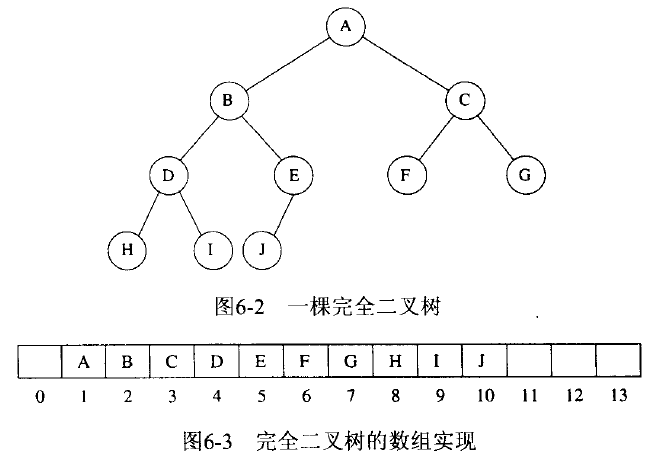
Figure 62: 二叉堆示例:用数组实现完全二叉树
6.1.1. 二叉堆 Insert 分析(上滤)
将一个元素 X 插入到堆中,我们首先在下一个空闲位置创建一个空穴。如果 X 可以放在空穴中而不破坏堆序性质,那么插入完成。 否则,把空穴的父节点上的元素移入空穴中,这样空穴朝着根的方向上行一步,继续该过程直到 X 能被放入到空穴中为止。这种策略被称为上滤(percolate up)。
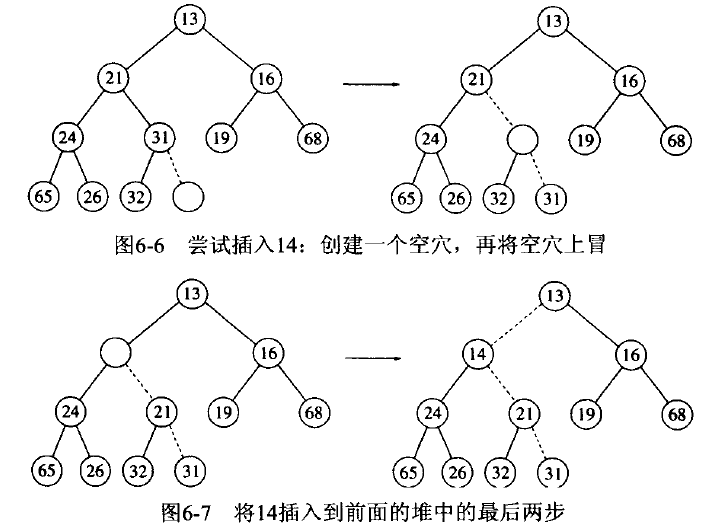
Figure 63: 二叉堆 Insert 分析(上滤)
6.1.2. 二叉堆 DeleteMin 分析(下滤)
找到最小元素(根节点)很容易,困难在于删除它。
当删除最小元素时,在根节点处产生了一个空穴,由于现在堆少了一个元素,因此堆中最后一个元素 X 必须移动到堆的某个地方。如果 X 可以被放入空穴中,那么 DeleteMin 完成。不过这一般不太可能, 因此我们将空穴的两个儿子中较小者移入空穴,这样就把空穴向下推了一层。重复该步骤直到 X 可以被放入到空穴中。这种策略被称为下滤(percolate down)。
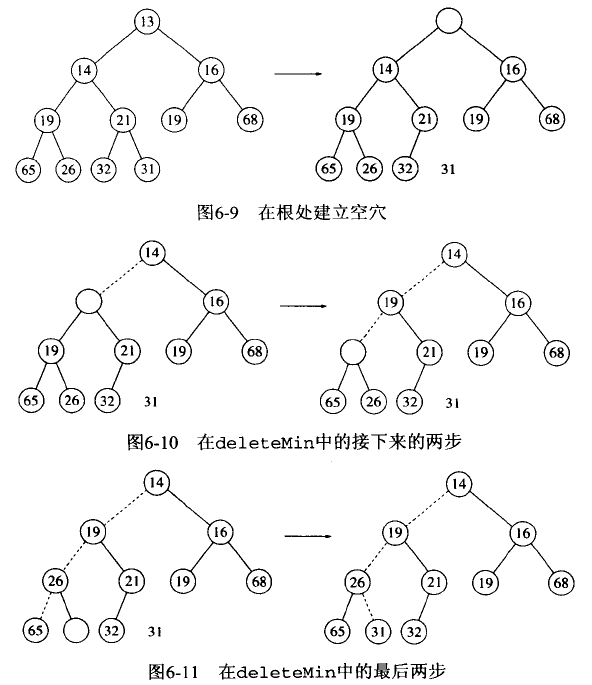
Figure 64: 二叉堆 DeleteMin 分析(下滤)
6.1.3. 二叉堆 BuildHeap 分析(可在线性时间内完成)
BuildHeap 不是 Priority Queue 的基本操作,它的功能是把 \(N\) 个关键字作为输入,将它们放入到空堆中。
显然,可以通过 \(N\) 次 Insert 操作来完成,其最坏时间界为 \(O(Nlog_{2}N)\) 。
我们还有更快的方法,其最坏时间界为 \(O(N)\) ,即:我们可以在线性时间内,把一个无序数组构造成为一个二叉堆。
算法是: 先以任意的顺序放到树中,并保持结构性质。再对前一半元素按“从后往前”的顺序(即从 \(N/2\) 处的元素开始,从后往前)进行“下滤”操作,这将创建一个具有堆序的树。
// BuildHeap
for (i = N/2; i > 0; i--)
PercolateDown(i); //PercolateDown是“下滤”操作,即DeleteMin中介绍的算法
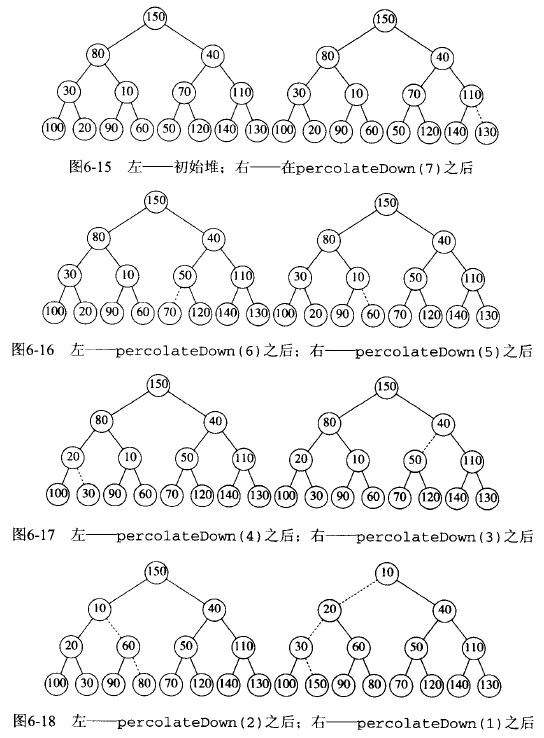
Figure 65: 二叉堆 BuildHeap 实例
在图 65 所示实例中,每条虚线对应两次比较:一次是找出较小的儿子节点,另一次是将较小的儿子与该节点比较。在这个实例中有 10 条虚线,对应 20 次比较。
为了确定 BuildHeap 的运行时间界(前面介绍过,时间界为 \(O(N)\) ),我们必须确定虚线的条数的界。这可以通过计算堆中“所有节点的高度的和”来得到,它是虚线的最大条数。这里不严格推导,直接给出结论:“所有节点的高度的和”为 \(O(N)\) ,即虚线的最大条数为 \(O(N)\) 。
6.1.4. 二叉堆实现
摘自:数据结构与算法分析——C 语言描述(原书第 2 版)
#include <stdio.h>
#include <stdlib.h>
#define MinPQSize (10)
#define MinData (-32767)
typedef int ElementType;
struct HeapStruct;
typedef struct HeapStruct *PriorityQueue;
struct HeapStruct
{
int Capacity;
int Size;
ElementType *Elements;
};
PriorityQueue
Initialize( int MaxElements )
{
PriorityQueue H;
if( MaxElements < MinPQSize )
printf( "Priority queue size is too small" );
H = malloc( sizeof( struct HeapStruct ) );
if( H ==NULL )
printf( "Out of space!!!" );
/* Allocate the array plus one extra for sentinel */
H->Elements = malloc( ( MaxElements + 1 ) * sizeof( ElementType ) );
if( H->Elements == NULL )
printf( "Out of space!!!" );
H->Capacity = MaxElements;
H->Size = 0;
H->Elements[ 0 ] = MinData;
return H;
}
/* H->Element[ 0 ] is a sentinel */
void
Insert( ElementType X, PriorityQueue H )
{
int i;
if( H->Size == H->Capacity ) {
printf( "Priority queue is full" );
return;
}
for( i = ++H->Size; H->Elements[ i / 2 ] > X; i /= 2 )
H->Elements[ i ] = H->Elements[ i / 2 ];
H->Elements[ i ] = X;
}
ElementType
DeleteMin( PriorityQueue H )
{
int i, Child;
ElementType MinElement, LastElement;
if( H->Size == 0 ) {
printf( "Priority queue is empty" );
return H->Elements[ 0 ];
}
MinElement = H->Elements[ 1 ];
LastElement = H->Elements[ H->Size-- ];
for( i = 1; i * 2 <= H->Size; i = Child ) {
/* Find smaller child */
Child = i * 2;
if( Child != H->Size && H->Elements[ Child + 1 ]
< H->Elements[ Child ] )
Child++;
/* Percolate one level */
if( LastElement > H->Elements[ Child ] )
H->Elements[ i ] = H->Elements[ Child ];
else
break;
}
H->Elements[ i ] = LastElement;
return MinElement;
}
int main()
{
PriorityQueue PQ = Initialize(100);
Insert(1, PQ);
Insert(2, PQ);
Insert(3, PQ);
printf("size %d\n", PQ->Size);
DeleteMin(PQ);
DeleteMin(PQ);
printf("size %d\n", PQ->Size);
return 0;
}
6.2. 优先队列的 Merge 操作
Merge 操作(将两个堆合并成一个堆)虽然不是 Priority Queue 的最基本操作,但高级的实现一般都支持快速 Merge 操作。
二叉堆无法高效地支持 Merge 操作。
后面讨论的数据结构(左式堆,斜堆,二项队列)都能高效地支持 Merge 操作。
6.3. Leftist Heap(左式堆)
左式堆能有效地支持 Merge 操作。
先介绍一个概念:节点 X 的零路径长(null path length, NPL)是指节点 X 到它子树的不满节点(不具有两个儿子的节点)的最短路径长度。
叶子节点或只有一个儿子的节点的 NPL 为 0,NULL 节点的 NPL 为-1。
显然,一个节点的 NPL 等于子节点 NPL 最小值加 1: \(NPL (X) = min(NPL(X->left), NPL(X->right)) + 1\)
左式堆是具有堆序性质的二叉树,同时它还满足性质: 堆中每个节点的左儿子的零路径长大于等于右儿子的零路径长。
下图两个树是具有堆序性质的二叉树,且 NPL 值标记在树节点中,显然仅左边的树是左式堆。
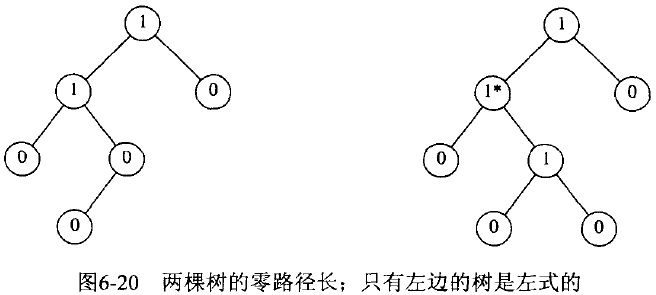
Figure 66: 零路径长示例
说明:上面介绍的这种左式堆是高度优先左高树(Height-Biased Leftist Tree, HBLT);还有一种叫做重量优先左高树(Weight-Biased Leftist Tree, WBLT),WBLT 和 HBLT 类似,只是用节点的重量(即其子树的节点数量)代替 NPL。
6.3.1. 左式堆 Merge 操作
假定有两个堆 H1 和 H2,且 H1 的根值小于 H2 的根值。
算法如下:
- 将具有大的根值的堆 H2 与具有小的根值的堆 H1 的右子堆 Merge;
- 让上步中得到的新堆成为 H1 的根的右儿子;
- 比较 H1 两个儿子的 NPL 值,如果右儿子 NPL 值较大,交换 H1 的左儿子和右儿子。
Merge 操作演示实例:
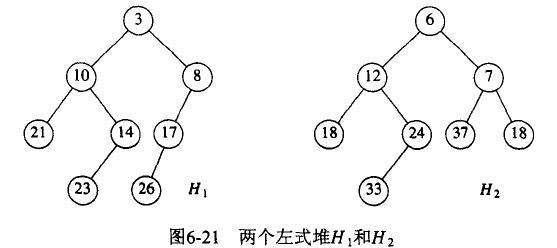
Figure 67: 左式堆 Merge 操作实例
具体 Merge 操作如下:
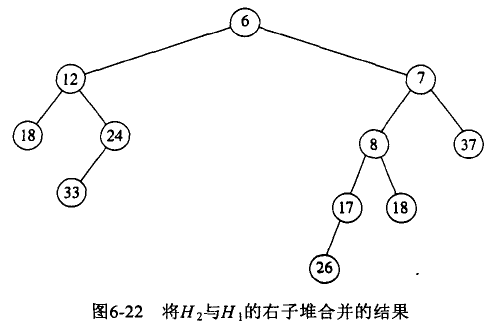
Figure 68: 左式堆 Merge 操作,步骤 1
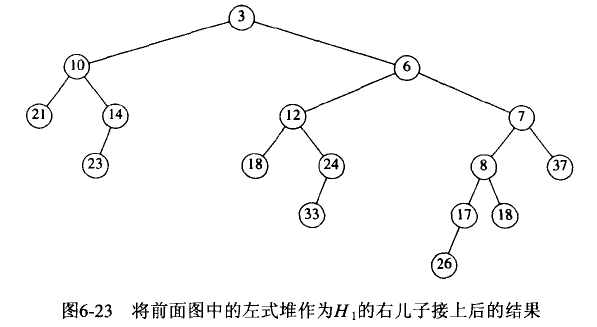
Figure 69: 左式堆 Merge 操作,步骤 2
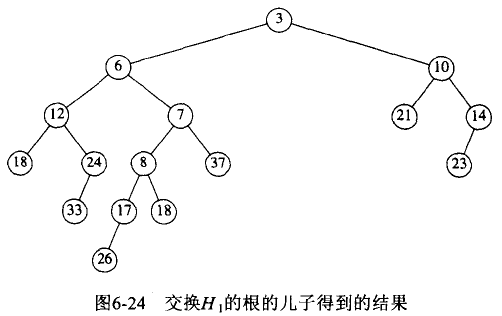
Figure 70: 左式堆 Merge 操作,步骤 3
6.3.2. 左式堆 Insert 和 DeleteMin 分析
Insert 可以看成是单节点堆和另一个堆的 Merge 操作。
DeleteMin,删除根后得到两个堆,然后再将这两个堆 Merge。
6.3.3. 左式堆实现
参考:《数据结构与算法分析——C 语言描述(原书第 2 版)》6.6 节
6.4. Skew Heap(斜堆,左式堆的自调节形式)
斜堆是左式堆的自调节形式。斜堆和左式堆的关系类似于伸展树和 AVL 树间的关系。
斜堆不需要节点的 NPL 值信息。
斜堆 Merge 操作和左式堆类似,仅最后一步有区别。
| 斜堆 Merge 操作 | 左式堆 Merge 操作 |
|---|---|
| 将具有大的根值的堆 H2 与具有小的根值的堆 H1 的右子堆 Merge; | 将具有大的根值的堆 H2 与具有小的根值的堆 H1 的右子堆 Merge; |
| 让上步中得到的新堆成为 H1 的根的右儿子; | 让上步中得到的新堆成为 H1 的根的右儿子; |
| 交换 H1 的左儿子和右儿子。 | 比较 H1 两个儿子的 NPL 值,如果右儿子 NPL 值较大,交换 H1 的左儿子和右儿子。 |
说明:如果斜堆不做最后一步(交换 H1 的左儿子和右儿子),Merge 操作虽然已经完成,但右儿子经过前面两个步骤后肯定会越来越高,这无法保证摊还时间界为 \(O(log_{2}N)\) 。
关于斜堆的摊还时间界,可参考:《数据结构与算法分析——C 语言描述(原书第 2 版)》11.3 节
6.5. Binomial Heap(二项堆,又称为二项队列)
Binomial Heap 的 Insert,DeleteMin,Merge 操作的最坏时间复杂度都为 \(O(log_{2}N)\) ,与左式堆和斜堆相比并不优势,它的优势在于 Insert 操作平均花费仅是常量时间,即 Insert 操作的平均时间复杂度为 \(O(1)\) 。
Binomial Heap(二项堆)又称为:Binomial Queue(二项队列)。
二项堆不是一棵堆序树,而是堆序树的集合。该集合中的每棵堆序树都是二项树。
6.5.1. 二项树
高度为 0 的二项树 \(B_{0}\) 是一棵单节点树;
高度为 k 的二项树 \(B_{k}\) 由二棵二项树 \(B_{k-1}\) 组成,其中一棵二项树 \(B_{k-1}\) 附接到另一棵二项树 \(B_{k-1}\) 的根上作为最右孩子(也可以是最左孩子,但要全部一致,不能同时存在)。
二项树例子如下:
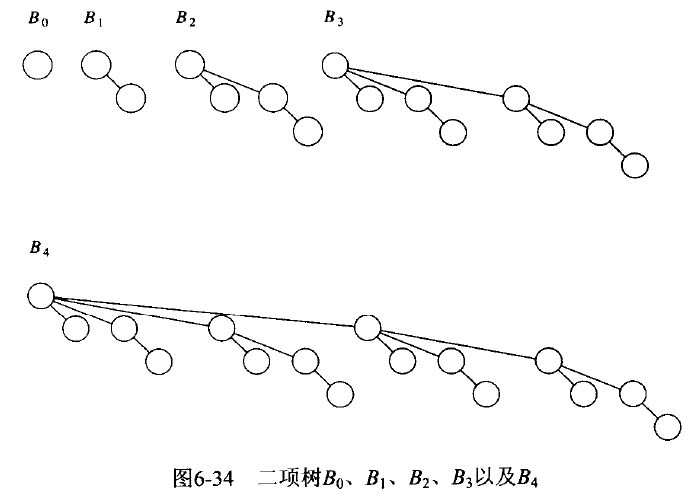
Figure 71: 二项树例子
高度为 k 的二项树 \(B_{k}\) 具有下面性质:
- 共有 \(2^{k}\) 个节点;
- 深度为 d 处的节点数是二项系数 \({k \choose d}\) 。
上面性质用数学归纳法容易证明,详情可参考:<Introduction to Algorithms, 2nd Edition, Section 19.1>
6.5.1.1. 二项系数(Binomial coefficient)
二项系数 \({n \choose r}\) 是 \((1+x)^{n}\) 展开后 \(x^{r}\) 的系数。
二项式定理(binomial theorem)如下:
\[(a+b)^{n}=\sum_{r=0}^{n}{n \choose r}a^{n-r}b^{r}\]
其中: \({n \choose r}=\frac{n!}{r!(n-r)!}\)
显然二项系数 \({n \choose r}\) 就是组合数: \(C_{n}^{r}\)
6.5.2. 二项堆 Merge 分析
二项堆可以用二项树的集合表示。例如,含 13 个元素的二项堆可用 \(B_{3}\),\(B_{2}\),\(B_{0}\) 表示(共容纳 8+4+1 个元素)。
Merge 两个二项堆从概念上是容易操作的, 只要合并两个二项堆中所有高度相同的二项树即可。
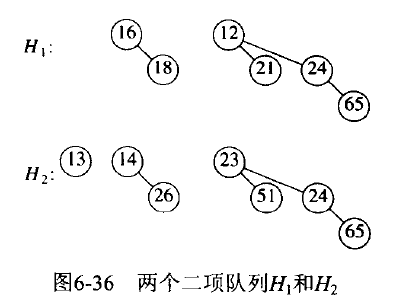
Figure 72: 二项堆 Merge 实例:待合并二项队列
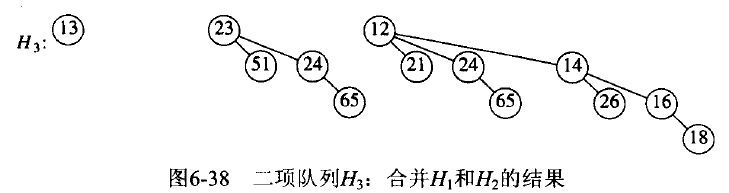
Figure 73: 二项堆 Merge 实例:合并后的结果
合并两个二项树花费常数时间,而二项堆存在 \(O(log_{2}N)\) 棵二项树,因此合并两个二项堆最坏情形下花费时间为 \(O(log_{2}N)\) 。
6.5.3. 二项堆 Insert 分析
二项堆 Insert 操作可以看作是一个仅含有一个二项树 \(B_{0}\) 的二项堆和另一个二项堆的 Merge 操作。Insert 操作的最坏运行时间为 \(O(log_{2}N)\) 。
由于二项堆中的每种二项树出现的概率均为 1/2,故 Insert 操作平均在两步后就能完成。Insert 操作的平均时间为 \(O(1)\) 。
Insert 操作实例:
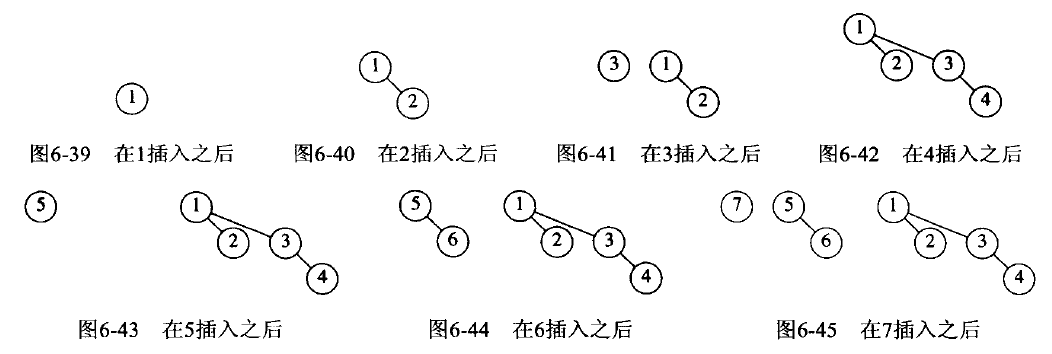
Figure 74: 二项堆 Insert 实例
6.5.4. 二项堆 DeleteMin 分析
DeleteMin 操作也可以通过 Merge 操作来完成。
首先在二项堆中找到含有最小根的二项树;其次在根处分解含有最小根的二项树;最后 Merge 所有除最小根外的二项树。
二项堆进行 DeleteMin 操作实例:
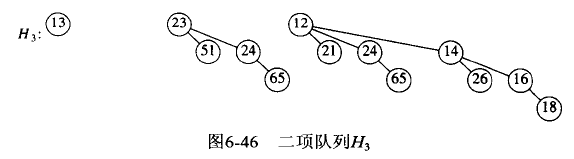
Figure 75: 二项堆 DeleteMin 实例
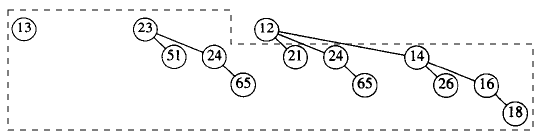
Figure 76: 二项堆 DeleteMin 实例:在根处分解含有最小根的二项树
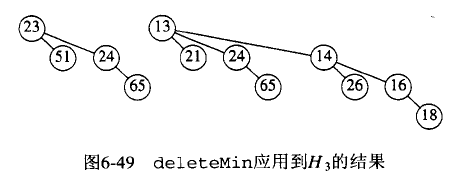
Figure 77: 二项堆 DeleteMin 实例:Merge 所有除最小根外的二项树
6.5.5. 二项堆的表示
二项树可以用“树的左孩子右兄弟表示法”来表示,二项堆可以用二项树的数组来表示。
注:用左孩子右兄弟表示法时, \(B_{k}\) 的左孩子是一个二项树 \(B_{k-1}\) 的根。
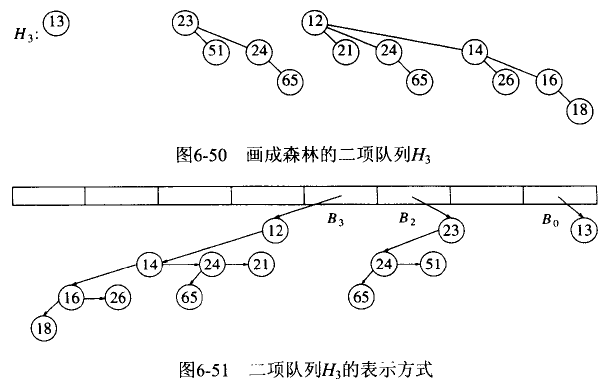
Figure 78: 二项堆的表示
上面两个图中同一层的节点的顺序是相反的。
如果我们改变 \(B_{k}\) 的定义,则不会有同层节点看上去顺序相反的问题。即改变 \(B_{k}\) 的定义为:高度为 k 的二项树 \(B_{k}\) 由二棵二项树 \(B_{k-1}\) 组成,其中一棵二项树 \(B_{k-1}\) 附接到另一棵二项树 \(B_{k-1}\) 的根上作为最左孩子。
合并两个等高二项树的图示如下:
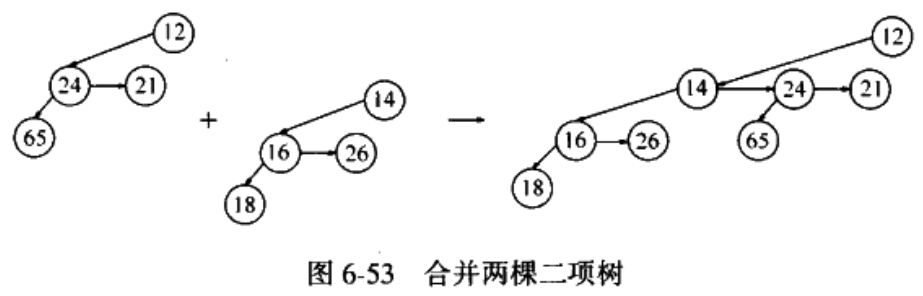
Figure 79: 合并两棵二项树
6.5.6. 二项堆的实现
摘自:《数据结构与算法分析——C 语言描述(原书第 2 版)》6.8 节。
注:这个实现是没有优化的。
#include <stdio.h>
#include <stdlib.h>
typedef long ElementType;
#define Infinity (30000L)
#define MaxTrees (14) /* Stores 2^14 -1 items */
#define Capacity (16383) /* 16383 = 2^14 -1 */
struct BinNode
{
ElementType Element;
struct BinNode * LeftChild;
struct BinNode * NextSibling;
};
typedef struct BinNode *BinTree;
struct Collection
{
int CurrentSize;
BinTree TheTrees[ MaxTrees ];
};
typedef struct Collection *BinQueue;
BinQueue
Initialize( void )
{
BinQueue H;
int i;
H = malloc( sizeof( struct Collection ) );
if( H == NULL )
printf( "Out of space!!!" );
H->CurrentSize = 0;
for( i = 0; i < MaxTrees; i++ )
H->TheTrees[ i ] = NULL;
return H;
}
/* Return the result of merging equal-sized T1 and T2 */
BinTree
CombineTrees( BinTree T1, BinTree T2 )
{
if( T1->Element > T2->Element )
return CombineTrees( T2, T1 );
T2->NextSibling = T1->LeftChild;
T1->LeftChild = T2;
return T1;
}
/* Merge two binomial queues */
/* Not optimized for early termination */
/* H1 contains merged result, H2 would be cleared */
BinQueue
Merge( BinQueue H1, BinQueue H2 )
{
BinTree T1, T2, Carry = NULL;
int i, j;
if( H1->CurrentSize + H2->CurrentSize > Capacity )
printf( "Merge would exceed capacity" );
H1->CurrentSize += H2->CurrentSize;
for( i = 0, j = 1; j <= H1->CurrentSize; i++, j *= 2 ) {
T1 = H1->TheTrees[ i ]; T2 = H2->TheTrees[ i ];
switch( !!T1 + 2 * !!T2 + 4 * !!Carry ) {
case 0: /* No trees */
case 1: /* Only H1 */
break;
case 2: /* Only H2 */
H1->TheTrees[ i ] = T2;
H2->TheTrees[ i ] = NULL;
break;
case 4: /* Only Carry */
H1->TheTrees[ i ] = Carry;
Carry = NULL;
break;
case 3: /* H1 and H2 */
Carry = CombineTrees( T1, T2 );
H1->TheTrees[ i ] = H2->TheTrees[ i ] = NULL;
break;
case 5: /* H1 and Carry */
Carry = CombineTrees( T1, Carry );
H1->TheTrees[ i ] = NULL;
break;
case 6: /* H2 and Carry */
Carry = CombineTrees( T2, Carry );
H2->TheTrees[ i ] = NULL;
break;
case 7: /* All three */
H1->TheTrees[ i ] = Carry;
Carry = CombineTrees( T1, T2 );
H2->TheTrees[ i ] = NULL;
break;
}
}
return H1;
}
/* Not optimized for O(1) amortized performance */
BinQueue
Insert( ElementType Item, BinQueue H )
{
BinTree NewNode;
BinQueue OneItem;
NewNode = malloc( sizeof( struct BinNode ) );
if( NewNode == NULL )
printf( "Out of space!!!" );
NewNode->LeftChild = NewNode->NextSibling = NULL;
NewNode->Element = Item;
OneItem = Initialize( );
OneItem->CurrentSize = 1;
OneItem->TheTrees[ 0 ] = NewNode;
return Merge( H, OneItem );
}
ElementType
DeleteMin( BinQueue H )
{
int i, j;
int MinTree; /* The tree with the minimum item */
BinQueue DeletedQueue;
BinTree DeletedTree, OldRoot;
ElementType MinItem;
if( H->CurrentSize == 0 ) {
printf( "Empty binomial queue" );
return -Infinity;
}
MinItem = Infinity;
for( i = 0; i < MaxTrees; i++ ) {
if( H->TheTrees[ i ] &&
H->TheTrees[ i ]->Element < MinItem ) {
/* Update minimum */
MinItem = H->TheTrees[ i ]->Element;
MinTree = i;
}
}
DeletedTree = H->TheTrees[ MinTree ];
OldRoot = DeletedTree;
DeletedTree = DeletedTree->LeftChild;
free( OldRoot );
DeletedQueue = Initialize( );
DeletedQueue->CurrentSize = ( 1 << MinTree ) - 1;
for( j = MinTree - 1; j >= 0; j-- ) {
DeletedQueue->TheTrees[ j ] = DeletedTree;
DeletedTree = DeletedTree->NextSibling;
DeletedQueue->TheTrees[ j ]->NextSibling = NULL;
}
H->TheTrees[ MinTree ] = NULL;
H->CurrentSize -= DeletedQueue->CurrentSize + 1;
Merge( H, DeletedQueue );
return MinItem;
}
#define MaxSize (12000)
int main( )
{
BinQueue H;
int i, j;
ElementType AnItem;
H = Initialize( );
for( i=0, j=MaxSize/2; i<MaxSize; i++, j=( j+71)%MaxSize ) {
printf( "Inserting %d\n", j );
H = Insert( j, H );
}
j = 0;
while( H->CurrentSize != 0 ) {
printf( "DeleteMin\n" );
if( DeleteMin( H ) != j++ )
printf( "Error in DeleteMin, %d\n", j );
}
if( j != MaxSize )
printf( "Error in counting\n" );
printf( "Done...\n" );
return 0;
}
6.6. Fibonacci Heap(斐波那契堆)
Fibonacci heap is a heap data structure consisting of a collection of trees. It has a better amortized running time than a binomial heap. The name of Fibonacci heap comes from Fibonacci numbers which are used in the running time analysis.
斐波那契堆各种操作的平摊运行时间都比较理想。除 DeleteMin 操作需要 \(O(log_{2}N)\) 平摊运行时间外,其它常见操作(如 FindMax, Insert, DecreaseKey, Merge)仅需 \(\Theta(1)\) 的平摊运算时间。
但实际应用中,由于斐波那契堆的常数因子和程序设计上的复杂性,使得它通常不如二叉堆(或 k 叉堆)合适。因此,斐波那契堆主要是具有理论上的意义。
斐波那契堆和二项堆一样,由一组树(不一定是二项树)构成。斐波那契堆的结构比二项堆更松散一些,从而可以改善渐近时间界。对结构的维护工作被延迟到方便时再做。
参考:
Introduction to Algorithms, 3rd Edition. Chapter 19 Fibonacci Heaps
6.7. Pairing Heap(配对堆)
斐波那契堆各种操作的平摊运行时间在理论上都比较理想;但实践中,它的实现比较复杂,实际运行时的性能不够优秀。
配对堆的实现更简单,同时也有较好的运行时间界。
参考:
Data Structures and Algorithm Analysis in C, 2nd Edition. 12.7 Pairing Heap
The Pairing-Heap: A New Form of Self-Adjusting Heap: https://www.cs.cmu.edu/~sleator/papers/pairing-heaps.pdf
6.8. 常见优先队列实现的时间复杂度
假设优先队列为“最小堆”,如果为“最大堆”则相关的函数名应改为 FindMax,DeleteMax,IncreaseKey。
| Operation | Binary Heap | Binomial Heap | Fibonacci Heap | Pairing Heap |
|---|---|---|---|---|
| FindMin | \(\Theta(1)\) | \(\Theta(1)\) | \(\Theta(1)\) | \(\Theta(1)\) |
| DeleteMin | \(\Theta(log_{2}N)\) | \(\Theta(log_{2}N)\) | \(O(log_{2}N)\) | \(\Theta(log_{2}N)\) |
| Insert | \(\Theta(log_{2}N)\) | \(\Theta(1)\) | \(\Theta(1)\) | \(\Theta(1)\) |
| DecreaseKey | \(\Theta(log_{2}N)\) | \(\Theta(log_{2}N)\) | \(\Theta(1)\) | \(O(log_{2}N)\) |
| Merge | \(\Theta(Mlog_{2}N)\) | \(O(log_{2}N)\) | \(\Theta(1)\) | \(\Theta(1)\) |
说明:N为堆的大小;Merge 操作中的 N 为大堆的大小,M为小堆的大小。
参考:https://en.wikipedia.org/wiki/Fibonacci_heap#Summary_of_running_times
6.9. 优先队列的应用
Priority queue applications:
- Bandwidth management
- Discrete event simulation
- Dijkstra’s algorithm
- Huffman coding
- Best-first search algorithms
- ROAM triangulation algorithm
- Prim’s Algorithm for Minimum Spanning Tree
7. Hash Table
哈希表以常数时间支持对象的插入、删除和查找。但任何需要排序信息的操作得不到有效的支持,如 FindMin,FindMax 等。
7.1. 哈希表基本思路
如果要保存对象的关键字是非负整数,如果建立一个数组 a[N],其中 N 为关键字中的最大整数,每个对象放入到数组中其关键字对应的位置中,这样能实现以常数时间支持对象的插入、删除和查找。
这种思路很好,但有两个明显问题。一是如果关键字的最大整数非常大,则会浪费巨大的内存;二是对象的关键字往往是字符串,而不是非负整数。这两个问题可以通过一个映射函数(称为 hash 函数)来解决,它把关键字映射到一个小的整数范围中。但不可避免地,存在两个关键字映射到同一整数的情况,这被称为哈希冲突(hash collision)。
7.2. 哈希函数
哈希函数的设计应尽可能减少冲突的发生,关键字在哈希表中均匀地分散。
如果关键字是整数,哈希函数简单地直接返回“key mod TableSize”即可。这个哈希函数在某种特殊情况下可能会发生较多不必要的冲突。如 key 的个位数都恰好为 0,且哈希表的大小为 10。为了避免这种情况的发生, 简单的解决办法是保证哈希表的大小是素数。
如果关键字是字符串,简单的想法是把字符串中每个字符的 ASCII 码值加起来后再对哈希表的大小取模。这种方法简单高效,但是当且哈希表的大小比较大时,可能不会均匀地分散关键字。如哈希表的大小的 10007,关键字最多 8 个字符长,哈希函数最多映射到范围 0 至 127*8。为了避免这种情况的发生,可以让关键字中每个字符乘上不同的因子后相加再对哈希表的大小取模,如计算 abcd 的哈希值,可以这样:(313a + 312b + 31c + d) mod 10007,用 Horner 法则简化多项式的计算,得如下 hash 函数:
//from: "The C Programming Language, 2nd, 1988" Section 6.6 Table Lookup
unsigned hash(char *s, int size) {
unsigned hashval;
for (hashval = 0; *s != '\0'; s++) {
hashval = *s + 31 * hashval;
}
return hashval % size;
}
为了加快 hash 函数的运算速度,我们用 32(即 2^5)代替 31,利用 C 语言中的移位运算实现乘法,得到下面的 hash 函数:
//from: 参考:《数据结构与算法分析——C语言描述(原书第2版)》5.2节
unsigned hash(char *s, int size) {
unsigned hashval;
for (hashval = 0; *s != '\0'; s++) {
hashval = *s + (hashval << 5);
}
return hashval % size;
}
参考:《数据结构与算法分析——C 语言描述(原书第 2 版)》5.2 节
7.3. 解决冲突
7.3.1. 分离链接法(separate chaining)
分离链接法的思想是将散列到同一个值的所有元素保存到一个链表中。 如图 80 所示。
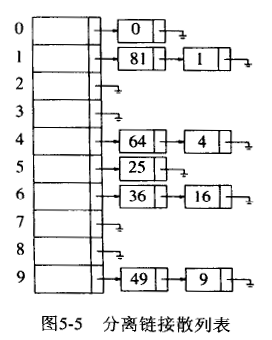
Figure 80: 分离链接法解决哈希冲突
这样在执行查找操作时,计算 hash 找到链表后需要遍历整个链表,性能会下降。
7.3.2. 开放寻址法(open addressing)
开放寻址法是另外一种解决冲突的方法。它的思路是,如果有冲突发生,那么就尝试选择另外的单元(如下一个空单元),直到找到空的单元为止。
由于所有的数据都要置入表内,所以开放寻址法所用的表要比分离链接法所用的表大。一般地,对于开放寻址法,装填因子(Hash 表中存放的元素个数和 Hash 表数组长度的比值)应该低于 0.5。
采用开放寻址法时,元素的删除一般要求是“惰性删除”。因为待删除的单元可能已经引起过冲突,其它元素可能绕过它存在了别处,为了不影响其它元素的查找操作,不能使用标准的删除操作。
7.4. 调整哈希表大小(Resizing)
随着哈希表中存放的元素越来越多时,冲突也越来越多,这时哈希表的性能会下降。为了保证哈希表的查找性能,我们需要重新调整哈希表的大小。
7.4.1. 复制所有元素
调整哈希表大小最直接的办法是:创建一个更大的哈希表,然后把旧哈希表中的元素重新计算哈希后,复制到新哈希表中,最后删除旧哈希表。
这种办法有个缺点:当旧哈希表本身比较大时,其代价较高,对于一些实时性要求高的应用来说是无法承受的。
7.4.2. 渐进式调整(Incremental Resizing)
下面介绍一种渐进式调整哈希表大小(Incremental Resizing)的办法:
- During the resize, allocate the new hash table, but keep the old table unchanged.
- In each lookup or delete operation, check both tables.
- Perform insertion operations only in the new table.
- At each insertion also move r elements from the old table to the new table.
- When all elements are removed from the old table, deallocate it.
To ensure that the old table is completely copied over before the new table itself needs to be enlarged, it is necessary to increase the size of the table by a factor of at least (r + 1)/r during resizing.
注:Redis 中采用的就是 Incremental Resizing 方法来调整哈希表大小。
7.5. 哈希表的简单实现
摘自:“The C Programming Language, 2nd, 1988” Section 6.6 Table Lookup
其中哈希冲突解决采用的是分离链接法。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct nlist {
struct nlist *next; // hash collision resolution(separate chaining)
char *name; // key
char *defn; // value
};
#define HASHSIZE 101
struct nlist *hashtab[HASHSIZE]; /* pointer(point to key-values ) table */
unsigned hash(char *s) {
unsigned hashval;
for (hashval = 0; *s != '\0'; s++) {
hashval = *s + 31 * hashval;
}
return hashval % HASHSIZE;
}
struct nlist *lookup(char *s) {
struct nlist *np;
for (np = hashtab[hash(s)]; np != NULL; np = np->next) {
if (strcmp(s, np->name) == 0) {
return np;
}
}
return NULL;
}
struct nlist *put(char *name, char *defn) {
struct nlist *np;
unsigned hashval;
if ((np = lookup(name)) == NULL) { // not found
np = (struct nlist *) malloc(sizeof(*np));
if (np == NULL || (np->name = strdup(name)) == NULL) {
return NULL;
}
hashval = hash(name);
// insert in front
np->next = hashtab[hashval];
hashtab[hashval] = np;
} else { // already there
free ((void *) np->defn); // free old
}
if ((np->defn = strdup(defn)) == NULL) {
return NULL;
}
return np;
}
int main() {
struct nlist *tmp;
put("key1", "value1");
put("key2", "value2");
put("key2", "value2-new"); //update previous record.
tmp = lookup("key1");
if (tmp != NULL) {
printf("%s\n", tmp->defn);
}
tmp = lookup("key2");
if (tmp != NULL) {
printf("%s\n", tmp->defn);
}
return 0;
}
7.6. Perfect hashing function(完美哈希函数)
如果哈希函数不会产生冲突(即哈希表的查找操作在最坏情况也为 \(O(1)\) ),则称为 perfect hashing function 。
一般情况下,完美哈希函数是针对“静态集合”,即仅对一个固定集合中的元素计算哈希值。
8. Disjoint-Set(Union–Find)
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that keeps track of a set of elements partitioned into a number of disjoint (nonoverlapping) subsets. It supports two useful operations: Find and Union.
Disjoint-Set(不相交集)支持下面 2 种操作:
- Union,作用是合并两个集合;
- Find,作用是查找元素所在的集合。
Disjoint-Set 主要用来解决“图中的动态连通性”问题:一张地图上有很多点,有些点之间有道路连通,而有些点之间则没有。我们想从点 A 走向点 B,一个关键问题是 A 和 B 是否是连通的。显然,如果 Find(A) == Find(B),那么 A 和 B 就是连通的。