Graph Algorithms
Table of Contents
1. 图的基本概念
图(Graph)由顶点(Vertex)和边(Edge)组成, \(G=(V,E)\) 。边 \(e \in E\) 是一个点对 \((v,w)\) ,其中 \(v,w \in V\) 。
如果边 \((v,w) \in E\) ,则称顶点 \(v\) 和 \(w\) 邻接(Adjacent)。
本文主要参考:《数据结构与算法分析——C 语言描述(原书第 2 版)》
1.1. 图的表示:邻接矩阵和邻接表
图有两种常见表示:邻接矩阵(Adjacency matrix)和邻接表(Adjacency matrix)。
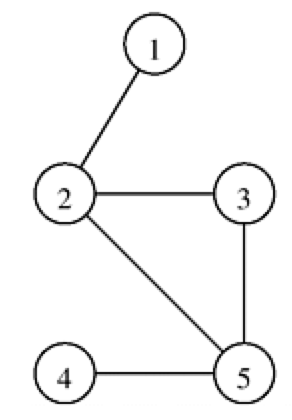
Figure 1: 无向图示例
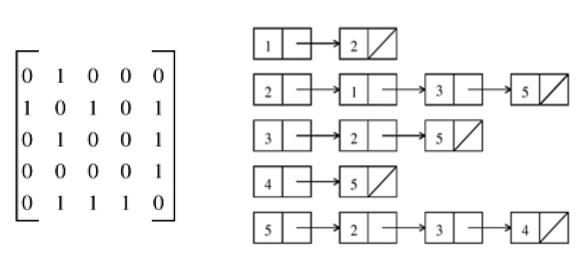
Figure 2: 邻接矩阵表示(左)和邻接表表示(右)
当图为稠密图时,使用邻接矩阵是可行的;但当图为稀疏图(这是更常见的情况)时,使用邻接表更合适。
参考:Introduction to Parallel Computing, Second Edition, By Ananth Grama. Chapter 10. Graph Algorithms
2. 图的遍历——深度优先搜索和广度优先搜索
深度优先搜索应用:有向无环图(DAG)的拓扑排序、查找强连通分支、欧拉回路等等。而图的最短路径算法里常常会用到广度优先搜索。
2.1. 深度优先搜索(DFS)
图的深度优先搜索(depth-first search)很像树的先序遍历。有两种基本实现:一是递归调用;二是使用显式栈。
递归调用实现深度优先搜索的伪代码如下:
void DFS (Vertex V)
{
visited[V] = true;
// Do something.
for each W adjacent to V
{
if ( !visited[W] )
{
DFS(W);
}
}
}
说明 1:全局数组 visited 初始化为 false,通过只对尚未被访问的节点递归调用函数 DFS,可以保证不会陷入无限循环中。
说明 2:如果图是无向的且不连通,或者有向的但非强连通的,上面方法可能会访问不到某些节点(这时可以对未访问顶点显式调用 DFS)。
2.2. 广度优先搜索(BFS)
在深度优先搜索中,使用了栈(递归调用可以看作是一个隐式栈),如果把这个“栈”换成“队列”,可以得到图的另外一种搜索策略——广度优先搜索(breadth-first search)。图的深度优先搜索很像树的层序遍历(level-order traversal)。
广度优先搜索的伪代码如下:
//广度优先搜索的伪代码(从顶点v开始)
把顶点v标记为已到达顶点;
初始化队列Q,其中仅包含一个元素v;
while (Q不为空)
{
从队列中删除顶点w;
令u为邻接于w的那些顶点;
while (u)
{
if (u尚未被标记) {
把u加入队列;
把u标记为已到达顶点;
}
u = 邻接于w的下一个顶点;
}
}
摘自《数据结构、算法与应用——C++语言描述,SartajSahni 著》12.10.1 节。
3. 拓扑排序
拓扑排序是对“有向无环图(Directed Acyclic Graph, DAG)”顶点的一种排序,它使得如果存在一条从 \(v_i\) 到 \(v_j\) 的路径,那么在排序中 \(v_j\) 出现在 \(v_i\) 的后面。拓扑排序不一定是唯一的,任何合理的排序都是可以的。
显然如果图中含有环,那么拓扑排序是不可能的,因为对于环上的两个顶点 \(v\) 和 \(w\) , \(v\) 先于 \(w\) ,但同时 \(w\) 又先于 \(v\) 。
课程表是一个拓扑排序的例子,有些课程必须在另外一些课程选修前修完。
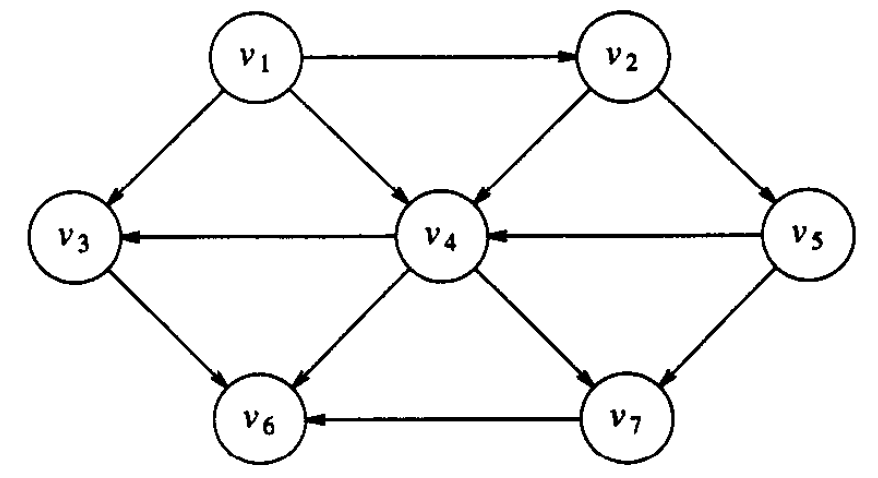
Figure 3: 有向无环图
对于图 3 所示的有向无环图, \(v_1,v_2,v_5,v_4,v_3,v_7,v_6\) 和 \(v_1,v_2,v_5,v_4,v_7,v_3,v_6\) 都是它的拓扑排序。
3.1. 拓扑排序算法
一个简单的拓扑排序算法是: 先找出任意一个没有入边的顶点,然后选择该点,同时将它和它的边一起从图中删除。然后,我们对图的其余部分应用同样的方法处理。
4. 单源最短路径算法
在一个有向图中,从一个顶点出发,求该顶点至所有可到达顶点的最短路径。
4.1. 无权最短路径
无权图可以看作是每条边都赋以权 1。
以图 3 为例,设 \(v_3\) 为出发顶点,如何找出它到其它各个顶点的最短路径?
思路如下( 广度优先搜索策略 ):
先寻找到 \(v_3\) 最短路径长为 1 的顶点,它们显然是和 \(v_3\) 邻接的顶点 \(v_1\) 和 \(v_6\) ,标记这两个顶点。
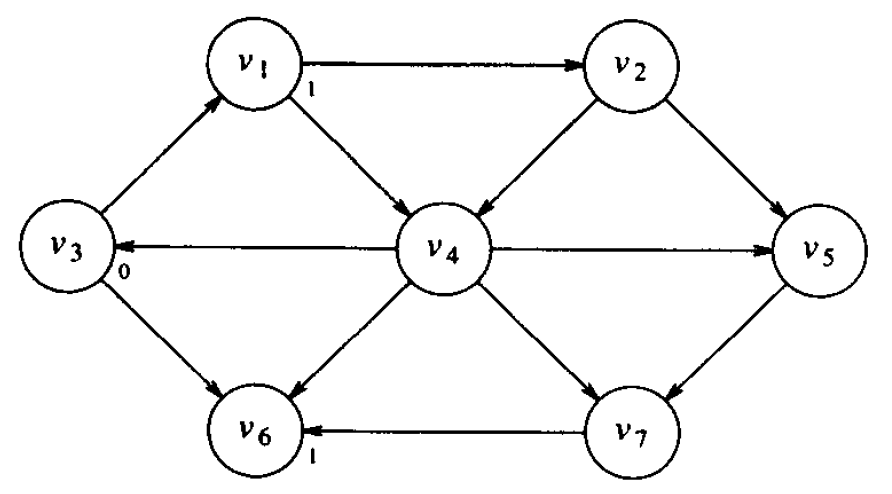
Figure 4: 标记到出发顶点路径长为 1 的顶点
然后,寻找从 \(v_3\) 出发最短路径为 2 的顶点,这可以从 \(v_1\) 和 \(v_6\) (它们是最路径为 1 的顶点)的邻接顶点中找到,只考虑未标记的顶点, \(v_2\) 和 \(v_4\) 满足要求,标记它们为最短路径为 2 的顶点。
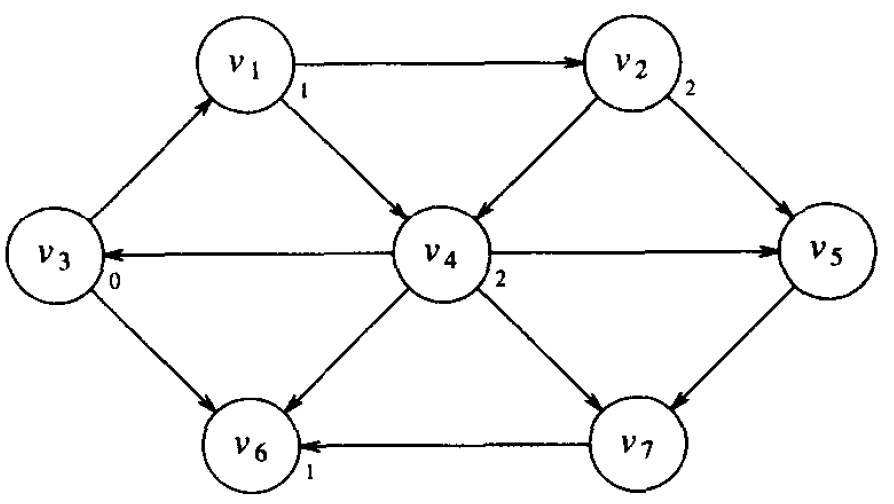
Figure 5: 标记到出发顶点路径长为 2 的顶点
按照同样的方法寻找从 \(v_3\) 出发最短路径为 3 的顶点,它们就是 \(v_2\) 和 \(v_4\) 未标记的邻接顶点 \(v_5\) 和 \(v_7\) 。至此所有顶点都已经被标记,算法结束。
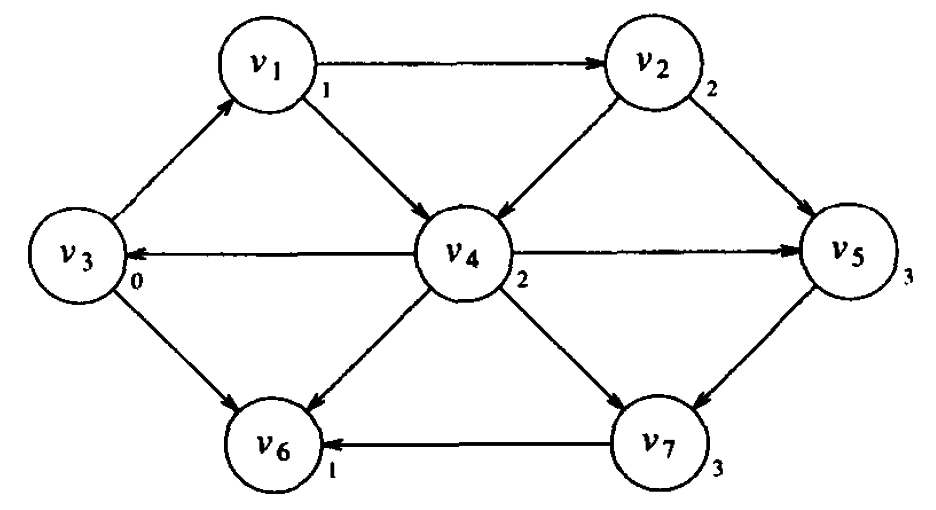
Figure 6: 无权最短路径算法的最后结果
4.2. 赋权图最路径(Dijkstra 算法)
对于赋权图,尽管比无权图复杂,我们仍然可以借鉴前面求无权图最短路径时的思路:从出发顶点进行广度优先搜索,从近到远计算其它顶点到出发顶点的最短路径。
4.2.1. Dijkstra 算法(贪心算法)描述
介绍 Dijkstra 算法前先介绍最短路径树(SPT,Shortest-Path Tree)定义:一个图和它的一个指定的源点(即出发顶点)s,s的最短路径树是指包含 s 以及从 s 可达的所有顶点,它们形成一棵以 s 为根的有向树,其中 每条树路径为图中的最短路径。
显然,Dijkstra 算法就是寻找最短路径树(SPT)的算法。
Dijkstra’s algorithm 的基本思想描述如下: 开始时,将源点放在 SPT 上,然后,一次一条边地生成 SPT,所取的下一条边总是从源点到非 SPT 上顶点的最短路径。换句话说,Dijkstra 算法就是哪个顶点离源点的距离近,就先添加到 SPT 中。 Dijkstra 算法是一种贪心算法。
Dijkstra 算法的具体步骤如下:
(1)、首先给出发顶点标上永久性标号 0,然后给每个与出发顶点直接相连的结点标上一个临时标号,标号值为连接出发顶点和该结点线路的权值。给其它没有和出发顶点相连的结点的临时标号为∞。
(2)、选择具有最小临时标号的结点(这就是贪心算法的策略),将该结点的临时标号改为永久性标号。
(3)、假设结点 i 是刚获得永久性标号的结点,搜索每个与结点 i 直接相连的结点 j,在“结点 j 目前的临时标号”和“结点 i 的永久性标号+边(i,j)的权值”两者间取一个较小的值对结点 j 的临时标号进行更新。
(4)、重复步骤(2)~(3),直到所有结点都具有永久性标号。永久性标号值就是出发顶点到该结点的最短距离。
说明:由于每次要选择具有最小临时标号的结点,所以在实现 Dijkstra 算法时往往要用到优先队列。
Dijkstra 算法的伪代码如下:
// Pseudocode (excerpted from wikipedia)
function Dijkstra(Graph, source):
create vertex set Q
for each vertex v in Graph: // Initialization
dist[v] ← INFINITY // Unknown distance from source to v
prev[v] ← UNDEFINED // Previous node in optimal path from source
add v to Q // All nodes initially in Q (unvisited nodes)
dist[source] ← 0 // Distance from source to source
while Q is not empty:
u ← vertex in Q with min dist[u] // Source node will be selected first
remove u from Q
for each neighbor v of u: // where v is still in Q.
alt ← dist[u] + length(u, v)
if alt < dist[v]: // A shorter path to v has been found
dist[v] ← alt
prev[v] ← u
return dist[], prev[]
4.2.1.1. 无环图
如果已知图是无环图,我们可以按拓扑顺序来选择顶点。由于选择和更新可以在拓扑排序执行的时候进行,所以 Dijkstra 算法可以一趟完成。
因为当一个顶点 \(v\) 被选取以后,按照拓扑排序的法则,它没有从未知顶点发出的进入边,因此它的距离 \(d_v\) 不再会被降低,所以这种选择法则是行得通的。
4.2.2. Dijkstra 算法实例分析
下图中线上所标注的数字为相邻结点之间的距离(即权值),设结点 1 为源点,求源点到其他各点的最短路径。
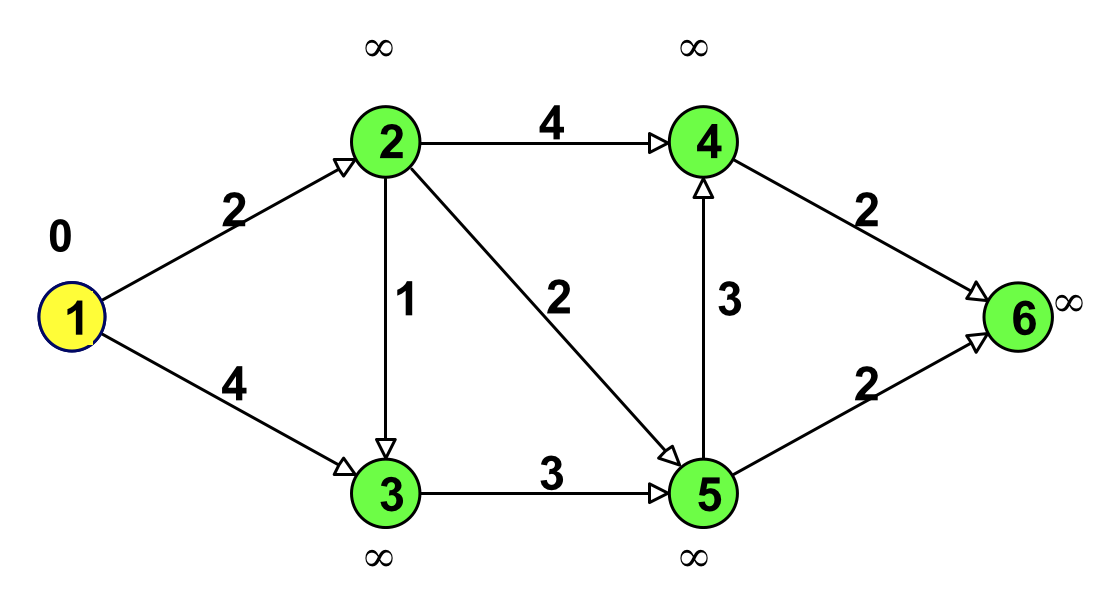
Figure 7: Dijkstra 算法实例(完成初始化)
注 1:黄色点表示“最小临时标号”的点,绿色点表示还未分析过的点,红色点表示永久性标号的点。
注 2:下面过程中,“选择”对应前面介绍算法中的步骤(2),“更新”对应步骤(3)。
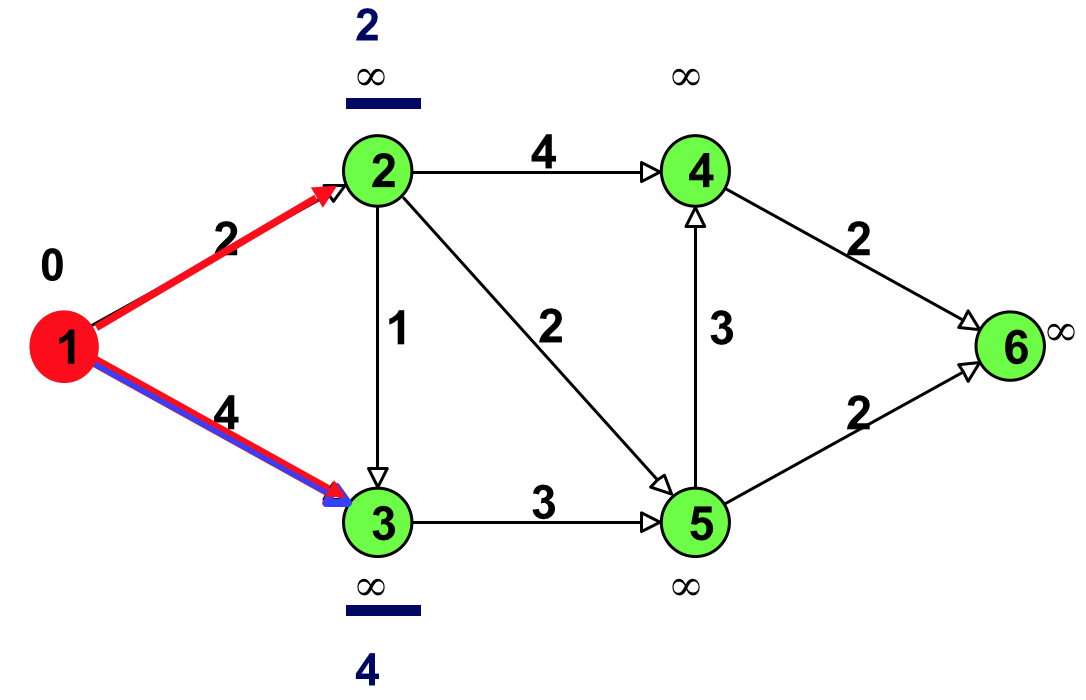
Figure 8: 更新(结点 1 邻接的点:结点 2 和结点 3)
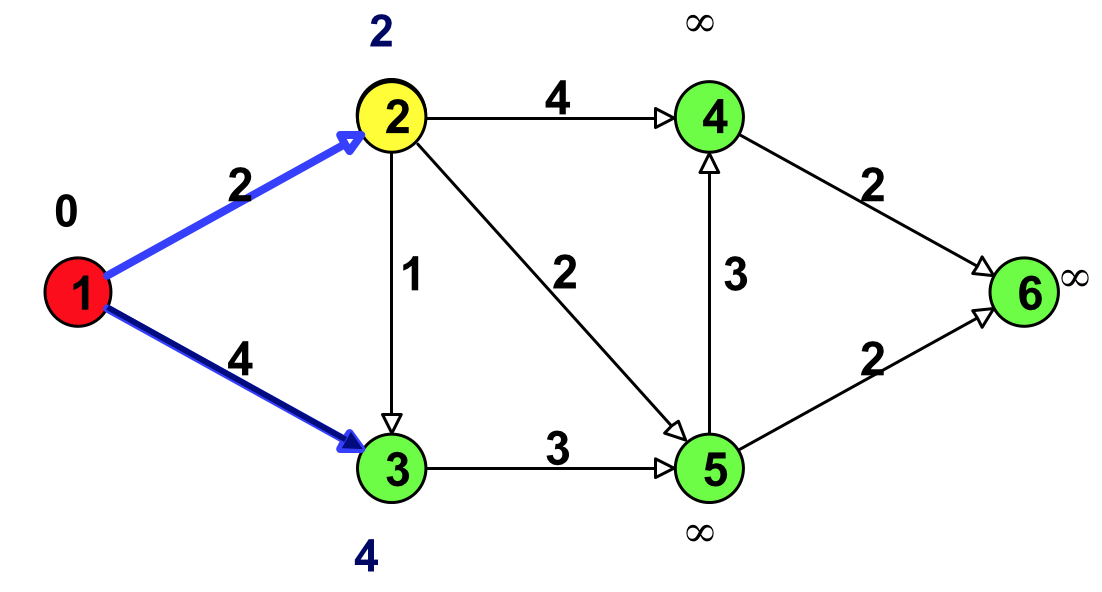
Figure 9: 选择具有最小临时标号的点(结点 2)
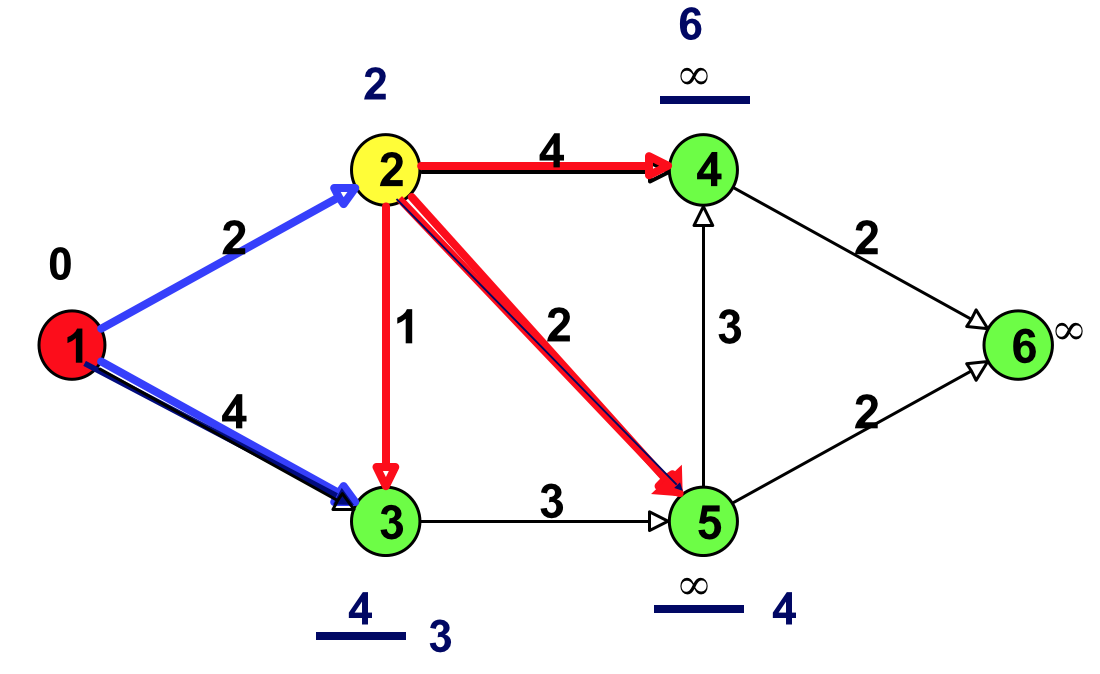
Figure 10: 更新(结点 2 邻接的点:结点 3、结点 4 和结点 5)
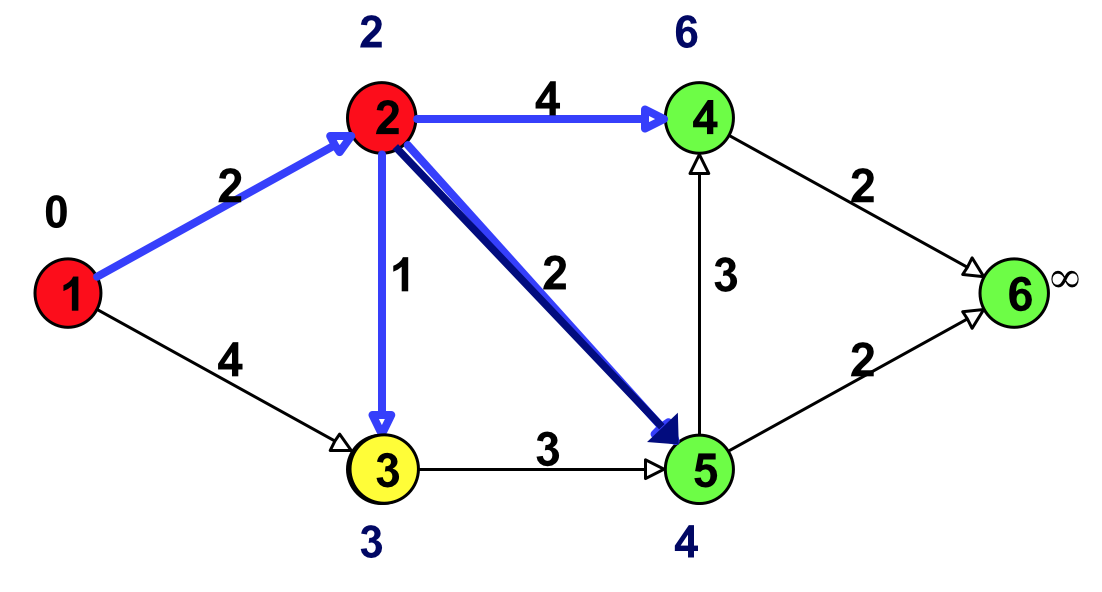
Figure 11: 选择具有最小临时标号的点(结点 3)
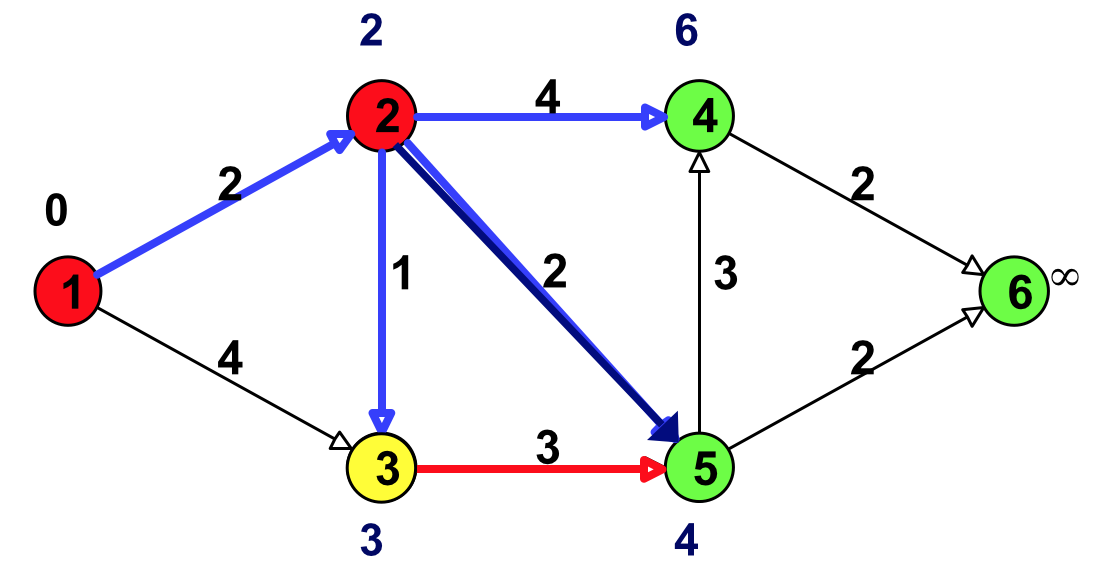
Figure 12: 更新(结点 3 邻接的点:结点 5)
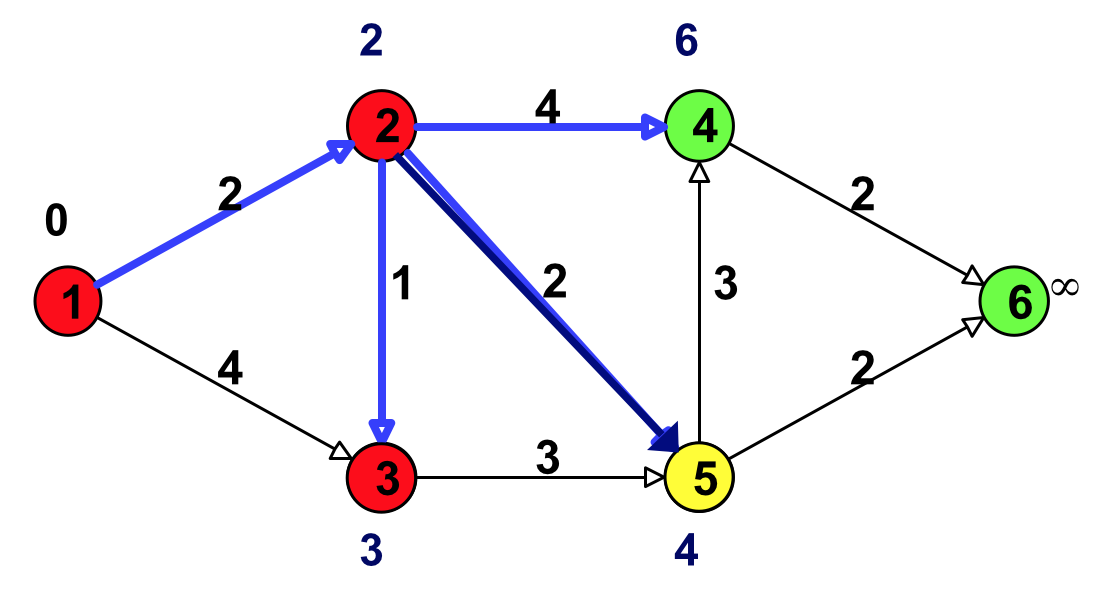
Figure 13: 选择具有最小临时标号的点(结点 5)
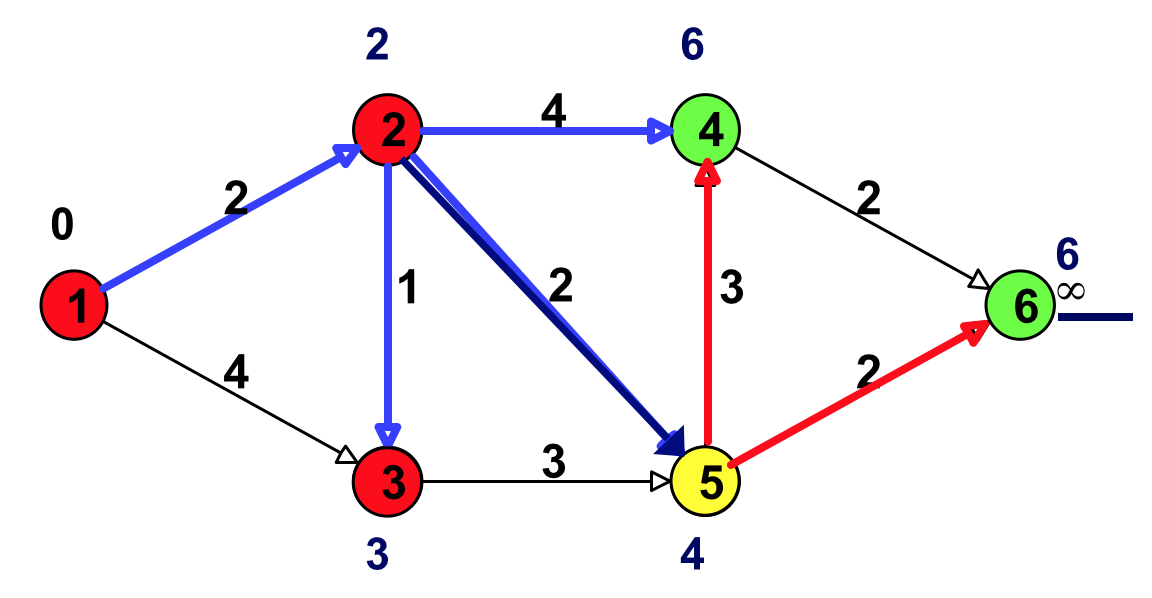
Figure 14: 更新(结点 5 邻接的点:结点 4 和结点 6)
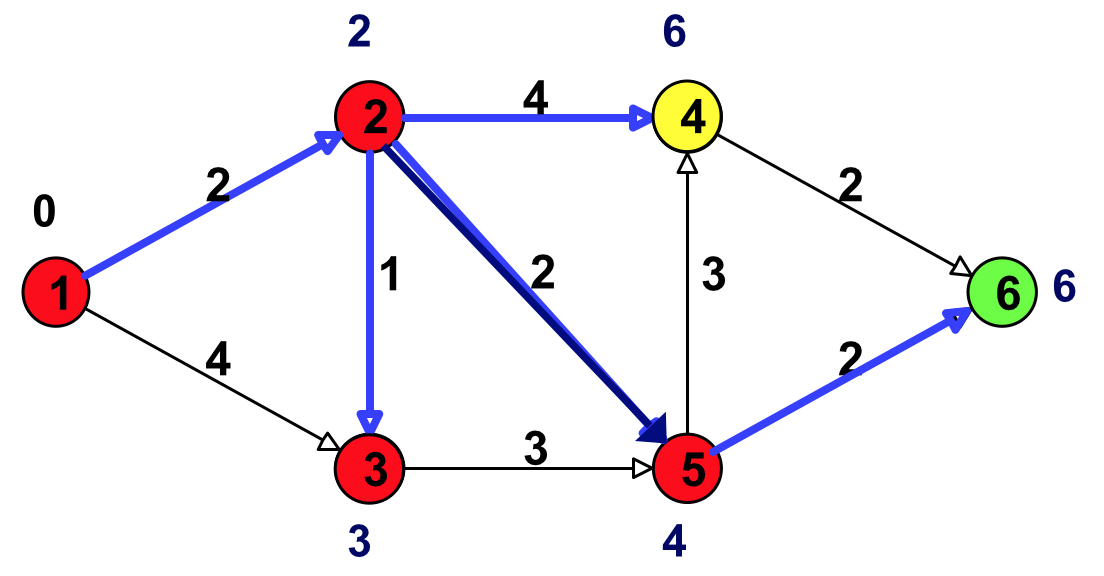
Figure 15: 选择具有最小临时标号的点(结点 5)
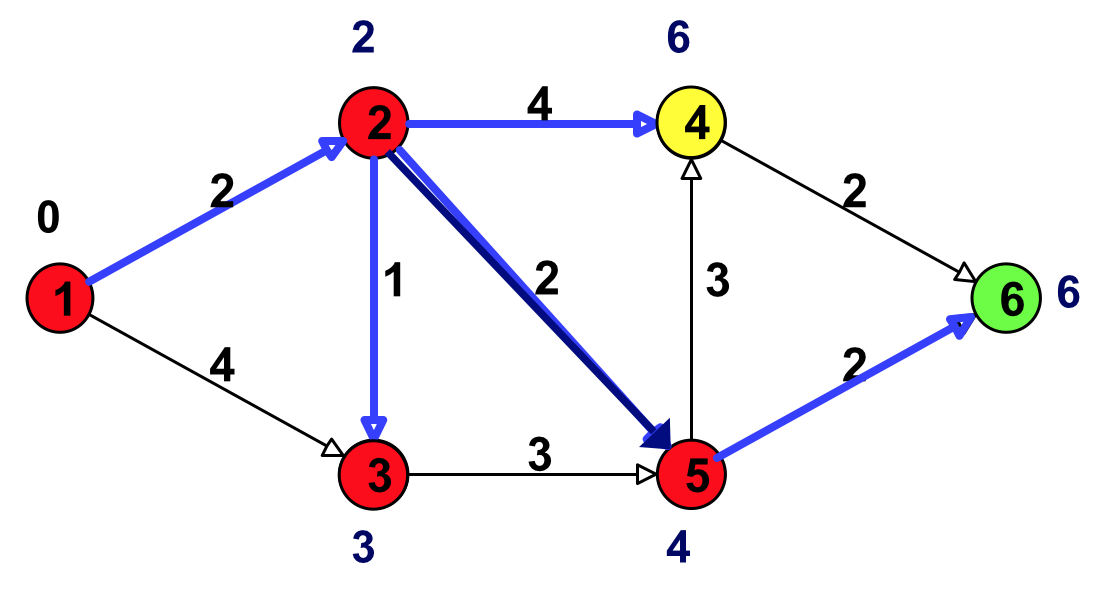
Figure 16: 更新(结点 5 邻接的点:结点 4 和结点 6)
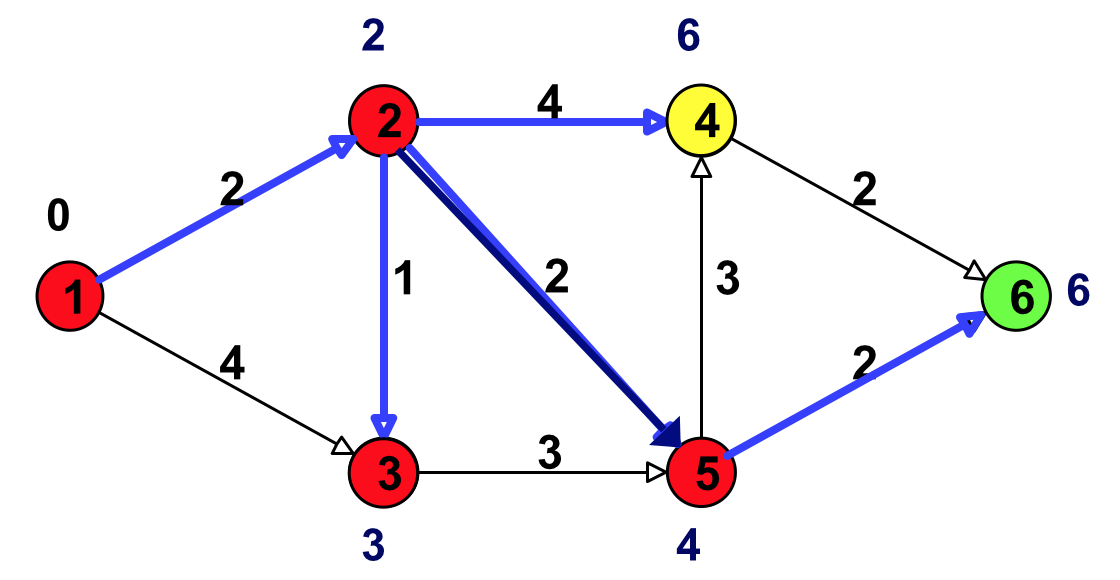
Figure 17: 选择具有最小临时标号的点(结点 4 和结点 6 都可以,这里选择结点 4)
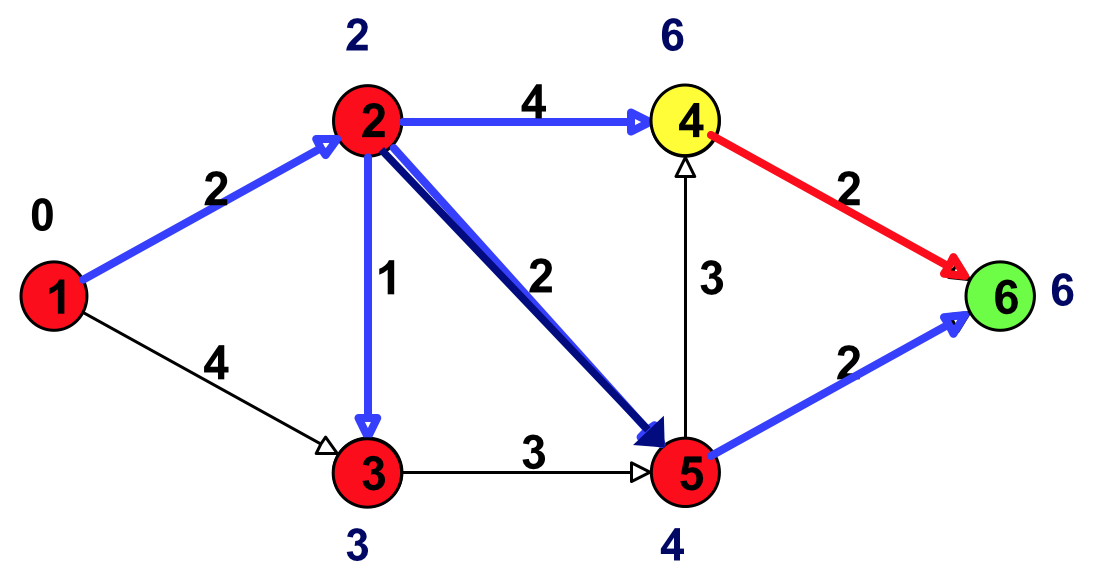
Figure 18: 更新(结点 4 邻接的点:结点 6)
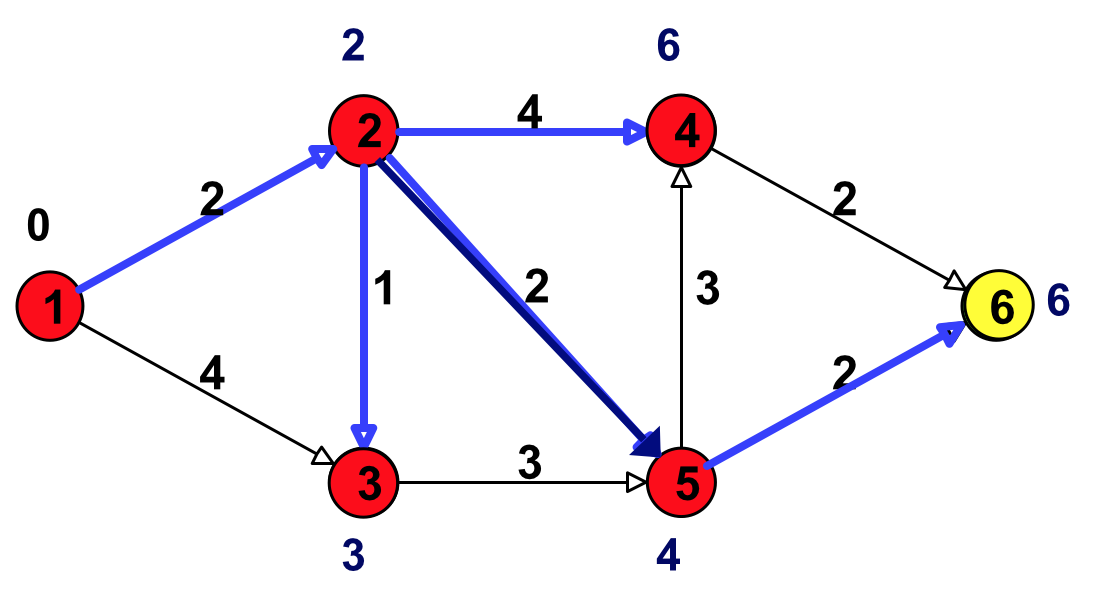
Figure 19: 选择具有最小临时标号的点(只剩下结点 6 了,选择它)
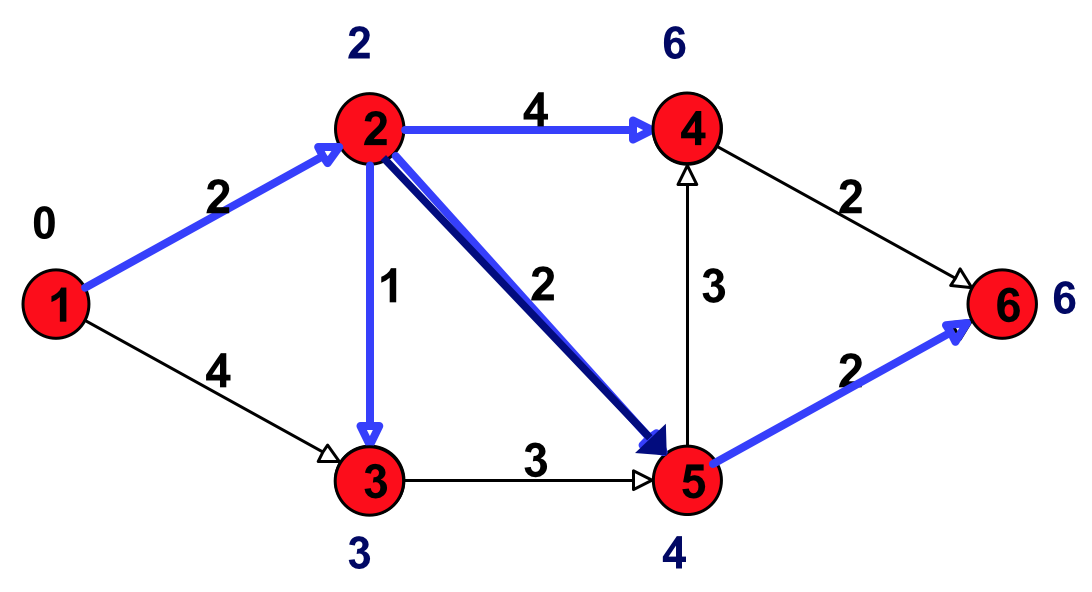
Figure 20: 所有结点都有了永久性标号,算法结束
算法结束后,可以通过回溯前驱结点找到最短路径树(SPT)。
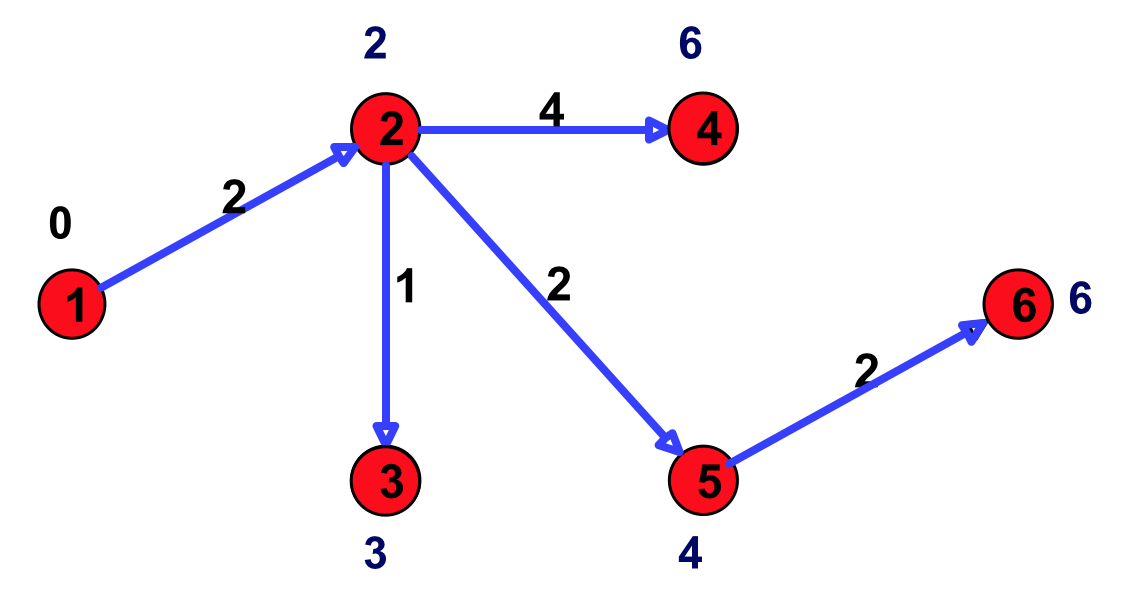
Figure 21: 最短路径树
参考:
http://wenku.baidu.com/view/8837010aba1aa8114431d9ec.html
http://www.utdallas.edu/~dzdu/cs6363/lect06.ppt
4.2.3. Dijkstra 算法实现
Dijkstra 算法的简单实现如下:
//Dijkstra算法的简单实现
//其中图用邻接矩阵表示
#include<iostream>
using std::cout;
using std::endl;
#define NoEdge 100000 //用NoEdge表示不邻接的结点间的权值。NoEdge的值远大于所有边的权值。
#define N 6 //图中的结点总数。
//功能,求从s点开发到各个结点的最短路径。
//w表示图的(带权)邻接矩阵。
//在数组d[]中返回结点到源点的最短距离。
//在数组p[]中返回最短路径树(SPT)中结点的前驱结点。
//w、s为输入参数,d、p为输出参数。
void Dijkstra(int w[][N], int s, int d[], int p[])
{
int known[N] = {0};
int i;
for (i = 0; i < N; i++) {//初始化d[]和p[]。
d[i] = w[s][i]; //给d[]赋初值,注意有向图中w[s][i]和w[i][s]是不同的。
if (d[i] <NoEdge)
p[i] = s; //把和源点s相连的结点的前驱结点标记为s。
else
p[i] = -1; //把和源点s不相连的结点的前驱结点标记为-1。
}
known[s] = 1; //known[i]=1时表示结点i已经加入到最短路径树(SPT)中,即它的最短路径已经确定。
//开始主循环,每次求得s到某个结点k的最短路径,并设置known[k]=1。
for (i = 1; i < N; i++) { //只要更新N-1次即可。i只是用来控制更新次数,在循环体中没有用到。
int t = NoEdge;
int k = s;
for (int j = 0; j < N; j++) { //每次在最短路径树(SPT)外的结点中找离s最近的结点,标记为k。
if((!known[j]) && (d[j] < t)) {
t = d[j];
k = j;
}
}
known[k] = 1;
for (int j = 0; j < N; j++) { //更新当前最短路径及距离
if((!known[j]) && (w[k][j] < NoEdge) && (d[j] > d[k] + w[k][j])) {
d[j] = d[k] + w[k][j];
p[j] = k;
}
}
}
}
//测试Dijkstra程序
int main()
{
int w[N][N] = {
{0,2,4,NoEdge,NoEdge,NoEdge},
{NoEdge,0,1,4,2,NoEdge},
{NoEdge,NoEdge,0,NoEdge,3,NoEdge},
{NoEdge,NoEdge,NoEdge,0,NoEdge,2},
{NoEdge,NoEdge,NoEdge,3,0,2},
{NoEdge,NoEdge,NoEdge,NoEdge,NoEdge,0}
};
int d[N];
int p[N];
Dijkstra(w,0,d,p);
cout<<"Vertex: "<<"Shortest Path: "<<"Predecessor Vertex:"<<endl;
for (int i = 0; i < N; i++) {
cout<<i+1<<" "<<d[i]<<" "<<p[i]+1<<endl; //+1仅仅是为了把起始结点号从0变为1。
}
return 0;
}
说明 1:上面的实现不是高效的,可以通过用“优先队列”代替数组 d 来提高效率。
说明 2:对于稀疏图用邻接矩阵是很低效的,应该使用邻接表。
上面程序中使用的测试数据来自上节介绍的实例。运行程序,得到下面输出:
Vertex: Shortest Path: Predecessor Vertex: 1 0 1 2 2 1 3 3 2 4 6 2 5 4 2 6 6 5
得到上面的输出结果容易得到对应的最短路径树,即图 21 。
4.2.4. Dijkstra 算法应用
开放最短路径优先(Open Shortest Path First, OSPF)算法是 Dijkstra 算法在网络路由中的一个具体实现。
4.2.5. Dijkstra 算法不足
Dijkstra 算法不适应有权值为负数的情况。
4.3. Bellman-Ford 算法(可适应权值为负数的情况)
Dijkstra 算法不能适应有边的权值为负数的情况, Bellman-Ford算法 可以处理有负数权值边的情况。
参考:算法导论(原书第 2 版),24.1 Bellman-Ford 算法
4.3.1. SPFA 算法
SPFA 全称 Shortest Path Faster Algorithm ,用于求单源最短路径(可以认为 SPFA 是对 Bellman-Ford 算法的优化)。
SPFA 是段凡丁(西南交通大学软件学院副院长)于 1994 年发表的。
有时,给定的图存在负权边,这时 Dijkstra 等算法便没有了用武之地,而 Bellman-Ford 算法的复杂度又过高,SPFA 算法便派上用场。
该算法在 NOIP(全国青少年信息学奥林匹克联赛)和 ACM-ICPC(ACM 国际大学生程序设计竞赛)竞赛中受到广泛的关注和学习,赢得了强烈的反响和好评。
4.4. A*算法
Dijkstra 算法计算源点到所有其他点的最短路径长度,A*(A Star)算法关注点到点的最短路径。
Dijkstra 算法用来求点到点的最短路径的话,它实际上毫无方向地向四周搜索,发现了目标点后即终止。而 A*算法用来求点对点最短路径的优点在于能保证最短路径的搜索始终向着终点的方向进行。
4.5. D*算法
前面介绍的算法(如 Dijkstra 算法,A*算法)都是静态路径最短路径算法,即外界环境不变的情况下,计算最短路径。
还有一类最短路径算法——动态路径最短路径算法,指外界环境不断发生变化(如权重等不断变化),即不能计算预测的情况下计算最短路。如在游戏中敌人或障碍物不断移动的情况下。典型的有 D*(D Star)算法,美国火星探测器核心的寻路算法就是采用的 D*算法。
5. 所有顶点对的最短路径
有时需要找出图中所有顶点对之间的最短路径,显然这可以通过运行多次单源最短路径算法来求解,但我们期望更快的算法来立即得到所有顶点对的最短路径。
5.1. 基于矩阵乘法的动态规划算法
略。参考:算法导论(原书第 2 版),25.1 最短路径与矩阵乘法
5.2. Floyd-Warshall 算法(动态规划算法)
Floyd-Warshall 算法有时也直接称为 Floyd 算法(弗洛伊德算法)。Floyd 算法在稠密图上的效果比较好,其效率要高于多次运用 Dijkstra 算法(假设图边权值都为正数),当然对于稀疏图,Floyd 算法并没有优势。
Floyd 算法是一种动态规划算法。可以看做是在 Warshall 算法(也是一种动态规划算法)基础上扩展而来的。
5.2.1. Warshall 算法(求解传递闭包)
Warshall 算法用来计算有向图的传递闭包(Transitive Closure)。
参考:《算法设计与分析基础,第 2 版,Anany Levitin 著》8.2 节。
5.2.1.1. 传递闭包
什么是有向图的传递闭包?一个 \(n\) 顶点有向图的传递闭包定义为一个 \(n\) 阶布尔矩阵 \(T=\{t_{ij}\}\) ,如果从第 \(i\) 个顶点到第 \(j\) 个顶点之间存在一条有效的有向路径, \(t_{ij}\) 就设为 1,否则 \(t_{ij}\) 为 0。
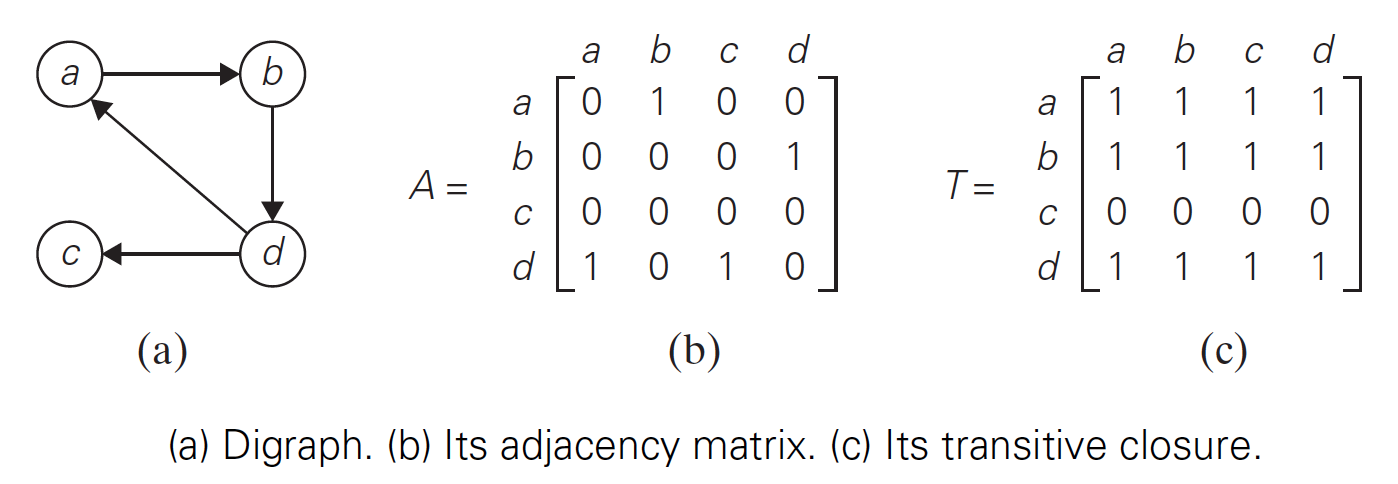
Figure 22: 传递闭包实例
显然,通过图的传递闭包能知道图的任意顶点之间是否存在着有向路径。
5.2.1.2. Warshall 算法描述
如何求有向图的传递闭包?
显然我们可以通过深度优先查找或广度优先查找得到,从第 \(i\) 个顶点开始,无论采用哪种遍历方法,都能够得到通过第 \(i\) 个顶点访问到的所有顶点的信息,再把传递闭包的第 \(i\) 行的相应列置为 1。这样的话,以每个顶点为起始点做一次这样的遍历就生成了整个图的传递闭包。
用上面的方法对有向图遍历了多次,有没有更好的算法?有,就是 Warshall 算法。
定义矩阵 \(R^{(k)}\) ,当且仅当,从第 \(i\) 个顶点到第 \(j\) 个顶点之间存在一条有向路径并且 路径的每一个中间顶点的编号不大于 \(k\) 时 , \(r_{ij}\) 就设置于为 1,否则为 0。这样对于含有 \(n\) 个顶点的有向图来说就有一系列矩阵:
\[R^{(0)}, R^{(1)}, \cdots , R^{(k-1)}, R^{(k)}, \cdots, R^{(n)}\]
根据上面定义,矩阵 \(R^{(0)}\) ,表示不允许它的路径中包含任何中间顶点,显然 \(R^{(0)}\) 就是有向图的邻接矩阵。矩阵 \(R^{(1)}\) ,表示允许使用第一个顶点作为中间顶点的路径信息,这样的话这个矩阵会比 \(R^{(0)}\) 包含更多的 1。推而广之, \(R^{(k)}\) 相对于 \(R^{(k-1)}\) 来说,允许增加一个顶点作为其路径上的顶点,所以 \(R^{(k)}\) 一般来说(不是必然)会比 \(R^{(k-1)}\) 包含更多的 1。
最后一个矩阵 \(R^{(n)}\) ,反映了能够以有向图中所有顶点作为中间顶点的路径,因此它就是有向图的传递闭包。
Warshall 算法的基本思路:利用 \(R^{(k-1)}\) 计算 \(R^{(k)}\) ,最后得到 \(R^{(n)}\) 。
怎么利用 \(R^{(k-1)}\) 计算 \(R^{(k)}\) 呢?当 \(r^{k}_{ij} = 1\) 时,要么 \(r^{k-1}_{ij} = 1\) ,要么 \(r^{k-1}_{ik} = 1\) 且 \(r^{k-1}_{kj} = 1\) 。即有:
\[r^{k}_{ij} = r^{k-1}_{ij} \; \text{or} \; ( r^{k-1}_{ik} \; \text{and} \; r^{k-1}_{kj})\]
上式就是 Warshall 算法的核心递推式!为什么会这样,请看下面分析。
(1) 如果 \(r^{(k-1)}_{ij}=1\) ,说明可以从顶点 \(i\) 走到顶点 \(j\) ,显然可得到 \(r^{(k)}_{ij}=1\) ;
(2) 如果 \(r^{(k-1)}_{ik}=1\) 且 \(r^{(k-1)}_{kj}=1\) ,说明可以从顶点 \(i\) 走到顶点 \(k\) ,从顶点 \(k\) 走到顶点 \(j\) ,当然也有 \(r^{(k)}_{ij}=1\) 。
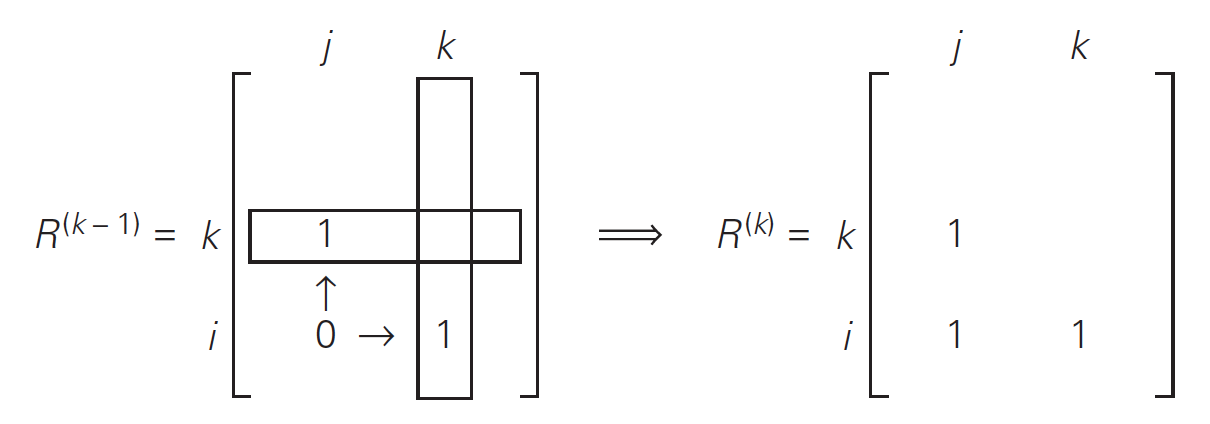
Figure 23: Warshall 算法将 0 变成 1 的规则
5.2.1.3. Warshall 算法实例
Warshall 算法实例如图 24 所示。
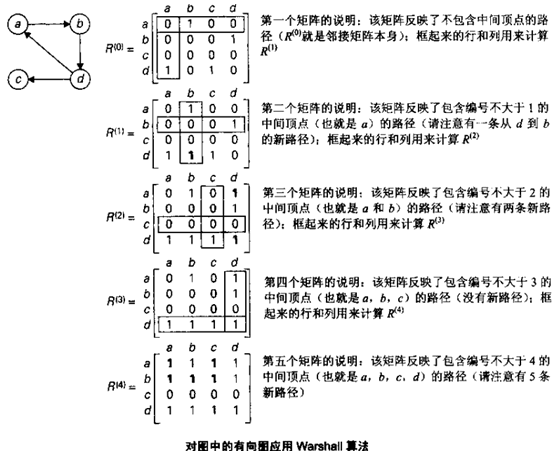
Figure 24: Warshall 算法实例
5.2.1.4. Warshall 算法伪代码
Warshall 算法伪代码如下:
//Implements Warshall’s algorithm for computing the transitive closure
//Input: The adjacency matrix A of a digraph with n vertices
//Output: The transitive closure of the digraph
R(0) ← A
for k←1 to n do
for i←1 to n do
for j←1 to n do
R(k)[i, j] ← R(k−1)[i, j] or ( R(k−1)[i, k] and R(k−1)[k, j] )
return R(n)
代码非常地简洁,3个 for 循环搞定,但其时间效率仅仅为 \(O(n^3)\) 。
5.2.2. Floyd-Warshall 算法
Floyd-Warshall 算法常常简称 Floyd 算法。
Floyd 算法几乎和 Warshall 算法完全一样,不同之处在于,它不使用逻辑运算来跟踪路径的存在,而检查每条边对应的路径来判断该边是否为新的更短路径的一部分。
为了方便起见,我们把最短路径的长度记录在 \(n\) 阶矩阵 \(D\) 中,这个矩阵称为路径矩阵(Distance Matrix)。如图 25 所示。
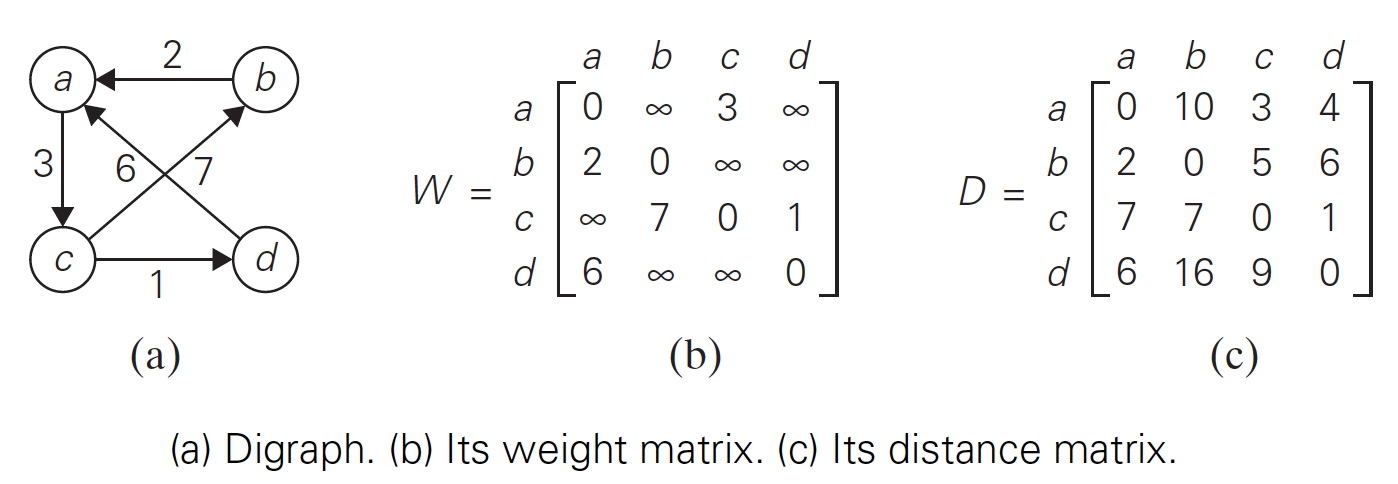
Figure 25: 路径矩阵实例
5.2.2.1. Floyd 算法描述
我们可以使用一种非常类似于 Warshall 算法的方式来生成这个距离矩阵,称为 Floyd 算法。
Floyd 算法通过一系列 \(n\) 阶矩阵来计算一个 \(n\) 顶点加权图的距离矩阵:
\[D^{(0)}, D^{(1)}, \cdots , D^{(k-1)}, D^{(k)}, \cdots, D^{(n)}\]
矩阵 \(D^{(k)}\) 的定义为:第 \(i\) 行第 \(j\) 列的元素 \(d^(k)_{ij}\) 等于从第 \(i\) 个顶点到第 \(j\) 个顶点之间所有路径中最短的那条的长度,并且 路径的每一个中间顶点的编号不大于 \(k\) 。
显然 \(D^{(0)}\) 是权重矩阵。序列最后一个矩阵 \(D^{(n)}\) 是能够以所有 \(n\) 个顶点为中间顶点的全部路径中最短路径的长度,因此它就是我们想要求的距离矩阵。
和 Warshall 算法一样,每一个 D(k)都可以通过它的直接前趋 D(k-1)计算得到。公式如下:
\[d^{(k)}_{ij} = min\{d^{(k-1)}_{ij}, d^{(k-1)}_{ik} + d^{(k-1)}_{kj} \}\]
也可以用另一种方法表述,如果要把当前距离矩阵 \(D^{(k-1)}\) 中的第 \(i\) 行第 \(j\) 列元素替换为第 \(i\) 行(同一行)第 \(k\) 列元素和第 \(k\) 行第 \(j\) 列(同一列)元素的和,当且仅当后者的和小于它的当前值。
5.2.2.2. Floyd 算法实例
图 26 是 Floyd 算法的一个具体实例。
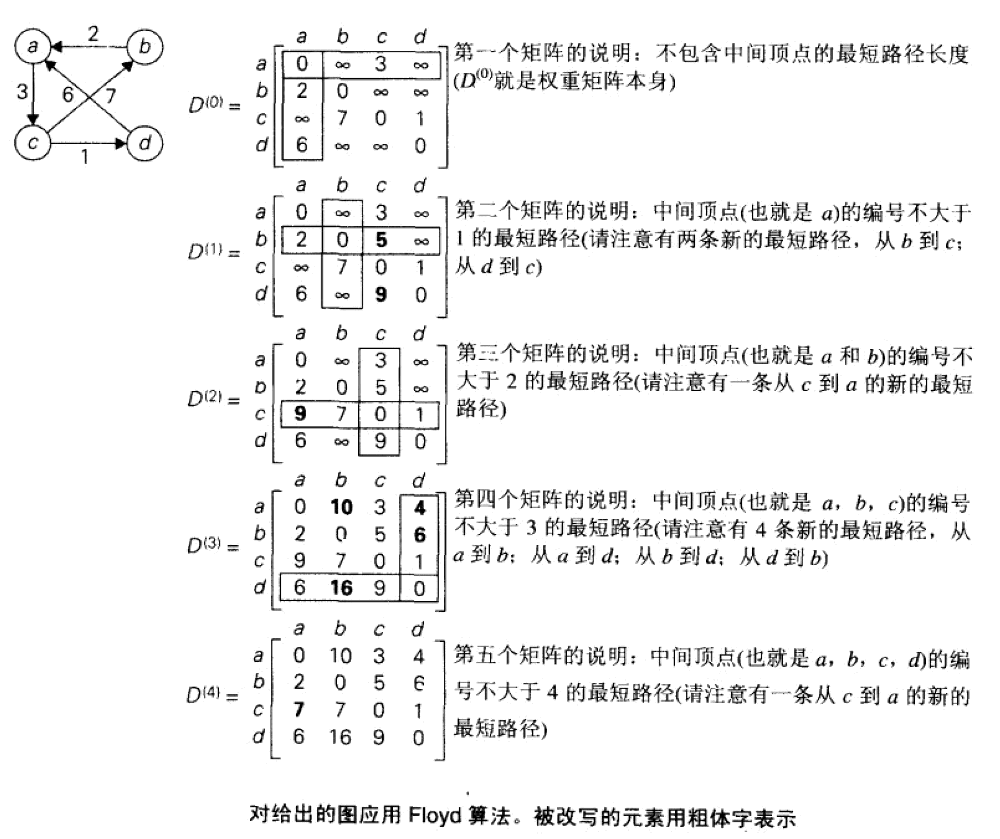
Figure 26: Floyd 算法实例
5.2.2.3. Floyd 算法伪代码
Folyd 算法的伪代码几乎和 Warshall 算法完全一样。
//Implements Floyd’s algorithm for the all-pairs shortest-paths problem
//Input: The weight matrix W of a graph with no negative-length cycle
//Output: The distance matrix of the shortest paths’ lengths
D←W //is not necessary if W can be overwritten
for k←1 to n do
for i←1 to n do
for j←1 to n do
D[i, j]←min{D[i, j], D[i, k] + D[k,j]}
return D
应该注意的是:3个 for 循环中一定是 \(k\) 在最外边!先固定了顶点 \(k\) ,把所有从顶点 \(i\) 到顶点 \(j\) 且经过顶点 \(k\) 的距离找出来,才能保证每次求的是 \(D^{(k)}\) ,且求值顺序是从 \(D^{(1)}\) 到 \(D^{(n)}\) ,这样才能保证最后结果的正确性。
5.2.2.4. Floyd 算法实现
Floyd 算法实现如下:
//Floyd-Warshall算法实现
#include<iostream>
using std::cout;
using std::endl;
#define NoEdge 100000 //用NoEdge表示不邻接的结点间的权值。NoEdge的值远大于所有边的权值。
#define N 6 //图中的结点总数。
//w为输入的带权邻接矩阵。
//在数组D[]中返回距离矩阵。
//在数组path[][]中返回顶点i到顶点j的路径上,顶点i的后继。
//path用来记录最短路径,在这里记录的是顶点i到顶点j的最短路径中顶点i的后继。
//当然path也可以改为记录顶点i到顶点j的最短路径中顶点j的前驱。
void Floyd(const int w[][N],int D[][N],int path[][N])
{
int i,j,k;
for(i=0; i < N; i++) {//初始化,把w里的值复制到D里,并设置path。
for(j=0; j < N; j++) {
if(w[i][j] <NoEdge) {
path[i][j] = j;
//path[i][j] = i; //如果不记录后继,而是记录顶点j的前驱的话。
} else {
path[i][j] = -1;
}
D[i][j]=w[i][j];
}
}
for(k=0; k < N; k++) { //3个for循环计算D。
for(i=0; i < N; i++) {
for(j=0; j < N; j++) {
if(D[i][j]>D[i][k]+D[k][j]) {
// 最好写为if(D[i][k]!=NoEdge && D[k][j]!=NoEdge && D[i][j]>D[i][k]+D[k][j])
// 防止潜在溢出所造成的错误,当然如果确定边的权值不是很大,不这样写也没关系。
D[i][j] = D[i][k]+D[k][j];
path[i][j] = path[i][k]; //更正顶点i的后继。
//path[i][j] = path[k][j]; //如果不记录后继,而是记录顶点j的前驱的话。
}
}
}
}
}
//测试Floyd程序。
int main()
{
const int w[N][N] = {
{0,12,18,NoEdge,17,NoEdge},
{12,0,10,3,NoEdge,5},
{18,10,0,NoEdge,21,11},
{NoEdge,3,NoEdge,0,NoEdge,8},
{17,NoEdge,21,NoEdge,0,16},
{NoEdge,5,11,8,16,0}
};
int D[N][N];
int path[N][N];
Floyd(w,D,path);
//输出距离矩阵
for(int i=0; i < N; i++) {
for(int j=0; j < N; j++) {
cout<<D[i][j]<<"\t";
}
cout<<endl;
}
cout<<endl;
for(int i=0; i < N; i++) {
for(int j=0; j < N; j++) {
cout<<path[i][j]<<"\t";
}
cout<<endl;
}
return 0;
}
5.3. 稀疏图上的 Johnson 算法
略。参考:算法导论(原书第 2 版),25.3 稀疏图上的 Johnson 算法
6. 最小生成树
一个无向连通图 G 的最小生成树(MST,Minimum Spanning Tree)就是由该图的那些连接 G 的所有顶点的边构成的树,且其总值最低。显然,最小生成树不一定是唯一的。
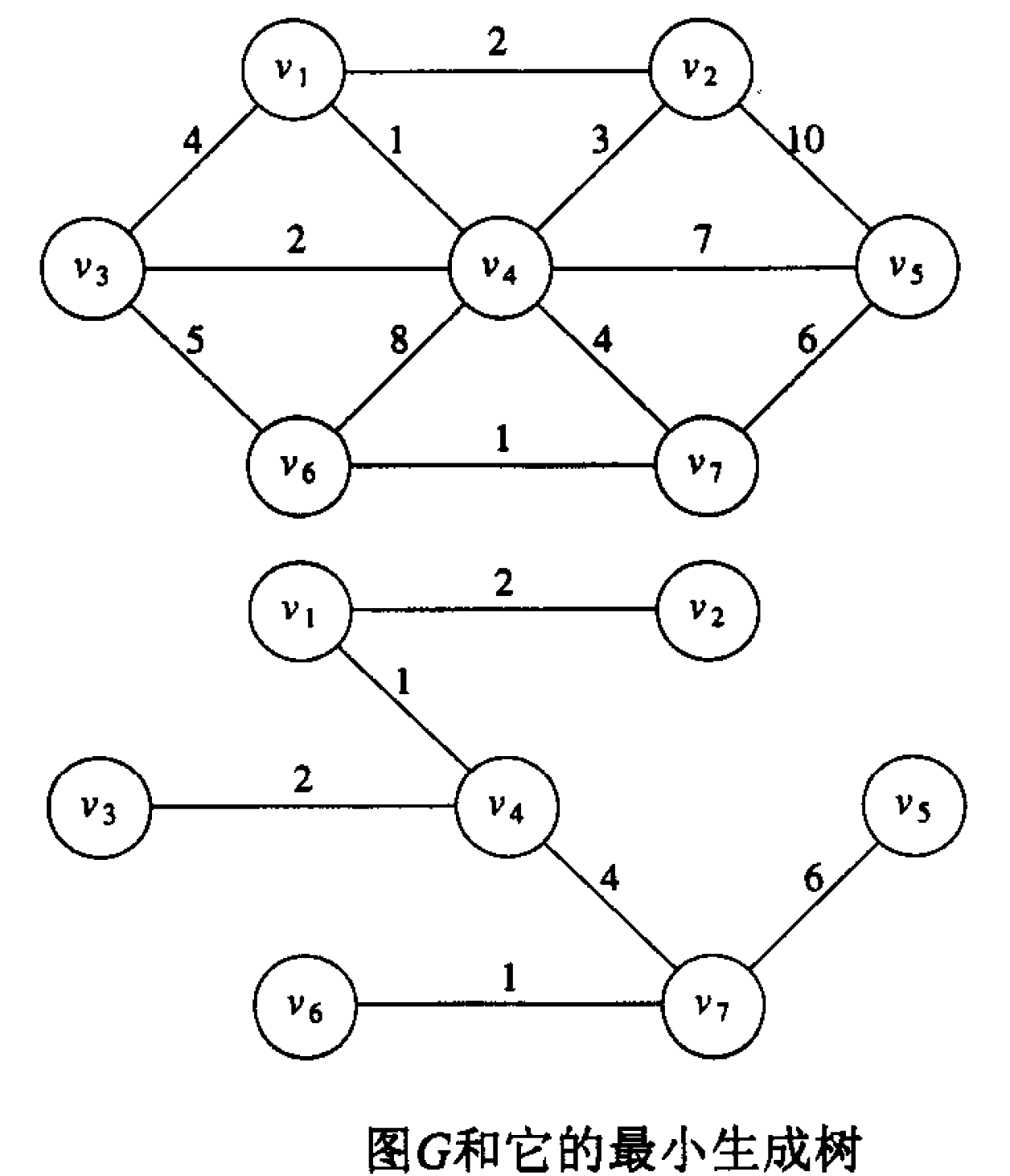
Figure 27: 最小生成树实例
下面介绍两种求最小生成树的算法:Prim 算法和 Kruskal 算法(都是贪心算法)。尽管不是所有贪心算法都是准确的,但这里介绍的两种贪心算法得到的一定是最小生成树。
关于 Prim 算法和 Kruskal 算法正确性的证明可以查看 SartajSahni 的《数据结构、算法与应用——C++语言描述》13.3.6 节。
6.1. Prim 算法(贪心算法)
Prim 算法思想:在每阶段都可以通过选择边(u,v),使得(u,v)的值是所有 u 在树上、但 v 不在树上的边的值中的最小者,从而找出一个新的顶点并把它添加到这棵树中。如图 28 所示。
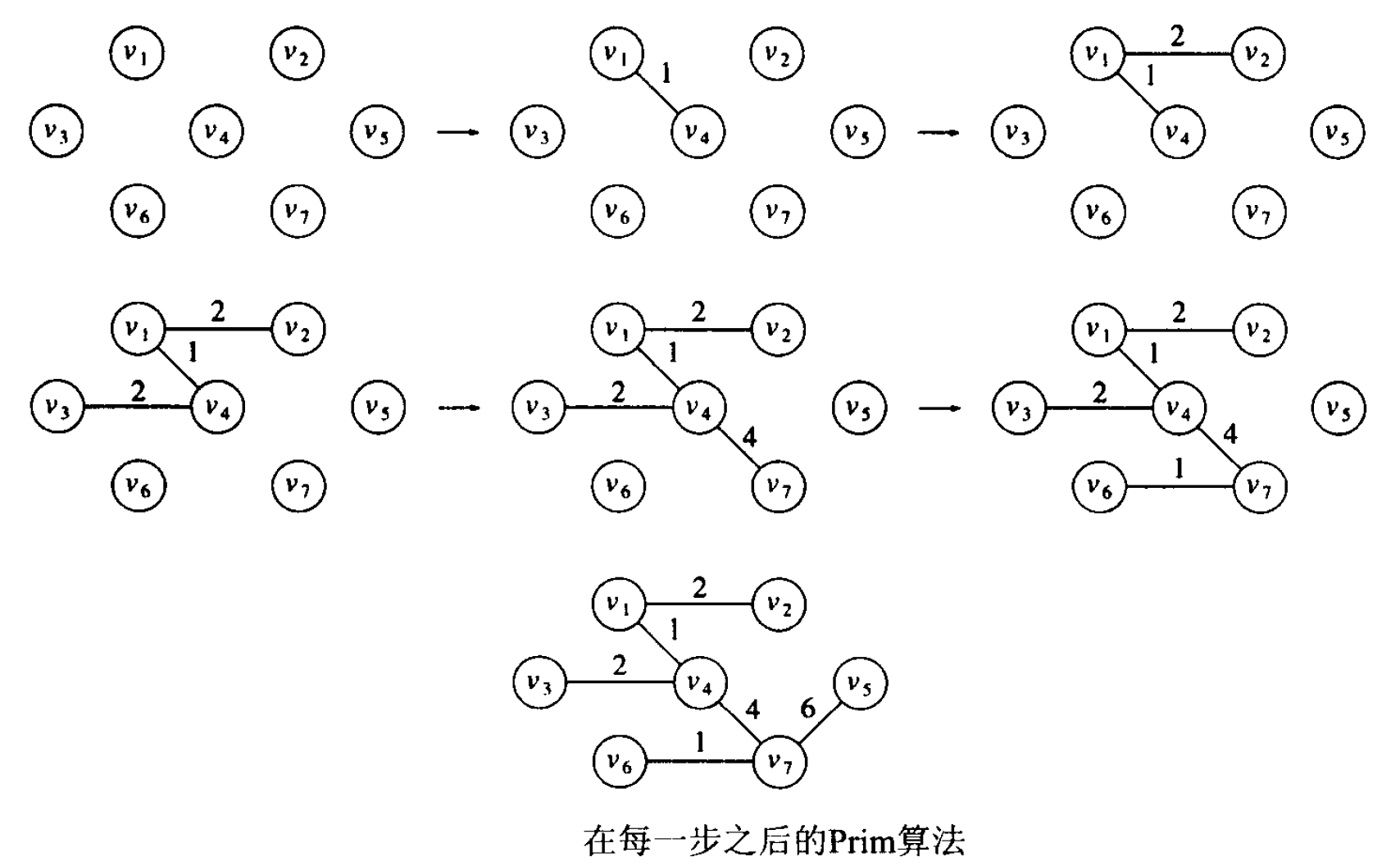
Figure 28: Prim 算法实例
6.2. Kruskal 算法(贪心算法)
Kruskal 算法思想:也是贪心算法,其贪心策略是连续按照最小的权值选择边,当所选的边不产生回路时就把它确定为取定的边。如图 29 所示。
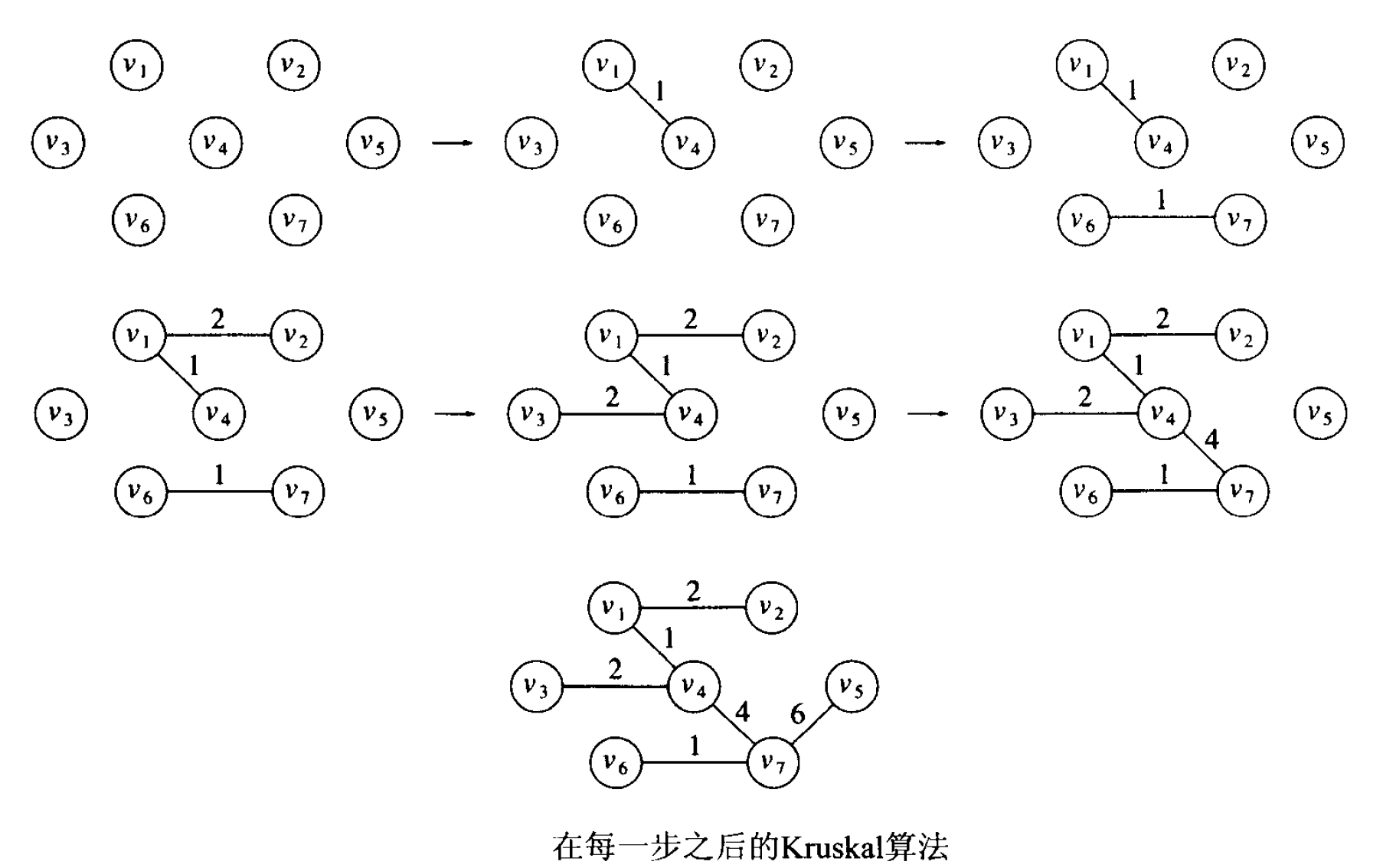
Figure 29: Kruskal 算法实例
注:不相交集的 Union/Find 算法在 Kruskal 算法中有用武之地。
7. 最大网络流
最大网络流问题(Maximum flow problem)是确定图中两点可以通过的最大流量。
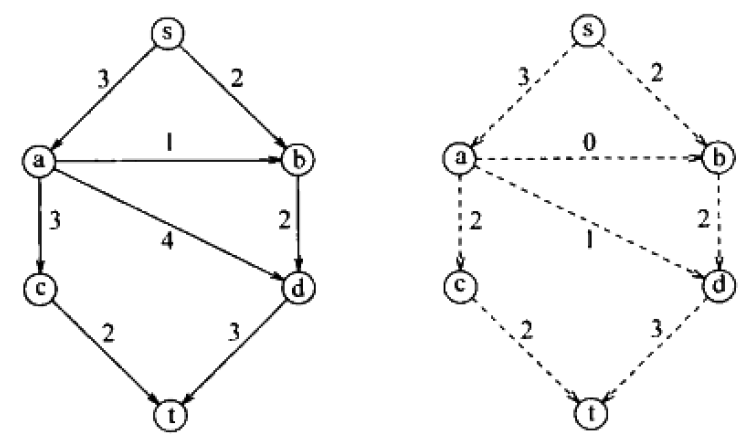
Figure 30: 最大网络流实例:图(左)及其最大流(右)
参考:
数据结构与算法分析——C语言描述(原书第2版),9.4 网络流问题
算法导论(原书第2版),26.2 Ford-Fulkerson方法