Automatic Differentiation

1. 求解微分
2. 自动微分法（Auto Diff）
3. 参考

1. 求解微分

求解微分（导数）是一个基本数学问题，应用场景很广，比如使用梯度下降法求解函数极值时，需要求解函数对各个参数的偏导数。

微分求解一般有下面 4 种方法：

手动求解法(Manual Differentiation)
数值微分法(Numerical Differentiation)
符号微分法(Symbolic Differentiation)
自动微分法(Automatic Differentiation, 又称 Algorithmic Differentiation)

本文重点介绍“自动微分法(Automatic Differentiation)”。在介绍它前，先了解下其它 3 种方法。

1.1. 手动求解法

手动求解法：先求解出导数公式，然后按公式编写代码，代入实际数值，得出真实的梯度。这很容易出错，而且每次我们修改模型后，都要修改对应的梯度求解公式，很是麻烦。

1.2. 数值微分法

数值微分法就是根据导数的原始定义进行求解。导数定义为：
$f^{'} (x) = lim_{h \to 0} \frac{f (x + h) - f (x)}{h}$
不过由于 Round-off error 和 Truncation error 的存在，使得它的应用很受限。为了减少误差，往往采用下面的“center difference”来求解导数：
$f^{'} (x) = lim_{h \to 0} \frac{f (x + h) - f (x - h)}{2 h}$
使用上式的误差比使用导数原始定义公式的误差相对更小。 由于数值微分法的实现非常简单，我们往往利用它来检验其他求导算法的正确性。

1.3. 符号微分法

符号微分法是一种利用代数软件（如 Mathematica, Maxima, Maple 等）来代替手动求解法的过程，相对于手动求解来说它不容易出错。它实现微分的一些公式，试图将问题转化为一个纯数学符号问题。符号微分的缺点是它经常导致复杂、晦涩难懂的表达式，最终出现“表达式膨胀”（expression swell）问题，导致最终求解速度变慢。

1.4. 自动微分法

自动微分法是本文介绍的重点，后面将专门介绍。

2. 自动微分法（Auto Diff）

自动微分法是一种介于符号微分和数值微分的方法：数值微分强调一开始直接代入数值近似求解；符号微分强调直接对代数进行求解，最后才代入问题数值；自动微分将符号微分法应用于最基本的算子，比如常数，幂函数，指数函数，对数函数，三角函数等，然后代入数值，保留中间结果，最后再应用于整个函数。因此它应用相当灵活，可以做到完全向用户隐藏微分求解过程，由于它只对基本函数或常数运用符号微分法则，所以它可以灵活结合编程语言的循环结构，条件结构等，使用自动微分和不使用自动微分对代码总体改动非常小，并且由于它的计算实际是一种图计算，可以对其做很多优化，这也是为什么该方法在现代深度学习系统中得以广泛应用。

摘自：https://blog.csdn.net/aws3217150/article/details/70214422

自动微分法有两种：前向模式（Forward Mode）和反向模式（Reverse Mode）。

介绍前向模式和反向模式时，我们将使用下面的函数作为例子：
$f (x_{1}, x_{2}) = \ln (x_{1}) + x_{1} x_{2} - \sin (x_{2})$
它可以转化为图 1 所示的计算图。

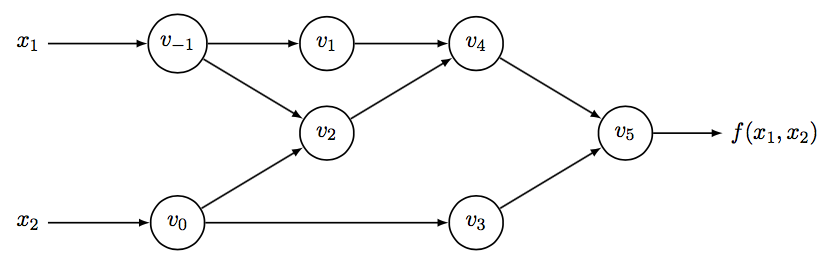
Figure 1: Computational graph of $f (x_{1}, x_{2}) = \ln (x_{1}) + x_{1} x_{2} - \sin (x_{2})$

图 1 中采用了下面的表示法：设函数为 $R^{n} \to R^{m}$ ，则，
变量 $v_{i - n} = x_{i}, i = 1, \dots, n$ 表示输入变量（如本例的 $v_{- 1}, v_{0}$ 分别表示输入变量 $x_{1}, x_{2}$ ）；
变量 $v_{i}, i = 1, \dots, l$ 表示中间变量（如本例的 $v_{1}, v_{2}, v_{3}, v_{4}, v_{5}$ 都是中间变量，其中 $v_{5}$ 还是输出变量）；
变量 $y_{m - i} = v_{l - i}, i = m - 1, \dots, 0$ 表示输出变量（如本例的 $v_{5}$ 表示输出变量）。

2.1. 前向模式（Forward Mode）

得到如图 1 所示的计算图后，我们容易分步地计算函数的值，并求得它每一步的导数值，最终求得 $\frac{\partial y}{\partial x_{1}}$ 和 $\frac{\partial y}{\partial x_{2}}$ 的导数值。

图 2 演示了使用前向模式的自动微分法求解 $\frac{\partial y}{\partial x_{1}}$ 的过程（请关注右子图），图中 ${\dot{v}}_{i} = \frac{\partial v_{i}}{\partial x_{1}}$ 。

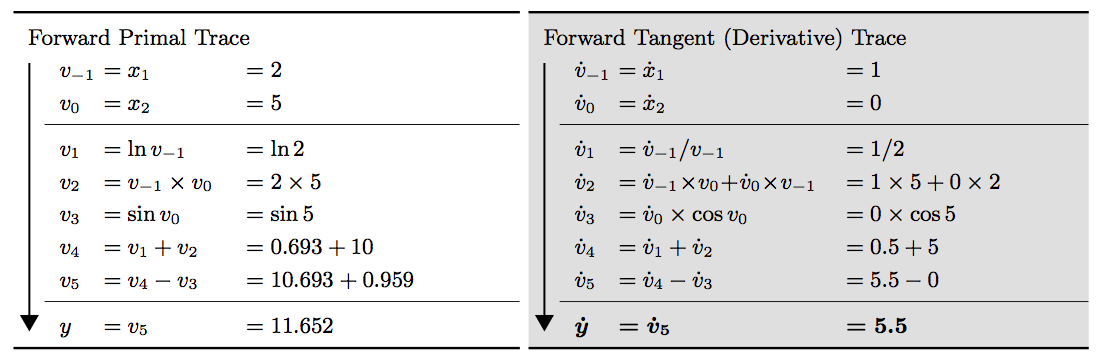
Figure 2: 使用自动微分法（前向模式）求解 $f (x_{1}, x_{2}) = \ln (x_{1}) + x_{1} x_{2} - \sin (x_{2})$ 在点 $(x_{1}, x_{2}) = (2, 5)$ 处的偏导数 $\frac{\partial y}{\partial x_{1}}$

采用类似的方法，我们可以求出在点 $(2, 5)$ 处的另一个偏导数 $\frac{\partial y}{\partial x_{2}}$ 。这时设 ${\dot{v}}_{i} = \frac{\partial v_{i}}{\partial x_{2}}$ ，则有：
$\begin{aligned} {\dot{v}}_{- 1} & = {\dot{x}}_{1} & = 0 \\ {\dot{v}}_{0} & = {\dot{x}}_{2} & = 1 \\ {\dot{v}}_{1} & = {\dot{v}}_{- 1} / v_{1} & = 0 \\ {\dot{v}}_{2} & = {\dot{v}}_{- 1} \times v_{0} + {\dot{v}}_{0} \times v_{- 1} & = 0 \times 5 + 1 \times 2 \\ {\dot{v}}_{3} & = {\dot{v}}_{0} \times \cos v_{0} & = 1 \times \cos 5 \\ {\dot{v}}_{4} & = {\dot{v}}_{1} + {\dot{v}}_{2} & = 0 + 2 \\ {\dot{v}}_{5} & = {\dot{v}}_{4} - {\dot{v}}_{3} & = 2 - \cos 5 \\ \dot{y} & = {\dot{v}}_{5} & = 1.716 \end{aligned}$

从上可知，设函数为 $R^{n} \to R^{m}$ ，求微分时我们需要计算 $n$ 趟（上面例子中 $n = 2$ ）。当输入变量维度很大时，效率不高。所以，前向模式的自动微分法不适合 $n > m$ 的情况。

2.2. 反向模式（Reverse Mode）

当输入维度大于输出维度时，使用自动微分法的反向模式更加高效。

图 3 演示了使用前向模式的自动微分法求解 $\frac{\partial y}{\partial x_{1}}$ 和 $\frac{\partial y}{\partial x_{2}}$ 的过程（请关注右子图，从下往上看），图中 ${\bar{v}}_{i} = \frac{\partial y_{j}}{\partial v_{i}}$ （在神经网络的反向传播算法中， $y_{j}$ 是损失 $E$ ，它只有一个维度，即 $m = 1$ ，这种情况下可把 $y_{j}$ 直接记为 $y$ ）。

Figure 3: 使用自动微分法（反向模式）求解 $f (x_{1}, x_{2}) = \ln (x_{1}) + x_{1} x_{2} - \sin (x_{2})$ 在点 $(x_{1}, x_{2}) = (2, 5)$ 处的偏导数 $\frac{\partial y}{\partial x_{1}}$ 和 $\frac{\partial y}{\partial x_{2}}$

注：与前向模式的自动微分法不同，反向模式的自动微分法仅计算一趟就得到了对各个输入分量的偏导数 $\frac{\partial y}{\partial x_{1}}$ 和 $\frac{\partial y}{\partial x_{2}}$ 。所以 反向模式的自动微分法特别适合于输入维度大，而输出维度小的情况（函数 $R^{n} \to R^{m}$ 中 $n ≫ m$ ）。

下面介绍一下 ${\bar{v}}_{0} = 1.716$ 的计算过程。首先从左子图可知， $v_{0}$ 只通过 $v_{2}$ 和 $v_{3}$ 影响到输出 $y$ ，所以有：
$\frac{\partial y}{\partial v_{0}} = \frac{\partial y}{\partial v_{2}} \frac{\partial v_{2}}{\partial v_{0}} + \frac{\partial y}{\partial v_{3}} \frac{\partial v_{3}}{\partial v_{0}}$
又可写为：
${\bar{v}}_{0} = {\bar{v}}_{2} \frac{\partial v_{2}}{\partial v_{0}} + {\bar{v}}_{3} \frac{\partial v_{3}}{\partial v_{0}}$
在图 3 的右子图中，上式的计算是通过下面两个步骤进行的：
${\bar{v}}_{0} = {\bar{v}}_{3} \frac{\partial v_{3}}{\partial v_{0}} and {\bar{v}}_{0} = {\bar{v}}_{0} + {\bar{v}}_{2} \frac{\partial v_{2}}{\partial v_{0}}$

2.3. Backpropagation VS. Reverse-Mode Auto Diff

Backpropagation refers to the whole process of training an artificial neural network using multiple backpropagation steps, each of which computes gradients and uses them to perform a Gradient Descent step. In contrast, reverse-mode auto diff is simply a technique used to compute gradients efficiently and it happens to be used by backpropagation.

注：反向传播算法描述的是求解神经网络的整个过程，它往往使用“反向模式的自动微分法”来进行梯度求解。

参考：https://stackoverflow.com/questions/49926192/what-is-the-difference-between-backpropagation-and-reverse-mode-autodiff

3. 参考

本文主要参考：Automatic differentiation in machine learning: a survey