Bayes Filter
Table of Contents
1. 非线性动态系统的状态空间模型
贝叶斯滤波可以对动态系统进行状态估计,比如估计物体的运动速度。我们用传感器可以直接得到物体状态,为什么还要滤波呢?因为 传感器不可靠,得到的测量数据不是真实数据,我们需要“去除测量数据中的噪声” ,“去噪声”在随机过程理论中称为滤波。
非线性动态系统的状态空间模型的离散差分方程如下:
\[\begin{aligned} \boldsymbol{x_k} &= f(\boldsymbol{x_{k-1}} , \boldsymbol{u_{k}} ) + \boldsymbol{w_{k}} \\
\boldsymbol{z_k} &= h(\boldsymbol{x_{k}}) + \boldsymbol{v_k} \end{aligned}\]
其中, \(\boldsymbol{x_k}\) 是 \(k\) 时刻系统的状态(如速度等), \(\boldsymbol{u_{k}}\) 是 \(k\) 时刻对系统的控制量(如方向盘转角等), \(f\) 是状态转移方程, \(\boldsymbol{w_{k}}\) 是过程噪声; \(\boldsymbol{z_k}\) 是 \(k\) 时刻系统状态的测量值, \(h\) 是测量方程, \(\boldsymbol{v_{k}}\) 是测试噪声。
参考:
https://en.wikipedia.org/wiki/State-space_representation#Nonlinear_systems
Modern Control Systems, 12th, by Richard C. Dorf, Robert H. Bishop, Chapter 3 State Variable Models
2. Bayes filter
2.1. 概率基本知识
随机变量 \(X\) 和 \(Y\) 的联合分布记为:
\[p(x,y) = p(X=x \; \text{and} \; Y=y)\]
如果 \(p(y) > 0\) ,我们称已经知道随机变量 \(Y=y\) 时,随机变量 \(X=x\) 的概率为条件概率,其定义为:
\[p(x \mid y) = \frac{p(x,y)}{p(y)}\]
全概率公式(Law of Total Probability)为:
\[\begin{aligned} p(x) & = \sum_y p(x \mid y) p(y) \quad \quad \text{(discrete case)} \\
p(x) & = \int p(x \mid y) p(y) \, \mathrm{d}y \quad \quad \text{(continuous case)} \end{aligned}\]
贝叶斯公式为:
\[p(x \mid y) = \frac{p(y \mid x )p(x)}{p(y)}\]
由于当 \(x\) 取不同值时,上式的分母 \(p(y)\) 是不会变的,所以常常记 \(\eta = \frac{1}{p(y)}\) ,这样贝叶斯公式也可以写为:
\[p(x \mid y) = \eta \, p(y \mid x )p(x)\]
2.1.1. 条件独立(Conditional Independence)
如果有:
\[p(x,y \mid z) = p(x \mid z) p (y \mid z)\]
则称随机变量 \(X,Y\) 关于 \(Z\) 条件独立 。上式相当于下面两式:
\[\begin{aligned} p(x \mid z) & = p(x \mid z, y) \\
p(y \mid z) & = p(y \mid z, x) \\
\end{aligned}\]
说明 1:在机器人概率建模时,常常用“条件独立”作为假设来简化模型。
说明 2:条件独立和相互独立没有必然联系,也就是说:
\[\begin{gathered} p(x,y \mid z) = p(x \mid z) p(y \mid z) \mathrel{\rlap{\hskip .5em/}}\Longrightarrow p(x,y) = p(x)p(y) \\
p(x,y) = p(x)p(y) \mathrel{\rlap{\hskip .5em/}}\Longrightarrow p(x,y \mid z) = p(x \mid z) p(y \mid z) \end{gathered}\]
2.2. 贝叶斯滤波
贝叶斯滤波(Beyes filter, or Recursive Bayesian estimation)为非线性动态系统的状态估计问题提供了一种基于概率分布形式的解决方案。 贝叶斯滤波的基本原理是:首先用系统模型预测出状态的概率密度,然后用最近的测量值对其进行修正得到“后验概率密度”。
2.2.1. 记法说明
后文中,将使用下面记法。
\(t_1\) 到 \(t_2\) 时刻的所有状态: \(x_{t_1:t_2} = x_{t_1}, x_{t_1 + 1}, x_{t_1 + 2}, \cdots, x_{t_2}\)
\(t_1\) 到 \(t_2\) 时刻的所有测量值: \(z_{t_1:t_2} = z_{t_1}, z_{t_1 + 1}, z_{t_1 + 2}, \cdots, z_{t_2}\)
\(t_1\) 到 \(t_2\) 时刻的所有控制量: \(u_{t_1:t_2} = u_{t_1}, u_{t_1 + 1}, u_{t_1 + 2}, \cdots, u_{t_2}\)
后文中,所有的概率分布都用 \(p\) 来表示,比如 \(p(x_0)\) 和 \(p(z_t \mid x_t)\) 等等,但它们显然是不同的分布,严格地说,应该写为 \(p_{x_0}(x_0)\) 和 \(p_{z_t \mid x_t}(z_t \mid x_t)\) ,为了简单,没有采用这种累赘的写法。
2.3. 贝叶斯滤波框架介绍
在贝叶斯滤波框架中,下面这些是已知的(可以认为它们是系统参数):
(1) 测量值(或称观察值) \(z_{t}\) 和对系统的控制量 \(u_{t}\)
(2) 传感器的模型(Measurements Model) \(p(z_t \mid x_t)\)
(3) 系统控制量的模型(Motion Model) \(p(x_t \mid u_t, x_{t-1})\)
(4) 初始时系统状态,即先验概率 \(p(x_0)\)
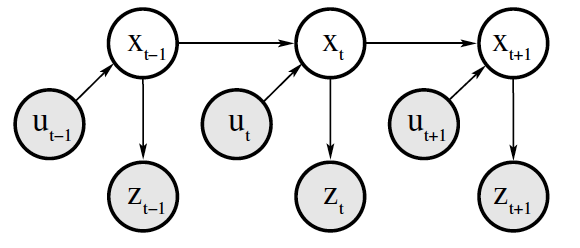
Figure 1: 贝叶斯滤波采用的状态空间模型(这个模型又叫Dynamic Bayesian Network)
贝叶斯滤波就是 求已知系统控制量(即 \(u_{1:t}\) )和状态测量值(即 \(z_{1:t}\) )时系统的状态,即后验概率: \(p(x_t \mid u_{1:t}, z_{1:t})\) ,一般我们把这个后验概率称为 Belief ,记为:
\[bel(x_t) := p(x_t \mid u_{1:t}, z_{1:t})\]
为了简化 \(bel(x_t)\) 的求解,我们假设系统满足马尔可夫性,请看下文。
2.3.1. 马尔可夫假设(即“状态完全”假设)
A state \(x_t\) will be called complete if it is the best predictor of the future. Put differently, completeness entails that knowledge of past states, measurements, or controls carry no additional information that would help us to predict the future more accurately. It it important to notice that our definition of completeness does not require the future to be a deterministic function of the state. Temporal processes that meet these conditions are commonly known as Markov chains.
参考:Probabilistic Robotics, by Sebastian Thrun, 2.3.1 State
由马尔可夫假设可得到一些结论,如:
\[\begin{aligned} p(x_t \mid x_{0:t-1}, z_{1:t-1}, u_{1:t}) &= p(x_t \mid x_{t-1}, u_t) \\
p(z_t \mid x_{0:t}, z_{1:t-1}, u_{1:t}) &= p(z_t \mid x_t) \end{aligned}\]
注 1:前一个式子表明系统当前状态仅和上一个状态及系统当前控制量有关。
注 2:后一个式子表明系统的测量值仅和当前状态有关,状态 \(x_t\) 足够预测 \(z_t\) 。
注 3:这两个式子右边都是系统参数(是已知的),其中 \(p(x_t \mid x_{t-1}, u_t)\) 就是系统控制量模型参数,而 \(p(z_t \mid x_t)\) 是系统传感器模型参数。
2.4. 贝叶斯滤波推导
本节主要参考:Probabilistic Robotics, by Sebastian Thrun, 2.4.3 Mathematical Derivation of the Bayes Filter
贝叶斯滤波推导,可以分为两步。
第一步,预测过程,即由 \(p(x_{t-1} \mid u_{1:t-1}, z_{1:t-1})\) (也就是 \(bel(x_{t-1})\) )推导出 \(p(x_{t} \mid u_{1:t}, z_{1:t-1})\) 。
我们把 \(p(x_{t} \mid u_{1:t}, z_{1:t-1})\) 记作 \(\overline{bel}(x_t)\) 。由全概率公式(Law of Total Probability)可得:
\[\begin{aligned} \overline{bel}(x_t) & = p(x_{t} \mid u_{1:t}, z_{1:t-1}) \\
& \stackrel{\text{Total Prob.}}{=} \int p(x_t \mid x_{t-1}, u_{1:t}, z_{1:t-1}) p(x_{t-1} \mid u_{1:t}, z_{1:t-1}) \, \mathrm{d} x_{t-1} \end{aligned}\]
由马尔可夫假设,有: \(p(x_t \mid x_{t-1}, u_{1:t}, z_{1:t-1}) = p(x_t \mid x_{t-1}, u_t)\)
观察上式中的 \(p(x_{t-1} \mid u_{1:t}, z_{1:t-1})\) ,由于 \(u_t\) 显然不会对过去的状态 \(x_{t-1}\) 产生影响,所以可以去掉它(因为如果 \(A,B\) 相互独立,有 \(P(A \mid B) = P(A)\) ),从而有: \(p(x_{t-1} \mid u_{1:t}, z_{1:t-1}) = p(x_{t-1} \mid u_{1:t-1}, z_{1:t-1})\)
综上,有:
\[\begin{aligned} \overline{bel}(x_t) & = \int p(x_t \mid x_{t-1}, u_{1:t}, z_{1:t-1}) p(x_{t-1} \mid u_{1:t}, z_{1:t-1}) \, \mathrm{d} x_{t-1} \\
& \stackrel{\text{Markov}}{=} \int p(x_t \mid x_{t-1}, u_t) p(x_{t-1} \mid u_{1:t}, z_{1:t-1}) \, \mathrm{d} x_{t-1} \\
& = \int p(x_t \mid x_{t-1}, u_t) p(x_{t-1} \mid u_{1:t-1}, z_{1:t-1}) \, \mathrm{d} x_{t-1} \\
& = \int p(x_t \mid x_{t-1}, u_t) bel(x_{t-1}) \, \mathrm{d} x_{t-1} \end{aligned}\]
第二步,更新过程,即由 \(p(x_{t} \mid u_{1:t}, z_{1:t-1})\) 推导出 \(p(x_{t} \mid u_{1:t}, z_{1:t})\) (也就是 \(bel(x_t)\) )。
由贝叶斯公式可以推导出 \(p(x \mid y,z) = \frac{p(y \mid x, z)p(x \mid z)}{p(y \mid z)}\) (这个式子称为 Bayes Rule with Background Knowledge),利用这个结论可得:
\[\begin{aligned} bel(x_t) & = p(x_{t} \mid u_{1:t}, z_{1:t}) \\
& = \frac{p(z_t \mid x_t, u_{1:t}, z_{1:t-1})p(x_t \mid u_{1:t}, z_{1:t-1})}{p(z_t \mid u_{1:t}, z_{1:t-1})} \\
& = \eta \, p(z_t \mid x_t, u_{1:t}, z_{1:t-1})p(x_t \mid u_{1:t}, z_{1:t-1})
\end{aligned}\]
其中, \(\eta\) 可看做是归一化常数,它当 \(x_t\) 取不同可能状态时是不变的,所以保证 \(x_t\) 取所有可能状态时 \(bel(x_t)\) 相加为 1 即可。
由马尔可夫假设,有: \(p(z_t \mid x_t, u_{1:t}, z_{1:t-1}) = p(z_t \mid x_t)\) ,所以:
\[\begin{aligned} bel(x_t) & = \eta \, p(z_t \mid x_t, u_{1:t}, z_{1:t-1})p(x_t \mid u_{1:t}, z_{1:t-1}) \\
& \stackrel{\text{Markov}}{=} \eta \, p(z_t \mid x_t) p(x_t \mid u_{1:t}, z_{1:t-1}) \\
& = \eta \, p(z_t \mid x_t) \overline{bel}(x_t)
\end{aligned}\]
结合第一步和第二步,我们已经推导出 贝叶斯滤波的递推公式为:
\[{\color{red}{bel(x_t)}} = \eta \, p(z_t \mid x_t) \int p(x_t \mid x_{t-1}, u_t) {\color{red}{bel(x_{t-1})}} \, \mathrm{d} x_{t-1}\]
具有极大后验概率密度 \(bel(x_t)\) 的状态可以作为系统状态的估计值。
从上面的公式知, 贝叶斯滤波需要知道三个概率分布:
(1) 传感器模型 \(p(z_t \mid x_t)\)
(2) 系统控制量模型 \(p(x_t \mid u_t, x_{t-1})\)
(3) 系统的初始状态概率分布 \(bel(x_0) = p(x_0)\)
贝叶斯滤波算法可简单描述为:

Figure 2: The general algorithm for Bayes filtering
2.4.1. 离散贝叶斯滤波
把前面推导的贝叶斯滤波算法应用到离散状态空间,即得离散贝叶斯滤波。离散贝叶斯滤波算法如图 3 所示。

Figure 3: Discrete Bayes Filter
2.5. 贝叶斯滤波系列算法
贝叶斯滤波需要进行积分运算,除了一些特殊的系统模型(如线性高斯系统,有限状态的离散系统)之外,对于一般的非线性、非高斯系统,贝叶斯滤波很难得到后验概率的封闭解析式。因此,现有的非线性滤波器多采用近似的计算方法解决积分问题,以此来获取估计的次优解。在系统的非线性模型可由在当前状态展开的线性模型有限近似的前提下,基于一阶或二阶 Taylor 级数展开的扩展 Kalman 滤波得到广泛应用。在一般情况下,逼近概率密度函数比逼近非线性函数容易实现。据此,Julier 与 Uhlmann 提出一种 Unscented Kalman 滤波器(UKF),通过选定的 sigma 点来精确估计随机变量经非线性变换后的均值和方差,从而更好的近似状态的概率密度函数,其理论估计精度优于扩展 Kalman 滤波(EKF)。获取次优解的另外一中方案便是基于蒙特卡洛模拟的粒子滤波器。
摘自:http://wenku.baidu.com/view/88896d2b453610661ed9f4b4.html
贝叶斯滤波算法是一个大的框架,一系列算法都可以认为是贝叶斯滤波算法的具体实现。
如下面这些都是贝叶斯滤波算法:
- Kalman filters
- Extended Kalman filters
- Particle filters
2.6. 贝叶斯滤波应用场景
贝叶斯滤波是一个大的框架,它可以用来作状态估计(状态估计是一个非常广的概念,如速度估计,位置估计等等)。
机器人的 Localization 算法(已知地图,估计自己的位置)基本上都是贝叶斯滤波或其变种。
3. 贝叶斯滤波实例
本节主要参考:Probabilistic Robotics, by Sebastian Thrun, 2.4.2 Example
下面以“移动机器人估计门的状态(打开或关闭)”为例说明贝叶斯滤波的基本思想。这个例子是一个简单的有限状态的离散系统。
Figure 4: A mobile robot estimating the state of a door.
首先给出贝叶斯滤波所需要的三个概率分布。
已知系统的初始状态概率分布为:
\[\begin{aligned} bel(X_0 = \text{open}) &= 0.5 \\
bel(X_0 = \text{closed}) &= 0.5 \end{aligned}\]
已知传感器模型(描述传感器噪声)为:
\[\begin{aligned} p(Z_t = \mathrm{sense\_open} \mid X_t = \mathrm{is\_open}) &= 0.6 \\
p(Z_t = \mathrm{sense\_closed} \mid X_t = \mathrm{is\_open}) &= 0.4 \\
p(Z_t = \mathrm{sense\_open} \mid X_t = \mathrm{is\_closed}) &= 0.2 \\
p(Z_t = \mathrm{sense\_closed} \mid X_t = \mathrm{is\_closed}) &= 0.8 \\
\end{aligned}\]
已知系统的控制量模型为:
\[\begin{aligned} p(X_t = \mathrm{is\_open} \mid U_t = \text{push}, X_{t-1} = \mathrm{is\_open}) &= 1 \\
p(X_t = \mathrm{is\_closed} \mid U_t = \text{push}, X_{t-1} = \mathrm{is\_open}) &= 0 \\
p(X_t = \mathrm{is\_open} \mid U_t = \text{push}, X_{t-1} = \mathrm{is\_closed}) &= 0.8 \\
p(X_t = \mathrm{is\_closed} \mid U_t = \text{push}, X_{t-1} = \mathrm{is\_closed}) &= 0.2 \\
p(X_t = \mathrm{is\_open} \mid U_t = \mathrm{do\_nothing}, X_{t-1} = \mathrm{is\_open}) &= 1 \\
p(X_t = \mathrm{is\_closed} \mid U_t = \mathrm{do\_nothing}, X_{t-1} = \mathrm{is\_open}) &= 0 \\
p(X_t = \mathrm{is\_open} \mid U_t = \mathrm{do\_nothing}, X_{t-1} = \mathrm{is\_closed}) &= 0 \\
p(X_t = \mathrm{is\_closed} \mid U_t = \mathrm{do\_nothing}, X_{t-1} = \mathrm{is\_closed}) &= 1 \\
\end{aligned}\]
假设,机器人的第一个行为是“什么都不做”,即 \(U_1 = \mathrm{do\_nothing}\) ,传感器测量出的结果是门是“打开的”,即 \(Z_1 = \mathrm{sense\_open}\) ,现在我们要估计门处于什么状态?
下面开始计算贝叶斯滤波的第一步,计算 \(\overline{bel}(x_1)\)
\[\begin{aligned} \overline{bel}(x_1) & = \int p(x_1 \mid x_0, u_1) bel(x_0) \, \mathrm{d} x_0 \\
& = \sum_{x_0} p(x_1 \mid x_0, u_1) bel(x_0) \\
& = p(x_1 \mid U_1 = \mathrm{do\_nothing}, X_0 = \mathrm{is\_open}) \, bel(X_0 = \mathrm{is\_open}) \\
& \quad + p(x_1 \mid U_1 = \mathrm{do\_nothing}, X_0 = \mathrm{is\_closed}) \, bel(X_0 = \mathrm{is\_closed}) \\
\end{aligned}\]
其中, \(x_1\) 有两个状态,即 \(X_1 = \mathrm{is\_open}\) 和 \(X_1 = \mathrm{is\_closed}\) ,分别代入上式,有:
\[\begin{aligned} \overline{bel}(X_1 = \mathrm{is\_open}) & = p(X_1 = \mathrm{is\_open} \mid U_1 = \mathrm{do\_nothing}, X_0 = \mathrm{is\_open}) \, bel(X_0 = \mathrm{is\_open}) \\
& \quad + p(X_1 = \mathrm{is\_open} \mid U_1 = \mathrm{do\_nothing}, X_0 = \mathrm{is\_closed}) \, bel(X_0 = \mathrm{is\_closed}) \\
& = 1 \cdot 0.5 + 0 \cdot 0.5 = 0.5 \\
\end{aligned}\]
以及:
\[\begin{aligned} \overline{bel}(X_1 = \mathrm{is\_closed}) & = p(X_1 = \mathrm{is\_closed} \mid U_1 = \mathrm{do\_nothing}, X_0 = \mathrm{is\_open}) \, bel(X_0 = \mathrm{is\_open}) \\
& \quad + p(X_1 = \mathrm{is\_closed} \mid U_1 = \mathrm{do\_nothing}, X_0 = \mathrm{is\_closed}) \, bel(X_0 = \mathrm{is\_closed}) \\
& = 0 \cdot 0.5 + 1 \cdot 0.5 = 0.5 \\
\end{aligned}\]
下面开始计算贝叶斯滤波的第二步,计算 \(bel(x_1)\)
\[bel(x_1) = \eta \, p(Z_1 = \mathrm{sense\_open} \mid x_1) \overline{bel}(x_1)\]
对于两种可能状态 \(X_1 = \mathrm{is\_open}\) 和 \(X_1 = \mathrm{is\_closed}\) ,分别代入上式,有:
\[\begin{aligned} bel(X_1 = \mathrm{is\_open} ) &= \eta \, p(Z_1 = \mathrm{sense\_open} \mid X_1 = \mathrm{is\_open}) \overline{bel}(X_1 = \mathrm{is\_open})\\
& = \eta \, 0.6 \cdot 0.5 = \eta \, 0.3
\end{aligned}\]
以及
\[\begin{aligned} bel(X_1 = \mathrm{is\_closed} ) &= \eta \, p(Z_1 = \mathrm{sense\_open} \mid X_1 = \mathrm{is\_closed}) \overline{bel}(X_1 = \mathrm{is\_closed})\\
& = \eta \, 0.2 \cdot 0.5 = \eta \, 0.1
\end{aligned}\]
其中, \(\eta\) 可以这样计算:
\[\eta = (0.3 + 0.1)^{-1} = 2.5\]
从而:
\[\begin{aligned} bel(X_1 = \mathrm{is\_open} ) = \eta \, 0.3 = 0.75 \\
bel(X_1 = \mathrm{is\_closed} ) = \eta \, 0.1 = 0.25
\end{aligned}\]
所以,这个阶段我们可以估计门是处于“打开的”。
现在假设,机器人的第二个行为是“推开门”,即 \(U_2 = \text{push}\) ,此时传感器测量出的结果是门是“打开的”,即 \(Z_2 = \mathrm{sense\_open}\) ,现在我们再次估计门处于什么状态?
过程和前面类似,具体过程省略,下面直接给出计算后的结果。
第一步结果:
\[\begin{aligned} \overline{bel}(X_2 = \mathrm{is\_open}) = 1 \cdot 0.75 + 0.8 \cdot 0.25 = 0.95 \\
\overline{bel}(X_2 = \mathrm{is\_closed}) = 0 \cdot 0.75 + 0.2 \cdot 0.25 = 0.05 \\
\end{aligned}\]
第二步结果:
\[\begin{aligned} bel(X_2 = \mathrm{is\_open}) = \eta \, 0.6 \cdot 0.95 \approx 0.983 \\
bel(X_2 = \mathrm{is\_closed}) = \eta \, 0.2 \cdot 0.05 \approx 0.017 \\
\end{aligned}\]
所以,这个阶段我们可以估计门是处于“打开的”。
4. Binary Bayes Filters With Static State
本节主要参考:Probabilistic Robotics, by Sebastian Thrun, 4.2 Binary Bayes Filters With Static State
考虑特殊的情况:待估计状态只有两种可能情况(比如门“打开”或“关闭”),且不会随时间而变化(比如假设门不会自动从“打开”变为“关闭”,这称状态为静态的)。由于状态是静态的,所以可以认为它只和测量值相关,而与控制量无关。这时有:
\[bel_t(\boldsymbol{x}) = p(\boldsymbol{x} \mid \boldsymbol{z}_{1:t}, \boldsymbol{u}_{1:t}) = p(\boldsymbol{x} \mid \boldsymbol{z}_{1:t})\]
其中,两个可能状态分别记为 \(x\) 和 \(\lnot x\) 。那么有: \(bel_t(x) = 1 - bel_t(\lnot x)\) 。在这里我们采用记法 \(bel_t(x)\) ,而不采用记法 \(bel(x_t)\) 是为了表明状态不会改变(状态仅在两个可能状态之间转换,而不会变为其它状态)。
对于这种情况当然可以直接使用离散贝叶斯滤波,不过,我们常常用下面介绍的方法来实现 Binary Bayes Filters With Static State.
事件 \(x\) 的对数发生比(log odds ratio)定义为:
\[l(x) := \log \frac{p(x)}{p(\lnot x)} = \log \frac{p(x)}{1- p(x)}\]
采用“对数发生比”比采用“Bayes 后验概率”来表达状态发生的可能性更加地合理。 因为“Bayes 后验概率”的取值范围只是 \(0 \; \text{to} \; 1\) ,而“对数发生比”的取值范围为 \(- \infty \; \text{to} \; \infty\) ,这样可以提高计算精度,避免一些不必要的计算截断误差。
4.1. Binary Bayes Filter 算法
定义 \(l_t(x) := \log \frac{bel_t(x)}{1 - bel_t(x)}\) ,Binary Bayes Filter 算法如图 5 所示。

Figure 5: Binary Bayes Filter
其中, \(p(x)\) 是状态 \(x\) 的先验概率,初始时 \(l_0(x) = \log \frac{p(x)}{1 - p(x)}\) 。
说明:Binary Bayes Filter 算法中使用了 \(p(x \mid z_t)\) (它被称为 Inverse Measurement Model),而没有使用贝叶斯滤波中的 \(p(z_t \mid x)\) 。
如果状态相对简单时, \(p(x \mid z_t)\) 比 \(p(z_t \mid x)\) 更加容易计算。
Inverse models are often used in situations where measurements are more complex than the binary state. An example of such a situation is the problem of estimating whether or not a door is closed, from camera images. Here the state is extremely simple, but the space of all measurements is huge. It is easier to devise a function that calculates a probability of a door being closed from a camera image, than describing the distribution over all camera images that show a closed door.
4.2. Binary Bayes Filter 算法推导
在前面推导 Bayes Filter 时,我们证明过:
\[\begin{aligned} bel(x_t) & = p(x_{t} \mid u_{1:t}, z_{1:t}) \\
& = \frac{p(z_t \mid x_t, u_{1:t}, z_{1:t-1})p(x_t \mid u_{1:t}, z_{1:t-1})}{p(z_t \mid u_{1:t}, z_{1:t-1})} \\
& = \frac{p(z_t \mid x_t, u_{1:t}, z_{1:t-1})p(x_t \mid u_{1:t}, z_{1:t-1})}{p(z_t \mid u_{1:t}, z_{1:t-1})} \\
\end{aligned}\]
在这里,相应地可简化为:
\[\begin{aligned} p(x \mid z_{1:t}) & = \frac{p(z_t \mid x, z_{1:t-1})p(x \mid z_{1:t-1})}{p(z_t \mid z_{1:t-1})} \\
& = \frac{p(z_t \mid x)p(x \mid z_{1:t-1})}{p(z_t \mid z_{1:t-1})} \\
\end{aligned}\]
又由贝叶斯公式有 \(p(z_t \mid x) = \frac{p(x \mid z_t)p(z_t)}{p(x)}\) ,所以上式进一步可化为:
\[p(x \mid z_{1:t}) = \frac{p(x \mid z_t)p(z_t) p(x \mid z_{1:t-1})}{p(x) p(z_t \mid z_{1:t-1})}\]
类似地,有:
\[p(\lnot x \mid z_{1:t}) = \frac{p(\lnot x \mid z_t)p(z_t) p(\lnot x \mid z_{1:t-1})}{p(\lnot x) p(z_t \mid z_{1:t-1})}\]
利用前面两式,对 \(l_t(x)\) 进行推导,有:
\[\begin{aligned} l_t(x) & := \log \frac{bel_t(x)}{1 - bel_t(x)} \\
& = \log \left( \frac{p(x \mid z_{1:t})}{p(\lnot x \mid z_{1:t})} \right) \\
& = \log \left( \frac{\frac{p(x \mid z_t)p(z_t) p(x \mid z_{1:t-1})}{p(x) p(z_t \mid z_{1:t-1})}}{\frac{p(\lnot x \mid z_t)p(z_t) p(\lnot x \mid z_{1:t-1})}{p(\lnot x) p(z_t \mid z_{1:t-1})}} \right) \\
& = \log \left( \frac{p(x \mid z_t)}{p(\lnot x \mid z_t)} \cdot \frac{p(x \mid z_{1:t-1})}{p(\lnot x \mid z_{1:t-1})} \cdot \frac{p(\lnot x)}{p(x)} \right) \\
& = \log \left( \frac{p(x \mid z_t)}{1 - p(x \mid z_t)} \cdot \frac{p(x \mid z_{1:t-1})}{1 - p(x \mid z_{1:t-1})} \cdot \frac{1 - p(x)}{p(x)} \right) \\
& = \log \frac{p(x \mid z_t)}{1 - p(x \mid z_t)} + \log \frac{p(x \mid z_{1:t-1})}{1 - p(x \mid z_{1:t-1})} + \log \frac{1 - p(x)}{p(x)} \\
& = \log \frac{p(x \mid z_t)}{1 - p(x \mid z_t)} + l_{t-1}(x) - \log \frac{p(x)}{1 - p(x)} \\
\end{aligned}\]
证毕。