Byzantine Generals Problem, BFT Algorithm
Table of Contents
1. 拜占庭将军问题(Byzantine Generals Problem)
在了解分布式一致性算法前,先来认识一下由 Leslie Lamport 于 1982 年在论文 The Byzantine Generals Problem 中提出的分布式系统中的著名问题——拜占庭将军问题(Byzantine Generals Problem)。
拜占庭是东罗马帝国的首都。由于当时拜占庭罗马帝国国土辽阔,为了防御目的,因此每个军队都分隔很远,将军与将军之间只能靠信差传消息。在战争的时候,拜占庭军队内所有将军必需达成一致的共识,决定是否有赢的机会才去攻打敌人的阵营。但是,在军队内有可能存有叛徒,左右将军们的决定,在进行共识时,结果并不代表大多数人的意见。这时候,在已知有成员不可靠的情况下,其余忠诚的将军在不受叛徒的影响下如何达成一致的协议,拜占庭问题就此形成。拜占庭将军问题是对现实世界的模型化,由于硬件错误、网络拥塞或断开以及遭到恶意攻击,计算机和网络可能出现不可预料的行为。
在讨论拜占庭将军问题时,有个基本的前提需要交待一下,那就是 信道必须是可靠的,也就是说:某人发出去的消息,“不会被别人篡改”。 如果这一点都无法满足,那么拜占庭问题是无解的。不过,信道上可能出现消息的延迟、丢失、重复。
注:关于信道可靠问题,另一个相关的问题是两军问题(Two Generals' Problem)。两军问题的结论是,在一个不可靠的通信链路上试图通过通信以达成一致是基本不可能的。
1.1. BFT, CFT
如果某节点故意不响应集群中其它节点的请求、故意向其它节点发送错误的数据、故意给不同的节点发送不一致消息等等,那么该节点属于“作恶节点”。
通常,我们把 随意性故障(可包含作恶节点)称为拜占庭故障(Byzantine Failure),能解决这类故障的算法被称为“Byzantine Fault Tolerance(BFT)算法”。 Lamport 在 1982 年的原论文中指出,如果有问题的节点数为 \(f\) ,那么总节点数 \(n\) 必须满足 \(n \ge 3f+1\) 才能达成一致的决策;Lamport 同时给出了复杂度为 \(O(n^{f+1})\) 的算法。1999 年,Miguel Castro 和 Barbara Liskov 提出的 Practical Byzantine Fault Tolerance(PBFT)算法的复杂度为 \(O(n^2)\) ,这从 Lamport 的“指数级”复杂度降低到了“多项式级”复杂度。
还有另外一类算法,解决的是 分布式系统中存在故障(消息延迟、丢失、重复),但不存在作恶节点的场景下的共识问题,这一类算法称为“Crash Fault Tolerance(CFT)”,故障容错算法,或者非拜占庭容错算法。 CFT 算法一般用于局域网场景下的分布式系统,如分布式数据库等等,Paxos 算法、Raft 算法等属于 CFT 算法。对于 CFT 算法,需要正常节点 \(n-f\) 大于故障节点 \(f\) 数量,才能达成一致的决策。也就是说,如果故障节点数为 \(f\) ,那么总节点数 \(n\) 满足 \(n \ge 2f + 1\) 才能达成一致的决策。
注: CFT 算法仅需要考虑“故障”情况,而 BFT 算法还需要考虑节点作恶情况。
2. 问题定义
论文把 \(n\) 个将军分为两个角色:指挥官(Commander)和副将(Lieutenant),且指挥官或者副将都可能是叛徒(Traitor)。指挥官的命令只有两类:进攻(Attack)和撤退(Retreat)。
“拜占庭将军问题”采用下面的定义:1 个指挥官发送一个命令给 \(n-1\) 个副将,且需要保证两个要求:
- 所有诚实的将军遵守统一的命令(即统一进攻或者统一撤退);
- 如果指挥官是诚实的,所有的诚实的将军必须准守指挥官的命令。
为了防止指挥官是叛徒,副将们显然不能直接执行指挥官的命令,因为如果指挥官要副将 1 进攻,而要副将 2 撤退,则无法满足前面提到的第 1 个要求了。所以副将之间肯定是要发送消息的。
3. 叛徒数为 f 时,少于 3f + 1 个将军是无解的
现在考虑简单的情况,系统中有 1 个叛徒,那么至少需要多少个将军才可能找到一个满足要求的解呢?答案是至少 4 个将军才有可能找到一个解。2 个的话,这个问题没啥意义;下面看看系统中共 3 个将军能否有解。
先看那个叛徒是副将的情况,不失一般性,假设副将 2 是叛徒(他欺骗副将 1 说指挥官要他撤退),如图 1 所示。这时,副将 1 会不知所措,他根本无法知道谁是叛徒。
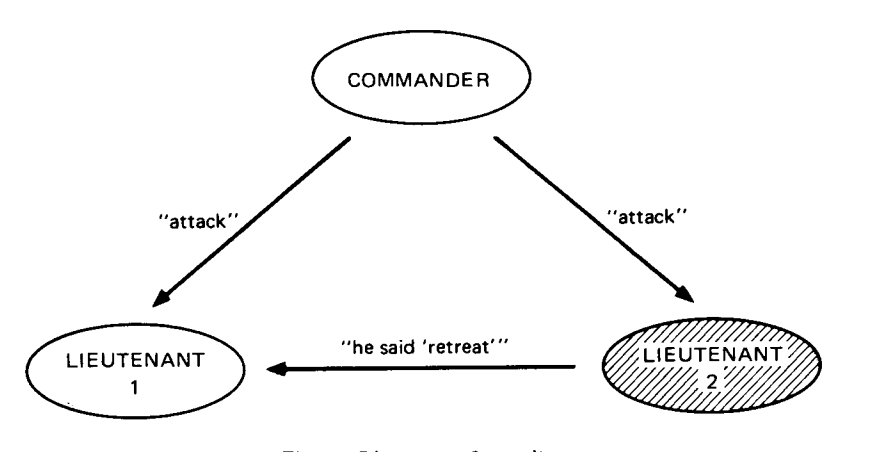
Figure 1: 共 3 个将军,副将 2 是叛徒
再看那个叛徒是指挥官的情况,这时,指挥官要副将 1 进攻,而要副将 2 撤退,由于副将 2 是诚实的,它告诉副将 1 说指挥官要他撤退。这时,副将 1 会不知所措,他根本无法知道谁是叛徒。
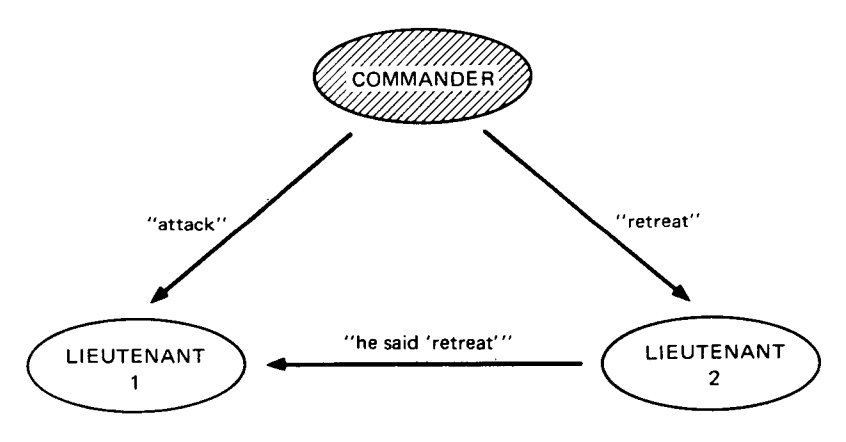
Figure 2: 共 3 个将军,指挥官是叛徒
从而,1 个叛徒时系统中只有 3 个将军是不够的。我们可以得到结论:1 个叛徒时,系统中至少要 4 个将军才可能达成一致决策(满足节 2 中提出的两个要求)。从而, \(f\) 个叛徒时,少于 \(3f + 1\) 个将军是无解的。注意:这个表述是严谨的, 这里并没有说一定有解(因为暂时没有证明存在解),只是说少于 \(3f + 1\) 个将军是无解的。
4. Oral Message 方案
Lamport 给出了一个基于口述消息(Oral Message)的方案。当系统中最多 1 个叛徒时,记为 OM(1),它的做法是: 副将收到指挥官发来的命令后,把命令转发给所有其他副将,副将收到哪种命令(进攻或撤退)多就执行哪种命令。 如图 3 所示。
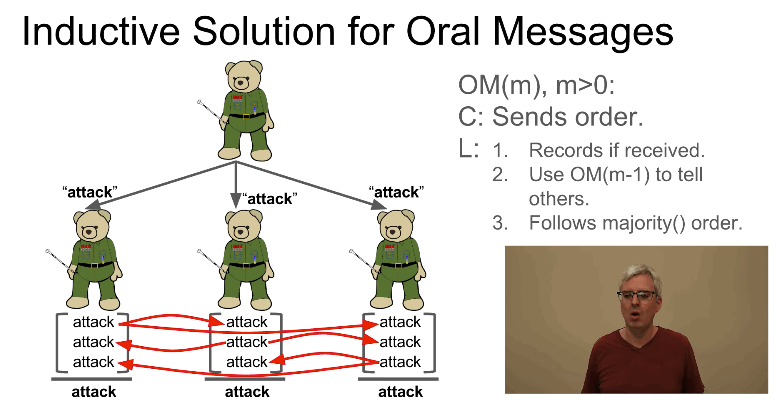
Figure 3: 副将收到哪种命令多就执行哪种命令
现在考虑 1 个叛徒的情况。假设指挥官是叛徒,则如图 4 所示。
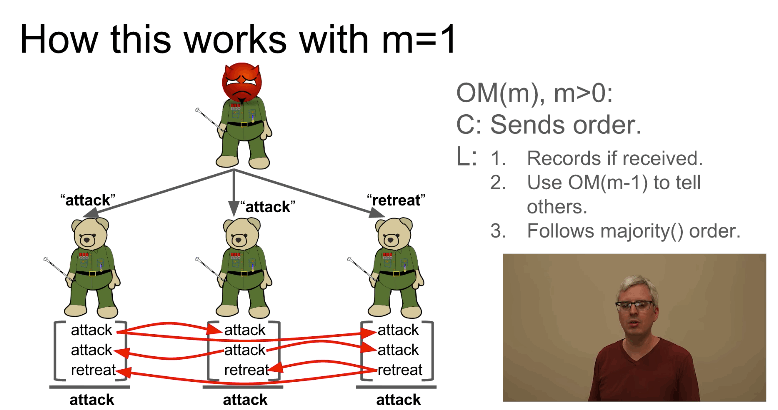
Figure 4: 指挥官是叛徒,副将收到哪种命令多就执行哪种命令,这里忠诚的将军的行为会一致
假设某个副将是叛徒,则如图 5 (注:图 3,4,5 都摘自 https://www.youtube.com/watch?v=_e4wNoTV3Gw&t=1357 )所示。
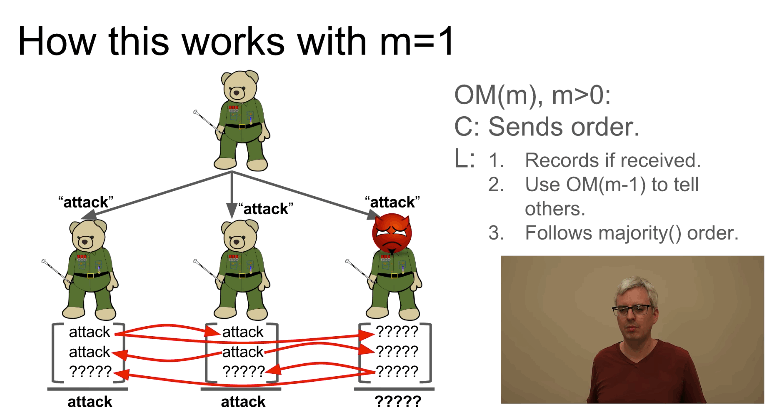
Figure 5: 1 个副将是叛徒,副将收到哪种命令多就执行哪种命令,这里忠诚的将军都会执行指挥官的命令(即进攻)
上面介绍了 OM(1) 的特殊情况。一般情况下,Oral Message 方案是一种递归算法,如图 6 所示。

Figure 6: Oral Message 方案
上面仅演示了系统中最多 1 个叛徒(总节点为 4)的情况,如果想具体地演示一下系统中可能有 2 个叛徒(总节点为 7)的情况,可参考 https://marknelson.us/posts/2007/07/23/byzantine.html
Oral Message 方案在副将之间需要发送很多消息,复杂度为 \(O(n^{f+1})\) 。所以, Oral Message 方案仅仅适应于“节点少”的场景。
注:Lamport 在论文中还给出了另一个方案(Signed Message):发送者对自己发出的消息进行签名。这样,叛徒往不同将军发送不一致消息时,总是会被发现(系统中可以找到矛盾的来自同个叛徒的签名消息),所以叛徒唯一能做的就是延迟(或不)发送消息,这种情况下,有 \(f\) 个叛徒,总将军数 \(n \ge 2f+1\) 即可达成共识。