Birthday Attack and Wagner Attack
Table of Contents
1. Birthday Attack
生日问题(Birthday Problem)是指:一个有 30 名学生的班级,存在两名学生同一天生日的概率是多少?答案是 70.63%,这是一个很可能发生的事件了,因为概率已经超过 50% 了,由于这个结论不符合人的直觉(直觉往往认为概率要比 70.63% 小得多,毕竟一年有 365 天),所以也称为“生日悖论”。
生日问题也可以换一种问法:在一个班级中,最少需要几人,当中两名学生同一天生日的概率才会过半?答案是 23 人。
这里省略具体的推导过程,可参考:阮一峰的网络日志,哈希碰撞与生日攻击 。
1.1. 相关密码学攻击
利用生日问题对密码学设施进行的攻击被称为生日攻击(Birthday Attack)。
比如,对于 64-bit 的哈希函数,有大概 \(1.8 \times 10^{19}\) 种输出,但仅仅需要进行约 \(50\) 亿次计算尝试就能找到哈希碰撞。
又如,Pollard's kangaroo algorithm 和 Pollard's rho algorithm for logarithms 都是利用了生日攻击来尝试破解离散对数问题。
2. Wagner's Generalized Birthday Attack
2002 年,David Wagner 在论文 A Generalized Birthday Problem 中把生日问题进行了推广。
2.1. k-sum 问题
Wagner 提出了一个更加一般化的生日问题(“k-sum 问题”):设有 \(k\) 个列表 \(L_1, L_2, \cdots, L_k\) ,每个列表中的元素都随机产生,元素比特位数为 \(n\) ,寻找 \(x_1 \in L_1, x_2 \in L_2, \cdots, x_k \in L_k\) 使其满足 \(x_1 \oplus x_2 \oplus \dots \oplus x_k = 0\) ,记号 \(\oplus\) 表示按位异或运算。
当 \(k=2\) 时,这就是一个经典的生日问题,因为两个数(学生生日的二进制编码)异或为零就是两个数相等(同一天生日)。
2.2. k-tree 算法(Wagner Attack)
对于 k-sum 问题,Wagner 给出了方法,并称之为 k-tree 算法(其它人一般叫它为 Wagner's Generalized Birthday Attack,简称 Wagner Attack),其中时间复杂度为 \(O(k \cdot 2^{n/(1+\lfloor \lg k \rfloor)})\) ,当 \(k\) 增大时,时间复杂度减少得比较慢。假设 \(k\) 没有限制,如果定义 \(k=2^{\sqrt{n} - 1}\) ,则时间复杂度为 \(O(2^{2\sqrt{n}})\) ,也就是说它是亚指数时间(subexponential)内可以解决 k-sum 问题。
下面以 \(k=4\) 为例介绍 k-tree 算法的主要思想(如图 1 所示):
- \(L_1,L_2,L_3,L_4\) 每个元素都有 \(n\) 比特位,首先我们从 \(L_1,L_2\) 中寻找部分低比特位(如低位置的 \(n/3\) 个比特位)相同的那些元素 \(x_1,x_2\) ,也就是说寻找满足 \(\text{low}_{n/3}(x_1 \oplus x_2) = 0\) 的 \(x_1,x_2\) ,我们得到新列表 \(L_{12} = \{ (x_1 \oplus x_2, x_1, x_2)\}\) ;
- 使用和上一步类似的方法处理 \(L_3,L_4\) ,得到满足 \(\text{low}_{n/3}(x_3 \oplus x_4) = 0\) 的新列表 \(L_{34} = \{ (x_3 \oplus x_4, x_3, x_4)\}\) ;
- 在 \((m, x_1, x_2) \in L_{12}\) 和 \((n, x_3, x_4) \in L_{34}\) 中寻找满足 \(m=n\) 的元组。由于 \(m,n\) 的低 \(n/3\) 个比特位已经都为 \(0\) ,只需要检查剩下的 \(2n/3\) 个比特位是否相同。一旦找到这样的 \(m,n\) ,对应的 \(x_1,x_2,x_3,x_4\) 显然会满足 \(x_1 \oplus x_2 \oplus x_3 \oplus x_4 = 0\) 。
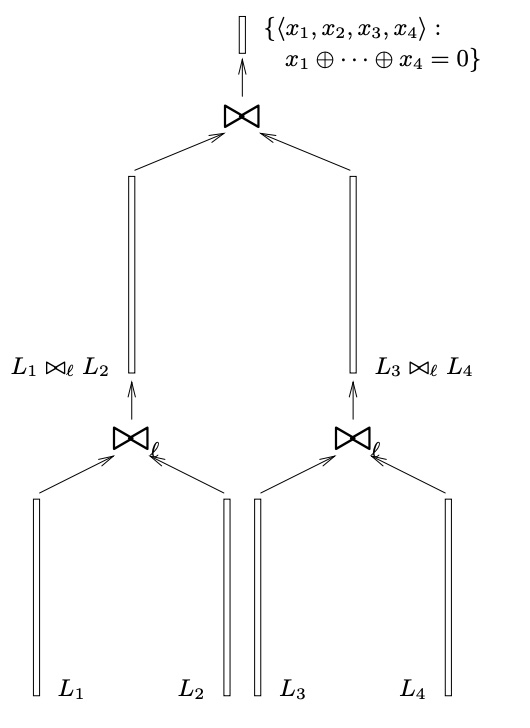
Figure 1: A pictorial representation of k-tree algorithm for the 4-sum problem
当 \(k > 4\) 时,只要 \(k\) 可以表示为 \(2\) 的次方形式,把图 1 中高为 \(2\) 的完全二叉树换成高为 \(\lg k\) 的完全二叉树,就可以得到类似的算法。如果 \(k\) 不能表示为 \(2\) 的次方形式,Wagner 论文中提到也能得到类似算法。
需要指出的是:k-sum 问题中 \(x_1 \oplus x_2 \oplus \dots \oplus x_k = 0\) 最右边的数字 \(0\) 不重要(它是一个不失一般性的选择),可以把这个 \(0\) 换为其它的常数,k-tree 算法一样工作,时间复杂度不变。
2.3. 相关密码学攻击
Wagner Attack 告诉我们: 如果一些随机串(比如 16 个)相加会得到某一个数,那么在不知道原始随机串情况下寻找出满足这个约束(即相加为某个指定数)的另外一些随机串并不是那么难,可以在亚指数时间( \(O(2^{2\sqrt{n}})\) ,其中 \(n\) 为随机串比特位数)内完成。
Wagner 在论文的第 4 节给出了受 k-tree 算法影响的协议,比如:
- Schnorr blind signatures
- Incremental hash (NASD incremental hashing, AdHash, The PCIHF hash)
- Low-weight parity checks
- Group signatures