Calculus
Table of Contents
1. 微积分简介
微积分学(Calculus ,拉丁语意为用来计数的小石头) 是研究极限、微分学、积分学和无穷级数等的一个数学分支。
微积分学在科学、经济学、商业管理学和工业工程学领域有广泛的应用,用来解决那些仅依靠代数学和几何学不能有效解决的问题。微积分学在代数学和解析几何学的基础上建立起来,并包括微分学、积分学二大分支。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行演绎。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法。
参考:
https://zh.wikipedia.org/wiki/%E5%BE%AE%E7%A7%AF%E5%88%86%E5%AD%A6
本文主要参考:“高等数学,同济大学数学系编”
2. 函数的极限
经常看到这样的式子 \(\lim\limits_{x \to x_0}{f(x)} = A\) ,它表示的是函数的极限,其严谨定义如下:
设函数 \(f(x)\) 在点 \(x_0\) 的某一去心邻域内有定义,如果存在常数 \(A\) ,对于任意给定的正数 \(\varepsilon\) (不论它多么小),总存在正数 \(\delta\) ,使得当 \(x\) 满足不等式 \(0 < |x - x_0| < \delta\) 时,对应的函数值 \(f(x)\) 都满足不等式:
\[|f(x) - A| < \varepsilon\]
那么常数 \(A\) 就叫做函数 \(f(x)\) 当 \(x \to x_0\) 时的极限,记作:
\[\lim_{x \to x_0}{f(x)} = A\]
说明:函数在某点处的极限和函数在该点处是否有定义没有关系。如 \(\lim\limits_{x \to 1}{\frac{x^2 - 1}{x-1}} = 2\) ,但 \(\frac{x^2 - 1}{x-1}\) 在 \(x=1\) 处无定义。
3. 导数(Derivative)和微分(Differential)
3.1. 引入导数概念的现实例子
在介绍导数概念前,先看两个现实例子。
3.1.1. 非匀速运动在某时刻的瞬时速度
设某个动点沿 \(y\) 轴作直线运动,已经其位移和时间的函数为 \(y=f(t)\) 。如果是匀速运动,则随意取一段时间,再求得这段时间内所经过的路程,最后拿路程和时间相除就得到了该点的速度。如果不是匀速运动,则如何求得该点在某个时间 \(t_0\) 的速度呢?
首先,取从时刻 \(t_0\) 到 \(t\) 这样一个时间间隔,在这段时间内,动点从位置 \(y_0 = f(t_0)\) 移动到了 \(y = f(t)\) ,在 \(t-t_0\) 这个时间段内动点的平均速度为:
\[\frac{y - y_0}{t - t_0} = \frac{f(t) - f(t_0)}{t - t_0}\]
如果时间间隔很短,则上面比值在实践中也可用来说明动点在时刻 \(t_0\) 的速度。令 \(t \to t_0\) ,取上式的极限,如果这个极限存在,设为 \(v\) ,即有:
\[v = \lim_{t \to t_0}{\frac{f(t) - f(t_0)}{t - t_0}}\]
这时就把这个极限值 \(v\) 称为动点在时刻 \(t_0\) 时刻的瞬时速度。
3.1.2. 切线的斜率
先介绍下曲线在某点处的切线的概念。设有曲线 C 及 C 上一点 M,在点 M 处另取 C 上一点 N,作割线 MN,当点 N 沿曲线 C 趋于点 M 时,如果割线 MN 绕点 M 旋转而趋于极限位置 MT,直线 MT 就称为曲线 C 在点 M 处的 切线 。下面将讨论如何求切线 MT 的斜率。
以曲线 C 为函数 \(y=f(x)\) 的图形为例。
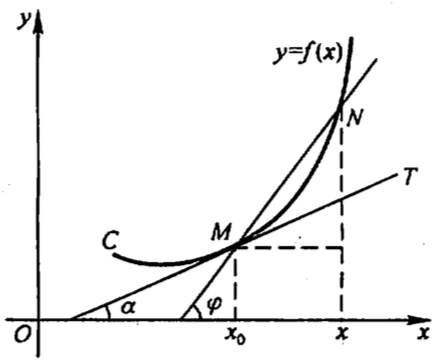
Figure 1: Tangent Line
割线 MN 的斜率为:
\[\tan \varphi = \frac{y - y_0}{x - x_0} = \frac{f(x) - f(x_0)}{x - x)}\]
当点 N 沿曲线 C 趋于点 M 时(即 \(x \to x_0\) ),如果上式的极限存在,设为 \(k\) ,即有:
\[k = \lim_{x \to x_0}{\frac{f(x) - f(x_0)}{x - x_0}}\]
这是就是曲线 C 在点 M 处的切线斜率。
3.2. 导数定义
导数的定义如下:
设函数 \(y=f(x)\) 在点 \(x_0\) 的某个领域内有定义,当自变量 \(x\) 在 \(x_0\) 处取得增量 \(\Delta x\) (点 \(x_0 + \Delta x\) 仍在该领域内)时,相应的函数取得增量 \(\Delta y=f(x_0 + \Delta x) - f(x_0)\) ;如果 \(\Delta y\) 与 \(\Delta x\) 之比当 \(\Delta x \to 0\) 时的极限存在,则称函数 \(y = f(x)\) 在点 \(x_0\) 处 可导 ,并称这个极限为函数 \(y=f(x)\) 在点 \(x_0\) 处的 导数 ,记为 \(f'(x_0)\) ,即:
\[f'(x_0) = \lim_{\Delta x \to 0}{\frac{\Delta y}{\Delta x}} = \lim_{\Delta x \to 0}{\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}}\]
\(f'(x_0)\) 还有其它一些记法: \(y'|_{x=x_0}\) 或者 \(\left.\frac{dy}{dx}\right\vert_{x=x_0}\) 或者 \(\left.\frac{df(x)}{dx}\right\vert_{x=x_0}\)
在 \(x_0\) 处的导数的定义式也可取不同的形式,常见的有:
\[f'(x_0) = \lim_{h \to 0}{\frac{f(x_0 + h) - f(x_0)}{h}}\]
和
\[f'(x_0) = \lim_{x \to x_0}{\frac{f(x) - f(x_0)}{x - x_0}}\]
上面讲的是函数在某一点处可导,如果函数 \(y=f(x)\) 在区间 \(I\) 内的每点处都可导,就称函数 \(f(x)\) 在区间 \(I\) 内可导,这时,对于任一 \(x \in I\) ,都对应着 \(f(x)\) 的一个确定的导数值,这样就构成了一个新的函数,这个函数叫做 \(y=f(x)\) 的导函数,记作 \(y'\) 或者 \(f'(x)\) 或者 \(\frac{dy}{dx}\) 或者 \(\frac{df(x)}{dx}\) ,即函数 \(f(x)\) 的导函数的定义为:
\[f'(x) = \lim_{\Delta x \to 0}{\frac{f(x + \Delta x) - f(x)}{\Delta x}}\]
导函数 \(f'(x)\) 简称导数(Derivative),而 \(f'(x_0)\) 就是 \(f'(x)\) 在 \(x_0\) 处的值。
3.2.1. 实例:求解导数
求函数 \(f(x) = C\) ( \(C\) 为常数) 的导数。
\[f'(x) = \lim_{h \to 0}{\frac{f(x+h) - f(x)}{h}} = \lim_{h \to 0}{\frac{C - C}{h}} = 0\]
即常数的导数等于零。
3.2.2. 基本初等函数求导公式

Figure 2: 基本初等函数求导公式
参考:
Common Derivatives and Integrals: http://tutorial.math.lamar.edu/pdf/Common_Derivatives_Integrals.pdf
The Most Important Derivatives and Antiderivatives to Know: http://www.dummies.com/how-to/content/the-most-important-derivatives-and-antiderivatives.html
3.2.3. 函数的和、差、积、商求导法则
设 \(u=u(x), v=v(x)\) 都可导,则:
(1) \((u \pm v)' = u' \pm v'\)
(2) \((uv)' = u'v + uv'\)
(3) \(\left( \dfrac{u}{v} \right) = \dfrac{u'v - uv'}{v^2}, v \ne 0\)
3.2.4. 复合函数求导法则(链式法则)
设 \(y = f(u)\) ,而 \(u=g(x)\) 且 \(f(u)\) 及 \(g(x)\) 都可导,则复合函数 \(y = f[g(x)]\) 的导数为:
\[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\]
注:复合函数的求导法则可以推广到三个或更多个中间变量的情形。
3.3. 函数的微分
3.3.1. 函数微分的定义
设函数 \(y = f(x)\) 在某区间内有定义, \(x_0\) 及 \(x_0 + \Delta x\) 在这个区间内,如果增量:
\[\Delta y = f(x_0 + \Delta x) - f(x_0)\]
可表示为:
\[\Delta y = A \Delta x + o(\Delta x)\]
其中, \(A\) 是不依赖于 \(\Delta x\) 的常数,那么称函数 \(y = f(x)\) 在点 \(x_0\) 是可微的,而 \(A \Delta x\) 叫做函数 \(y = f(x)\) 在点 \(x_0\) 相应于自变量增量 \(\Delta x\) 的 微分(Differential) ,记作 \(dy\) ,即有:
\[dy = A \Delta x\]
如果把式 \(\Delta y = A \Delta x + o(\Delta x)\) 两边除以 \(\Delta x\) ,可得: \(\frac{\Delta y}{\Delta x} = A + \frac{o(\Delta x)}{\Delta x}\) 。从而,当 \(\Delta x \to 0\) 时,有:
\[A = \lim_{\Delta x \to 0}{\frac{\Delta y}{\Delta x}} = f'(x_0)\]
函数 \(y=f(x)\) 在任意点 \(x\) 的微分,称为 函数的微分 ,记作 \(dy\) 或 \(df(x)\) ,有:
\[dy = f'(x) \Delta x\]
总结: 微分是对函数的局部变化的一种线性描述。
3.3.2. 实例:计算函数的微分
实例:求函数 \(y=x^2\) 在 \(x=1\) 和 \(x=3\) 处的微分。
解:函数 \(y=x^2\) 在 \(x=1\) 处的微分为: \(dy|_{x=1} = (x^2)'|_{x=1} \Delta x = 2 \Delta x\) ;在 \(x=3\) 处的微分为: \(dy|_{x=3} = (x^2)'|_{x=3} \Delta x = 6 \Delta x\) 。
实例:求函数 \(y=x^3\) 当 \(x=2, \Delta x = 0.02\) 时的微分。
解: \(dy \Bigr|_{\substack{x=2 \\ \Delta x = 0.02}} = (x^3)' \Delta x \Bigr|_{\substack{x = 2 \\ \Delta x = 0.02}} = 3 \cdot 2^2 \cdot 0.02 =0.24\)
3.3.3. 微分在近似计算中的应用
在工程问题中,经常遇到一些复杂的计算公式,直接计算比较麻烦,利用微分可以把复杂的计算公式用简单的近似公式来代替(用 \(dy\) 近似代替 \(\Delta y\) )。
由前面介绍的知识,有:
\[\Delta y \approx dy = f'(x_0) \Delta x, \qquad (\Delta x \to 0)\]
上式也可写为:
\[\Delta y = f(x_0 + \Delta x) - f(x_0) \approx f'(x_0) \Delta x, \qquad (\Delta x \to 0)\]
或:
\[f(x_0 + \Delta x) \approx f(x_0) + f'(x_0) \Delta x, \qquad (\Delta x \to 0)\]
上面这些式子都可以用来作近似计算。
3.3.3.1. 实例:估算球体镀层体积
实例:有一批半径为 1 cm 的球,为了提高球面的光洁度,要镀上一层铜,厚度定为 0.01 cm,估计一下每只球需要用多少克铜(铜的密度为 8.9 克/立方厘米)?
解:因为镀层的体积等于两个球体的体积之差,所以它就球体体积 \(V=\frac{4}{3} \pi R^3\) 当 \(R\) 自 \(R_0\) 取得增量 \(\Delta R\) 时的增量 \(\Delta V\) 。
\[\Delta V \approx dV = \left.\left(\frac{4}{3} \pi R^3\right)' \right|_{\substack{R=R_0=1 \\ \Delta R = 0.01}} \Delta R = 4 \times 3.14 \times 1^2 \times 0.01 \approx 0.13 (cm^3)\]
所以,需要的铜为 \(0.13 \times 8.9 \approx 1.16 (g)\) 。
3.3.3.2. 实例:工程中常用近似公式
工程中有一些常用的近似公式(当 \(|x|\) 很小时适用),如:
- \(\sqrt[n]{1+x} \approx 1 + \frac{1}{n} x\)
- \(\sin x \approx x\)
- \(\tan x \approx x\)
- \(e^x \approx 1 + x\)
- \(\ln (1 + x) \approx x\)
上面这些近似公式可以由 \(f(x_0 + \Delta x) \approx f(x_0) + f'(x_0) \Delta x\) 推导出来。
实例:计算 \(\sqrt{1.05}\) 的近似值。
解: \(\sqrt{1.05} = \sqrt{1 + 0.05} \approx 1 + \frac{1}{2}(0.05) = 1.025\)
说明:如果直接开方,可得 \(\sqrt{1.05} = 1.02470\) 将两个结果比较,可以看出上面近似值的误差很小。
4. 导数应用
4.1. 求函数的极值
在函数取得极值处,曲线的切线是水平的,但曲线上有水平切线的地方,函数不一定取得极值。如下图中 \(x=x_3\) 处有水平切线,但 \(f(x_3)\) 不是极值。
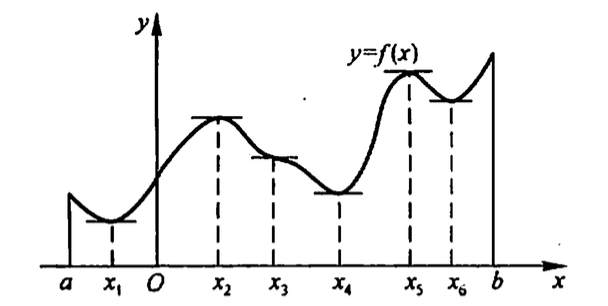
Figure 3: 函数极值
关于利用导数求函数极值,有下面三个定理。
定理(必要条件):设函数 \(f(x)\) 在 \(x_0\) 处可导,且在 \(x_0\) 处取得极值,那么 \(f'(x_0)=0\) 。
定理(第一充分条件):设函数 \(f(x)\) 在 \(x_0\) 处连续,且在 \(x_0\) 的某去心邻域 \(\mathring{U}(x_0, \delta)\) 内可导,有:
(1) 若 \(x \in (x_0 - \delta, x_0)\) 时, \(f'(x) > 0\) ,而 \(x \in (x_0, x_0 + \delta\) 时, \(f'(x) < 0\) ,则 \(f(x)\) 在 \(x_0\) 处取得极大值;
(2) 若 \(x \in (x_0 - \delta, x_0)\) 时, \(f'(x) < 0\) ,而 \(x \in (x_0, x_0 + \delta\) 时, \(f'(x) > 0\) ,则 \(f(x)\) 在 \(x_0\) 处取得极小值;
(3) 若 \(x \in \mathring{U}(x_0, \delta)\) 时, \(f'(x)\) 的符号保持不变,则 \(f(x)\) 在 \(x_0\) 处没有极值。
定理(第二充分条件):设函数 \(f(x)\) 在 \(x_0\) 处具有二阶导数且 \(f'(x_0) = 0, f''(x_0) \ne 0\) ,那么:
(1) 当 \(f''(x_0) < 0\) 时,函数 \(f(x)\) 在 \(x_0\) 处取得极大值;
(2) 当 \(f''(x_0) > 0\) 时,函数 \(f(x)\) 在 \(x_0\) 处取得极小值。
4.2. 泰勒公式(用多项式表示复杂函数)
对于一些复杂的函数,这了便于研究,往往希望用一些简单的函数来近似。
泰勒公式:如果函数 \(f(x)\) 在含有 \(x_0\) 的某个开区间 \((a,b)\) 内具有直到 \((n+1)\) 阶的导数,则对任一 \(x \in (a,b)\) ,有:
\[f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}{2!} (x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x)\]
其中
\[R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} = o[(x-x_0)^n] \qquad (\xi \, \text{between} \, x_0 \, \text{and} \, x)\]
实例:我们知道 \((e^x)'=e^x\) ,利用泰勒公式容易求得:
\[e^x = 1 + x + \frac{x^2}{2!} + \cdots + \frac{x^n}{n!} + \frac{e^{\theta x}}{(n+1)!}x^{n+1} \qquad (0 < \theta < 1)\]
如果省掉高阶无穷小量,可得近似公式:
\[e^x \approx 1 + x + \frac{x^2}{2!} + \cdots + \frac{x^n}{n!}\]
5. 不定积分
前面介绍了如何求一个函数的导函数,现在将讨论它的反问题,即如果寻找一个可导函数,便它的导数等于已知函数。这就是积分学的基本问题之一。
先介绍一下“原函数”的概念。
如果在区间 \(I\) 上,可导函数 \(F(x)\) 的导函数为 \(f(x)\) ,即有:
\[F'(x) = f(x), \qquad x \in I\]
那么函数 \(F(x)\) 就称为 \(f(x)\) 在区间 \(I\) 上的 原函数 。
5.1. 不定积分定义
在区间 \(I\) 上,函数 \(f(x)\) 的带有任意常数项的原函数称为 \(f(x)\) (或 \(f(x)dx\) )在区间 \(I\) 上的 不定积分(Indefinite Integral) ,记作:
\[\int f(x) \, \mathrm{d}x\]
其中记号 \(\int\) 称为积分号, \(f(x)\) 称为被积函数, \(f(x) \, \mathrm{d}x\) 称为被积表达式, \(x\) 称为积分变量。
显然,如果 \(F(x)\) 是 \(f(x)\) 在区间 \(I\) 上的一个原函数,那么有:
\[\int f(x) \, \mathrm{d}x = F(x) + C\]
其中 \(C\) 是任意常数项。
5.1.1. 实例:求不定积分
实例:求 \(\int x^2 \, \mathrm{d}x\)
解:由于 \(\left( \frac{x^3}{3} \right)' = x^2\) ,所以 \(\frac{x^3}{3}\) 是 \(x^2\) 的一个原函数,从而 \(\int x^2 \, \mathrm{d}x = \frac{x^3}{3} + C\)
6. 定积分
6.1. 定积分定义
设函数 \(f(x)\) 在 \([a,b]\) 上有界,在 \([a,b]\) 中任意插入若干个分点
\[a = x_0 < x_1 < x_2 < \cdots < x_{n-1} < x_n = b\]
把区间 \([a,b]\) 分成 \(n\) 个小区间
\[[x_0, x_1], [x_2,x_3], \cdots, [x_{n-1}, x_n]\]
各个小区间的长度依次为
\[\Delta x_1 = x_1 - x_0, \Delta x_2 = x_2 - x_1, \cdots, \Delta x_n = x_n - x_{n-1}\]
在每个小区间 \([x_{i-1}, x_i]\) 上任取一点 \(\xi_i \, (x_{i-1} \le \xi_i \le x_i)\) ,作函数值 \(f(\xi_i)\) 与小区间长度 \(\Delta x_i\) 的乘积 \(f(\xi_i) \Delta x_i \, (i=1,2,\cdots,n)\) ,并作出和
\[S= \sum_{i=1}^n f(\xi_i) \Delta x_i\]
记 \(\lambda = \max \{ \Delta x_i, \Delta x_2, \cdots, \Delta x_n \}\) ,如果不论对 \([a,b]\) 怎样划分,也不论在小区间 \([x_{i-1}, x_i]\) 上点 \(\xi_i\) 怎样选取,只要当 \(\lambda \to 0\) 时,和 \(S\) 总趋于确定的极限 \(I\) ,那么称这个极限 \(I\) 为函数 \(f(x)\) 在区间 \([a,b]\) 上的定积分,简称 积分(Integral) ,记作 \(\int_a^b f(x) \, \mathrm{d}x\) ,即有:
\[\int_a^b f(x) \, \mathrm{d}x = \lim_{\lambda \to 0} \sum_{i=1}^{n} f(\xi_i) \Delta x_i\]
6.1.1. 定积分几何意义
定积分 \(\int_a^b f(x) \, \mathrm{d}x\) 在几何上表示曲线 \(y=f(x)\) 、两条直线 \(x=a\) 和 \(x=b\) 与 \(x\) 轴所围成的曲边梯形的面积。如果所围图形出现在 \(x\) 轴的下方,则 \(\int_a^b f(x) \, \mathrm{d}x\) 表示 \(x\) 轴上方图形面积减去 \(x\) 轴下方图形面积所得之差。
Figure 4: 定积分几何意义(摘自 Integral Wikipedia)
6.2. 微积分基本定理(牛顿-莱布尼茨公式)
直接用定积分的定义来求解定积分是比较繁琐的。我们需要寻找更简单的方法。
微积分基本定理:如果函数 \(F(x)\) 是连续函数 \(f(x)\) 在区间 \([a,b]\) 上的一个原函数,则:
\[\int_a^b f(x) \, \mathrm{d}x = F(b) - F(a)\]
上式也记作:
\[\int_a^b f(x) \, \mathrm{d}x = [F(x)]_a^b\]
这个定理又称 牛顿-莱布尼茨公式 。
这个定理表明: 一个连续函数在区间 \([a,b]\) 上的定积分等于它的任一个原函数在区间 \([a,b]\) 上的增量,这大大简化了定积分的计算过程。
微积分基本定理的证明可参考:
Fundamental theorem of calculus: https://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus
6.2.1. 实例:计算定积分
实例:计算定积分 \(\int_0^1 x^2 \, \mathrm{d}x\)
解:由于 \(\frac{x^3}{3}\) 是 \(x^2\) 的一个原函数,根据牛顿-莱布尼茨公式,有
\[\int_0^1 x^2 \, \mathrm{d}x = \left[ \frac{x^3}{3} \right]_0^1 = \frac{1}{3} - 0 = \frac{1}{3}\]
6.3. 积分表
常见函数的积分,有现成的表可查。
参考:
Integral Table: http://www.mathwords.com/i/integral_table.htm
Lists of integrals: https://en.wikipedia.org/wiki/Lists_of_integrals
7. 多元函数微积分(Vector Calculus)
前面内容中讨论的函数都是一元函数(只有一个自变量)。在很多实际问题中,经常会遇到多个变量之间的依赖关系,如圆柱体的体积 \(V\) 和它的底半径 \(r\) 和高 \(h\) 之间具有关系 \(V = \pi r^2 h\) 。
后面将讨论多元函数(有多个自变量的函数)的微积分,重点研究二元函数。
说明:概念“multivariable calculus”和“vector calculus”是相同的。
参考:
Vector Calculus, by Michael Corral(online pdf book): http://www.mecmath.net/calc3book.pdf
7.1. 偏导数(Partial Derivative)
对于一元函数时,导数就是函数的变化率。多元函数的自变量不止一个,因变量和自变量的关系要比一元函数复杂得多。多元函数关于其中一个自变量(把其它自变量看做常量)的变化量称为关于这个自变量的偏导数。
偏导数定义:设函数 \(z = f(x,y)\) 在点 \((x_0, y_0)\) 的某一邻域内有定义,当 \(y\) 固定在 \(y_0\) 而 \(x\) 在 \(x_0\) 处有增量 \(\Delta x\) 时,相应的函数有增量 \(f(x_0 + \Delta x, y_0) - f(x_0, y_0)\) ,如果下面极限
\[\lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x, y_0) - f(x_0, y_0)}{\Delta x}\]
存在,则称此极限为函数 \(x=f(x,y)\) 在点 \((x_0, y_0)\) 处 对 \(x\) 的偏导数 ,记作:
\(\left. \frac{\partial z}{\partial x} \right|_{\substack{x=x_0 \\ y=y_0}}\) 或者 \(\left. \frac{\partial f}{\partial x} \right|_{\substack{x=x_0 \\ y=y_0}}\) 或者 \(\left. z_y \right|_{\substack{x=x_0 \\ y=y_0}}\) 或者 \(f_x(x_0, y_0)\) 。故有:
\[\left. \frac{\partial z}{\partial x} \right|_{\substack{x=x_0 \\ y=y_0}} = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x, y_0) - f(x_0, y_0)}{\Delta x}\]
类似地,函数 \(z=f(x,y)\) 在点 \((x_0, y_0)\) 处 对 y 的偏导数 为:
\[\left. \frac{\partial z}{\partial y} \right|_{\substack{x=x_0 \\ y=y_0}} = \lim_{\Delta y \to 0} \frac{f(x_0, y_0 + \Delta y) - f(x_0, y_0)}{\Delta y}\]
如果函数 \(z=f(x,y)\) 在区域 \(D\) 内每一点 \((x,y)\) 处对 \(x\) 的偏导数都存在,那么这个偏导数就是 \(x\) 和 \(y\) 的函数,它被称为函数 \(z=f(x,y)\) 对自变量 \(x\) 的偏导函数(Partial derivative) ,记作: \(\frac{\partial z}{\partial x}\) 或者 \(\frac{\partial f}{\partial x}\) 或者 \(z_x\) 或者 \(z'_x\) 或者 \(f_x(x,y)\) 或者 \(f'_x(x,y)\) 。类似地,可以定义函数 \(z=f(x,y)\) 对自变量 \(y\) 的偏导数 ,记作:\(\frac{\partial z}{\partial y}\) 或者 \(\frac{\partial f}{\partial y}\) 或者 \(z_y\) 或者 \(z'_y\) 或者 \(f_y(x,y)\) 或者 \(f'_y(x,y)\) 。
7.1.1. 求多元函数的偏导数
求多元函数的偏导数,并不需要新方法,因为只有一个自变量在变动,另一个自变量是看做固定的。
实例:求 \(z = x^2 + 3xy + y^2\) 的偏导数。
解:把 \(y\) 看做常量,得 \(\frac{\partial z}{\partial x} = 2x + 3y\) ;把 \(x\) 看做常量,得 \(\frac{\partial z}{\partial y} = 3x + 2y\) 。
7.1.2. 偏导数的几何意义(函数值沿坐标轴方向的变化率)
二元函数 \(z = f(x,y)\) 在点 \((x_0, y_0)\) 的偏导数有下述几何意义。
设 \(M_0 (x_0, y_0, f(x_0,y_0)\) 为曲面 \(z = f(x,y)\) 上的一点,过 \(M_0\) 作平面 \(y=y_0\) ,截此曲面得一曲线,此曲线在平面 \(y=y_0\) 上的方程为 \(z = f(x, y_0)\) ,则偏导数 \(f_x (x_0, y_0)\) 就是这曲线在点 \(M_0\) 处的切线 \(M_0 T_x\) 对 \(x\) 轴的斜率。
同样,偏导数 \(f_y (x_0, y_0)\) 的几何意义是曲面被平面 \(x = x_0\) 所截得的曲线在点 \(M_0\) 处的切线 \(M_0 T_y\) 对 \(y\) 轴的斜率。
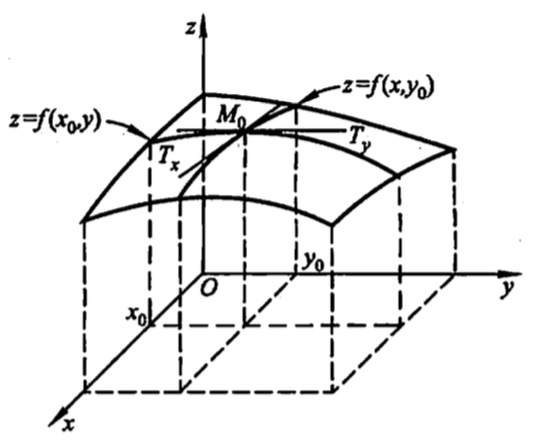
Figure 5: 偏导数的几何意义
总结: 多元函数的偏导数反映了函数值沿坐标轴方向的变化率。
7.1.3. 高阶偏导数
设函数 \(z = f(x,y)\) 在区域 \(D\) 内具有偏导数 \(f_x(x,y)\) 和 \(f_y(x,y)\) ,在 \(D\) 内它们都是 \(x,y\) 的函数。如果这两个函数的偏导数也存在,则称它们是函数 \(z = f(x,y)\) 的 二阶偏导数 。按照对变量求导次序的不同,有下列四个二阶偏导数:
\[\frac{\partial}{\partial x} \left( \frac{\partial z}{\partial x} \right) = \frac{\partial^2 z}{\partial x^2} = f_{xx}(x,y)\]
\[\frac{\partial}{\partial y} \left( \frac{\partial z}{\partial x} \right) = \frac{\partial^2 z}{\partial x \partial y} = f_{xy}(x,y)\]
\[\frac{\partial}{\partial x} \left( \frac{\partial z}{\partial y} \right) = \frac{\partial^2 z}{\partial y \partial x} = f_{yx}(x,y)\]
\[\frac{\partial}{\partial y} \left( \frac{\partial z}{\partial y} \right) = \frac{\partial^2 z}{\partial y^2} = f_{yy}(x,y)\]
其中第二、三个偏导数称为混合偏导数(可以证明它们是相等的)。类似地,可得其他更高阶的偏导数。
7.2. 偏导数应用——求多元函数的极值
7.2.1. 二元函数无条件极值
对于函数的自变量,除了限制在函数的定义域内以处,并不其他条件,这称为无条件极值。函数的无条件极值问题,可以利用下面定理求得。
定理(必要条件):设函数 \(z = f(x,y)\) 在点 \((x_0, y_0)\) 具有偏导数,且在点 \((x_0, y_0)\) 处有极值,则有: \(f_x(x_0,y_0) = 0, \quad f_y(x_0,y_0) = 0\) 。
定理(充分条件):设函数 \(z = f(x,y)\) 在点 \((x_0, y_0)\) 的某邻域内连续且有一阶及二阶连续偏导数,又 \(f_x(x_0,y_0) = 0, \quad f_y(x_0,y_0) = 0\) ,令
\[f_{xx}(x_0,y_0) = A, \, f_{xy}(x_0,y_0) = B, \, f_{yy}(x_0,y_0) = C\]
则 \(f(x,y)\) 在 \((x_0, y_0)\) 处是否取得极值的条件如下:
(1) \(AC-B^2 > 0\) 时具有极值,且当 \(A < 0\) 时有极大值,当 \(A > 0\) 时有极小值;
(2) \(AC-B^2 < 0\) 时没有极值;
(3) \(AC-B^2 = 0\) 时可能有极值,也可能没有极值,还需另作讨论。
说明:上面定理可以推广到求解三元或更多元函数的极值,请看下节。
7.2.2. 多元函数无条件极值
假设 \(n\) 元函数 \(f(x_1,x_2,\cdots,x_n)\) 在定义域内二阶连续可导,如何求解它的极值呢?
第一步,求驻点。
求解下面方程组:
\[\begin{cases}
\frac{\partial f}{\partial x_1} = 0 \\
\frac{\partial f}{\partial x_2} = 0 \\
\vdots \\
\frac{\partial f}{\partial x_n} = 0 \\
\end{cases}\]
求得的解即为驻点,设共有 \(k\) 个解,记作 \(M_i, (i=1,2,\cdots,k)\)
第二步,判断驻点是否为极值点。
求函数 \(f(x_1,x_2,\cdots,x_n)\) 的 Hessian 矩阵:
\[\nabla^2 f(\boldsymbol{x}) = \left( \begin{array}{cccc} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \\
\end{array} \right)\]
依次验证每个驻点 \(M_i, (i=1,2,\cdots,k)\) :
(1) 如果 \(\nabla^2 f(M_i)\) 是正定矩阵,则该点是一个极小值;
(2) 如果 \(\nabla^2 f(M_i)\) 是负定矩阵,则该点是一个极大值;
(3) 如果 \(\nabla^2 f(M_i)\) 是不定矩阵,则该点不是极值点。
注:正定矩阵等概念请参考线性代数或矩阵论相关资料。
7.2.3. 条件极值(拉格朗日乘数法)
除前面讨论的无条件极值。在实例问题中,对可能会对自变量附加条件,这称为条件极值(这里只讨论附加约束条件为等式的情况)。
例如,求表面积为 \(a^2\) 而体积为最大的长方体的体积问题。可化为满足条件 \(2(xy+yz+zx)=a^2\) ,求 \(V=xyz\) 的极值。对于这个条件极值问题,可以用下面方法转换为无条件极值问题:由 \(2(xy+yz+zx)=a^2\) 求出 \(z\) 关于 \(x,y\) 的函数,再代入到 \(V=xyz\) 中,可得到 \(V= \frac{xy}{2} \left( \frac{a^2 - 2xy}{x+y} \right)\) ,这样就把条件极值问题化为了无条件极值问题。
但在很多情形下,将条件极值问题化为了无条件极值问题是很困难的。下面介绍的拉格朗日乘数法可以帮助我们求解条件极值。
拉格朗日乘数法(Lagrange multiplier):要找函数 \(z = f(x,y)\) 在附加条件 \(\varphi(x,y)=0\) 下的可能极值点,可以先作拉格朗日函数
\[L(x,y) = f(x,y) + \lambda \varphi(x,y)\]
其中 \(\lambda\) 为参数,求其对 \(x\) 与 \(y\) 的一阶偏导数,并使之为零,然后与方程 \(\varphi(x,y)=0\) 联立起来,组成方程组:
\[\begin{cases}
f_x(x,y) + \lambda \varphi_x(x,y) = 0 \\
f_y(x,y) + \lambda \varphi_y(x,y) = 0 \\
\varphi(x,y) = 0
\end{cases}\]
由上面方程组解出 \(x\) 和 \(y\) 就是函数 \(f(x,y)\) 在附加条件 \(\varphi(x,y) = 0\) 下的可能极值点。
说明 1:至于可能极值点是否是极值点,在实际问题中往往可根据问题本身的性质来判定。
说明 2:极值点是极小值点还是极大值点,可以由 \(f\) 的 Hessian 矩阵在该点是否是正定矩阵来判断。如果 Hessian 矩阵在极值点是正定矩阵,则该极值点为极小值点;如果 Hessian 矩阵在极值点是负定矩阵,则该极值点为极大值点。
上面方法可以推广到自变量多于两个,条件多于一个的情形。如 \(u = f(x,y,z,t)\) 在两个附加条件 \(\varphi(x,y,z,t) = 0, \; \phi(x,y,z,t) = 0\) 下的极值,可以先作拉格朗日函数\(L(x,y,z,t) = f(x,y,z,t) + \lambda \varphi(x,y,z,t) + \mu \phi(x,y,z,t)\) ,对它关于 \(x,y,z,t\) 求一阶偏导数再与附加条件联立得到一个方程组,方程组的解即是可能的极值点。
参考:
Lagrange Multiplier: http://mathworld.wolfram.com/LagrangeMultiplier.html
7.2.4. 实例:拉格朗日乘数法求条件极值
例:求表面积为 \(a^2\) 而体积为最大的长方体的体积。
解:设长方体的三棱长为 \(x,y,z\) ,则问题就是在条件
\[\varphi(x,y,z) = 2(xy + yz + zx) - a^2 =0\]
下,求函数
\[V=xyz \quad (x>0, y>0, z>0)\]
的最大值。
作拉格朗日函数
\[L(x,y,z) = xyz + \lambda (2xy + 2yz + 2zx - a^2)\]
求其对 \(x,y,z\) 的偏导数,并使之为零。再和 \(\varphi(x,y,z) = 0\) 联立,得到方程组:
\[\begin{cases}
yz + 2 \lambda (y+z) = 0 \\
xz + 2 \lambda (x+z) = 0 \\
xy + 2 \lambda (y+x) = 0 \\
2(xy + yz + zx) - a^2 = 0
\end{cases}\]
由上面方程组,可以求得:
\[x=y=z=\frac{\sqrt{6}}{6}a\]
这是唯一可能的极值点。由于问题本身可知最大值一定存在,所以最大值就在这个可能的极值点处取得。故表面积为 \(a^2\) 的长方体的最大体积为 \(V=\frac{\sqrt{6}}{36}a^3\)
7.3. 方向导数(Directional Derivative)和梯度(Gradient)
多元函数的偏导数反映了函数值沿坐标轴方向的变化率,而许多实际问题中常常还需要掌握函数在某点处沿某一指定方向的变化率。例如,热空气要向冷的地方流动,气象学中要确定大气温度、气压沿某个方向的变化率。这就引出了方向导数的概念。
参考:
“方向导数、梯度” http://math.fudan.edu.cn/gdsx/KEJIAN/%E6%96%B9%E5%90%91%E5%AF%BC%E6%95%B0%E5%92%8C%E6%A2%AF%E5%BA%A6.pdf
7.3.1. 方向导数定义
函数方向导数定义如下:
设 \(f\) 是定义于 \(R^n\) 中某个区域 \(D\) 上的函数,点 \(P_0 \in D\) , \(l\) 为一给定的非零向量, \(P\) 为一动点,向量 \(P_0P\) 与 \(l\) 的方向始终一致。如果极限
\[\lim_{||P_0P|| \to 0}\frac{f(P) - f(P_0)}{||P_0P||}\]
存在,则称此极限为 函数 \(f\) 在 \(P_0\) 处沿 \(l\) 方向的方向导数 ,记作 \(\left. \frac{\partial f}{\partial l} \right|_{P_0}\) ,即有:
\[\left. \frac{\partial f}{\partial l} \right|_{P_0} = \lim_{||P_0P|| \to 0}\frac{f(P) - f(P_0)}{||P_0P||}\]
常用下面定理求解方法导数:
若函数 \(f(x_1, x_2, \cdots, x_n)\) 在点 \(P_0\) 处可微,那么函数在该点沿任一方向 \(l\) 的方向导数存在,且有:
\[\left. \frac{\partial f}{\partial l} \right|_{P_0} = \left. \frac{\partial f}{\partial x_1} \right|_{P_0} \cos \alpha_1 + \left. \frac{\partial f}{\partial x_2} \right|_{P_0} \cos \alpha_2 + \cdots + \left. \frac{\partial f}{\partial x_n} \right|_{P_0} \cos \alpha_n \]
其中, \(\cos \alpha_1, \cos \alpha_2, \cdots, \cos \alpha_n\) 是方向 \(l\) 的方向余弦。
方向余弦的定义如下:
设 \(l\) 是一个 \(n\) 维非零向量, \(l_0 = \frac{l}{||l||}\) ,即 \(l_0\) 是与 \(l\) 同向的单位向量。取 \(0 \le \alpha_i \le \pi\) ,使 \(l_0 = (\cos \alpha_1, \cos \alpha_2, \cdots, \cos \alpha_n)\) ,显然会有 \(\cos^2 \alpha_1 + \cos^2 \alpha_2 + \cdots + \cos^2 \alpha_n = 1\) ,称 \(\cos \alpha_1, \cos \alpha_2, \cdots, \cos \alpha_n\) 为 向量 \(l\) 的方向余弦 。
7.3.2. 实例:求方向导数
实例:求 \(f(x,y,z) = xy + yz + zx\) 在点 \((1,1,2)\) 沿方向 \(l\) 的方向导数,其中 \(l\) 的方向角分别为 \(60^o,45^o,60^o\)
解:方向 \(l\) 的方向余弦为:
\[(\cos60^o, \cos45^o, \cos60^o) = (\frac{1}{2}, \frac{\sqrt{2}}{2}, \frac{1}{2})\]
又,函数 \(f(x,y,z)\) 在点 \((1,1,2)\) 处对 \(x,y,z\) 的偏导数为:
\[\left. \frac{\partial f}{\partial x} \right|_{(1,1,2)} = \left. (y+z) \right|_{(1,1,2)} = 3\]
\[\left. \frac{\partial f}{\partial y} \right|_{(1,1,2)} = \left. (x+z) \right|_{(1,1,2)} = 3\]
\[\left. \frac{\partial f}{\partial z} \right|_{(1,1,2)} = \left. (y+x) \right|_{(1,1,2)} = 2\]
所以有:
\[\left. \frac{\partial f}{\partial l} \right|_{(1,1,2)} = 3 \cdot \frac{1}{2} + 3 \cdot \frac{\sqrt{2}}{2} + 2 \cdot \frac{1}{2} = \frac{1}{2}(5 + 3 \sqrt{2})\]
7.3.3. 梯度(是个向量,这个方向上函数值增加最快)
设二元函数 \(f(x,y)\) 在平面区域 \(D\) 内具有一阶连续偏导数,则对于每一点 \(P_0(x_0,y_0) \in D\) ,向量 \(\left. \frac{\partial f}{\partial x}\right|_{(x_0,y_0)} \boldsymbol{i} + \left. \frac{\partial f}{\partial y}\right|_{(x_0,y_0)} \boldsymbol{j}\) 称为函数 \(f(x,y)\) 在点 \(P_0(x_0,y_0)\) 处的 梯度(Gradient) ,记作 \(\text{grad}f(x_0,y_0)\) 或者 \(\nabla f(x_0,y_0)\) ,即有:
\[\nabla f(x_0,y_0) = \left. \frac{\partial f}{\partial x}\right|_{(x_0,y_0)} \boldsymbol{i} + \left. \frac{\partial f}{\partial y}\right|_{(x_0,y_0)} \boldsymbol{j}\]
其中 \(\nabla = \frac{\partial}{\partial x} \boldsymbol{i} + \frac{\partial}{\partial y} \boldsymbol{j}\) 称为(二维的)“向量微分算子”或者“Nabla 算子”。对于平面区域 \(D\) 上的每一点都有梯度,记为:
\[\nabla f = \frac{\partial f}{\partial x} \boldsymbol{i} + \frac{\partial f}{\partial y} \boldsymbol{j}\]
以上梯度概念可以容易地推广到三维和更高维的情况。
说明: 沿梯度方向,函数值增加最快。同样可知,沿梯度的相反方向函数值的减少最快。
7.3.4. 实例:利用梯度求函数值增加最快的方向
实例:设 \(f(x,y,z) = x^3 - xy^2 - z\) ,问 \(f(x,y,z)\) 在 \(P_0(1,1,0)\) 处沿什么方向增加最快?
解:由于 \(\nabla f = f_x \boldsymbol{i} + f_y \boldsymbol{j} + f_z \boldsymbol{k} = (3x^2 - y^2) \boldsymbol{i} - 2xy \boldsymbol{j} - \boldsymbol{k}\) ,从而 \(f(x,y,z)\) 在 \(P_0(1,1,0)\) 处沿 \(\nabla f(1,1,0) = 2 \boldsymbol{i} - 2 \boldsymbol{j} - \boldsymbol{k}\) 的方向增加最快。
7.4. 再议拉格朗日乘数法
前面介绍过求条件极值的拉格朗日乘数法,这里将再次讨论它。
7.4.1. 用“Nabla 算子”表示拉格朗日乘数法
拉格朗日乘数法求解条件极值可以表述为:
\(f\) 在 \(M\) 个约束条件 \(g_1 = 0, g_2=0, \cdots, g_M =0\) 下的可能极值点是满足下面方程组的解:
\[\begin{cases}
\nabla f + \sum_{k=1}^{M} \lambda_k \nabla g_k = 0 \\
g_1 = g_2 = \cdots = g_M = 0
\end{cases}\]
其中 \(\nabla f + \sum_{k=1}^{M} \lambda_k \nabla g_k = 0\) 是一个向量方程。
实例:求解 \(u = f(x,y,z,t)\) 在两个附加条件 \(g_1(x,y,z,t) = 0, \, g_2(x,y,z,t) = 0\) 下的极值。
可以先作拉格朗日函数 \(L(x,y,z,t) = f(x,y,z,t) + \lambda_1 g_1(x,y,z,t) + \lambda_2 g_2(x,y,z,t)\) ,对它关于 \(x,y,z,t\) 求一阶偏导数再与附加条件联立成方程组,得:
\[\begin{cases}
\frac{\partial f}{\partial x} + \lambda_1 \frac{\partial g_1}{\partial x} + \lambda_2 \frac{\partial g_2}{\partial x} = 0 \\
\frac{\partial f}{\partial y} + \lambda_1 \frac{\partial g_1}{\partial y} + \lambda_2 \frac{\partial g_2}{\partial y} = 0 \\
\frac{\partial f}{\partial z} + \lambda_1 \frac{\partial g_1}{\partial z} + \lambda_2 \frac{\partial g_2}{\partial z} = 0 \\
\frac{\partial f}{\partial t} + \lambda_1 \frac{\partial g_1}{\partial t} + \lambda_2 \frac{\partial g_2}{\partial t} = 0 \\
g_1(x,y,z,t) = 0 \\
g_2(x,y,z,t) = 0
\end{cases}\]
上面方程组可简写为如下“Nabla 算子”形式:
\[\begin{cases}
\nabla f + \lambda_1 \nabla g_1 + \lambda_2 \nabla g_2 = 0 \\
g_1 = g_2 = 0
\end{cases}\]
7.4.1.1. 简写拉格朗日乘数法为一个表达式
接着看上面的例子,如果我们把拉格朗日函数 \(L(x,y,z,t) = f(x,y,z,t) + \lambda_1 g_1(x,y,z,t) + \lambda_2 g_2(x,y,z,t)\) ,写为:
\[\mathcal{L}(x,y,z,t,\lambda_1, \lambda_2) = f(x,y,z,t) + \lambda_1 g_1(x,y,z,t) + \lambda_2 g_2(x,y,z,t)\]
即把 \(\lambda_1,\lambda_2\) 也看做“变量”,则联立的方程组可简写为一个方程。如含 4 个自变量的函数在两个约束条件下,拉格朗日乘数法可以简单表述为:
\[\nabla_{x,y,z,t,\lambda_1, \lambda_2} \mathcal{L}(x,y,z,t,\lambda_1, \lambda_2) = 0\]
其中, \(\nabla_{x,y,z,t} \mathcal{L}(x,y,z,t,\lambda_1, \lambda_2) = 0\) 相当于 \(\nabla f + \lambda_1 \nabla g_1 + \lambda_2 \nabla g_2 = 0\) ,而 \(\nabla_{\lambda_1,\lambda_2} \mathcal{L}(x,y,z,t,\lambda_1, \lambda_2) = 0\) 则隐含着约束条件 \(g_1 = g_2 = 0\) 。
7.4.2. 如何理解拉格朗日乘数法
如何理解拉格朗日乘数法呢?
如下图所示,求曲面 \(f(x,y)\) 在约束 \(g(x,y) = c\) 下的最大值。
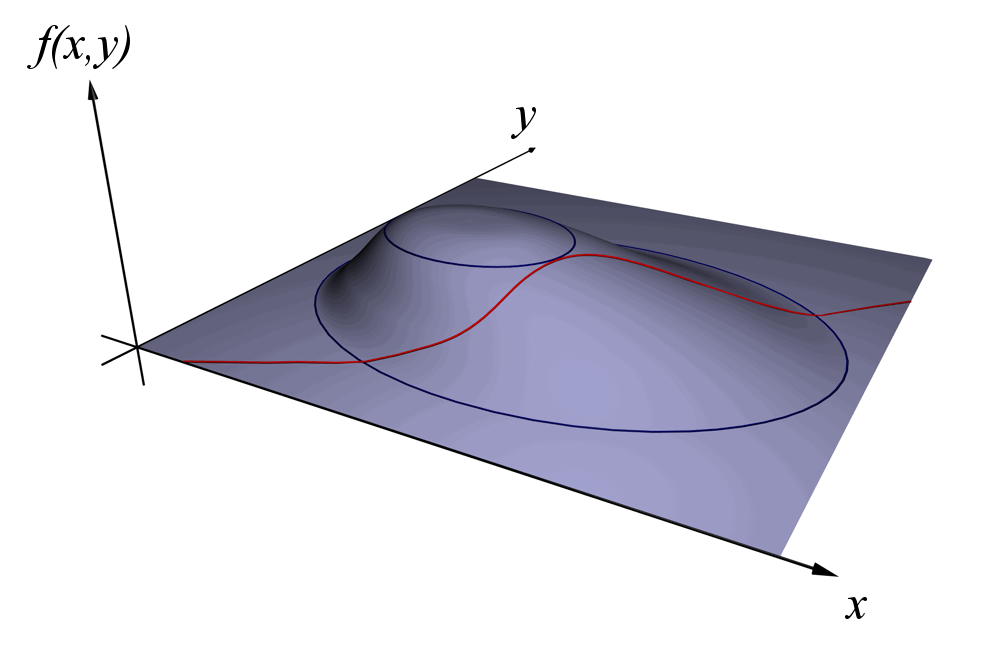
Figure 6: 求曲面 \(f(x,y)\) 在约束 \(g(x,y) = c\) (用红线表示)下的最大值(图片摘自 Lagrange multiplier Wikipedia)
上图对应的“等高线图”如下图所示,蓝虚线为等高线。极值出现在红线(约束条件)和蓝虚线(等高线)相切的点。如果 \(g(x,y) = c\) 和等高线相交,则意味着还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与 \(g(x,y) = c\) 的交点的值更大或者更小, 所以只有当等高线与 \(g(x,y) = c\) 相切的时候,才可能取得极值。 又由于 \(d_1 > d_2\) ,所以极值为最大值。
Figure 7: 上图对应的“等高线图”,蓝虚线为曲面 \(f(x,y)\) 的等高线,与红线相切时取得极值(图片摘自 Lagrange multiplier Wikipedia)
极值点处等高线与约束条件的曲线相切(这时它们的梯度方向相同或相反), 这就是拉格朗日乘数法的方程: \(\nabla f = -\lambda \nabla g\) 。

