Context-free Grammar, Part I Top-down Parsing
Table of Contents
1. 上下文无关文法简介
上下文无关文法(Context-free Grammar, CFG)是一类非常重要的文法,程序设计语言一般是上下文无关文法,它在 Chomsky 文法体系中属于“2 型文法”,如表 1 所示。
| Chomsky 文法类别 | 生成的语言 | 产生式特点 |
|---|---|---|
| 0 型文法 | 无限制语言 | 产生式左边至少含有一个非终结符 |
| 1 型文法 | 上下文有关语言 | 产生式左边字符串长度小于等于右边字符串长度 |
| 2 型文法 | 上下文无关语言 | 产生式左边是单个非终结符 |
| 3 型文法 | 正则语言 | 产生式左边是单个非终结符,产生式右边是“一个终结符”或“一个终结符和一个非终结符” |
说明:上下文无关文法的产生式左边是单个非终结字符。这说明无论左边那个非终结符出现在何处,都可被右边的语句所替代,这就是名字“上下文无关”的含义!
可以看到:1型文法产生式的限制最少,2型文法次之,3型文法产生式的限制最多。
1.1. CFG 相关分析算法
上下文无法文法的相关分析算法如下:
| 大分类 | 分析算法 | 适应文法举例 | 备注 |
|
自顶向下的分析法 |
递归下降分析法 | 自顶向下的通用方法,可能回溯,效率不高 | |
| 预测分析法(递归下降分析法的特例) | LL(1)文法 | 局限于 LL(1)语法,不需要回溯 | |
|
自底向上的分析法 |
Operator Precedence parsing | 《编译原理》第 2 版中已经删掉了这个算法的介绍 | |
| LR(0) parsing | LR(0)文法 | ||
| SLR(1) parsing | SLR(1)文法 | ||
| LR(1) parsing | LR(1)文法 | LR(1) parsing 又称为 Canonical LR parsing | |
| LALR(1) parsing | LALR(1)文法 | ||
| GLR parsing | Generalized LR,又称 Tomita 分析法。这是一种并行的分析算法 | ||
| 其它 | CYK 算法、Earley 算法等 | 通用算法,但效率低 |
注 1:1965 年,D.Knuth 首先提出了 LR(k)文法及 LR(k)分析技术。对于 LR(k)文法的理论研究业已证明:①每一 LR(k)文法都是无二义性文法;②一个由 LR(k)文法所产生的语言也可由某一 LR(1)文法产生。同时,由于通常的程序设计语言一般均能由 LR(1)文法来产生。因此,对程序设计语言的编译来说,我们可仅考虑 k≤1,即 LR(0)和 LR(1)的情况。
注 2:在名字“LL(1)”中,第一个“L”表示从左向右扫描输入,第二个“L”表示分析过程中将用“最左推导”,而“1”则表示在每一步中只需要向前看一个输入符号来决定语法分析动作。
注 3:一般来说,算符优先分析法(Operator Precedence parsing)是自底向上的语法分析方法。不过,Pratt 在 1973 年提出了一种自顶向下的算符优先分析法,称为Pratt Parser。
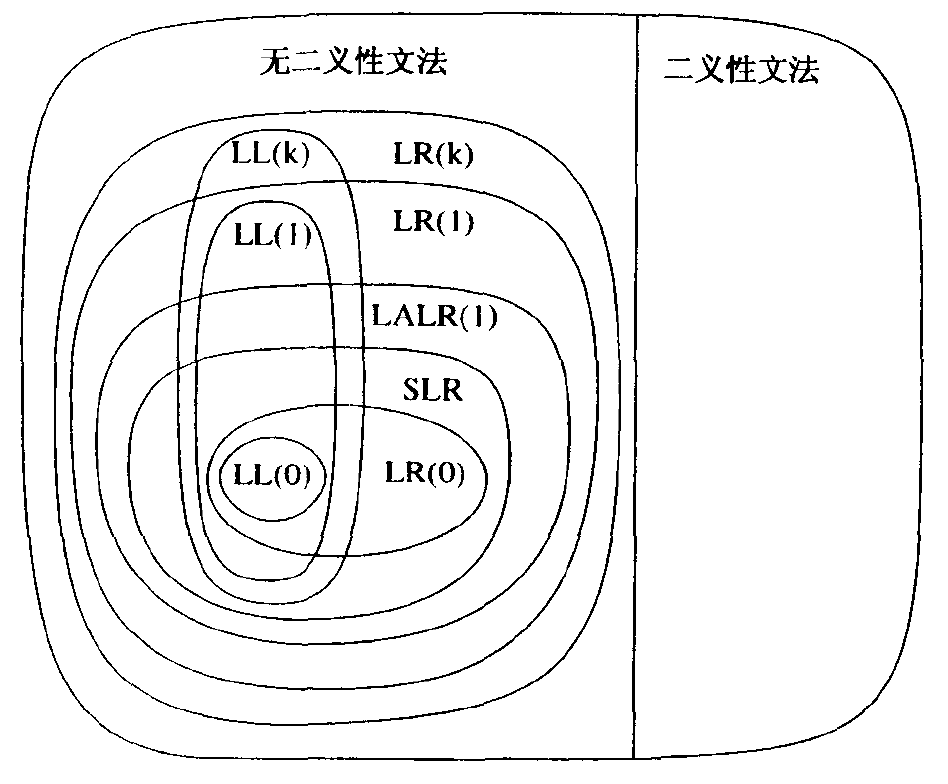
Figure 1: 几个文法类之间的关系(摘自虎书 3.3.6 节)
从图 1 中可以看到,LR 文法能够比对应的 LL 文法描述更多的语言。
2. 自顶向下分析法(Top-down)
2.1. First 集合和 Follow 集合
在自顶向下语法分析过程中,First 集合和 Follow 集合使得我们可以根据下一个输入符号来选择应用哪个产生式。
First 集:通熟地讲,First(α)的定义就是可以由α生成的一个或多个终结符号串的第一个符号的集合。α是任意的文法符号串。
通常情况下,如果α以一个终结符号开头,此时该终结符号就是 First(α)中的唯一符号;如果α以一个非终结符号开头,且该非终结符的所有产生式体都以终结符号开头,那么这些终结符号就是 First(α)的所有成员。
Follow 集: 对于非终结符 A,Follow(A)就是可能在某些句型中紧跟在 A 右边的终结符号的集合。
注:自顶向下分析中,我们并不需要显式地构造 First 集合和 Follow 集合。
递归下降程序分析和 LL(1)分析一般地都要求计算先行集合,它们分别称作 First 集合和 Follow 集合。由于无需显式地构造出这些集合就可以构造出简单的自顶向下的分析程序,所以在基本算法的介绍之后我们再讨论它们。
摘自:编译原理及实践(冯博琴译),第 4 章
人们进行 First 集合和 Follow 集合的计算是为了对早期错误进行探测。
摘自:编译原理及实践(冯博琴译),4.1.3 其他决定问题
2.2. 递归下降分析法
下面介绍递归下降分析法的特例——预测分析法,预测分析法仅适应于 LL(1)文法。
2.2.1. 预测分析法(递归)
预测分析法的效率比一般的递归下降分析法高。 预测分析法仅适应于 LL(1)文法。LL(1)文法有个重要特点:只需要检查当前输入符号就可以为一个非终结符号选择正确的产生式。 LL(1)文法已经足以描述大部分程序设计语言构造,虽然为程序语言设计适当的文法时需要多加小心。比如,左递归的文法和二义性的文法都不可能是 LL(1)的。
假设有下面文法(C或 Java 中的某些语句):
stmt -> expr;
| if (expr) stmt
| for (optexpr; optexpr; optexpr) stmt
| other
optexpr -> ε
| expr
对应的预测分析伪代码为:
void stmt() {
switch ( lookahead ) {
case expr:
match(expr); match(';'); break;
case if:
match(if); match('('); match(expr); match(')'); stmt();
break;
case for:
match(for); match('(');
optexpr(); match (';'); optexpr(); match (';'); optexpr();
match(')'); stmt(); break;
case other:
match(other); break;
default:
report("syntax error");
}
}
void optexpr() {
if (lookahead == expr) match(expr);
}
void match(terminal t) {
if (lookahead == t) lookahead = nextTerminal;
else report("syntax error");
}
显然上面是一个递归的算法,因为 stmt 函数中有对它自身即 stmt 函数的调用。
参考:《编译原理(第 2 版)》2.4.2 节。
2.2.2. 预测分析法实例(C递归实现)
下面给出一个递归下降分析法的完整实例,它可以计算支持加减乘法和括号的中缀表达式。
//摘自《编译原理及实践》4.1.2节。
//Simple intger arithmetic calculator according to the EBNF:
// <exp>-><term>{<addop><term>}
// <addop>->+|-
// <term>-><factor>{<mulop><factor>}
// <mulop>->*
// <factor>->(<exp>)|Number
//
// Inputs a line of text from stdin
// Outputs "ERROR" or the result.
#include <stdio.h>
#include <stdlib.h>
char token; //global token variable
//function prototypes for recursive call;
int exp(void);
int term(void);
int factor(void);
void error(void) {
fprintf(stderr, "Error\n");
exit(1);
}
void match(char expectedToken) {
if(token == expectedToken)
token = getchar();
else
error();
}
int main() {
int result;
token = getchar(); //load token with first character for lookahead
result = exp();
if(token == '\n') //check for end of line
printf("Result = %d\n", result);
else
error(); //extraneous chars on line
return 0;
}
int exp(void) {
int temp = term();
while((token == '+')||(token == '-')) {
switch(token) {
case '+':
match('+');
temp += term();
break;
case '-':
match('-');
temp -= term();
break;
}
}
return temp;
}
int term(void) {
int temp = factor();
while(token == '*') {
match('*');
temp *= factor();
}
return temp;
}
int factor(void) {
int temp;
if(token == '(') {
match('(');
temp = exp();
match(')');
} else if(isdigit(token)) {
ungetc(token, stdin);
scanf("%d", &temp);
token = getchar();
} else
error();
return temp;
}
2.2.3. 预测分析法(非递归)
用非递归的预测分析法,显式维护栈结构关键是要得到预测分析表。预测分析表可以由 First 和 Follow 集合得到(具体方法可参见:《编译原理(第 2 版)》P142,算法 4.31)。
2.2.4. 预测分析法实例(C++非递归实现)
To explain an LL(1) parser’s workings we will consider the following small LL(1) grammar:
S → F S → ( S + F ) F → a
and parse the following input:
( a + a )
//摘自:http://en.wikipedia.org/wiki/LL_parser
//关于parser table如何产生,请参考上面链接。
// parser table: (表中1,2,3为rule的编号)
// |---+---+---+---+---+---|
// | | ( | ) | a | + | $ |
// |---+---+---+---+---+---|
// | S | 2 | - | 1 | - | - |
// | F | - | - | 3 | - | - |
// |---+---+---+---+---+---|
#include <iostream>
#include <stack>
/* List of tokens (terminals), begins with 1 */
enum {
T_OP = 1, /* ( */
T_CP, /* ) */
T_A, /* a */
T_PLUS, /* + */
T_EOF, /* $ */
T_ERROR /* Just for errors */
};
/* Non-terminals names */
enum {
N_S = 1,
N_F
};
/* Array of terminals/non-terminals to be pushed into the stack. Notes:
* Terminals are negative.
* First element is the number of elements in the array.
*/
/* S ->F */
static const int rule_s1[] = {1, N_F};
/* S ->'('S '+'F ')'*/
static const int rule_s2[] = {5, -T_OP, N_S, -T_PLUS, N_F, -T_CP};
/* F ->'a'*/
static const int rule_f1[] = {1, -T_A};
/* The parse table, the order of the rows and columns */
static const int * parse_table[][T_EOF] = {
/* ( ) a + $ */
/* S */ {rule_s2, NULL, rule_s1, NULL, NULL},
/* F */ {NULL , NULL, rule_f1, NULL, NULL},
};
/*********************************************************************/
/* Simple tokenizer */
class Tokenizer {
std::string src;
size_t i;
int current;
int CheckNext(bool increment)
{
for(;;) {
switch(src[i]) {
case '': i++; break;
case '(': current = T_OP; goto done;
case ')': current = T_CP; goto done;
case 'a': current = T_A; goto done;
case '+': current = T_PLUS; goto done;
case '\0': current = T_EOF; return T_EOF;
default : return T_ERROR;
}
}
done:
if(increment) i++;
return current;
}
public:
Tokenizer(const std::string&src) : src(src), i(0)
{ current = CheckNext(false); }
int GetNext()
{ return CheckNext(true); }
int PeekNext()
{ return CheckNext(false); }
};
/*********************************************************************/
int
main(void)
{
Tokenizer tokenizer("(a + a)");
std::stack<int>stack;
/* Initialize the stack with the start symbol and EOF */
stack.push(-T_EOF);
stack.push(N_S);
/* While there is something on the stack */
while(!stack.empty()) {
/* Check if the top is a terminal, negative value */
if(stack.top() <0) {
/* Get the top value, negate it! */
int terminal = -stack.top();
int token = tokenizer.GetNext();
/* Tokenizer error? */
if(token == T_ERROR) {
std::cerr <<"Error (1): Unrecognised token.\n";
return -1;
}
/* The terminal matches the input token? */
else if(terminal != token) {
std::cerr <<"Error (2): Unexpected token.\n";
return -1;
}
/* Remove it from the stack */
stack.pop();
}
else {
/* Fetch the rule */
const int *rule = parse_table[stack.top()-1][tokenizer.PeekNext()-1];
/* Invalid rule */
if(rule == NULL) {
std::cerr <<"Error (3): No matching grammar for this token.\n";
return -1;
}
/* Log the rule */
if(rule == rule_s1) { std::cerr <<"S ->F\n"; }
else if(rule == rule_s2) { std::cerr <<"S ->'('S '+'F ')'\n"; }
else if(rule == rule_f1) { std::cerr <<"F ->'a'\n"; }
/* Remove the symbol from the stack */
stack.pop();
/* Push the grammar to the stack in reverse order! */
for(size_t i = rule[0]; i >0 ; i--) {
stack.push(rule[i]);
}
}
}
/* Input is valid */
std::cerr <<"OK!\n";
return 0;
}
2.3. 左递归
自顶向下分析方法不能处理左递归文法,必须消除左递归。
2.3.1. EBNF 可以减少左递归
为什么说“Extended BNF relieves the need for left-recursion to some extent.”(EBNF 能减少左递归的使用)?

Figure 2: EBNF 可以减少左递归(摘自:《编译原理及实践,4.1.2 节》)
又如:JavaCC 是自顶向下语法分析器,无法处理左递归,但它支持 EBNF 描述形式,现实实践中真正遇到左递归的情况会很少。参考:http://cs.lmu.edu/~ray/notes/javacc/