Context-free Grammar, Part II Botton-Up Parsing
Table of Contents
1. 自底向上分析法(Bottom-up)
An LR parser scans and parses the input text in one forward pass over the text. The parser builds up the parse tree incrementally, bottom up, and left to right, without guessing or backtracking.
Figure 1: Bottom-up parse of A*2 + 1
1.1. 可行前缀和句柄
本节内容详细请参考:编译原理及实践(冯博琴译),5.1 节。
在介绍可行前缀之前先介绍一下什么是最右句型(right sentential form)。
我们知道,推导可分为最左推导(每一步推导时替换最左边的非终结符)和最右推导(每一步推导时替换最右边的非终结符),自顶向下分析对应着输入串的最左推导过程,自底向上分析对应着输入串的最右推导过程。
最右句型是指最右推导过程中的每一个中间串。
例如,有文法
E' -> E E -> E + n | n
图 2 展示了串 n + n 使用这个文法的自底向上分析过程。
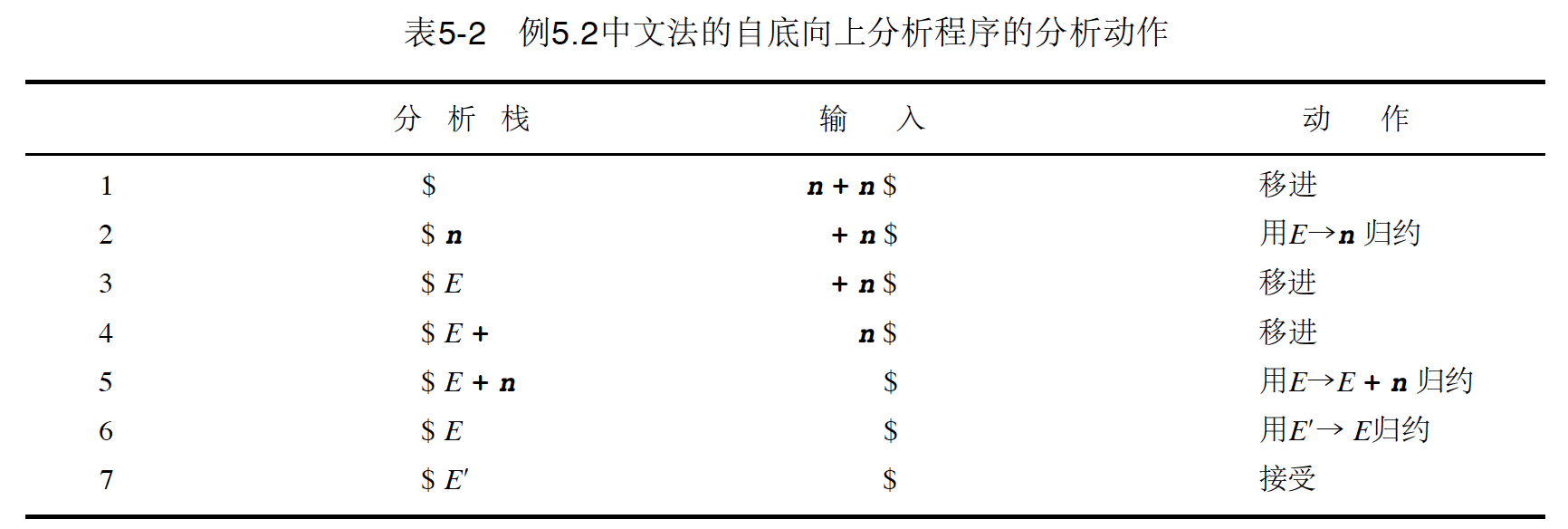
Figure 2: 串 n + n 使用上面文法的自底向上分析过程
在图 2 中的“动作”那列中,由下往上可以得到其对应的推导(最右推导)是: E' => E => E + n => n + n 。
在分析过程中,最右句型被分析栈和输入分隔开。
分析栈中的符号序列称为最右句型的可行前缀。 上面例子中,E、E +和 E + n 都是最右句型 E + n 的可行前缀;ε和 n 是最右句型 n + n 的可行前缀,注意 n +不是 n + n 的可行前缀。
分析过程中, 发生归约动作时使用的产生式称为句柄(一般仅指产生式的右部分),句柄在被识别之前总是位于分析栈的顶部。 上面例子中,句柄有:n,E + n,E,它们都是归约动作中使用的产生式,且出现在分析栈的顶部。
由于“移进”和“归约”是自底向上分析过程中的两个主要动作,所以“自底向上分析程序”有时也称为“移进——归约分析程序”。 识别句柄是“移进——归约分析程序”的主要任务。
1.2. LR(0)分析
1.2.1. 利用自动机进行自底向上语法分析
下面将以 LR(0)分析为例描述有限自动机和语法分析的关系。详细请参考:编译原理及实践(冯博琴译),5.2.1 节。
基本流程为: 产生式----->LR(0)项----->NFA(LR(0)项作为 NFA 有限自动机的状态,这个有限自动机保存着移进——归约分析的过程)----->DFA
DFA 构造好后,就可以用它来识别某个具体的输入串了。
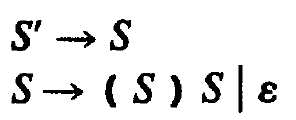
Figure 3: 产生式(扩充文法)

Figure 4: 对应的 LR(0)项
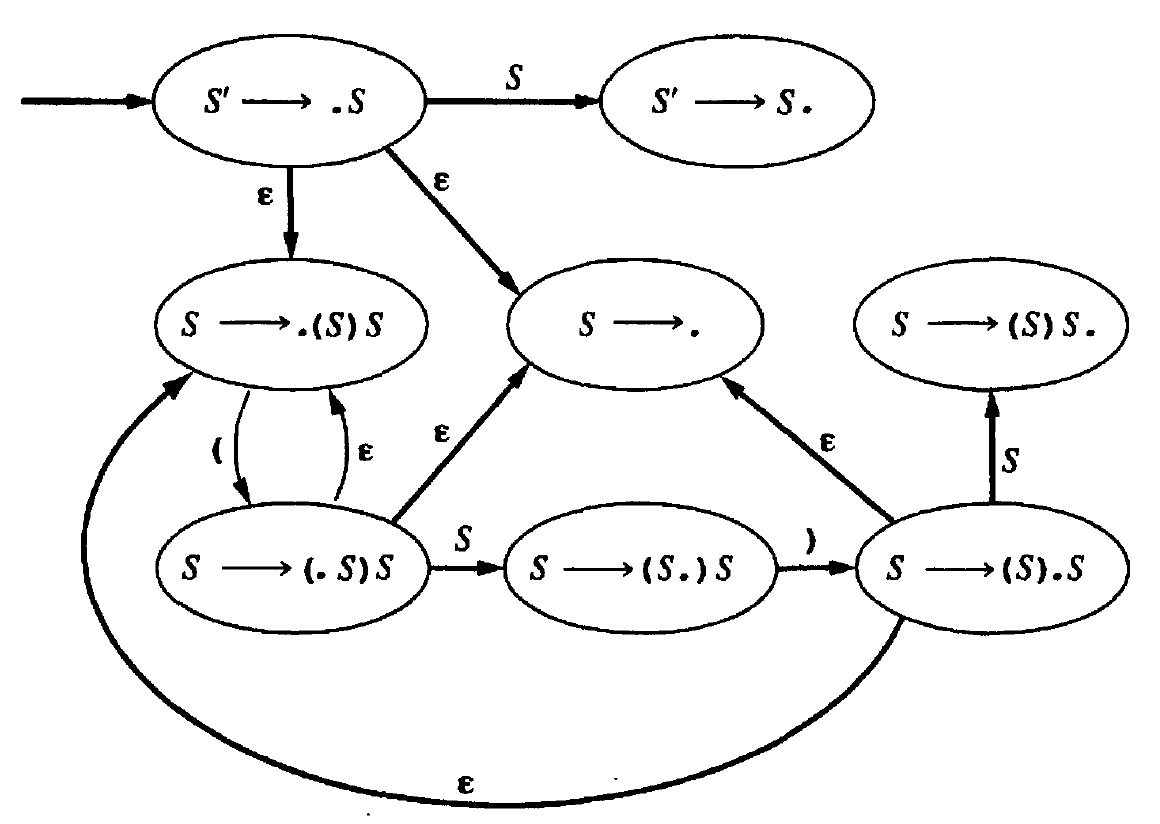
Figure 5: 对应的 NFA
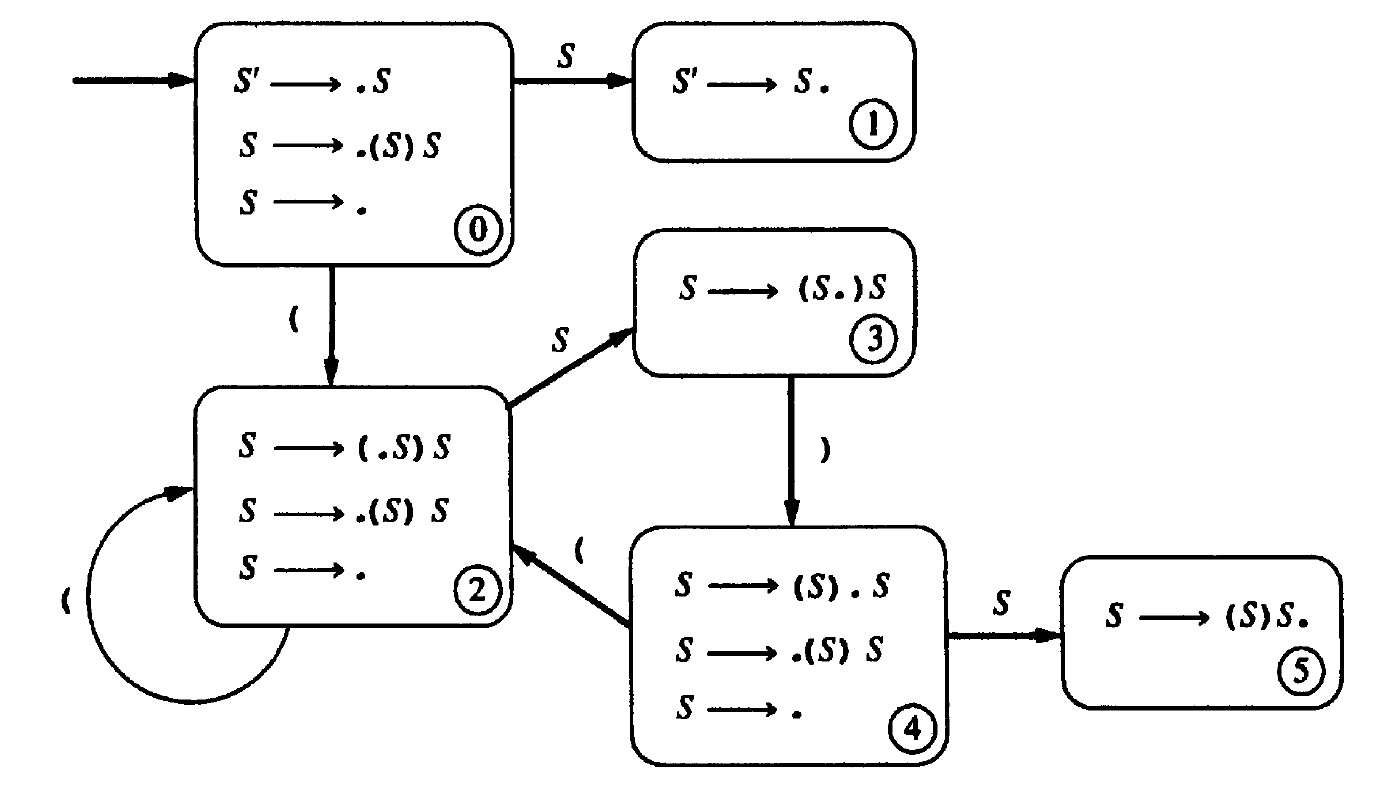
Figure 6: 对应的 DFA
注:当然 yacc 等工具不用中间生成 NFA,可以直接从产生式得到 DFA。
1.2.2. 什么是 LR(0)项
LR(0)项就是在其右边带有“位置信息”的产生式选择。 一般用一个点号来表示这个位置信息。

Figure 7: 摘自《编译原理(第 2 版)》4.6.2 节
LR(0)项可以作为一个保存有分析栈和移进——归约分析过程的信息的有穷自动机状态来使用。
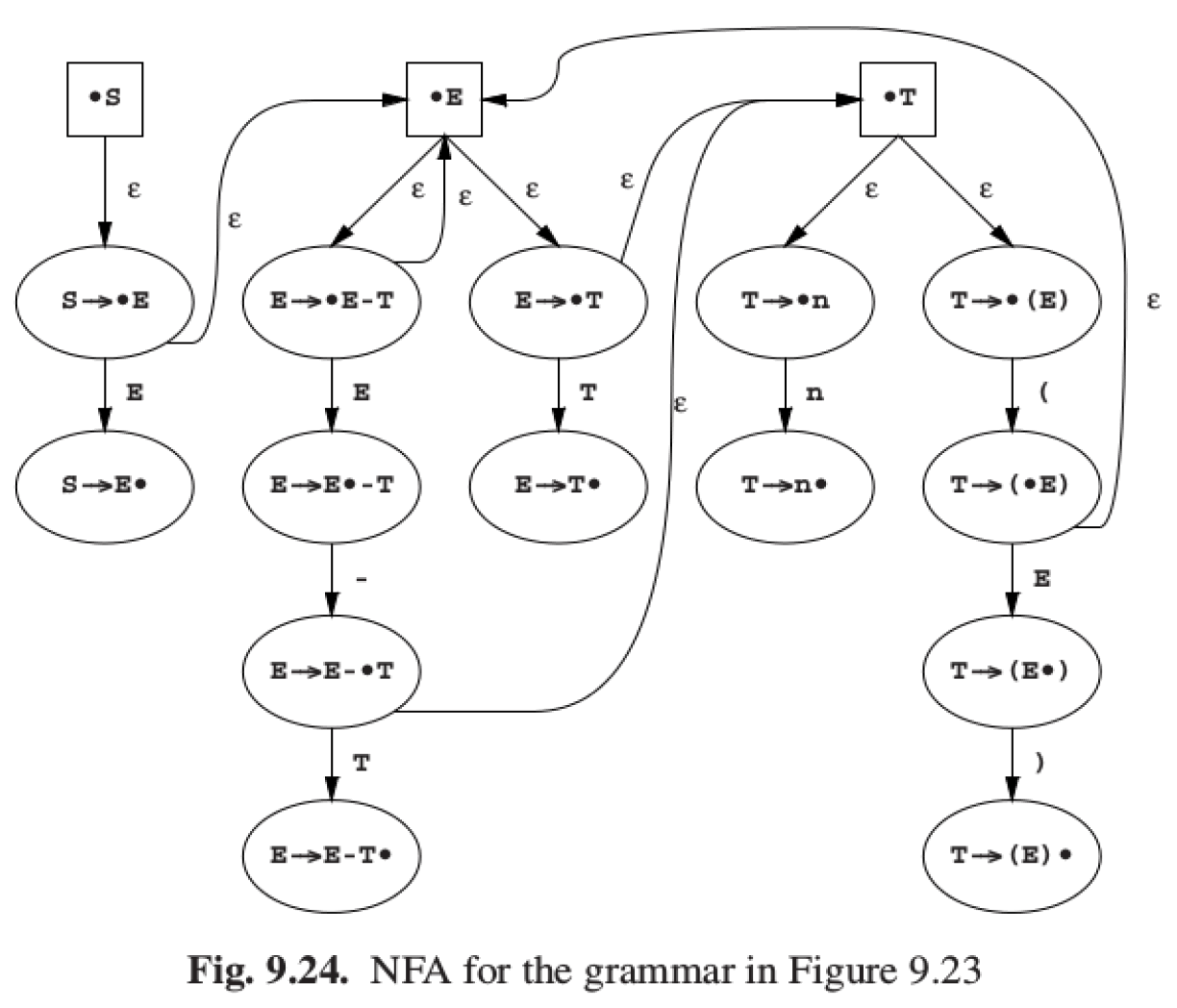
1.2.3. 由 LR(0)项构造 NFA(定义状态转换规则)
要构造 LR(0)项对应的 NFA,首先得定义自动机状态间的转换规则。详细请参考:编译原理及实践(冯博琴译),5.2.2 节。
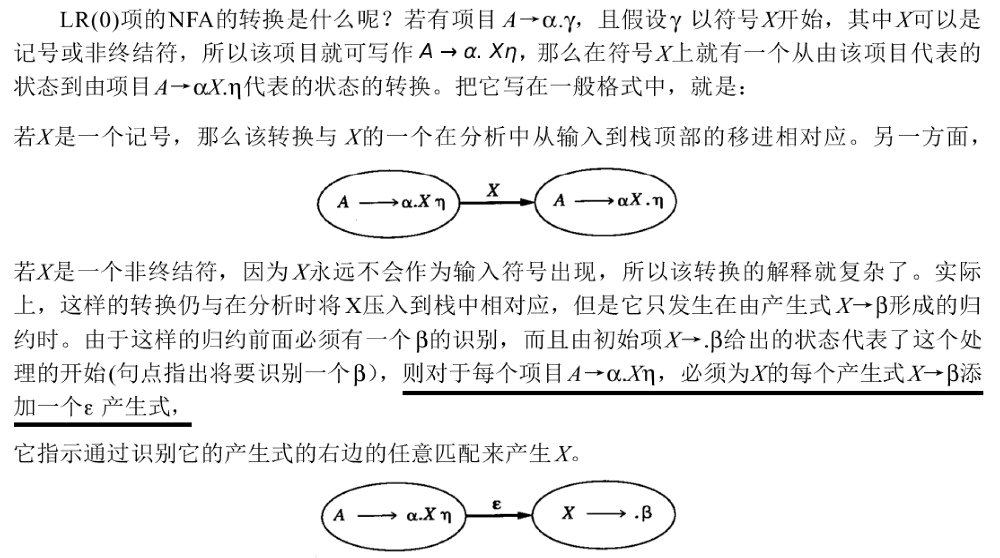
Figure 8: 由 LR(0)项构造 NFA
从上面分析知,由 LR(0)项构造 NFA 包含两种情况。第一种情况是显而易见的,第二种情况说明了 如何添加“ε-转换”,即对每个 A->α.Xβ,添加ε-转换到所有可能的 X->.β
如,下面有 8 个 LR(0)项,它们对应的 NFA 是什么呢?

Figure 9: 对应的 LR(0)项
8 个 LR(0)项对应着 NFA 的 8 个状态,由前面介绍的构造 LR(0)项对应 NFA 的规则可以得到其 NFA 为(下图中, ε-转换是这样添加的:对每个 A->α.Xβ,添加ε-转换到所有可能的 X->.β ):

Figure 10: 对应的 NFA
有了 NFA,就可以通过子集构造法得到 DFA(如图 6 所示)了,有了 DFA,再加上 LR(0)分析算法指定的动作,就可以得到文法的分析表了。
1.2.4. LR(0)项中内核项和非内核项(又称为闭包项)
在介绍内核项和非内核项(闭包项)前,先介绍项集的闭包。以 LR(0)项为例。

Figure 11: 项集的闭包
由上面的定义知,如果某个点在最左端的 B 产生式被加入到 I 的闭包中,则所有点在最左端的 B 产生式都会被加入到这个闭包中。由于有这个性质,我们可以少关注那些可以通过闭包运算得到的项(闭包项)。
我们把项分为下面两类:
(1) 内核项:包括初始产生式 S' -> .S 和点不在最左端的所有项。
(2) 非内核项(闭包项):除了 S' -> .S 之外的点在最左端的所有项。
区分内核项和非内核项(闭包项)的重要意义在于:若有一个文法,内核项唯一地判断出状态以及它的转移,那么只需要指出内核项就可以完整地表示出项目集合的 DFA 来。
LR(0)项的闭包实际上体现的就是 LR(0)项的自动机中转换规则定义中的第二情况(如何添加“ε-转换”)。
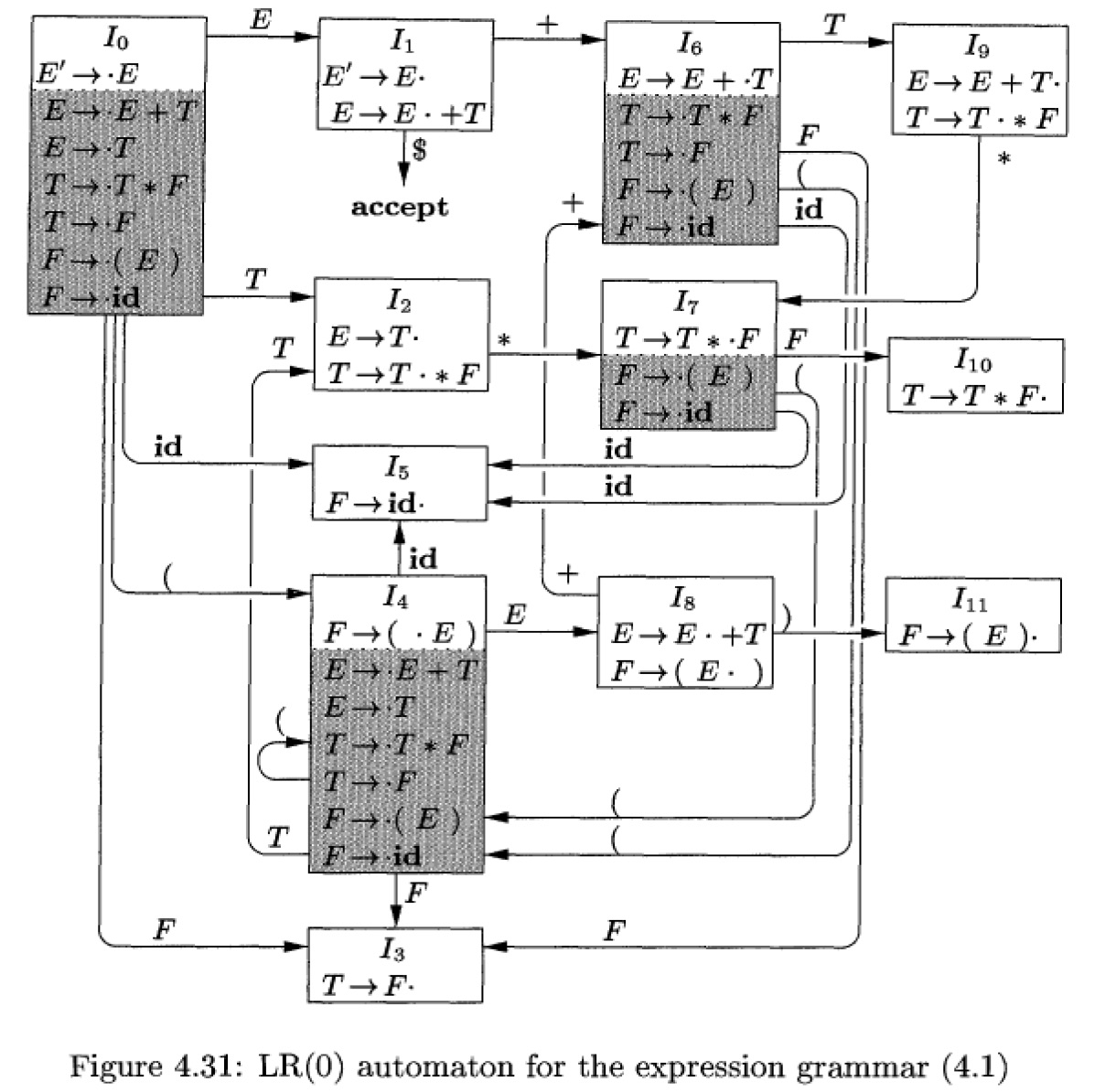
Figure 12: DFA 中阴影部分的项是非内核项(摘自《编译原理(第 2 版)》4.6.2 节)
显然,所有非内核项(闭包项)都会出现在项集 \(I_0\) 中。
1.2.5. LR(0)分析算法
详细请参考:编译原理及实践(冯博琴译),5.2.3 节。
LR(0)分析算法很简单,描述如下:
令 s 为当前 state(位于分析栈顶部),则动作定义为:
1.如果 s 中包含了形式为 A->α.Xβ的项(称为“移入”项),其中 X 是一个终结符。则动作是将当前的输入记号移入栈中,若输入记号为 X,则压入栈中的新 state 为包含了 A->αX.β的 state;若输入记号不为 X,则报错。
2.如果 s 中包含了形式为 A->γ.的项(称为“完整”项)。则动作是用产生式 A->γ归约,分析栈按下面规则更新:首先把γ和相应的 state 从分析栈中删除,这样分析栈回到了构造γ前的 state(这个 state 肯定含有一个形式为 B->α.Aβ的项),把 A 压入到分析栈,再压入那个包含项 B->αA.β的 state。
若某文法用上面的分析算法没有歧义,则称它为 LR(0)文法。 显然很少有实用的文法为 LR(0)文法。
1.2.6. LR(0)文法的等价描述
一个文法是 LR(0)文法当且仅当它的 DFA 中每个 state 要么仅包含一个或多个“移入”项,要么仅包含单个“完整”项 (显然,按照 LR(0)算法,若某个 state 中既含有“移入”项又含有“完整”项则会出现 shift/reduce 冲突,若某个 state 中含有多个“完整”项则会出现 reduce/reduce 冲突)。
从上可知,LR(0)对文法的限制是很严格的。
1.2.7. LR(0)文法实例
考虑文法:A -> (A) | a
它对应的 LR(0)项的 DFA 如下图所示,这是一个 LR(0)文法,因为 state 0, state 3, state 4 仅包含“移入”项,而 state 1, state 2, state 5 都是单个“完整”项。
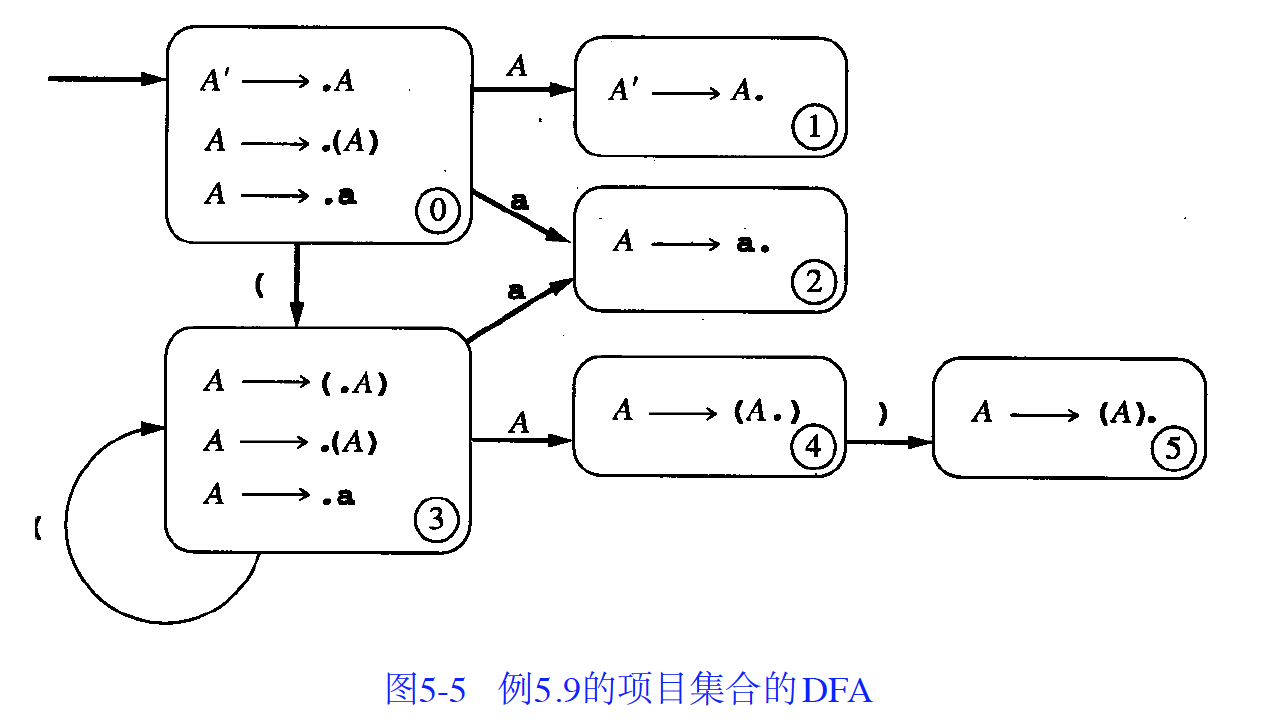
Figure 13: 文法“A -> (A) | a”对应的 DFA
下图详细说明了如何用上面的 DFA 来分析串((a))的过程。

Figure 14: 分析串((a))的过程
DFA 常用文法分析表来表示,文法“A -> (A) | a”对应的分析表:
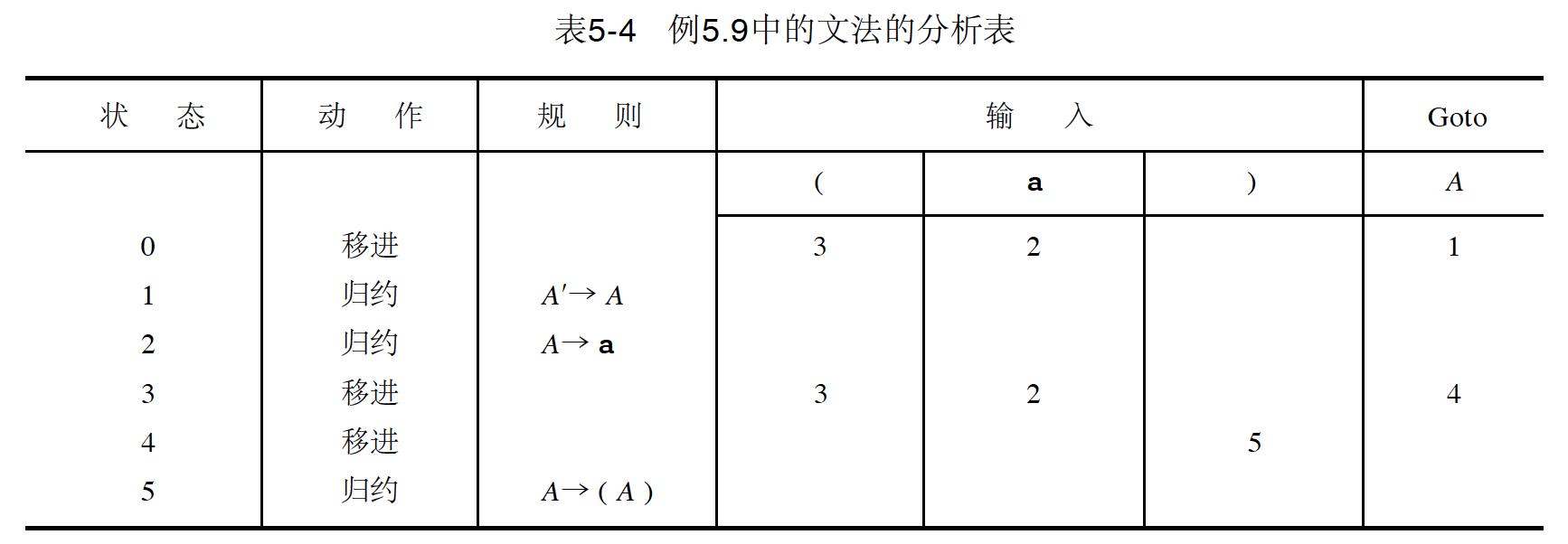
Figure 15: 文法“A -> (A) | a”对应的分析表(空白的地方表示出错)
1.2.8. 另解 LR(0)自动机
LR(0)自动机也可用可行前缀和句柄来表达。
The LR(0) automaton is a DFA which accepts viable prefixes of right sentential forms, ending in a handle.
1.3. SLR(1)分析
1.3.1. 构造 SLR(1)对应的自动机
SLR(1)分析使用的自动机就是 LR(0)项对应的自动机。
它通过使用输入串中的下一个记号来指导它的动作,使得分析能力大大提高。
1.3.2. SLR(1)分析算法
SLR(1)分析是在 LR(0)上的一个简单有效的扩展(SLR(1)通过向前看符号的信息使得其分析能力得到增强),这个扩展使得 SLR(1)能处理很多实际的语言结构。
SLR(1)分析算法如下所示:

Figure 16: The SLR(1) parsing algorithm
如果用上面的算法分析文法没有歧义产生,则该文法称为 SLR(1)文法。
参考:编译原理及实践(冯博琴译),5.3.1 节。
1.3.3. SLR(1)文法的等价描述
SLR(1)文法的定义不是很直观。下面描述一个等价的直观描述。
当且仅当任何状态 s 满足下面两个条件时,文法就为 SLR(1)文法:
条件 1、对于在 s 中的任何项 A->α.Xβ,其中 X 是终结符,是向前看符号,则 s 中可以包含“完整”项,但不能包含这样的“完整”项 B->γ.,其中 X 在 Follow(B)中。
条件 2、对于在 s 中的任何两个“完整”项 A->α.和 A->β.,Follow(A) ∩ Follow(B)为空。
说明 1:条件 1 中,如果包含了“完整”项 B->γ.,其中 X 在 Follow(B),就会出现 shift-reduce 冲突(A->α.Xβ可以 shift,而 B->γ.可以 reduce);条件 2 中,如果两个“完整”项 A->α.和 A->β.,Follow(A) ∩ Follow(B)不为空,就会出现 reduce-reduce 冲突。
说明 2:前面提到,LR(0)文法的限制的重要特点是:DFA 的每个 state 只有两种可能性:1.全部为“移入”项;2.仅有 1 个“完整”项。 SLR(1)文法对 LR(0)文法的两个限制都进行了放宽。
1.3.4. SLR(1)分析实例
以文法:S -> (S)S | ε为例,它对应的 SLR(1)分析表如下:
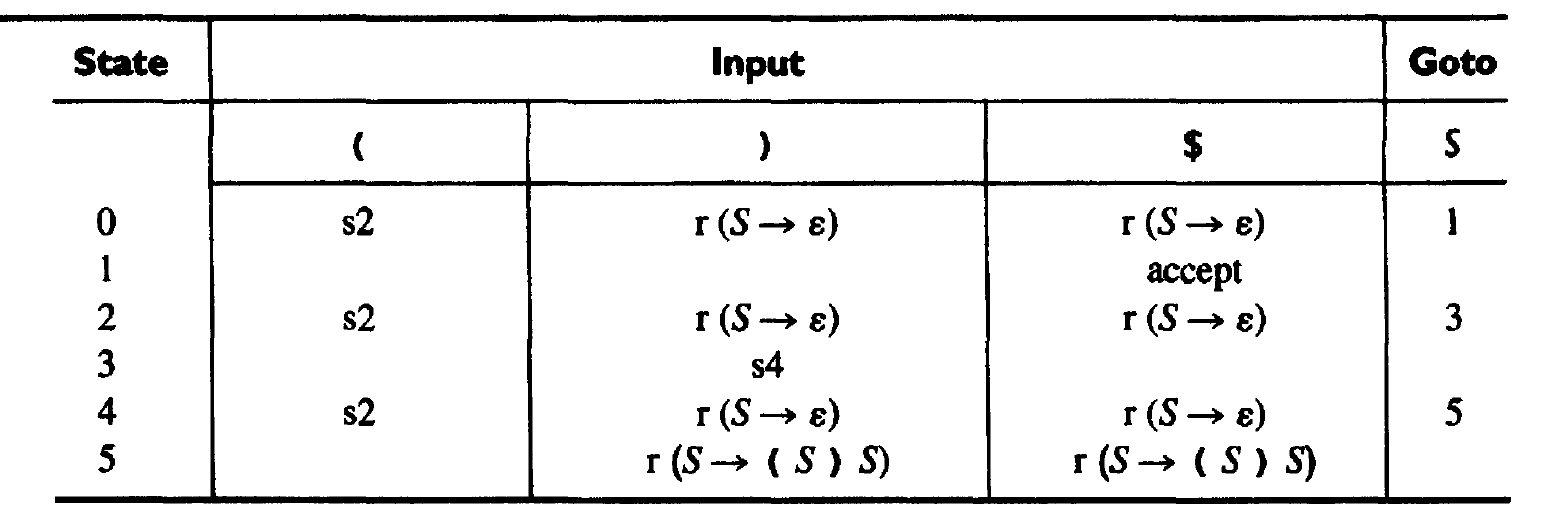
Figure 17: 文法“S -> (S)S | ε”的分析表,accept 表示 r(S'->S)
用它来分析输入串()()的过程如下:
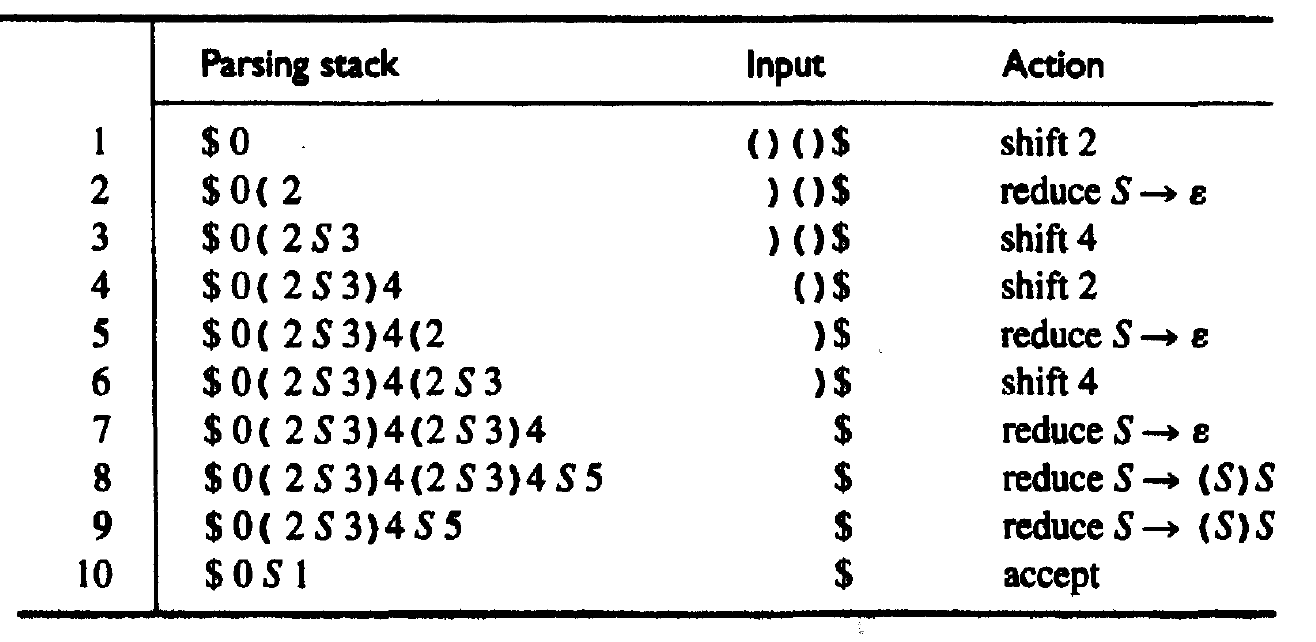
Figure 18: 利用上面文法分析输入串()()的过程
1.3.5. SLR(1)不够强大
《编译原理(第 2 版)》4.6.4 节例 4.48 的文法不是 SLR(1),例 4.61 表明这个文法属于 LALR(1)。
1.4. LR(1)分析(即 Canonical LR 分析)
在 SLR(1)算法中,“先行符号”已经被利用来指导动作。
LR(1)的思想是除了用“先行符号”来指导动作外,再进一步利用“先行符号”,把“先行符号”的信息构建在 DFA 中!
这个新的 DFA 使用的是 LR(1)项,而不是 LR(0)项。LR(1)项是由 LR(0)项和一个先行记号组成。可以用中括号将 LR(1)项写为下面形式:
\[[A \to \alpha . \beta , \, a]\]
其中,A->α.β是 LR(0)项,而 a 是一个先行记号,LR(0)项和先行记号之间用逗号分开。
1.4.1. 构造 LR(1)项对应的自动机
首先,定义 LR(1)项之间的转换。详细请参考:编译原理及实践(冯博琴译),5.4.1 节。

Figure 19: LR(1)项之间的转换
定义由两部分组成。第一部分定义中,转换状态前后的先行符号是相同的;第二部分定义“创建”了新的先行。
第一部分定义很简单,它和 LR(0)项转换规则的第一部分定义基本类似:
\[[A\to\alpha.X\gamma,\,a]\overset{X}{\longrightarrow}[A\to\alpha X.\gamma,\,a]\]
第二部分定义也不难理解。它比 LR(0)项转换规则第二部分定义更加精细!就是这点精细使得 LR(1)分析时产生冲突的机会变小,分析能力大大提高。
下面来说明第二部分定义的由来。显然,B为非终结符时,有下面“ε-转换”:
\[[A\to\alpha.B\gamma,\,a]\overset{\epsilon}{\longrightarrow}[B\to . \beta,\,lookahead]\]
如果不特别限制 lookahead,则 lookahead 显然是 Follow(B)中的元素。其实我们可以合理地缩小 lookahead 的范围(这样分析时产生冲突的机会会变小),把 lookahead 限制在 First(γa)中,即:
\[[A\to\alpha.B\gamma,\,a]\overset{\epsilon}{\longrightarrow}[B\to . \beta,\,b]\quad b\in First(\gamma a)\]
这样做是合理的, 项 \([A\to\alpha.B\gamma,\,a]\) 说明了在分析的这一点上可能要识别 B,再识别γ,最后移入 a。所是当识别 B 时可以限制 lookahead 在 First(γa)中。

Figure 20: 识别非终结符 B 时可以限制 lookahead 在 First(γa)中
1.4.2. LR(1)项中的内核项和非内核项
对于 Gnu bison,下面第一个命令仅会报告内核项,而第二个命令会报告内核项和非内核项(闭包项):
$ bison --report=state calc.y # 仅会报告内核项 $ bison --report=itemset calc.y # 报告内核项和非内核项(闭包项)
注:yacc 默认只报告内核项。
1.4.3. LR(1)项集族的构造(如何产生 LR(1)的 DFA)

Figure 21: LR(1)项集族的构造
参考:《编译原理(第 2 版)》4.7.2 节。
1.4.4. 实例说明“LR(1)项的 NFA 和 DFA”
下面例子摘自:Parsing Techniques - A Practical Guide,2nd, 9.6.1 节。
假设有下面文法:
S -> ABc A -> a B -> b B -> ε
上面 LR(1)文法其对应的 NFA 为(图中 LR(1)项省略了中括号,且是用空格而不是逗号分开 LR(0)项和先行符号,用#而不是$表示结束符):
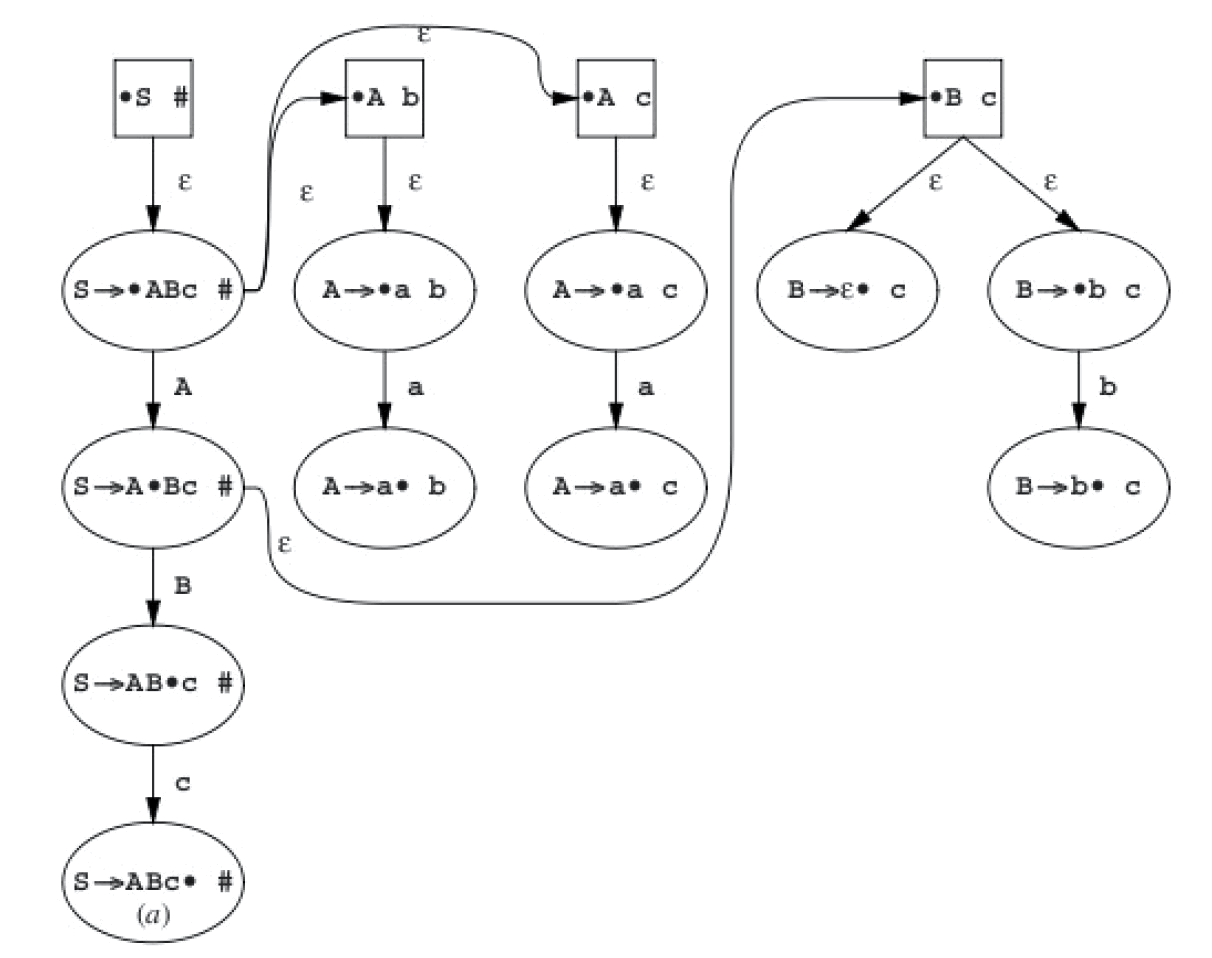
Figure 22: LR(1)项对应的 NFA
转换为 DFA 为:
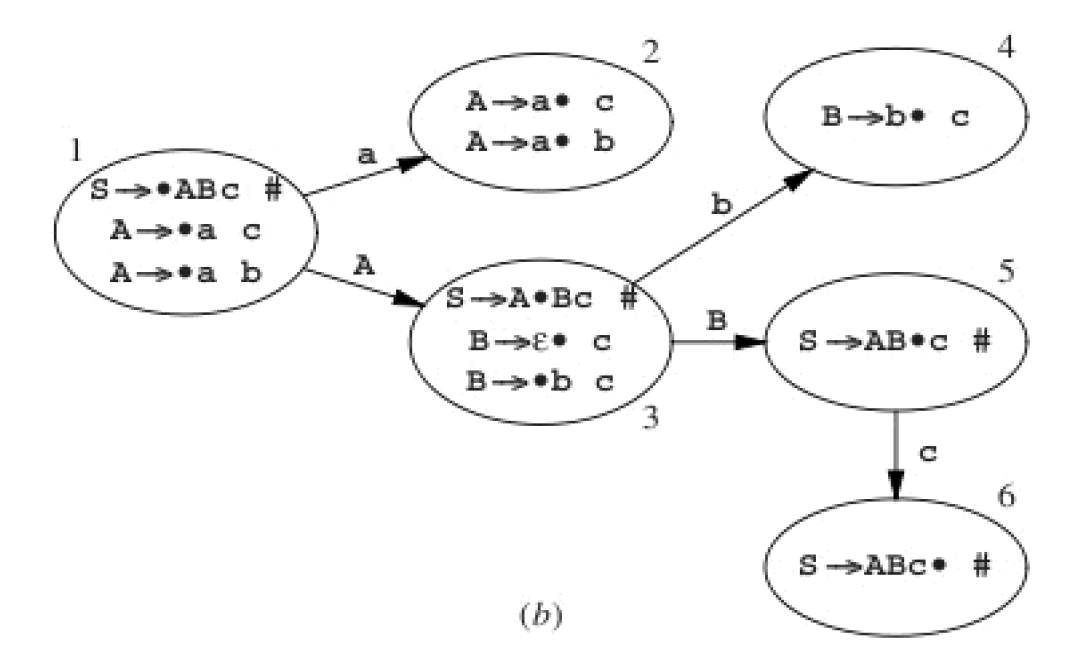
Figure 23: LR(1)项对应的 DFA
1.4.5. LR(1)分析算法
LR(1)分析算法和 SLR(1)分析算法很相似。

Figure 24: LR(1)分析算法
参考:编译原理及实践(冯博琴译),5.4.2 节。
1.4.6. LR(1)文法的等价描述
LR(1)文法的直观且等价的描述:
当且仅当任何状态 s 满足下面两个条件时,文法就为 LR(1)文法:
条件 1、对于在 s 中的任何项[A->α.Xβ , a],其中 X 是终结符,则 s 中不能有格式为[B->γ. , X]的项(否则就有一个 shift/reduce 冲突)。
条件 2、在 s 中没有同时出现格式[A->α. , a]和[B->β. , a]的两个项(否则就有一个 reduce/reduce 冲突)。
说明 1:LR(1)文法的特点和 SLR(1)文法的特点比较类似。
说明 2:LR(1)文法比 SLR(1)文法更强大,具体强大在哪里可参见《编译原理(第 2 版)》4.7.1 节。
1.4.7. LR(1)分析表
和前面描述 LR(0)文法相同,我们仍然考虑文法:A -> (A) | a。
它对应 LR(1)项的 DFA 为:
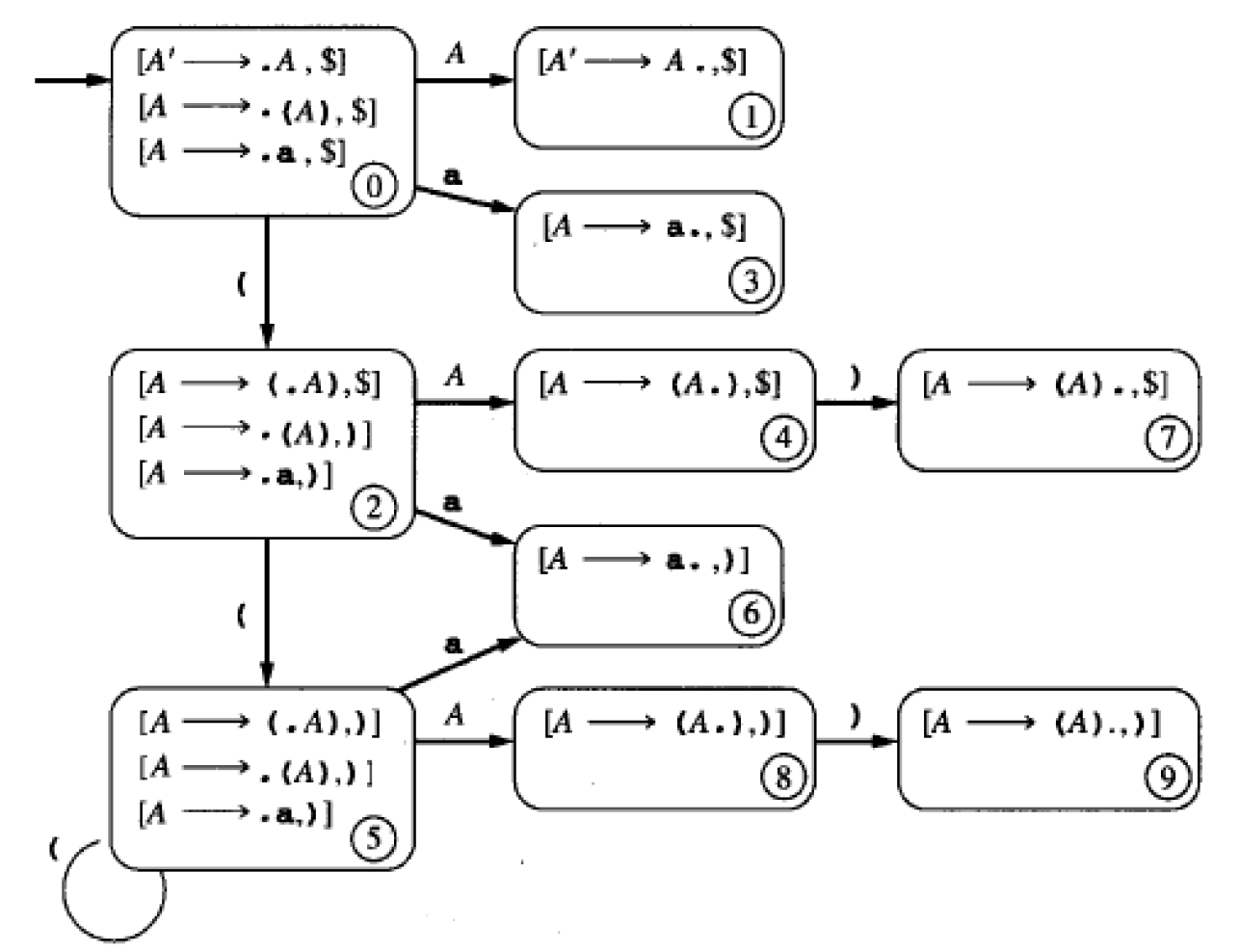
Figure 25: 文法“A -> (A) | a”对应 LR(1)项的 DFA
把这个 DFA 转换为 LR(1)分析表,如下表所示:
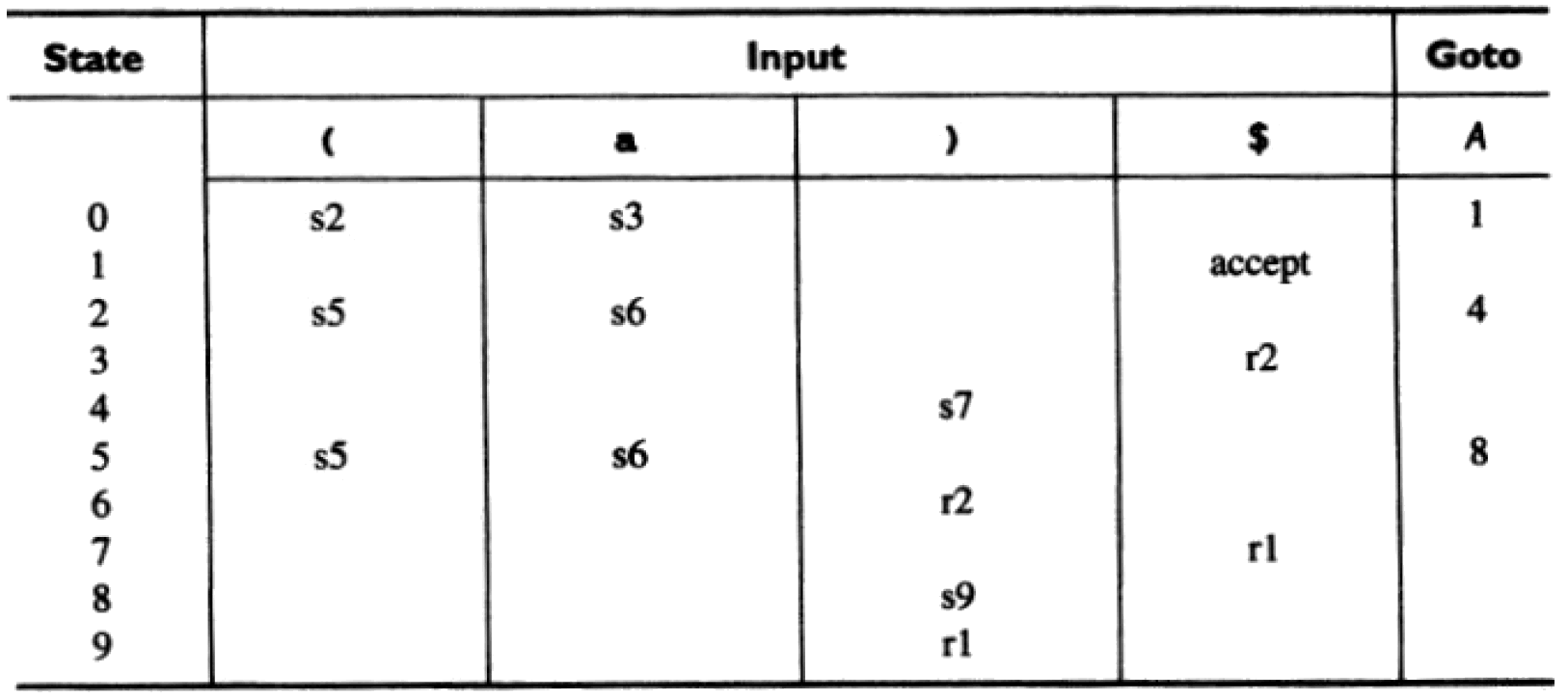
Figure 26: 文法“A -> (A) | a”对应 LR(1)分析表
说明 1:accept 代表 reduce(A'->A) 。
说明 2:用编号 1 和 2 分别表示产生式 A->(A)和 A->a,即:r1 代表 reduce(A->(A)) ,r2 代表 reduce(A->a) 。
说明 3:空白的地方表示出错。
用 LR(1)分析表来分析特定字符串的步骤和用 SLR(1)分析表(或 LR(0)分析表)的分析步骤是相同的。也就是说 LR(1)算法的难点在于 LR(1)分析表的构造!
1.5. LALR(1)分析
参考:编译原理及实践(冯博琴译),5.4.3 节。
LALR(1)的功能比 SLR(1)强,比 LR(1)弱,但 LALR(1)同时具有 SLR(1)状态数量少的优点及 LR(1)适用范围广的优点。
1.5.1. LALR(1)的基础——LR(1)项的 DFA 的两个特点
定义 LR(1)项的 DFA 中的状态的核心是由 LR(1)项的第 1 个成分组成的 LR(0)项的集合(也就是说核心不包含向前看符号)。
由于 LR(1)项的 DFA 的构造方法和 LR(0)项的 DFA 构造方法有很多类似的地方,我们可以得到 LR(1)项的 DFA 有两个基本特点:
(1) LR(1)项的 DFA 的状态的核心是 LR(0)项的 DFA 的一个状态;
(2) 若有具有相同核心的 LR(1)项的 DFA 的两个状态 s1 和 s2,假设在符号 X 上有一个从 s1 到状态 t1 的转换,则在 X 上一定还有一个从状态 s2 到状态 t2 的转换,且状态 t1 和 t2 具有相同的核心。
这两个基本特点是 LALR(1)算法的基础。
LALR(1)项的 DFA 由下面方法得到:合并 LR(1)项的 DFA 中具有相同核心的状态,并把对应先行符号求并集作为 LALR(1)项的第 2 部分。这种合并会不会引入冲突呢?结论是:不会引入 shift/reduce 冲突,但可能引入 reduce/reduce 冲突。 (参见:编译原理第 2 版,4.7.4 节)。
和前面一样,仍然考虑文法:A -> (A)|a,它的 LR(1)项的 DFA 在前面已经给出,它的 LALR(1)项的 DFA 如下图,显示它比 LR(1)项对应 DFA 的状态数要少。
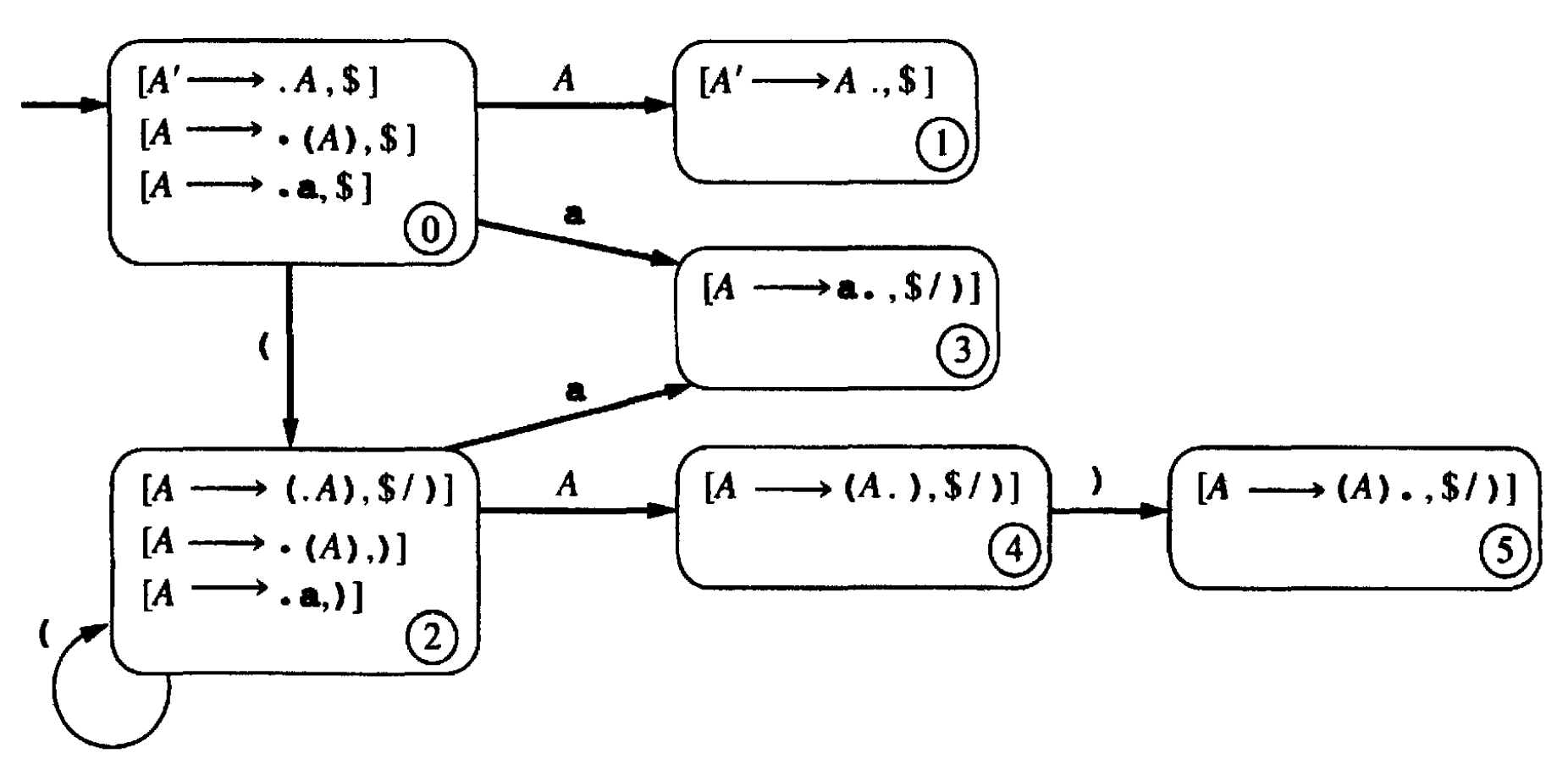
Figure 27: 文法“A -> (A) | a”的 LALR(1)项对应的 DFA
1.5.2. LALR(1)和 LR(1)的区别
SLR, LALR and LR parsers can all be implemented using exactly the same table-driven machinery.
The difference between LALR and LR has to do with the table generator. LR parser generators keep track of all possible reductions from specific states and their precise lookahead set; you end up with states in which every reduction is associated with its exact lookahead set from its left context. This tends to build rather large sets of states. LALR parser generators are willing to combine states if the GOTO tables and lookahead sets for reductions are compatible and don't conflict; this produces considerably smaller numbers of states, at the price of not be able to distinguish certain symbol sequences that LR can distinguish. So, LR parsers can parse a larger set of languages than LALR parsers, but have very much bigger parser tables. In practice, one can find LALR grammars which are close enough to the target languages that the size of the state machine is worth optimizing; the places where the LR parser would be better is handled by ad hoc checking outside the parser.
摘自:http://stackoverflow.com/questions/2676144/what-is-the-difference-between-lr-slr-and-lalr-parsers
1.5.3. 是 LR(1)但不是 LALR(1)的例子
编译原理第 2 版,例 4.58 是一个典型的例子。
下面再给出一个和上书中类似的是 LR(1)但不是 LALR(1)的例子:
It is well known that there are grammars which are LR(1) but not LALR(1). For exemple:
S -> aEa | bEb | aFb | bFa E -> e F -> e
Why? Please refer to:
http://stackoverflow.com/questions/8496065/why-is-this-lr1-grammar-not-lalr1
http://compilers.iecc.com/comparch/article/03-11-026
1.5.4. LALR(1)分析表构造
从理论上讲,构造 LALR(1)分析表非常简单,合并 LR(1)分析表中相同核心的项,并把先行符号求并集即可。
但问题是对于实用的文法来说,LR(1)分析表一般都非常庞大,无法完整地构造出 LR(1)分析表(当然随着内存容量越来越大,完整构造 LR(1)已成为可能)。
LALR(1)分析表构造算法有很多,Parsing Techniques,2nd 一书中对其进行了总结。
典型的有:“Aho 和 Ullman 提出的方法(他们都是龙书的作者,该方法在 AT&T Yacc 中使用)”和“DeRemer 和 Pennello 提出的方法(该方法在 Gnu Bison 中使用)”。
1.5.5. 构造 LALR(1)分析表的经典算法——Yacc,Lemon 所用算法
这种方法通过“传播和自发生成”的过程来生成先行符号,直接从 LR(0)项的 DFA 得到 LALR(1)项的 DFA。
什么是自发生成的向前看符号?什么是传播来的向前看符号?

Figure 28: “自发生成的”和“传播来的”向前看符号(摘自《编译原理,第 2 版》4.7.5 节)
怎么得到“自发生成的”和“传播来的”向前看符号呢?

Figure 29: 发现“自发生成的”和“传播来的”向前看符号(摘自《编译原理,第 2 版》4.7.5 节)
构造 LALR(1)分析表的算法如下所示:

Figure 30: 构造 LALR(1)分析表(摘自《编译原理,第 2 版》4.7.5 节,算法 4.63)
它的主要思想是: 首先计算出所有项的产生式中“自发生成”的先行符号以及先行符号的传播途径(这个传播途径可方便地用表格表示,实例见“编译原理,第 2 版”4.7.4 节 P175,例 4.64 中的图 4-46),之后用传播的方法增加先行符号。
1.5.5.1. 为什么要把先行符号分为自发生成的和传播的?
把 LALR(1)项的先行符号分为自发生成的和传播来的,这充分利用了 LALR(1)项先行符号的下面特点:
(1) 传播关系不取决于某个特定的先行符号,也就是说要么所有的先行符号都从一个项传播到另一个项,要么都不传播。
(2) 传播来的先行符号,既然是从上一个项是传播过来的,那么它最开始也源于自发生成的先行符号。
由上面两点知, 只要知道自发生成的先行符号和先行符号的传播途径,就能推算出所有先行符号。
1.5.6. 更快地构造 LALR(1)分析表——Bison 所用算法
参考:Efficient Computation of LALR(1) Look-Ahead Sets(Frank DeRemer, Thomas Pennello, 1982)
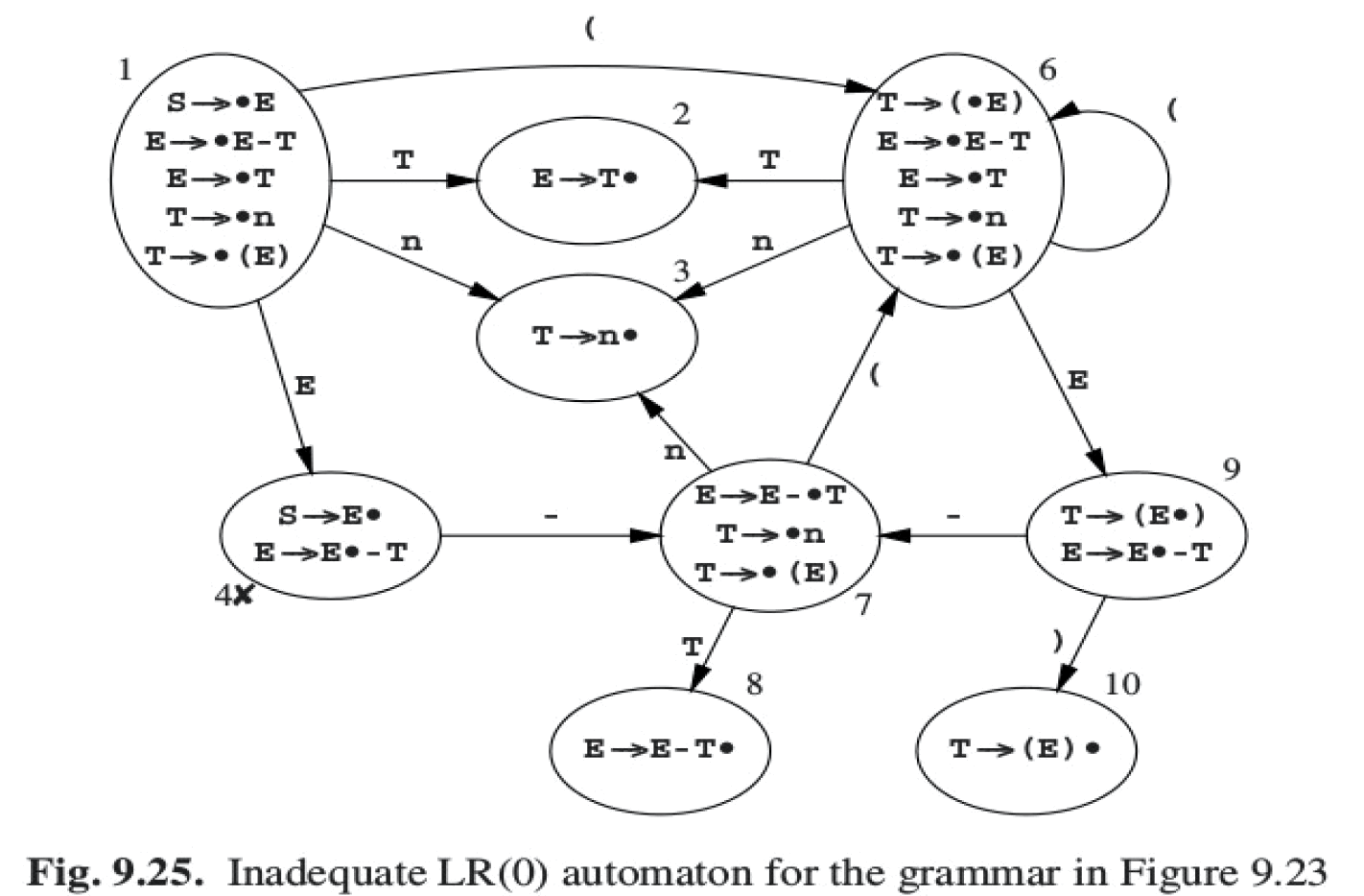
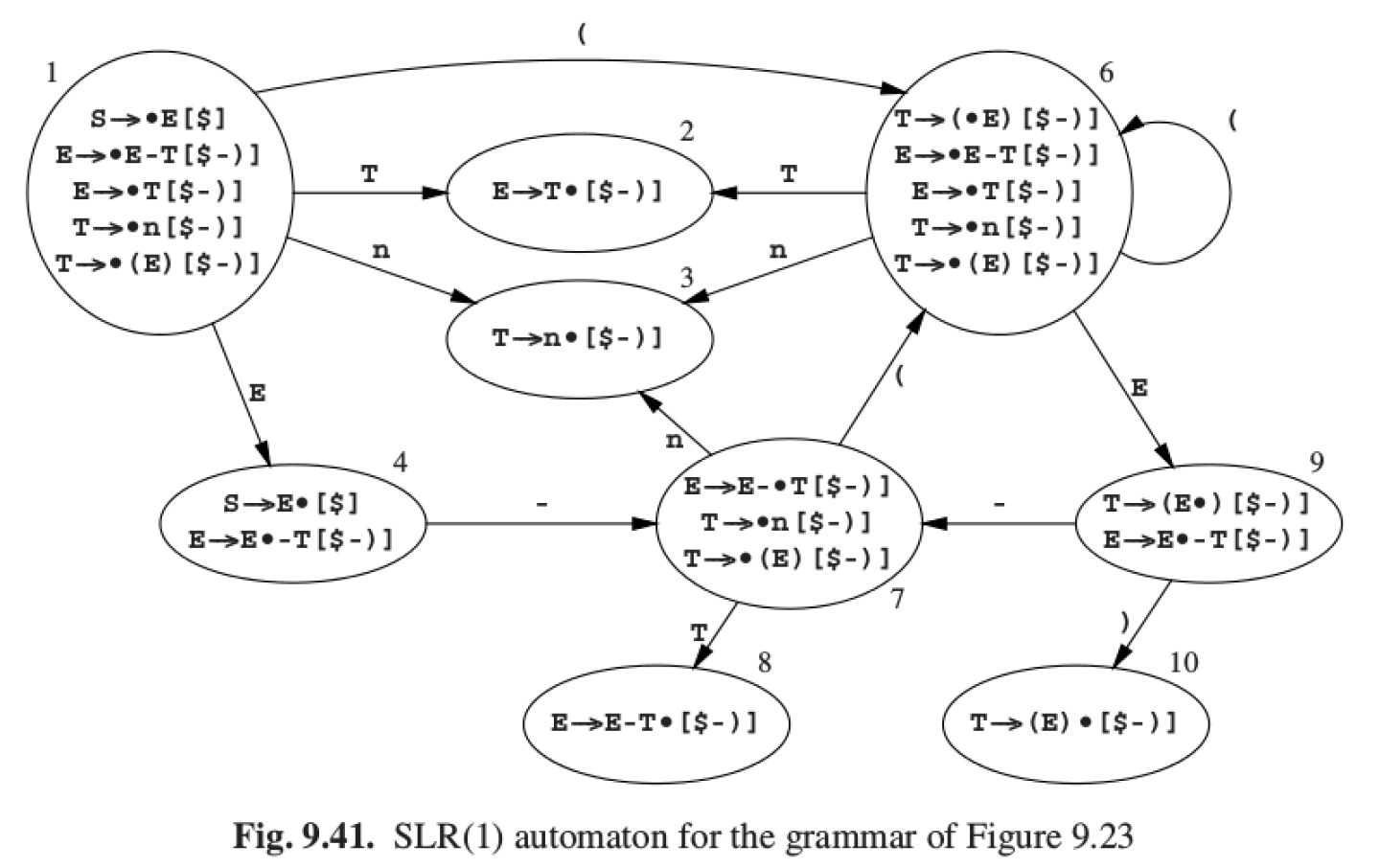
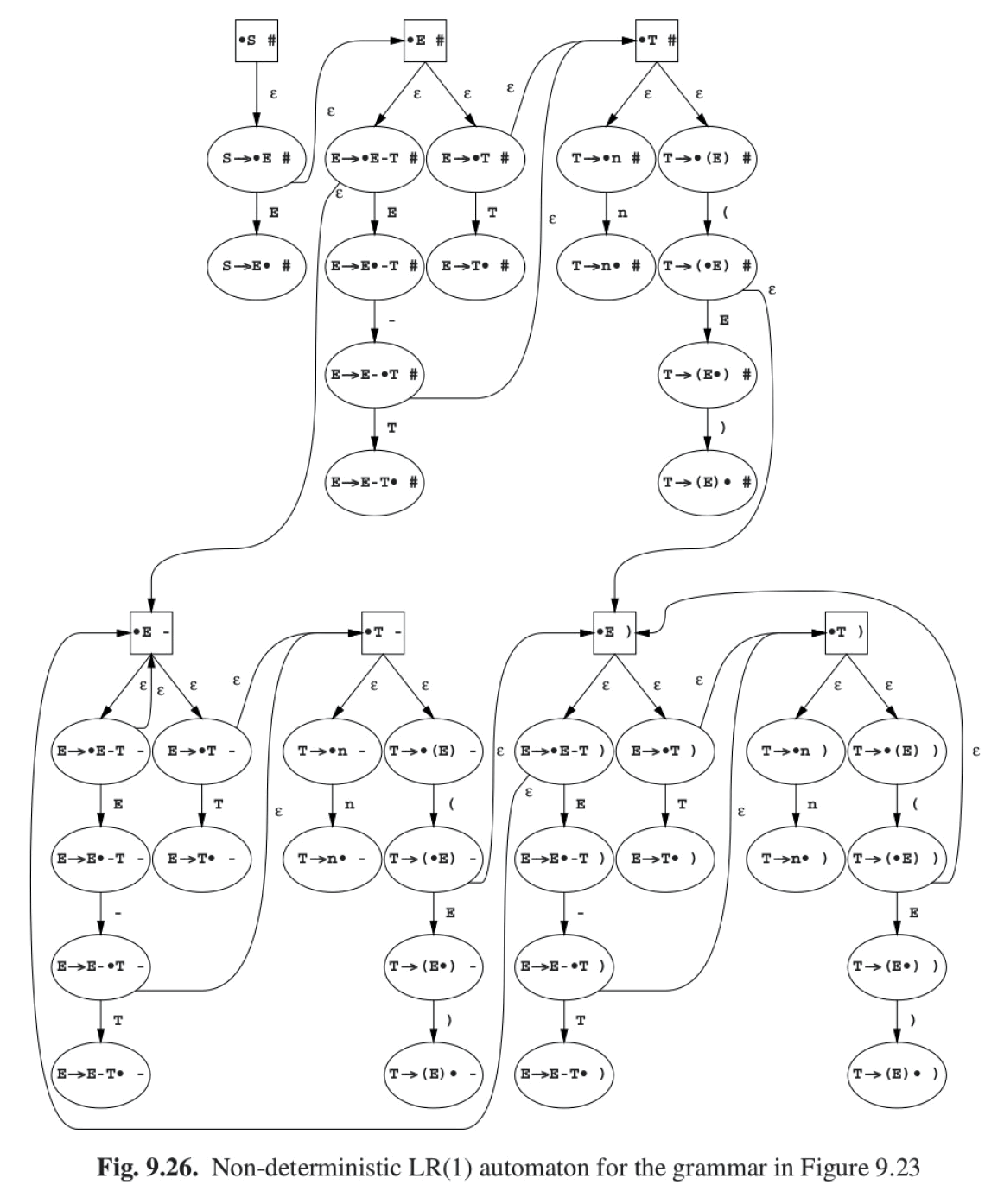
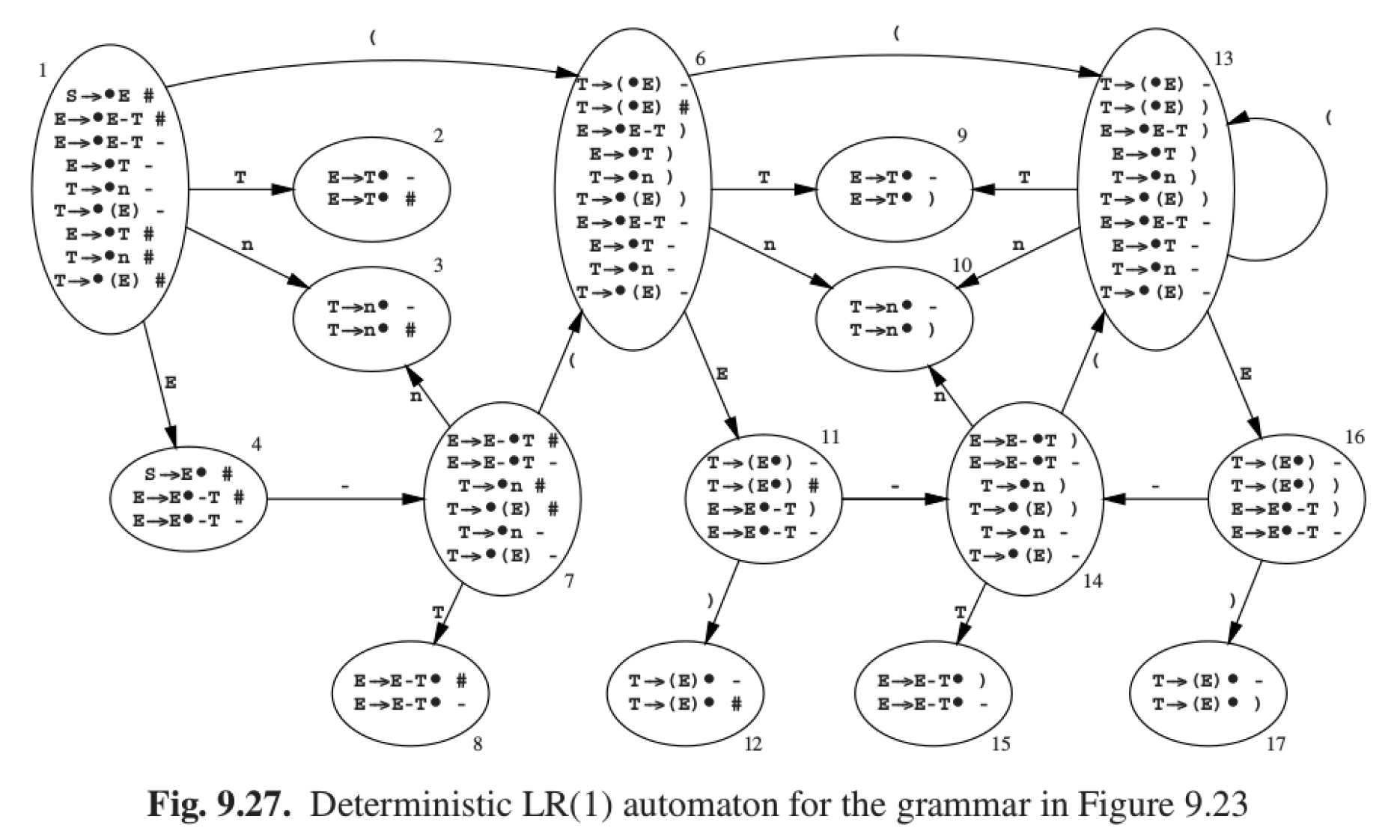
1.6. 实例:从 LR(0)到 SLR 到 LR(1)
下面例子摘自:Parsing Techniques - A Practical Guide,2nd

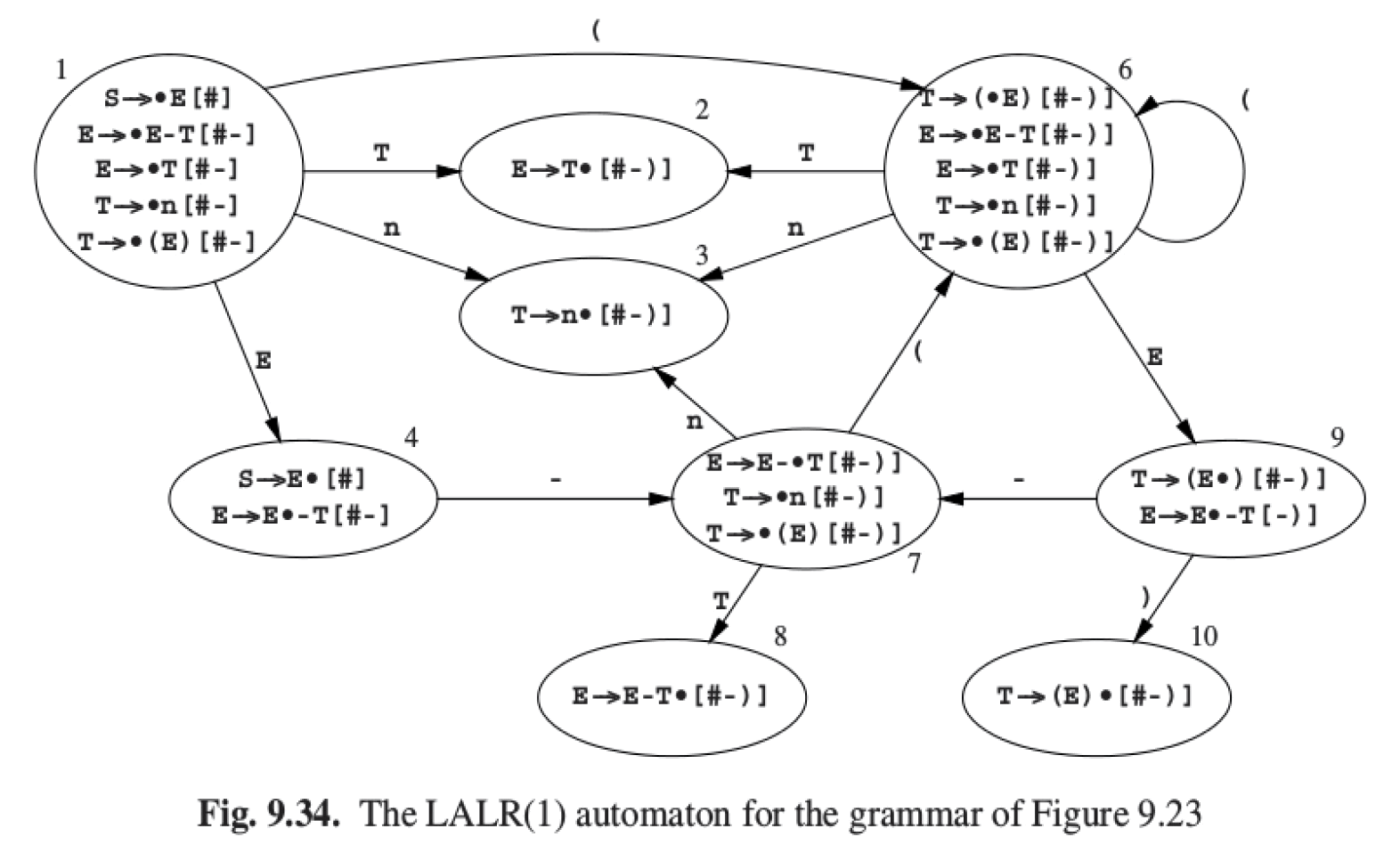
2. Bottom-up 和 Top-down 的比较
Bottom-up(LR)和 Top-down(LL)分析树的建立过程如图 31 所示。
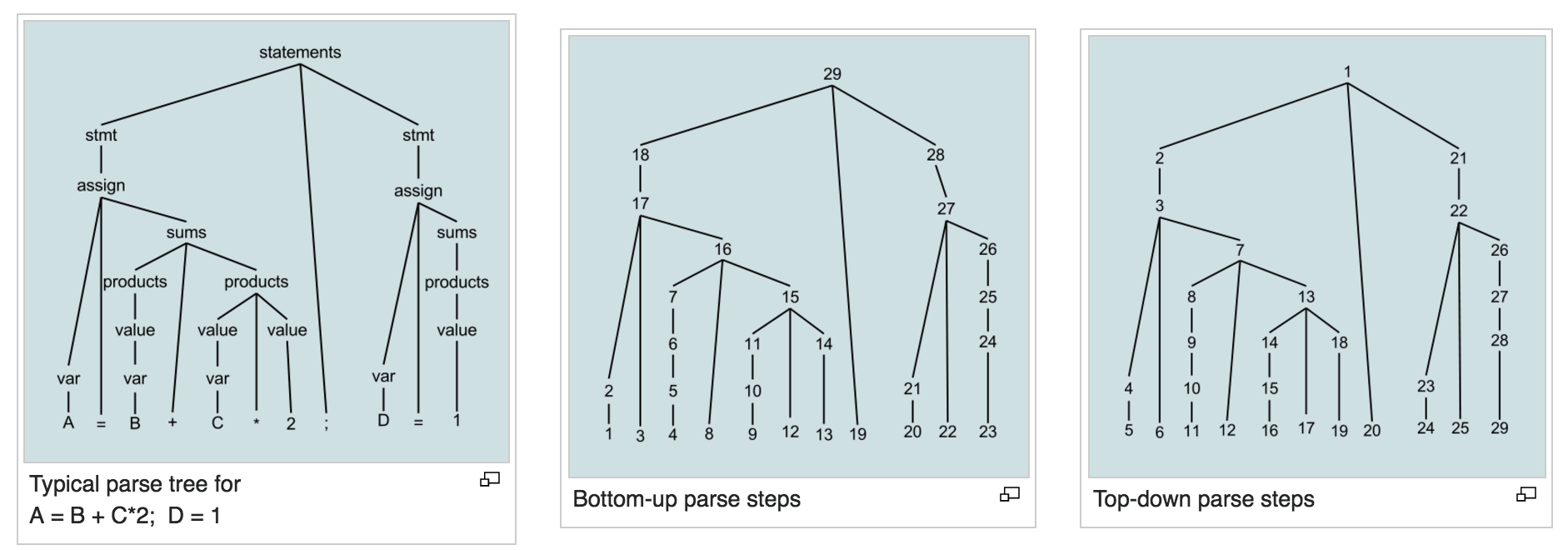
Figure 31: Bottom-up 和 Top-down 建立分析树过程(摘自:https://en.wikipedia.org/wiki/Bottom-up_parsing)
下面引用两处关于 Bottom-up 和 Top-down 的比较。
Bottom-up 和 Top-down 的比较一,如图 32 所示(摘自:http://www.montefiore.ulg.ac.be/~geurts/Cours/compil/2011/03-syntaxanalysis-3.pdf)。

Figure 32: Top-down versus Bottom-up parsing
Bottom-up 和 Top-down 的比较二:
LL or LR?
This question has already been answered much better by someone else, so I'm just quoting his news message in full here:
I hope this doesn't start a war...
First - - Frank, if you see this, don't shoot me. (My boss is Frank DeRemer, the creator of LALR parsing...)
(I borrowed this summary from Fischer&LeBlanc's "Crafting a Compiler")
Simplicity - - LL
Generality - - LALR
Actions - - LL
Error repair - - LL
Table sizes - - LL
Parsing speed - - comparable (me: and tool-dependent)
Simplicity - - LL wins
========
The workings of an LL parser are much simpler. And, if you have to debug a parser, looking at a recursive-descent parser (a common way to program an LL parser) is much simpler than the tables of a LALR parser.
Generality - - LALR wins
========
For ease of specification, LALR wins hands down. The big difference here between LL and (LA)LR is that in an LL grammar you must left-factor rules and remove left recursion.
Left factoring is necessary because LL parsing requires selecting an alternative based on a fixed number of input tokens.
Left recursion is problematic because a lookahead token of a rule is always in the lookahead token on that same rule. (Everything in set A is in set A...) This causes the rule to recurse forever and ever and ever and ever...
To see ways to convert LALR grammars to LL grammars, take a look at my page on it:
http://www.jguru.com/thetick/articles/lalrtoll.html
Many languages already have LALR grammars available, so you'd have to translate. If the language doesn't have a grammar available, then I'd say it's not really any harder to write a LL grammar from scratch. (You just have to be in the right "LL" mindset, which usually involves watching 8 hours of Dr. Who before writing the grammar... I actually prefer LL if you didn't know...)
Actions - - LL wins
=====
In an LL parser you can place actions anywhere you want without introducing a conflict
Error repair - - LL wins
==========
LL parsers have much better context information (they are top-down parsers) and therefore can help much more in repairing an error, not to mention reporting errors.
Table sizes - - LL
=========
Assuming you write a table-driven LL parser, its tables are nearly half the size. (To be fair, there are ways to optimize LALR tables to make them smaller, so I think this one washes...)
Parsing speed - comparable (me: and tool-dependent)
