Cryptography
Table of Contents
1. 密码学
密码学中,有两类密码体制:“对称密钥密码体制”和“公钥密码体制”。 对称密钥密码体制使用同一个密钥进行加密和解密。而公钥密码体制的加密密钥和解密密码是不同的。
2. 对称密钥密码体制
对称密钥密码体制使用“同一个密钥”进行加密和解密。
Kerckhoff’s principle 告诉我们,依赖于不公开算法进行加密解密的方法都不可靠。
Kerckhoff’s principle: All algorithms must be public; only the keys are secret.
用对称密钥密码体制进行加密和解密的过程如图 1 (图片摘自:https://technet.microsoft.com/en-us/library/cc962028.aspx) 所示。
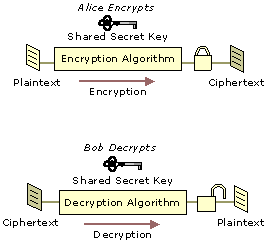
Figure 1: Encryption and Decryption with a Symmetric Key
一些常见的对称密钥算法如表 1 所示(摘自:Computer Networks, by A Tanenbaum, 5th, 8.2.4 Other Ciphers)。
| Cipher | Author | Key length | Comments | Published |
|---|---|---|---|---|
| DES | IBM | 56 bits | Too weak to use now | 1975 |
| RC4 | Ronald Rivest | 1-2048 bits | Caution: some keys are weak | 1994 |
| RC5 | Ronald Rivest | 128-256 bits | Good, but patented | 1994 |
| Triple DES | IBM | 168 bits | Good, but getting old | 1995 |
| CAST5 (CAST-128) | Carlisle Adams and Stafford Tavares | 40-128 bits | 1996 | |
| AES (Rijndael) | Daemen and Rijmen | 128-256 bits | Best choice | 1998 |
| Serpent | Anderson, Biham, Knudsen | 128-256 bits | Very strong | 1998 |
| Twofish | Bruce Schneier | 128-256 bits | Very strong; widely used | 1998 |
| Camellia | Mitsubishi Electric and NTT of Japan | 128, 192, 256 bits | 2000 | |
| Salsa20 | Daniel J. Bernstein | 128, 256 bits | 20 means “20 rounds” | 2007 |
| ChaCha20 | Daniel J. Bernstein | 128, 256 bits | Successor of Salsa20 | 2008 |
2.1. 分组密码
把明文信息划分为不同的组(或块)结构,分别对每个组(或块)进行加密、解密,称为分组密码。 DES,AES 等都是分组密码。
注:除分组密码外,还有流密码。
2.1.1. 填充方案(PKCS7Padding,ISO10126Padding)
对于分组密码,明文字节必须按照块进行填充对齐,才能方便进行加密运算。
最简单的填充方案是全部填充 0,其它填充方案有 PKCS7Padding, ISO10126Padding等。
PKCS7Padding 填充方案的策略为填充“填充的长度”。 比如,块为 8 字节大小,而数据有 9 字节,采用 PKCS7Padding 方案,则第 2 个块(最后一个块)的剩下的 7 字节全部填充 07 。
## PKCS7Padding F1 F2 F3 F4 F5 F6 F7 F8 ## 第1块 F9 07 07 07 07 07 07 07 ## 第2块
ISO10126Padding 填充方案的策略为填充“随机数,最后一个字节为填充的长度”。 比如,块为 8 字节大小,而数据有 9 字节,采用 ISO10126Padding 方案填充后为:
## ISO10126Padding F1 F2 F3 F4 F5 F6 F7 F8 ## 第1块 F9 XX XX XX XX XX XX 07 ## 第2块,XX为随机数
注:PKCS5Padding 和 PKCS7Padding 基本相同,区别在于 PKCS5Padding 要求块大小为 8 字节,不过很多时候 PKCS5Padding 和 PKCS7Padding 可以交替使用,表示的是同一种填充方案。
参考:
https://crypto.stackexchange.com/questions/9043/what-is-the-difference-between-pkcs5-padding-and-pkcs7-padding
https://en.wikipedia.org/wiki/Padding_(cryptography)
2.1.2. 工作模式(ECB/CBC/CFB/OFB/CTR)
分组密码的工作模式如表 2 所示。
| 模式 | 描述 | 典型应用 |
|---|---|---|
| 电码本(ECB,Electronic Code Book) | 这是最简单的工作模式。对明文分组后,对每一组进行单独加密 | 单个数据的安全传输(如一个加密密钥) |
| 密文分组链接(CBC,Cipher Block Chaining) | 加密算法的输入是上一个密文组和下一个明文组的异或 | 面向分组的通用传输;认证 |
| 密文反馈(CFB,Cipher FeedBack) | 一次处理 s 位,上一块密文作为加密算法的输入,产生的伪随机数输出与明文异或作为下一单元的密文 | 面向数据流的通用传输;认证 |
| 输出反馈(OFB,Output FeedBack) | 与 CFB 类似,只是加密算法的输人是上一次加密的输出,且使用整个分组 | 噪声信道上的数据流的传输(如卫屋通信) |
| 计数器(CTR,Counter) | 每个明文分组都与一个经过加密的计数器相异或。对每个后续分组计数器递增 | 面向分组的通用传输;用于高速需求 |
2.1.2.1. 具备认证功能的工作模式
在加密的同时,还具备认证功能(参考节 6.1.1)的工作模式如表 3 所示。
| 模式 | 描述 |
|---|---|
| Galois/Counter Mode (GCM) | 把分组加密(或称块加密)转换为了流加密,所以不需要 padding 方案了。它的优点是性能非常好 |
| Counter with CBC-MAC (CCM) | |
| Synthetic Initialization Vector (SIV) | 优点是重用 IV 值(nonce 值)时,不会影响安全性,这时仅得到确定的密文,参考 RFC 8452 |
| AES-GCM-SIV | 同时具备 GCM 优点(性能好)和 SIV 的优点(重用 nonce 值不影响安全性),参考 RFC 8452 |
3. 公钥密码体制
对称密钥密码体制有一个重要的问题是:加密解密都需要这个密钥,所以不能把密钥藏起来,必须把密钥分发给系统中的所有人,这很难保证密钥的安全(密钥容易泄露给系统外的人)。
1976 年 Diffie 和 Hellman 在他们的文章“New Directions in Cryptography”中提出了一个新想法:在发送端和接收端之间不传递密钥也可以完成解密,这对密码学产生了深远的影响。
Diffie 和 Hellman 使人们意识到:加密密钥和解密密钥可以不同。1977 年 Rivest, Adi Shamir 和 Leonard Adleman 提出了第一个公钥密码算法,即 RSA算法。
说明:Rivest, Adi Shamir 和 Leonard Adleman 获得了 2002 年的图灵奖。(补充:Diffie 和 Hellman 获得了 2015 年的图灵奖。)
在公钥密码体制中,每个参与者都有两个密钥:公钥和私钥。公钥是公开的,私钥则只有自己知道。用户 B 给用户 A 发送消息时,首先用户 B 使用用户 A 的公钥对消息进行加密,用户 A 收到密文后用自己的私钥对密文进行解密。利用公钥密码系统进行加密和解密的过程如图 2 (图片摘自https://technet.microsoft.com/en-us/library/cc962028.aspx) 所示。
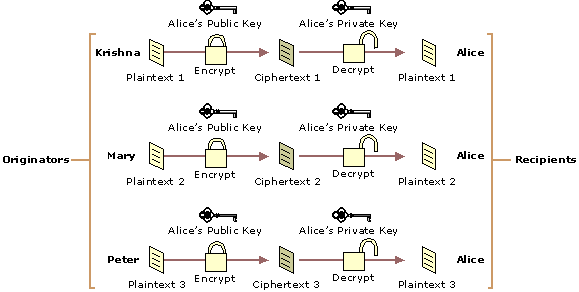
Figure 2: Encryption and Decryption with Asymmetric Keys
3.1. RSA 算法
3.1.1. RSA 算法描述
RSA 算法的描述分为两个部分:如何生成公钥和私钥,如何进行加密及解密。
RSA 算法生成公钥和私钥的方法如下:
- 选择两个随机大素数 \(p\) 和 \(q\) ( \(p\) 和 \(q\) 是保密的,生成完公钥和私钥后就销毁)
- 计算大素数 \(p\) 和 \(q\) 的乘积 \(n=p \times q\) ( \(n\) 是公开的)
- 计算 \(z = (p-1) \times (q-1)\) ( \(z\) 是保密的,生成完公钥和私钥后就销毁)
- 随机选择整数 \(e\) (在实践中, \(e\) 往往取固定值 65537),满足 \(\text{gcd}(e, z) =1\) ,其中 \(\text{gcd}\) 是最大公约数,即表示 \(e,z\) 互素( \(e\) 是公开的)。
- 计算 \(d\) ,满足 \(d \times e = 1 \pmod z\) ( \(d\) 是保密的)
完成上面步骤后, \((e,n)\) 就是公钥,而 \((d,n)\) 是私钥。
RSA 算法的加密及解密过程如下:
- 假设明文为 \(P\) ,则其对应的密文 \(C\) 的计算方法(使用公钥进行加密的过程)为: \(C = P^e \pmod n\)
- 假设密文为 \(C\) ,则其对应的明文 \(P\) 的计算方法(使用私钥进行解密的过程)为: \(P = C^d \pmod n\)
说明 1:RSA 算法的安全性来源于: 给定两个素数 \(p\) 和 \(q\) 容易求得它们的乘积 \(n\) ,但对 \(n\) 进行因式分解求出 \(p,q\) 却很困难。
说明 2:使用 RSA 算法时,明文 \(P\) 对应数字必须要小于模数 \(n\) ,否则解密会出错。用一个简单的例子来说明原因。假设 \(e=d=1\) ,则加密过程为 \(C=P (\bmod n)\) ,解密过程为 \(P' = C (\bmod n)\) ,当 \(P \ge n\) 时,容易验证 \(P'\) 和 \(P\) 不相同,解密失败,从而明文 \(P\) 对应数字必须小于模数 \(n\) 。
说明 3:公钥中的 \(e\) 往往为固定值 65537,而私钥中的 \(d\) 往往很大,如 2048 比特位。这样,加密过程比较快,而解密过程相对加密过程则要慢很多。节 3.1.3 中介绍了利用中国剩余定理加快 RSA 解密过程的算法。
3.1.2. RSA 算法实例
图 3 是用 RSA 算法对明文“SUZANNE”进行加密和解密的演示实例。
在这个例子中,选择素数 \(p=3,q=11\) ,从而 \(n=3 \times 11=33, z = 2 \times 10=20\) ,可以选择 \(e=3\) (因为 3 和 20 是互素的,所以满足要求),从方程 \(d \times 3 = 1 (\bmod 20)\) 中,求解得出 \(d=7\) 。所以,加密过程为 \(C=P^3 (\bmod 33)\) ,解密过程为 \(P = C^7 (\bmod 33)\)
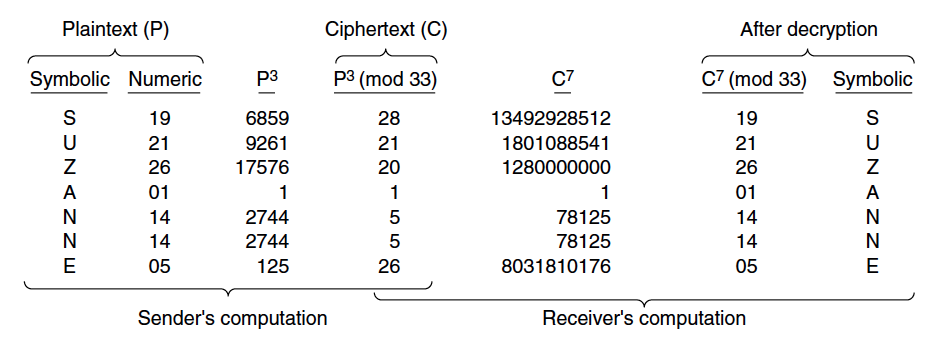
Figure 3: An example of the RSA algorithm
说明:在上面例子中,除了对单个字母进行分别加密外,还可以把“SUZANNE”作为整体转换为一个数字后,运行一次 RSA 算法进行加密(不过这时要求选择一个更大的 \(n\) ,因为 RSA 算法要求模数 \(n\) 必须大于明文)。
参考:Computer Networks, by A Tanenbaum, 5th, 8.3.1 RSA
3.1.3. 使用 CRT 加快 RSA 解密过程
如果知道 RSA 公钥 \(n\) 的两个素因子 \(p,q\) ,则可以利用 Chinese Remainder Theorem (CRT) 加快 RSA 的解密过程。
我们往往在生成 RSA 私钥时,除保存私钥 \((d,n)\) 外,还保存下面这些数据:
- RSA 公钥 \(n\) 的两个素因子 \(p,q\)
- \(d_{P}=d{\pmod {p-1}}\)
- \(d_{Q}=d{\pmod {q-1}}\)
- \(q_{\text{inv}}=q^{-1}{\pmod {p}}\)
RSA 解密时,采用下面方式计算明文比直接使用 \(m=c^d {\pmod {pq}}\) 计算明文要快很多:
- \(m_{1}=c^{d_{P}}{\pmod {p}}\)
- \(m_{2}=c^{d_{Q}}{\pmod {q}}\)
- \(h=q_{\text{inv}}(m_{1}-m_{2}){\pmod {p}}\)
- \(m=m_{2}+hq{\pmod {pq}}\)
参考:https://en.wikipedia.org/wiki/RSA_(cryptosystem)#Using_the_Chinese_remainder_algorithm
3.2. 其它公钥密码算法
除 RSA 外,还有其它一些公钥密码算法,如:ElGamal 和 Elliptic curve cryptography (ECC) 等等。
3.2.1. 椭圆曲线密码学(ECC)
ECC (Elliptic Curves Cryptography)是另一种著名的公钥密码算法,它由 1985 年由 Neal Koblitz 和 Victor S. Miller 提出。
和 RSA 公钥密码算法相比,ECC 具有下面优点:
- 在相同安全性级别下,ECC 的 public key 的长度更短。For example, a 256-bit elliptic curve public key should provide comparable security to a 3072-bit RSA public key.
- 加解密速度更快,占用的 CPU 和内存资源更少。
参考:
ECC 加密算法入门介绍:https://www.pediy.com/kssd/pediy06/pediy6014.htm
Elliptic Curve Cryptography (ECC) Certificates Performance Analysis
3.2.2. ElGamal
ElGamal 是 Taher Elgamal 在 1985 年发明的公钥密码算法。
Key Generation:
The first party, Alice, generates a key pair as follows:
- Generate an efficient description of a cyclic group \(G\), of order \(q\), with generator \(g\).
- Choose an integer \(x\) randomly from \(\{1,\ldots ,q-1\}\).
- Compute \(h:=g^{x}\).
- The public key consists of the values \((G,q,g,h)\). Alice publishes this public key and retains \(x\) as her private key, which must be kept secret.
Encryption:
A second party, Bob, encrypts a message \(M\) to Alice under her public key \((G,q,g,h)\) as follows:
- Map the message \(M\) to an element \(m\) of \(G\) using a reversible mapping function.
- Choose an integer \(r\) randomly from \(\{1, \ldots, q-1\}\).
- Compute \(s:=h^{r}\). This is called the shared secret.
- Compute \(c_{1}:=g^{r}\).
- Compute \(c_{2}:=m\cdot s = m \cdot h^r\).
- Bob sends the ciphertext \((c_{1},c_{2}) = (g^{r}, m \cdot h^r)\) to Alice.
Decryption:
Alice decrypts a ciphertext \((c_{1},c_{2})\) with her private key \(x\) as follows:
- Compute \(s:=c_{1}^{x}\). Since \(c_{1}^{x}=(g^r)^x=g^{xr} = h^{r}\), and thus it is the same shared secret that was used by Bob in encryption.
- Compute \(s^{-1}\), the inverse of \(s\) in the group \(G\).
- Compute \(m:=c_{2}\cdot s^{-1}\).
- Map \(m\) back to the plaintext message \(M\).
ElGamal 的不足:ElGamal encryption is unconditionally malleable, and therefore is not secure under chosen ciphertext attack. For example, given an encryption \((c_{1},c_{2})\) of some (possibly unknown) message \(m\), one can easily construct a valid encryption \((c_1, 2 c_2)\) of the message \(2m\). 为了解决这个缺点,Ronald Cramer 和 Victor Shoup 在 1998 年扩展了 ElGamal,提出了 Cramer–Shoup cryptosystem,这种算法在 Chosen Ciphertext Attack 下也是安全的。
3.2.2.1. 乘同态
ElGamal 具有“乘同态”(Multiplicative Homomorphic)性质。
通过前面的内容我们知道,对数据 \(m\) 进行 ElGamal 加密后的得到的密文由两个部分 \((c_1,c_2) = (g^r, m \cdot h^r)\) 组成,记 ElGamal 加密过程为 \(E(m,r) = (g^r, m h^r)\) ,定义密文上的乘法运算为 \((c_1,c_2) \cdot (c_3,c4) \triangleq (c_1 \cdot c_3, c_2 \cdot c_4)\) 。
所谓乘同态就是指:仅已知公钥和两个加密后的消息 \(E(m_1,r_1)\) 和 \(E(m_2,r_2)\) ,不接触私钥(也就是说不解密)情况下,可以计算出两个明文 \(m_1\) 和 \(m_2\) 相乘后(即 \(m_1m_2\) )再加密的结果。
下面计算一下两个密文的乘积: \[\begin{aligned} E(m_1,r_1) \cdot E(m_2,r_2) & = (g^{r_1}, m_1 \cdot h^{r_1}) \cdot (g^{r_2}, m_2 \cdot h^{r_2}) \\ & = (g^{r_1}g^{r_2}, m_1 h^{r_1} m_2 h^{r_2}) \\ & = (g^{r_1+r_2}, m_1m_2 h^{r_1+r_2}) \end{aligned}\] 如果我们对两个明文的乘积 \(m_1m_2\) 使用随机数 \(r_1+r_2\) 进行加密,则会得到密文: \[E(m_1m_2, r_1+r_2) = (g^{r_1+r_2}, m_1m_2 h^{r_1+r_2})\] 显然,它和前面介绍的两个密文的乘积 \(E(m_1,r_1) \cdot E(m_2,r_2)\) 是相同的,所以 ElGamal 具有乘同态性质。
3.2.2.2. 加同态(Exponential ElGamal)
正常情况下,ElGamal 加密不具体“加同态”(Additive Homomorphic)性质,不过通过一定调整可以让 ElGamal 具备加同态性质。
所谓加同态就是指:仅已知公钥和两个加密后的消息 \(E(m_1,r_1)\) 和 \(E(m_2,r_2)\) ,不接触私钥(也就是说不解密)情况下,可以计算出两个明文 \(m_1\) 和 \(m_2\) 相加后(即 \(m_1+m_2\) )再加密的结果。
我们知道,正常的 ElGamal 加密过程为: \[E(m,r) = (g^r, m h^r)\] 为了让 ElGamal 具备加同态性质,我们定义 \[E'(m,r) = (g^r, g^m h^r)\] 这相当于加密时,不直接操作 \(m\) ,而是操作 \(g^m\) ,这种变种被称为 Exponential ElGamal。
在这个定义下,我们计算一下两个密文的乘积: \[\begin{aligned} E'(m_1,r_1) \cdot E'(m_2,r_2) & = (g^{r_1}, g^{m_1} h^{r_1}) \cdot (g^{r_2}, g^{m_2} h^{r_2}) \\ & = (g^{r_1}g^{r_2},g^{m_1} h^{r_1} g^{m_2} h^{r_2}) \\ & = (g^{r_1+r_2}, g^{m_1+m_2} h^{r_1+r_2}) \end{aligned}\] 如果我们对两个明文的和 \(m_1+m_2\) 使用随机数 \(r_1+r_2\) 进行加密,则会得到密文: \[E'(m_1+m_2, r_1+r_2) = (g^{r_1+r_2}, g^{m_1+m_2} h^{r_1+r_2})\] 显然,它和前面介绍的两个密文的乘积 \(E'(m_1,r_1) \cdot E'(m_2,r_2)\) 是相同的,所以 ElGamal 具有加同态性质。
注 1:我们一般不能直接用 Exponential ElGamal 算法来加密大数字 \(m\) 。因为解密后得到的是 \(g^m\) ,从它是无法反推出原始数据 \(m\) 来的。一般的只有当 \(m\) 比较小时,我们可以用穷举法得到原始数据 \(m\) ,这时才可以使用 Exponential ElGamal 加密。
注 2:当使用原始的 ElGamal 加密时具备“乘同态”性质(这时没有“加同态”性质),而使用 Exponential ElGamal 加密时具备“加同态”性质(这时没有“乘同态”性质)。没有一种方案使 ElGamal 既具备“乘同态”性质,又具备“加同态”性质。
3.2.2.3. ElGamal 的安全假设 CDH 和 DDH
下面介绍一下 Computational Diffie–Hellman Assumption(CDH):
设循环群 \(G\) 的 order 为 \(q\) ,给定一个三元组 \((g,g^a,g^b)\) (其中 \(g\) 是随机选择的生成元, \(a,b\) 是从 \([0,\cdots,q-1]\) 是随机选择的数)后,想要计算出 \(g^{ab}\) 是困难的,这就是 CDH 假设。
下面介绍一下 Decisional Diffie–Hellman Assumption(DDH):
设循环群 \(G\) 的 order 为 \(q\) ,给定两组数据 \((g,g^a,g^b,g^{ab})\) 和 \((g,g^a,g^b,g^r)\) (其中 \(g\) 是随机选择的生成元, \(a,b,r\) 是从 \([0,\cdots,q-1]\) 是随机选择的数),则这两组数据是不可区分的。 也就是说你不知道 \(g^{ab}\) 和 \(g^r\) 这两个值中哪个值会和 \(g^a,g^b\) 相关。
ElGamal 加解密依赖于 CDH 假设,具体来说:已知 \((g,g^x,g^r)\) ,别人不能容易地计算出 shared secret \(g^{xr}\) ,只有知道私钥 \(x\) 的人才可以计算 \(g^{xr}\) 。不过,如果要证明 ElGamal 具备 Semantic security,则会依赖于 DDH 假设。参考:https://en.wikipedia.org/wiki/ElGamal_encryption#Security
注 1:CDH/DDH 基于离散对数假设(Discrete Logarithm Assumption),如果离散对数假设不成立,则 CDH/DDH 不会成立。
注 2: DDH 并不总是成立。如果循环群 \(G\) 拥有 Pairing 特性,那么 DDH 可能不成立。 因为,我们利用 Pairing 可以把 \(g^a,g^b\) 转换为 \(g_{T}^{ab}=e(g^a,g^b)\) ,类似地利用 Pairing 把 \(g,g^{ab}\) 转换为 \(g_{T}^{ab}=e(g,g^{ab})\) ,利用 Pairing 把 \(g,g^{r}\) 转换为 \(g_{T}^{r}=e(g,g^r)\) ,这样群 \(G_T\) 中计算出了三个值,其中有两个是相等的(都是 \(g_{T}^{ab}\) ),剩下的那个( \(g_{T}^{r}\) )则是由 \((g,g^r)\) 计算而来,从而可以区分两组数据 \((g,g^a,g^b,g^{ab})\) 和 \((g,g^a,g^b,g^r)\) 了,这样就解决了 DDH 问题。不过,这里还涉及到 Pairing 有效计算的问题(当 Embedding Degree 太大时,无法有效计算 Pairing)。参考:https://en.wikipedia.org/wiki/Decisional_Diffie%E2%80%93Hellman_assumption#Groups_for_which_DDH_is_assumed_to_hold
注 3:使用 ElGamal 时,我们会选择没有 Pairing 特性的循环群,原因上面已经介绍。
3.2.3. Paillier Cryptosystem
Paillier 密码系统是 Pascal Paillier 于 1999 年发明的,它是一种公钥密码算法。除此外, Paillier 具备“加同态”性质。
3.3. 公钥的分配
假设用户 Alice 要和 Bob 进行加密通信,Alice 怎么得到 Bob 的公钥呢?Bob 可以把他的公钥放到他的网站主页上,Alice 下载即可。但是,这是不可靠的。Alice 访问 Bob 的主页时,黑客 Trudy 可能拦截 Alice 的请求,并把 Bob 的公钥(设为 \(E_B\) )替换为他自已的公钥(设为 \(E_T\) ),Alice 得到的是 Trudy 的公钥(但她不知道)。
Alice 发送消息给 Bob 时,用公钥(Trudy 的公钥)加密后发送出去,被 Trudy 拦截,Trudy 利用自已的私钥解密了消息(甚至解密后还可以修改消息),并用 Bob 的公钥重新加密发送给 Bob。整个过程 Alice 和 Bob 是不知情的。具体过程如图 4 所示。
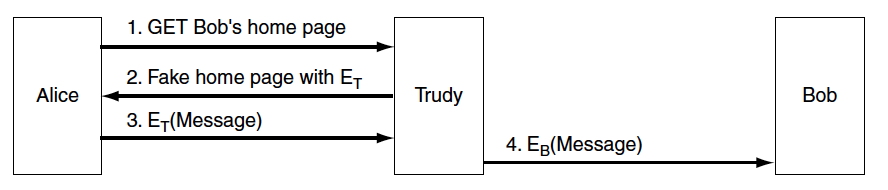
Figure 4: A way for Trudy to subvert public-key encryption
所以,Bob 把他的公钥放在他主页上让别人下载的做法是不安全的。
那怎么办呢?一个作法是把公钥放到一个安全的 Key Distribution Center (KDC, 注:KDC 常常用于“对称密钥算法”中密钥的分配)中,需要时就去下载,但是 KDC 必须 24 小时在线,而且可能成为瓶颈。
人们想到了另外的办法,克服 Key Distribution Center 需要随时 24 小时在线并可能成为瓶颈的缺点。这就是用证书(Certificates)证明公钥属于某个人或组织,请看下文介绍。
参考:Computer Networks, by A Tanenbaum, 5th, 8.5 Management of Public Keys
3.3.1. 证书(Certificates)
证书(Certificates)可以证明公钥属于某个人或组织。能够证明公钥属于某个人或组织的机构称为 CA (Certification Authority)。
还是以前面的场景作例子。Bob 为了使别人知道和他通信是安全的,他首先把它的公钥提交给 CA(很可能要交付一定的费用),CA 给他颁发一个证书,证明这个公钥确实属于 Bob。证书用 CA 的私钥进行了数字签名(后文将介绍数字签名),别人无法伪造。证书的大概内容如图 5 所示。

Figure 5: A possible certificate and its signed hash
Alice 想和 Bob 通信,首先从 Bob 主页上下载得到了 Bob 的公钥及公钥的证书。(如果这个过程被 Trudy 拦截,Trudy 把 Bob 的公钥及公钥的证书换成了自己的公钥及自己公钥的证书,Alice 打开证书时就可以发现证书中公显示公钥是 Trudy 的,而不是 Bob 的!证书有 CA 的签名,Trudy 无法伪造证书。)
Alice 确认 Bob 的公钥及其证书后,利用 Bob 的公钥进行消息加密,就可以向 Bob 发送加密信息了。
3.3.1.1. 证书格式(X.509)
如果每个 CA 采用不同的证书格式,则管理起来比较麻烦。一般地,大家都使用 X.509 作为证书格式的标准。
X.509 的基本字段如表 4 所示。
| Field | Meaning |
|---|---|
| Version | Which version of X.509 |
| Serial | number This number plus the CA’s name uniquely identifies the certificate |
| Signature | algorithm The algorithm used to sign the certificate |
| Issuer | X.500 name of the CA |
| Validity | period The starting and ending times of the validity period |
| Subject | name The entity whose key is being certified |
| Public | key The subject’s public key and the ID of the algorithm using it |
| Issuer | ID An optional ID uniquely identifying the certificate’s issuer |
| Subject | ID An optional ID uniquely identifying the certificate’s subject |
| Extensions | Many extensions have been defined |
| Signature | The certificate’s signature (signed by the CA’s private key) |
3.3.1.2. Public Key Infrastructures (PKI)
还有一些其它问题需要解决,如 CA 的一些操作规范,如何废止证书等等。这一系列其他问题都在公钥基础设施(Public Key Infrastructures, PKI)中有规范。
3.4. 密钥的编码标准
密钥有不同的编码标准,如表 5 所示。
| 支持 RSA | 支持其它算法 | 可编码私钥 | 可编码公钥 | BEGIN Tag | |
|---|---|---|---|---|---|
| PKCS#1 (RFC8017) | ✓ | ✓ | ✓ | -----BEGIN RSA PRIVATE KEY-----, -----BEGIN RSA PUBLIC KEY----- |
|
| PKCS#8 (RFC5958) | ✓ | ✓ | ✓ | -----BEGIN PRIVATE KEY-----, -----BEGIN ENCRYPTED PRIVATE KEY----- |
|
| PKI X.509 (RFC5280) | ✓ | ✓ | ✓ | -----BEGIN PUBLIC KEY----- |
每种标准都支持 PEM(文本形式)格式和 DER(二进制形式)格式。
4. 数字签名(Digital Signatures)
书信或文件可以根据亲笔签名或印章来证明其真实性。电子消息怎么实现这一点呢?这是“数字签名”所要完成的任务。一般地,数字签名要满足下面三个要求:
- The receiver can verify the claimed identity of the sender.
- The sender cannot later repudiate the contents of the message.
- The receiver cannot possibly have concocted the message himself.
4.1. RSA Digital Signature Process
用 RSA 算法进行数字签名的过程如图 6 (图片摘自:https://technet.microsoft.com/en-us/library/cc962021.aspx) 所示。
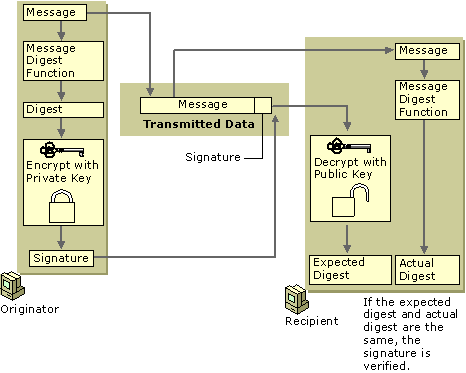
Figure 6: Basic RSA Data Security Digital Signature Process
说明 1:图示中 Originator 用自己的私钥对消息摘要进行 RSA 加密操作的过程就是“RSA 签名过程”。私钥怎么可以用来加密呢(前面介绍过的都是用别人公钥进行加密,用自己私钥进行解密)?RSA 算法的加密操作步骤和解密操作步骤是一样的(只是使用的密钥不同),所以你不用关心到底叫“加密”还是“解密”,只需关心用“公钥”还是“私钥”处理数据。正常的加密解密过程是“先使用公钥操作数据,再使用私钥操作数据”(即 \(D(E(P))=P\) )。RSA 算法还有一个特性就是“先使用私钥操作数据,再使用公钥操作数据”也可以得到原始数据( \(E(D(P))=P\) ),用 RSA 进行数字签名正是利用了 RSA 的这个特性。
说明 2:图示中,对消息本身是没有加密的,如果有需求可以进行额外的加密操作。即有数字签名,又有加密过程的示意图如图 7 所示。
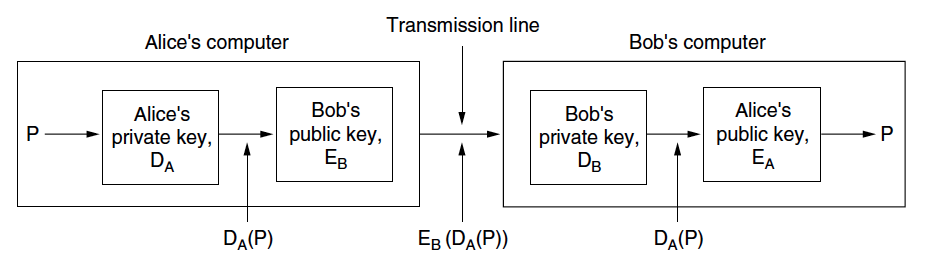
Figure 7: Digital signatures using public-key cryptography(Alice 用自已私钥处理数据的过程就是“签名”)
4.2. ElGamal Signature
ElGamal 签名方案由密码学家 Taher Elgamal 于 1985 年提出。
ElGamal 签名方案有两个 Domain 参数: \(p,g\) ,其中 \(p\) 是素数,而 \(g\) 是群的一个生成元,需要满足 \(g < p\) 。
用户密钥对的产生步骤:
- 从 \(\{1,2,\cdots, p-2\}\) 中随机选择一个数 \(x\) ,这就是用户的私钥;
- 计算 \(y = g^x \pmod p\) ,得到的 \(y\) 是用户的公钥。
ElGamal 对消息 \(m\) 进行签名的过程如下:
- 从 \(\{2,3,\cdots, p-2\}\) 中随机选择一个数 \(k\) ,要求 \(k\) 和 \(p-1\) 互素;
- 计算 \(r = g^k \pmod p\) ;
- 计算 \(s = k^{-1} \cdot (\text{Hash}(m) - x \cdot r) \pmod {p-1}\) ,其中 \(k^{-1}\) 由 \(k^{-1} \cdot k \pmod {p-1} = 1\) 计算而来;
- 如果得到的 \(s\) 为零(出现的可能性很小),则重新选择 \(k\) ,再进行上面的过程。
上面步骤中得到的 \((r,s)\) 就是消息 \(m\) 的签名数据。
验证签名的过程:
- 验证 \(0 < r < p, 0 < s < p-1\) ;
- 如果 \(g^{\text{Hash}(m)} = y^r r^s \pmod p\) 成立,则通过签名验证。
4.2.1. ElGamal 实例
假设 ElGamal 的参数为:
p = 19 # 素数 g = 10 # 10 < 23
假设 Alice 的私钥和公钥为:
x = 16 # 这是私钥,从 2,3,...,p-2 中随机选择 y = 4 # 这是公钥,y = g^x mod p = 4
Alice 对消息进行签名的过程如下:
H(m) = 14 # 假设消息的哈希为 14
k = 5 # 从 2,3,...,p-2 中随机选择,和 p-1 = 18 互素
r = 3 # r = 10^5 mod 19 = 3
i = 15 # 这是 k^{-1},由 k * i mod (p-1) = 1 得到 i = 11
s = 4 # s = i * (H(m) - r*x) mod (p-1) = 11 * (14 - 3 * 16) mod 18 = 4
\((3, 4)\) 就是签名。
Bob 对签名进行验证的过程如下:
H(m) = 14 # 消息哈希
g^{H(m)} mod p = 16 # 10^{14} mod 19 = 16
y^r * r^s mod p = 16 # 4^3 * 3^4 mod 19 = 16
由于 \(g^{\text{Hash}(m)} = y^r r^s \pmod p\) 成立,所以通过验证。
4.3. Schnorr Signature
Schnorr 签名方案由德国密码学家 Claus Schnorr 提出,这个方案在 1990 年申请了专利,不过相关专利已于 2008 年过期。
注:EdDSA 签名方案可以看作是 Schnorr 签名方案采用 Twisted Edwards Curve 时的变种。
4.3.1. Schnorr 签名及验证过程
Schnorr 签名中的运算定义在群上,记 \(g\) 是群的生成元。
设待签名的消息为 \(m\) ,签名者的私钥为 \(x\) ,则公钥为 \(y=g^x\) ,Schnorr 签名方案如下:
- 选择随机数 \(k\) ;
- 计算 \(r=g^k\) ;
- 计算 \(s=k - \text{Hash}(r || m) \cdot x\) ;其中 \(||\) 是 concatenation,这里表示把 \(r\) 所表示的 bit string 和输入消息 \(m\) 进行连接;
- 输出签名 \((r, s)\) 。
验证签名的过程:检查 \(r = g^s \cdot y^{\text{Hash}(r || m)}\) 是否成立,成立就通过验证。
签名验证的正确性证明(从右边往左边推): \[g^s \cdot y^{\text{Hash}(r || m)} = g^{k - \text{Hash}(r || m) \cdot x} \cdot g^{x \cdot \text{Hash}(r || m)} = g^k = r\]
说明:在生成签名数据计算 \(s\) 时,也可以定义 \(s=k + \text{Hash}(r || m) \cdot x\) ,相应地在验证签名时换个形式即可,即检查 \(g^s = r \cdot y^{\text{Hash}(r || m)}\) 是否成立,成立就通过验证。
4.4. Digital Signature Algorithm (DSA)
Digital Signature Algorithm(DSA)是另一种广泛使用的数字签名技术,它是在 ElGamal 和 Schnorr 签名方案的基础上发展而来的。下面介绍一下 DSA 算法流程(不证明)。
4.4.1. DSA 参数和密钥对
DSA 算法有 3 个参数 \((p,q,g)\) :
- \(p\) ,是个 \(L\) bits 长的素数。 \(L\) 是 64 的倍数,原始的规范要求范围是 512 到 1024。NIST 800-57 推荐使用更大的 \(L\) ,如 2048 或者 3072;
- \(q\) ,它是 \(p-1\) 的素因子,即满足 \(q \mid p-1\) ;
- \(g\) ,由 \(g=h^{(p-1)/q} \pmod p\) 计算而来, \(h=2\) 采用比较多。
用户的密钥对根据上面三个参数 \((p,q,g)\) 计算而来:
- 从 \(\{1,2,\cdots, q-1\}\) 中随机选择一个数 \(x\) ;
- 计算 \(y=g^x \pmod p\) 。
上面过程中 \(x\) 就是私钥,而 \(y\) 就是公钥。
4.4.2. DSA 签名过程
签名过程如下(假设消息是 \(m\) ,而 \(H(m)\) 是计算消息的哈希):
- 从 \(\{1,2,\cdots, q-1\}\) 中随机选择一个数 \(k\) ;
- 计算 \(r=(g^k \pmod p) \pmod q\) ;如果发现 \(r\) 等于 0,则要重新选择一个 \(k\) 再重新计算;
- 计算 \(s=(k^{-1}(H(m) + x \cdot r)) \pmod q\) ,如果发现 \(s\) 等于 0,则重新选择一个 \(k\) 再重新计算;
上面过程中,得到的 \((r, s)\) 就是签名。
4.4.3. DSA 验证签名过程
验证签名的过程如下:
- 验证 \(0 < r < q, 0 < s < q\) ;
- 计算 \(w=s^{-1} \pmod q\) ;
- 计算 \(u_1 = H(m) \cdot w \pmod q\) ;
- 计算 \(u_2 = r \cdot w \pmod q\) ;
- 计算 \(v = (g^{u_1}y^{u_2} \pmod p) \pmod q\) ;
如果 \(v=r\) 则通过签名验证。
4.4.4. DSA 实例
假设 DSA 的参数为:
p = 7 # 素数
q = 3 # 它是 p-1 的素因子
g = 4 # 取 h=2,则 g = 2^{(7-1)/3} mod 7 = 4
假设 Alice 的私钥和公钥为:
x = 5 # 这是私钥,从 1,2,...,6 中随机选择 y = 2 # 这是公钥,y = 4^5 mod 7 = 2
Alice 对消息进行签名的过程如下:
H(m) = 3 # 假设消息的哈希为 3
k = 2 # 从 1,2,...,6 中随机选择
r = 2 # r = (4^2 mod 7) mod 3 = 2
i = 5 # 这是 k^{-1},由 k * i mod q = 1 得到 i = 5
s = 2 # s = i*(H(m)+r*x) mod q = 5*(3+2*5) mod 3 = 2
\((r, s) = (2, 2)\) 就是签名。
Bob 对签名进行验证的过程如下:
H(m) = 3 # 消息哈希
w = 5 # s*w mod q = 1 得到 w = 5
u1 = 0 # u1 = h*w mod q = 3*5 mod 3 = 0
u2 = 1 # u2 = r*w mod q = 2*5 mod 3 = 1
v = 2 # v = (((g^{u1})*(y^{u2})) mod p) mod q = 2
由于 \(v=r\) 成立,所以通过验证。
参考:http://www.herongyang.com/Cryptography/DSA-Introduction-Algorithm-Illustration-p7-q3.html
4.5. Rabin Signature Algorithm
Rabin Signature Algorithm 是 Rabin 于 1979 年发明的数字签名算法。下面介绍的 Rabin Signature Algorithm 并不是 Rabin 在原始论文中描述的版本,而是更加安全并且简化的版本。
密钥对生成过程:
- 选择两个素数 \(p, q\) ,它们需要满足条件 \(p \equiv 3 \pmod{4}, q \equiv 3 \pmod{4}\) ;
- 记 \((p, q)\) 为私钥;
- 记乘积 \(n=pq\) 为公钥。
生成签名过程:
- 记待签名数据为 \(m\) ;
- 随机选择 \(U\) ,计算 \(\text{Hash(m || U)}\) 。这里 \(m || U\) 表示 \(m\) 和 \(U\) 进行 concatenate;
- 计算 \(x=\left(\left(p^{q-2}\text{Hash(m || U)}^{\frac {q+1}{4}}{\bmod {q}}\right)p+\left(q^{p-2}\text{Hash(m || U)}^{\frac {p+1}{4}}{\bmod {p}}\right)q\right){\bmod (p\cdot q)}\)
- 测试 \(x^2 \equiv \text{Hash(m || U)} \pmod{n}\) 是否成立,如果不成立则回到第 2 步重新选择 \(U\) 。
- 得到的 \((x, U)\) 就是签名数据。
验证签名过程:验证 \(x^2 \equiv \text{Hash(m || U)} \pmod{n}\) 是否成立;如果成立则签名合法。
Rabin Signature Algorithm 的关键在于,不知道私钥 \((p,q)\) 的情况下,很难找到满足条件 \(x^2 \equiv \text{Hash(m || U)} \pmod{n}\) 的 \((x, U)\) ;而知道私钥 \((p,q)\) 后,可以根据签名过程的第 3 步中的公式快速地找到满足条件 \(x^2 \equiv \text{Hash(m || U)} \pmod{n}\) 的 \((x, U)\) 。
关于签名过程的第 3 步中求解 \(x\) 的公式是如何推导出来的,这里不详细介绍,可参考:https://aaron67.cc/2021/07/10/rabin-signatures/
5. Secret Key Exchange(密钥交换)
目前,公钥密码算法的处理速度远远慢于对称密钥算法,所以一般不会直接使用公钥密码算法加解密大量数据。
当使用对称密钥算法用作网络通信时,一个重要的问题是如何传输或者约定一个密钥?这称为 Secret Key Exchange。通常有两种方法:
(1) RSA key exchange process
(2) Diffie-Hellman Key Agreement algorithm
参考:https://technet.microsoft.com/en-us/library/cc962035.aspx
5.1. RSA Key Exchange Process
用 RSA 算法传输密钥的过程如图 8(图片摘自:https://technet.microsoft.com/en-us/library/cc962035.aspx) 所示。

Figure 8: Basic RSA Key Exchange
5.2. Diffie-Hellman Key Agreement algorithm
Diffie–Hellman key exchange (D–H) 算法可以使通信双方通过一定方式生成一个相同密钥。其基本流程如图 9 (图片摘自:https://technet.microsoft.com/en-us/library/cc962035.aspx) 所示。
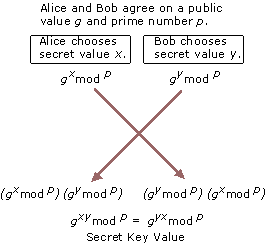
Figure 9: Diffie-Hellman Key Agreement
图 10 (图片摘自https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange) 是 Diffie-Hellman Key Agreement 算法的另一个图示。
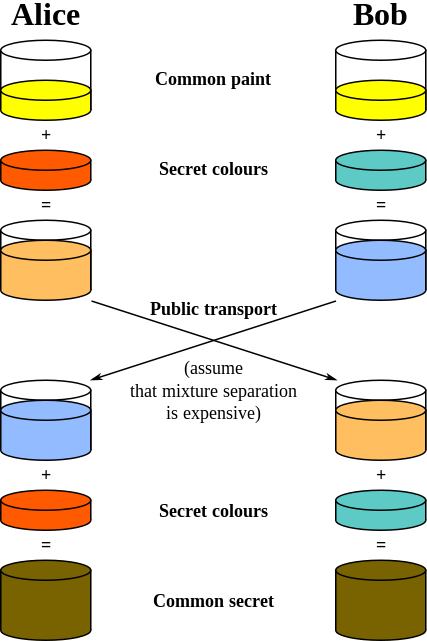
Figure 10: Illustration of the Diffie–Hellman Key Exchange
说明: Diffie-Hellman Key Agreement algorithm 并没有传输密钥本身,它是通过一定方式让通信双方生成一个相同密钥。
5.3. Secret Key Exchange 应用
Secret Key Exchange 相关算法在 SSH1 和 SSH2 中广泛使用。SSH2 避免了 RSA 的专利问题(专利现在已经过时),采用 Diffie-Hellman 算法代替 RSA 来完成对称密钥的交换。
参考:http://docstore.mik.ua/orelly/networking_2ndEd/ssh/ch03_09.htm
For protocol 2, forward security is provided through a Diffie-Hellman key agreement. This key agreement results in a shared session key. The rest of the session is encrypted using a symmetric cipher, currently 128-bit AES, Blowfish, 3DES, CAST128, Arcfour, 192-bit AES, or 256-bit AES.
摘自: man sshd
6. 消息认证码(MAC)
消息认证码(Message Authentication Code)也称为密码学校验,它在实际中得到广泛使用。
消息认证码的原理(如图 11 所示)如下: 它利用密钥来生成一个固定长度的短数据块,并将该数据块附加在消息之后一起发送出去。 在这种方法中,假定通信双方比如 A 和 B,共享密钥 K。若 A 向 B 发送消息时,则 A 计算 MAC,它是消息和密钥的函数,即:
\[\text{MAC}= C(K, Message)\]
其中,Message 为输人消息;C 为 MAC 函数;K 为共享的密钥;MAC 为计算得到的消息认证码。
消息和 MAC 一起被发送给接收方。接收方对收到的消息用相同的密钥进行相同的计算,得出新的 MAC,并将接收到的 MAC 与其计算出的 MAC 进行比较,如果假定只有收发双方知道该密钥,那么若接收到的 MAC 与计算得出的 MAC 相等,则:
(1) 接收方可以相信消息未被修改。 如果攻击者改变了消息,但他无法改变相应的 MAC,所以接收方计算出的 MAC 将不等于接收到的 MAC。因为我们已假定攻击者不知道密钥,所以他不知道应如何改变 MAC 才能使其与修改后的消息相一致。
(2) 接收方可以相信消息来自真正的发送方,不是来自其它的第三方。 因为其他各方均不知道密钥,因此他们不能产生具有正确 MAC 的消息。
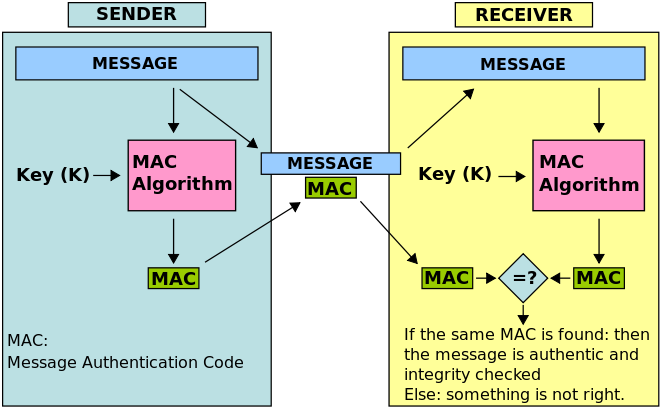
Figure 11: MAC 原理
6.1. MAC 和对称加密
对整个消息进行对称加密也可以提供认证功能。
不过,使用 MAC 可以将认证和保密性分离开来。 MAC 适应于不关心消息的保密性,而关心消息认证的情况。 例如简单网络管理协议(SNMPv3)就是如此,管理系统应对其收到的 SNMP 消息进行认证,这一点非常重要,尤其是当消息中包含修改系统参数的命令时更是如此,但对这些应用不必加密 SNMP 传输。
6.1.1. AEAD
Authenticated Encryption with Associated Data (AEAD) 是一种同时具备“保密性”和“可认证性”的加密形式。
单纯的对称加密算法,其解密步骤是无法确认密钥是否正确的。也就是说,加密后的数据可以用任何密钥执行解密运算,得到一组疑似原始数据,但却不知道密钥是否是正确的,也不知道解密出来的原始数据是否正确。如果有手段可以确认解密步骤是否正确,这就具备了“可认证性”。
要同时实现“保密性”和“可认证性”,显然可以把加密算法和认证算法两者组合起来,如图 12, 13, 14 的方式(摘自 https://en.wikipedia.org/wiki/Authenticated_encryption)。
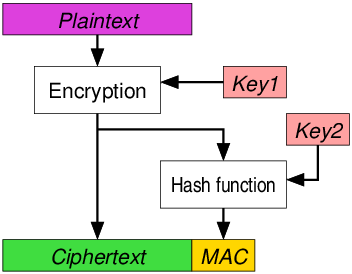
Figure 12: Encrypt-then-MAC
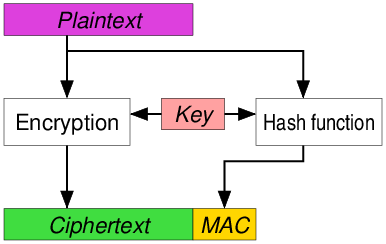
Figure 13: Encrypt-and-MAC
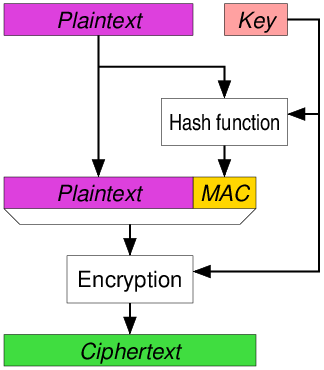
Figure 14: MAC-then-Encrypt
不过,通过组合加密算法和认证算法来实现“保密性”和“可认证性”的方式,被发现有一些安全问题。近年来, 人们提出需要在算法的内部同时实现加密和认证,而不是人为地去组合两种算法,这被称为 AEAD。 例如,下面这些算法都是同时具备“保密性”和“可认证性”的 AEAD 算法:
- AES 的 GCM 模式,如 AES-128-GCM/AES-192-GCM/AES-256-GCM
- ChaCha20-IETF-Poly1305 (rfc8439)
AEAD 算法一般会提供两个方法:
Seal(key, nonce, aad, pt):
Encrypt and authenticate plaintext pt with associated data aad (which contains the data to be authenticated, but not encrypted) using secret key key and nonce nonce, yielding ciphertext and tag ct
Open(key, nonce, aad, ct):
Decrypt ciphertext ct using associated data aad with secret key key and nonce nonce, returning plaintext message pt or the error
6.2. MAC 和数字签名的区别
在安全功能方面,MAC 与数字签名共享一些属性,因为它们都提供“消息完整性”和“消息验证”。与数字签名不同的是,MAC 采用的是对称密钥方案,MAC 不提供不可否认性(通信双方 A 和 B 都知道对称密钥,所以出现分歧时法官无法确定带有消息认证码的消息是由 A 还是 B 产生的)。MAC 的一个优势就是它们的速度比数字签名要快很多,因为它们要么基于分组密码(如 CBC-MAC),要么基于哈希函数(如 HMAC)。
7. Key Size 和安全强度的关系
不同算法的 Key Size 不能直接比较,NIST 给出了不同算法的 Key Size 和安全强度之间的对应关系,如图 15 所示(摘自:https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-57pt1r5.pdf )。
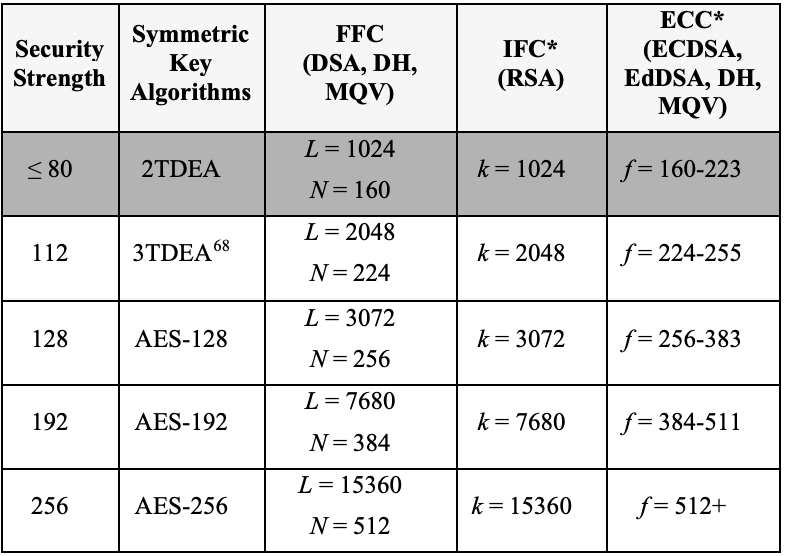
Figure 15: Comparable security strengths of symmetric block cipher and asymmetric-key algorithms
从图中可见,3072 bits 的 RSA Key 的安全强度和 128 bits 的 AES 算法的安全强度相当。
8. 大整数分解问题和离散对数问题
大整数分解问题(Integer factorization)也称为“质因数分解”,是将一个正整数写成几个约数的乘积。例如,给出 45 这个数,它可以分解成 \(3^{2}\times 5\) 。根据算术基本定理(Fundamental theorem of arithmetic),这样的分解结果是独一无二的。 对于大整数,目前并没有有效的算法能找到它的分解方式。 也就是说大整数分解是一个很难的问题,很多密码学算法的安全性是基于这个难题的,比如 RSA 算法、Paillier 算法等。随着量子计算机的来临,大整数分解不再很难,数学家 Peter Shor 在 1994 年提出了量子计算机中可在多项式时间内进行整数分解的算法,该被称为 Shor's algorithm。
离散对数问题(Discrete Logarithm Problem,简称 DLP),是指:给定 \(p\) 阶有限乘法群 \(G\) ,且 \(g\) 是 \(G\) 中的一个生成元,它是公开的参数,假设 \(x, h\) 满足 \(g^x \bmod p = y\) ,我们知道已知 \(x\) 求解 \(y\) 比较容易, 但当 \(p\) 很大时,已知 \(y\) 求解 \(x\) 是很困难的。 DLP 问题也可以表达为加法群的形式:设 \(H\) 是有限加法群, \(P\) 和 \(Q\) 是群 \(H\) 中的两个已知元素,且满足 \(nP=Q\) ,求解 \(n\) 是很困难的。很多密码学算法的安全性基于 DLP 难题,比如 ElGamal、Diffie–Hellman Key Exchange、DSA、ECDSA、EdDSA、Schnorr、BLS Digital Signature 等等。Shor 也指出量子计算机中可在多项式时间内解决离散对数问题。
参考:
Algorithms for quantum computation: Discrete logarithms and factoring, by Peter W. Shor
Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer, by Peter W. Shor
8.1. 其它难题
大整数分解问题和离散对数问题是目前绝大部分密码学算法的基础,随着量子计算机的发展,它们可能被攻破。为了对抗量子计算机攻击,人们提出了格密码(Lattice-based cryptography)。
9. Tips
9.1. RSA 算法、Diffie-Hellman 算法及 DSA 算法在应用上的比较
9.2. 公钥密码体制 VS. 对称密钥密码体制
公钥密码算法一般比对称密钥密码算法慢好几个数量级。 一般公钥密码算法用于密钥(对称密钥算法所使用的 key 称为密钥)管理和数字签名等任务。公钥密码体制并没有取代对称密钥密码体制,它们将长期并存。