DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
Table of Contents
1. DBSCAN 简介
DBSCAN (Density-Based Spatial Clustering of Applications with Noise)是一种著名的基于密度的聚类算法。
1.1. 一些密度描述概念
DBSCAN 算法基于一组“邻域”参数 \((\epsilon, MinPts)\) 来刻画样本分布的紧密程度。给定数据集 \(D= \{ \boldsymbol{x_1}, \boldsymbol{x_1}, \cdots, \boldsymbol{x_m} \}\) ,定义下面这几个概念:
- \(\epsilon - \text{邻域}\) :对 \(\boldsymbol{x_j} \in D\) ,其 \(\epsilon - \text{邻域}\) 包含样本集 \(D\) 中与 \(\boldsymbol{x_j}\) 的距离不大于 \(\epsilon\) 的样本,即 \(N_{\epsilon}(\boldsymbol{x_j}) = \{ \boldsymbol{x_i} \in D \mid \text{dist}(\boldsymbol{x_i}, \boldsymbol{x_j}) \le \epsilon \}\) ;其中 \(\text{dist}(\cdot,\cdot)\) 往往为欧式距离。
- 核心对象(core object):若 \(\boldsymbol{x_j}\) 的 \(\epsilon - \text{邻域}\) 至少包含 \(MinPts\) 个样本,即 \(N_{\epsilon}(\boldsymbol{x_j}) \ge MinPts\) ,则 \(\boldsymbol{x_j}\) 是一个核心对象。
- 密度直达(directly density-reachable):若 \(\boldsymbol{x_j}\) 位于 \(\boldsymbol{x_i}\) 的 \(\epsilon - \text{邻域}\) 中,且 \(\boldsymbol{x_i}\) 是核心对象,则称 \(\boldsymbol{x_j}\) 由 \(\boldsymbol{x_i}\) 密度直达。密度直达关系通常不满足对称性。
- 密度可达(density-reachable):对 \(\boldsymbol{x_i}\) 与 \(\boldsymbol{x_j}\) ,若存在样本序列 \(\boldsymbol{p_1}, \boldsymbol{p_2}, \cdots, \boldsymbol{p_n}\) ,其中 \(\boldsymbol{p_1} = \boldsymbol{x_i}, \boldsymbol{p_n} = \boldsymbol{x_j}\) 且 \(\boldsymbol{p_{i+1}}\) 由 \(\boldsymbol{p_i}\) 密度直达,则称 \(\boldsymbol{x_j}\) 由 \(\boldsymbol{x_i}\) 密度可达。密度可达关系满足传递性,但不满足对称性。
- 密度相连(density-connected):对 \(\boldsymbol{x_i}\) 与 \(\boldsymbol{x_j}\) ,若存在 \(\boldsymbol{x_k}\) 使得 \(\boldsymbol{x_i}\) 与 \(\boldsymbol{x_j}\) 均由 \(\boldsymbol{x_k}\) 密度可达,则称 \(\boldsymbol{x_i}\) 由 \(\boldsymbol{x_j}\) 密度相连。密度相连关系满足对称性。
图 1 给出了上述概念的直观显示。
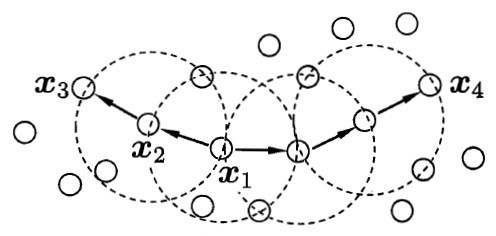
Figure 1: DBSCAN 定义的基本概念(\(MinPts=3\));虚线显示出 \(\epsilon - \text{邻域}\), \(\boldsymbol{x_1}\) 是核心对象, \(\boldsymbol{x_2}\) 由 \(\boldsymbol{x_1}\) 密度直达, \(\boldsymbol{x_3}\) 由 \(\boldsymbol{x_1}\) 密度可达, \(\boldsymbol{x_3}\) 与 \(\boldsymbol{x_4}\) 密度相连
2. DBSCAN 算法
基于前面定义的概念。DBSCAN 将“簇”定义为: 由密度可达关系导出的最大密度相连的样本集合。
一个 DBSCAN 簇里一定有一个或多个核心对象。如果只有一个核心对象,则簇里其他的非核心对象都在这个核心对象的 \(\epsilon - \text{邻域}\) 里;如果有多个核心对象,则簇里的任意一个核心对象的 \(\epsilon - \text{邻域}\) 中一定有一个其他的核心对象,否则这两个核心对象无法密度可达。这些核心对象的 \(\epsilon - \text{邻域}\) 里所有的样本组成了一个 DBSCAN 聚类簇。数据集 \(D\) 中不属于任何簇的样本被认为是噪声或异常样本。
2.1. DBSCAN 算法描述
那么,如何从数据集 \(D\) 中找出满足上面定义的聚类簇(由密度可达关系导出的最大密度相连的样本集合)呢?DBSCAN 使用了如下方法:它任意选择一个没有类别的核心对象作为种子,然后找到所有这个核心对象能够密度可达的样本集合,即为一个聚类簇。接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合,这样就得到另一个聚类簇。一直运行到所有核心对象都有类别为止。
DBSCAN 算法如图 2 所示。

Figure 2: DBSCAN 算法
在第 1-7 行中,算法先根据给定的邻域参数 \((\epsilon, MinPts)\) 找出所有核心对象;然后在第 10-24 行中,以任一核心对象为出发点,找出由其密度可达的样本生成聚类簇,直到所有核心对象均被访问过为止。
2.2. DBSCAN 应用实例
以图 3 所示的西瓜相关数据集为例,假定邻域参数 \((\epsilon, MinPts)\) 设置为 \(\epsilon = 0.11, MinPts = 5\) 。请用 DBSCAN 算法进行聚类处理。
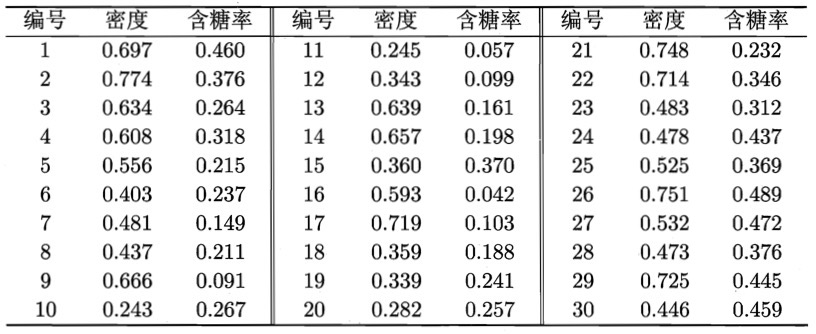
Figure 3: 西瓜数据集
DBSCAN 算法先找出各样本的 \(\epsilon - \text{邻域}\) 并确定核心对象集合:
\[\Omega = \{\boldsymbol{x_3}, \boldsymbol{x_5}, \boldsymbol{x_6}, \boldsymbol{x_8}, \boldsymbol{x_9}, \boldsymbol{x_{13}}, \boldsymbol{x_{14}}, \boldsymbol{x_{18}}, \boldsymbol{x_{19}}, \boldsymbol{x_{24}}, \boldsymbol{x_{25}}, \boldsymbol{x_{28}}, \boldsymbol{x_{29}} \}\]
然后,从 \(\Omega\) 中随机选取一个核心对象作为种子,找出由它密度可达的所有样本,这就构成了第一个聚类簇。不失一般性,假定核心对象 \(\boldsymbol{x_8}\) 被选中作为种子,则 DBSCAN 算法生成的第一个聚类簇为:
\[C_1 = \{ \boldsymbol{x_6}, \boldsymbol{x_7}, \boldsymbol{x_8}, \boldsymbol{x_{10}}, \boldsymbol{x_{12}}, \boldsymbol{x_{18}}, \boldsymbol{x_{19}}, \boldsymbol{x_{20}}, \boldsymbol{x_{23}}\}\]
然后,DBSCAN 算法将 \(C_1\) 中包含的核心对象从 \(\Omega\) 中去除:
\[\Omega = \Omega \setminus C_1 = \{\boldsymbol{x_3}, \boldsymbol{x_5}, \boldsymbol{x_9}, \boldsymbol{x_{13}}, \boldsymbol{x_{14}}, \boldsymbol{x_{24}}, \boldsymbol{x_{25}}, \boldsymbol{x_{28}}, \boldsymbol{x_{29}} \}\]
再从更新后的集合 \(\Omega\) 中随机选取一个核心对象作为种子来生成下一个聚类簇。上述过程不断重复,直至 \(\Omega\) 为空。 \(C_1\) 之后生成的聚类簇为
\[\begin{aligned} C_2 & = \{\boldsymbol{x_3}, \boldsymbol{x_4}, \boldsymbol{x_5}, \boldsymbol{x_9}, \boldsymbol{x_{13}}, \boldsymbol{x_{14}}, \boldsymbol{x_{16}}, \boldsymbol{x_{17}}, \boldsymbol{x_{21}} \} \\
C_3 & = \{\boldsymbol{x_1}, \boldsymbol{x_2}, \boldsymbol{x_{22}}, \boldsymbol{x_{26}}, \boldsymbol{x_{29}} \} \\
C_4 & = \{\boldsymbol{x_{24}}, \boldsymbol{x_{25}}, \boldsymbol{x_{27}}, \boldsymbol{x_{28}}, \boldsymbol{x_{30}} \} \\
\end{aligned}\]
图 4 显示出 DBSCAN 算法先后生成聚类簇的情况。
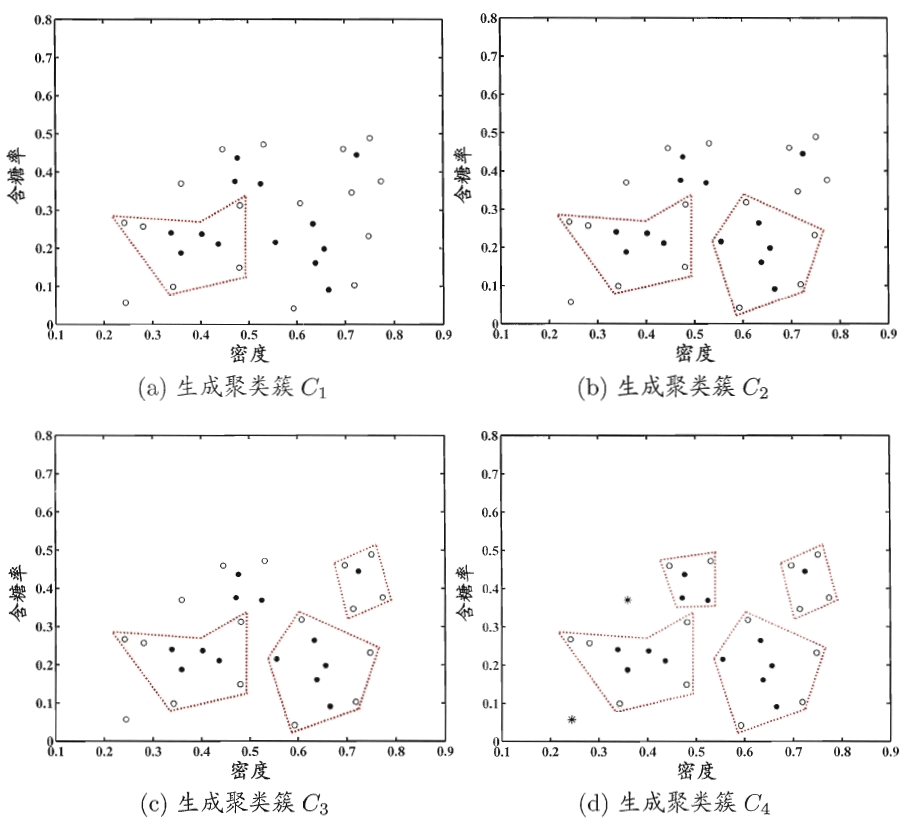
Figure 4: DBSCAN 算法(\(\epsilon = 0.11, MinPts = 5\))生成聚类簇的先后情况。核心对象、非核心对象、噪声样本分别用“●”,“○”和“*”表示,红色虚线显示出簇划分
3. DBSCAN 算法的优缺点
DBSCAN 的优点:
1、相比 K-means 算法和 GMM 算法,DBSCAN 算法不需要用户提供聚类数量。
2、DBSCAN 能分辨噪音点,对数据集中的异常点不敏感。
DBSCAN 的缺点:
1、如果样本集的点有不同的密度,且该差异很大,这时 DBSCAN 将不能提供一个好的聚类结果,因为不能选择一个适用于所有聚类的 \((\epsilon, MinPts)\) 参数组合。注:OPTICS(Ordering Points To Identify the Clustering Structure)是 DBSCAN 算法的变种,它能较好地处理样本密度相差很大时的情况。
2、它不是完全决定性的算法。某些样本可能到两个核心对象的距离都小于 \(\epsilon\) ,但这两个核心对象由于不是密度直达,又不属于同一个聚类簇,这时如何决定这个样本的类别呢?一般来说,DBSCAN 采用先来后到,先进行聚类的类别簇会标记这个样本为它的类别。注:可以把交界点视为噪音,这样就有完全决定性的结果。
4. 参考
本文主要摘自:《机器学习,周志华,2016》,9.5,密度聚类