Digital Image Processing Basics
Table of Contents
- 1. 基本概念
- 2. 灰度变换和空间滤波(Intensity Transformation and Spatial Filtering)
- 3. 形态学图像处理(Morphological Image Processing)
- 4. 图像分割(Image Segmentation)
- 4.1. 孤立点、线、边缘的检测
- 4.2. 阈值处理(Thresholding)
- 4.3. 使用形态学分水岭(Watershed)的分割
1. 基本概念
数字图像处理(Digital Image Processing)是通过计算机对图像进行去除噪声、增强、复原、分割、提取特征等处理的方法和技术。
本文主要参考:
《数字图像处理(第三版),冈萨雷斯》
Image Processing, Analysis, and Machine Vision, 3rd Edition, 2007
1.1. 什么是数字图像、像素
一幅图像可定义为一个二维函数 \(f(x,y)\) ,其中 \(x\) 和 \(y\) 是空间(平面)坐标,而在任何一对空间坐标 \((x,y)\) 处的幅值 \(f\) 称为图像在该点处的 强度 或 灰度 。当 \(x,y\) 和灰度值 \(f\) 是有限的离散数值时,该图像就称为 数字图像 。
为表达清楚和方便起见,我们对离散坐标使用整数值: \(x=0,1,2,\cdots,M-1\) 和 \(y=0,1,2,\cdots,N-1\) ,数字图像 \(f\) 可表示为如下矩阵:
\[f(x,y) = \left( \begin{array}{cccc}
f(0,0) & f(0,1) & \cdots & f(0,N-1) \\
f(1,0) & f(1,1) & \cdots & f(1,N-1) \\
\vdots & \vdots & \ddots & \vdots \\
f(M-1,0) & f(M-1,1) & \cdots & f(M-1,N-1)
\end{array} \right)\]
上式右边是一个实数矩阵,该矩阵中的每个元素称为 像素 。
习惯上,数字图像的原点位于左上角,正 \(x\) 轴向下延伸,正 \(y\) 轴向右延伸。这种表示基于这样的事实:许多图像显示(如电视显示器)扫描都是从左上角开始的,然后一次向下移动一行。这还基于一个事实就是矩阵的第一个元素按惯例应在阵列的左上角。
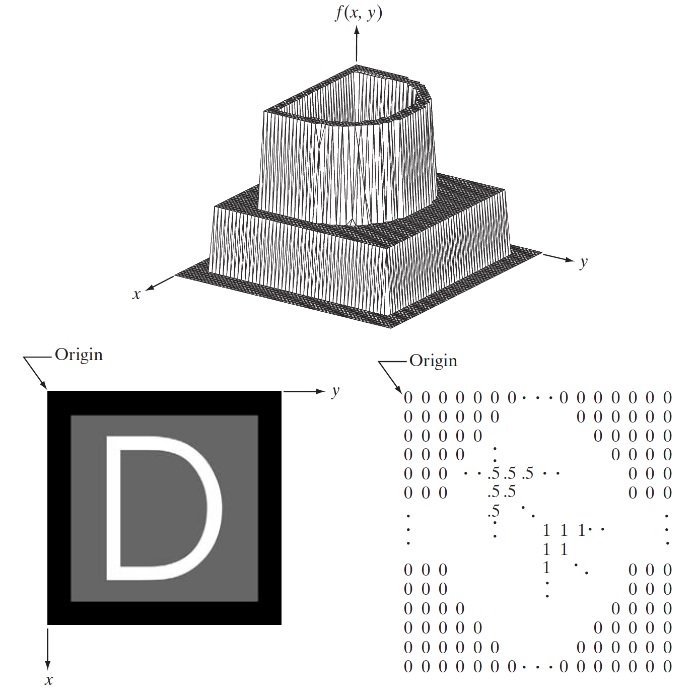
Figure 1: 图像的表示(矩阵中 0/0.5/1 分别表示黑色/灰色/白色)
根据每个像素所代表的信息不同,可分为二值图像、灰度图像,RGB 图像等等。
1.2. 像素间的一些基本关系
1.2.1. 距离
像素 \((x_1,y_1)\) 和 \((x_2,y_2)\) 的距离有不同的度量方法,如:
一,欧氏距离(Euclidean Distance),可记为 \(D_E = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\)
二,城区距离(City-Block Distance),两点间只允许横向和纵向的移动,可记为 \(D_4 = \vert x_1 - x_2 \vert + \vert y_1 - y_2 \vert\)
三,棋盘距离(Chessboard Distance),两点间还允许对角线方向的移动(国际象棋里国王从一处移动到另一处的步数),可记为 \(D_8 = \max\{\vert x_1 - x_2 \vert, \vert y_1 - y_2 \vert\}\)
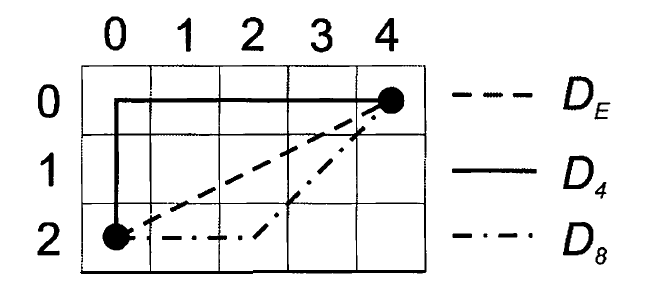
Figure 2: 欧氏距离、城区距离、棋盘距离的实例
1.2.2. 邻接性
距离为 1 的两点是邻接的(采用城区距离时称为 4-邻接,采用棋盘距离时称为 8-邻接)。
1.3. 空间分辩率
直观上看,空间分辩率是图像中可辨别的最小细节的度量。空间分辩率有很多方法来说明,其中“每英寸点数(Dots per inch, dpi)”是最常用的度量。一般地,报纸用 75dpi 的分辩率来印刷,杂志是 133dpi。
1.4. 图像插值(Image Interpolation)
插值(Interpolation)是在诸如放大、收缩、旋转和几何校正等任务中广泛使用的基本工具。这里将主要介绍插值在调整图像大小(缩小或放大)时的应用。
当缩小图像时,目标图像的像素会映射为原图像中的多个像素,这时需要插值;当放大图像时,目标图像上的像素可能无法在原图像中找到精确对应的像素,这时也需要进行插值。
插值是用已知数据来估计未知位置的数值的处理过程。 下面介绍几种常用的插值算法。
1.4.1. 最近邻插值(Nearest neighbor interpolation)
从一个简单的例子开始讨论。假设一幅大小为 \(500 \times 500\) 像素的图像要放大 1.5 倍到 \(750 \times 750\) 像素。一种简单的放大方法是创建一个 \(750 \times 750\) 网格,它与原始图像有相同的间隔,然后将其收缩,使它准确地与原图像匹配。显然,收缩后的 \(750 \times 750\) 网格的像素间隔要小于原图像的像素间隔。为了对覆盖的每一个点赋以灰度值,我们在原图像中寻找最接近的像素,并把该像素的灰度赋给 \(750 \times 750\) 网格中的新像素。当完成对网格中覆盖的所有点的灰度赋值后,就把图像扩展到原来规定的大小,得到放大后的图像。
上面描述的方法称为最近邻插值(Nearest neighbor interpolation),因为这种方法把原图像中最近邻的灰度赋给了每个新位置。
1.4.2. 双线性插值(Bilinear interpolation)
前面讨论的最近邻插值算法比较简单,但其效果不是很好,如可能导致直边缘严重失真。双线性插值是一种更实用的方法。
在介绍双线性插值前,先了解一下线性插值(Linear interpolation)。线性插值非常简单,使用连接两个已知量的直线来确定在这两个已知量之间的一个未知量的值的方法。线性插值的一个实例如图 3 所示。
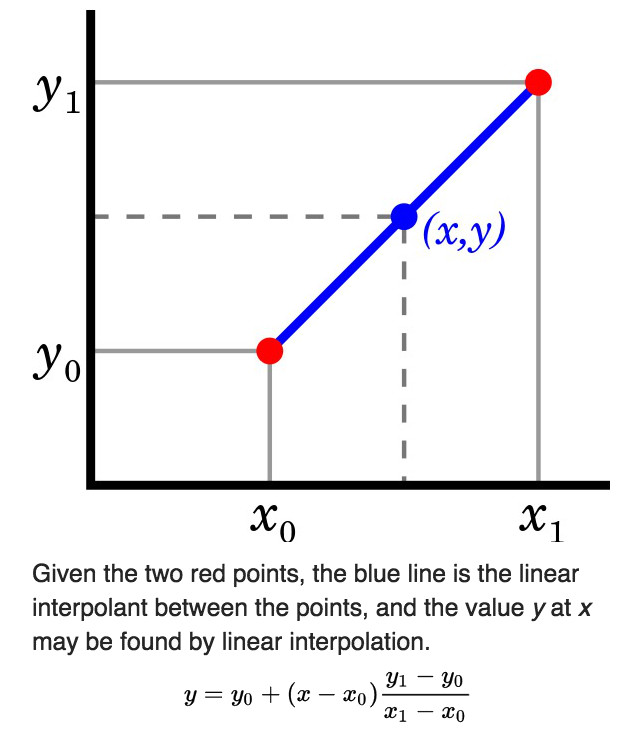
Figure 3: 线性插值实例
双线性插值(Bilinear interpolation)是线性插值算法在二维空间的扩展。 双线性插值利用 4 个最近邻点的灰度值来估计点的灰度值,如图 4 中,已知 4 个最近邻点的灰度值分别为 91,210,162,95,需要估计点 \((20.2, 14.5)\) 处的灰度值。
双线性插值的具体步骤如下:
第 1 步,用线性插值法求得点 \((20, 14,5)\) 和点 \((21, 14.5)\) 的估计灰度值,即:
\[\begin{aligned} I_{(20, 14.5)} = \frac{15-14.5}{15-14} \cdot 91 + \frac{14.5 - 14}{15 -14} \cdot 210 = 150.5 \\
I_{(21, 14.5)} = \frac{15-14.5}{15-14} \cdot 162 + \frac{14.5-14}{15-14} \cdot 95 = 128.5 \end{aligned}\]
第 2 步,再次用线性插值法求得得 \((20.2, 14.5)\) 的估计灰度值,即:
\[I_{(20.2, 14.5)} = \frac{21-20.2}{21-20} \cdot 150.5 + \frac{20.2-20}{21-20} \cdot 128.5 = 146.1\]
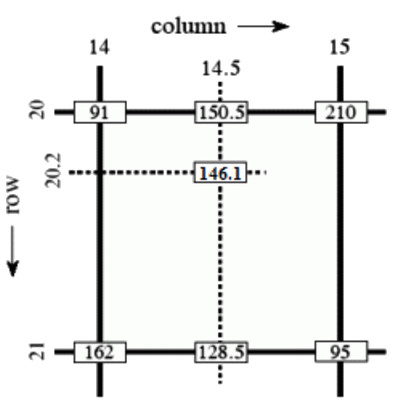
Figure 4: 双线性插值实例
1.4.3. 双三次插值(Bicubic interpolation)
双三次插值(Bicubic interpolation)通过 16 个最近邻点来估计点的灰度值,它比双线性插值(通过 4 个最近邻点来估计点的灰度值)得到的效果更好。双三次插值是商业图像编辑程序(比如 Adobe Photoshop 和 Corel Photopaint)的标准插值方法。
这里不详细介绍双三次插值的具体算法。
2. 灰度变换和空间滤波(Intensity Transformation and Spatial Filtering)
这里将介绍图像空间域(空间域就是简单的包含图像像素的平面)处理技术,它直接以图像的像素操作为基础。这是相对于变换域中的图像处理而言的,变换域中的图像处理先把图像变换到变换域,在变换域中进行处理,然后通过反变换把处理结果返回到空间域。 某些图像处理任务在空间域中执行更容易,而另一些任务则可能更适合在变换域中处理。通常,空间域处理技术在计算上更有效,且在执行上需要较少的处理资源。
这里的大部分例子都是“图像增强”,增强处理是对图像进行加工,使其结果对于特定的应用比原始图像更合适的一种处理。
2.1. 基本的灰度变换函数
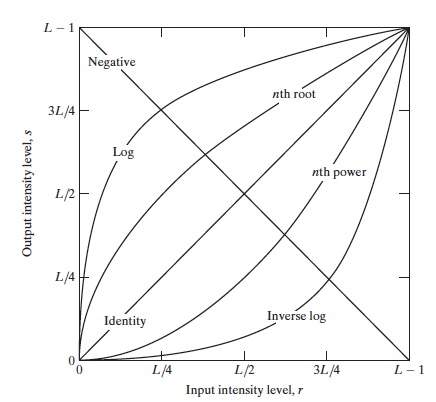
Figure 5: 基本的灰度变换函数
2.1.1. 反转变换
对于灰度级范围为 \([0, L-1]\) 的图像,其反转图像由下式给出:
\[s = L-1-r\]
其中, \(r\) 是输入灰度级, \(s\) 是输出灰度级。
这种类型的处理特别适用于增强嵌入在一幅图像的暗区域中的白色或灰色细节,特别是当黑色面积在尺寸上占主导地位时。 比如,图 6 左边图像是乳房 X 射线照片,显然分析乳房组织时使用反转图像会容易得多。
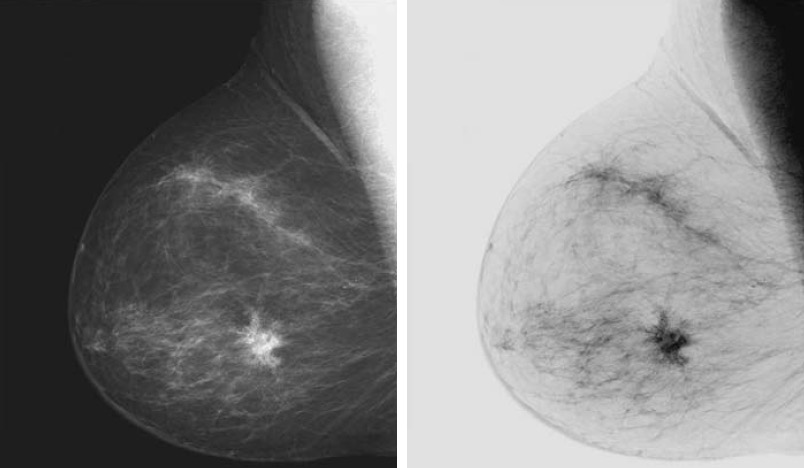
Figure 6: 乳房 X 线照片及其反转图像(其反转图像更容易分析)
2.1.2. 对数变换
对数变换的通用形式为:
\[s = c \log(1+r)\]
其中, \(c \ge 0\) 是一个常数。r是输入灰度级,s是输出灰度级。
从图 5 中曲线的形状可知,对数变换会将输入中“范围较窄的低灰度值”映射为输出中“范围较宽的灰度值”,这样较暗的区域对比度将得到提升,从而增强图像较暗区域的细节。反对数变换的作用与此相反(它能增强图像较亮区域的细节)。不过,后文介绍的“幂律(伽马)变换”也能实现灰度级的扩展/压缩,而且“幂律(伽马)变换”更为通用。
对数变换的主要应用场景在于压缩像素值变化较大的图像的动态范围。 像素值有较大动态范围的一个典型应用是傅里叶频谱,频谱的动态范围可从 0 到 \(10^6\) ,甚至更高。图像的显示系统通常无法真实地再现如此大范围的灰度值。当作线性地缩放显示时,最亮的像素将支配该显示,频谱中的低值(恰恰是重要的)将损失掉。因而,最终结果是许多重要的灰度细节在傅里叶频谱的显示中丢失(无法察觉)了。 通过对数变换可以压缩像素值变化较大的图像的动态范围,通过这种非线性地变换,图像的一些细节将展示地更清楚。 图 7 中左边是傅里叶频谱,右边是应用对数变换(c=1)后的结果。

Figure 7: 傅里叶频谱(左图),及应用对数变换(c=1)后的结果(右图)
2.1.3. 幂律(伽马)变换
幂律(伽马)变换的基本形式为:
\[s = c r^{\gamma}\]
其中, \(c\) 和 \(\gamma\) 为正常数。r是输入灰度级,s是输出灰度级。有时考虑到偏移量(即输入为 0 时的一个可度量输出),上式也写为 \(s=c(r+\varepsilon)^{\gamma}\) ,不过,偏移量一般是显示标定(display calibration)问题。
不同伽马 \(\gamma\) 值(假设所有情形 c=1)的 \(s = c r^{\gamma}\) 曲线如图 8 所示。
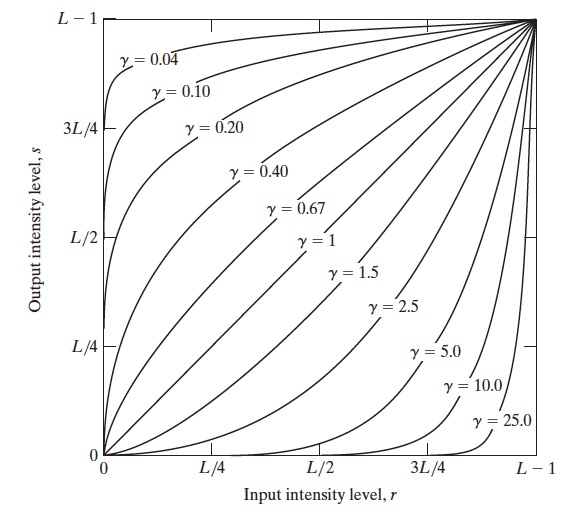
Figure 8: 不同伽马 \(\gamma\) 值(假设所有情形 c=1)的 \(s = c r^{\gamma}\) 曲线
从图 8 中分析易知, 当 \(\gamma\) 值小于 1 时,伽马变换把“范围较窄的低灰度值”转换为“范围较宽的灰度值”,这样可以增强图像较暗区域的对比度。当 \(\gamma\) 值大于 1 时,伽马变换把“范围较窄的高灰度值”转换为“范围较宽的灰度值”,这样可以增强图像较亮区域的对比度。
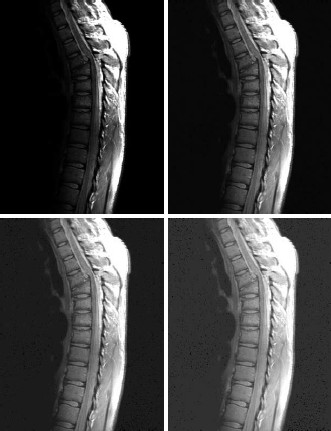
Figure 9: 伽马变换实例(增加暗部对比度):左上角为原图,其它 3 个是伽马变换后的图像(c均为 1, \(\gamma\) 值分别为 0.6,0.4,0.3)

Figure 10: 伽马变换实例(增加亮部对比度):左上角为原图,其它 3 个是伽马变换后的图像(c均为 1, \(\gamma\) 值分别为 3.0,4.0,5.0)
2.2. 直方图处理(Histogram Processing)
首先,介绍一下直方图的概念。 灰度级范围为 \([0, L-1]\) 的数字图像的直方图是离散函数 \(h(r_k) = n_k\) ,其中 \(r_k\) 是第 \(k\) 级灰度值, \(n_k\) 是图像中灰度为 \(r_k\) 的像素的个数。
如果把它归一化后,则直方图可表示为:
\[p(r_k) = \frac{n_k}{MN}\]
其中, \(M\) 和 \(N\) 是图像的行和列的维数(即 \(MN\) 为像素总数)。
图像及其直方图的实例如图 11 所示。
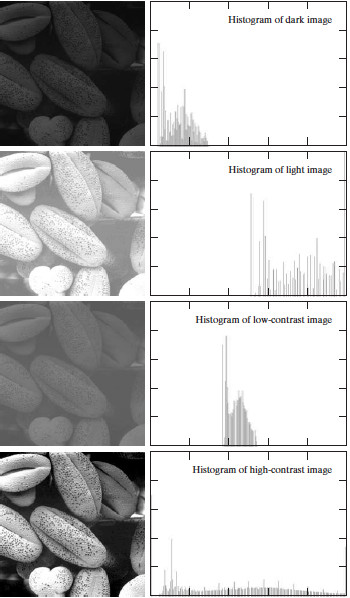
Figure 11: 图像及其直方图(横轴为灰度值,竖轴为对应像素的个数)
2.2.1. 直方图均衡(Histogram Equalization)
图像的直方图,表示了其灰度分布的特性。 直方图均衡(Histogram Equalization)的目的是使图像的灰度分布平均化(即各个灰度值的像素的个数差不多相等)。也就是说,直方图均衡就是把给定图像的直方图分布改变成“均匀”分布直方图分布。
直方图均衡对于处理背景和前景太亮或者太暗的图像非常有用,这种方法尤其是可以显示 X 射线图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。图 12 是直方图均衡的一个实例图。
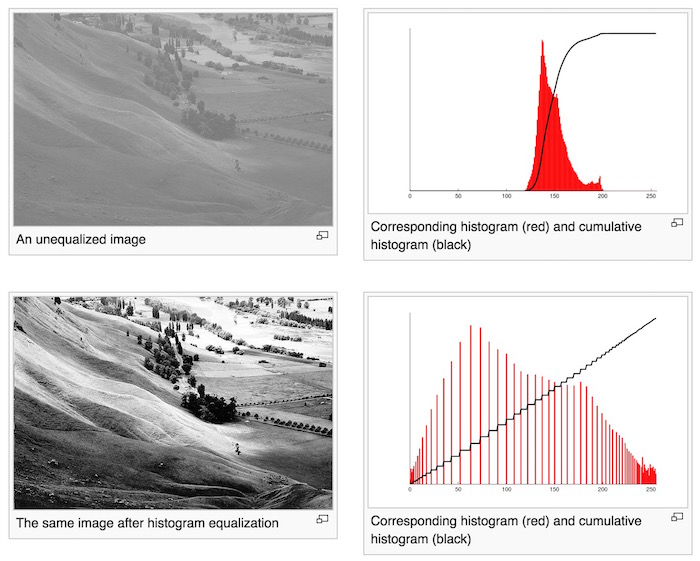
Figure 12: 直方图均衡实例(处理后图像的直方图累积分布函数基本上是一条“直线”,实例摘自Wikipedia)
图 13 是直方图均衡的另一个例子。
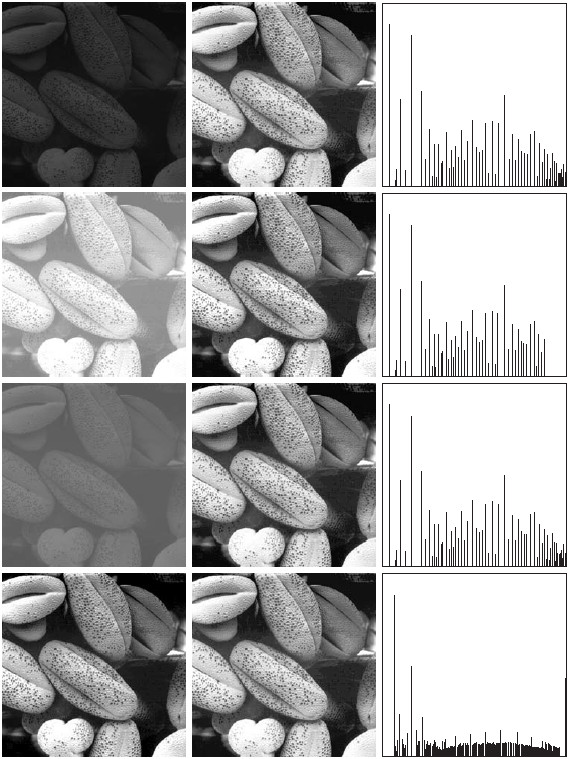
Figure 13: 直方图均衡实例(左边是原图,中间是均衡后的图像,右边是中间图像的直方图)
2.2.1.1. 直方图均衡算法
直方图均衡化的目的是把灰度值尽量平均化(每个灰度值的像素数量差不多)。当然,它需要满足这个的基本条件: 灰度无论怎么变换,需要保证原来的大小关系不变,较亮的区域,变换后依旧是较亮的,较暗依旧暗,只是对比度增大,明暗关系绝对不能颠倒!
用变量 \(r\) 表示待处理图像的灰度。通常,我们假设 r 的取值区间为 \([0, L-1]\) ,且 \(r=0\) 表示黑色, \(r=L-1\) 表示白色。
通过推导(这里不介绍推导过程,可参考《数字图像处理(第三版)冈萨雷斯》第 3.3 节),我们可知进行下面的灰度变换后,得到的图像其灰度基本上是平均化的,而且满足前面提到的基本条件(明暗关系绝对不能颠倒)。
其中, \(MN\) 是图像中像素的总数, \(n_j\) 是灰度为 \(r_j\) 的像素的个数, \(L\) 是图像中可能的灰度级的数量(对 8 比特图像来说, \(L\) 为 256)。上式就是“直方图均衡”的转换公式。注意:上面公式计算的转换后的灰度值往往为小数,这时可以用“四舍五入”法得到最接近的整数作为“直方图均衡”的最终灰度值。
2.2.1.2. 直方图均衡算法实例
下面通过一个简单的例子来说明直方图均衡的工作原理。假设一幅大小为 \(8 \times 8\) 像素(即 \(MN\) 为 64)的 8 比特图像(即 L=256)如图 14 所示。
Figure 14: 直方图均衡实例,原图的灰度矩阵
要实现“直方图均衡”处理,实现前面介绍的公式 \(s_k = T(r_k) = (L-1) \sum_{j=0}^{k}\frac{n_j}{MN}, \; k = 0,1,2,\cdots,L-1\) 即可。具体过程如下所述。
第一步:计算每一个灰度出现次数。
第二步:计算灰度的累积概率,即式中的 \(\sum_{j=0}^{k}\frac{n_j}{MN}\)
第二步:由上一步计算的累积概率乘以 255(即 L-1),并作“四舍五入”得到最终灰度值,即为均衡化后的灰度值。
| 原始灰度值 | 出现次数 | 概率 | 累积概率 | 灰度值 | 取整后即为均衡化后的灰度值 |
|---|---|---|---|---|---|
| 52 | 1 | 1/64 | 1/64 | 255*(1/64)=3.98 | 4 |
| 55 | 3 | 3/64 | 4/64 | 255*(4/64)=15.93 | 16 |
| 58 | 2 | 2/64 | 6/64 | 255*(6/64)=23.90 | 24 |
| 59 | 3 | 3/64 | 9/64 | 255*(9/64)=35.85 | 36 |
| 60 | 1 | 1/64 | 10/64 | 255*(10/64)=39.84 | 40 |
| 61 | 4 | 4/64 | 14/64 | 255*(14/64)=55.78 | 56 |
| 62 | 1 | 1/64 | 15/64 | 255*(15/64)=59.76 | 60 |
| 63 | 2 | 2/64 | 17/64 | 255*(17/64)=67.73 | 68 |
| 64 | 2 | 2/64 | 19/64 | 255*(19/64)=75.70 | 76 |
| 65 | 3 | 3/64 | 22/64 | 255*(22/64)=87.65 | 88 |
| 66 | 2 | 2/64 | 24/64 | 255*(24/64)=95.62 | 96 |
| 67 | 1 | 1/64 | 25/64 | 255*(25/64)=99.60 | 100 |
| 68 | 5 | 5/64 | 30/64 | 255*(30/64)=119.53 | 120 |
| 69 | 3 | 3/64 | 33/64 | 255*(33/64)=131.48 | 131 |
| 70 | 4 | 4/64 | 37/64 | 255*(37/64)=147.42 | 147 |
| 71 | 2 | 2/64 | 39/64 | 255*(39/64)=155.39 | 155 |
| 72 | 1 | 1/64 | 40/64 | 255*(40/64)=159.37 | 159 |
| 73 | 2 | 2/64 | 42/64 | 255*(42/64)=167.34 | 167 |
| 75 | 1 | 1/64 | 43/64 | 255*(43/64)=171.32 | 171 |
| 76 | 1 | 1/64 | 44/64 | 255*(44/64)=175.31 | 175 |
| 77 | 1 | 1/64 | 45/64 | 255*(45/64)=179.29 | 179 |
| 78 | 1 | 1/64 | 46/64 | 255*(46/64)=183.28 | 183 |
| 79 | 2 | 2/64 | 48/64 | 255*(48/64)=191.25 | 191 |
| 83 | 1 | 1/64 | 49/64 | 255*(49/64)=195.23 | 195 |
| 85 | 2 | 2/64 | 51/64 | 255*(51/64)=203.20 | 203 |
| 87 | 1 | 1/64 | 52/64 | 255*(52/64)=207.18 | 207 |
| 88 | 1 | 1/64 | 53/64 | 255*(53/64)=211.17 | 211 |
| 90 | 1 | 1/64 | 54/64 | 255*(54/64)=215.15 | 215 |
| 94 | 1 | 1/64 | 55/64 | 255*(55/64)=219.14 | 219 |
| 104 | 2 | 2/64 | 57/64 | 255*(57/64)=227.10 | 227 |
| 106 | 1 | 1/64 | 58/64 | 255*(58/64)=231.09 | 231 |
| 109 | 1 | 1/64 | 59/64 | 255*(59/64)=235.07 | 235 |
| 113 | 1 | 1/64 | 60/64 | 255*(60/64)=239.06 | 239 |
| 122 | 1 | 1/64 | 61/64 | 255*(61/64)=243.04 | 243 |
| 126 | 1 | 1/64 | 62/64 | 255*(62/64)=247.03 | 247 |
| 144 | 1 | 1/64 | 63/64 | 255*(63/64)=251.01 | 251 |
| 154 | 1 | 1/64 | 64/64 | 255*(64/64)=255 | 255 |
最后,把原始图像中的每个灰度值替换为对应的“均衡化后的灰度值”即可完成直方图均衡处理。
说明:这个例子的原始图像摘自 Wikipedia ,但 Wikipedia 中的“直方图均衡”公式和本文使用公式(摘自《数字图像处理(第三版),冈萨雷斯》)有点小区别,它们都是正确的,都能使图像直方图基本平均。
2.2.1.3. 直方图均衡优缺点
直方图均衡优点:无需参数,仅靠输入图像就能自动实现对比度增强。
直方图均衡缺点:
1)变换后图像的灰度级可能减少,某些细节可能丢失;
2)它对处理的数据不加选择,它可能会增加背景噪声的对比度并且降低有用信号的对比度;
3)某些图像,如直方图有高峰,经处理后对比度不自然的过分地增强了。
2.2.2. Histogram Matching (Specification)
直方均衡可以得到一个灰度直方图分布平均的图像,直方图均衡的结果是唯一的。这是优点,也可以说是缺点。优点在于,无需多余的参数,就可以实现对比度的增强。缺点在于,没有参数,对于结果无法调整。
图 15 是一个“直方图均衡”处理后效果不是很好的例子。
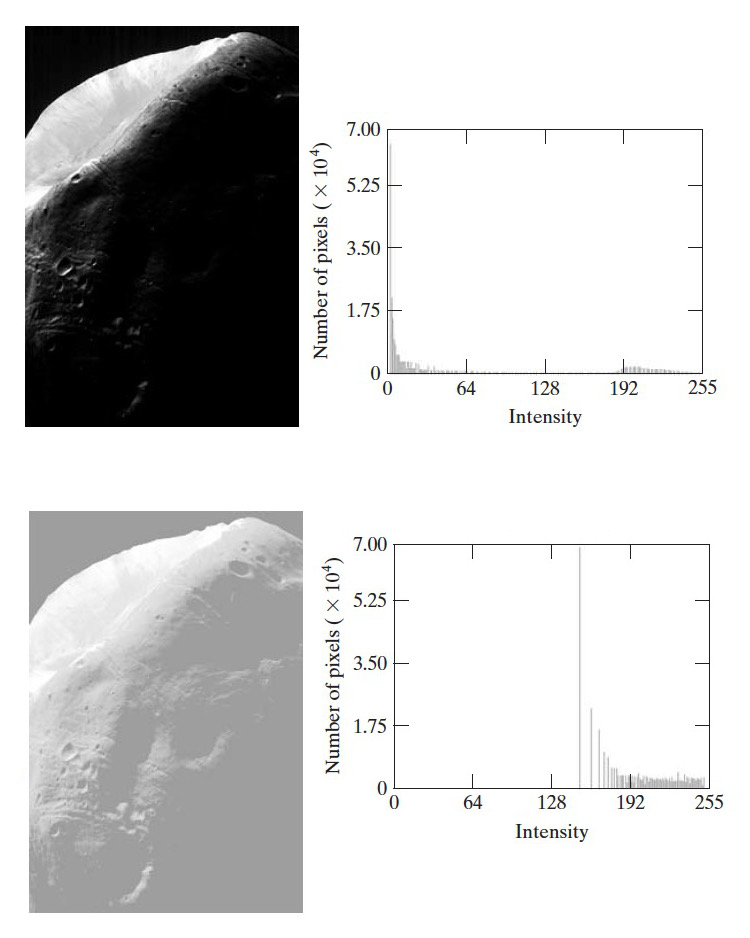
Figure 15: 一幅很黑的图像(上图)在“直方图均衡”处理后(下图)变得灰蒙蒙
在上面例子中,我们发现原图中的一个细节已经显示出来了,只是整个图像偏白而已,如果能够把处理后的图像的直方图向左移一些,则效果可能会好很多(不会这么偏白)。但“直方图均衡”无法调整,为了解决这个不足,就有了直方图匹配(规定化)。
产生处理后的图像具有特殊直方图的方法称为直方图匹配(或称为直方图规定化)。
这里不详细介绍“直方图匹配”过程。不过,很多时候“直方图匹配”都是试凑的过程。
2.2.3. 直方图统计(灰度均值,灰度方差)
令 \(r\) 表示在区间 \([0, L-1]\) 上代表灰度值的一个离散随机变量,并令 \(p(r_i)\) 表示对应于 \(r_i\) 值的归一化直方图分量。图像的灰度均值(即平均灰度)为:
\[m = \sum_{i=0}^{L-1} r_i p(r_i)\]
灰度方差为:
\[\sigma^2 = \sum_{i=0}^{L-1} (r_i - m)^2 p(r_i)\]
灰度方差是图像对比度的度量。
对于均值和方差,通常直接从取样值来估计它们,而不必计算直方图。这些估计值称为“取样均值”和“取样方差”。它们可以根据基本的统计学知识由下面的形式给出:
\[m = \frac{1}{MN} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x,y)\]
和
\[\sigma^2 = \frac{1}{MN} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} [ f(x,y) - m ]^2\]
2.3. 空间滤波基础
空间域处理可由下式表示:
\[g(x,y) = T[f(x,y)]\]
其中, \(f(x,y)\) 是输入图像, \(g(x,y)\) 是处理后的图像, \(T\) 是在点 \((x,y)\) 的邻域上定义的关于 \(f\) 的一种算子。设点 \((x,y)\) 是图像中的一个任意位置,点 \((x,y)\) 的邻域是包含该点的小区域。典型地,邻域是中心在 \((x,y)\) 的矩形,其尺寸比图像小得多。
空间域处理的基本过程为:邻域原点从一个像素向另一个像素移动,对邻域中的像素应用算子 \(T\) ,并在该位置产生输出。 这样,对于任意指定的位置 \((x,y)\) ,输出图像 \(g\) 在这些坐标处的值就等于对 \(f\) 中以 \((x,y)\) 为原点的邻域应用算子 \(T\) 的结果。
例如:假设邻域的大小为 \(3 \times 3\) 的正方形,算子 \(T\) 定义为“计算该邻域的平均灰度”。考虑图像中的任意位置,如 \((100, 150)\) 。假设该邻域的原点位于其中心处,则在该位置的结果 \(g(100, 150)\) 是计算 \(f(100, 150)\) 和它的 8 个邻点的和,再除以 9(即由邻域包围的像素灰度的平均值)。然后,邻域的原点移动到下一个位置,并重复前面的过程,产生下一个输出图像 \(g\) 的值。 典型地,该处理从输入图像的左上角开始,以水平扫描的方式逐像素地处理,每次一行。当该邻域的原点位于图像的边界上时,部分邻域将位于图像的外部。此时,不是在用 \(T\) 做指定的计算时忽略外侧邻点,就是用 0 或其他指定的灰度值填充图像的边缘,被填充边界的厚度取决于邻域的大小。
上面描述的过程被称为“空间滤波”,其中,邻域和预定义的操作一起称为空间滤波器(spatial filter),也称为空间掩模(spatial mask)、核(kernel)、模板(template)或窗口(window)。
2.3.1. 空间滤波机理
前面提到过,空间滤波器由下面两部分组成:
(1)一个邻域(典型地是一个较小的矩形);
(2)对该邻域包围的图像像素执行的预定义操作。
如果在图像像素上执行的预定义操作是线性操作,则该滤波器称为“线性空间滤波器”。否则,滤波器就称为“非线性空间滤波器”。
2.3.1.1. 线性空间滤波器(其操作可概括为“乘积求和”)
图 16 说明了使用 \(3 \times 3\) 邻域的线性空间滤波器的机理。在图像中的任意一点 \((x,y)\) ,滤波器的响应 \(g(x,y)\) 是滤波器系数与由该滤波器包围的图像像素的乘积之和:
\[g(x,y) = w(-1,-1)f(x-1,y-1) + w(-1,0)f(x-1,y) + \cdots + w(0,0)f(x,y) + \cdots + w(1,1) f(x+1,y+1)\]
很明显,滤波器的中心系数 \(w(0,0)\) 对准位置 \((x,y)\) 的像素。对于大小为 \(m \times n\) 的模板,为简化索引,我们仅关注奇数尺寸的滤波器,假设 \(m=2a+1, n=2b+1\) ,其中 \(a,b\) 为正整数。
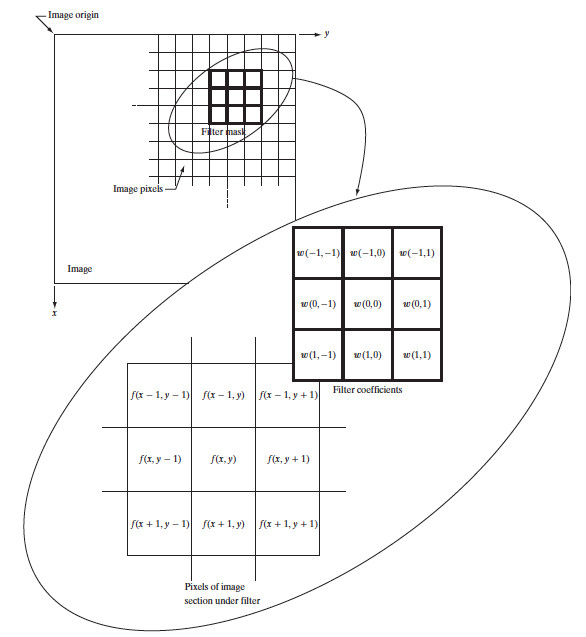
Figure 16: 使用大小为 \(3 \times 3\) 的滤波器模板的线性空间滤波器
更一般地,使用大小为 \(m \times n\) (设 \(m,n\) 都为奇数,且 \(m=2a+1, n=2b+1\) )的滤波器对大小为 \(M \times N\) 的图像进行“线性空间滤波”,可由下式表示:
\[g(x,y) = \sum_{s=-a}^{a} \sum_{t=-b}^{b} w(s,t) f(x+s, y+t)\]
其中, \(x\) 和 \(y\) 是可变的,以便 \(w\) 中的每个像素可访问 \(f\) 中的每个像素。
说明: 一般地,为了简化线性空间滤波器的表达形式,我们设定滤波器模板的中心坐标为 \((0,0)\) ,这和图像的坐标选择是不同的,图像一般设定左上角坐标为 \((0,0)\) 。
2.3.2. 线性空间滤波的相关与卷积(Spatial Correlation and Convolution)
在执行线性空间滤波时,必须清楚地理解两个相近的概念:一个是相关(Correlation),另一个是卷积(Convolution)。如上面描述的那样, 相关是滤波器模板移过图像并计算每个位置乘积之和的处理(前文已经介绍过)。卷积的机理相似,但滤波器首先要旋转 \(180^{\circ}\) 。 下面将详细介绍“相关”和“卷积”处理过程。
一个大小为 \(m \times n\) 的滤波器 \(w(x,y)\) 与一幅图像 \(f(x,y)\) 做“相关”操作,可表示为 \(w(x,y) \mathbin{☆} f(x,y)\) ,在上一节中已经给出过其公式,为方便起见重写如下:
这一等式对所有位移变量 \(x\) 和 \(y\) 求值,以便 \(w\) 的所有元素访问 \(f\) 的每一个像素,其中假设 \(f\) 已被适当地填充(比如在边缘进行零填充,后文将介绍)。式中 \(a=(m-1)/2, b = (n-1)/2\) ,且假设 \(m,n\) 是奇整数。
类似地, \(w(x,y)\) 和 \(f(x,y)\) 的“卷积”表示为 \(w(x,y) \star f(x,y)\) ,它的定义由下式给出:
其中,等式右侧的减号表示翻转 \(f\) (即旋转 \(180^{\circ}\) )。为简化符号表示,我们遵循惯例,翻转和移位 \(w\) 而不是 \(f\) ,得到的结果是一样的(因为“卷积”满足交换律)。
显然, 如果滤波器矩阵是对称矩阵,则“卷积”操作和“相关”操作将得到相同的结果。
2.3.2.1. “相关”和“卷积”实例
下面用例子来说明“相关”和“卷积”的处理过程及其区别。这个例子摘自 Example of 2D Convolution
假设输入图像 \(f\) 的大小为 \(3 \times 3\) (这里仅为介绍“相关”和“卷积”的处理过程,为简单起见选择了一个非常小的图像尺寸),如图 17 所示。
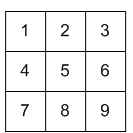
Figure 17: Input f(x,y)
滤波器 \(w\) 的大小为 \(3 \times 3\) (这是常用的滤波器大小),如图 18 所示。
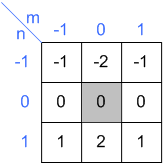
Figure 18: Kernel w(x,y)
“相关”操作 \(w(x,y) \mathbin{☆} f(x,y)\) 的计算过程如图 19 所示。
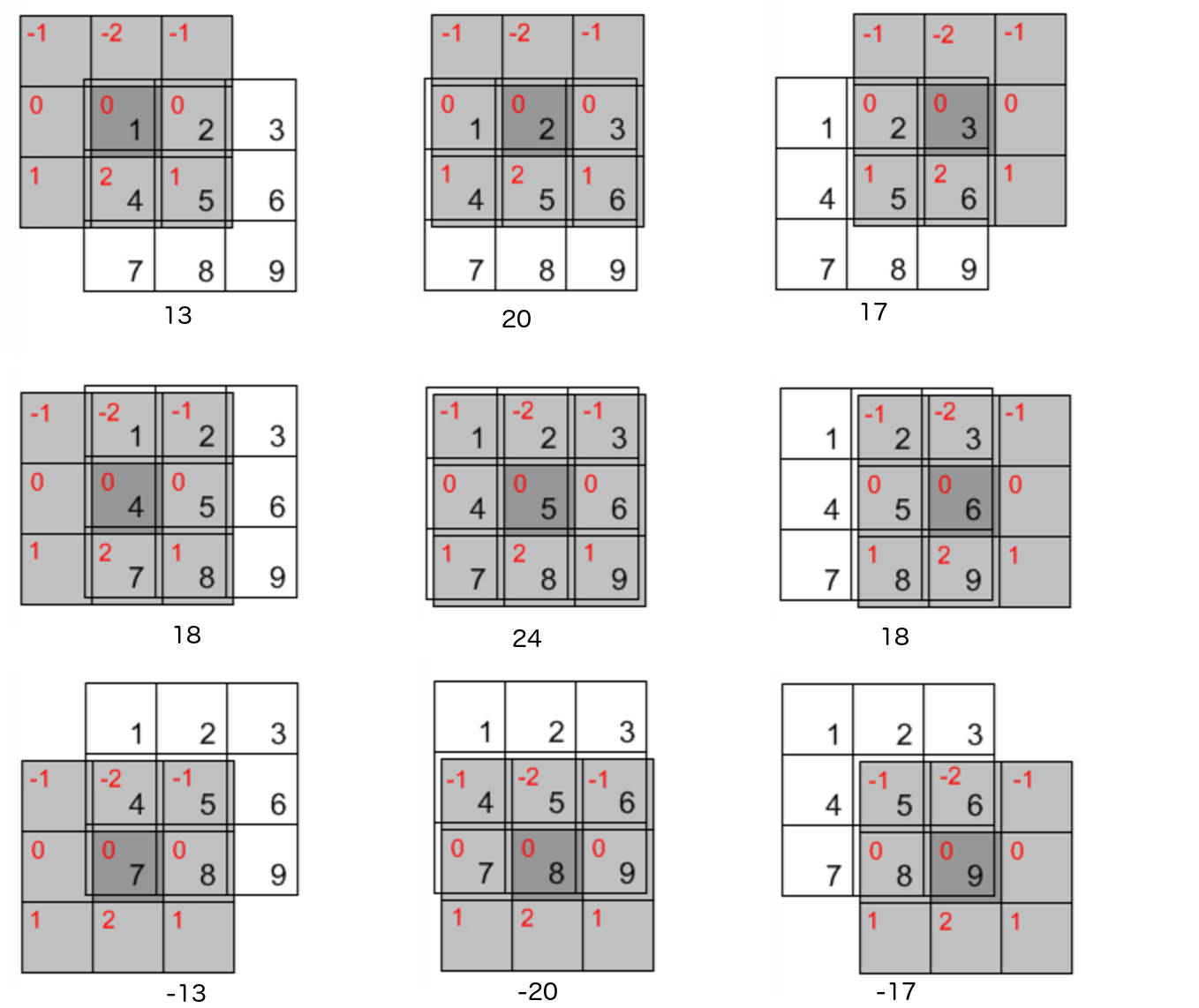
Figure 19: “相关”操作 \(w(x,y) \mathbin{☆} f(x,y)\)
设“相关”操作后的结果矩阵为 \(g_1\) ,详细计算过程(这个例子中对于图像边缘进行的是“零填充”,当然也可以进行其它方式的填充)如下:
\[\begin{aligned}g_1(0,0) &= 0 \times (-1) + 0 \times (-2) + 0 \times (-1) + 0 \times 0 + 1 \times 0 + 2 \times 0 + 0 \times 1 + 4 \times 2 + 5 \times 1 = 13 \\
g_1(0,1) &= 0 \times (-1) + 0 \times (-2) + 0 \times (-1) + 1 \times 0 + 2 \times 0 + 3 \times 0 + 4 \times 1 + 5 \times 2 + 6 \times 1 = 20 \\
g_1(0,2) &= 0 \times (-1) + 0 \times (-2) + 0 \times (-1) + 2 \times 0 + 3 \times 0 + 0 \times 0 + 5 \times 1 + 6 \times 2 + 0 \times 1 = 17 \\
g_1(1,0) &= 0 \times (-1) + 1 \times (-2) + 2 \times (-1) + 0 \times 0 + 4 \times 0 + 5 \times 0 + 0 \times 1 + 7 \times 2 + 8 \times 1 = 18 \\
g_1(1,1) &= 1 \times (-1) + 2 \times (-2) + 3 \times (-1) + 4 \times 0 + 5 \times 0 + 6 \times 0 + 7 \times 1 + 8 \times 2 + 9 \times 1 = 24 \\
g_1(1,2) &= 2 \times (-1) + 3 \times (-2) + 0 \times (-1) + 5 \times 0 + 6 \times 0 + 0 \times 0 + 8 \times 1 + 9 \times 2 + 0 \times 1 = 18 \\
g_1(2,0) &= 0 \times (-1) + 4 \times (-2) + 5 \times (-1) + 0 \times 0 + 7 \times 0 + 8 \times 0 + 0 \times 1 + 0 \times 2 + 0 \times 1 = -13 \\
g_1(2,1) &= 4 \times (-1) + 5 \times (-2) + 6 \times (-1) + 7 \times 0 + 8 \times 0 + 9 \times 0 + 0 \times 1 + 0 \times 2 + 0 \times 1 = -20 \\
g_1(2,2) &= 5 \times (-1) + 6 \times (-2) + 0 \times (-1) + 8 \times 0 + 9 \times 0 + 0 \times 0 + 0 \times 1 + 0 \times 2 + 0 \times 1 = -17 \end{aligned}\]
即通过“相关”操作后得到的输出如图 20 所示(结果中有负数,真实做图像处理时要处理这种情况)。
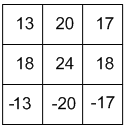
Figure 20: Correlation Output
“卷积”操作和“相关”操作是类似的,唯一不同在于做“卷积”操作时要提前把滤波器旋转(包括水平方向和垂直方向) \(180^{\circ}\)
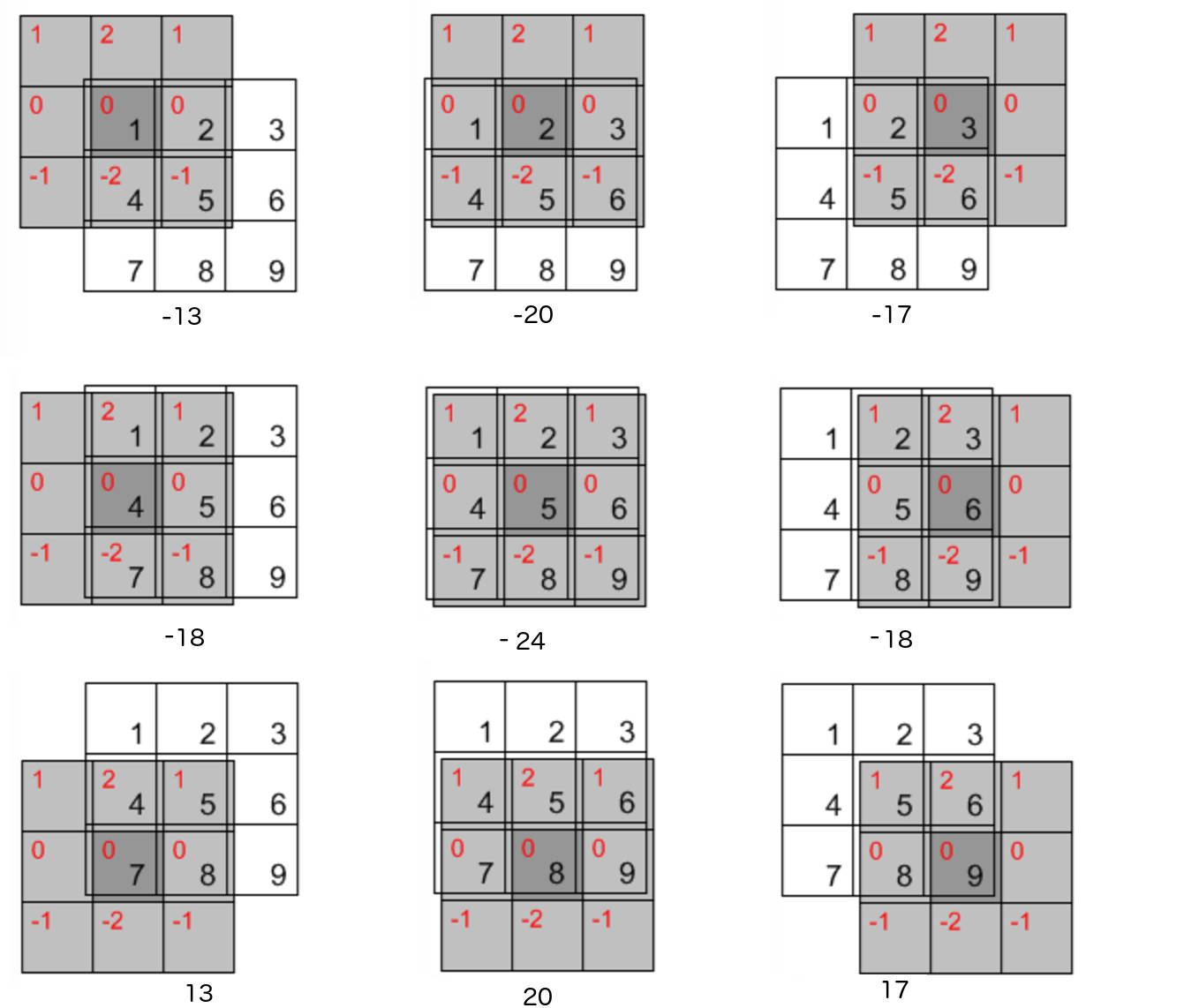
Figure 21: “卷积”操作 \(w(x,y) \star f(x,y)\) (滤波器已经旋转了 \(180^{\circ}\) )
通过“卷积”操作 \(w(x,y) \star f(x,y)\) 后,得到的输出如图 22 所示(结果中有负数,真实做图像处理时要处理这种情况)。
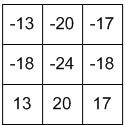
Figure 22: Convolution Output
2.3.2.2. 关于术语的说明
在图像处理文献中,我们可能会遇到“卷积滤波器”、“卷积模板”或“卷积核”这些术语。按惯例,这些术语用来表示一种空间滤波器,并且滤波器不一定用于真正的卷积。类似地,“模板与图像的卷积”通常用于表示滑动乘积求和处理,没有区分相关和卷积间的差别,它通常用于表示两种操作之一。这一不太严密的术语是产生混淆的根源。
线性空间滤波时,要不要把滤波器首先旋转 \(180^{\circ}\) 其实不重要,重要的是在给定的滤波任务中,按对应于期望操作的方式来指定滤波模板。
2.3.3. 应用软件对线性空间滤波的支持
ImageMagick 和 GIMP 支持定制线性空间滤波的模板。
参考:
ImageMagick v6 Examples -- Convolution of Images
GIMP Convolution Matrix
2.4. 平滑空间滤波器
平滑滤波器用于模糊处理和降低噪声。模糊处理经常用于预处理任务中,例如在(大)目标提取之前去除图像中的一些琐碎细节,以及桥接直线或曲线的缝隙。
2.4.1. 平滑线性滤波器(均值滤波器)
平滑线性空间滤波器使用滤波模板确定的邻域内像素的平均灰度值代替图像中每个像素的值,这种处理的结果降低了图像灰度的“尖锐”变化。这些滤波器有时也称为均值滤波器(Averaging Filters)。显然,它们属于低通滤波器(Lowpass Filters)。
图 23 是两个 \(3 \times 3\) 平滑线性滤波器的示例。左边的平滑线性滤波器的所有系数都相等(都为 \(1/9\) ),有时也称为盒状滤波器(Box Filter)。右边的平滑线性滤波器实现是的“加权平均”,突出了处于模板中心位置的像素的重要性比其它像素的重要性要更大。不过,实践中,由于模板在一幅图像中任何一个位置所跨过的区域很小,通常很难看出使用图 23 中两个模板或类似方式进行平滑处理后的图像的区别。
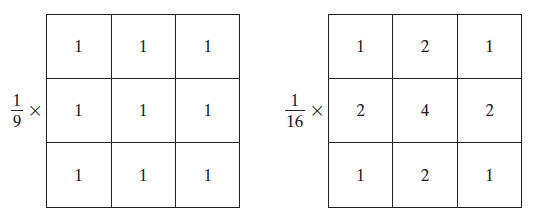
Figure 23: 两个 \(3 \times 3\) 平滑线性滤波器的示例
图 24 是使用不同尺寸的模板对图像进行平滑处理后的效果。

Figure 24: 不同尺寸的模板对图像进行平滑处理后的效果(第一个图是原图像,其它是分别使用 m=3,5,9,15,35 的方形均值滤波器处理后的效果)
2.4.2. 高斯模糊(Gaussian blur)
高斯模糊(Gaussian blur)是图像处理常用滤波器,可以用它来 减少图像噪声,降低细节层次。
二维高斯函数为:
\[G(x,y) = \frac{1}{2 \pi \sigma^2} e^{- \frac{x^2 + y^2}{2 \sigma^2}}\]
它是各向同性的(isotropic),函数图形如 25 所示。
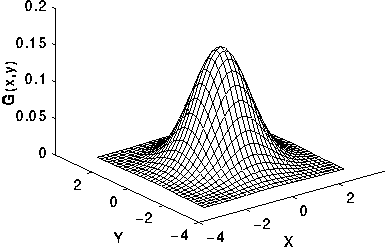
Figure 25: 二维高斯函数
图 26 是高斯滤波器(标准差 \(\sigma=1\) ,核大小为 \(5\times 5\) )的一个离散近似。
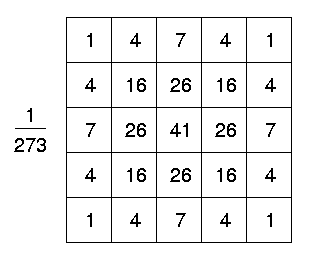
Figure 26: 高斯滤波器(标准差 \(\sigma=1\) ,核大小为 \(5\times 5\) )
下面是高斯滤波器(标准差 \(\sigma=0.84089642\) ,核大小为 \(7\times 7\) )的另一个离散近似。
| 0.00000067 | 0.00002292 | 0.00019117 | 0.00038771 | 0.00019117 | 0.00002292 | 0.00000067 |
| 0.00002292 | 0.00078634 | 0.00655965 | 0.01330373 | 0.00655965 | 0.00078633 | 0.00002292 |
| 0.00019117 | 0.00655965 | 0.05472157 | 0.11098164 | 0.05472157 | 0.00655965 | 0.00019117 |
| 0.00038771 | 0.01330373 | 0.11098164 | 0.22508352 | 0.11098164 | 0.01330373 | 0.00038771 |
| 0.00019117 | 0.00655965 | 0.05472157 | 0.11098164 | 0.05472157 | 0.00655965 | 0.00019117 |
| 0.00002292 | 0.00078633 | 0.00655965 | 0.01330373 | 0.00655965 | 0.00078633 | 0.00002292 |
| 0.00000067 | 0.00002292 | 0.00019117 | 0.00038771 | 0.00019117 | 0.00002292 | 0.00000067 |
显然,高斯滤波器的输出是“邻域像素的加权平均”,同时离中心越近的像素权重越高。因此, 相对于均值滤波高斯滤波器的平滑效果更柔和,而且边缘保留的也更好。
计算高斯函数的离散近似时,在 \(3\sigma\) 距离之外的离散值可以认为不起作用,所以, 用户不指定核大小时,核大小可以由 \(\sigma\) 自动决定,为 \((6\sigma + 1) \times (6\sigma + 1)\) 。
2.4.3. 统计排序(非线性)滤波器
统计排序滤波器是一种非线性空间滤波器,这种滤波器的响应以滤波器包围的图像区域中所包含的像素的排序为基础,然后使用统计排序结果决定的值代替中心像素的值。这一类中最知名的滤波器是中值滤波器(Median Filter),正如其名暗示的那样,它是将像素邻域内灰度的中值代替该像素的值。
2.5. 锐化空间滤波器
锐化处理的主要目的是突出灰度的过渡部分。图像锐化的用途多种多样,应用范围从电子印刷和医学成像到工业检测和军事系统的制导等。从前面介绍的内容中,我们了解到,图像模糊可通过在空间域用像素邻域平均法实现。因为均值处理和积分类似,在逻辑上,我们可以得出锐化处理可由空间微分来实现这一结论。事实上,的确如此,下面将介绍由数字微分来定义和实现锐化算子的各种方法。
2.5.1. 数字函数微分基础
数字函数的微分描述的是“差别”,有不同的方式来定义这些“差别”。 不过,对于一阶微分的任何定义都必须满足以下几点:(1) 在恒定灰度区域的微分值为零;(2) 在灰度台阶或斜坡的开始位置微分值非零;(3) 沿着斜坡的微分值为非零。类似地,任何二阶微分的定义必须满足以下几点:(1) 在恒定区域微分值为零;(2) 在灰度台阶或斜坡的开始和结束位置微分值非零;(3) 沿着斜坡的微分值为零。
对于一维函数 \(f(x)\) ,其一阶微分的基本定义是差值:
\[\frac{\partial f}{\partial x} = f(x+1) - f(x)\]
对上式关于 \(x\) 再次微分,得到二阶微分:
\[\begin{aligned} \frac{\partial^2 f}{\partial x^2} & = f'(x+1) - f'(x) \\
& = f(x+2) - f(x+1) - f(x+1) + f(x) \\
& = f(x+2) - 2f(x+1) + f(x) \\
\end{aligned}\]
但这一展开是关于点 \(x+1\) 的,我们感兴趣的是关于点 \(x\) 的二阶微分,故将上式中变量都减 1。即,我们将一维函数的二阶微分定义为如下差值:
\[\frac{\partial^2 f}{\partial x^2} = f(x+1) + f(x-1) - 2f(x)\]
注:这里使用偏导数符号仅仅是为了和二维函数在形式上一致。
容易验证这两个定义都满足前面所说的条件。
图 28 是一幅图像中一段水平灰度剖面对应一维数字函数的一阶微分和二阶微分。
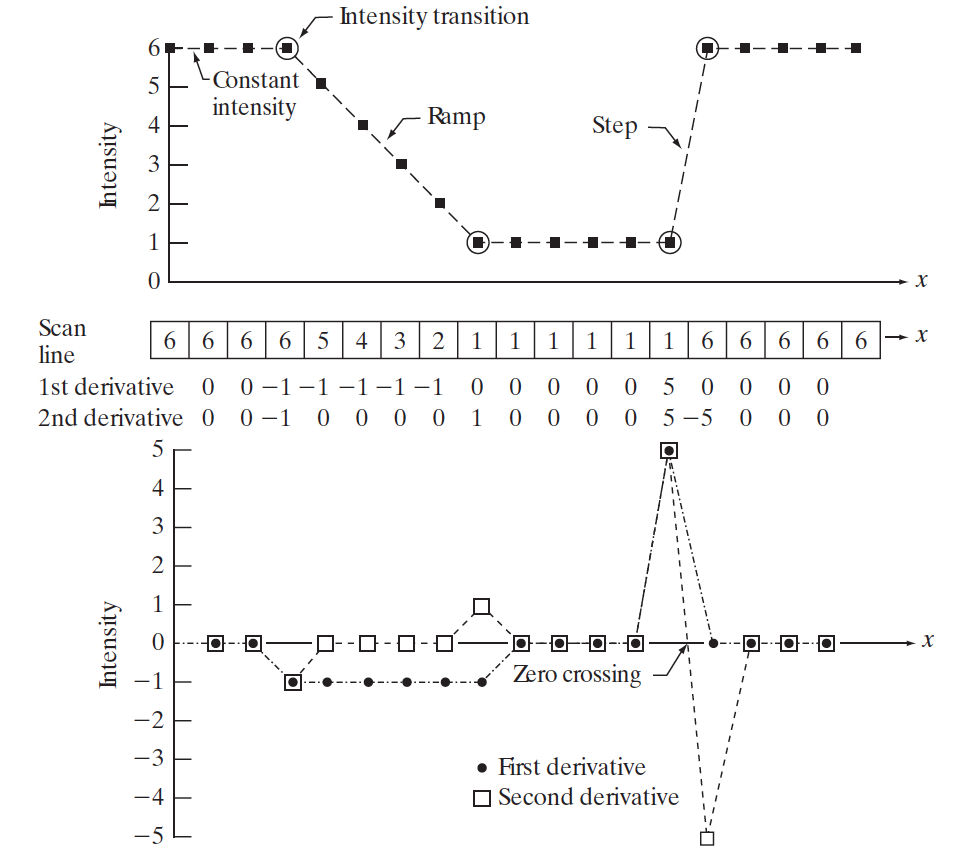
Figure 28: 一幅图像中一段水平灰度剖面对应一维数字函数的一阶微分和二阶微分
在上面例子中,在灰度台阶的过渡中,二阶微分出现了“零交叉”,这对于边缘定位是非常有用的。
2.5.2. 使用二阶微分进行图像锐化——拉普拉斯算子
一个二维图像函数 \(f(x,y)\) 的拉普拉斯算子定义为:
\[\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\]
由于任意阶微分都是线性操作,所以拉普拉斯算子也是一个线性算子。为了以离散形式描述这一公式,和前面介绍的一维函数二阶微分的定义类似,对二维函数二阶微分可以这样定义,在 \(x\) 方向上:
\[\frac{\partial^2 f}{\partial x^2} = f(x+1,y) + f(x-1,y) - 2f(x,y)\]
在 \(y\) 方向上:
\[\frac{\partial^2 f}{\partial y^2} = f(x,y+1) + f(x,y-1) - 2f(x,y)\]
由上面三个公式,从而得 两个变量的离散拉普拉斯算子为:
\[\nabla^2 f(x,y) = f(x+1,y) + f(x-1,y) + f(x,y+1) + f(x,y-1) - 4f(x,y)\]
图 29 所示模板是上面离散拉普拉斯算子的滤波模板实现。
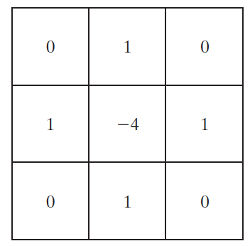
Figure 29: 拉普拉斯算子的滤波模板
通过拉普拉斯算子得到的图像(称为拉普拉斯图像),体现了原图像灰度的突变。那些原图像中灰度恒定的区域在拉普拉斯图像中对应区域的灰度会为零(表现为黑色)。
图 30 是拉普拉斯图像的一个例子。
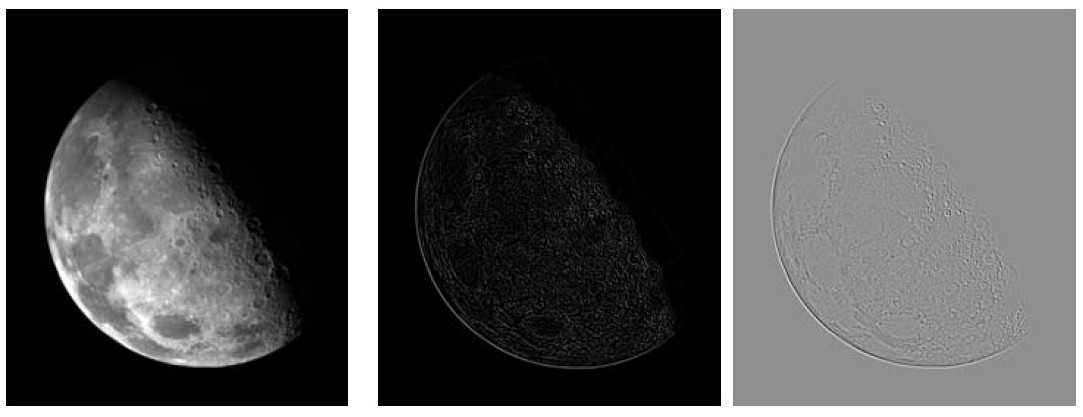
Figure 30: 左图为原图,中间为拉普拉斯图像(出现负数时直接修剪为 0),右边是映射到整个灰色范围[0,L-1]的拉普拉斯图像
在实践中,除了图 29 所示的拉普拉斯模板外,还有其它三个拉普拉斯模板。图 31 是常用的拉普拉斯滤波模板实现的总结。
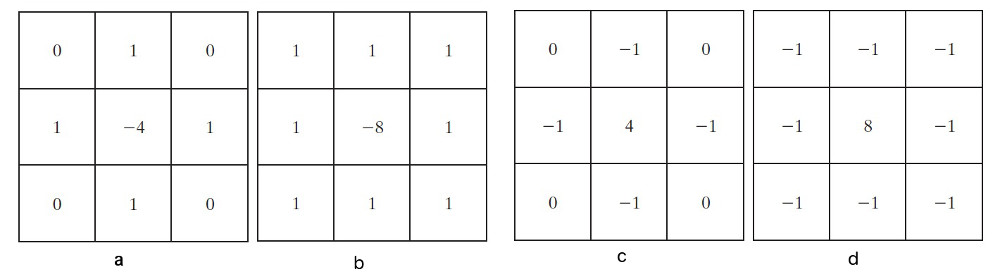
Figure 31: 拉普拉斯滤波模板实现 (a)拉普拉斯“基本模板”;(b)实现带有对角项的拉普拉斯“扩展模板”;(c)和(d)是常用的其他两个拉普拉斯实现
将拉普拉斯滤波后的图像和原图像合并(相加或相减)时,可以达到锐化原图像的效果。至于到底是相加还是相减,取决于拉普拉斯算子中心系数的符号(当中心系数的符号为负时,两图像相减;当中心系数的符号为正时,两图像相加)。即,用拉普拉斯滤波模板进行锐化处理的方法可用下式表示:
\[g(x,y) = \begin{cases} f(x,y) - \nabla^2 f(x,y) \qquad \text{如果拉普拉斯模板的中心系数为负} \\ f(x,y) + \nabla^2 f(x,y) \qquad \text{如果拉普拉斯模板的中心系数为正} \end{cases}\]
图 32 是用拉普拉斯滤波模板进行锐化处理的实例。从图中可知,右图锐化效果更加明显,因为它使用的是拉普拉斯“扩展模板”,在对角方向上产生了额外的锐化。

Figure 32: 拉普拉斯锐化实例(左图是原图,中图是使用拉普拉斯“基本模板”锐化处理效果图,右图是拉普拉斯“扩展模板”锐化处理效果图)
2.5.2.1. 各向同性滤波器(Isotropic Filter)
各向同性滤波器(Isotropic Filter)是旋转不变的,即将原图像旋转后进行滤波处理给出的结果与先对图像滤波然后再旋转的结果相同。
图 31 中 4 个拉普拉斯滤波器的实现中,其中(a)和(c)对 \(90^{\circ}\) 增幅的结果是各向同性的,(b)和(d)对 \(45^{\circ}\) 增幅的结果是各向同性的。
2.5.3. 非锐化掩蔽(Unsharp Masking)和高提升滤波(Highboost Filtering)
非锐化掩蔽(Unsharp Masking)是在印刷和出版界已用了多年的图像锐化处理技术。非锐化掩蔽的处理过程如下:
第 1 步:模糊原图像;
第 2 步:从原图像中减去模糊图像(产生的差值图像称为模板);
第 3 步:将模板加到原图像上,将得到锐化图像。
非锐化掩蔽的原理如图 33 所示。
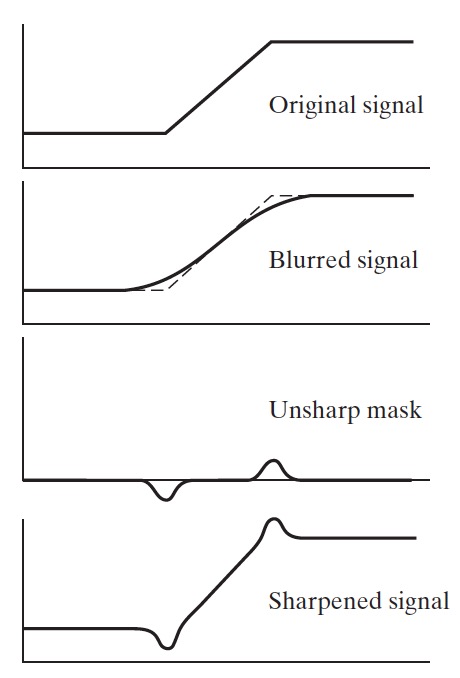
Figure 33: 非锐化掩蔽的原理(将原始信号减去模糊后的信号得到钝化模板,将原信号加上钝化模板将得到锐化后的信号)
令 \(\overline{f}(x,y)\) 表示模糊后的图像,非锐化掩蔽用公式描述如下。首先,得到模板:
\[g_{\text{mask}}(x,y) = f(x,y) - \overline{f}(x,y)\]
然后,在原图像上加上该模板的一个权重部分:
\[g(x,y) = f(x,y) + k \times g_{\text{mask}}(x,y) \qquad (k \ge 0)\]
上式中,当 \(k=1\) 时,就是前面介绍的非锐化掩蔽。当 \(k < 1\) 时,该处理过程不强调钝化模板的贡献。 当 \(k > 1\) 时,该处理过程称为高提升滤波(Highboost Filtering)。
2.5.4. 使用一阶微分进行图像锐化(非线性)——梯度
图像处理中的一阶微分是用梯度幅值来实现的。对于函数 \(f(x,y)\) , \(f\) 在坐标 \((x,y)\) 处的梯度定义为二维列向量:
\[\nabla f \equiv \text{grad}(f) \equiv \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}\]
该向量具有重要的几何特性,即它指出了在位置 \((x,y)\) 处 \(f\) 的最大变化率的方向(函数值增加最快的方向)。
向量 \(\nabla f\) 的幅度值(Magnitude)表示为 \(M(x,y)\) ,即:
\[M(x,y) = \sqrt{ \left(\frac{\partial f}{\partial x} \right)^2 + \left(\frac{\partial f}{\partial y} \right)^2}\]
它是梯度向量方向变化率在 \((x,y)\) 处的值。 当 \(x\) 和 \(y\) 在 \(f\) 中所有像素变化时计算每个 \(M(x,y)\) 得到与原图像大小相同的图像,该图像通常称为梯度图像(当含义很清楚时,可简称为梯度)。
在某些实现中,用绝对值来近似平方和平方根操作更适合计算,即:
\[M(x,y) \approx |\frac{\partial f}{\partial x}| + |\frac{\partial f}{\partial y}| \]
和拉普拉斯滤波的情况类似,我们需要对上面公式定义一个离散近似,并由此形成合适的滤波模板。
为了简化下面的讨论,我们将使用图 34 中的符号来表示一个 \(3 \times 3\) 区域内的图像点的灰度。使用这些符号,中心点 \(z_5\) 表示任意位置 \((x,y)\) 处的 \(f(x,y)\) , \(z_1\) 表示为 \(f(x-1,y-1)\) ,等等。
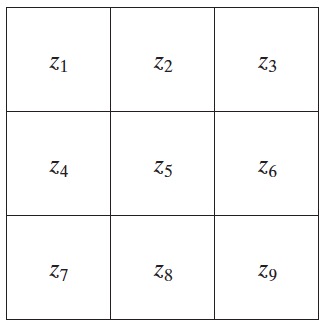
Figure 34: 一幅图像的 \(3 \times 3\) 区域,中心点 \(z_5\) 表示任意位置 \((x,y)\) 处的 \(f(x,y)\)
由节 2.5.1 中介绍的知识可知,一阶微分的最简近似是 \(\frac{\partial f}{\partial x} = z_8 - z_5\) 和 \(\frac{\partial f}{\partial y} = z_6 - z_5\) 。在早期数字图像处理的研究中,由 Roberts 提出的其他两个定义使用了交叉差分: \(\frac{\partial f}{\partial x} = z_9 - z_5\) 和 \(\frac{\partial f}{\partial y} = z_8 - z_6\) ,用线性滤波器模板表示,如图 35 所示,它们被称为罗伯特交叉梯度算子(Roberts cross gradient operators)。
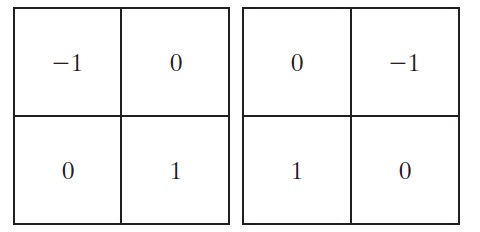
Figure 35: Roberts cross gradient operators
这时,对应的梯度图像为:
\[M(x,y) = \sqrt{(z_9 - z_5)^2 + (z_8 - z_6)^2}\]
或者近似为:
\[M(x,y) = |z_9 - z_5| + |z_8 - z_6|\]
2.5.4.1. Sobel Operator
Sobel算子 是一个流行的梯度算子。它使用下面公式对一阶微分进行近似:
\[\begin{aligned} \frac{\partial f}{\partial x} &= (z_7 + 2 z_8 + z_9) - (z_1 + 2 z_2 + z_3) \\
\frac{\partial f}{\partial y} &= (z_3 + 2 z_6 + z_9) - (z_1 + 2 z_4 + z_7) \end{aligned}\]
用模板表示,如图 36 所示。
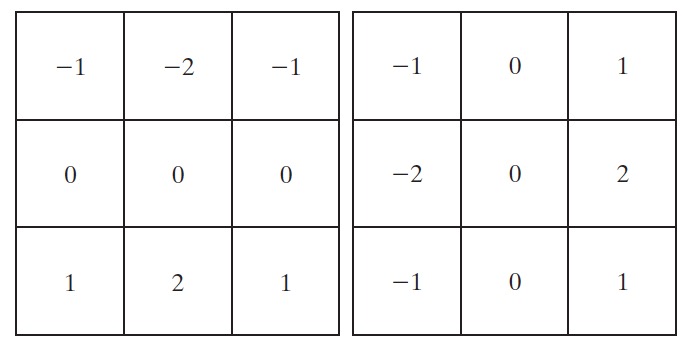
Figure 36: Sobel Operator
这时,对应的梯度图像为:
\[M(x,y) = \sqrt{\left((z_7 + 2 z_8 + z_9) - (z_1 + 2 z_2 + z_3) \right)^2 + \left((z_3 + 2 z_6 + z_9) - (z_1 + 2 z_4 + z_7) \right)^2}\]
或者近似为:
\[M(x,y) = |(z_7 + 2 z_8 + z_9) - (z_1 + 2 z_2 + z_3)| + |(z_3 + 2 z_6 + z_9) - (z_1 + 2 z_4 + z_7)|\]
2.5.5. Tips: 微分算子的模板系数相加为零
前面介绍的微分算子(如拉普拉斯算子,Sobel 算子),其模板系数相加都为零。这体现了节 2.5.1 所描述的定义微分的条件(恒定灰度区域的微分值为零)。
3. 形态学图像处理(Morphological Image Processing)
形态学(Morphology)一词通常表示生物学的一个分支,该分支主要研究动植物的形态和结构。这里,我们使用同一词语表示数学形态学(Mathematical morphology)的内容,将数字形态学作为图像处理工具。
首先,我们将讨论简单的二值图像(要么为黑要么为白,没有灰度级别),介绍一些基本算法后,最后再将讨论扩展到灰度图像。
\(\mathbb{Z}^2\) 中的集合可表示二值图像中的对象(集合的元素是图像中所有白色像素,或者所有黑色像素)。
3.1. 数学形态学基本知识
数学形态学的主要工具是“集合论”。
3.1.1. 集合基本操作
基本集合操作包括:
(1) 子集。如果集合 A 中的每个元素又是另一个集合 B 中的一个元素,则称 A 为 B 的子集,表示为:
\[A \subseteq B\]
(2) 并集。如果某个集合 C 包含集合 A 和 B 中的所有元素,则称 C 为集合 A 和 B 的并集,表示为:
\[C = A \cup B\]
(3) 交集。如果某个集合 D 包含的元素同时属于集合 A 和 B,则称 D 为集合 A 和 B 的交集,表示为:
\[D = A \cap B\]
(4) 补集。集合 A 的补集是不包含于集合 A 的元素所组成的集合,表示为:
\[A^c = \{ w \mid w \notin A \}\]
(5) 差集。集合 A 和 B 的差集是属于集合 A,而不属于集合 B 的元素组成的集合,表示为:
\[A-B = \{ w \mid w \in A, w \notin B \} = A \cap B^c\]
3.1.2. 反射(Reflection)和平移(Translation)
除了上面这些基本的操作外,集合的“反射(Reflection)”和“平移(Translation)”的概念在形态学中应用非常广泛。
一个集合 B 的反射(Reflection)可记为 \(\hat{B}\) ,定义如下:
\[\hat{B} = \{ w \mid w = -b, b \in B \}\]
如果 B 是描述图像中物体的像素(二维点)的集合,则 \(\hat{B}\) 是 B 中 \((x,y)\) 坐标被 \((-x,-y)\) 替代的点的集合。
集合 B 按照点 \(z=(z_1, z_2)\) 的平移(Translation)可记为 \((B)_z\) ,定义如下:
\[(B)_z = \{ c \mid c = b + z, b \in B \}\]
如果 B 是描述图像中物体的像素(二维点)的集合,则 \((B)_z\) 是 B 中 \((x,y)\) 坐标被 \((x+z_1, y+z_2)\) 替代的点的集合。
集合反射和平移例子如图 37 所示。
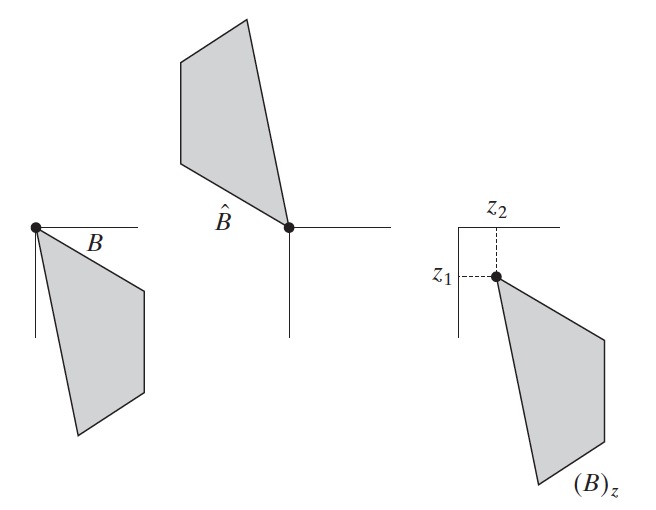
Figure 37: 集合(图像)的反射和平移
3.1.3. 结构元(Structuring Element)
在形态学中, 结构元(Structuring Element)是一个小集合(子图像),用它来研究图像中感兴趣的特征。
结构元都有一个“原点”,一般用实心黑点表示(如果结构元是对称的,且未明确画出原点时,常常假定结构元原点就是结构元的对称中心)。
当对图像操作时,为便于操作,一般要求结构元是矩形阵列,这可以通过“添加最小可能数量”的背景元素形成一个矩阵阵列来实现。
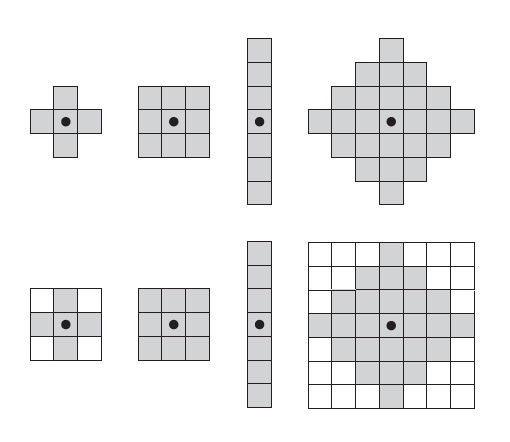
Figure 38: 第一行为结构元例子,第二行是转换为矩形阵列的结构元。
用结构元对图像进行处理时,图像边界处也往往需要添加适当的背景元素。
如何使用结构元对图像进行处理呢?我们通过一个例子来说明。
假定我们定义一个用结构元 B 在集合 A 上的操作如下:通过让 B 在 A 上运行,以便结构元 B 的原点访问 A 的每一个元素,来创建一个新集合。在 B 的每个原点位置,如果 B 完全被 A 包含,则将该位置标记为新集合的一个成员;否则,将该位置标记为非新集合的成员。 图 39 显示了这一操作结果。我们注意到,当 B 的原点位于 A 的边界元素上时,B的一部分将不再包含在 A 中,按照约定的规则,从而 B 处在中心位置的点没有成为新集合的成员。 最终结果是集合 A 的边界被腐蚀掉了。
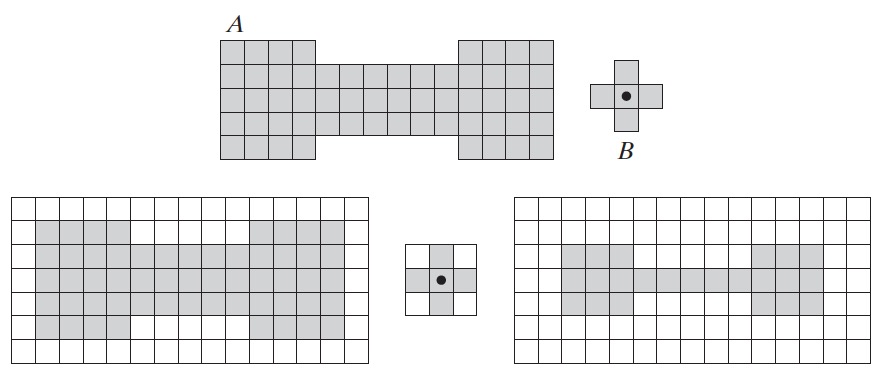
Figure 39: 第一行分别是集合 A 和结构元 B,第二行是:填充过的集合 A,填充过的结构元 B,由结构元 B 按约定规则处理 A 后形成的集合
关于“腐蚀”的数字公式表述在后文将介绍。
3.2. 腐蚀(Erosion)和膨胀(Dilation)
腐蚀(Erosion)和膨胀(Dilation)这两个操作是形态学处理的基础,很多形态学算法都以这两种原始操作为基础。
3.2.1. 腐蚀(Erosion)
A 和 B 是 \(\mathbb{Z}^2\) 中的集合,集合 B 对集合 A 的“腐蚀”定义为:
\[A \ominus B=\{z \mid (B)_{z} \subseteq A\}\]
即 B 对 A 的腐蚀是一个用 z 平移的 B,那些满足“B 包含在 A 中”的所有的点 z 的集合。
腐蚀还有其他一些等价的定义形式,如:
\[A \ominus B=\{z \mid (B)_z \cap A^c = \varnothing \}\]
图 40 是用结构元 B 对图像 A 进行腐蚀的两个例子。
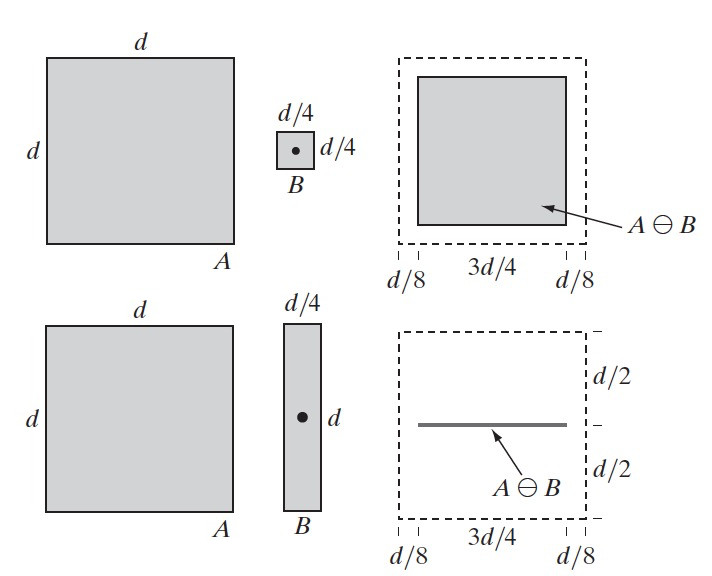
Figure 40: 结构元 B 对图像 A 进行腐蚀的两个例子
图 41 是用形态相同但大小不同的结构元对同一图像进行腐蚀的例子。
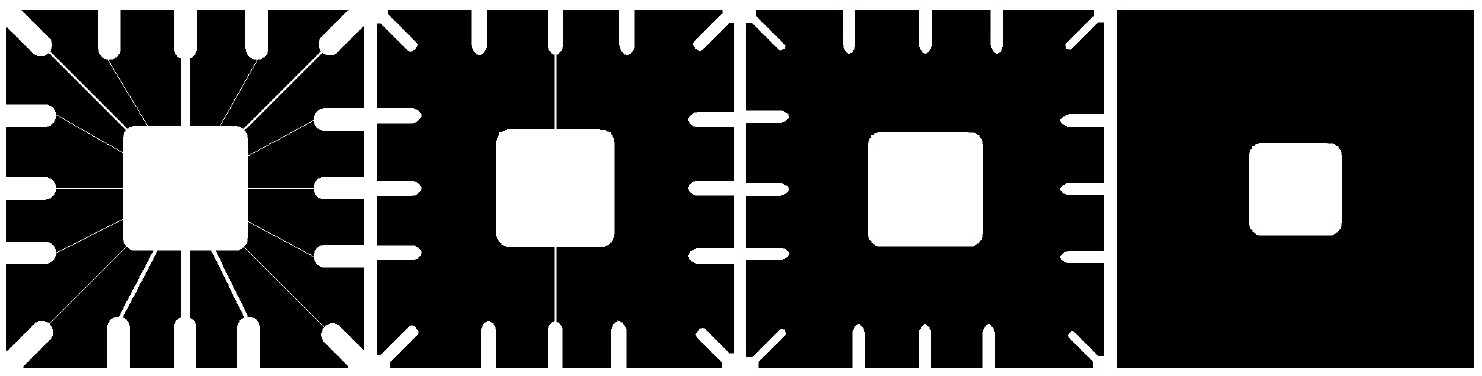
Figure 41: 第一个是原图像(486x486),后面三个图像分别用 11x11,15x15,45x45 的结构元(元素全为 1)进行腐蚀处理后的结果
3.2.2. 膨胀(Dilation)
A 和 B 是 \(\mathbb{Z}^2\) 中的集合,集合 B 对集合 A 的“膨胀”定义为:
\[A \oplus B=\{z \mid (\hat{B})_{z} \cap A \neq \varnothing \}\]
集合 B 对集合 A 的“膨胀”就是用 z 平移的 B 关于原点的映像 \(\hat{B}\) ,那些满足“ \(\hat{B}\) 和 A 至少有一个元素是重叠的”的所有的点 z 的集合。
图 42 是用结构元 B(它是关于原点对称的,所以 \(\hat{B}=B\) )对图像 A 进行膨胀的两个例子。
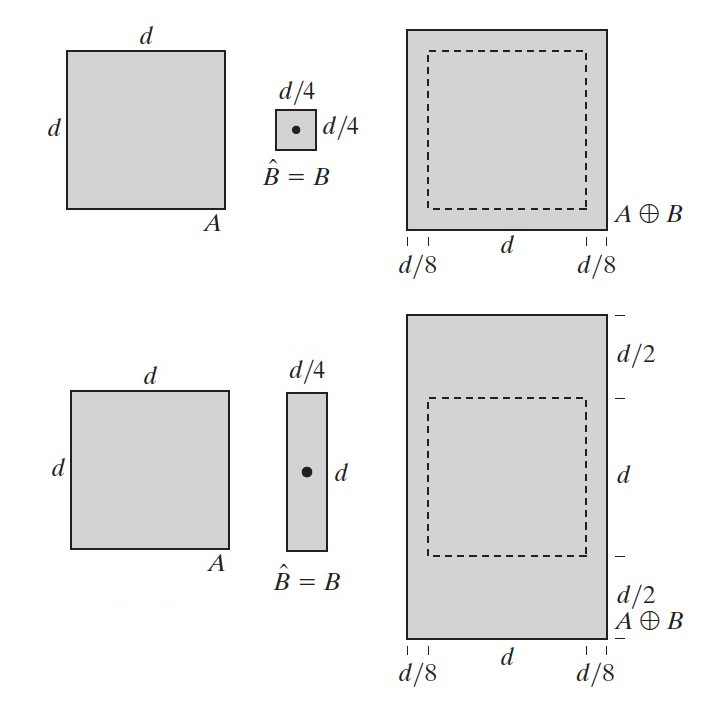
Figure 42: 结构元 B 对图像 A 进行膨胀的两个例子
3.2.3. 腐蚀和膨胀的对偶性
可以证明,腐蚀和膨胀彼此关于集合求补运算和反射运算是对偶的,即:
\[\begin{aligned} (A \ominus B)^c = A^c \oplus \hat{B} \\
(A \oplus B)^c = A^c \ominus \hat{B} \end{aligned}\]
上面两式表明,B对 A 的腐蚀是 \(\hat{B}\) 对 \(A^c\) 的膨胀的补;B对 A 的膨胀是 \(\hat{B}\) 对 \(A^c\) 的腐蚀的补。
当结构元 B 关于其原点对称时(通常如此),有 \(\hat{B}=B\) ,这时对偶性特别有用。这样,我们可以用相同的结构元简单地使用 B 膨胀图像 A 的背景(即膨胀 \(A^c\) ),并对该结果求补就可得到 B 对图像 A 的腐蚀。
3.3. 开操作(Opening)和闭操作(Closing)
开操作(Opening)和闭操作(Closing)是形态学的另外两个重要操作。
3.3.1. 开操作(先腐蚀后膨胀)
结构元 B 对集合 A 的开操作,表示为 \(A\circ B\) ,其定义为:
\[A\circ B=(A\ominus B) \oplus B\]
即开操作是“先腐蚀后膨胀”。
开操作有一个简单的几何解释。假设我们把结构元 B 视为一个“转球”, \(A\circ B\) 的边界由 B 中的点建立: 当 B 在 A 的边界内侧滚动时,B所能达到的 A 的边界的最远点组成了 \(A\circ B\) 的边界。 图 43 是开操作的一个实例。
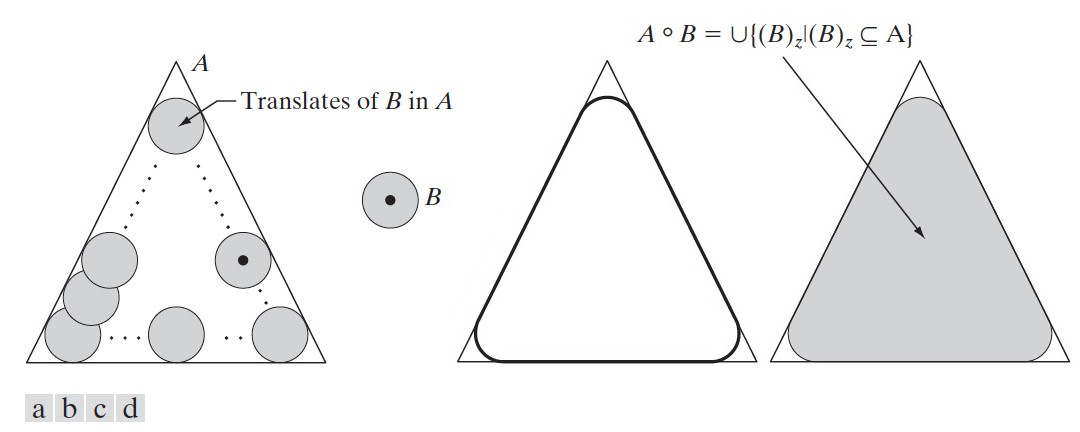
Figure 43: (a)结构元 B 沿集合 A 的“内侧边界”滚动,(b)结构元,(c)粗线是开操作的外部边界,(d)阴影部分就是开操作 \(A\circ B\) 的结果
结构元 B 对集合 A 的开操作还可以表示为:
\[A\circ B= \bigcup \{ (B)_z \mid (B)_z \subseteq A \}\]
其中,记号 \(\bigcup \{ \cdot \}\) 表示大括号中所有集合的并集。
3.3.2. 闭操作(先膨胀后腐蚀)
结构元 B 对集合 A 的闭操作,表示为 \(A\bullet B\) ,其定义为:
\[A\bullet B=(A\oplus B) \ominus B\]
即闭操作是“先膨胀后腐蚀”。
和开操作类似,闭操作也有一个简单的几何解释(不同在于开操作是沿“内侧边界”滚动,而闭操作是沿“外侧边界”滚动)。如图 44 所示。
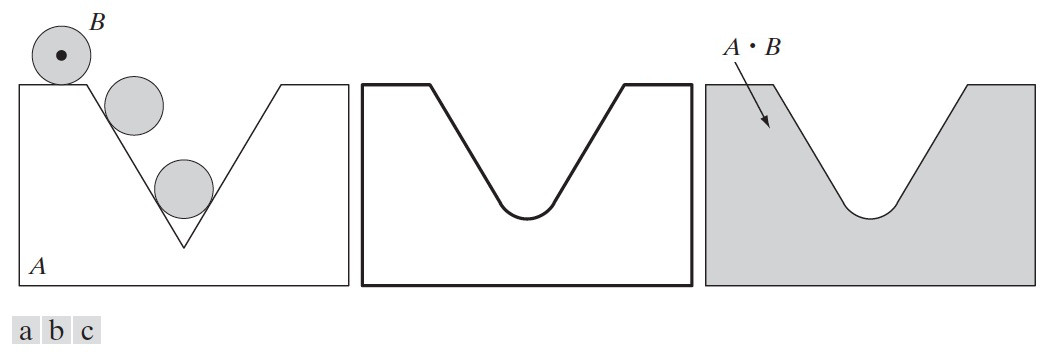
Figure 44: (a) 结构元 B 沿集合 A“外侧边界”滚动,(b)粗线是闭操作的外部边界,(d)阴影部分就是闭操作 \(A\bullet B\) 的结果
3.3.3. 开操作和闭操作的对偶性
和腐蚀和膨胀类似,开操作和闭操作彼此关于集合求补运算和反射运算是对偶的,即:
\[\begin{aligned} (A \circ B)^c = A^c \bullet \hat{B} \\
(A \bullet B)^c = A^c \circ \hat{B} \end{aligned}\]
3.3.4. 实例:腐蚀、膨胀、开操作、闭操作
图 45 是形态学基本操作(腐蚀、膨胀、开操作、闭操作)的实例。
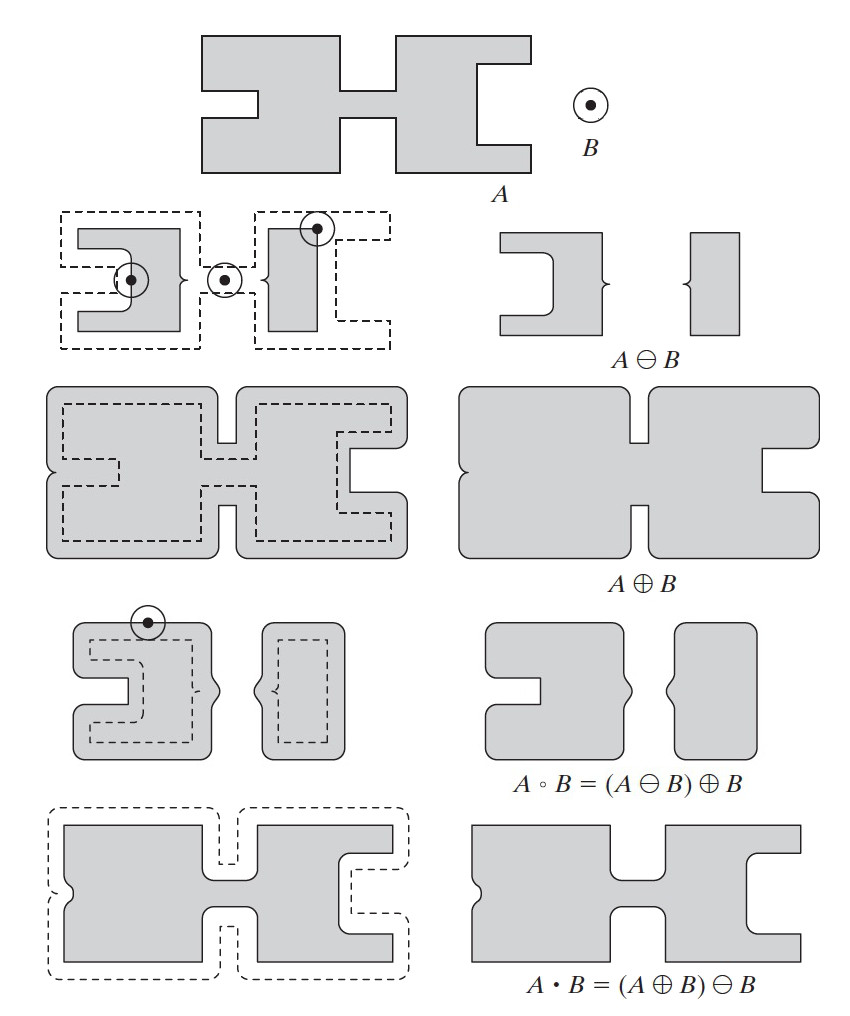
Figure 45: 形态学基本操作(腐蚀、膨胀、开操作、闭操作)的实例
3.4. 灰度级形态学
前面介绍的形态学基本操作都是基于二值图像,这里我们把它们扩展到灰度级图像。
设 \(f(x,y)\) 是灰度级图像, \(b(x,y)\) 是一个结构元。
如果结构元 \(b(x,y)\) 的所有灰度值都相等,则称为“平坦结构元”,否则称为“非平坦结构元”(很少用)。
灰度级形态学中结构元的反射的定义如下:
\[\hat{b}(x,y) = b(-x, -y)\]
3.4.1. 腐蚀和膨胀
当结构元 b 的原点位于 \((x,y)\) 处时,用一个平坦结构元 b 在 \((x,y)\) 处对图像 f 的“腐蚀”的定义为:图像 f 中与 b 重合区域的最小值。灰度图像的“腐蚀”用公式表示为:
\[[f \ominus b] (x,y) = \min_{(s,t) \in b} \{ f(x+s, y+t) \}\]
平坦结构元 b 在 \((x,y)\) 处对图像 f 的“膨胀”的定义为:图像 f 中与 \(\hat{b}\) (即 \(b(-x, -y)\) )重合区域的最大值。灰度图像的“膨胀”用公式表示为:
\[[f \oplus b] (x,y) = \max_{(s,t) \in b} \{ f(x-s, y-t) \}\]
3.4.2. 开操作和闭操作
灰度图像的开操作和闭操作的表达式与二值图像的对应操作具有相同的形式。
结构元 b 对图像 f 的开操作为:
\[f \circ b = (f \ominus b) \oplus b\]
结构元 b 对图像 f 的闭操作为:
\[f \bullet B = (f \oplus b) \ominus b\]
灰度图像的开操作和闭操作同样具有简单的几何解释。假设我们将一个图像 \(f(x,y)\) 看成是一个三维表面,也就是说,它的灰度值可解释为 \(xy\) 平面上的高度值。
b 对 f 的开操作的几何解释为: 在 b 的原点位置,从 f 的下表面垂直向上推动结构元 b 时,b的任何部分所达到的最高值。当 b 的原点访问 f 的每一个坐标 \((x,y)\) 所得到的所有值组成的集合就是 b 对 f 的开操作的结果。 闭操作的几何解释和开操作类似,只是“向上推”改为“向下推”,能达到的“最高值”改为“最低值”。
图 46 以一维的形式说明了灰度图像的开操作和闭操作的几何解释。
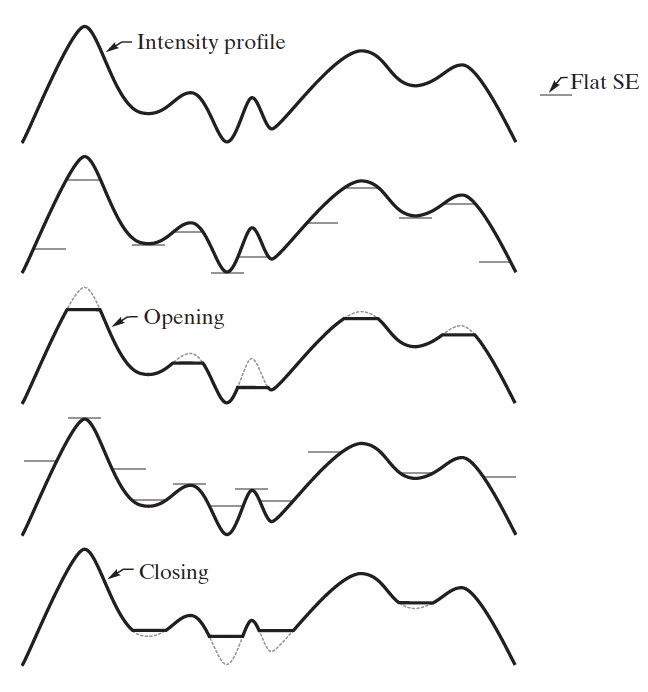
Figure 46: 一维情形下的开操作和闭操作
显然, 开操作可去除“比结构元小”的明亮细节,而闭操作可去除“比结构元小”的暗部细节。
3.4.2.1. 开操作和闭操作实例
前面介绍过,开操作可去除“比结构元小”的明亮细节,而闭操作可去除“比结构元小”的暗部细节。
图 47 是灰度图像开操作和闭操作实例。

Figure 47: 左为原图(448x425 的灰度级图像),中图为使用半径为 3 像素的圆形结构元得到的开操作的结果(原图中较小的白点被去除了);右图为使用半径为 5 像素的圆形结构元得到的闭操作的结果(原图中较小的黑点被去除了)
3.4.3. 一些基本的灰度级形态学算法
3.4.3.1. 形态学梯度(Morphological gradient)
膨胀图和腐蚀图之差为形态学梯度(Morphological gradient),其定义为:
\[g = (f \oplus b) - (f \ominus b)\]
膨胀粗化一幅图像中的区域,而腐蚀则细化它们;膨胀和腐蚀的差会强调区域间的边界,而同质区域会被忽略,从而产生“类似于微分(梯度)”的效果。
图 48 是形态学梯度的一个实例。
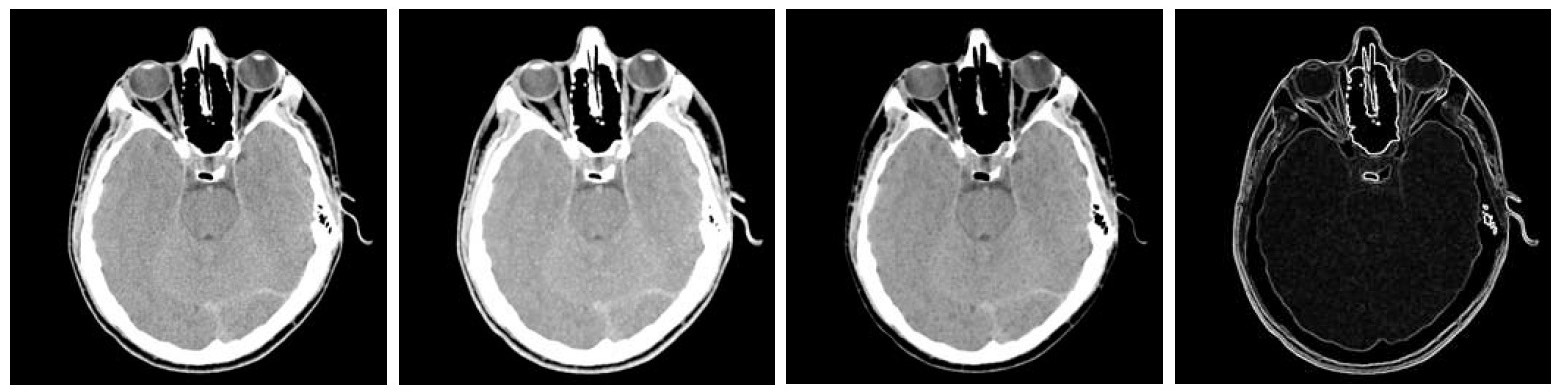
Figure 48: 从左到右依次为原图(头部 CT 图像)、膨胀图、腐蚀图、形态学梯度图
3.4.3.2. 顶帽和底帽变换(Top-hat and bottom-hat transformation)
灰度级图像 f 的顶帽变换(Top-hat transformation)定义为 \(f\) 减去其“开操作”:
\[T_{hat}(f) = f - (f \circ b)\]
灰度级图像 f 的底帽变换(Bottom-hat transformation)定义为“闭操作”减去 \(f\) :
\[B_{hat}(f) = (f \bullet b) - f\]
顶帽变换常用于校正不均匀光照的影响,增强图像对比度。 图 49 是顶帽变换增强对比度的实例。

Figure 49: (a)大小为 600x600 的原图(对比度低),(b)直接进行阈值处理(右下角出现了错误),(c)进行开操作的图像(结构元为半径为 50 的圆,结果只剩下了背景),(d)顶帽变换后的图像(对比度高),(e)对(d)图进行阈值处理(不再有错误)
4. 图像分割(Image Segmentation)
分割是将图像细分为构成它的子区域或物体。细分的程序取决于要解决的问题。
4.1. 孤立点、线、边缘的检测
孤立点、线、边缘是图像中“灰度剧烈变化”的位置。数学上,可以用微分(导数)来描述变化。使用线性空间滤波器(滤波器为梯度算子或微分算子)可以计算每个像素位置处的一阶导数和二阶导数。线性空间滤波器可参考 2.3.1.1 。
4.1.1. 孤立点的检测(拉普拉斯算子)
使用拉普拉斯算子(参考 2.5.2 ),如果在某点处该滤波器(模板)的响应的绝对值超过了一个指定的阈值,那么可以认为模板中心位置 \((x,y)\) 处的该点已经被检测到了。 在输出图像中,这样的点被标注为 1(表示找到孤立点),而所有其他点则被标注为 0,从而产生一幅二值图像。

Figure 50: (a)点检测(拉普拉斯)模板,(b)原图像(带有一个通孔的涡轮叶片 X 射线图),(c)模板和图像卷积的结果,(d)对(c)图阈值处理后的二值图像(找到了一个点)
4.1.3. 边缘检测原理:一阶导数和二阶导数
一阶导数和二阶导数都可以找到边缘,如图 52 所示。
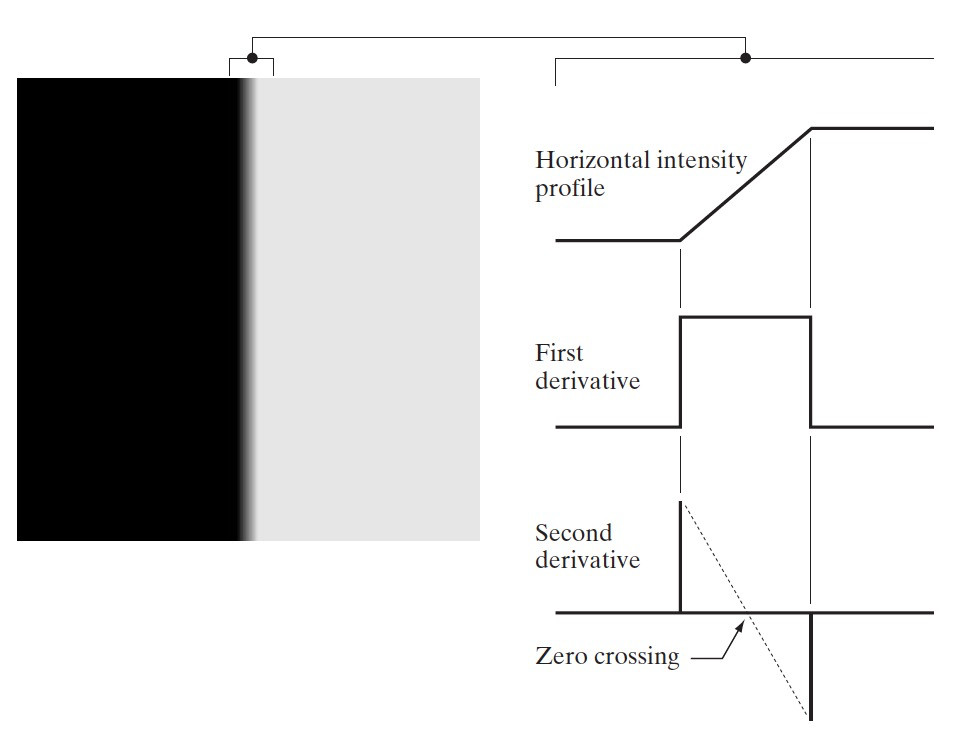
Figure 52: 左图被界线明显地分为两个区域,右图是界线的剖面图及其一阶导数和二阶导数
在灰度斜坡开始处并沿着整个灰度斜坡,一阶导数都不为零,这会导致一阶导数产生比较“粗”的边缘。
对于图像中的每条边缘,二阶导数生成两个值(被称为双线效应,Double-line effect,这是一个副作用,需要处理); 二阶导数的正负符号可以用于确定边缘的方向(从亮到暗,还是从暗到亮);二阶导数的“零交叉点”可以用于定位边缘的中心。
4.1.4. 基本的边缘检测:梯度算子(Prewitt, Sobel, Kirsch Compass, Robinson Compass)
边缘是灰度变化较大的位置。用一阶导数(即梯度)可以检测灰度变化。相关基本知识可参考 2.5.4 。
这里列举一些常见的边缘检测梯度算子,如图 53 所示。
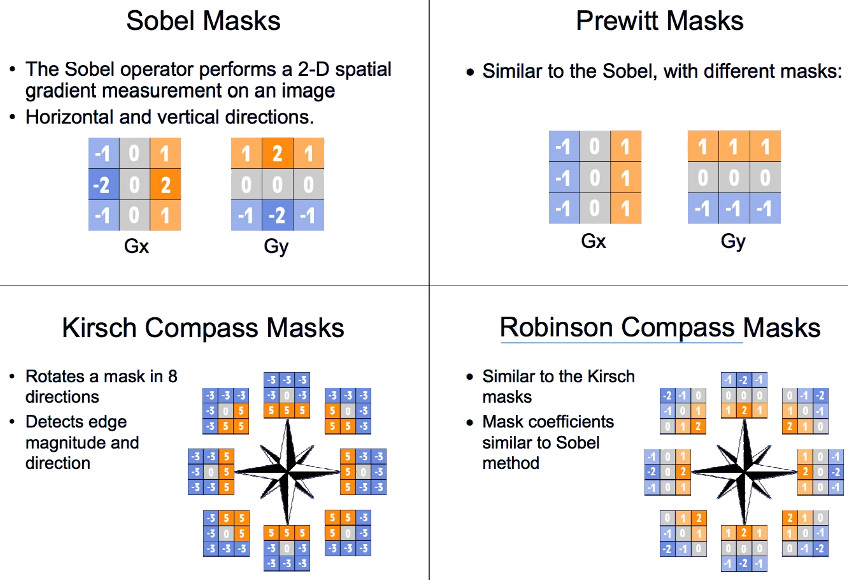
Figure 53: 常见的边缘检测梯度算子(摘自:http://www.cs.tau.ac.il/~turkel/notes/sem.pdf)
4.1.5. 先进的边缘检测:Marr-Hildreth edge detector (LoG, DoG)
节 2.5.2 中介绍过,使用二阶微分可以提取出图像中灰度变化较快的部分。但是,直接对图像使用拉普拉斯算子 \(\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\) ,得到的结果中图像的噪声很可能被放大。
一个更好的作法是先使用“高斯模糊滤波器(参考2.4.2)”抑制图像中的噪声,再使用二阶微分得到其拉普拉斯图像,最后寻找拉普拉斯图像中的零交叉点即可得到图像边缘。这就是 Marr-Hildreth 边缘检测算法的思想。
Marr-Hildreth 边缘检测算法 总结如下:
第一步:用“高斯模糊滤波器 \(G(x,y)\) ”对输入图像 \(f(x,y)\) 进行平滑处理。
第二步:计算去噪后图像(第一步的结果)的拉普拉斯图像:
\[g(x,y) = \nabla^2 [G(x,y) \star f(x,y)]\]
其中, \(\star\) 是卷积运算(由于高斯模糊滤波器是对称的,“相关”和“卷积”的结果是相同的,一般提到 Marr-Hildreth 算法时,习惯于使用卷积一词)。
第三步:计算 \(g(x,y)\) 的“零交叉点”,即为图像中物体边缘。
注:第一、二步往往合并为一步,后文会介绍。
第三步中,如何寻找 \(g(x,y)\) 中的零交叉点呢? 由于噪声或计算不准确,试图通过查找满足 \(g(x,y)=0\) 的坐标都找零交叉点是不实际的。 寻找零交叉点的一种可行方法描述如下:
在滤波后的图像 \(g(x,y)\) 的任意像素 \(p\) 处,观察以 \(p\) 为中心的一个 \(3 \times 3\) 邻域,如果 \(p\) 为零交叉点,则意味着至少存在“相对的邻域像素的正负符号不同”,这有 4 种情况需要测试:左/右、上/下、和两个对角。存在一种情况“相对的邻域像素的正负符号不同”,并且它们的数值差的绝对值还超过某个阈值(这很重要),则我们称 \(p\) 为一个零交叉像素。
4.1.5.1. Laplacian of Gaussian(LoG, Mexican hat operator)
在 Marr-Hildreth 边缘检测算法中,计算 \(g(x,y) = \nabla^2 [G(x,y) \star f(x,y)]\) 时,由于“高斯模糊运算”和“求拉普拉斯图像”都是线性操作(线性空间滤波器),所以有:
\[g(x,y) = [ \nabla^2 G(x,y) ] \star f(x,y)\]
这意味着,我们可以先求 \(\nabla^2 G(x,y) = \frac{\partial^2}{\partial x^2} G(x,y) + \frac{\partial^2}{\partial y^2} G(x,y)\) ,再把它和图像进行卷积。
二维高斯函数为(省略了归一化系数):
\[G(x,y) = e^{- \frac{x^2 + y^2}{2 \sigma^2}}\]
它对 \(x\) 的一阶偏导数:
\[\frac{\partial}{\partial x} G(x,y) = \frac{\partial}{\partial x} e^{- (x^2 + y^2)/2 \sigma^2} = - \frac{x}{\sigma^2} e^{- (x^2 + y^2)/2 \sigma^2}\]
对 \(x\) 的二阶偏导数:
\[\frac{\partial^2}{\partial x^2} G(x,y) = \frac{x^2}{\sigma^4} e^{- (x^2 + y^2)/2 \sigma^2} - \frac{1}{\sigma^2} e^{- (x^2 + y^2)/2 \sigma^2} = \frac{x^2 - \sigma^2}{\sigma^4} e^{- (x^2 + y^2)/2 \sigma^2}\]
从而:
\[\begin{aligned} \nabla^2 G(x,y) & = \frac{\partial^2}{\partial x^2} G(x,y) + \frac{\partial^2}{\partial y^2} G(x,y) \\
& = \frac{x^2 - \sigma^2}{\sigma^4} e^{- (x^2 + y^2)/2 \sigma^2} + \frac{y^2 - \sigma^2}{\sigma^4} e^{- (x^2 + y^2)/2 \sigma^2} \\
& = \frac{x^2 + y^2 - 2 \sigma^2}{\sigma^4} e^{- (x^2 + y^2)/2 \sigma^2} \\
\end{aligned}\]
上面这个式子被称为 Laplacian of Gaussian(LoG),即:
\[\text{LoG}(x,y) \triangleq \nabla^2 G(x,y) =\frac{x^2+y^2-2\sigma^2}{\sigma^4} e^{-\frac{(x^2+y^2)}{2\sigma^2}}\]
LoG 的负函数的三维图如图 54 (a)所示,其形状像个帽子,有时 LoG 函数也被称为墨西哥草帽算子(Mexican hat operator)。
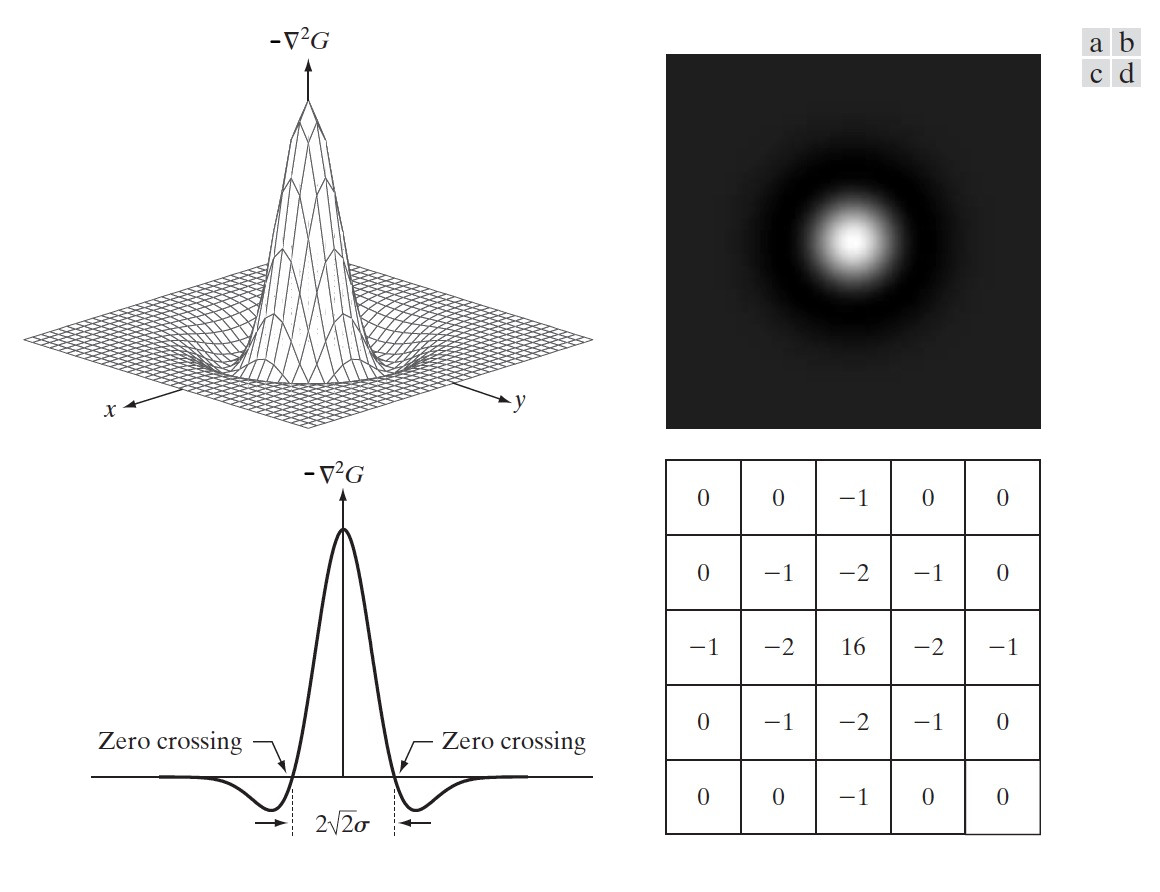
Figure 54: (a)负 LoG 的三维图,(b)以图像形式显示负 LoG,(c)图(a)的横截面(注意零交叉点),(d)负 LoG 的一个 \(5\times5\) 离散近似模板
4.1.5.2. Difference of Gaussian(DoG)
在实践中,我们常常用高斯函数的差分(Difference of Gaussian, DoG)来近似 LoG,即:
\[\text{LoG}(x,y) \approx \text{DoG}(x,y) = \frac{1}{2 \pi \sigma_1^2} e^{- \frac{(x^2 + y^2)}{2 \sigma_1^2}} - \frac{1}{2 \pi \sigma_2^2} e^{- \frac{(x^2 + y^2)}{2 \sigma_2^2}}\]
为了使 LoG 和 DoG 具有相同的零交叉点, \(\sigma\) 和 \(\sigma_1, \sigma_2\) 需要满足下面条件:
\[\sigma^2 = \frac{\sigma_1^2 \sigma_2^2}{\sigma_1^2 - \sigma_2^2} \ln \left[ \frac{\sigma_1^2}{\sigma_2^2} \right]\]
4.1.6. 更先进的边缘检测:Canny edge detector
Canny edge detector是目前讨论过的边缘检测算法中最优秀的。
Canny 算法分为如下几个步骤:
(1) 用高斯滤波器平滑输入图像;
(2) 计算梯度幅值图像和梯度角度图像;
(3) 对梯度幅值图像应用“非最大抑制(Non-maximum suppression)”算法;
(4) 用“双阈值处理(Double threshold)”和来检测边缘;
(5) 用特征综合方法收集来自多尺度的最终的边缘信息(不过,通常的算法实现都省略了这一步)。
由第(2)步知,Canny 算法是利用一阶导数来检测边缘的,但由于一阶导数得到的边缘往往会较粗; 第(3)步使用非最大抑制(Non-maximum suppression)算法的目的是“细化上一步得到的边缘”。 后文将介绍非最大抑制(Non-maximum suppression)算法。
“双阈值处理”的目的是减少伪边缘点,其具体过程为:设置两个阈值,上限和下限。如果一个像素的梯度大于上限阈值,则认为是边缘像素;如果低于下限阈值,则不认为是边缘像素,被抛弃;如果介于二者之间,只有当其“与高于上限阈值的像素连接”时才被接受。
图 55 是用不同算法对同一图像进行边缘检测的例子。从这个例子可知 Canny 算法的效果最好。
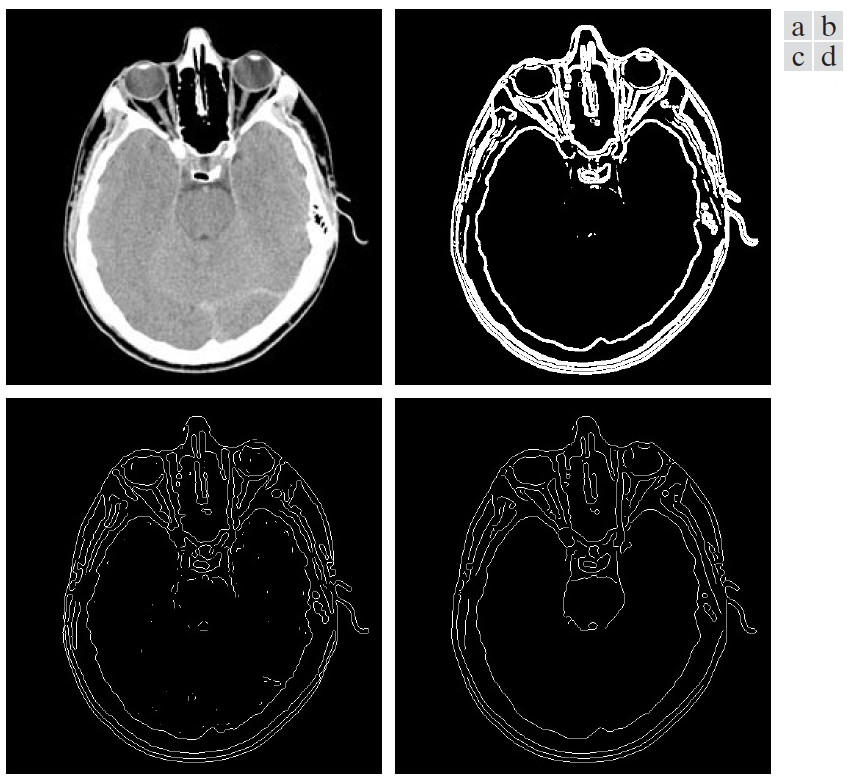
Figure 55: (a)原始的头部 CT 图像,(b)阈值处理后的梯度图像,(c)用 Marr-Hildreth 算法得到的图像,(d)用 Canny 算法得到的图像
4.1.6.1. 非最大抑制(Non-maximum suppression)
非最大抑制(Non-maximum suppression)是一个边缘细化算法。
假设通过高斯滤波器平滑后的图像为 \(f_s\) ,其梯度幅值图像和梯度角度图像(描述的是边缘法线方向)分别为:
\[M(x,y) = \sqrt{(\frac{\partial f_s}{\partial x})^2 + (\frac{\partial f_s}{\partial y})^2}\]
和
\[\alpha(x,y) = \arctan \left[ \frac{\frac{\partial f_s}{\partial y}}{\frac{\partial f_s}{\partial x}} \right]\]
显然, \(M(x,y)\) 和 \(\alpha(x,y)\) 是与原图像尺寸相同的阵列。
怎么细化边缘(边缘保存在 \(M(x,y)\) 中)呢?
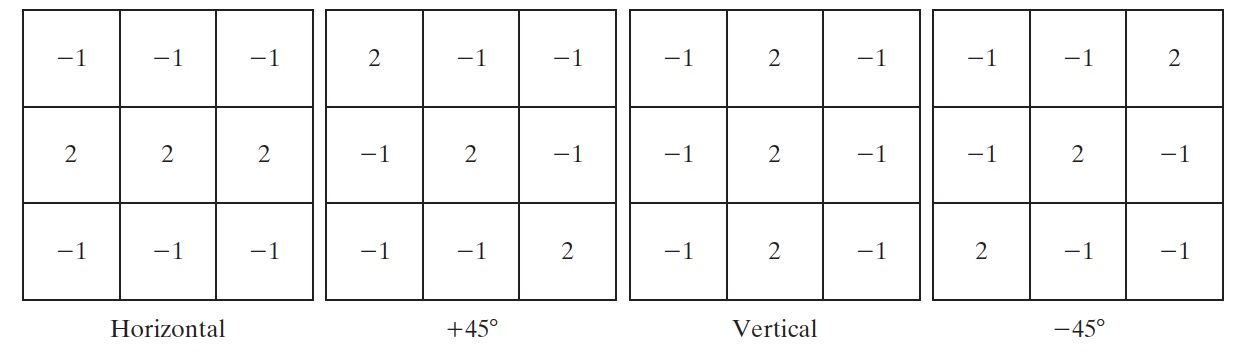
在 \(M(x,y)\) 的每一个 \(3 \times 3\) 区域内,对于一个通过该区域中心点的边缘,我们定义四个方向范围:水平,垂直、+45 度、-45 度(分别用 \(d_1, d_2, d_3, d_4\) 表示),如图 56 (c)所示(说明,水平方向和 \(x\) 轴方向一致,在图中是上下方向,并不是左右方向)。
记细化后的梯度(幅值)图像为 \(g_N(x,y)\) 。
非最大抑制算法计算 \(g_N(x,y)\) 中某一个像素的过程如下:
(1) 把“和区域中心点的梯度角度 \(\alpha(x,y)\) 最接近的方向”记为 \(d_k\) (前面介绍的四个方向之一);
(2) 在 \(M(x,y)\) 图像中,如果区域中心点的值大于其沿着 \(d_k\) 方向的两个相邻点,则保留下来(即 \(g_N(x,y) = M(x,y)\) ),否则就抑制它(即 \(g_N(x,y) = 0\) )。这就是“非最大抑制”算法名字的由来。
例如,在图 56 (b)中,和 \(p_5\) 处的梯度角度 \(\alpha(x,y)\) 最接近的方向范围是 \(d_1\) ,则我们只关心 \(d_1\) 方向上和 \(p_5\) 相邻的两点 \(p_2\) 和 \(p_8\) 。如果 \(p_5\) 比 \(p_2\) 和 \(p_8\) 都要大,则 \(p_5\) 的值就作为 \(g_N(x,y)\) 图像中对应位置上的值,否则以 0 作为 \(g_N(x,y)\) 图像中对应位置上的值。这样,用相同的方法处理完 \(M(x,y)\) 中的所有点后,得到的 \(g_N(x,y)\) 显然比 \(M(x,y)\) 要多很多零值点(边缘被细化了)。
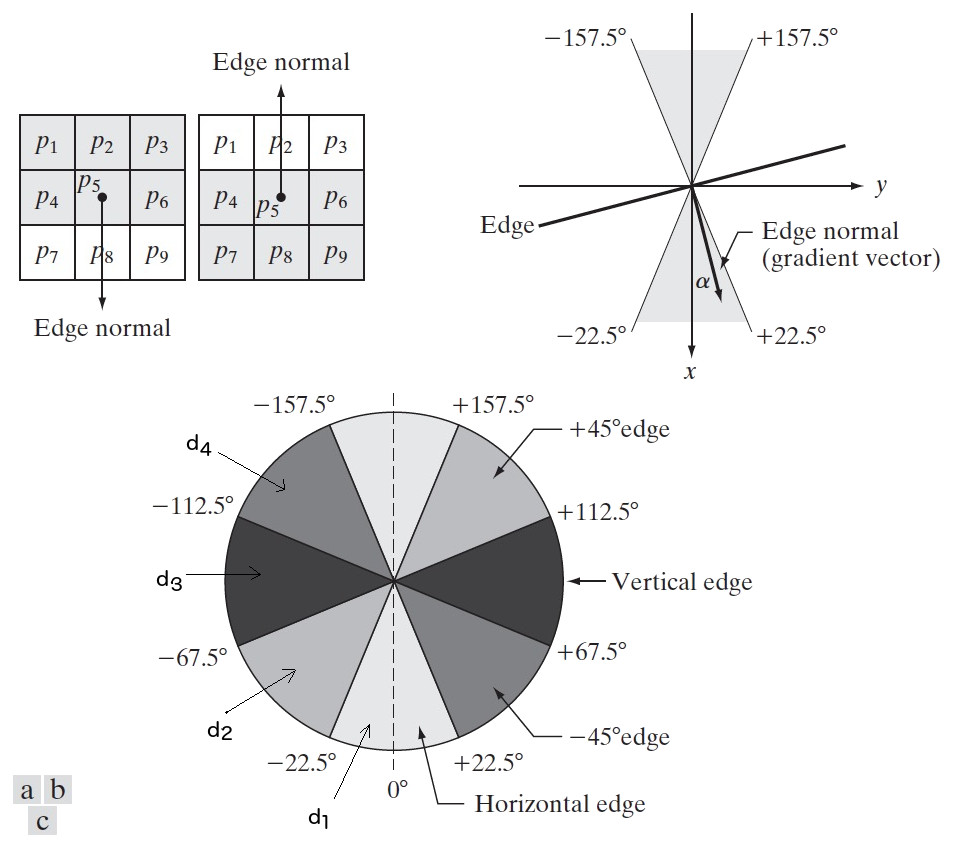
Figure 56: 非最大抑制(normal 是“法线”的意思)
4.1.7. 用霍夫变换(Hough Transform)检测形状
霍夫变换(Hough Transform)可以用来寻找图像中的直线,扩展后可以用来寻找其他的形状(如圆形等等)。
下面用检测直线来说明霍夫变换的基本思想。假设直线由两点 \(A=(x_1,y_1)\) 和 \(B=(x_2,y_2)\) 定义(如图 57 (a)所示)。 通过点 \(A\) 的所有直线可用 \(y_1 = k x_1 + q\) 表示。 同一个方程可以解释为参数空间 \(k,q\) 的方程,因此通过点 \(A\) 的所有直线可以表示为方程 \(q = -x_1 k +y_1\) (如图 57 (b)所示),类似地, 通过点 \(B\) 的所有直线可以表示为方程 \(q = -x_2 k +y_2\) 。在参数空间 \(k,q\) 中,两条直线的唯一公共点是在原图像空间中表示连接点 \(A\) 和 \(B\) 的唯一存在的直线。这样,我们在参数空间中检测相交的点就相当于在原图像空间中检测直线,后文将介绍这个过程。
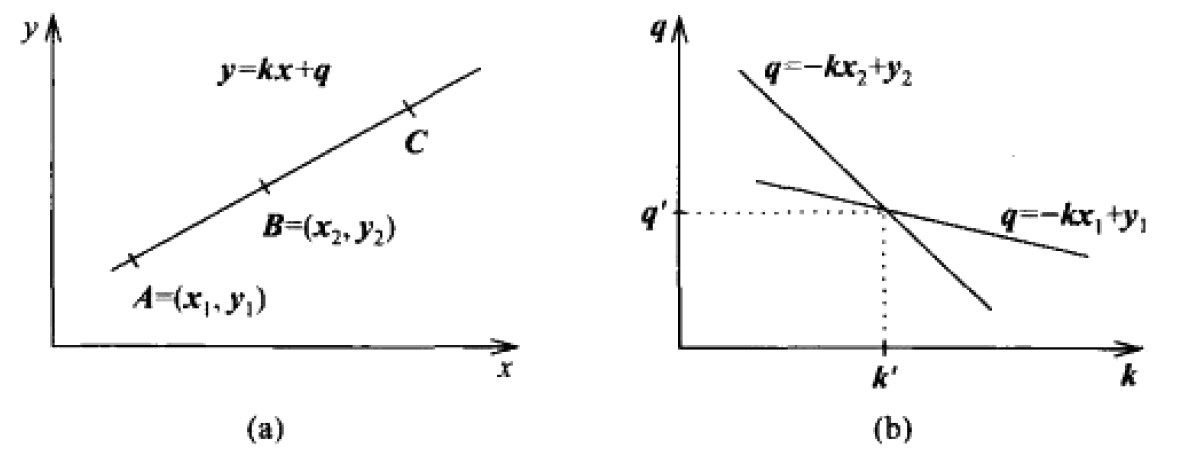
Figure 57: Hough 变换原理。(a)原图像空间,(b)参数空间
不过,当直线逼近垂直方向时,直线的斜率 \(k\) 会趋于无限大,比较难处理,这时可以把直线表达为下面形式(这时参数空间为 \(\rho, \theta\) ): \(x \cos \theta + y \sin \theta = \rho\) ,经过原图像空间某点的所有直线,在参数空间 \(\rho, \theta\) 中是一条正弦曲线,如图 58 所示。
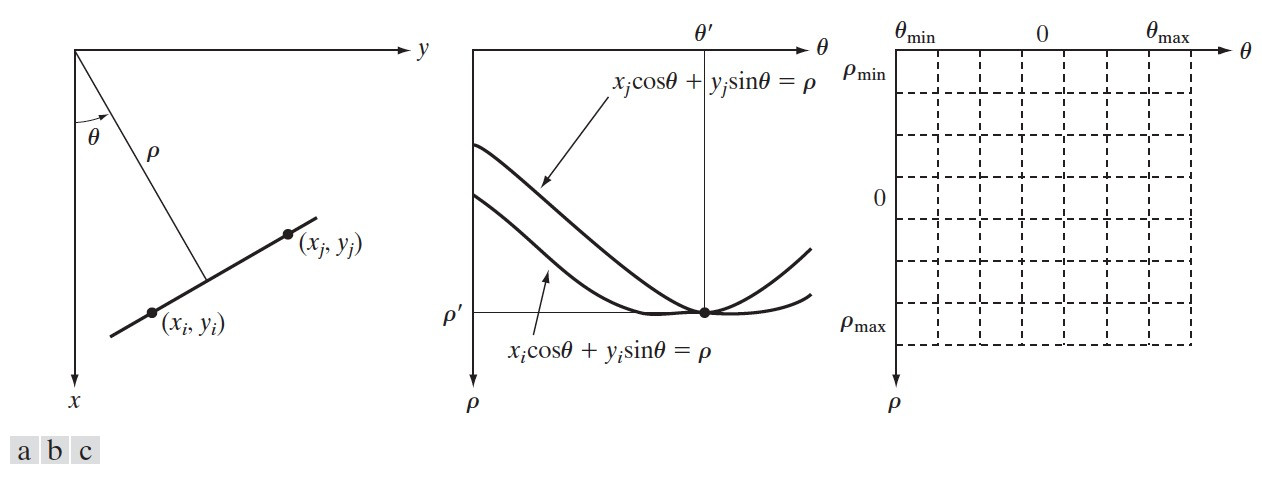
Figure 58: (a)原图像空间,(b)参数空间 \(\rho, \theta\) ,(c)把 \(\rho, \theta\) 空间划分为累加单元(某个累加单元的点非常多时就说明找到了原图像空间的直线)
一般来说,由于噪声或计算误差,原图像空间中的直线不会精确地被变换到参数空间中的一个点,而是一个点群,点群中心可以作为原图像空间直线的参数。我们在参数空间寻找点群的方法是:把 \(\rho, \theta\) 空间划分为累加单元(如图 58 (c)所示),哪个累加单元的点非常多,就说明找到了原图像空间的直线。
详情可参考:《图像处理、分析与机器视觉(第 3 版,艾海舟等译)》,6.2.6 霍夫变换
4.1.7.1. 霍夫变换对噪声不敏感
霍夫变换有个重要性质:它对图像中直接的残缺部分、噪声以及其他共存的非直线结构不敏感。 如图 59 所示。

Figure 59: (a)原始图像,(b)边缘图像,(c)Hough 变换的参数空间,(d)Hough 变换检测到的直线
4.2. 阈值处理(Thresholding)
阈值处理直观、实现简单、计算速度快,它在图像分割应用中处于核心地位。利用阈值处理,可以基于灰度值的特性将图像直接划分为不同区域。
4.2.1. 阈值处理基础知识
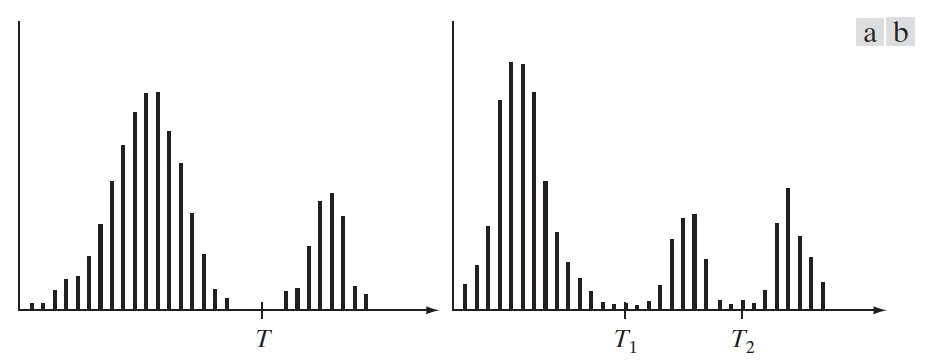
Figure 60: (a)可被单阈值分隔的灰度直方图,(b)可被双阈值分隔的灰度直方图
假设某图像 \(f(x,y)\) 由暗色的背景和较亮的物体组成,其灰度直方图如图 60 (a)所示,从这个图像的背景中提取物体的一种明显方法是选择一个合适的阈值 \(T\) ,使得背景点都满足 \(f(x,y) \le T\) ,而物体像素点都满足 \(f(x,y) > T\) 。换句话说,分割后的图像 \(g(x,y)\) 由下式给出:
\[g(x,y) = \begin{cases} 1, & f(x,y) > T \\ 0, & f(x,y) \le T \end{cases}\]
如果 \(T\) 是一个适用于整个图像的常数,则上面公式给出的处理称为 “全局阈值处理” 。当 \(T\) 值在一幅图像上改变时,称为 “可变阈值处理” (有时也称为“局部阈值处理”或者“区域阈值处理”)。可以把阈值从单个扩展到多个(如图 60 (b)所示),这称为“多阈值处理”。
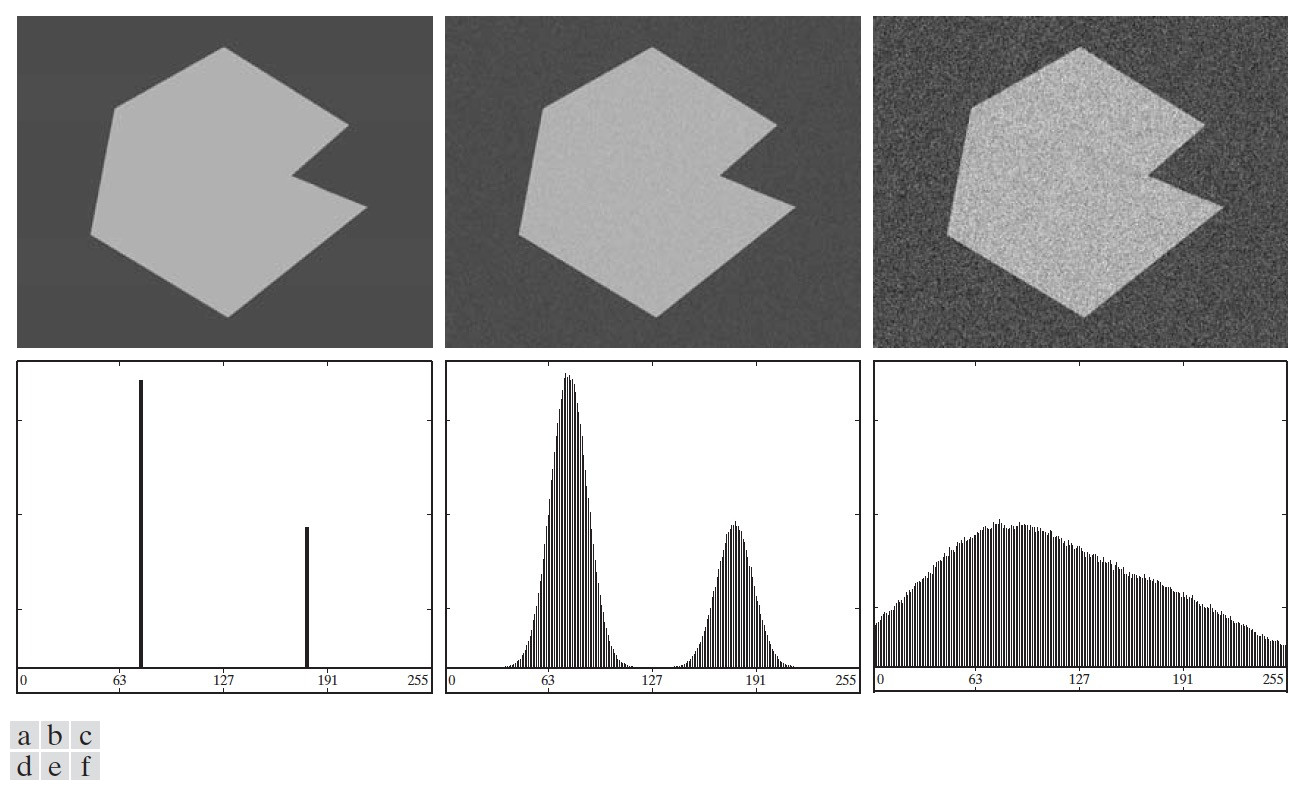
4.2.1.1. 噪声对阈值处理的影响
4.2.1.2. 光照和反射对阈值处理的影响
图 62 (c)显示了非均匀光照对一幅图像的直方图的影响,我们无法直接使用阈值处理来分割它的背景和物体。如果光照是均匀的,但图像的反射不均匀也会得到类似的结果。
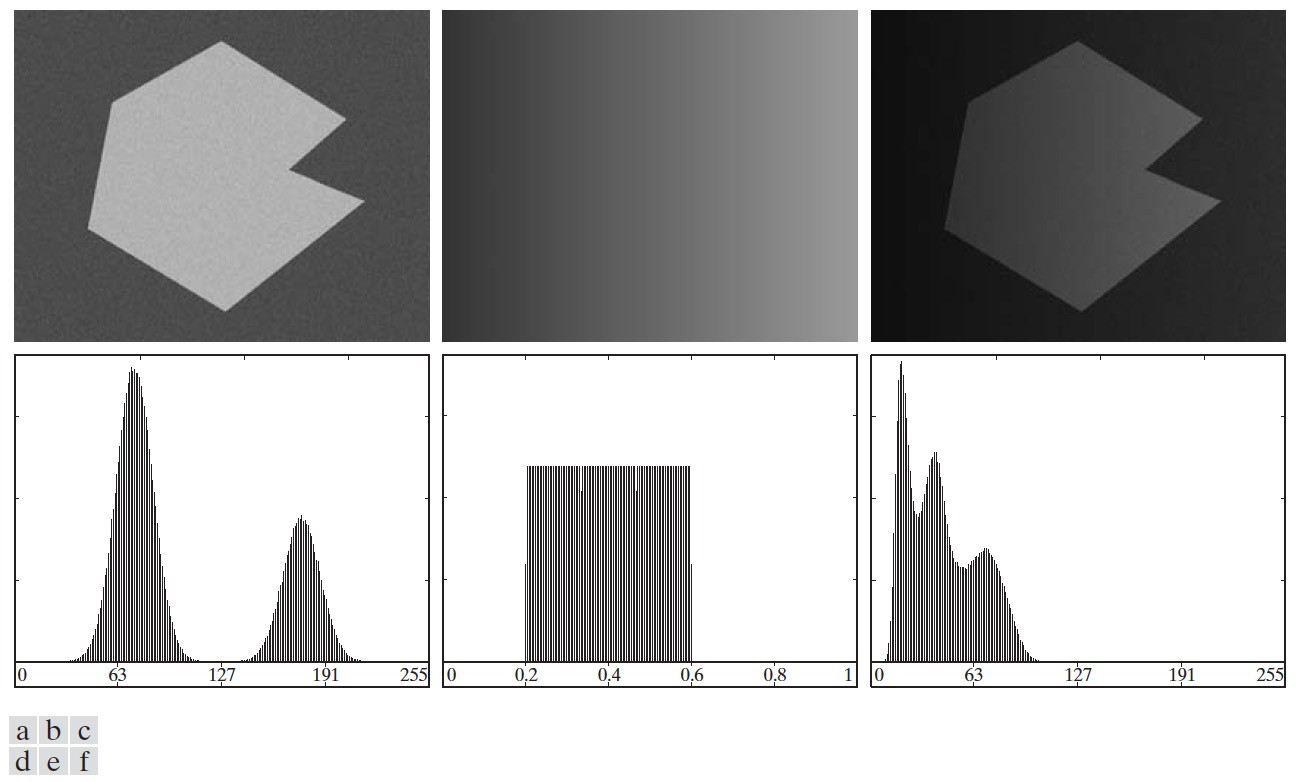
Figure 62: (a)带有噪声的图像,(b)一个灰度斜坡图像,(c)图(a)和图(c)相乘的图像(可模拟非均匀光照图像),(d)~(f)相应的直方图
对于光照或反射不均匀造成无法直接使用阈值处理来分割背景和物体的问题,一般有三种办法来解决:
(1) 直接校正这种阴影模式。例如,非均匀光照可以用相反的模式与图像相乘来校正;
(2) 可尝试使用 3.4.3.2 中介绍的顶帽变换来校正全局阴影模式;
(3) 可尝试使用 4.2.6 中介绍的可变阈值处理。
4.2.2. 基本全局阈值处理
当物体和背景像素的灰度分布相差明显时,可以用全局阈值处理来分割背景和物体。但如何找到一个合适的阈值呢?
可以使用下面的迭代算法来寻找全局阈值 \(T\) :
(1) 为全局阈值 \(T\) 选择一个初始估计值;
(2) 用阈值 \(T\) 分割该图像。这将产生两组像素: \(G_1\) 由灰度值大于 \(T\) 的所有像素组成, \(G_2\) 由灰度值小于等于 \(T\) 的所有像素组成。
(3) 对 \(G_1\) 和 \(G_2\) 的像素分别计算平均灰度值,记为 \(m_1\) 和 \(m_2\) 。
(4) 计算一个新的阈值:
\[T = \frac{1}{2} (m_1 + m_2)\]
(5) 重复步骤 2 到步骤 4,直到连续迭代中的 \(T\) 值间的差小于一个预定义的参数 \(\Delta T\) 为止。
图 63 是全局阈值处理的一个例子。
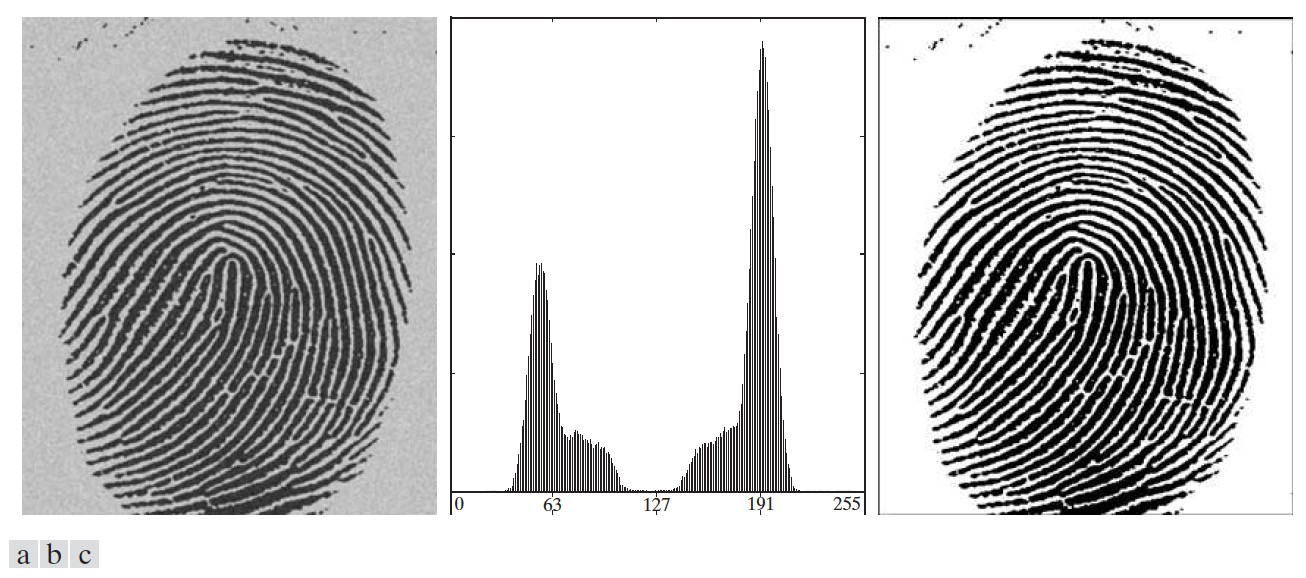
Figure 63: (a)带噪声的指纹,(b)图(a)的直方图,(c)使用全局阈值处理的结果(迭代后得到的阈值 \(T\) 为 125.4)
4.2.3. 用 Otsu 方法(类间最大方差法)进行全局阈值处理
Otsu方法 是由日本学者 Nobuyuki Otsu 于 1979 年提出的一种对图像进行全局阈值处理的算法。
Otsu 方法的基本思想为:按图像的灰度特性,将图像分成背景和物体二个部分时,背景和目标之间的方差越大,说明图像的这二个部分的差别会越大,分类效果越好。 但怎么描述背景和目标之间的方差(称为类间方差)呢?请看下文说明。
介绍“类间方差”前,先介绍一些基本知识。
假设图像阈值化处理后为两类 \(C_1\) 和 \(C_2\) ,其中 \(C_1\) 由图像中灰度值在范围 \([0,k]\) 内的所有像素组成, \(C_2\) 由灰度值在范围 \([k+1, L-1]\) 内的所有像素组成。则,像素被分到类 \(C_1\) 中的概率 \(P_1(k)\) 为:
\[P_1(k) = \sum_{i=0}^{k} p_i\]
其中, \(p_i\) 是归一化直方图中灰度为 \(i\) 时的值。
像素被分到类 \(C_2\) 中的概率 \(P_2(k)\) 为:
\[P_2(k) = 1 - P_1(k)\]
记 \(m_1(k)\) 和 \(m_2(k)\) 分别为 \(C_1\) 和 \(C_2\) 的灰度均值, \(m_G\) 为整个图像的灰度均值(它和 \(m_1(k)\) 和 \(m_2(k)\) 之间存在关系: \(P_1(k) m_1(k) + P_2(k) m_2(k) = m_G\) )。
由节 2.2.3 知识可知,整个图像的灰度方差为:
\[\sigma_G^2 = \sum_{i=0}^{L-1} (i - m_G)^2 p_i\]
为了使记号不过于累赘,下面的讨论我们暂时省略 \(k\) 。
记 \(\sigma_B^2\) 为类间方差(between-class variance),其定义为:
\[{\color{red}{\sigma_B^2 = P_1 (m_1 - m_G)^2 + P_2 (m_2 - m_G)^2}}\]
利用关系式 \(P_1 m_1 + P_2 m_2 = m_G\) ,类间方差还可以化为下面形式:
\[\sigma_B^2 = P_1 P_2 (m_1 - m_2)^2\]
从上式可以看出, 两个类的灰度均值 \(m_1\) 和 \(m_2\) 彼此相隔越远时, \(\sigma_B^2\) 会越大,这表明类间方差 \(\sigma_B^2\) 是类之间的可分性度量。
\(C_1\) 和 \(C_2\) 类是以阈值 \(k\) 为分类依据的, \(k\) 取不同的值时,可得到不同的类间方差 \(\sigma_B^2(k)\) , Otsu 方法的核心 就是求当 \(\sigma_B^2(k)\) 取得最大值时,对应的阈值 \(k^{*}\) 作为最终的阈值。用公式表达就是:
\[\sigma_B^2(k^*) = \max_{0 \le k \le L-1} \sigma_B^2(k)\]
4.2.3.1. 可分性度量
找到一个全局阈值后,怎么评价它的好坏呢?引入下面归一化的度量值:
\[\eta(k) = \frac{\sigma_B^2(k)}{\sigma_G^2}\]
\(0 \le \eta(k) \le 1\) ,当 \(\eta(k)\) 越接近于 1 时,说明阈值 \(k\) 的可分性越好。
4.2.4. 利用图像平滑改善全局阈值处理
4.2.5. 利用边缘改善全局阈值处理
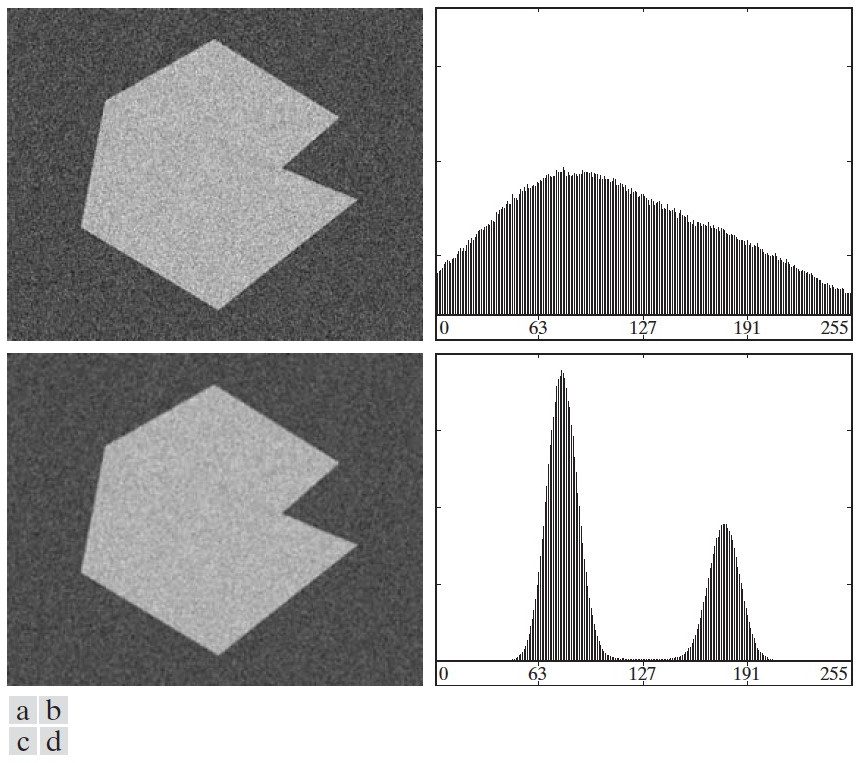
节 4.2.4 中介绍的利用平滑方法并不能改善所有的全局阈值处理,如图 66 所示,背景中的物体太小,经过平滑处理后,没有产生新的波峰,还是无法使用全局阈值处理。
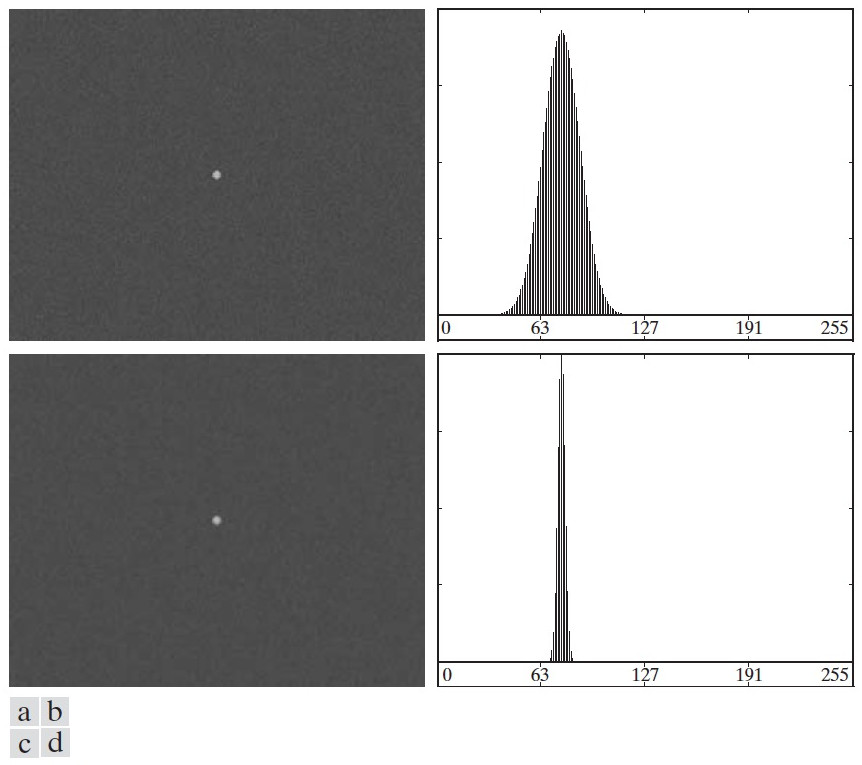
Figure 66: (a)原始图像,(b)图(a)直方图,(c)对图(a)使用 \(5\times5\) 均值模板进行平滑处理后的结果,(d)图(c)的直方图(还是没有产生新的波峰)
这时怎么办呢?改进直方图形状的另一种思路是: 仅考虑那些位于或靠近“物体和背景的过渡位置(即边缘)”的像素,这些部分像素构成一个子图,用全局阈值处理(如 Ostu 方法)从这个子图中得到一个阈值,再利用这个阈值处理整个原始图像。
但,完整的边缘信息在用阈值处理进行分割操作期间是不可用的,因为寻找边缘正好是分割所要做的工作。利用梯度幅度图像或拉普拉斯绝对值图像可以得到边缘的基本信息。
下面通过一个例子来说明如何利用边缘来改善全局阈值处理。如图 67 所示。
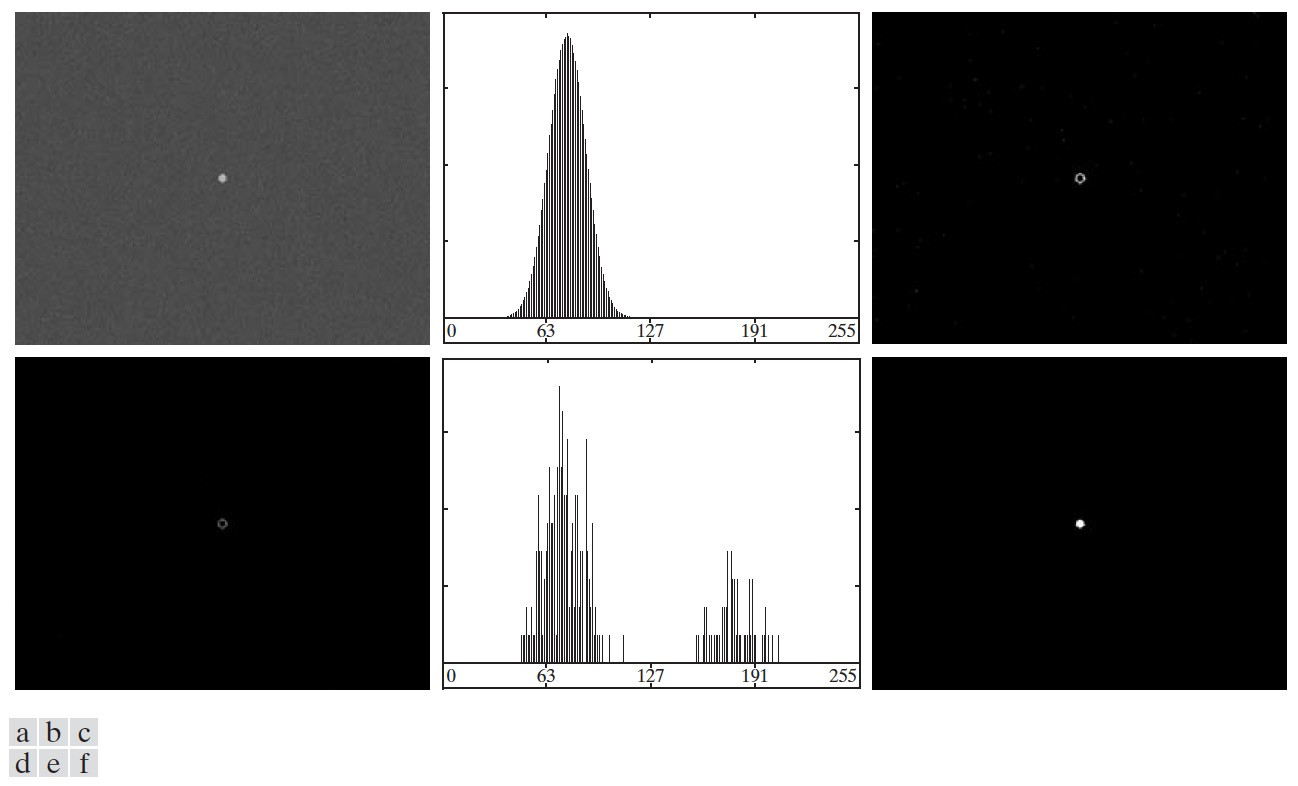
Figure 67: (a)原始图像,(b)图(a)直方图,(c)梯度图像(阈值处理为二值图像),(d)图(a)和图(c)的对应像素相乘(非零像素构成的子图是原始图像中位于或靠近的像素点),(e)图(d)中非零像素的直方图,(f)用 Otsu 方法处理直方图(e),得到阈值(为 134)后,用该阈值处理原始图像的结果
4.2.6. 可变阈值处理(局部阈值处理/区域阈值处理/动态阈值处理/自适应阈值处理)
可变阈值处理(又称为“局部阈值处理”或者“区域阈值处理”)是指阈值 \(T\) 在整个图像中是可变的。当阈值 \(T\) 取决于空间坐标 \((x,y)\) 时,可变阈值处理通常称为“动态阈值处理”,或者“自适应阈值处理”。
4.2.6.1. 图像分块
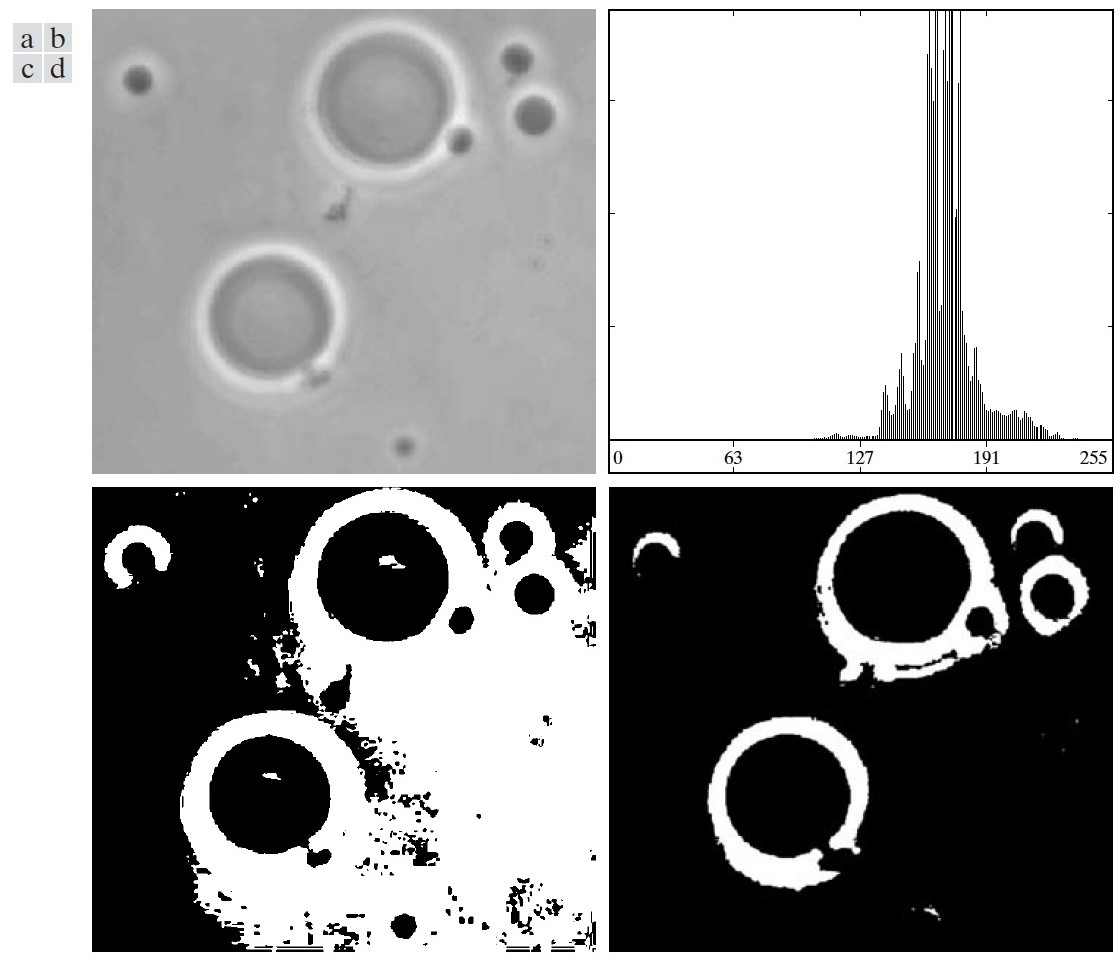
可变阈值处理最简单的方法之一是把一幅图像分成不重叠的矩形(这种方法称为“图像分块”)。这种方法可用于补偿光照或反射不均匀性。选择的矩形要足够小,以便每个矩形的光照都近似是均匀的。图 68 显示了“图像分块”进行可变阈值处理的例子。
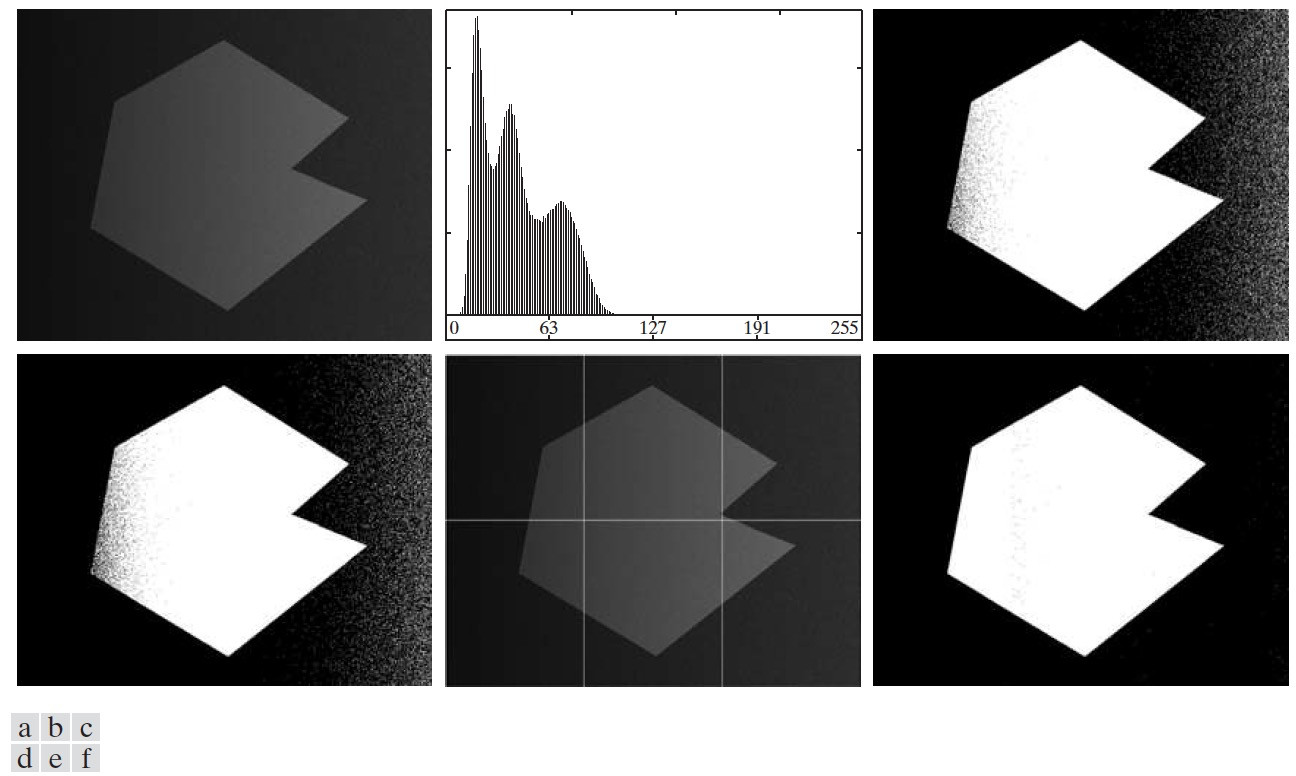
Figure 68: (a)带噪声阴影的图像,(b)图(a)的直方图,(c)用基本全局阈值处理的结果,(d)用 Otsu 方法得到的结果,(e)把图(a)分为 6 个子图像,(f)对图(e)每一幅子图像应用 Otsu 方法的结果
图 68 (e)的 6 个子图像的直方图如图 69 所示,显然对每个图像直接用阈值处理即可分割背景和物体了。
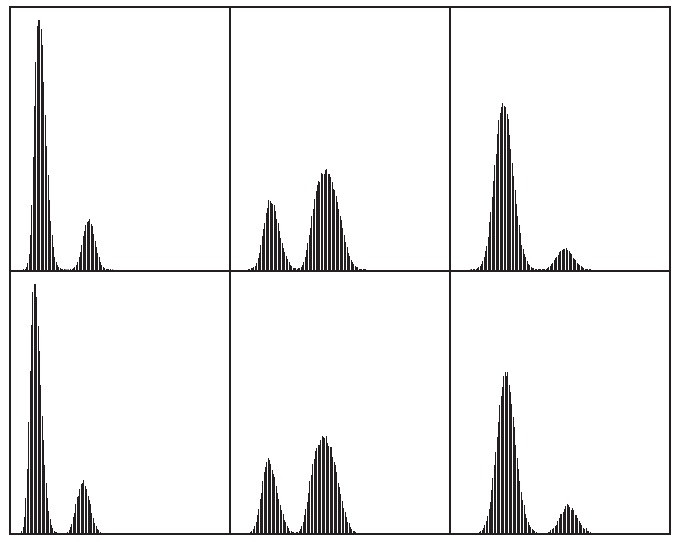
Figure 69: 图 68 (e)的 6 个子图像的直方图
4.2.6.2. 基于局部图像特性的可变阈值处理
与前面讨论的图像细分方法相比,更为一般的方法是在一幅图像中的每一点 \((x,y)\) 处计算阈值。一般来说,每一点处的阈值由该点的一个邻域内的像素的“灰度标准差”和“灰度均值”来决定,因为这两个量分别是局部对比度和局部平均灰度的描述子。令 \(\sigma_{xy}\) 和 \(m_{xy}\) 分别表示一幅图像中以坐标 \((x,y)\) 为中心的邻域所包含的像素集合的“灰度标准差”和“灰度均值”(关于它们的计算可参考节 2.2.3 )。
可变阈值处理的通用形式为:
\[T_{xy} = a \sigma_{xy} + b m_{xy}\]
其中, \(a\) 和 \(b\) 为非负常数(它们往往通过试验来确定)。
分割后的图像计算如下:
\[g(x,y) = \begin{cases} 1, & f(x,y) > T_{xy} \\ 0, & f(x,y) \le T_{xy} \end{cases}\]
其中, \(f(x,y)\) 是输入图像。
4.2.6.3. 使用移动平均(Using moving average)
这一节介绍的内容是上一节内容(可变阈值处理)的特殊情形,它使用点 \((x,y)\) 处邻域内像素的“灰度均值”来计算 \((x,y)\) 点的局部阈值,即 \(T_{xy} = b m_{xy}\) 。
“移动平均(Moving average)”采用下面方式计算 \(m_{xy}\) :把图像以 Z 字形展开为一维序列,表示为 \(z_1, z_2, \cdots\) ,图 70 是移动平均的原理。
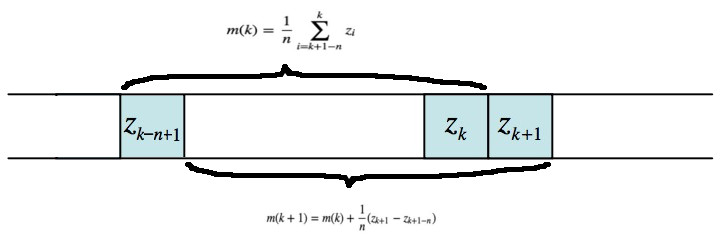
Figure 70: “移动平均”原理(一个新的灰度值加入时,同时剔出一个旧的灰度值,无需每次都重新将逐个数值加起来求平均)
可以用下面方式求“移动平均”:
\[m_{xy} = m(k+1) = \frac{1}{n} \sum_{i=k+2-n}^{k+1} z_i = m(k) + \frac{1}{n}(z_{k+1} - z_{k+1-n})\]
其中, \(n\) 表示用于计算平均灰度的点数,且 \(m(1) = z_1/n\) ,这个初始值严格来说并不正确,因为单点的平均值是该点自身的值。从另外一个角度看,如果图像的边界填充了 \(n-1\) 个 0,那么 \(m(1) = z_1/n\) 是合理的。
图 71 是“移动平均”可变阈值对手写文本图像进行处理的实例( \(n\) 的经验值是平均笔画宽度的 5 倍,在这里平均笔画宽度是 4 像素,所以 \(n\) 取 20,而 \(b\) 可取 0.5)。

Figure 71: 每一排的左图是原图,中图是 Otsu 方法处理的结果,右图是用“移动平均”进行可变阈值处理的结果
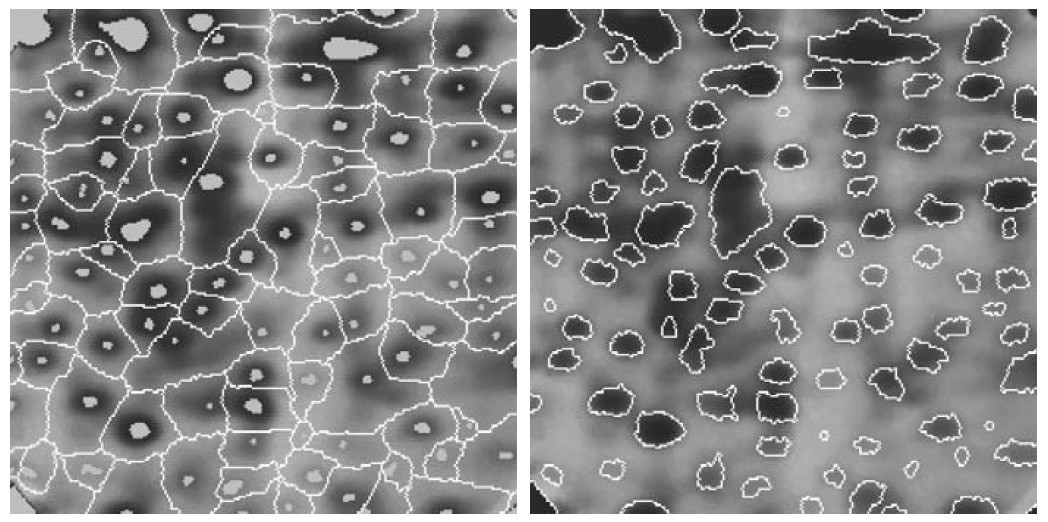
4.3. 使用形态学分水岭(Watershed)的分割
分水岭(Watershed)和集水盆地(Catchment basins)是地形学中广泛使用的概念。分水岭分开每个集水盆地。
在“地形学”解释中,我们考虑三种类型的点:(a)属于一个区域最小值的点;(b)把一点看成是一个水滴,如果把这些点放在任意位置上,水滴一定会下落到一个单一的最小值点;(c)处在该点的水会等可能性地流向不止一个这样的最小值点。其中,满足条件(b)的点的集合称为集水盆地;满足条件(c)的点形成的地表面的峰线,称为“分水线(Watershed lines)”。
基于这些概念的分割算法的主要目标是找出分水线。其基本思想比较简单:假设在每个区域的最小值上打一个洞,并且让水通过洞以均匀的速率上升,从低到高淹没整个地形。当不同的集水盆地中上升的水聚集时,修建一个水坝来阻止这种聚合,当水继续上升,最后只剩下了水坝。这些水坝就是用分水岭算法提取出来的边界。 如图 72 所示。
由前面的分析可知,分水岭算法可以保证分割区域的连续性和封闭性,消除了分割线断裂的问题。
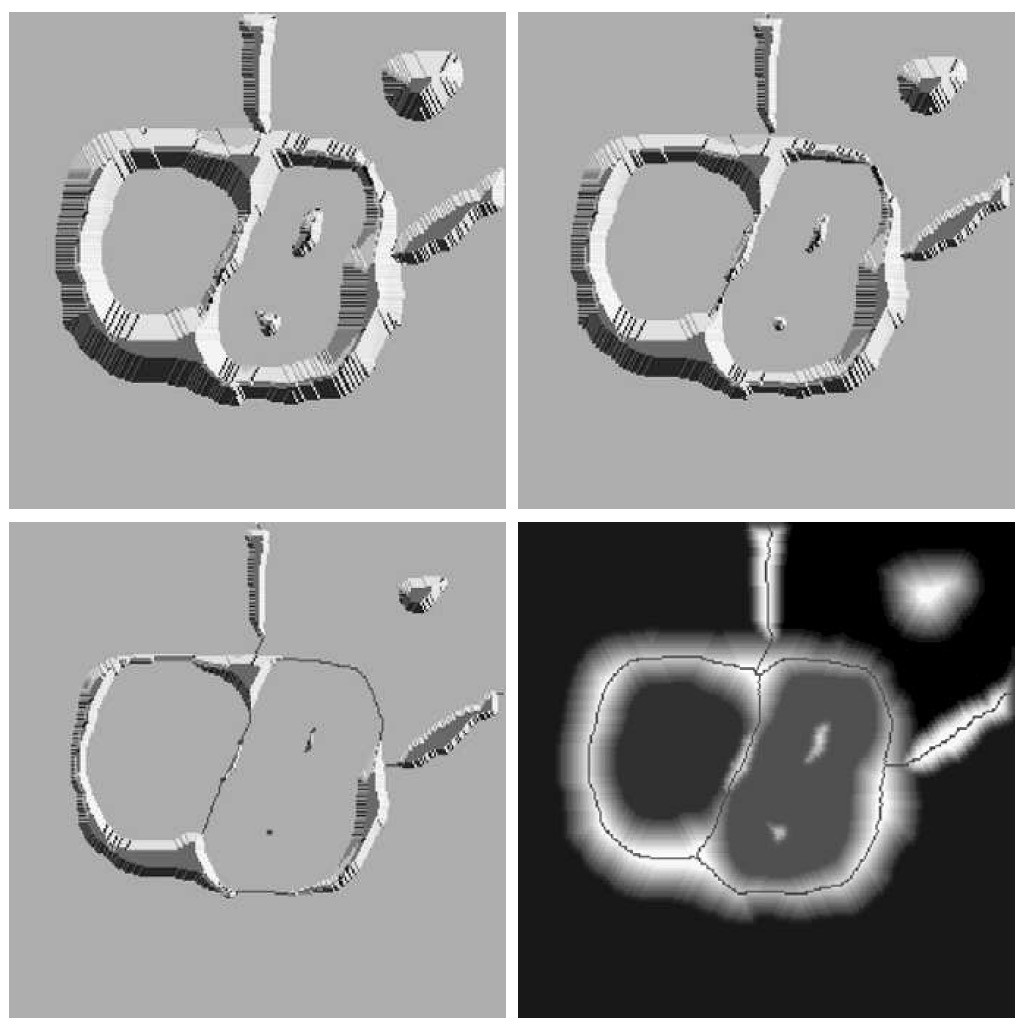
Figure 72: 分水岭算法原理:当水从低到高淹没整个地形时,修建水坝来阻止不同的集水盆地中的水聚集
由于变化较小的灰度对应的区域有较小的梯度值,所以分水岭算法作用于图像的梯度图像,而不是图像本身。