Lagrangian Dual Problem
Table of Contents
1. 前言
阅读本文前,请先了解拉格朗日乘数法和 KKT 最优化条件(拉格朗日乘数法的推广)。本文讨论的内容“拉格朗日对偶问题”在关于“凸优化”的相关书籍中可以找到。
参考:
http://ocw.nctu.edu.tw/course/np982/Lecture12.pdf
http://cbio.ensmp.fr/~jvert/teaching/2006insead/slides/4_duality/duality.pdf
《统计学习方法,李航著》
2. 拉格朗日对偶问题
这里讨论的问题就是 KKT 最优化条件所适用的含不等式约束条件的最优化问题。
原始问题为:
假设 \(f(\boldsymbol{x}),g_i(\boldsymbol{x}),h_i(\boldsymbol{x})\) 是定义在 \(\mathbb{R}^n\) 上的连续可微函数。考虑下面最优化问题:
\[\begin{aligned}
& \text{minimize} & & f(\boldsymbol{x}) \\
& \text{subject to} & & g_i(\boldsymbol{x}) \le 0, \; i = 1,2,\cdots,m \\
&&& h_j(\boldsymbol{x}) = 0, \; j = 1,2,\cdots,n
\end{aligned}\]
“KKT 最优化条件”指出当 \(f(\boldsymbol{x})\) 取最小值时, \(\boldsymbol{x}\) 满足下面的方程组:
\[\begin{cases}
\nabla f(\boldsymbol{x}) + \sum_{i=1}^{m} \mu_i \nabla g_i(\boldsymbol{x}) + \sum_{j=1}^{n} \lambda_j \nabla h_j(\boldsymbol{x}) = 0 \\
g_i(\boldsymbol{x}) \le 0, \, \forall i = 1, \cdots, m \\
h_j(\boldsymbol{x}) = 0, \, \forall j = 1, \cdots, n \\
\mu_i \ge 0, \, \forall i = 1, \cdots, m \\
\mu_i g_i(\boldsymbol{x}) = 0, \, \forall j = 1, \cdots, m
\end{cases}\]
求解上面方程组,可以得到原问题的解。
但我们还有其它的办法——先求解这个问题的对偶问题(有时求解对偶问题比求解上面方程组更加容易),从而由对偶问题的解得到原问题的解。
2.1. 对偶问题
引入广义拉格朗日函数:
\[\mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol{x}) + \sum_{i=1}^{m}\mu_i g_i(\boldsymbol{x}) + \sum_{j=1}^{n}\lambda_j h_j(\boldsymbol{x})\]
定义关于 \(\boldsymbol{x}\) 的函数:
\[\phi(\boldsymbol{x}) = \max_{\boldsymbol{\lambda},\boldsymbol{\mu};\mu_i \ge 0} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})\]
下面分析一下函数 \(\phi(\boldsymbol{x})\) :
(1) 如果 \(\boldsymbol{x}\) 满足原问题约束条件 \(g_i(\boldsymbol{x}) \le 0, \; i = 1,2,\cdots,m\) 及 \(h_j(\boldsymbol{x}) = 0, \; j = 1,2,\cdots,n\) ,则有:
\[\begin{aligned}
\mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) & =
f(\boldsymbol{x}) + \underbrace{\sum_{i=1}^{m}\mu_i g_i(\boldsymbol{x})}_{\le 0} + \underbrace{\sum_{j=1}^{n}\lambda_j h_j(\boldsymbol{x})}_{= 0} \\
& \le
f(\boldsymbol{x})
\end{aligned}\]
从而:
\[\phi(\boldsymbol{x}) = \max_{\boldsymbol{\lambda},\boldsymbol{\mu};\mu_i \ge 0} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol{x})\]
(2) 如果 \(\boldsymbol{x}\) 不满足原问题的约束条件,则可得: \(\phi(\boldsymbol{x}) = \max \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \to +\infty\) ,这是因为:
(2.1) 如果存在某个 \(i\) 使得 \(g_i(\boldsymbol{x}) > 0\) ,则可以令 \(\mu_i \to +\infty\) ,从而 \(\phi(\boldsymbol{x}) = \max \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \to +\infty\)
(2.2) 如果存在某个 \(j\) 使得 \(h_j(\boldsymbol{x}) \ne 0\) ,则可令 \(\lambda_j h_j(\boldsymbol{x}) \to + \infty\) ,从而 \(\phi(\boldsymbol{x}) = \max \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \to +\infty\)
综上所述,有:
\[\phi(\boldsymbol{x}) = \max_{\boldsymbol{\lambda},\boldsymbol{\mu};\mu_i \ge 0} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = \begin{cases}
f(\boldsymbol{x}), & \boldsymbol{x}\text{满足原始问题的约束条件} \\
+\infty, & \text{otherwise}
\end{cases}\]
由上式可知,如果我们考虑 \(\phi(\boldsymbol{x})\) 的最小化问题,那么它显然和原问题是等价的。即原问题等价于下面优化问题:
\[\underset{\boldsymbol{x}}{\text{minimize}} \max\limits_{\boldsymbol{\lambda},\boldsymbol{\mu};\mu_i \ge 0} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})\]
上面问题还不是原问题对偶问题,再考虑上面优化问题的变换形式(把“先求最大值再求最小”值转换成了“先求最小值再求最大值”):
\[\begin{aligned}
& \underset{\boldsymbol{\lambda},\boldsymbol{\mu}}{\text{maximize}} && \min\limits_{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\
& \text{subject to} && \mu_i \ge 0, \; i = 1,2,\cdots,m
\end{aligned}\]
我们定义这个问题为 原问题的拉格朗日对偶问题(Lagrangian dual problem)。
2.1.1. 对偶问题总结
对前面介绍知识简单总结如下:
\[\begin{array}{l|l|l}
\text{Primal problem} & \text{和原问题等价的优化问题} & \text{Lagrangian Dual problem} \\
\hline \\
\underset{\boldsymbol{x}}{\text{minimize}} \; f(\boldsymbol{x}) & \underset{\boldsymbol{x}}{\text{minimize}} \max\limits_{\boldsymbol{\lambda},\boldsymbol{\mu};\mu_i \ge 0} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) & \underset{\boldsymbol{\lambda},\boldsymbol{\mu}}{\text{maximize}} \min\limits_{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\
\text{subject to}: g_i(\boldsymbol{x}) \le 0, \; i = 1,2,\cdots,m & & \text{subject to}: \mu_i \ge 0, \; i = 1,2,\cdots,m \\
\qquad \qquad h_j(\boldsymbol{x}) = 0, \; j = 1,2,\cdots,n & & \\
\end{array}\]
其中, \(\mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol{x}) + \sum_{i=1}^{m}\mu_i g_i(\boldsymbol{x}) + \sum_{j=1}^{n}\lambda_j h_j(\boldsymbol{x})\)
说明:对偶问题中的目标函数称为 对偶函数 ,即对偶函数定义为: \(\Theta(\boldsymbol{\lambda}, \boldsymbol{\mu}) = \min\limits_{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})\)
3. 对偶问题解和原问题解的关系
3.1. Weak Duality Theorem(对偶问题的最优值小于等于原问题的最优值)
弱对偶定理:
如果原问题和其对偶问题都存在最优值,设原问题的最优值(最小值)为 \(p^{*}\) ,对偶问题的最优值(最大值)为 \(d^{*}\) ,则
\[d^{*} \le p^{*}\]
证明如下:
设原问题取最小值时: \(\boldsymbol{x} = \boldsymbol{\overline{x}}\) ,即有 \(p^{*} = f(\boldsymbol{\overline{x}})\) ;对偶问题取最大值时: \(\boldsymbol{\lambda} = \boldsymbol{\overline{\lambda}}, \boldsymbol{\mu} = \boldsymbol{\overline{\mu}}\) ,即有 \(d^{*} = \min\limits_{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\overline{\lambda}}, \boldsymbol{\overline{\mu}})\)
推导如下:
\[\begin{aligned}
d^{*} & = \min\limits_{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\overline{\lambda}}, \boldsymbol{\overline{\mu}}) \\
& \le \mathcal{L}(\overline{\boldsymbol{x}}, \boldsymbol{\overline{\lambda}}, \boldsymbol{\overline{\mu}}) \\
& = f(\overline{\boldsymbol{x}}) + \underbrace{\sum_{i=1}^{m}\mu_i g_i(\overline{\boldsymbol{x}})}_{\le 0} + \underbrace{\sum_{j=1}^{n}\lambda_j h_j(\overline{\boldsymbol{x}})}_{= 0} \\
& \le f(\overline{\boldsymbol{x}}) \\
& = p^{*}
\end{aligned}\]
证毕。
说明: 弱对偶定理说明“对偶函数在其约束条件下的最大值”比“原函数在其约束条件下的最小值”还小(或相等)。这样,极大化对偶函数可以逼近原函数最优解。
如果原问题是个求最大值的优化问题,那么类似地有:“对偶函数在其约束条件下的最小值”比“原函数在其约束条件下的最大值”还大(或相等)。
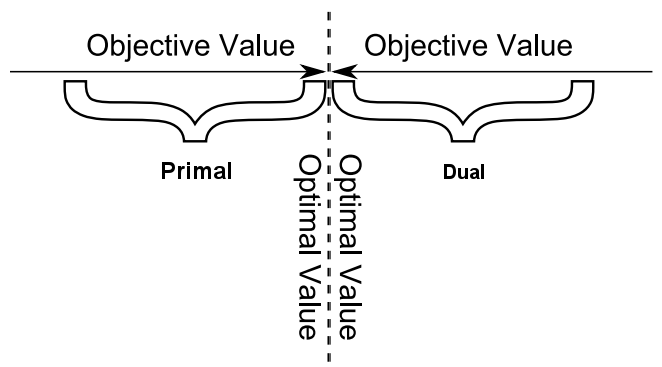
Figure 1: 对偶问题和原问题的最优值的关系
3.2. Strong Duality Theorem(一定条件下对偶问题的最优值等于原问题的最优值)
强对偶定理(这里仅给出结论,其证明从略):
如果:
(1) 函数 \(f(\boldsymbol{x})\) 和 \(g_i(\boldsymbol{x})\) 是凸函数,函数 \(h_j(\boldsymbol{x})\) 是仿射函数;
(2) 满足 Slater 条件 ,即存在一个 \(\boldsymbol{x}\) ,对所有 \(i\) 有 \(g_i(\boldsymbol{x}) < 0, h_i(\boldsymbol{x}) = 0\) (这时称不等式约束条件 \(g_i(\boldsymbol{x})\) 为严格可行的);
则存在 \(\overline{\boldsymbol{x}}, \boldsymbol{\overline{\lambda}}, \boldsymbol{\overline{\mu}}\) ,使 \(\overline{\boldsymbol{x}}\) 是原问题的解, \(\boldsymbol{\overline{\lambda}}, \boldsymbol{\overline{\mu}}\) 是对偶问题的解,并且有:
\[d^{*} = p^{*} = \mathcal{L}(\overline{\boldsymbol{x}}, \boldsymbol{\overline{\lambda}}, \boldsymbol{\overline{\mu}})\]
注:函数 \(h(\boldsymbol{x})\) 称为仿射函数(affine function),如果它满足 \(h(\boldsymbol{x}) = \boldsymbol{a} \cdot \boldsymbol{x} + b, \; a \in \mathbb{R}^n, b \in \mathbb{R}, x \in \mathbb{R}^n\) 。
4. 实例:通过求解对偶问题求解原问题(来源于 SVM)
设 \(\boldsymbol{w} = (w^{(1)}, w^{(2)})^{\mathrm{T}}, \Vert \boldsymbol{w}\Vert = \sqrt{{w^{(1)}}^2 + {w^{(2)}}^2}\) ,求解下面最优化问题:
\[\begin{aligned}
& \underset{\boldsymbol{w},b}{\text{minimize}} & & \dfrac{1}{2} \Vert \boldsymbol{w}\Vert^2 \\
& \text{subject to} & & 3w^{(1)} + 3w^{(2)} + b \ge 1 \\
&&& 4w^{(1)} + 3w^{(2)} + b \ge 1 \\
&&& -w^{(1)} - w^{(2)} - b \ge 1 \\
\end{aligned}\]
注:这个优化问题摘自《统计学习方法,李航著,例 7.1》,其背景来源于支持向量机(SVM)。
下面将用两种方法(直接求解和通过对偶问题求解)来解决这个最优化问题。
我们记:
\[f(\boldsymbol{w},b) = \frac{1}{2} \Vert \boldsymbol{w}\Vert^2 = \frac{1}{2} ({w^{(1)}}^2 + {w^{(2)}}^2)\]
广义拉格朗日函数为: \[\mathcal{L}(\boldsymbol{w},b, \boldsymbol{\alpha}) = \frac{1}{2} ({w^{(1)}}^2 + {w^{(2)}}^2) + \alpha_1(-3 w^{(1)} - 3 w^{(2)} -b + 1) + \alpha_2(-4 w^{(1)} - 3 w^{(2)} -b + 1) + \alpha_3(w^{(1)} + w^{(2)} + b + 1)\]
4.1. 方法一:直接求解原问题
我们用 KKT 最优化条件直接求解这个问题。
原问题的解满足 KKT 条件:
\[\begin{cases}
\dfrac{\partial \mathcal{L}}{\partial {w^{(1)}}} = w^{(1)} - 3 \alpha_1 - 4 \alpha_2 + \alpha_3 = 0 \\
\dfrac{\partial \mathcal{L}}{\partial {w^{(2)}}} = w^{(2)} - 3 \alpha_1 - 3 \alpha_2 + \alpha_3 = 0 \\
\dfrac{\partial \mathcal{L}}{\partial b} = - \alpha_1 - \alpha_2 + \alpha_3 = 0 \\
-3 w^{(1)} - 3 w^{(2)} -b + 1 \le 0 \\
-4 w^{(1)} - 3 w^{(2)} -b + 1 \le 0 \\
w^{(1)} + w^{(2)} + b + 1 \le 0 \\
\alpha_1 \ge 0 \\
\alpha_2 \ge 0 \\
\alpha_3 \ge 0 \\
\alpha_1(-3 w^{(1)} - 3 w^{(2)} -b + 1) = 0 \\
\alpha_2(-4 w^{(1)} - 3 w^{(2)} -b + 1) = 0 \\
\alpha_3(w^{(1)} + w^{(2)} + b + 1) = 0 \\
\end{cases}\]
求解上面方程组比较麻烦,可以按照下面的思路分情况讨论:
case 1: \(\alpha_1 = 0, \alpha_2 = 0, \alpha_3 = 0\) ,可得到 \(w^{(1)} = w^{(2)} = 0\) ,但这和方程组中第 5、6 式矛盾;
case 2: \(\alpha_1 = 0, \alpha_2 = 0, \alpha_3 > 0\) ,和方程组中第 3 式矛盾;
case 3: \(\alpha_1 = 0, \alpha_2 > 0, \alpha_3 = 0\) ,和方程组中第 3 式矛盾;
case 4: \(\alpha_1 = 0, \alpha_2 > 0, \alpha_3 > 0\) ,方程组无解(推导细节略);
case 5: \(\alpha_1 > 0, \alpha_2 = 0, \alpha_3 = 0\) ,和方程组中第 3 式矛盾;
case 6: \(\alpha_1 > 0, \alpha_2 = 0, \alpha_3 > 0\) ,得 \(\alpha_1=\alpha_4=\frac{1}{4}, w^{(1)} = w^{(2)}=\frac{1}{2}, b = -2\)
case 7: \(\alpha_1 > 0, \alpha_2 > 0, \alpha_3 = 0\) ,和方程组中第 3 式矛盾;
case 8: \(\alpha_1 > 0, \alpha_2 > 0, \alpha_3 > 0\) ,从方程组中最后 3 个式子可推出矛盾。
综上所述,有:
当 \(w^{(1)} = w^{(2)}=\frac{1}{2}, b = -2\) 时, \(f(\boldsymbol{w},b) = \frac{1}{2} \Vert \boldsymbol{w}\Vert^2\) 取约束条件下的最小值。
4.2. 方法二:先求解对偶问题再求解原问题
原问题的拉格朗日对偶问题为:
\[\begin{aligned}
& \underset{\boldsymbol{\alpha}}{\text{maximize}} && \min\limits_{\boldsymbol{w},b} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha}) \\
& \text{subject to} && \alpha_i \ge 0, \; i = 1,2,3
\end{aligned}\]
要求对偶问题的解,需要先求 \(\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})\) 对 \(\boldsymbol{w},b\) 的极小,再求对 \(\boldsymbol{\alpha}\) 的极大。
第一步:求 \(\min\limits_{\boldsymbol{w},b} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})\)
这是一个普通的多元函数极值问题。极值点处偏导数为 0。所以有:
\[\begin{cases}
\dfrac{\partial \mathcal{L}}{\partial {w^{(1)}}} = w^{(1)} - 3 \alpha_1 - 4 \alpha_2 + \alpha_3 = 0 \\
\dfrac{\partial \mathcal{L}}{\partial {w^{(2)}}} = w^{(2)} - 3 \alpha_1 - 3 \alpha_2 + \alpha_3 = 0 \\
\dfrac{\partial \mathcal{L}}{\partial b} = - \alpha_1 - \alpha_2 + \alpha_3 = 0
\end{cases}\]
得:
\[\begin{cases}
w^{(1)} = 3 \alpha_1 + 4 \alpha_2 - \alpha_3 \\
w^{(2)} = 3 \alpha_1 + 3 \alpha_2 - \alpha_3 \\
\alpha_1 + \alpha_2 - \alpha_3 = 0
\end{cases}\]
把上面方程组中第 1、2 式代入到广义拉格朗日函数 \(\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})\) 中,再尽可能利用方程组中第 3 式简化得到的结果,最后可以得到:
\[\min\limits_{\boldsymbol{w},b} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha}) = -\frac{1}{2}(18 \alpha_1^2 + 25 \alpha_2^2 + 2 \alpha_1^2 + 42 \alpha_1 \alpha_2 - 12 \alpha_1 \alpha_3 -14 \alpha_2 \alpha_3) + \alpha_1 + \alpha_2 + \alpha_3 \]
第二步:求 \(\min\limits_{\boldsymbol{w},b} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})\) 对 \(\boldsymbol{\alpha}\) 的极大。
由上面计算的结果知,对偶问题为:
\[\begin{aligned}
& \underset{\boldsymbol{\alpha}}{\text{maximize}} && -\frac{1}{2}(18 \alpha_1^2 + 25 \alpha_2^2 + 2 \alpha_1^2 + 42 \alpha_1 \alpha_2 - 12 \alpha_1 \alpha_3 -14 \alpha_2 \alpha_3) + \alpha_1 + \alpha_2 + \alpha_3 \\
& \text{subject to} && \alpha_1 + \alpha_2 - \alpha_3 = 0 \\
&&& \alpha_i \ge 0, \; i = 1,2,3 \\
\end{aligned}\]
显然,它等价于:
\[\begin{aligned}
& \underset{\boldsymbol{\alpha}}{\text{minimize}} && \frac{1}{2}(18 \alpha_1^2 + 25 \alpha_2^2 + 2 \alpha_1^2 + 42 \alpha_1 \alpha_2 - 12 \alpha_1 \alpha_3 -14 \alpha_2 \alpha_3) - \alpha_1 - \alpha_2 - \alpha_3 \\
& \text{subject to} && \alpha_1 + \alpha_2 - \alpha_3 = 0 \\
&&& \alpha_i \ge 0, \; i = 1,2,3 \\
\end{aligned}\]
容易求解这个问题(详细过程略)的解为: \(\alpha_1 = \frac{1}{4}, \alpha_2 = 0, \alpha_3 = \frac{1}{4}\)
第三步:由对偶问题的解得到原问题的解。
原问题满足“强对偶定理”的条件,利用“强对偶定理”知,对偶问题的解 \(\alpha_1 = \frac{1}{4}, \alpha_2 = 0, \alpha_3 = \frac{1}{4}\) 就是原问题取得最小值时广义拉格朗日函数 \(\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})\) 中 \(\boldsymbol{\alpha}\) 的值。有了这个信息,原问题的 KKT 最优化条件迎刃而解,原问题也迎刃而解。得原问题的解为: \(w^{(1)} = w^{(2)}=\frac{1}{2}, b = -2\) ,这和直接求解原问题得到的结果一致。