Elliptic Curve Cryptography (ECC)
Table of Contents
1. 实数域上的椭圆曲线
在实数域上,椭圆曲线(Elliptic curve)的定义(“Weierstrass Normal Form”形式)如下: \[y^2 = x^3 + ax + b\] 其中, \(a,b\) 为实数,且需满足 \(4a^3 + 27b^2 \neq 0\) ,这个不等式约束是为了保证曲线上所有点都是非奇异的(或称为光滑的)。显然,“Weierstrass Normal Form”的椭圆曲线是关于 \(x\) 轴对称的。
当 \(a,b\) 取不同值时,椭圆曲线的形状实例如图 1 所示。
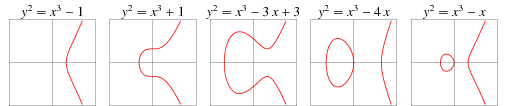
Figure 1: 当 \(a,b\) 取不同值时,椭圆曲线的形状变化(摘自:Wolfram MathWorld)
除 Weierstrass Normal Form 外,还有 Weierstrass Long Form,它可表示为 \[y^2 + a_1 xy + a_3 y = x^3 + a_2 x^2 + a_4 x + a_6\] 通过一定技巧可以把它转换为 Normal Form,这里不介绍它。
1.1. 椭圆曲线上的加法运算
前面我们已经展示过几个椭圆曲线的图像,但点与点之间好像没有什么联系。我们能不能建立一个类似于在实数轴上加法的运算法则呢?数学家们定义了一个这样的运算法则。
椭圆曲线上两个点“加法”算法的定义: 任意取椭圆曲线上两点 \(P\) 和 \(Q\) (若 \(P\) 和 \(Q\) 两点重合,则做 \(P\) 点的切线)做直线交于椭圆曲线的另一点 \(R'\) ,过 \(R'\) 做 \(y\) 轴的平行线交于 \(R\) 。我们定义点 \(R\) 就是点 \(P\) 和 \(Q\) 相加的结果,记为: \(P+Q=R\) 。
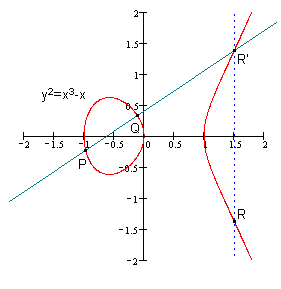
Figure 2: 加法实例(不同点相加): \(R=P+Q\)
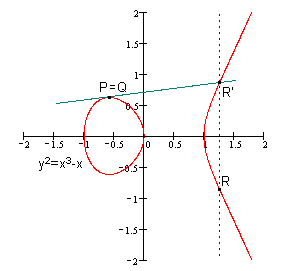
Figure 3: 加法实例(相同点相加): \(R=P+P=2P\)
注 1:我们称 \(y\) 轴的平行线与椭圆曲线的两个交点互为“负元”,图 2 和 3 的例子中 \(-R=R'\) 。
注 2: \(k\) 个相同的点 \(P\) 相加,我们记作 \(kP\) ,如图 3 例子中有 \(R=2P\) ,再如图 4 例子中有 \(P+P+P=2P+P=3P\) 。
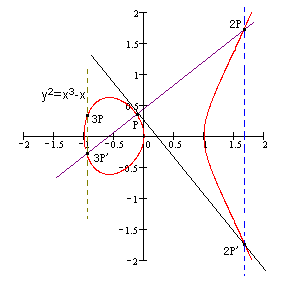
Figure 4: \(P+P+P=2P+P=3P\)
1.2. 加法运算公式
前面介绍了椭圆曲线上加法运算的定义,这节介绍它的计算公式。需要注意的是椭圆曲线上的加法不是实数中普通的加法,而是从普通加法中抽象出来的加法,他具备普通加法的一些性质,但其运算规则显然与普通加法不同。
设有椭圆曲线 \(y^2 = x^3 + ax + b\) ,点 \(P=(x_P,y_P)\) 和 \(Q=(x_Q,y_Q)\) 是椭圆曲线上的两点,求 \(P+Q\) 。
把点 \(P+Q\) 记为 \(R=(x_R,y_R)\) ,当点 \(P\) 和点 \(Q\) 是不同点时(不考虑 \(x_P = x_Q\) 的特殊情况),记斜率 \(m=\frac{y_P - y_Q}{x_P - x_Q}\) ,过这两点直线为:
\[y=m (x - x_Q) + y_Q\]
由椭圆曲线上加法运算的定义知, \(P=(x_P,y_P),Q=(x_Q,y_Q),-R=R'=(x_R, -y_R)\) 三点共线,从而这三点的坐标满足下面方程组:
\[\begin{cases}
y^2 = x^3 + ax + b \\
y=m (x - x_Q) + y_Q \\
\end{cases}\]
求解方程组可得 \(R\) 的坐标为:
\[\begin{cases}
x_R & = m^2 - x_P - x_Q \\
y_R & = - m (x_R - x_P) - y_P \\
\end{cases}\]
当点 \(P\) 和点 \(Q\) 是同一点时,按照定义,我们需要先求过 \(P\) 点的切线,再求切线与椭圆曲线联立方程组求得交点 \(-R=R'=(x_R, -y_R)\) ,详细过程省略,这里直接给出结论:很巧的是,它也可以化为上面的形式(即和点 \(P,Q\) 是不同点的形式相同),不过此时式中的 \(m = \frac{3 x^2_P + a}{2y_P}\) 。
总结,椭圆曲线 \(y^2 = x^3 + ax + b\) 上加法运算 \((x_R,y_R) = (x_P,y_P) + (x_Q,y_Q)\) 的计算公式:
\[\begin{cases}
x_R & = m^2 - x_P - x_Q \\
y_R & = - m (x_R - x_P) - y_P \\
\end{cases}\]
上式中,当点 \(P\) 和点 \(Q\) 是不同点时 \(m=\frac{y_P - y_Q}{x_P - x_Q}\) ,当点 \(P\) 和点 \(Q\) 是同一点时 \(m = \frac{3 x^2_P + a}{2y_P}\) 。
1.2.1. 加法运算实例
设有椭圆曲线 \(y^2 = x^3 -7x + 10\) ,椭圆上两点 \(P = (1,2), Q=(3,4)\) ,求 \(P + Q\) 和 \(2P\) 。
解:设 \(R = P + Q\) ,由于 \(P\) 和 \(Q\) 不同,利用上一节介绍的公式,可知:
\[\begin{aligned}
m &= \frac{y_P - y_Q}{x_P - x_Q} = \frac{2 - 4}{1 - 3} = 1 \\
x_R &= m^2 - x_P - x_Q = 1^2 - 1 - 3 = -3\\
y_R &= - m (x_R - x_P) - y_P = - 1 (- 3 - 1) - 2 = 2 \\
\end{aligned}\]
从而 \(R=(-3, 2)\) 即为所求,如图 5 所示。
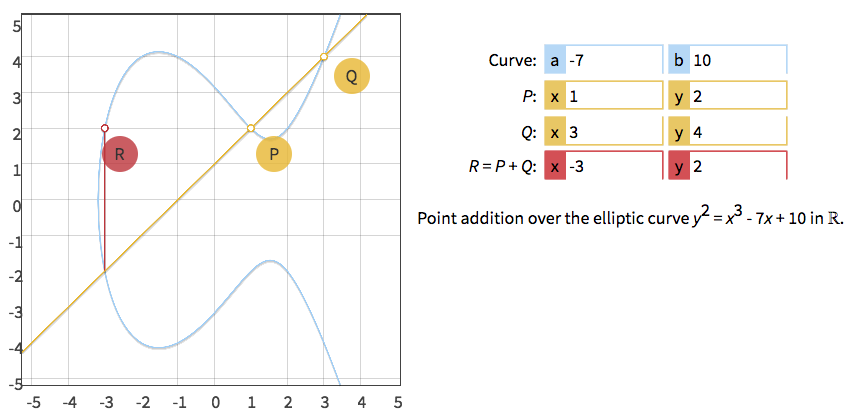
Figure 5: \(R = P + Q\)
现在设 \(R = 2P = P + P\) ,是两个相同点相加,利用上一节介绍的公式,可知:
\[\begin{aligned}
m &= \frac{3 x^2_P + a}{2y_P} = \frac{3 \cdot 1^2 - 7}{2 \cdot 2} = -1 \\
x_R &= m^2 - x_P - x_P = (-1)^2 - 1 - 1 = -1 \\
y_R &= - m (x_R - x_P) - y_P = 1 \cdot (-1 - 1) - 2 = -4 \\
\end{aligned}\]
从而 \(R=(-1, -4)\) 即为所求,如图 6 所示。
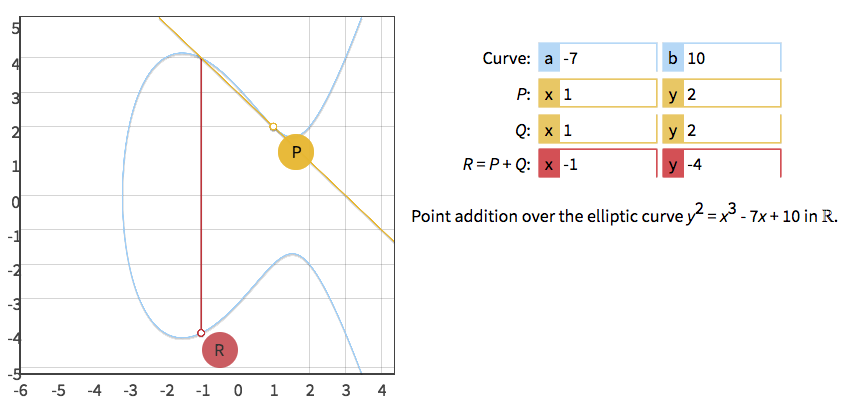
Figure 6: \(R = 2P\)
注:图 5 和图 6 摘自:https://cdn.rawgit.com/andreacorbellini/ecc/920b29a/interactive/reals-add.html
2. 密码学中的椭圆曲线
前面介绍的椭圆曲线是连续的(点的两个坐标均定义在 \(R\) 上),它可表示为:
\[\begin{array}{rcl}
\left\{(x, y) \in \mathbb{R}^2 \right. & \left. | \right. & \left. y^2 = x^3 + ax + b, \right. \\
& & \left. 4a^3 + 27b^2 \ne 0\right\}
\end{array}\]
这种连续的椭圆曲线并不适合用于加密(如连续的椭圆曲线中容易出现浮点数,可能有计算误差等问题)。在密码学中,我们把椭圆曲线定义在有限域 \(\mathbb{F}_p\) (其中 \(p\) 为素数)上(有限域的概念请参考近世代数相关书籍),这里我们可以简单地认为点的两个坐标是集合 \(\{0, 1, 2, \cdots, p-1\}\) 中的值。
在密码学中,我们把椭圆曲线定义为:
\[\begin{array}{rcl}
\left\{(x, y) \in (\mathbb{F}_p)^2 \right. & \left. | \right. & \left. y^2 \equiv x^3 + ax + b \pmod{p}, \right. \\
& & \left. 4a^3 + 27b^2 \not\equiv 0 \pmod{p}\right\} \cup\ \left\{ \mathcal{O} \right\}
\end{array}\]
注 1: \(\mathcal{O}\) 是什么?为什么还要单独增加这样一个点,这里请忽略,后文将说明。
注 2: 上式定义的椭圆曲线是离散的点,一点都不像椭圆 ,下面给出几个具体的例子。
取 \(a=-1, b=0\) ,素数 \(p=61\) ,其椭圆曲线的图形如图 7 所示。
Figure 7: Elliptic curve \(y^2 = x^3 − x\) over finite field \(\mathbb{F}_{61}\)
图 7 中取两点 \((4, 11), (4, 50)\) ,验证如下:
\[\begin{aligned}
x^3 − x = 4^3 - 4 = 60 \pmod {61} \\
y^2 = 11^2 = 121 \equiv 60 \pmod {61} \\
y^2 = 50^2 = 2500 \equiv 60 \pmod {61} \\
\end{aligned}\]
再看一个例子,取 \(a=-1, b=0\) ,素数 \(p=71\) ,其椭圆曲线的图形如图 8 所示。
Figure 8: Elliptic curve \(y^2 = x^3 − x\) over finite field \(\mathbb{F}_{71}\)
2.1. 从椭圆曲线到“群”
在近世代数中,“群”是集合再加上集合上一个二元运算(比如加法)满足下面条件后组成的代数结构:
- 封闭性: \(\forall a_1, a_2 \in A, \; a_1 + a_2 \in A\)
- 结合律: \(\forall a_1, a_2, a_3 \in A, \; (a_1 + a_2) + a_3 = a_1 + ( a_2 + a_3)\)
- 具有单位元: \(\exists e \in A, \; s.t. \; \forall a \in A, \; e + a = a + e = a\)
- 都有逆元素: \(\forall a \in A, \; \exists a^{-1} \in A, \; s.t. \; a + a^{-1} = e\)
把上一节中椭圆曲线所对应的离散点作为群的集合,仿照实数域椭圆曲线加法运算的定义(参见节 1.1 ),我们把群上的二元运算记为 \(+\) ,设 \(P=(x_P, y_P), Q=(x_Q, y_Q)\) ,把 \(R = P + Q\) 定义为:
\[\begin{aligned}
x_R &= m^2 - x_P - x_Q \pmod p \\
y_R &= -m (x_R - x_P ) - y_P \pmod p \\
\end{aligned}\]
当 \(P \neq Q\) 时, \(m = \frac{y_P - y_Q}{x_P - x_Q} \pmod p\) ;当 \(P=Q\) 时, \(m = \frac{3 x_P^2 + a}{2 x_P} \pmod p\) 。
设 \(P,Q\) 在椭圆曲线上,按上面定义计算的点 \(P+Q\) 一定也在椭圆曲线上(即“封闭性”) ,为什么会这样呢?这里不证明,有兴趣的话可参考 An Elementary Proof Of The Group Law For Elliptic Curves(文章中也有关于“结合律”的证明)。我们通过一个具体的例子来验证一下“封闭性”。设椭圆曲线 \(y^2 \equiv x^3 − x \pmod {61}\) (参考图 7 ),易知点 \(P=(4,11), Q=(8,4)\) 都在椭圆曲线,通过上面的加法定义公式可求得 \(P+Q=(33, 55)\) ,容易验证点 \((33, 55)\) 确实也在椭圆曲线上。不仅如此,椭圆曲线上任意两点相加的结果都会在椭圆曲线上。
现在考察椭圆曲线上是否具有“单位元”,即是否存在点 \(\mathcal{O}\) (单位元)使所有点都满足:
\[P + \mathcal{O} = P\]
事实上, 椭圆曲线满足上面条件的点 \(\mathcal{O}\) 是不存在的。为了满足群定义,我们将一个抽象的无穷点 \((x, \infty)\) 定义为单位元 \(\mathcal{O}\) ,这个无穷点可以看作是位于 \(y\) 轴正半轴的无穷远处,或 \(y\) 轴负半轴的无穷远处。
现在考察椭圆曲线上每个点是否都有“逆元素”,即对每一个点 \(P\) ,是否可以找到 \(-P\) 满足:
\[P + (-P) = \mathcal{O}\]
答案是肯定的, \(-P\) 可以这样定义(可以证明它一定存在于椭圆曲线上):
\[-P = (x_P, - y_P \bmod p)\]
比如,按上面公式可求椭圆曲线 \(y^2 \equiv x^3 − x \pmod {61}\) 上的点 \((4, 11)\) 的逆元素为 \((4, 50)\) ,容易验证它确实也在椭圆曲线上。
2.2. Elliptic Curves over Finite Fields
有限素域 \(\mathbb{F}_{p}\) 上的椭圆曲线记为 \(E(\mathbb{F}_{p})\) ,它由下面这些点组成: \[E(\mathbb{F}_{p}) = \{(x, y): x,y \in \mathbb{F}_{p} \;\text{satisfy}\; y^2 = x^3 + ax + b \} \cup \{ \mathcal{O} \}\]
本文中,还采用类似 \(y^2 \equiv x^3 − x \pmod {61}\) 的记号表示有限素域 \(\mathbb{F}_{61}\) 上的椭圆曲线 \(y^2 = x^3 − x\) 。
2.2.1. 实例: \(\mathbb{F}_{13}\) 上的椭圆曲线 \(y^2 = x^3 + 3x + 8\)
\(\mathbb{F}_{13}\) 上的椭圆曲线 \(y^2 = x^3 + 3x + 8\) 有多少个点呢?我们可以采用穷举法,设 \(x=0,1,\cdots,12\) 检查是否有满足条件的 \(y\) 。比如 \(x=0\) ,这时我们找不到 \(\mathbb{F}_{13}\) 上的 \(y\) 满足 \(y^2 = 8 \bmod 13\) ;然后再设 \(x=1\) ,我们可以发现 \(y=5,8\) 会满足 \(y^2 = 1 + 3 + 8 \bmod 13\) ,也就是说点 \((1,5)\) 和 \((1,8)\) 在 \(E(\mathbb{F}_{13})\) 中。依次类推,我们最终可以得到: \[E(\mathbb{F}_{13}) = \{ \mathcal{O}, (1,5), (1, 8), (2, 3), (2, 10), (9,6), (9,7), (12, 2), (12, 11) \}\] 也就是说这个曲线上一共有 9 个点。
根据定义,我们容易计算出这 9 个点的加法表,如图 9 所示(摘自 An Introduction to Mathematical Cryptography, Second Edition 6.2 节 Elliptic Curves over Finite Fields)。
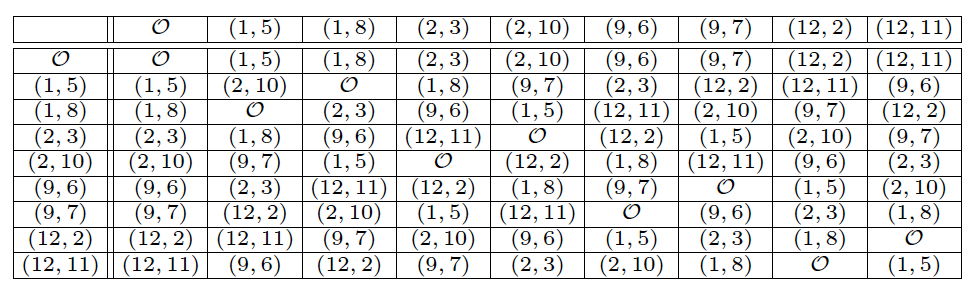
Figure 9: Addition table for E: \(y^2 = x^3 + 3x + 8\) over \(\mathbb{F}_{13}\)
2.3. 椭圆曲线上有多少个点(群的阶)
椭圆曲线,如 \(y^2 \equiv x^3 − x \pmod {61}\) 上(包含 \(\mathcal{O}\) )有多少个点呢(注:群中元素个数又称为群的阶)?这里素数 \(p\) 比较小,我们把 \(x\) 从 \(0\) 到 \(p-1\) 遍历一次,每个 \(x\) 看是否可以求出合法的 \(y\) 也满足 \(y \in \{0, 1, \cdots, p-1\}\) ,即可统计出所有满足要求的点。当 \(x\) 固定时最多有 2 个 \(y\) ,再加上一个额外的 \(\mathcal{O}\) ,所以我们知道 \(\mathbb{F}_{p}\) 上的椭圆曲线的点的数量肯定不会超过 \(2p+1\) 。这种方法当素数 \(p\) 很大时效率很慢,可以用 Schoof's algorithm 快速计算椭圆曲线上点的个数。
对于有限素域 \(\mathbb{F}_{p}\) 上的椭圆曲线,其点的个数记为 \(\#E(\mathbb{F}_{p})\) 。
2.3.1. Hasse 定理
Hasse's theorem 表明有限素域 \(\mathbb{F}_{p}\) 上的椭圆曲线的点的个数 \(\#E(\mathbb{F}_{p})\) 会满足下面约束: \[\mid \#E(\mathbb{F}_{p}) - (p + 1) \mid \le 2 \sqrt{p}\]
比如,前面介绍的 \(\mathbb{F}_{13}\) 上的曲线 \(y^2 = x^3 + 3x + 8\) ,我们已经知道: \(\#E(\mathbb{F}_{p})=9\) ,容易验证 \(\mid 9 - (13+1) \mid \le 2 \sqrt{13}\) 是成立的。
2.4. 标量乘法和循环子群
我们定义下面记号:
\[nP = \underbrace{P + P + \cdots + P}_{n \text{ times}}\]
定义 \(0P = \mathcal{O}\) 。以 \(y^2 \equiv x^3 + 2x + 3 \pmod {97}\) 为例,取 \(P=(3,6)\) ,我们计算一下 \(P, 2P, 3P, 4P, 5P, 6P \cdots\) ,由群的“封闭性”可知,它们都属于椭圆曲线所在“群”。
\[\begin{aligned}
0P &= \mathcal{O} \\
1P &= (3, 6) \\
2P &= (80, 10) \\
3P &= (80, 87) \\
4P &= (3, 91) \\
5P &= \mathcal{O} \\
6P &= (3, 6) \\
7P &= (80, 10) \\
8P &= (80, 87) \\
8P &= (3, 91) \\
10P &= \mathcal{O} \\
\cdots \\
\end{aligned}\]
我们可以发现, \(P\) 的倍数只有 5 个点,而椭圆曲线上其他的点没有出现在 \(P\) 的倍数中。
可以证明 \(\mathcal{O}, (3, 6), (80, 10), (80, 87), (3, 91)\) 在椭圆曲线群所定义的加法运算下也构成群,它称为椭圆曲线群的“子群”,由于这个子群的每个元素可通过对 \(P=(3, 6)\) 重复进行群运算而生成,所以这个子群又称为“循环子群”,其中 \(P\) 称为循环子群的 Base Point(或者 Generator)。
2.4.1. Generator 的选择
在循环子群中,除 \(\mathcal{O}\) 外,每个点都可以作为 Generator。那么怎么从中选择一个 Generator 作为椭圆曲线的参数呢?我们 一般从中选择 \(x\) 坐标较小的点,对于 \(x\) 坐标一样小时可能存在的两个点中,一般从中选择 \(y\) 坐标较小的点。
2.4.2. 循环子群的元素个数(子群的阶)
拉格朗日定理(Lagrange's theorem):设 \(G\) 为有限群, \(A\) 是 \(G\) 的子群,则 \(A\) 的元素个数(子群的阶)是 \(G\) 的元素个数的因数。
上面定理阐述了子群的阶和群的阶的关系。
实例 1:椭圆曲线群 \(y^2 \equiv x^3 - x + 3 \pmod {37}\) (包含点 \(\mathcal{O}\) )的阶经过计算可知为 \(N=42\) ,则其子群的阶 \(n\) 只可能是 \(42\) 的因数,即 \(n=1,2,3,6,7,14,21,42\) 。在椭圆曲线取一点 \(P=(2,3)\) ,计算可知 \(P \neq \mathcal{O}, 2P \neq \mathcal{O}, \cdots, 6P \neq \mathcal{O}, 7P = \mathcal{O}, 8P = P, \cdots\) ,显然由点 \(P\) 生成的循环子群的阶为 \(7\) ,它确实是 \(42\) 的因数,这从侧面印证了拉格朗日定理。
实例 2:椭圆曲线群 \(y^2 \equiv x^3 - x + 1 \pmod {29}\) (包含点 \(\mathcal{O}\) )的阶经过计算可知为 \(N=37\) 。 由于 \(N=37\) 是素数,它只有两个因数,即 \(n=1, 37\) 。由拉格朗日定理知,子群的阶要么是 \(1\) ,要么是 \(37\) 。当 \(n=1\) 时,子群仅包含 \(\mathcal{O}\) ,当 \(n=37\) 时,子群就是椭圆曲线群本身。
注:设 \(N\) 为椭圆曲线群的阶, \(n\) 为由 \(P\) (Base Point)生成的循环子群的阶,我们称 \(h=N/n\) 为相应循环子群的余因子(cofactor)。
2.5. 离散对数问题
在椭圆曲线的循环子群中(设循环子群的阶为 \(n\) ),考虑式子 \(Q=kP\) ,对于给定的 \(k\) 和 \(P\) 计算 \(Q\) 相对容易(可以使用 Double-and-add 算法);而如果已知点 \(P\) 和 \(Q\) ,求 \(k\) 则比较困难(当然我们并不能证明它很“难”,只是说目前没有找到有效的算法来计算上式中的 \(k\) ),这个问题称为椭圆曲线离散对数问题(Elliptic-Curve Discrete-Logarithm Problem, ECDLP)。
如果要暴力求解 \(k\) 的话,你需要设 \(k=1,2,\cdots,n\) ,对于每一个 \(k\) 直接使用加法计算公式验证其是否满足 \(Q = \underbrace{P + P + \cdots + P}_{k \text{ times}}\) ,当 \(n\) 非常大时,暴力求解没有应用价值。
注:在 Digital Signature Algorithm(DSA)或者 Diffie-Hellman Key Exchange 算法中,我们也会说到“离散对数问题”,它指的是另一个问题: \(k\) 和 \(y\) 满足 \(y \equiv g^k \pmod p\) ,其中 \(g,p\) 是参数,已知 \(y\) 时请问 \(k\) 是多少?这个问题也很“难”(目前没有找到有效算法),这里不介绍。
3. Elliptic Curve Cryptography
3.1. Domain Parameters
使用基于椭圆曲线的密码学算法时,各个参与方首先需要约定好椭圆曲线的各个参数,它们被称为 Domain Parameters。
下面是 ECC 的 Domain Parameters:
- The prime \(p\) that specifies the size of the finite field.(注: \(p\) 一般取很大的素数)
- The coefficients \(a\) and \(b\) of the elliptic curve equation. 到此,我们可以确定椭圆曲线群 \(E(\mathbb{F}_{p})\) 了,参见节 2.2
- The base point (generator) \(G=(x_G, y_G)\) that generates our subgroup. 有了 Generator 后,我们可以确定 \(E(\mathbb{F}_{p})\) 上的一个循环子群了,参见节 2.4
- The order \(n\) of the subgroup. \(n\) 就是上一步得到的循环子群的元素个数
- The cofactor \(h=N/n\) of the subgroup. 这里 \(N=\#E(\mathbb{F}_{p})\) ,即 \(N\) 是椭圆曲线群 \(E(\mathbb{F}_{p})\) 所包含的所有点的个数,由拉格朗日定理(参见节 2.4.2)可知, \(h\) 一定是一个整数。显然,当 \(h=1\) 时,由 \(G\) 确定的椭圆曲线的所有点就是椭圆曲线群 \(E(\mathbb{F}_{p})\) 本身,比如曲线 Secp256k1 的 \(h\) 就是 1。曲线 Curve25519 的 cofactor \(h=8\) ,所以它的 Generator 得到的循环子群的元素个数是椭圆曲线群 \(E(\mathbb{F}_{p})\) 元素个数的 \(1/8\) 。需要说明的是,当 \(h>1\) 时,有一些安全问题需要注意:比如可能遭受 Small-Subgroup Attack,还可能存在 Non-injective behavior/Covert channels/Implementation-defined behavior/Nontrivial modifications 等问题,具体可参考:Decaf: Eliminating cofactors through point compression, 1.1 Pitfalls of a cofactor。区块链 Monero 上出现过由于 \(Cofactor>1\) 而引起的安全漏洞,参考:Disclosure of a Major Bug in CryptoNote Based Currencies
一般使用 \((p, a, b, G, n, h)\) 表示 ECC 的 Domain Parameters。需要说明的是: 当 \(p,a,b,G\) 确定后, \(n\) 和 \(h\) 也就确定了,也就是说 \(n,h\) 是由 \(p,a,b,G\) 计算出来的参数。
3.1.1. Random Curves (seed \(S\))
前面说过,椭圆曲线离散对数问题的困难的。这不完全正确,如当满足条件 \(p=hn\) 时的所有椭圆曲线都比较容易破解。
为了减少潜在的风险,我们可以增加一个随机种子 \(S\) ,用它来产生参数 \(a,b\) ,或者 \(G\) ,或者这两者。这样,椭圆曲线变得不可预测。
3.1.2. 选择合适的椭圆曲线
关于选择椭圆曲线有很多不同的“标准”,如:
- ANSI X9.62 (1999).
- IEEE P1363 (2000).
- SEC 2 (2000).
- NIST FIPS 186-2 (2000).
- ANSI X9.63 (2001).
- Brainpool (2005).
- NSA Suite B (2005).
- ANSSI FRP256V1 (2011).
如何选择一个“安全的”?可参考:SafeCurves: choosing safe curves for elliptic-curve cryptography (注:Bitcoin 使用的 secp256k1 ,在该网页中被标记为 Unsafe)。
3.1.3. Secp256k1
Bitcoin 使用的椭圆曲线是 secp256k1 ,它的参数如下:
\[\begin{aligned}
p &= \texttt{0xffffffff ffffffff ffffffff ffffffff ffffffff ffffffff fffffffe fffffc2f} \\
a &= \texttt{0} \\
b &= \texttt{7} \\
x_G &= \texttt{0x79be667e f9dcbbac 55a06295 ce870b07 029bfcdb 2dce28d9 59f2815b 16f81798} \\
y_G &= \texttt{0x483ada77 26a3c465 5da4fbfc 0e1108a8 fd17b448 a6855419 9c47d08f fb10d4b8} \\
n &= \texttt{0xffffffff ffffffff ffffffff fffffffe baaedce6 af48a03b bfd25e8c d0364141} \\
h &= \texttt{1} \\
\end{aligned}\]
3.1.4. Secp256k1 VS. Secp256r1 (NIST P-256)
美国国家安全局建议使用的椭圆曲线是 secp256r1(也被称为 NIST P-256),secp256r1 使用的参数是:
p = 0xffffffff00000001000000000000000000000000ffffffffffffffffffffffff a = 0xffffffff00000001000000000000000000000000fffffffffffffffffffffffc b = 0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b x_G = 0x6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296 y_G = 0x4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5 n = 0xffffffff00000000ffffffffffffffffbce6faada7179e84f3b9cac2fc632551 h = 0x1
曲线 secp256k1 和 secp256r1 的名称只有一字之差,k 和 r 的不同。其中 k 表示 Koblitz(他是 ECC 发明人);而 r 表示随机,即参数是随机选取的,但美国国家安全局并没有公布随机数的挑选规则,所以外界一直存在疑虑,怀疑 NSA 可能对随机数生成器动过手脚,让破解难度大幅降低。
注 1:secp256r1 曲线还有其它的别名:prime256v1 或者 nist256p1 或者 NIST P-256,参考:https://www.ietf.org/rfc/rfc4492.html#appendix-A
注 2:在区块链领域,Secp256k1 使用更广泛;不过在区块链以外的其它领域,Secp256r1 使用更广泛,比如 Android/iOS 的硬件安全密钥都支持 Secp256r1,而不支持 Secp256k1。
3.2. Elliptic Curve Diffie-Hellman (ECDH)
下面介绍使用椭圆曲线进行密钥交换(Key Exchange)的过程,它是 Diffie-Hellman algorithm 算法的变种,一般称为 Elliptic curve Diffie-Hellman (ECDH)。
Alice 和 Bob 想进行通信,为了加密(基于效率考虑往往会采用对称密钥算法,如 AES 等)通信的数据,他们需要约定同一个密钥(称为“Shared Secret”)。
使用 ECDH 算法约定“Shared Secret”的过程(和 Diffie-Hellman 密钥交换算法基本类似)如下。
第一步,选择一个椭圆曲线(即确定 Domain parameters),你可以从 Standards for Efficient Cryptography, SEC 2: Recommended Elliptic Curve Domain Parameters 中选择一个推荐的参数。
第二步,为 Alice 和 Bob 分别生成 private key/public key。比如,Alice 生成 private key/public key 的过程如下:
1、从 \(\{1, 2, \cdots, n - 1\}\) ( \(n\) 在 Domain parameters 中指定的循环子群的阶)中随机选择一个数 \(d_A\) 作为 private key。
2、计算 \(Q_A=d_A G\) ( \(G\) 是 Domain parameters 中的 Base Point), \(Q_A\) 就是 public key。(注:这就是由私钥生成公钥的过程,直接按多次加法求解比较慢,可采用 Double-and-add 算法进行优化。这里有一个使用 Double-and-add 算法计算公钥的例子:https://bitcoin.stackexchange.com/questions/25024/how-do-you-get-a-bitcoin-public-key-from-a-private-key)
类似的过程,Bob 生成一个 private key/public key,分别记为 \(d_B, Q_B\) ,有 \(Q_B=d_B G\) 。
第三步,Alice 和 Bob 分别把自己的公钥传送给对方,传递过程被别人偷看也没关系,由公钥无法容易地计算出私钥。
第四步, Alice 用自己的私钥和 Bob 的公钥计算 \(Secret_1=d_A Q_B\) ,同样地,Bob 用自己的私钥和 Alice 的公钥计算 \(Secret_2=d_B Q_A\) ,由于 \(Secret_1 = Secret_2\) (因为 \(d_A Q_B = d_A (d_B G) = d_B (d_A G) = d_B Q_A\) ),所以它可作为“Shared Secret”。
3.2.1. Ephemeral ECDH (ECDHE)
如果通信双方不使用固定的 private key/public key,而是在建立连接时才动态生成各自的 private key/public key(注:这次通信结束,下次连接时重新生成各自的 private key/public key),这称为 Ephemeral ECDH (ECDHE)。
3.3. 公钥表达形式(Uncompressed and Compressed)
在椭圆曲线中,私钥 \(d \in \{1, 2, \cdots, n - 1\}\) 是整数;而公钥 \(Q =d G\) 则是椭圆曲线上的一个“点”,它有 \(x_Q, y_Q\) 两个坐标,每个坐标都是整数。下面是 secp256k1 曲线上公钥的一个例子:
\[\begin{aligned}
x_Q &= \texttt{0x50863AD64A87AE8A2FE83C1AF1A8403CB53F53E486D8511DAD8A04887E5B2352} \\
y_Q &= \texttt{0x2CD470243453A299FA9E77237716103ABC11A1DF38855ED6F2EE187E9C582BA6} \\
\end{aligned}\]
我们容易验证这个公钥确实是 secp256k1 曲线上的一个点:
Python 3.6.8 (default, Oct 7 2019, 12:59:55) [GCC 8.3.0] on linux Type "help", "copyright", "credits" or "license" for more information. >>> p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f >>> x = 0x50863AD64A87AE8A2FE83C1AF1A8403CB53F53E486D8511DAD8A04887E5B2352 >>> y = 0x2CD470243453A299FA9E77237716103ABC11A1DF38855ED6F2EE187E9C582BA6 >>> y**2 % p - (x**3 + 7) % p 0
一般地,我们往往用“一个数”来表达椭圆曲线中的公钥,如何用一个数来表达两个坐标呢?有两种方案:“Uncompressed format”和“Compressed format”(Compressed format 有 ansiX962_compressed_prime 和 ansiX962_compressed_char2 标准,这里不介绍它们)。
下面介绍一下“Uncompressed format”,它的规则很简单,把 \(x_Q\) 和 \(y_Q\) 直接连接在一起,再在前面加个 0x04 前缀即可。例如有:
\[\begin{aligned}
x_Q &= \texttt{0x50863AD64A87AE8A2FE83C1AF1A8403CB53F53E486D8511DAD8A04887E5B2352} \\
y_Q &= \texttt{0x2CD470243453A299FA9E77237716103ABC11A1DF38855ED6F2EE187E9C582BA6} \\
\end{aligned}\]
则公钥(十六进制)可表示为:
Q = 0450863AD64A87AE8A2FE83C1AF1A8403CB53F53E486D8511DAD8A04887E5B23522CD470243453A299FA9E77237716103ABC11A1DF38855ED6F2EE187E9C582BA6
3.4. Elliptic Curve Digital Signature Algorithm (ECDSA)
前面介绍了使用椭圆曲线进行密钥交换(Key Exchange)的过程,这里将介绍如何使用椭圆曲线进行数字签名,简称 ECDSA。ECDSA 是椭圆曲线应用于 DSA 的成果,其基本思路和 DSA 很相似。
数字签名的场景为:Alice 用他的私钥 \(d_A\) 对消息进行签名,而其它人(如 Bob)可以使用 Alice 的公钥 \(Q_A\) 来验证这个消息确实是 Alice 发送的。
3.4.1. ECDSA 签名及验证过程
本节介绍 ECDSA 签名及验证的具体过程(下一节将证明其正确性)。
假设 Alice 的私钥为 \(d_A\) ,公钥为 \(Q_A\) 。需要签名的消息为 \(m\) ,首先对消息 \(m\) 进行下面处理:
- 对原始消息计算哈希(需要使用 Cryptographic hash function),得到 \(e=\text{Hash}(m)\) ,把 \(e\) 当做一个大整数;
- 如果 \(e\) 的比特长度大于 \(n\) ( \(n\) 在 Domain parameters 中指定的循环子群的阶)的比特长度,则把截断 \(e\) ,只留下左边和 \(n\) 同样比特长的部分,后文直接用 \(\text{Hash}(m)\) 表示经过这样处理后的摘要消息,它是一个大整数。
Alice 签名过程:
- 从 \(\{1, 2, \cdots, n - 1\}\) 中随机选择一个数,记为 \(k\) ;
- 计算 \(R = k G\) (其中 \(G\) 是 Domain parameters);
- 计算整数 \(r = x_R \pmod n\) (其中 \(x_R\) 是上一步计算的点 \(R\) 的横坐标);
- 如果 \(r=0\) ,则随机选择另外一个 \(k\) ,重新计算前面两步;
- 计算整数 \(s= k^{-1}(\text{Hash}(m) + rd_A) \pmod n\) (其中 \(d_A\) 是 Alice 的私钥, \(k^{-1}\) 是满足 \(k k^{-1} = 1 \pmod n\) 的整数);
- 如果 \(s=0\) ,则随机选择另外一个 \(k\) ,重新计算前面步骤。
经常上面步骤得到的 整数对 \((r, s)\) 就是摘要消息 \(\text{Hash}(m)\) 的数字签名。
Bob 验证签名的过程:
- 计算整数 \(u_1 = s^{-1} Hash(m) \pmod n\) (其中 \(s^{-1}\) 是满足 \(s s^{-1} = 1 \pmod n\) 的整数);
- 计算整数 \(u_2 = s^{-1} r \pmod n\) ;
- 计算点 \(R = u_1 G + u_2 Q_A\) (其中 \(Q_A\) 是 Alice 的公钥)。
- 如果 \(r = x_R \pmod n\) (这里 \(x_R\) 是上一步计算的点 \(R\) 的横坐标)成立,则验证签名通过,否则验证失败。
3.4.1.1. ECDSA 正确性证明
前面介绍的签名过程和验证签名过程为什么正确呢?下面来证明它的正确性。
首先,在验证签名时,有(后面推导将省写 \(\text{mod } n\) ):
\[\begin{aligned} R &= u_1 G + u_2 Q_A \\
& = u_1 G + u_2 d_A G \\
& = (u_1 + u_2 d_A) G \\
& = (s^{-1} \text{Hash}(m) + s^{-1} r d_A) G \\
& = s^{-1} (\text{Hash}(m) + r d_A) G \\
\end{aligned}\]
在生成签名时,有:
\[\begin{aligned} R & = k G \\
& = s^{-1} (\text{Hash}(m) + r d_A) G \\
\end{aligned}\]
所以,通过两种方法得到了 \(R\) 的相同表达形式,而我们在生成签名时定义了 \(r = x_R \pmod n\) ,所以如果这个式子在验证签名过程中也成立,则说明验证通过。
3.4.1.2. 重复使用随机数 k 会导致私钥泄露
随机数 \(k\) 用完就丢弃,不能使用相同的 \(k\) 来对其它消息进行签名。 如果对于两个不同的消息 \(m_1,m_2\) 签名时,如果使用了同一个 \(k\) 则会导致私钥泄露。 下面介绍一下这种情况下私钥泄露的细节。
假设对 \(m_1\) 签名时使用的随机数为 \(k\) ,得到的结果为 \((r, s_1)\) ;对 \(m_2\) 签名时也是使用 \(k\) ,得到的结果为 \((r, s_2)\) 。由于 \(r\) 的计算只和随机数 \(k\) 有关,所以这两个签名结果中 \(r\) 是相同的。按照签名的计算公式有:
\[\begin{aligned}
s_1 &= k^{-1}(\text{Hash}(m_1) + r d) \\
s_2 &= k^{-1}(\text{Hash}(m_2) + r d) \\
\end{aligned}\]
把上面两个式子中,只有 \(k\) 和私钥 \(d\) 是未知的,如果把式中的 \(k\) 消去,就可以得到私钥 \(d\) 的计算公式:
\[d = (s_2 \text{Hash}(m_1) - s_1 \text{Hash}(m_2)) (r(s_1-s_2))^{-1}\]
3.4.1.3. ECDSA Signature Malleability(一个签名修改后还是有效签名)
当 \((r,s)\) 是一个 ECDSA 有效签名时,则 \((r, n-s)\) 也是 ECDSA 有效签名,这被称为 Signature Malleability(签名延展性)。 签名延展性可能带来一些问题,参考:https://github.com/bitcoin/bips/blob/master/bip-0062.mediawiki
解决“签名延展性”的办法:
- 对于签名生成者:在生成完 \((r,s)\) 后,检查 \(s <= n/2\) 是否成立,如果成立则 \((r,s)\) 就是签名数据;如果不成立则输出 \((r,n-s)\) 为最终的签名数据。这样保证了最终输出的签名数据 \(s\) 一定满足 \(s <= n/2\) ,从而 \(s\) 具备了唯一确定性。
- 对于签名验证者:在验证签名时,只接受满足 \(s <= n/2\) 的 \(s\) ,拒绝 \(s > n/2\) 时的 \(s\) ,这样保证了签名不再具有延展性。
参考:
https://github.com/bitcoin/bips/blob/master/bip-0062.mediawiki
https://github.com/ethereum/EIPs/blob/master/EIPS/eip-2.md
3.4.2. 从 ECDSA 签名数据中恢复公钥
可以从 ECDSA 签名数据中恢复出公钥,具体的算法如图 10 所示,摘自 SEC 1: Elliptic Curve Cryptography 中的 4.1.6 节 Public Key Recovery Operation。

Figure 10: 从签名中恢复公钥
图 10 所示算法中,有两个嵌套的 \(for\) 循环,一个是 \(j\) 从 0 到 \(h\) (对于 Secp256k1 来说 \(h=1\) ),而另一个是 \(k\) 从 1 到 2;组合起来,则对于 Secp256k1 来说,恢复公钥,最多要计算 4 次 candidate public key。找到正确的公钥前可能要拒绝 0 到 3 次 candidate public key,我们把这个拒绝的次数记为 Recovery Id。也就是说 Recovery Id 的可能值为 0/1/2/3,不过需要说明的是在 99.999999999···% 的情况下 Recovery Id 都会为 0/1。
编程时,如何计算 Recovery Id 呢?可采用下面公式:
recid = R.y & 1; // Where (R.x, R.y) = k * G; if (s > curve.n / 2) recid = recid ^ 1; // i.e. if (s > curve.n - s) recid = recid ^ 1;
在有的 ECDSA 实现中增加了一个额外的 \(v\) 来表示 Recovery Id,这样签名从以前的 \((r,s)\) 变为了 \((r,s,v)\) ,这样的签名数据被称为“Extended ECDSA signature”。
从签名中恢复公钥在带宽受限的环境中比较实用。
参考:
https://bitcoin.stackexchange.com/questions/83035/how-to-determine-first-byte-recovery-id-for-signatures-message-signing
https://ethereum.stackexchange.com/questions/42455/during-ecdsa-signing-how-do-i-generate-the-recovery-id
3.4.3. Deterministic ECDSA
在前面介绍的 ECDSA 中,有个一次一用的随机数 \(k\) ,它将导致对同一个消息进行签名时,每次产生的签名数据都不相同。
在 RFC6979 中定义了一种“确定性的”ECDSA,这个模式下,随机数 \(k\) 是由私钥和待签名消息一起推导出来的,从而对同一个消息的多次签名都会产生相同的签名数据。
3.4.4. ECDSA VS. EC-Schnorr
设签名者的私钥为 \(d\) ,公钥为 \(P=d \cdot G\) ,表 1 以对比的形式同时给出了 ECDSA 和 EC-Schnorr 签名方案(注:这里是 Schnorr 签名方案使用椭圆曲线时的情况,Schnorr 签名方案也可不使用椭圆曲线)。
| ECDSA signing | EC-Schnorr signing |
|---|---|
| 1. 选择随机数 \(k\) | 1. 选择随机数 \(k\) |
| 2. 计算 \(R=k \cdot G\) | 2. 计算 \(R=k \cdot G\) |
| 3. 计算 \(r=x_R \pmod n\) ,其中 \(x_R\) 是上一步计算的点 \(R\) 的 \(x\) 坐标 | |
| 4. 计算 \(s=k^{-1} \cdot (\text{Hash}(m) + r \cdot d) \pmod n\) | 3. 计算 \(s=k + \text{Hash}(P, R, m) \cdot d \pmod n\) |
| 5. 输出签名 \((r, s)\) | 4. 输出签名 \((R, s)\) |
| 验证签名:检查 \((\text{Hash}(m) \cdot s^{-1}) \cdot G + (r \cdot s^{-1}) \cdot P\) 的 \(x\) 坐标是否为 \(r\) | 验证签名:检查 \(s \cdot G = R + \text{Hash}(P, R, m) \cdot P\) 是否成立 |
表 1 中,只有用户的私钥 \(d\) 以及随机数 \(k\) (这个随机数是一次一用的,每次签名都在生成新的)是不能泄露的。
EC-Schnorr 签名验证的正确性:
3.4.4.1. EC-Schnorr 签名的优点
EC-Schnorr 签名方案有一些 ECDSA 所没有的优点,比如 批量验证(Batch Validation)。 假设有 1000 个签名需要验证,则无需挨个验证,仅验证下面一个式子即可: \[(s_1 + s_2 + \cdots + s_{1000}) \cdot G = (R_1 + \cdots + R_{1000}) + \text{Hash}(P_1, R_1, m_1) \cdot P_1 + \cdots + \text{Hash}(P_{1000}, R_{1000}, m_{1000}) \cdot P_{1000}\] 这样,涉及的计算更小,验证的效率要比单独验证要高。
EC-Schnorr 签名方案还有其它一些优点,详情可参考:https://medium.com/cryptoadvance/how-schnorr-signatures-may-improve-bitcoin-91655bcb4744
3.4.4.2. EC-Schnorr 签名有各种不同方案
EC-Schnorr 签名有各种不同方案,如:
上面例子中 first component/second component 分别指签名数据的第 1/2 部分。
参考:https://crypto.stackexchange.com/questions/34863/ec-schnorr-signature-multiple-standard
3.5. ECDSA 的 Python 实现
下面是 ECDSA 的 Python 实现(注:pip 上已有现成的库 ecdsa):
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# 代码摘自:https://github.com/andreacorbellini/ecc/blob/master/scripts/ecdsa.py
import collections
import hashlib
import random
EllipticCurve = collections.namedtuple('EllipticCurve', 'name p a b g n h')
curve = EllipticCurve(
'secp256k1',
# Field characteristic.
p=0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f,
# Curve coefficients.
a=0,
b=7,
# Base point.
g=(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798,
0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8),
# Subgroup order.
n=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141,
# Subgroup cofactor.
h=1,
)
# Modular arithmetic ##########################################################
def inverse_mod(k, p):
"""Returns the inverse of k modulo p.
This function returns the only integer x such that (x * k) % p == 1.
k must be non-zero and p must be a prime.
"""
if k == 0:
raise ZeroDivisionError('division by zero')
if k < 0:
# k ** -1 = p - (-k) ** -1 (mod p)
return p - inverse_mod(-k, p)
# Extended Euclidean algorithm.
s, old_s = 0, 1
t, old_t = 1, 0
r, old_r = p, k
while r != 0:
quotient = old_r // r
old_r, r = r, old_r - quotient * r
old_s, s = s, old_s - quotient * s
old_t, t = t, old_t - quotient * t
gcd, x, y = old_r, old_s, old_t
assert gcd == 1
assert (k * x) % p == 1
return x % p
# Functions that work on curve points #########################################
def is_on_curve(point):
"""Returns True if the given point lies on the elliptic curve."""
if point is None:
# None represents the point at infinity.
return True
x, y = point
return (y * y - x * x * x - curve.a * x - curve.b) % curve.p == 0
def point_neg(point):
"""Returns -point."""
assert is_on_curve(point)
if point is None:
# -0 = 0
return None
x, y = point
result = (x, -y % curve.p)
assert is_on_curve(result)
return result
def point_add(point1, point2):
"""Returns the result of point1 + point2 according to the group law."""
assert is_on_curve(point1)
assert is_on_curve(point2)
if point1 is None:
# 0 + point2 = point2
return point2
if point2 is None:
# point1 + 0 = point1
return point1
x1, y1 = point1
x2, y2 = point2
if x1 == x2 and y1 != y2:
# point1 + (-point1) = 0
return None
if x1 == x2:
# This is the case point1 == point2.
m = (3 * x1 * x1 + curve.a) * inverse_mod(2 * y1, curve.p)
else:
# This is the case point1 != point2.
m = (y1 - y2) * inverse_mod(x1 - x2, curve.p)
x3 = m * m - x1 - x2
y3 = y1 + m * (x3 - x1)
result = (x3 % curve.p,
-y3 % curve.p)
assert is_on_curve(result)
return result
def scalar_mult(k, point):
"""Returns k * point computed using the double and point_add algorithm."""
assert is_on_curve(point)
if k % curve.n == 0 or point is None:
return None
if k < 0:
# k * point = -k * (-point)
return scalar_mult(-k, point_neg(point))
result = None
addend = point
while k:
if k & 1:
# Add.
result = point_add(result, addend)
# Double.
addend = point_add(addend, addend)
k >>= 1
assert is_on_curve(result)
return result
# Keypair generation and ECDSA ################################################
def make_keypair():
"""Generates a random private-public key pair."""
private_key = random.randrange(1, curve.n)
public_key = scalar_mult(private_key, curve.g)
return private_key, public_key
def hash_message(message):
"""Returns the truncated SHA512 hash of the message."""
message_hash = hashlib.sha512(message).digest()
e = int.from_bytes(message_hash, 'big')
# FIPS 180 says that when a hash needs to be truncated, the rightmost bits
# should be discarded.
z = e >> (e.bit_length() - curve.n.bit_length())
assert z.bit_length() <= curve.n.bit_length()
return z
def sign_message(private_key, message):
z = hash_message(message)
r = 0
s = 0
while not r or not s:
k = random.randrange(1, curve.n)
x, y = scalar_mult(k, curve.g)
r = x % curve.n
s = ((z + r * private_key) * inverse_mod(k, curve.n)) % curve.n
return (r, s)
def verify_signature(public_key, message, signature):
z = hash_message(message)
r, s = signature
w = inverse_mod(s, curve.n)
u1 = (z * w) % curve.n
u2 = (r * w) % curve.n
x, y = point_add(scalar_mult(u1, curve.g),
scalar_mult(u2, public_key))
if (r % curve.n) == (x % curve.n):
return 'signature matches'
else:
return 'invalid signature'
print('Curve:', curve.name)
private, public = make_keypair()
print("Private key:", hex(private))
print("Public key: (0x{:x}, 0x{:x})".format(*public))
msg = b'Hello!'
signature = sign_message(private, msg)
print()
print('Message:', msg)
print('Signature: (0x{:x}, 0x{:x})'.format(*signature))
print('Verification:', verify_signature(public, msg, signature)) # 验证通过
msg = b'Hi there!' # 使用不同的消息,会验证失败
print()
print('Message:', msg)
print('Verification:', verify_signature(public, msg, signature))
private, public = make_keypair() # 使用不同的公钥,会验证失败
msg = b'Hello!'
print()
print('Message:', msg)
print("Public key: (0x{:x}, 0x{:x})".format(*public))
print('Verification:', verify_signature(public, msg, signature))
3.6. Elliptic Curve 加解密方案
3.6.1. Elliptic Curve Integrated Encryption Scheme (ECIES)
ECIES is a hybrid encryption system proposed by Victor Shoup in 2001. ECIES has been standardized in ANSI X9.63, IEEE 1363a, ISO/IEC 18033-2, and SECG SEC-1.
ECIES 方案是一种框架,并不是某个具体算法,如图 11 所示(摘自:https://cryptobook.nakov.com/asymmetric-key-ciphers/ecies-public-key-encryption )。
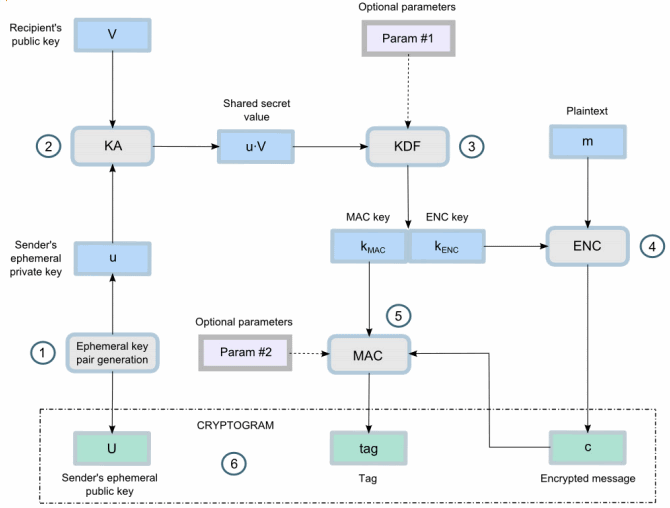
Figure 11: ECIES encryption scheme
四种 ECIES 标准的比较如图 12 所示(摘自 A Comparison of the Standardized Versions of ECIES )。
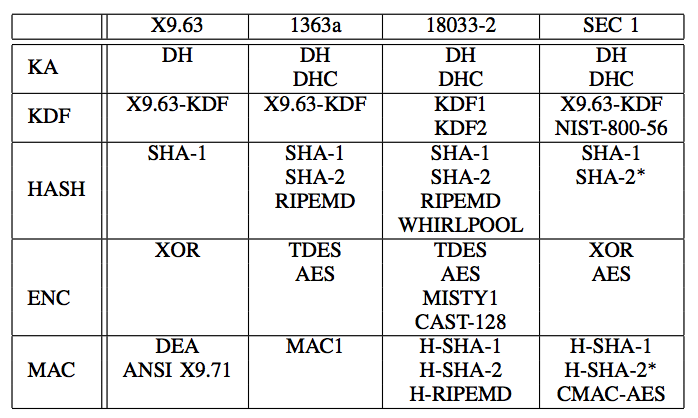
Figure 12: 四种 ECIES 标准
例如,Apple 的 Secure Enclave 支持的 SecKeyAlgorithm.eciesEncryptionCofactorVariableIVX963SHA256AESGCM 就是一种 ECIES 方案,参考:https://darthnull.org/secure-enclave-ecies/
3.6.1.1. ECIES 伪代码实现
下面是 ECIES 的伪代码实现:
# 下面是 ECIES 加密数据的过程 # Input: # pub_key 是接收者的公钥 # msg 是等待加密的消息 # Output: # ephemeral_pub_key 是临时公钥,接收者用它进行 ECDH 可以得到 AES 对称加密所用的密钥(具体来说就是接收者私钥乘以这个临时公钥) # iv 是 AES 算法的初始化变量 # tag 是消息认证码 # ciphertext 是密文 encrypt(pub_key, msg): ephemeral_pri_key, ephemeral_pub_key = gen_key(); shared_secret = ephemeral_pri_key * pub_key; // 这是 ECDH 计算临时 shared_secret 的过程,ECIES 的 KA 过程 iv = gen_random(); // AES 算法需要的 iv 值 // 注意:在实现 ECIES 时一般不会直接把上面的 shared_secret 当作 AES 的密钥; // 而是使用 X9.63 KDF 或者 HKDF https://en.wikipedia.org/wiki/HKDF 等 KDF 函数处理后,把结果当作 AES 密钥 // 不过,这个例子中省略了这个步骤 // aes gcm 本身是一种 AEAD 算法(这样不需要分别进行 ECIES 的 MAC/ENC 操作了),它的 tag 就是消息认证所需的 mac 值 ciphertext, tag = aes_gcm_encrypt(shared_secret, iv, msg); return ephemeral_pub_key, iv, tag, ciphertext # 下面是 ECIES 解密数据的过程 # Input: # pri_key 是接收者的私钥 # ephemeral_pub_key/iv/tag/ciphertext 是加密过程的输出,这里作为解密过程的输入 # Output: # plaintext 是解密后的明文 decrypt(pri_key, ephemeral_pub_key, iv, tag, ciphertext): shared_secret = pri_key * ephemeral_pub_key // 这是 ECDH 计算临时 shared_secret 的过程 // 注意:在实现 ECIES 时一般不会直接把上面的 shared_secret 当作 AES 的密钥; // 而是使用 X9.63 KDF 或者 HKDF https://en.wikipedia.org/wiki/HKDF 等 KDF 函数处理后,把结果当作 AES 密钥 // 不过,这个例子中省略了这个步骤 plaintext = aes_gcm_decrypt(shared_secret, iv, tag, ciphertext) return plaintext
3.6.2. Provably Secure Elliptic Curve encryption (PSEC)
Provably Secure Elliptic Curve encryption (PSEC) 是日本 NTT 实验室提出的一种基于椭圆曲线的公钥加密方案。
关于 PSEC 的标准文档,可以参考 Specifications for PSEC-KEM 或者 ISO/IEC 18033-2 。
3.6.3. Hybrid Public Key Encryption (HPKE)
Hybrid Public Key Encryption (HPKE) 是一个关于公钥加密的新标准,于 2022 年在 RFC 9180 中被标准化。
已经有了 ECIES,为什么还需要 HPKE 呢?这是因为 ECIES 标准提出比较早,其中有一些算法已经过时;加密和认证是通过 ENC/MAC 两个过程分开处理的,它没有使用 AEAD 这种更安全的方法;而且不能证明满足 IND-CCA2 安全,RFC 9180 中对 ECIES 的缺点是这样描述的:
All these existing schemes have problems, e.g., because they rely on outdated primitives, lack proofs of indistinguishable (adaptive) chosen-ciphertext attack (IND-CCA2) security, or fail to provide test vectors.
参考:
RFC 9180 Hybrid Public Key Encryption
HPKE: Standardizing public-key encryption (finally!)
3.6.4. NaCl crypto_box
NaCl 提出的 crypto_box 和 ECIES 有些类似,不过它们在一些底层算法上有很多不同,如表 2 所示。
| crypto_box | ECIES | |
|---|---|---|
| 密钥交换 | X25519 | ECDH |
| 对称加密 | XSalsa20 | AES |
| 消息认证 | Poly1305 | HMAC |
3.7. 其它坐标系
3.7.1. Jacobian 射影坐标(避免求逆运算)
笛卡尔坐标(Cartesian Coordinates)是一种特殊的仿射坐标(Affine Coordinates),下面的讨论将不区分这两种坐标。
在仿射坐标下,把椭圆曲线上的两个点相加会涉及到“求逆运算”,一般采用扩展欧几里得算法,但比较低效。如果采用“雅可比射影坐标(Jacobian Projective Coordinates)”,则椭圆曲线上的两个点相加运算可以避免求逆运算。OpenSSL 也使用了雅可比射影坐标表示点,参见 https://github.com/openssl/openssl/blob/OpenSSL_1_1_1-stable/crypto/ec/ec_local.h#L295
“雅可比射影坐标”和“仿射坐标”的转换关系为:
\[\begin{aligned} \text{Affine 坐标转换为 Jacobian 坐标的公式:} & \quad (X,Y) \to (X,Y,1) \\
\text{Jacobian 坐标转换 Affine 坐标的公式:} & \quad (X,Y,Z) \to (X/Z^2, Y/Z^3) \end{aligned}\]
参考:https://en.wikipedia.org/wiki/Jacobian_curve#Addition_and_doubling_in_projective_coordinates
3.7.2. Edwards Coordinates
2007 年,Harold Edwards 在论文 A NORMAL FORM FOR ELLIPTIC CURVES 中提出椭圆曲线的新形式 \[x^2 + y^2 = 1+x^2 y^2\] 这被称为 Edwards curve。
同一年,Daniel J. Bernstein 和 Tanja Lange 在论文 Faster addition and doubling on elliptic curves 中对 Edwards form 进行了扩展 \[a x^2 + y^2 = 1+x^2 y^2\] 这被称为 Twisted Edwards curve。
参考:Elliptic Curves Number Theory And Cryptography, Second Edition, 2.6.3 Edwards Coordinates
4. 参考
http://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/
http://andrea.corbellini.name/2015/05/23/elliptic-curve-cryptography-finite-fields-and-discrete-logarithms/
http://andrea.corbellini.name/2015/05/30/elliptic-curve-cryptography-ecdh-and-ecdsa/
An Introduction to Mathematical Cryptography, Second Edition

