EdDSA and Ed25519
Table of Contents
1. EdDSA 简介
EdDSA 由 Bernstein 等人于 2011 年在论文 High-speed high-security signatures 中提出的,正如原论文标题所写的那样,它是一种非常快的签名算法。EdDSA 可以看作是 Schnorr 签名方案采用 Twisted Edwards Curve 时的变种。
EdDSA 在 RFC8032 中被标准化。目前 EdDSA 有两个方案:Ed25519 和 Ed448。Ed25519 采用的哈希函数为 SHA-512(SHA-2),曲线为 Curve25519;而 Ed448 采用的哈希函数为 SHAKE256(SHA-3),曲线为 Curve448。后文将重点介绍 Ed25519。
1.1. Twisted Edwards Curve
Twisted Edwards Curve 由下式定义: \[ax^{2}+y^{2}=1+dx^{2}y^{2}\] Twisted Edwards Curve 上两个点 \((x_1,y_1), (x_2,y_2)\) ,其加法的定义为 \[(x_{1},y_{1})+(x_{2},y_{2})=\left({\frac {x_{1}y_{2}+y_{1}x_{2}}{1+dx_{1}x_{2}y_{1}y_{2}}},{\frac{y_{1}y_{2}-ax_{1}x_{2}}{1-dx_{1}x_{2}y_{1}y_{2}}}\right)\] 单位元(Identity element)为 \((0,1)\) ,容易验证对于任意点 \((x_1,y_1)\) ,式子 \((x_1,y_1) + (0,1) = (x_1,y_1)\) 都会成立。点 \((x_1, y_1)\) 的逆为 \((-x_1, y_1)\) ,容易验证 \((x_1, y_1) + (-x_1, y_1)\) 总是为单位元 \((0,1)\) ,即点加上它的逆总是单位元。
1.1.1. Curve25519
对于 Curve25519, \(a=-1, d=-\frac{121665}{121666}\) ,也就是 Curve25519 曲线为: \[-x^2 + y^2 = 1 -\frac{121665}{121666} x^2 y^2\]
如果采用 Montgomery Curve 形式,则 Curve25519 可以表示为: \[y^2 = x^3 + 486662 x^2 + x\]
关于作者是如何选择数字 486662 的?可以参考论文 Curve25519: new Diffie-Hellman speed records :
The smallest positive choices for A are 358990, 464586, and 486662. I rejected A = 358990 because one of its primes is slightly smaller than 2^{252}, raising the question of how standards and implementations should handle the theoretical possibility of a user's secret key matching the prime; discussing this question is more difficult than switching to another A. I rejected 464586 for the same reason. So I ended up with A = 486662.
2. EdDSA, Ed25519
2.1. 11 个参数
EdDSA 一共定义了 11 个参数。对于 Ed25519,这 11 个参数分别为:
+-----------+-------------------------------------------------------+
| Parameter | Value |
+-----------+-------------------------------------------------------+
| p | p of edwards25519 in [RFC7748] (i.e., 2^255 - 19) |
+-----------+-------------------------------------------------------+
| b | 256 |
+-----------+-------------------------------------------------------+
| encoding | 255-bit little-endian encoding of {0, 1, ..., p-1} |
| of GF(p) | |
+-----------+-------------------------------------------------------+
| H(x) | SHA-512(x) [RFC6234] |
+-----------+-------------------------------------------------------+
| c | base 2 logarithm of cofactor of edwards25519 in |
| | [RFC7748] (i.e., 3) |
+-----------+-------------------------------------------------------+
| n | 254 |
+-----------+-------------------------------------------------------+
| d | d of edwards25519 in [RFC7748] (i.e., -121665/121666 |
| | = 370957059346694393431380835087545651895421138798432 |
| | 19016388785533085940283555) |
+-----------+-------------------------------------------------------+
| a | -1 |
+-----------+-------------------------------------------------------+
| B | (X(P),Y(P)) of edwards25519 in [RFC7748] (i.e., (1511 |
| | 22213495354007725011514095885315114540126930418572060 |
| | 46113283949847762202, 4631683569492647816942839400347 |
| | 5163141307993866256225615783033603165251855960)) |
+-----------+-------------------------------------------------------+
| L | order of edwards25519 in [RFC7748] (i.e., |
| | 2^252+27742317777372353535851937790883648493). |
+-----------+-------------------------------------------------------+
| PH(x) | x (i.e., the identity function) |
+-----------+-------------------------------------------------------+
2.1.1. 点(如公钥)的编码(32 字节)
对于 \(ax^{2}+y^{2}=1+dx^{2}y^{2}\) 上的点,已知 \(x\) 可以求出两个 \(y\) ,已知 \(y\) 也可以求出两个 \(x\) 。要唯一确定一个点,仅有 \(x\) 或者仅有 \(y\) 是不够的。
Ed25519 的参数 \(p\) 选择比较仔细,导致曲线上点的 \(y\) 坐标以小端形式进行编码后,其最高有效位一定是 0。所以这一个比特位还可以利用来编码点的 \(x\) 坐标的正负。这样,Ed25519 曲线上点可以编码为 \(b=256\) 个比特位:其中 \(b-1=255\) 个比特位为 \(y\) 坐标,有 1 个比特位为 \(x\) 的符号位( \(x\) 为负数时这个比特位为 1, \(x\) 为正数时这个比特位为 0)。
总结: Ed25519 的点(如公钥 \(A\) ,签名数据 \(R\) 都是曲线上的点)编码为了 32 字节(256 比特位),其中有 255 个比特位编码了 \(y\) 坐标,而其中 1 个比特位编码的是 \(x\) 的符号位。
+--------+--------+--------+-- --+--------+--------+
| p[0] | p[1] | p[2] | ...... | p[30] | p[31] |
+--------+--------+--------+-- --+--------+--------+
^
|
|
由于是小端形式,所以最后一字节的最高比特位才表示 x 的正负
当然,也可以使用 255 个比特位编码 \(x\) 坐标,而用 1 个比特位编码 \(y\) 的符号位,之所以没有采用这种方案,是为了避免专利,参考:https://crypto.stackexchange.com/questions/106106/why-ed25519-encodes-y-coordinates-rather-than-x-coordinates
参考:
https://datatracker.ietf.org/doc/html/rfc8032#section-5.1.2
https://datatracker.ietf.org/doc/html/rfc8032#section-3.1
2.2. 生成私钥和公钥
EdDSA 的私钥是 \(b\) 个比特位的随机串,一般记为 \(k\) 。
为了计算公钥,我们对私钥 \(k\) 进行哈希运算,确保结果占 \(2b\) 比特位,得结果 \(H(k) = (h_0, h_1, ..., h_{2b-1})\) 。记: \[s \triangleq 2^n + \sum_{c \le i < n} 2^i \cdot h_i\] 这个 \(s\) 相当于 Schnorr 签名中的私钥。 EdDSA 的公钥记为 \(A\) ,由下式得到: \[A \triangleq s \cdot B\]
特别地,对于 Ed25519( \(b=256,n=254,c=3\) ),哈希运算为 SHA-512,其公钥可以用下式计算: \[A = \left(2^{254} + \sum_{i=3}^{253} 2^i \cdot h_i \right) \cdot B\] 式中 \(B\) 是曲线的 Base Point(Generator)。
注 1: Ed25519 公钥从 Ed25519 私钥哈希 \(\text{SHA-512}(k)\) “左半部分的 256 比特位”计算而来, 但也没有全部使用这 256 比特位,而是修改了其中的 5 个比特位,具体来说就是:把下标为 0,1,2 的比特位(低 3 位)设置为 0(因为上面式子中 \(i\) 直接从 3 开始,低 3 位直接忽略了),把第 255 比特位设置为 0,把第 254 比特位设置为 1。为什么要这样做呢?请参考节 2.2.1 。
注 2:后文我们可以看到私钥哈希 \(\text{SHA-512}(k)\) 的“右半部分”用于签名。
注 3:尽管 \(s\) 不是 Ed25519 私钥(它是 Ed25519 私钥哈希的左半部分),但我们不能泄露它,我们需要把它等同于私钥 \(k\) 对待,有了 \(s\) 就可以生成签名了(没有私钥 \(k\) 不能得到签名计算中的 \(r\) ,但随机生成 \(r\) 也是合法的签名,参考节 2.3 )。
2.2.1. 修改 Schnorr 私钥比特位(Bit Clamping)
在由 EdDSA 私钥推导 Schnorr 私钥时(参考节 2.2),为什么不直接使用左边的 256 比特位,而是要做下面修改呢?
- 把第 0,1,2 比特位(最低 3 位)设置为 0;
- 把第 255 比特位设置为 0,把第 254 比特位设置为 1;
这样做的原因分别为:
- 把第 0,1,2 比特位(最低 3 位)设置为 0 的原因是:为了避免 Small-Subgroup Attack(注:当椭圆曲线的 Cofactor 大于 1 时,可能遭受 Small-Subgroup Attack(参考节 6.1),而 Curve25519 的 Cofactor 为 8)。需要说明的是 就算我们不把最低 3 位设置为 0,其实 Ed25519 也不会遭受 Small-Subgroup Attack。因为 Ed25519 中没有 Small-Subgroup Attack 中“自己秘密值和别人提供的数据相乘”的场景出现。而之所以把最低 3 位设置为 0,是为了让 Ed25519 的密钥同时也可以安全地作为 X25519(key-exchange)协议的密钥。
- 而把第 255 比特位设置为 0,把第 254 比特位设置为 1 的原因:让 Curve25519 可以利用 Montgomery ladder 优化手段来加快 Scalar Multiplication 运算。这个设置也不是必要的,因为 Scalar Multiplication 还有其它更快的优化手段。
详情可参考:https://www.jcraige.com/an-explainer-on-ed25519-clamping
2.3. 生成签名
记: \[r \triangleq H(h_b || ... || h_{2b-1} || M)\] 其中 \(||\) 表示的是 concatenation。显然计算 \(r\) 时只使用了私钥哈希 \(H(k)\) 的“右半部分”,因为只取了 \(H(k)\) 的 \(b\) 到 \(2b-1\) 位。 \(r\) 由私钥和待签名消息完全确定。
定义: \[R \triangleq r \cdot B\] 定义: \[S \triangleq (r + s \cdot H(R||A||M)) \pmod L\] 式中的 \(s\) 在前一节中有定义,是利用私钥哈希 \(H(k)\) 的“左半部分”计算而来的 Schnorr 私钥。
得到的 \((R,S)=(r \cdot B, r + s \cdot H(R||A||M))\) 就是 EdDSA 签名。 \(R\) 是曲线上的点,而 \(S\) 是大整数。
对于 Ed25519,则取哈希函数为 \(\text{SHA-512}\) ,取 \[b=256, L = 2^{252} + 27742317777372353535851937790883648493\] 即可。
注:标准的 Schnorr 签名算法中每次签名时都要生成一个不能复用的随机数, EdDSA 签名算法中使用 \(r\) 来代替这个随机数。 \(r\) 由私钥哈希的右半部分和待签名消息 \(M\) 决定,所以对于同一个消息,每次得到的签名是相同的。
2.4. 验证签名
有了签名数据 \((R,S)\) 和公钥 \(A\) ,如果下式成立: \[(2^c \cdot S) \cdot B = 2^c \cdot R + (2^c \cdot H(R||A||M)) \cdot A\] 则通过签名验证。对于 Ed25519,则取哈希函数为 \(\text{SHA-512}\) ,取参数 \(c=3\) 即可。
特别地,为了防止 Signature Malleability,在验证签名 \((R,S)\) 是否合法时,还需要检测 \(S < L\) 是否成立,不成立就认为是非法签名,详情可参考节 3.2。
2.4.1. 证明
EdDSA 的证明:
2.4.2. 验证签名时无法检测 \(s\) 和 \(r\) 是否符合 RFC8032
RFC8032 中规定了:
- Schnorr 私钥 \(s\) (它由 EdDSA 私钥推导出来),需要把其进行 Clamping 操作(参考节 2.2.1 ,即最低 3 位设置为 0,最高位设置为 0,次高位设置为 1);
- 签名时使用的 \(r\) 值由 \(H(h_b || ... || h_{2b-1} || M)\) 计算而来。
如果签名者不遵守上面两个要求(比如对 \(s\) 不进行 Clamping,而 \(r\) 则随机产生),验证者也是不知道的。
因为验证签名时,从签名数据 \((R,S)\) 和公钥 \(A\) 中并不能判断签名者是否遵守上面两个要求。
2.5. 签名总结
Ed25519 密钥对生成和签名过程可总结为图 1 所示(摘自:https://blog.mozilla.org/warner/2011/11/29/ed25519-keys/ )。
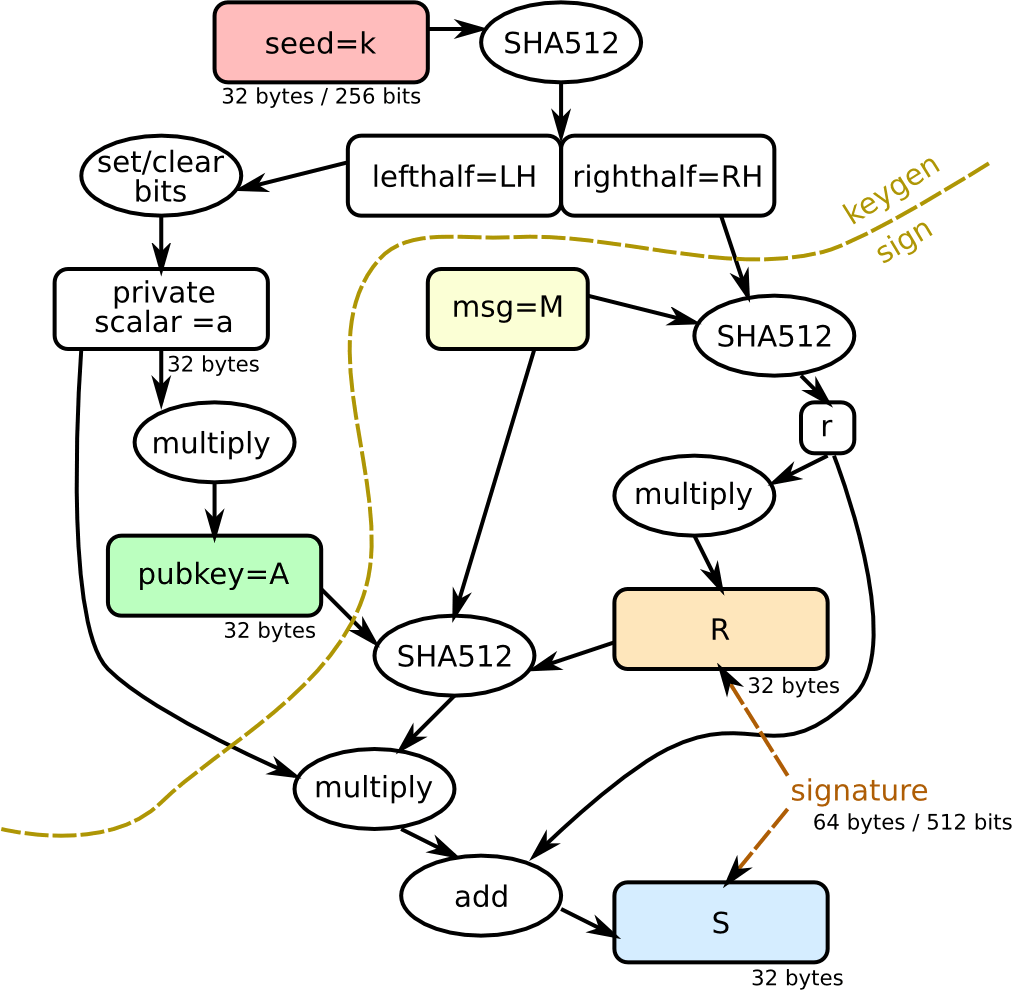
Figure 1: Ed25519 密钥对生成和签名过程(图中 a 是前面介绍的 Schnorr 私钥 s)
3. Ed25519 实现
在 RFC8032 第 6 节中有 Ed25519 的一个 Python 实现。在 https://ed25519.cr.yp.to/software.html 中也有 Ed25519 的一个 Python 实现。
3.1. Ed25519 实现漏洞之“假公钥”
Ed25519 协议本身目前还没有发现有漏洞,不过不恰当的实现可能导致安全漏洞。
出于效率考虑,一些库在实现 Ed25519 时,公钥 \(A\) 往往不会重新计算,而是被暂存起来。在签名的时候,公钥 \(A\) 作为已有值,直接参与签名计算。比如库可能提供下面函数进行签名: \(sign(k, A, M)\) ,其中 \(k\) 是 Ed25519 私钥, \(A\) 是公钥,而 \(M\) 待签名消息。
攻击者对同一个消息 \(M\) 发起两次签名,每次签名时使用不同公钥(比如分别使用 \(A\) 和 \(A'\) ,有一个公钥是假的,或者两个都是假的)可实现攻击。
第一次签名,假设输入的公钥为 \(A\) ,待签名消息为 \(M\) ,签名结果为:
第二次签名,假设输入的公钥为 \(A'\) ,待签名消息为 \(M\) ,签名结果为:
由于 \(M\) 相同,所以 \(r\) 相同,两次签名的 \(R\) 也相同。由于 \(R, A, M\) 是公开的,所以 \(H(R || A || M)\) 可以计算出来;同样 \(H(R || A' || M)\) 也可以计算出来。
把两次签名得到的 \(S\) 相减,有:
从而有: \[s = (S - S') \left( H(R || A || M) - H(R || A' || M) \right)^{-1}\]
我们可以求得 \(s\) ,它并不是 Ed25519 的私钥。不过,只知道 \(s\) 也可以生成一个合法的签名。
避免这种攻击的办法:不提供签名方法 \(sign(k, A, M)\) ,而是直接提供签名方法 \(sign(k, M)\) ,在函数内部通过 \(k\) 计算出公钥 \(A\) 。
3.2. Ed25519 实现漏洞之 Signature Malleability
什么是 Signature Malleability?在不知道私钥的情况下,如果通过修改一个已知的合法签名,可以得到另一个合法签名,这就称为 Signature Malleability。Signature Malleability 可能被黑客用于攻击,我们需要避免 Signature Malleability。
假设 \((R,S)\) 是一个已知的 Ed25519 合法签名数据( \(R\) 是曲线上的点,而 \(S\) 是大整数),那么 \((R, L + S)\) 也能满足 Ed25519 的签名校验(这里 \(L\) 是 Ed25519 的参数,即循环子群的阶 \(L=2^{252}+27742317777372353535851937790883648493\) ),也就是说 \((R, L + S)\) 也是一个合法签名。这样,不知道私钥的情况下,得到了另一个合法签名,这就是 Signature Malleability。
下面证明一下,为什么 \((R,S)\) 是合法签名时, \((R,L+S)\) 也会是合法签名。也就是说,为什么 \((2^c \cdot S) \cdot B = 2^c \cdot R + (2^c \cdot H(R||A||M)) \cdot A\) 成立时, \((2^c \cdot (L + S)) \cdot B = 2^c \cdot R + (2^c \cdot H(R||A||M)) \cdot A\) 一定成立。
两个等式的右边是一样的,我们只要证明两个等式的左边相等即可,即证明 \((2^c \cdot S) \cdot B = (2^c \cdot (L + S)) \cdot B\) 即可。
循环子群的阶为 \(L\) ,设 \(B\) 是 Generator,则由椭圆曲线循环子群的定义有 \(L \cdot B = \mathcal{O}\) 。
根据上面的证明过程可知,当 \((R,S)\) 是合法签名时,不仅 \((R, L + S)\) 是合法签名, \((R, 2L + S), (R, 3L + S)\) 等也都是合法签名。
为了避免 Signature Malleability,在 RFC8032 中规定了在校验签名 \((R,S)\) 是否正确时,必须额外检查 \(S < L\) 是否成立,不成立就认为它是非法签名。这样, \((R, L + S), (R, 2L + S), (R, 3L + S)\) 等显然无法通过这个额外检查了。
不过,在实现时可能忽视了这个检查,如 OpenSSL 以前就忽视过,参见:https://github.com/openssl/openssl/issues/7693
4. BIP32
有人指出在 Hierarchical Deterministic (HD) 场景中如果多次使用 Bit Clamping(参见节 2.2.1)可能不安全,参见:https://moderncrypto.org/mail-archive/curves/2017/000858.html ,有人给出了解决办法,参见:https://moderncrypto.org/mail-archive/curves/2017/000866.html
论文 BIP32-Ed25519: Hierarchical Deterministic Keys over a Non-linear Keyspace 中提出了如何调整 BIP32 来为 Ed25519 曲线推导分层确定性(HD)密钥。不过有人指出,如果 BIP32-Ed25519 中允许很长的 Derivation Path,则可能被恢复出私钥,参考:https://github.com/w3f/hd-ed25519
5. Threshold EdDSA
EdDSA 标准中要求 Nonce 值是确定性的(即由私钥和消息唯一确定)。但是在验证签名时,验证者无法知道签名者有没有使用 EdDSA 标准所规定的 Nonce 值。也就是说随机生成的 Nonce 值,也能通过 EdDSA 的签名验证。
对于 Threshold EdDSA,如果不要求签名时使用确定性 Nonce(即随机生成 Nonce 是可接受的),则可以使用 Schnorr 门限签名,因为 EdDSA 是 Schnorr 的变种,Schnorr 门限签名比较简单。
对于 Threshold EdDSA,如果要求签名时使用确定性 Nonce,会比较麻烦,这里不详细介绍,可以参考下面论文:
5.1. 还原区块链私钥
有一些区块链(比如 Solana)采用 EdDSA 签名,为了提高私钥的安全性,我们可以采用门限 EdDSA 签名。
先回顾一下 EdDSA 的私钥和公钥的关系:
Seed --- SHA512 ---> 521Bits --- Set/clear bits of --> Private scalar -----> Public Key ^ Lefehalf(521Bits) ^ ^ | | | | | | 标准 中间产生的 标准 EdDSA 公钥 EdDSA Schnorr (也是 Schnorr 公钥) 私钥 私钥
在我们实现门限 EdDSA 签名时,通常采用门限 Schnorr 签名的变种。也就是说, 我们得到的分片并不是“标准 EdDSA 私钥”的分片;而是“中间产生的 Schnorr 私钥“的分片。这么做的原因是更加简单:如果生成的是“标准 EdDSA 私钥”的分片,那么 MPC 签名过程中会涉及到 SHA512 的 MPC 运算,这个过程是很复杂的。为了避免这种复杂性,我们往往直接生成“中间产生的 Schnorr 私钥“的分片。
但是,这带来了一个新问题:我们通过分片还原出来的完整私钥,并不是标准 EdDSA 私钥,而是“中间产生的 Schnorr 私钥”。还原出来的私钥没有办法被标准的 EdDSA 库所使用。
对于这个问题有两种解决方案。
方案 1:为用户单独提供一套专有的 EdDSA 库。这个库可以直接从“中间产生的 Schnorr 私钥“开始进行签名(标准的 EdDSA 库只能从“标准 EdDSA 私钥”开始进行签名)。
方案 2:两套分片(key shares)方案。 Distributed Key Generation 结束后,生成的 key share 我们称它为第一套 key share,它的作用仅仅用于恢复 EdDSA 私钥,它并不用于 MPC 签名。而第二套 key share 的产生过程如下:从第一套 key share 恢复出完整私钥,作为标准 EdDSA 私钥,然后进行 SHA512 运算,再取左边 256 bits,再进行 Set/clear 操作,得到 Private scalar(中间产生的 Schnorr 私钥),再把这个 Private scalar 拆分为多个分片。这就是第二套 key share,它用于 MPC 签名,不用于恢复私钥(因为它恢复出来的仅仅是“中间产生的 Schnorr 私钥“)。
这两种方案的优缺点如表 1 所示。
| 优点 | 缺点 | |
|---|---|---|
| 方案 1 | 更安全,需要 Trust Dealer | 不能恢复出标准 EdDSA 私钥,和标准 EdDSA 库的兼容性不好 |
| 方案 2 | 兼容性好,可恢复标准 EdDSA 私钥 | 需要 Trust Dealer 还原第一套分片,拆分第二套分片 |
6. 附录
6.1. Small-Subgroup Attack
当 Cofactor 不为 1 时,可能存在 Small-Subgroup Attack,这里以 Diffie Hellman Key Exchange 协议来介绍下什么是 Small-Subgroup Attack。
The operations are usually implemented in the prime order subgroup of the full Curve. Let’s take the example of Diffie Hellman to understand the small subgroup attack. Let’s say our curve is of order 8p where p is a prime & 8 is the cofactor. The main group of order 8p is a finite cyclic Group. By the fundamental theorem of finite cyclic groups, the 2 subgroups of order 8 & order p are also finite cyclic subgroups. Let G be a generator of the prime order subgroup. Let a & b be Alice’s & Bob’s private key respectively. This is how a typical Diffie Hellman key exchange works.
Alice −−−−−−--−−aG−−−−−−−−−−−→ Bob
Alice ←−−−−−−−--bG−−−−−−−−−−−− Bob
Alice calculates a⋅bG, Bob calculates b⋅aG and the shared secret is derived from abG by both parties.
If Bob is a malicious participant, he can launch a small subgroup attack which can leak some information about Alice’s private key. The protocol depends on operating in the prime order subgroup (i.e. the subgroup of order p). Since G is a generator of the prime order subgroup, abG also falls in the prime order subgroup (because of closure). But the full curve group also contains other subgroups - one of which is of order 8. The points of the subgroup of order 8 are not in the prime order subgroup (other than the identity). Let H be a generator of the subgroup of order 8. Now, if Bob instead of sending bG to Alice sends just H to Alice. So Alice calculates aH (instead of abG) & derives the share secret using that. Alice then encrypts a message using the shared secret & sends it to Bob. Now if Alice’s shared secret had been derived from abG, then number of possible values abG could have is p which is a very large prime - for e.g. for Curve25519, \(p=2^{252}+27742317777372353535851937790883648493\) so brute forcing the encrypted message to recover the shared secret is not possible. However, Bob has tricked Alice into deriving her shared secret from aH. Since H is a generator of subgroup of order 8, aH is a point of the subgroup of order 8 because of closure in the subgroup. So aH can only be one of 8 points instead one of p points. Now brute forcing the secret key is much simpler for Bob. So Bob can recover aH. It’s possible to recover the value of a mod 8 from aH - which is the lower 3 bits of a.
To understand this better, let’s take the example of a simple additive group of order 8p where p=11 and the cofactor is 8. This is the group ℤ/88ℤ. This has the elements {0,1,2,3,4,….87} (I am omitting the coset notation for simplicity)
This has multiple subgroups including
- the prime order subgroup of order 11 - {0,8,16,24,32,40,48,56,64,72,80}
- the cofactor subgroup of order 8 - {0,11,22,33,44,55,66,77}
Let the generator chosen for the DH exchange be 8. So Alice would send a⋅8 & Bob would send b⋅8 & the shared secret would be derived from ab8. A malicious Bob instead of sending b⋅8, sends a generator of the cofactor subgroup - i.e he sends 11. So now Alice computes 11a. Irrespective of what a is chosen by Alice, a⋅11 always is restricted to 8 different elements instead of the bigger group of 11 different elements if Bob was a honest participant. Alice now derives the shared secret from a⋅11 & she encrypts a message with it & sends it to Bob. Because of the attack, Bob now has to only bruteforce by doing an exhaustive search through 8 different elements instead of 11 different elements. In our toy example, reduction from 11 to 8 is not a significant reduction, but in the case of actual cryptographic curves, the reduction in search is huge - from searching through a really large set of size p to searching through just 8 points. So now Bob knows aH. If you iterate through all possible 88 values of a & calculate aH, you will see that aH falls into 8 different values depending on value of a mod 8. So if you know the shared secret, you know a mod 8 which is the lower 3 bits of a.
This is the small subgroup attack.
There are also a couple of other attacks similar to the one we described.
- Instead of sending bG, Bob can send bG+H to Alice. So Alice now calculates abG+aH. Now since Bob knows abG, this again leaks a mod 8.
- Instead of Bob launching the above attack, a man in the middle (Mallory) intercepts bG sent by Bob & replace it with H, then he can brute force the secret key generated by Alice (aH) because it can only be one of 8 points.
In DH, leaking a mod 8 matters only if Alice reuses a. However, above attack is not limited to DH, but also applicable to many other Cryptographic protocols. In some protocols like like PAKE, MQV etc, the attack can have far worse effects.
Mitigation for the small subgroup attack - cofactor clearing
If you have a cyclic group of order np (where p is a prime), then scalar multipliying any element of the group by the cofactor (n) gives you an element of the prime order subgroup irrespective irrespective of which subgroup it was in originally. This can be easily done by both parties - i.e. Alice after choosing a private key a, she multiplies it by 8 & uses 8a as the private key. So when she receives bG from Bob, the shared secret is derived from 8abG instread of from abG. Likewise Bob does the same. Now if Bob is a malicious player, then what is leaked is 8a mod 8 instead of a mod 8. Since 8a mod 8 is always 0, nothing of significance is leaked. Thus, mutliplying the private key by the cofactor mitigates the small subgroup attack.
摘自:https://risencrypto.github.io/CofactorClearing/
简单总结下 Small-Subgroup Attack:在进行 Diffie Hellman Key Exchange 时,Bob 发给 Alice 的数据期望是从大子群中来(bG),但 Bob 如果使坏不发送大子群中的 bG,而是把小子群中元素 H 发给 Alice,那么 Alice 得到的 shared secret 就是 aH,当 Alice 使用 shared secret aH 加密数据发送给 Bob 后,Bob 可以通过暴力搜索破解出 aH(因为 H 所在小子群只有 8 个元素,从而 aH 的可能情况也只有 8 个)。Bob 知道 aH 后,可能从中得到 Alice 的秘密 a 的部分信息(因为大子群中的任意数 a 和小子群 H 相乘后得到的数会在小子群中,也就是只有 8 种可能,这相当于泄露了 a 的最低 3 个比特位)。
之所以会泄露 Alice 的秘密 a 的部分信息,是由于 Alice 把 a 和 Bob 提供的恶意数据相乘后发送给了 Bob。有一种方法可以避免 Small-Subgroup Attack:Alice 在使用 a 前,先把 a 乘以 Cofactor(8),由于这样操作后,其结果的最低 3 位会是 0,这样就不会泄露原先的 a 了。
注:在椭圆曲线中,把自己秘密值和别人提供的公钥相乘是一个危险的操作,比如在 Dangers of using secp256k1 for encryption - Twist Attacks 中提到了一种攻击方式可能会使 secp256k1 的私钥被泄露。