AdaBoost (Adaptive Boosting)
Table of Contents
1. 提升方法简介
提升(Boosting)方法是一种常用的统计学习方法,应用广泛且有效。在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。
提升方法是多种学习方法的集成,属于“集成学习(Ensemble learning)”。
参考:
本文主要摘自:《统计学习方法,李航著》第 8 章 提升方法
The Elements of Statistical Learning(2nd), Chapter 10 Boosting and Additive Trees
1.1. 提升方法的基本思路
提升算法基于这样一种思路:对于一个复杂任务来说,将多个专家的判断进行适当的综合所得出的判断,要比其中任何一个专家单独的判断好。实际上,就是“三个臭皮匠顶个诸葛亮”的道理。
历史上,Kearns 和 Valiant 首先提出了“强可学习(strongly learnable)”和“弱可学习(weakly learnable)”的概念。指出:在概率近似正确(probably approximately correct,PAC)学习框架中,一个概念(一个类),如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么就称这个概念是强可学习的;一个概念,如果存在一个多项式的学习算法能够学习它,学习的正确率仅比随机猜测略好,那么就称这个概念是弱可学习的。非常有趣的是 Schapire 后来证明 强可学习与弱可学习是等价的 ,也就是说,在 PAC 学习的框架下,一个概念是强可学习的充分必要条件是这个概念是弱可学习的。
这样一来,问题便成为,在学习中,如果已经发现了“弱学习算法”,那么能否将它提升(boost)为“强学习算法”。大家知道, 发现弱学习算法通常要比发现强学习算法容易得多。那么如何具体实施提升,便成为开发提升方法时所要解决的问题。 关于提升方法的研究很多,有很多算法被提出。最具代表性的是 AdaBoost 算法(AdaBoost algorithm)。
2. AdaBoost
对于分类问题而言,提升方法通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。这样,有两个问题需要回答:一是在每一轮如何改变训练数据的权值分布;二是如何将弱分类器组合成为一个强分类器。
关于第 1 个问题,AdaBoost 算法的做法是,提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。这样一来,那些没有得到正确分类的数据,由于其权值的加大而受到后轮的弱分类器的更大关注。于是,分类问题被一系列的弱分类器“分而治之”。至于第 2 个问题,即弱分类器的组合,AdaBoost 采取加权多数表决的方法。具体地,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用,减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。
AdaBoost 是如何实践上面的思路,请看下文分解。
2.1. AdaBoost 算法
AdaBoost 算法描述如下:
输入:训练数据集 \(T={(\boldsymbol{x_1},y_1), (\boldsymbol{x_2},y_2), \cdots (\boldsymbol{x_N},y_N)}\) ,其中 \(\boldsymbol{x_i} \in \mathcal{X} \subseteq \mathbb{R}^n, y_i \in \mathcal{Y} = \{ -1 , +1 \}, i=1,2,\cdots, N\) ,其中 \(y_i\) 是 \(\boldsymbol{x_i}\) 的类标记;弱学习算法。
输出:最终分类器 \(G(x)\) 。
第 1 步,初始化训练数据的权值分布:
\[D_1 = \{w_{1,1}, w_{1,2}, \cdots, w_{1,i}, \cdots, w_{1,N} \}, \quad w_{1,i} = \frac{1}{N}, \quad i = 1,2,\cdots,N\]
第 2 步,对 \(m=1,2,\cdots,M\) ( \(M\) 表示迭代的次数,即基本分类器个数)依次执行下面过程:
(a) 使用具有权值分布 \(D_m\) 的训练数据集学习,得到基本分类器:
\[G_m: \mathcal{X} \mapsto \{ -1 , +1\}\]
(b) 计算 \(G_m(\boldsymbol{x})\) 在训练数据集上的分类误差率:
\[e_m=P(G_m(\boldsymbol{x_i}) \neq y_i)= \sum_{i=1}^{N} w_{m,i}I(G_m(\boldsymbol{x_i}) \neq y_i)\]
注:上式中 \(I(G_m(\boldsymbol{x_i}) \neq y_i)\) 是指示函数,当参数为真(即不等号成立)时其值为 1,否则为 0。
(c) 计算基本分类器 \(G_m(\boldsymbol{x})\) 的系数:
\[\alpha_m = \frac{1}{2} \ln \frac{1-e_m}{e_m}\]
(d) 更新训练数据集的权值分布:
\[D_{m+1} = \{w_{m+1,1}, w_{m+1,2}, \cdots, w_{m+1,i}, \cdots, w_{m+1,N} \}\]
其中:
\[w_{m+1,i} = \begin{cases} \dfrac{w_{m,i}}{Z_m} e^{- \alpha_m}, & G_m(\boldsymbol{x_i}) = y_i \quad \text{注:即当该样本被正确分类时} \\ \dfrac{w_{m,i}}{Z_m} e^{\alpha_m}, & G_m(\boldsymbol{x_i}) \neq y_i \quad \text{注:即当该样本被错误分类时} \end{cases}\]
利用 \(y_i \in \{ -1 , +1 \}\) ,上式还可以写为:
\[w_{m+1,i} = \dfrac{w_{m,i}}{Z_m} e^{- \alpha_m y_i G_m(\boldsymbol{x_i})}, \quad i = 1,2,\cdots, N\]
这里, \(Z_m\) 是规范化因子,为:
\[Z_m = \sum_{i=1}^{N} w_{w,i} e^{- \alpha_m y_i G_m(\boldsymbol{x_i})}\]
它使 \(D_{m+1}\) 成为一个概率分布。
第 3 步,构建基本分类器的线性组合:
\[f(x) = \sum_{m=1}^M \alpha_m G_m(\boldsymbol{x})\]
得到最终分类器:
\[G(x) = sign(f(x)) = sign \left( \sum_{m=1}^M \alpha_m G_m(\boldsymbol{x}) \right)\]
算法完。
说明 1:上面算法中, \(w_{m+1,i} = \begin{cases} \dfrac{w_{m,i}}{Z_m} e^{- \alpha_m}, & G_m(\boldsymbol{x_i}) = y_i \\ \dfrac{w_{m,i}}{Z_m} e^{\alpha_m}, & G_m(\boldsymbol{x_i}) \neq y_i\end{cases}\) 使得被基本分类器 \(G_m(\boldsymbol{x})\) 误分类样本的权值得以扩大,而被正确分类样本的权值却得以缩小。两相比较, 误分类样本的权值被放大 \(e^{2\alpha_m}=\frac{e_m}{1-e_m}\) 倍 。因此,误分类样本在下一轮学习中起更大的作用。不改变所给的样本数据,而不断改变训练数据权值的分布,使得训练数据在基本分类器的学习中起不同的作用,这是 AdaBoost 的一个特点。
说明 2:线性组合 \(f(x)\) 实现 \(M\) 个基本分类器的 加权表决 。系数 \(\alpha_m\) 表示了基本分类器 \(G_m(\boldsymbol{x})\) 的重要性,这里,所有 \(\alpha_m\) 之和并不为 1。 \(f(x)\) 的符号决定实例 \(\boldsymbol{x}\) 的类别, \(f(x)\) 的绝对值表示分类的确信度。利用基本分类器的线性组合构建最终分类器是 AdaBoost 的另一特点。
AdaBoost 算法的实践过程可以形象地用图 1 (图片摘自“The Elements of Statistical Learning(2nd), Chapter 10 Boosting and Additive Trees”)展示。
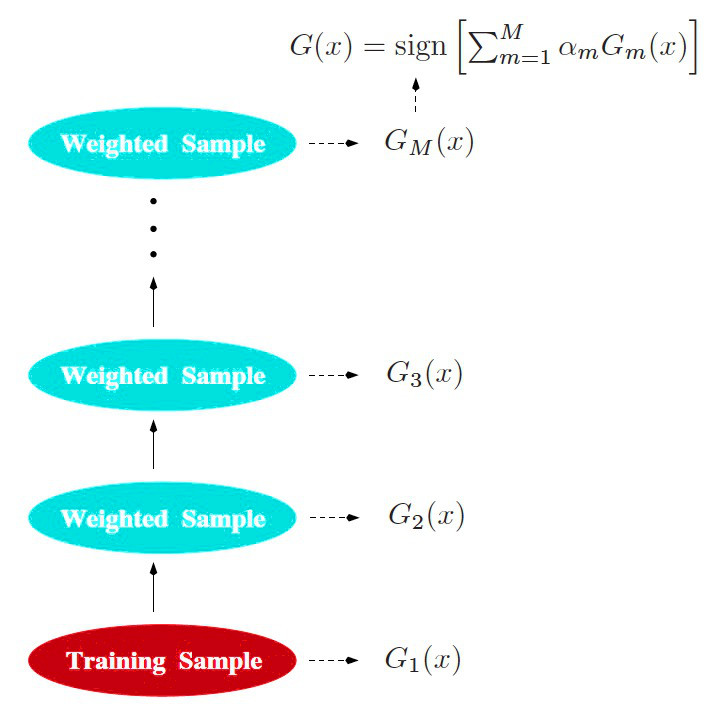
Figure 1: AdaBoost 算法图示
2.2. AdaBoost 应用实例
给定如表 1 所示训练数据。假设弱分类器由 \(x < v\) 或 \(x > v\) 产生,其阈值 \(v\) 使该分类器在训练数据集上分类误差率最低。试用 AdaBoost 算法学习一个强分类器。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| \(y\) | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
解:初始化数据权值分布:
\[D_1 = (w_{1,1}, w_{1,2}, \cdots, w_{1,10})\]
其中, \(w_{1,i} = 0.1, \quad i = 1,2, \cdots, 10\)
迭代过程 1,对 \(m=1\) ,有
(a) 在权值分布为 \(D_1\) 的训练数据上,容易求得阈值 \(v\) 取 2.5 时的分类误差率最低(这时误差点为 \(x=6,7,8\) ),故第 1 个基本分类器为:
\[G_1(x) = \begin{cases} 1, & x < 2.5 \\ -1, & x > 2.5 \end{cases}\]
(b) \(G_1(x)\) 在训练数据集上的误差率: \(e_1=P(G_1(x_i) \neq y_i) = 0.3\)
(c) 计算 \(G_1(x)\) 的系数:
\[\alpha_1 = \frac{1}{2} \ln \frac{1-e_1}{e_1}=0.4236\]
(d) 更新训练数据的权值分布:
\[\begin{aligned} w_{2,i} &= \frac{w_{1,i}}{Z_1} e^{-\alpha_1 y_i G_1(x)}, \quad i = 1,2, \cdots, 10 \\
D_2 &= (w_{2,1}, w_{2,2}, \cdots, w_{2,10}) \\
&= (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715) \\
f_1(x) &= 0.4236 G_1(x)
\end{aligned}\]
分类器 \(sign[f_1(x)]\) 在训练数据集上有 3 个误分类点。
迭代过程 2,对 \(m=2\) ,有
(a) 在权值分布为 \(D_2\) 的训练数据上,容易求得阈值 \(v\) 取 8.5 时的分类误差率最低,故第 2 个基本分类器为:
\[G_2(x) = \begin{cases} 1, & x < 8.5 \\ -1, & x > 8.5 \end{cases}\]
(b) \(G_2(x)\) 在训练数据集上的误差率: \(e_2=P(G_2(x_i) \neq y_i) = 0.2143\)
(c) 计算 \(G_2(x)\) 的系数:
\[\alpha_2 = \frac{1}{2} \ln \frac{1-e_2}{e_2}=0.6496\]
(d) 更新训练数据的权值分布:
\[\begin{aligned} D_3 &= (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455) \\
f_2(x) &= 0.4236 G_1(x) + 0.6496 G_2(x)
\end{aligned}\]
分类器 \(sign[f_2(x)]\) 在训练数据集上有 3 个误分类点。
迭代过程 3,对 \(m=3\) ,有
(a) 在权值分布为 \(D_3\) 的训练数据上,容易求得阈值 \(v\) 取 5.5 时的分类误差率最低,故第 2 个基本分类器为:
\[G_3(x) = \begin{cases} 1, & x < 5.5 \\ -1, & x > 5.5 \end{cases}\]
(b) \(G_3(x)\) 在训练数据集上的误差率: \(e_3 = 0.1820\)
(c) 计算 \(G_3(x)\) 的系数:
\[\alpha_3 = 0.7514\]
(d) 更新训练数据的权值分布:
\[\begin{aligned} D_4 &= (0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125) \\
f_3(x) &= 0.4236 G_1(x) + 0.6496 G_2(x) + 0.7514 G_3(x)
\end{aligned}\]
分类器 \(sign[f_3(x)]\) 在训练数据集上误分类点个数为 0。
于是,最终分类器为:
\[G(x) = sign[f_3(x)] = sign[0.4236 G_1(x) + 0.6496 G_2(x) + 0.7514 G_3(x)]\]
2.3. AdaBoost 算法缺点
AdaBoost 算法缺点:对异常点非常敏感。 它不断增加误分类样本的权重(指数上升),但如果数据样本是异常点(outlier),则可能极大的干扰后面基本分类器的学习。
3. 加法模型及 AdaBoost 算法解释
AdaBoost 算法可以看作是“模型为加法模型、损失函数为指数函数、学习算法为前向分布算法”时的二类分类学习方法。
3.1. 加法模型和前向分布算法
考虑加法模型(additive model):
\[f(x) = \sum_{m=1}^M \beta_m b(x; \gamma_m)\]
其中, \(b(x; \gamma_m)\) 为基函数, \(\gamma_m\) 为基函数的参数, \(\beta_m\) 为基函数的系数。显然, AdaBoost 算法最终分类器是一个加法模型。
在给定训练数据及损失函数 \(L(y, f(x))\) 的条件下,学习加法模型 \(f(x)\) 就是损失函数极小化问题:
\[\min_{\beta_m, \gamma_m} \sum_{i=1}^N L \left(y_i, \sum_{m=1}^M \beta_m b(x_i; \gamma_m) \right)\]
通常这是一个复杂的优化问题。前向分布算法(forward stagewise algorithm)求解这一优化问题的想法是:因为学习的是加法模型,那如果能够从前向后,每一步只学习一个基函数及其系数,然后逐步逼近上面的优化目标式,那么就可以简化优化的复杂度。具体的,每步只需优化如下损失函数:
\[\min_{\beta, \gamma} \sum_{i=1}^N L \left(y_i, \beta b(x_i; \gamma) \right)\]
这样, 前向分布算法将同时求解从 \(m=1\) 到 \(M\) 的所有参数 \(\beta_m, \gamma_m\) 的优化问题简化为逐次求解各个 \(\beta_m, \gamma_m\) 的优化问题。
3.1.1. 前向分布算法
给定训练数据集 \(T={(\boldsymbol{x_1},y_1), (\boldsymbol{x_2},y_2), \cdots (\boldsymbol{x_N},y_N)}\) ,其中 \(\boldsymbol{x_i} \in \mathcal{X} \subseteq \mathbb{R}^n, y_i \in \mathcal{Y} = \{ -1 , +1 \}, i=1,2,\cdots, N\) 。损失函数 \(L(y, f(\boldsymbol{x}))\) 和基函数的集合 \(\{ b(\boldsymbol{x}; \boldsymbol{\gamma}) \}\) 。学习加法模型 \(f(\boldsymbol{x})\) 的前向分步算法描述如下。
前向分布算法:
输入:训练数据集 \(T={(\boldsymbol{x_1},y_1), (\boldsymbol{x_2},y_2), \cdots (\boldsymbol{x_N},y_N)}\) ;损失函数 \(L(y, f(\boldsymbol{x}))\) 和基函数的集合 \(\{ b(\boldsymbol{x}; \boldsymbol{\gamma}) \}\) 。
输出:加法模型 \(f(\boldsymbol{x})\) 。
第 1 步,初始化 \(f_0(\boldsymbol{x}) = 0\)
第 2 步,迭代执行下面步骤,对 \(m=1,2, \cdots, M\)
(a) 极小化损失函数:
\[(\beta_m, \boldsymbol{\gamma}_m) = \operatorname{arg} \underset{\boldsymbol{\beta, \boldsymbol{\gamma}}}{\min} \sum_{i=1}^N L(y_i, f_{m-1}(\boldsymbol{x_i}) +\beta b(\boldsymbol{x_i}; \boldsymbol{\gamma}) )\]
得到参数 \(\beta_m, \boldsymbol{\gamma}_m\)
(b) 利用上步求得的 \(\beta_m, \boldsymbol{\gamma}_m\) 更新下面式子:
\[f_m(\boldsymbol{x}) = f_{m-1}(\boldsymbol{x}) + \beta_m b(\boldsymbol{x}; \boldsymbol{\gamma}_m)\]
第 3 步,得到加法模型:
\[f(\boldsymbol{x}) = f_M(\boldsymbol{x}) = \sum_{m=1}^{M} \beta_m b(\boldsymbol{x}; \boldsymbol{\gamma})\]
3.2. AdaBoost 算法的推导
AdaBoost 算法可以看作是损失函数为指数损失时的前向分布算法。关于它的推导可参考:
(1) 《统计学习方法,李航著》 8.3.2 前向分步算法与 AdaBoost
(2) The Elements of Statistical Learning(2nd), 10.4 Exponential Loss and AdaBoost
3.3. 不同损失函数及相应的 Boost 方法
按照损失函数的不同,表 2 给出了 4 种不同的 Boost 方法。
| Name | Loss | Algorithm |
|---|---|---|
| 平方损失 | \(\frac{1}{2}(y_i - f(\boldsymbol{x_i}))^2\) | L2Boosting (Least Squares Boosting) |
| 绝对损失 | \(\mid y_i - f(\boldsymbol{x_i}) \mid\) | Gradient boosting |
| 指数损失 | \(e^{(-\tilde{y}_i f(\boldsymbol{x_i}))}\) | AdaBoost |
| 对数损失 | \(\log(1+e^{-\tilde{y}_i f(\boldsymbol{x_i})})\) | LogitBoost |
参考:Machine Learning - A Probabilistic Perspective, 16.4 Boosting