GBDT (Gradient Boosting Decision Tree)
Table of Contents
1. 梯度提升简介(GBDT, MART, GTB, GBT, GBRT)
梯度提升树(GBDT, 全称为 Gradient Boosting Decision Tree)。它还有其它一些名字,如 Multiple Additive Regression Tree(MART), Gradient Tree Boosting(GTB), Gradient Boosting Tree(GBT), Gradient Boosting Regression Tree(GBRT).
注: “梯度提升”是集成学习 Boosting 家族的成员。 “梯度提升”是一个通用的框架,我们往往使用 CART 回归树作为“基本回归算法”,这时梯度提升称为梯度提升决策树(GBDT)。GBDT 是回归树,更适合做回归,当然也可以用作分类(如二分类时设定一个阈值即可)。GBDT 几乎可用于所有回归问题(线性/非线性),相对于 Logistic Regression 仅能用于线性回归,GBDT 的适用面更广。
参考:
梯度提升原始论文:Jerome H. Friedman. Greedy Function Approximation: A Gradient Boosting Machine: http://statweb.stanford.edu/~jhf/ftp/trebst.pdf
统计学习方法,李航著
1.1. 梯度提升基本思想
下面通过一个例子来说明梯度提升的基本思想。
有数据 \(\{(\boldsymbol{x_1},y_1), (\boldsymbol{x_2},y_2), \cdots, (\boldsymbol{x_N},y_N)\}\) ,你的任务是拟合这些样本点(即求回归模型),使平方误差最小。
假设你朋友提供了一个现成的模型 \(F(\boldsymbol{x})\) 给你,你检查后发现这个模型不错,但还不够完美。如模型输出 \(F(\boldsymbol{x}_1)=0.8\) ,而实际上 \(y_1=0.9\) ;模型输出 \(F(\boldsymbol{x}_2)=1.4\) ,而实际上 \(y_2=1.3\) 等等。你如何基于朋友的模型,得到一个更好的模型呢?
一个简单的想法是:你在 \(F\) 基础上增加一个回归模型 \(h\) ,这样新的回归模型为 \(F(\boldsymbol{x}) + h(\boldsymbol{x})\) 。也就是说,你增加的回归模型 \(h\) 满足下面条件:
\[\begin{aligned} F(\boldsymbol{x_1}) + h(\boldsymbol{x_1}) & = y_1 \\
F(\boldsymbol{x_1}) + h(\boldsymbol{x_1}) & = y_1 \\
F(\boldsymbol{x_2}) + h(\boldsymbol{x_2}) & = y_2 \\
\cdots \\
F(\boldsymbol{x_N}) + h(\boldsymbol{x_N}) & = y_N
\end{aligned}\]
上面式子等价于:
\[\begin{aligned} h(\boldsymbol{x_1}) & = y_1 - F(\boldsymbol{x_1}) \\
h(\boldsymbol{x_2}) & = y_2 - F(\boldsymbol{x_2}) \\
\cdots \\
h(\boldsymbol{x_N}) & = y_N - F(\boldsymbol{x_N})
\end{aligned}\]
也就说, \(h\) 可以看作是数据 \({(\boldsymbol{x_1}, y_1 - F(\boldsymbol{x_1})), (\boldsymbol{x_2},y_2 - F(\boldsymbol{x_2})), \cdots (\boldsymbol{x_N},y_N - F(\boldsymbol{x_N}))}\) 的拟合。
我们把 \(y_i - F(\boldsymbol{x_i})\) 称为 残差(\(\color{red}{\text{residuals}}\)) 。残差是回归模型 \(F\) 做的不好的地方, \(h\) 的作用是补偿 \(F\) 的不足。
对于新的模型 \(F+h\) ,如果发现它仍然不够好,我们可以重复上面的思路,在 \(F+h\) 基础上再增加一个回归模型,这样迭代进行下去。
这就是梯度提升的基本思路。但这和“梯度”(Gradient)有什么关系呢?下面的分析将说明:采用平方损失函数时,残差就是负梯度。
在数据拟合过程中,采用平方损失函数 \(L(y, F(\boldsymbol{x})) = \frac{1}{2} (y -F(\boldsymbol{x}))^2\) ,拟合目标是最小化总损失函数 \(J = \sum_{i=1}^N L(y_i, F(\boldsymbol{x}_i))\) 。
注意到 \(F(\boldsymbol{x}_1), F(\boldsymbol{x}_2), \cdots, F(\boldsymbol{x}_N)\) 就是一些数字,我们把 \(F(\boldsymbol{x}_i)\) 看作是参数,对它们求偏导数:
\[\frac{\partial J}{\partial F(\boldsymbol{x}_i)} = \frac{\partial \sum_{i=1}^N L(y_i, F(\boldsymbol{x}_i))}{\partial F(\boldsymbol{x}_i)} = \frac{\partial L(y_i, F(\boldsymbol{x}_i))}{\partial F(\boldsymbol{x}_i)} = F(\boldsymbol{x}_i) - y_i\]
上式表明, 采用平方误差时,残差就是负梯度 :
\[y_i - F(\boldsymbol{x}_i) = - \frac{\partial J}{\partial F(\boldsymbol{x}_i)}\]
参考:
A Gentle Introduction to Gradient Boosting: http://www.chengli.io/tutorials/gradient_boosting.pdf
1.2. 采用“负梯度”,而非“残差”
平方损失函数(Square loss)有一个缺点:它对异常点(outliers)比较敏感。其它一些损失函数,如绝对损失函数(Absolute loss),Huber loss 函数能更好地处理异常点。 表 1 是三种损失函数 Square loss/Absolute loss/Huber loss 对异常点的处理情况。
| \(y_i\) | 0.5 | 1.2 | 2 | \(5^{\color{red}{*}}\) |
| \(F(\boldsymbol{x}_i)\) | 0.6 | 1.4 | 1.5 | 1.7 |
| Square loss | 0.005 | 0.02 | 0.125 | 5.445 |
| Absolute loss | 0.1 | 0.2 | 0.5 | 3.3 |
| Huber loss(\(\delta= 0.5\)) | 0.005 | 0.02 | 0.125 | 1.525 |
在前面的介绍中,我们知道 采用 Square loss 为损失函数时,负梯度和残差相等。不过,当我们采用 Absolute loss/Huber loss 等其它损失函数时,负梯度只是残差的近似。
GBDT 算法用“负梯度”来取代“残差”。不过需要说明的是,这时新模型不再是 \(F+h\) (这个 \(h\) 是“残差”的拟合)了,而是 \(F+ \rho h\) (这个 \(h\) 是“负梯度”的拟合)。我们把“负梯度”称为“伪残差”(\(\color{red}{\text{pseudo-residuals}}\))。
为什么不直接使用“残差”,而使用“负梯度”呢(注:也有一些实现直接使用“残差”)?因为使用“负梯度”有时能够减小异常点的影响。 下面以 Huber loss 函数以例进行说明。
Huber loss 定义如下:
\[L(y, F) = \begin{cases} \frac{1}{2} (y - F)^2, & |y-F| \le \delta \\ \delta (|y-F| - \delta/2), & |y-F| > \delta \end{cases}\]
如果采用“残差”的话,则有:
\[h(\boldsymbol{x}_i) = y_i - F(\boldsymbol{x}_i)\]
如果采用“负梯度”的话,则有:
\[h(\boldsymbol{x}_i) = - \frac{\partial L(y_i, F(\boldsymbol{x}_i))}{\partial F(\boldsymbol{x}_i)} = \begin{cases} y_i - F(\boldsymbol{x}_i), & |y-F| \le \delta \\ \delta sign(y_i - F(\boldsymbol{x}_i)), & |y-F| > \delta \end{cases}\]
对比上面两式,可以发现,采用“负梯度”时异常点(会满足 \(|y-F| > \delta\))产生的影响会变小。
2. 梯度提升算法
前面从“残差”的角度介绍了梯度提升算法的基本思想(动机)。
梯度提升算法可以看作是“最速下降方法(Steepest Descent Method)”。 不过,和普通的最速下降方法(定义域为 \(R^n\) )不一样,这里目标函数(损失函数)的定义域是所有可行的“弱函数集合”,提升算法通过迭代的选择一个负梯度方向上的基函数来逐渐逼近局部极小值。下面简单地对此进行说明(不是严格推导)。
设损失函数为 \(L\) ,则总损失为:
\[J(F) = \sum_{i=1}^N L(y_i, F(\boldsymbol{x}_i))\]
总损失 \(J\) 取极小值时对应的 \(F\) 就是我们想求的 \(F\) ,即:
\[\hat{F} = \operatorname{arg} \underset{F}{\min} J(F)\]
上式很难求解。取近似,把 \(F(\boldsymbol{x})\) 看作是点 \(F(\boldsymbol{x}_1), F(\boldsymbol{x}_2), \cdots, F(\boldsymbol{x}_N)\) 的函数。采用梯度下降法(Steepest Descent)迭代求取 \(J(F)\) 取极小值时的 \(F(\boldsymbol{x})\) :
\[\begin{aligned} F_m (\boldsymbol{x}) & = F_{m-1}(\boldsymbol{x}) - \rho_m \left[ \frac{\partial J(F)}{\partial F(\boldsymbol{x})} \right]_{F(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x})} \\
& = F_{m-1}(\boldsymbol{x}) + \rho_m \underbrace{\left( - \left[ \frac{\partial J(F)}{\partial F(\boldsymbol{x})} \right]_{F(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x})} \right)}_{\text{负梯度,即“伪残差”}}
\end{aligned}\]
每次迭代过程中(假设当前是第 \(m\) 轮迭代),假设下面数据(伪残差)的拟合结果为 \(h_m(\boldsymbol{x})\) 。
\[\left(\boldsymbol{x_1}, - \left[ \tfrac{\partial L(y_1, F(\boldsymbol{x}_1))}{\partial F(\boldsymbol{x}_1)} \right]_{F(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x})} \right), \left(\boldsymbol{x_2}, - \left[ \tfrac{\partial L(y_2, F(\boldsymbol{x}_2))}{\partial F(\boldsymbol{x}_2)} \right]_{F(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x})} \right) , \cdots, \left(\boldsymbol{x_N}, - \left[ \tfrac{\partial L(y_N, F(\boldsymbol{x}_N))}{\partial F(\boldsymbol{x}_N)} \right]_{F(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x})} \right)\]
则 \(F_m (\boldsymbol{x})\) 可记为:
\[F_m (\boldsymbol{x}) = F_{m-1}(\boldsymbol{x}) + \rho_m h_m(\boldsymbol{x})\]
使用“line search”(一维搜索,即求解单变量函数的极小化问题),可以求得步长 \(\rho_m\) 为:
\[\rho_m=\operatorname{arg} \underset{\rho}{\min} \sum_{i=1}^N L(y_i, F_{m-1}(\boldsymbol{x}_i) + \rho h_m(\boldsymbol{x}_i))\]
2.1. Generic Gradient Boosting
下面是“梯度提升算法”的总结。
输入:训练数据 \(\{(\boldsymbol{x_1},y_1), (\boldsymbol{x_2},y_2), \cdots, (\boldsymbol{x_N},y_N)\}\) ,可微损失函数 \(L(y, F(\boldsymbol{x}))\) ,基本回归算法,迭代次数 \(M\) 。
输出:训练数据对应的回归模型 \(F_M(\boldsymbol{x})\)
算法步骤:
第 1 步:初始化 \(F_0(\boldsymbol{x})\) 为常量:
\[F_0(\boldsymbol{x}) = \operatorname{arg} \underset{\rho}{\min} \sum_{i=1}^N L(y_i, \rho)\]
第 2 步:令 \(m=1,2, \cdots, M\) ,按下面 4 个步骤求 \(F_m(\boldsymbol{x})\) :
(a) 计算“伪残差”:
\[r_{m,i} = - \left[ \frac{\partial L(y_i, F(\boldsymbol{x}_i))}{\partial F(\boldsymbol{x})} \right]_{F(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x})}, \quad\quad i=1,2,\cdots,N\]
(b) 使用“基本回归算法”拟合数据 \(\{(\boldsymbol{x_1}, r_{m,1}), (\boldsymbol{x_2}, r_{m,2}), \cdots, (\boldsymbol{x_N}, r_{m,N}) \}\) ,得到 \(h_m(\boldsymbol{x})\)
(c) 计算 \(\rho_m\) (方法为“line search”):
\[\rho_m = \operatorname{arg} \underset{\rho}{\min} \sum_{i=1}^N L(y_i, F_{m-1}(\boldsymbol{x}_i) + \rho h_m(\boldsymbol{x}))\]
(d) 更新 \(F_m\) 为:
\[F_m(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x}) + \rho_m h_m(\boldsymbol{x})\]
第 3 步:训练数据对应的回归模型即为 \(F_M(\boldsymbol{x})\)
说明:当我们选择 \(L\) 为平方损失时,容易验证 \(F_0(\boldsymbol{x})\) 就是 \(y_1,y_2,\cdots,y_N\) 的平均值,即:
\[F_0( \boldsymbol{x}) = \frac{1}{N} \sum_{i=1}^N y_i\]
2.2. GBDT
前面介绍的是通用的梯度提升算法。不过,实践中往往 采用 CART 回归树(参见附录)作为其基本回归算法,这时,梯度提升算法称为“梯度提升决策树”(GBDT, Gradient Boosting Decision Tree)。
GBDT 算法(“梯度提升算法+CART 回归树作为基本回归算法”)描述如下:
输入:训练数据 \(\{(\boldsymbol{x_1},y_1), (\boldsymbol{x_2},y_2), \cdots, (\boldsymbol{x_N},y_N)\}\) ,可微损失函数 \(L(y, F(\boldsymbol{x}))\) ,迭代次数 \(M\) 。
输出:训练数据对应的回归模型 \(F_M(\boldsymbol{x})\)
算法步骤:
第 1 步:初始化 \(F_0(\boldsymbol{x})\) 为常量:
\[F_0(\boldsymbol{x}) = \operatorname{arg} \underset{\rho}{\min} \sum_{i=1}^N L(y_i, \rho)\]
第 2 步:令 \(m=1,2, \cdots, M\) ,按下面 4 个步骤求 \(F_m(\boldsymbol{x})\) :
(a) 计算“伪残差”:
\[r_{m,i} = - \left[ \frac{\partial L(y_i, F(\boldsymbol{x}_i))}{\partial F(\boldsymbol{x})} \right]_{F(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x})}, \quad\quad i=1,2,\cdots,N\]
(b) 使用 CART 回归树拟合数据 \(\{(\boldsymbol{x_1}, r_{m,1}), (\boldsymbol{x_2}, r_{m,2}), \cdots, (\boldsymbol{x_N}, r_{m,N}) \}\) ,得到第 \(m\) 棵树的叶结点区域 \(R_{m,j}\) 其中 \(j=1,2,\cdots, J_m\) 。
(c) 对 \(j=1,2,\cdots, J_m\) 计算:
\[\gamma_{m,j} = \operatorname{arg} \underset{\gamma}{\min} \sum_{\boldsymbol{x}_i \in R_{m,j}} L(y_i, F_{m-1}(\boldsymbol{x}_i) + \gamma )\]
(d) 更新 \(F_m\) 为:
\[F_m(\boldsymbol{x}) = F_{m-1}(\boldsymbol{x}) + \sum_{j=1}^{J_m} \gamma_{m,j} I(\boldsymbol{x} \in R_{m,j})\]
第 3 步:训练数据对应的回归模型即为 \(F_M(\boldsymbol{x})\)
说明 1:假设第 \(m\) 次迭代求得的 CART 回归树为 \(h_m(\boldsymbol{x})=\sum_{j=1}^{J_m}c_{m,j} I(\boldsymbol{x} \in R_{m,j})\) ,上面算法描述中符号 \(\gamma_{m,j}\) 是前一节“梯度提升算法”描述中的步长 \(\rho_m\) 和 CART 回归树参数 \(c_{m,j}\) 的结合体,即 \(\gamma_{m,j} = \rho_m c_{m,j}\) 。
说明 2:其它细节,比如为什么有 \(\gamma_{m,j} = \operatorname{arg} \underset{\gamma}{\min} \sum_{\boldsymbol{x}_i \in R_{m,j}} L(y_i, F_{m-1}(\boldsymbol{x}_i) + \gamma )\) 可以参考“Jerome H. Friedman. Greedy Function Approximation: A Gradient Boosting Machine, 4.3 Regression tress”
3. 梯度提升的高效实现
3.1. XGBoost
XGBoost(eXtreme Gradient Boosting)是梯度提升的高效实现(且有很多改进),它是 Kaggle 比赛冠军选手最常用的工具。
参考:
XGBoost: A Scalable Tree Boosting System
Complete Guide to Parameter Tuning in XGBoost (with codes in Python)
3.2. LightGBM
LightGBM 是微软推出的比 XGBoost 更快的梯度提升工具包。
4. 附录:CART 回归树(最小二乘回归树)
这里简单地介绍一下 CART 回归树。为了简单起见,假设数据只有二个维度(即两个特征,用 \(X_1,X_2\) 表示)。
CART 的思路是把特征空间分为多个区域(后文将介绍具体如何划分,现在假定划分已经完成)。例如图 1 所示,特征空间分为了 5 个区域 \(R_1,R_2,\cdots,R_5\) 。
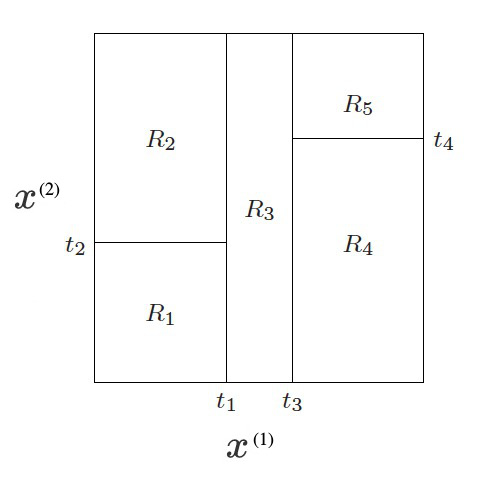
Figure 1: CART Regions
这时,我们把 CART 回归模型写为:
\[f(\boldsymbol{x}) = \sum_{m=1}^5 c_m I(\boldsymbol{x} \in R_m)\]
其中, \(I\) 为指示函数,也就是说 \(\boldsymbol{x} \in R_m\) 成立时, \(I(\boldsymbol{x} \in R_m)\) 为 1,否则为 0,由于想要预测的数据 \(\boldsymbol{x}\) 只可能处于 \(R_1,R_2,\cdots,R_5\) 中的某一个区域中,所以上式中,求和的 5 个项目中一定有 4 项为 0。也就是说上式就是:
\[f(\boldsymbol{x}) = \begin{cases} c_1, & \quad \text{if} \; \boldsymbol{x} \in R_1 \\ c_2, & \quad \text{if} \; \boldsymbol{x} \in R_2 \\ c_3, & \quad \text{if} \; \boldsymbol{x} \in R_3 \\ c_4, & \quad \text{if} \; \boldsymbol{x} \in R_4 \\ c_5, & \quad \text{if} \; \boldsymbol{x} \in R_5 \end{cases}\]
其中, \(c_1,c_2,\cdots,c_5\) 由训练数据求得。如何求解它们呢? CART 回归树采用的办法是取平方损失 \(\sum_{m=1}^5 (y_i - f(\boldsymbol{x}_i))^2\) 最小值时的相应值(这是 CART 回归树又称为最小二乘回归树的原因)。 容易推导出:当 \(c_i\) 取对应区域 \(R_i\) 中所有训练数据输出值的平均值(average)时平方损失会取得最小值,即:
\[c_m = \text{ave}(y_i \mid \boldsymbol{x}_i \in R_m)\]
总结: 对于 CART 回归树,新输入数据 \(\boldsymbol{x}\) (假设它位于区域 \(R_i\) 中)的输出值 \(y\) 就是区域 \(R_i\) 中所有训练数据的平均输出值。
如果通过训练数据我们求得 \(c_1=-5,c_2=-7,c_3=0,c_4=2,c_5=4\) ,则图 1 对应的 CART 回归树为图 2 所示,也可以表示为图 3 所示形式。
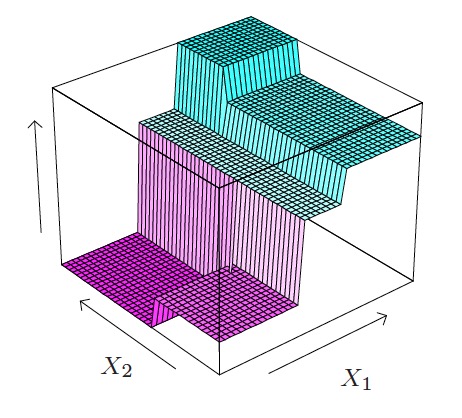
Figure 2: 图 1 对应的一个 CART 回归树的直观展示
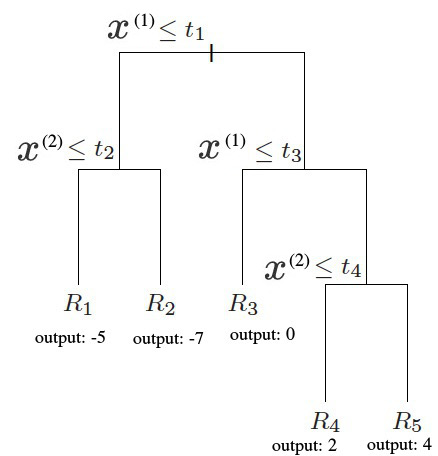
Figure 3: 图 1 对应的一个 CART 回归树
图 4 (摘自 https://support.sas.com/resources/papers/proceedings13/089-2013.pdf )演示了一个更复杂的 CART 回归树。
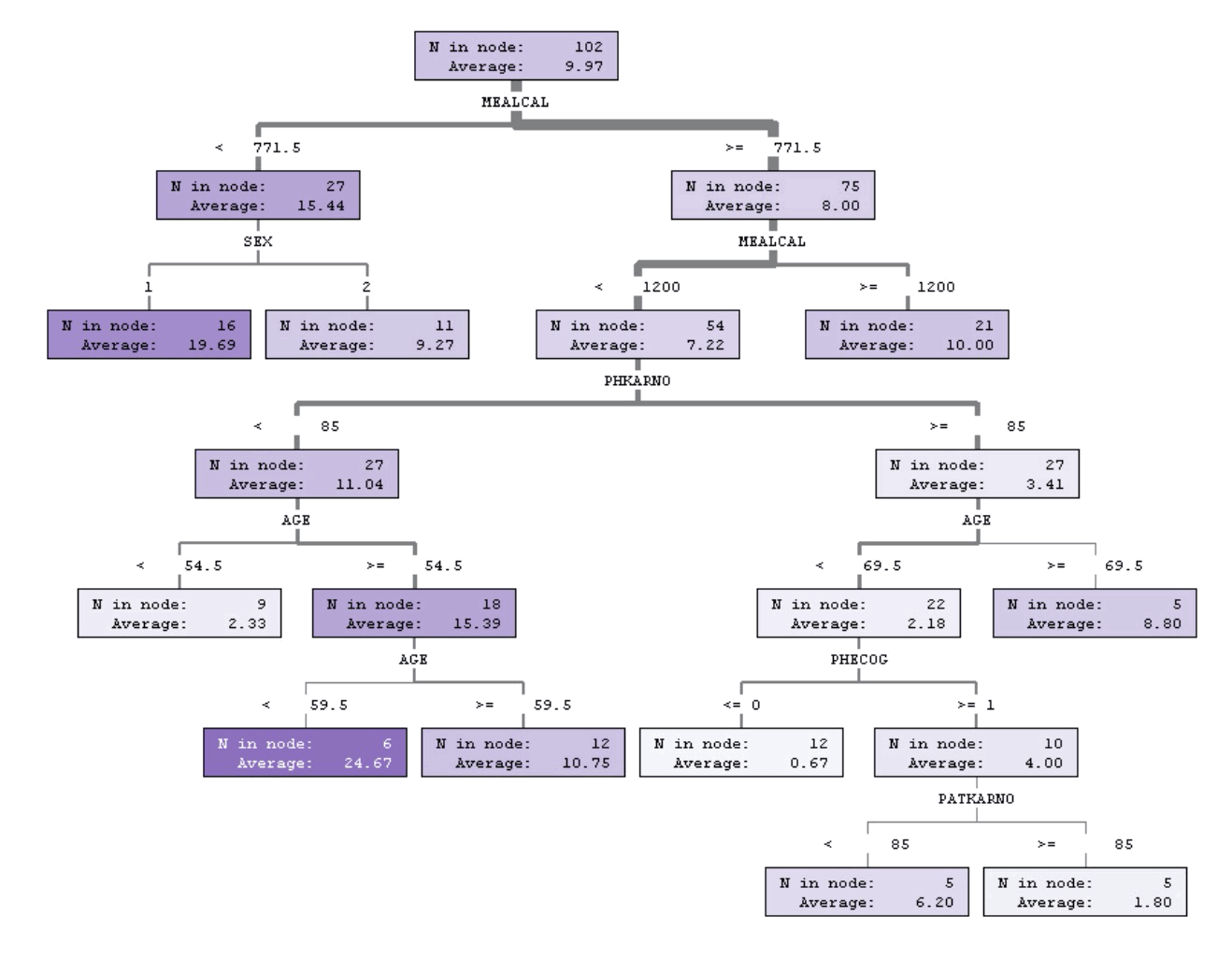
Figure 4: CART 回归树实例
4.1. 叶结点区域划分规则(递归二分分割)
前面还未介绍如何把特征空间划分为多个区域(称为叶结点区域)。CART 采用迭代方式(每次迭代把一个区域分为两个子区域)来划分特征空间。描述如下:
选择第 \(j\) 个特征 \(x^{(j)}\) 及它的取值 \(s\) ,把它们分别称为切分变量(splitting variable)和切点分(splitting point)。并定义两个区域:
\[\begin{aligned} R_1(j,s) & = \{\boldsymbol{x} \mid x^{(j)} \le s \} \\
R_2(j,s) & = \{\boldsymbol{x} \mid x^{(j)} > s \}
\end{aligned}\]
如何找到当前迭代中的最优切分变量 \(j\) 和最优切分点 \(s\) 呢?它们是下式(平方损失)达到最小值时对应的 \(j,s\) :
\[\min_{j,s}\left[ \min_{c_1} \sum_{\boldsymbol{x}_i \in R_1(j,s)} (y_i - c_1)^2 + \min_{c_2} \sum_{\boldsymbol{x}_i \in R_2(j,s)} (y_i - c_2)^2 \right]\]
怎么求解呢?首先,固定切分变量 \(j\) ,对固定的切分变量 \(j\) 扫描切分点 \(s\) ,找到使上式最小的 \(s\) ;然后,遍历所有特征,就可找到最优的切分变量 \(j\) 和它相应的最优切分点 \(s\) (后文将通过例子详细介绍这个过程)。
通过上面过程,我们把输入特征空间划分为了两个区域。接着,对每个区域重复上述划分过程,直到满足停止条件为止,这样就生成了 CART 回归树的各个 Regions。
注 1:图 3 所示 CART 回归树中,第一次迭代求得的切分变量为 \(x^{(1)}\) ,相应切分点为 \(t_1\) 。
注 2:迭代求解 Regions 的过程每次会把一个区域一分为二,所以图 5 所示分割肯定不会是 CART 分割过程的结果。
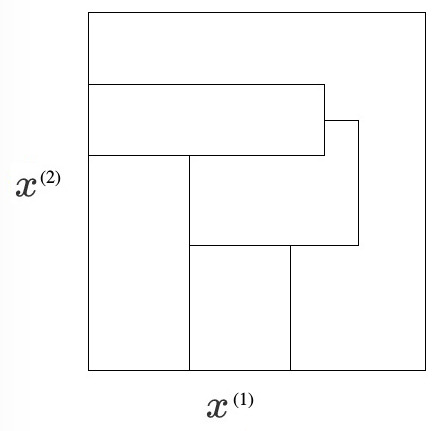
Figure 5: 这肯定不会是 CART 分割过程的结果
4.2. CART 回归树实例
下面通过一个 CART 回归树实例(摘自《统计学习方法,李航著》例 8.2)来重点描述下前面介绍的叶结点区域划分规则。
例子:给定表 2 所示训练数据, \(x\) 的取值范围为区间 \([0.5, 10.5]\) ,限制叶结点区域个数为 2(仅是为了使例子更简单),求其 CART 回归树。
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(y_i\) | 5.56 | 5.70 | 5.91 | 6.40 | 6.80 | 7.05 | 8.90 | 8.70 | 9.00 | 9.05 |
求 CART 回归树,重点是求解叶结点区域划分。
这个例子中特征空间是一维的,无需寻找最优切分变量。
设 \(R_1 = \{ x \mid x \le s \}, R_2 = \{ x \mid x > s \}\) ,下面我们来求解最优切分点 \(s\) 。
通过以下优化问题:
\[\min_{s} \left[ \min_{c_1} \sum_{x_i \in R_1} (y_i - c_1)^2 + \min_{c_2} \sum_{x_i \in R_2} (y_i - c_2)^2 \right]\]
可以求得训练数据的最优切分点 \(s\) 。
步骤如下:
容易求得, \(R_1,R_2\) 内部的平方损失(即 \(\sum_{x_i \in R_1} (y_i - c_1)^2\) 和 \(\sum_{x_i \in R_2} (y_i - c_2)^2\) )达到最小值时的 \(c_1,c_2\) 是 \(R_1,R_2\) 内部所有训练数据输出值的平均值,即:
\[c_1 = \frac{1}{N_1} \sum_{x_i \in R_1} y_i, \quad c_2 = \frac{1}{N_2} \sum_{x_i \in R_2} y_i\]
这里 \(N_1,N_2\) 是 \(R_1,R_2\) 中训练数据的个数。
根据所给数据,考虑如下切分点:
\[1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5\]
对于各个切分点,不难求出相应的 \(R_1,R_2,c_1,c_2\) 。记:
\[m(s) = \min_{c_1} \sum_{x_i \in R_1} (y_i - c_1)^2 + \min_{c_2} \sum_{x_i \in R_2} (y_i - c_2)^2\]
显然原优化问题,就是最小化 \(m(s)\) 。
当 \(s=1.5\) 时,有 \(R_1=\{ 1 \},R_2=\{2,3,\cdots,10 \},c_1 = 5.56, c_2=7.50\) ,从而:
\[m(s)=\min_{c_1} \sum_{x_i \in R_1} (y_i - c_1)^2 + \min_{c_2} \sum_{x_i \in R_2} (y_i - c_2)^2=0+15.72=15.72\]
类似地,对应其它切分点,我们都可以求得相应的 \(m(s)\) 值,其计算结果如表 3 所示。
| \(s\) | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| \(m(s)\) | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
从表 3 中可知,当 \(s=6.5\) 时 \(m(s)\) 达到最小值。所以 \(s=6.5\) 就是最优切分点。这时对应的 \(R_1=\{1,2,\cdots,6 \}, R_2=\{ 7,8,9,10\}, c_1=6.24, c_2=8.91\) 。从而 CART 回归树为:
\[f(x) = \begin{cases} 6.24, \quad & x \le 6.5 \\ 8.91, \quad & x > 6.5 \end{cases}\]
注 1:为简单起见,例子中特征空间是一维的(如果是多维的,步骤也类似,只是求最优切分变量时,还需遍历一下其它特征)。
注 2:为简单起见,我们限制叶结点区域个数为 2,这样只用进行一次迭代就得到 CART 回归树。当叶结点区域个数大于 2 时,步骤是类似的。比如叶结点区域个数为 3 时,我们可以按照同样的步骤在生成的两个区域中寻找另外一个最优切分点(由于只有一个特征,不用寻找最优切分变量了)。
4.3. CART 回归树 vs. 线性回归
假设输入变量(特征空间)是二维的,图 6 (摘自 https://rafalab.github.io/pages/649/section-11.pdf )演示了 CART 回归树和线性回归的区别。
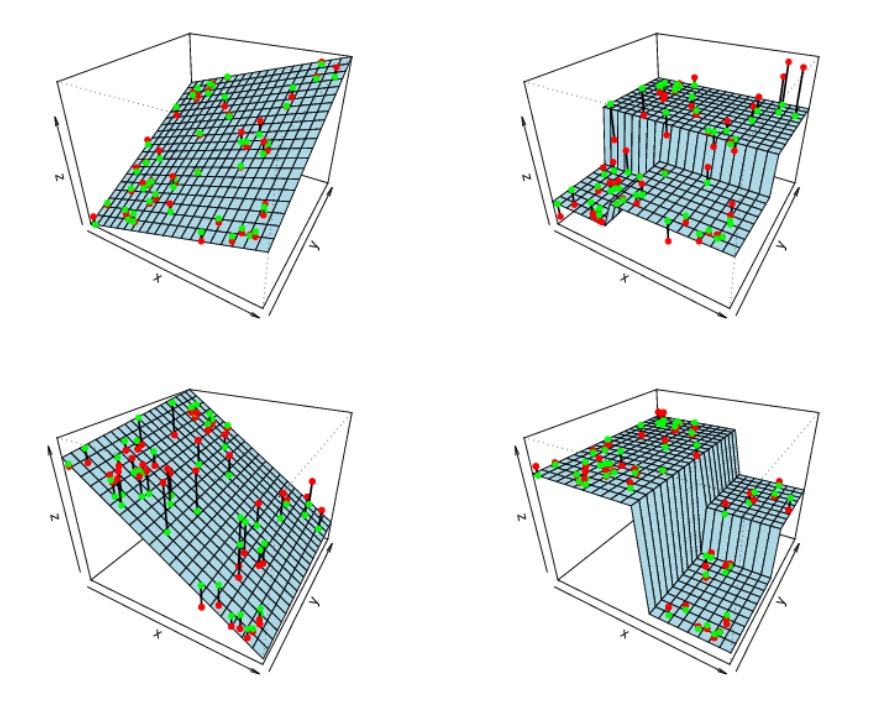
Figure 6: CART 回归树(右边两个图) vs. 线性回归(左边两个图)