Expectation–maximization algorithm
Table of Contents
1. EM 算法简介
In statistics, an expectation–maximization (EM) algorithm is an iterative method for finding maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables.
最大期望算法经过两个步骤交替进行计算:
第一步是计算期望(E步),利用对隐藏变量的现有估计值,计算其最大似然估计值;
第二步是最大化(M步),最大化在 E 步上求得的最大似然值来计算参数的值。
在 M 步中找到的参数估计值被用于下一个 E 步计算中,这个过程不断交替进行。
参考:
https://zh.wikipedia.org/wiki/%E6%9C%80%E5%A4%A7%E6%9C%9F%E6%9C%9B%E7%AE%97%E6%B3%95
EM 算法常用于求解 GMM(高斯混合模型)的参数:http://aandds.com/blog/gmm.html
2. EM 算法实例说明
假设有两枚硬币 A 和 B,它们正面朝上的概率分别记为 \(\theta_A, \theta_B\) ,但它们是未知的,想通过抛掷实验(实验过程如下:随机选择一个硬币,抛 10 次,把出现正面的情况记为 H,反面的情况记为 T。重复 5 次实验)来确定 \(\theta_A, \theta_B\) 。
如果我们知道当前实验的硬币是 A 还是 B,则估计 \(\theta_A, \theta_B\) 很简单,简单地统计一下正反面出现次数即可(最大似然估计)。如图 1 中(a)所示。
但如果不知道当前实验的硬币是 A 还是 B,这时得到的实验数据是“不完全数据集(Incomplete Data Set)”,无法直接使用最大似然估计,那这时怎么估计 \(\theta_A, \theta_B\) 呢?可以用 EM 算法,如图 1 中(b)所示。
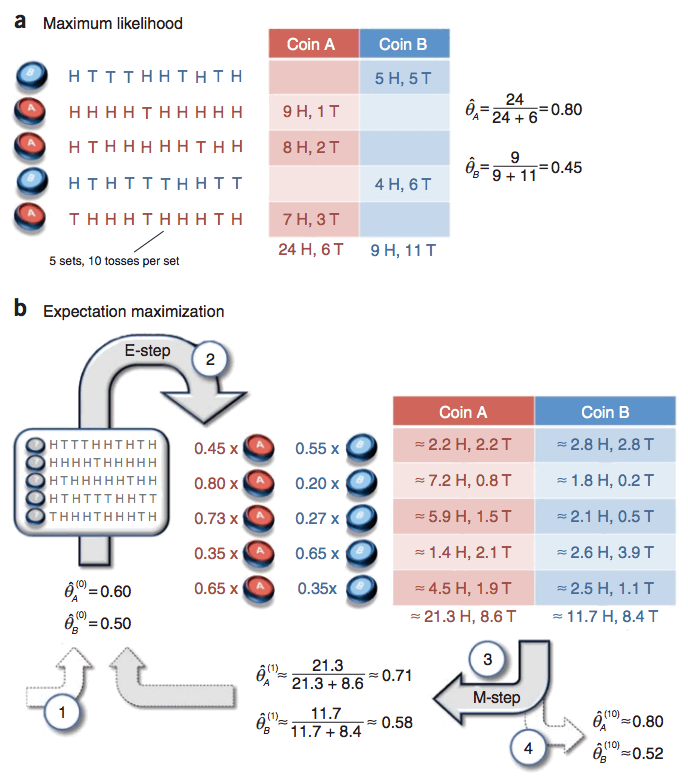
Figure 1: EM 算法演示
图 1 中(b)所示 EM 算法的 4 个步骤的说明如下:
(1). EM starts with an initial guess of the parameters.
(2). In the E-step, a probability distribution over possible completions is computed using the current parameters. The counts shown in the table are the expected numbers of heads and tails according to this distribution.
(3). In the M-step, new parameters are determined using the current completions.
(4). After several repetitions of the E-step and M-step, the algorithm converges.
下面说明“E step/M step”的具体计算过程。抛掷硬币是伯努利试验,服从二项分布,可用 \(p_i(k) = {10 \choose k} \theta_i^{k}(1-\theta_i)^{10-k}, k = 0,1,2, \cdots, 10\) 表示硬币 \(i \; (i \in \{A, B \})\) 正面出现 \(k\) 次的概率。其中 \(\theta_A = 0.6, \; \theta_B=0.5\) 。
这里仅以第二行数据为例进行说明。第二行数据中,正面出现了 9 次,反面出现了 1 次。不考虑前面的相同因子 \({10 \choose k}\) ,有:
\[\begin{gathered} \theta_A^9 (1-\theta_A)^{10-9} \simeq 0.004 \\
\theta_B^9 (1-\theta_B)^{10-9} \simeq 0.001 \end{gathered}\]
从而有:
\[\begin{gathered} \frac{0.004}{0.004+0.001}=0.8 \\
\frac{0.001}{0.004+0.001}=0.2 \end{gathered}\]
上式说明,得到第二行数据时,“当前硬币是 A”的概率是 0.8,而“当前硬币是 B”的概率为 0.2。那么,9次正面朝上中可以把 7.2 次划给硬币 A,1.8 次划给硬币 B;1 次反面朝上中可以把 0.8 次划给硬币 A,0.2 次划给硬币 B。有了这些数据,我们可以使用最大似然估计(和图 1 (a)的计算类似)来求解参数了(准确说是参数新的估计值)。
参考:
What is the expectation maximization algorithm?
http://math.stackexchange.com/questions/25111/how-does-expectation-maximization-work
http://stats.stackexchange.com/questions/72774/numerical-example-to-understand-expectation-maximization
2.1. EM 算法代码实现
前面介绍的例子,可以用下面程序实现对应的 EM 算法。
#!/usr/bin/env python
import numpy as np
import math
#### E-M Coin Toss Example as given in the EM tutorial paper by Do and Batzoglou* ####
def get_mn_log_likelihood(obs,probs):
""" Return the (log)likelihood of obs, given the probs"""
# Multinomial Distribution Log PMF
# ln (pdf) = multinomial coeff * product of probabilities
# ln[f(x|n, p)] = [ln(n!) - (ln(x1!)+ln(x2!)+...+ln(xk!))] + [x1*ln(p1)+x2*ln(p2)+...+xk*ln(pk)]
multinomial_coeff_denom= 0
prod_probs = 0
for x in range(0,len(obs)): # loop through state counts in each observation
multinomial_coeff_denom = multinomial_coeff_denom + math.log(math.factorial(obs[x]))
prod_probs = prod_probs + obs[x]*math.log(probs[x])
multinomial_coeff = math.log(math.factorial(sum(obs))) - multinomial_coeff_denom
likelihood = multinomial_coeff + prod_probs
return likelihood
# 1st: Coin B, {HTTTHHTHTH}, 5H,5T
# 2nd: Coin A, {HHHHTHHHHH}, 9H,1T
# 3rd: Coin A, {HTHHHHHTHH}, 8H,2T
# 4th: Coin B, {HTHTTTHHTT}, 4H,6T
# 5th: Coin A, {THHHTHHHTH}, 7H,3T
# so, from MLE: pA(heads) = 0.80 and pB(heads)=0.45
# represent the experiments
head_counts = np.array([5,9,8,4,7])
tail_counts = 10-head_counts
experiments = zip(head_counts,tail_counts)
# initialise the pA(heads) and pB(heads)
pA_heads = np.zeros(100); pA_heads[0] = 0.60
pB_heads = np.zeros(100); pB_heads[0] = 0.50
# E-M begins!
delta = 0.001
j = 0 # iteration counter
improvement = float('inf')
while (improvement>delta):
expectation_A = np.zeros((5,2), dtype=float)
expectation_B = np.zeros((5,2), dtype=float)
for i in range(0,len(experiments)):
e = experiments[i] # i'th experiment
ll_A = get_mn_log_likelihood(e,np.array([pA_heads[j],1-pA_heads[j]])) # loglikelihood of e given coin A
ll_B = get_mn_log_likelihood(e,np.array([pB_heads[j],1-pB_heads[j]])) # loglikelihood of e given coin B
weightA = math.exp(ll_A) / ( math.exp(ll_A) + math.exp(ll_B) ) # corresponding weight of A proportional to likelihood of A
weightB = math.exp(ll_B) / ( math.exp(ll_A) + math.exp(ll_B) ) # corresponding weight of B proportional to likelihood of B
expectation_A[i] = np.dot(weightA, e)
expectation_B[i] = np.dot(weightB, e)
pA_heads[j+1] = sum(expectation_A)[0] / sum(sum(expectation_A));
pB_heads[j+1] = sum(expectation_B)[0] / sum(sum(expectation_B));
improvement = max( abs(np.array([pA_heads[j+1],pB_heads[j+1]]) - np.array([pA_heads[j],pB_heads[j]]) ))
j = j+1
print(pA_heads[j]) # output 0.796465637923
print(pB_heads[j]) # output 0.520047189003
3. EM 算法和初值相关
EM 算法和初值的选择相关。 在前面介绍的例子中,如果选择的初值为: \(\theta_A = 0.5, \; \theta_B=0.6\) ,则收敛后得到的估计值为: \(\theta_A = 0.52, \; \theta_B=0.80\) 。
所以在应用时,常常选择不同的初值进行迭代,然后对得到的估计值进行比较,从中选择较好的。
4. EM算法不一定是全局最优解
EM算法得到的是局部最优解,不一定是全局最优解。