Polynomial Multiplication (Vector Convolution) and FFT
Table of Contents
1. 多项式
一个以 \(x\) 为变量的多项式 \(A(x)\) 是指: \[a_0 + a_1 x + a_2 x^2 + \cdots + a_j x^j\] 也可以记为 \(A(x) = \sum_{j=0}^{n-1} a_j x^j\) ,我们称 \(a_0, a_1, \cdots, a_{n-1}\) 为这个多项式的“系数”。如果一个多项式 \(A(x)\) 的最高次的非零系数是 \(a_k\) ,则称 \(A(x)\) 的“次数”是 \(k\) ,记为 \(degree(A) = k\) 。任何严格大于一个多项式次数的整数都是该多项式的“次数界”,因此,对于次数界为 \(n\) 的多项式,其次数可以是 \(0 \sim n-1\) 之间的任何整数,包括 \(0\) 和 \(n-1\) 。
1.1. 多项式加法
我们在多项式上可以定义很多不同的运算。对于多项式加法,如果 \(A(x)=\sum_{j=0}^{n-1} a_j x^j\) 和 \(B(x)=\sum_{j=0}^{n-1} b_j x^j\) 是次数界为 \(n\) 的多项式,那么它们的和也是一个次数界为 \(n\) 的多项式 \(C(x)=\sum_{j=0}^{n-1} c_j x^j\) ,对所有属于定义域的 \(x\) ,都有 \(c_j = a_j + b_j\) 。例如,如果有多项式 \(A(x) = 6x^3 + 7x^2 - 10x + 9\) 和 \(B(x) = -2x^3 + 4x - 5\) ,那么 \(C(x) = 4x^3 + 7x^2 - 6x + 4\) 。
1.2. 多项式乘法(向量卷积)
对于多项式乘法,如果 \(A(x)\) 和 \(B(x)\) 皆是次数界为 \(n\) 的多项式,则它们的乘积 \(C(x)\) 是一个次数界为 \(2n-1\) 的多项式(注:如果 \(A(x)\) 是次数界为 \(n_a\) 的多项式, \(B(x)\) 是次数界为 \(n_b\) 的多项式,那么 \(C(x)\) 是次数界为 \(n_a + n_b - 1\) 的多项式)。具体做法是 把 \(A(x)\) 中的每一项与 \(B(x)\) 中的每一项相乘,然后再合并同类项。 例如,我们可以对两个多项式 \(A(x)=6x^3 + 7x^2 - 10x + 9\) 和 \(B(x)=-2x^3 + 4x - 5\) 相乘(这里 \(A(x)\) 和 \(B(x)\) 的次数界都是 4,它们相乘结果的次数界是 7;如果使用次数表述,则 \(A(x)\) 和 \(B(x)\) 的次数都是 3,它们相乘结果的次数是 6),过程如图 1 所示。
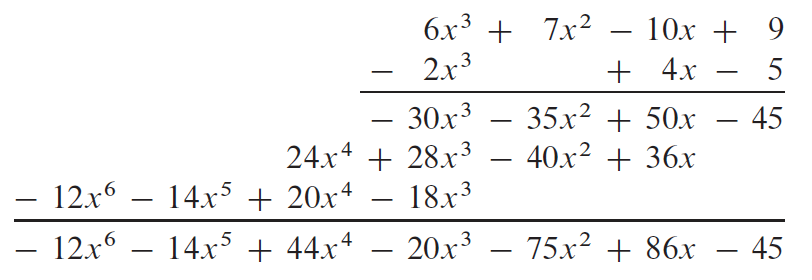
Figure 1: 多项式乘法实例
多项式 \(A(x)\) 和 \(B(x)\) 的乘积可记为: \[C(x) = \sum_{j=0}^{2n-2} c_j x^j\] 其中: \[c_j = \sum_{k=0}^j a_k b_{j-k}\]
由上式给出的系数向量 \(c\) 也称为输入向量 \(a\) 和 \(b\) 的“卷积”(Convolution),表示成: \[c = a \otimes b\]
1.3. 多项式的表示
这节介绍两种表示多项式的方法:系数表达和点值表达。
1.3.1. 系数表达
对一个次数界为 \(n\) 的多项式 \(A(x)=\sum_{j=0}^{n-1}a_j x^j\) 而言,其系数表达是一个由系数组成的向量 \(a=(a_0, a_1, \cdots, a_{n-1})\) 。
采用系数表达对于多项式的某些运算是很方便的。例如,对多项式 \(A(x)\) 在给定点 \(x_0\) 的求值运算就是计算 \(A(x_0)\) 的值。使用霍纳法则,我们可以在 \(\Theta(n)\) 时间复杂度内完成求值运算: \[A(x_0) = a_0 + x_0(a_1 + x_0(a_2 + \cdots + x_0(a_{n-2} + x_0(a_{n-1})) \cdots ))\]
类似地,对两个分别用系数向量 \(a = (a_0, a_1, \cdots, a_{n-1})\) 和 \(b=(b_0, b_1, \cdots, b_{n-1})\) 表示的多项式进行相加时,设结果多项式的系数向量为 \(c=(c_0, c_1, \cdots, c_{n-1})\) ,则 \(c_j = a_j + b_j\) ,显然所需的时间是 \(\Theta(n)\) 。
现在来考虑两个用系数形式表示的、次数界为 \(n\) 的多项式 \(A(x)\) 和 \(B(x)\) 的乘法运算。如果直接使用定义多项式乘法时的公式,那么完成多项式乘法所需时间就是 \(\Theta(n^2)\) ,因为向量 \(a\) 中的每个系数必须与向量 \(b\) 中的每个系数相乘。本文的主要目标就是 讨论如何降低多项式乘法的时间复杂度。
1.3.2. 点值表达
一个次数界为 \(n\) 的多项式 \(A(x)\) 的点值表达就是一个由 \(n\) 个点值对所组成的集合 \[\{(x_0, y_0), (x_1, y_1), \cdots, (x_{n-1}, y_{n-1})\}\] 其中 \(y_k=A(x_k)\) ,且对 \(k=0,1,\cdots, n-1\) ,所有 \(x_k\) 各不相同。
一个多项式可以有很多不同的点值表达,因为可以采用 \(n\) 个不同的点 \(x_0, x_1, \cdots, x_{n-1}\) 构成的集合作为这种表示方法的基。
1.3.3. 求值和插值(系数表达和点值表达的相互转换)
对一个用系数形式表达的多项式来说,在原则上计算其点值表达是简单易行的,因为我们所要做的就是选取 \(n\) 个不同 \(x_0, x_1, \cdots, x_{n-1}\) ,然后对 \(k=0,1, \cdots, n-1\) 求出 \(A(x_k)\) 。根据霍纳法则,求一个点值所需时间复杂度为 \(\Theta(n)\) ,求这 \(n\) 个点值所需时间复杂度为 \(\Theta(n^2)\) 。在稍后可以看到, 如果我们巧妙地选取点 \(x\) ,就可以加速这一计算过程,使其运行时间变为 \(\Theta(n \lg n)\) 。
从一个多项式的“点值表达”确定其“系数表达”形式称为“插值”。下面定理说明, 当插值多项式的“次数界”等于已知的点值对的数目时,插值是明确的。
定理(插值多项式的唯一性):对于任意 \(n\) 个点值对组成的集合 \(\{(x_0, y_0), (x_1, y_1), \cdots, (x_{n-1}, y_{n-1})\}\) ,其中所有的 \(x_k\) 都不同;那么存在唯一的次数界为 \(n\) 的多项式 \(A(x)\) ,满足 \(y_k=A(x_k), k=0,1, \cdots, n-1\) 。
这个定理表明,给定任意两个不同点,就可以唯一地确定一条直线(即一次多项式);给定任意三个不同点,就可以唯一地确定一条抛物线(即二次多项式)。需要注意,上面定理表述中使用的是“次数界”,而不是“次数”,这两者的关系参见节 1 。
拉格朗日公式: \[A(x) = \sum_{k=0}^{n-1} y_k \frac{\prod_{j \neq k} (x - x_j)}{\prod_{j \neq k}(x_k - x_j)}\] 可以完成这个插值操作,不过拉格朗日公式的时间复杂度为 \(\Theta(n^2)\) ,我们在本文中并不会采用它。
因此, \(n\) 个点的求值运算与插值运算是定义完备的互逆运算,它们将多项式的系数表达与点值表达进行相互转化。
1.3.4. 点值表达下的加法和乘法
对许多多项式相关的操作,点值表达是很便利的。对于加法,如果 \(C (x) = A (x) + B(x)\) ,则对任意点 \(x_k\) ,满足 \(C(x_k) = A(x_k) +B(x_k)\) 。更准确地说,如果已知 A 的点值表达 \[\{(x_0, y_0), (x_1, y_1), \cdots, (x_{n-1}, y_{n-1})\}\] 和 B 的点值表达 \[\{(x_0, y_0'), (x_1, y_1'), \cdots, (x_{n-1}, y_{n-1}')\}\] (注意,A 和 B 在相同的 \(n\) 个位置求值),则 C 的点值表达是 \[\{(x_0, y_0+y_0'), (x_1, y_1+y_1'), \cdots, (x_{n-1}, y_{n-1} + y_{n-1}')\}\]
因此,对两个点值形式表示的次数界为 \(n\) 的多项式相加,所需时间复杂度为 \(\Theta(n)\) 。
类似地,对于多项式乘法,点值表达也是方便的。如果 \(C(x) = A(x)B(x)\) ,则对于任意点 \(x_k\) , \(C(x_k) = A(x_k)B(x_k)\) ,并且对 A 的点值表达和 B 的点值表达进行“逐点相乘”,就可得到 C 的点值表达。不过,我们也必须面对这样一个问题,即 \(degree(C) = degree (A) + degree (B)\) ,参见节 1.2 。这意味着对于次数界为 \(n\) 的多项式 \(A(x)\) 和 \(B(x)\) ,如果我们分别取 \(n\) 个点值对,则它们逐点相乘后得到的 \(C\) 并不是确定的(因为 \(C\) 的次数会变大,但逐点相乘后点值对的数目不变,由上一节的知识可知这无法通过插值唯一地确定 \(C\) )。为了解决这个问题,对于次数界为 \(n\) 的多项式 \(A(x)\) 和 \(B(x)\) ,我们取 \(n\) 个点值对不够,要“扩展”为取 \(2n\) 个点值对参与计算。
给定 \(A\) 的扩展点值表达: \[\{(x_0, y_0), (x_1, y_1), \cdots, (x_{2n-1}, y_{2n-1})\}\] 和 \(B\) 的对应扩展点值表达: \[\{(x_0, y_0'), (x_1, y_1'), \cdots, (x_{2n-1}, y_{2n-1}')\}\] 则多项式 \(A\) 和 \(B\) 的乘积 \(C\) 的点值表达为: \[\{(x_0, y_0y_0'), (x_1, y_1y_1'), \cdots, (x_{2n-1}, y_{2n-1} y_{2n-1}')\}\]
给定两个点值扩展形式的输入多项式,我们可以看到使其相乘而得到点值形式的结果需要 \(\Theta(n)\) 时间,比采用系数形式表达的多项式相乘所需时间少得多。
2. 多项式的快速乘法
通过前面的介绍,我们有了两种计算多项式乘法的方法,如图 2 所示。
Figure 2: 两种求多项式乘法的方法,时间复杂度都是 \(\Theta(n^2)\)
图 2 中的两种方法的时间复杂度都是 \(\Theta(n^2)\) 。在方法二中,我们可以采用任何点作为求值点,但 通过精心地挑选求值点,可以把多项式“系数表达”和“点值表达”之间转化所需的时间复杂度变为 \(\Theta(n \lg n)\) 。
如何去“精心地挑选求值点”呢?请看下文。
2.1. 离散傅里叶变换(DFT)
在进一步介绍前,我们先了解一下离散傅里叶变换(DFT)。
向量 \(a=(a_0, a_1, \cdots, a_{n-1})\) 的离散傅里叶变换为另外一个向量 \(y=(y_0, y_1, \cdots, y_{n-1})\) ,该向量中每个元素的定义为: \[y_k=\sum_{j=0}^{n-1}a_j w_n^{kj}\]
上式中 \(w_n^k, \; k=0,1,\cdots,n-1\) 分别是满足 \(w^n=1\) 的 \(n\) 个单位复数根中的第 \(k\) 个。
如果我们恰好在“单位复数根” \(w_n^k\) 处求值 \(A(x)\) ,则显然这样得到的 \(A(w_n^k)=\sum_{j=0}^{n-1}a_j w_n^{kj}\) 就是系数向量 \(a=(a_0, a_1, \cdots, a_{n-1})\) 的离散傅里叶变换。
快速傅里叶变换(FFT)是计算离散傅里叶变换(DFT)的快速算法,它的时间复杂度是 \(\Theta(n \lg n)\) ;同样快速傅里叶逆变换(IFFT)是计算离散傅里叶逆变换(IDFT)的快速算法,它的时间复杂度也是 \(\Theta(n \lg n)\) 。
本文不详细介绍快速傅里叶变换的细节,可以参考 http://aandds.com/blog/fourier.html
2.2. FFT 加快多项式乘法
基于前面的介绍,我们可以得到了图 3 中的方法二来加快多项式乘法的计算,它的时间复杂度为 \(\Theta(n \lg n)\) 。
Figure 3: 方法二的时间复杂度变为了 \(\Theta(n \lg n)\)
下面是使用 FFT 加快加速多项式乘法计算的具体操作步骤:
- 加倍次数界:通过加入 \(n\) 个系数为 0 的高阶系数,把多项式 \(A(x)\) 和 \(B(x)\) 变为次数界为 \(2n\) 的多项式,并构造其系数表达;
- 求值:通过应用 \(2n\) 阶的 FFT 计算出 \(A(x)\) 和 \(B(x)\) 的长度为 \(2n\) 的点值表达。这些点值表达中包含了两个多项式在 \(2n\) 次单位根处的取值;
- 逐点相乘:把 \(A(x)\) 的值与 \(B(x)\) 的值逐点相乘,可以计算出多项式 \(C(x)=A(x)B(x)\) 的点值表达,这个表示中包含了 \(C(x)\) 在每个 \(2n\) 次单位根处的值;
- 插值:通过对 \(2n\) 个点值对应用 IFFT,计算其逆 DFT,就可以构造出多项式 \(C(x)\) 的系数表达。
图 4(摘自:https://bruceoutdoors.wordpress.com/2017/03/15/the-programmers-guide-to-fft-part-1-dft/ )是使用 FFT 进行多项式 \(6x^3 + 7x^2 - 10 x + 9\) 和 \(-2x^3 + 4x - 5\) 相乘的例子,得到的结果和图 1 是一样的。

Figure 4: 使用 FFT 进行多项式相乘的例子
3. 多项式除法
通过一定技巧,也可以把 FFT 应用于多项式除法,这里不介绍,详情可参考 http://people.csail.mit.edu/madhu/ST12/scribe/lect06.pdf 或者 http://web.cs.iastate.edu/~cs577/handouts/polydivide.pdf
4. 参考
本文主要参考:算法导论,第 3 版第 30 章

