Floating-point Number

Table of Contents

1. 浮点数

浮点表示通过将数字编码为 \(V= x \times 2^y\) 的形式来近似地表示实数。 它对执行涉及非常大的数字（即 \(|V| \gg 0\) ）、非常接近于 0（即 \(|V| \ll 1\) ）的数字，以及更普遍地作为实数运算的近似值的计算，是很有用的。

直到 20 世纪 80 年代，每个计算机制造商都设计了自己的表示浮点数的规则，以及对浮点数执行运算的细节。另外，它们常常不会太多地关注运算的精确性，而把实现的速度和简便性看得比数字精确性更重要。

大约在 1985 年，这些情况随着 IEEE 标准 754 的推出而改变了，这是一个仔细制订的表示浮点数及其运算的标准。这项工作是从 1976 年开始由 Intel 赞助的，在 8087 设计的同时，8087 是一种为 8086 处理器提供浮点支持的芯片。他们请 William Kahan（加州大学伯克利分校的一位教授）作为顾问，帮助设计未来处理器浮点标准。他们支持 Kahan 加人一个 IEEE 资助的制订工业标准的委员会。这个委员会最终采纳的标准非常接近于 Kahan 为 Intel 设计的标准。目前，实际上所有的计算机都支持这个后来被称为 IEEE 浮点的标准。这大大提高了科学应用程序在不同机器上的可移植性。

IEEE 754 浮点标准是定义在一组“小而一致”的原则上的，所以它实际上是相当优雅和容易理解的。

2. 二进制小数

理解浮点数的第一步是考虑含有小数值的二进制数字。首先，让我们来看看更熟悉的十进制表示法。十进制表示法使用的表示形式为： \(d_m d_{m-1} \cdots d_1 d_0 d_{-1} d_{-2} \cdots d_n\) ，其中每个十进制数 \(d_i\) 的取值范围是 \(0 \sim 9\) 。这个表示方法描述的数值 \(d\) 定义如下：
\[d = \sum_{i=-n}^{m} 10^i \times d_i\]

数字权的定义与十进制小数点符号（‘.’）相关，这意味着小数点左边的数字的权是 10 的正幂，得到整数值，而小数点右边的数字的权是 10 的负幂，得到小数值。例如， \(12.34_{10}\) 表示数字 \(1 \times 10^1 + 2 \times 10^0 + 3 \times 10^{-1} + 4 \times 10^{-2} = 12 \frac{34}{100}\) 。

类似地，考虑一个形如 \(b_m b_{m-1} \cdots b_1 b_0 b_{-1} b_{-2} \cdots b_n\) 的表示法，其中每个二进制数字，或者称为位， \(b_i\) 的取值范围是 0 和 1，如图 1 所示。这种表示方法表示的数 \(b\) 定义如下：
\[b = \sum_{i=-n}^{m} 2^i \times b_i\]

符号‘.’现在变为了二进制的点，点左边的位的权是 2 的正幂，点右边的位的权是 2 的负幂。例如， \(101.11_2\) 表示数字 \(1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 + 1 \times 2^{-1} + 1 \times 2^{-2} = 4+0+1+\frac{1}{2}+\frac{1}{4}=5\frac{3}{4}\) 。

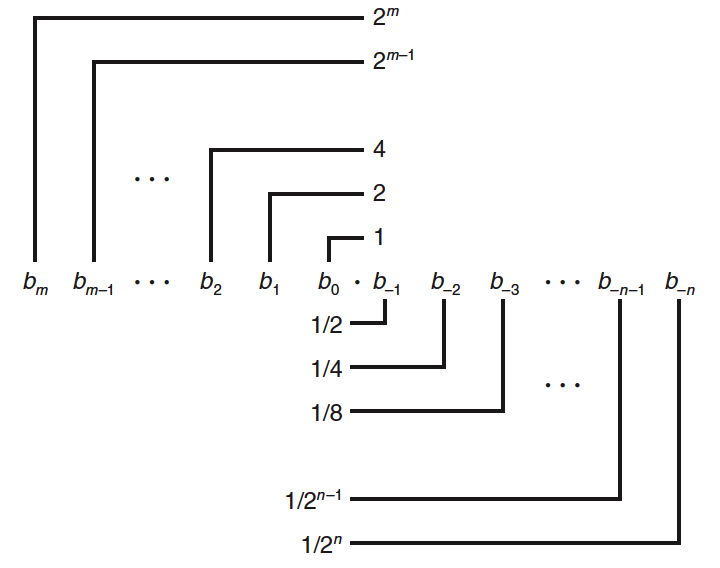
floating_point_number_fractional_binary.png

Figure 1: 小数的二进制表示。二进制点左边的数字的权重形如 \(2^i\) ，而右边的数字的权重形如 \(1/2^i\)

假定我们仅考虑有限长度的编码，那么十进制表示法不能准确地表达像 \(\frac{1}{3}\) 和 \(\frac{5}{7}\) 这样的数。类似地，小数的二进制表示法只能表示那些能够被写成 \(x \times 2^y\) 的数。其他的值只能够被近似地表示。例如，数字 \(\frac{1}{5}\) 可以用十进制小数 0.20 精确表示。不过， 我们并不能把 \(0.20\) 准确地表示为一个二进制小数，我们只能近似地表示它，增加二进制表示的长度可以提高表示的精度，如表 1 所示。

Table 1: 不能把 \(0.20\) 准确地表示为一个二进制小数
二进制小数表示 值 十进制
\(0.0_2\) \(\frac{0}{2}\) \(0.0_{10}\)
\(0.01_2\) \(\frac{1}{4}\) \(0.25_{10}\)
\(0.010_2\) \(\frac{2}{8}\) \(0.25_{10}\)
\(0.0011_2\) \(\frac{3}{16}\) \(0.1875_{10}\)
\(0.00110_2\) \(\frac{6}{32}\) \(0.1875_{10}\)
\(0.001101_2\) \(\frac{13}{64}\) \(0.203125_{10}\)
\(0.0011010_2\) \(\frac{26}{128}\) \(0.203125_{10}\)
\(0.00110011_2\) \(\frac{51}{256}\) \(0.19921875_{10}\)

3. IEEE 浮点表示

前一节中谈到的二进制小数是一种定点表示法，它有一个缺点：不能很有效地表示非常大的数字。例如，表达式 \(5 \times 2^{100}\) 如果用定点表示法，则是 \(101_2\) 后面跟随 \(100\) 个零组成的位模式来表示。相反地，我们希望通过给定 \(x\) 和 \(y\) 的值，来表示形如 \(x \times 2^y\) 的数。

IEEE 754 浮点标准用 \(V=(-1)^s \times M \times 2^E\) 的形式来表示一个数：

  • \(s\) 为符号位（sign），它决定这个数是负数（ \(s=1\) ）还是正数（ \(s=0\) ）。
  • \(M\) 称为尾数，或有效数字（significand），它是一个二进制小数。
  • \(E\) 称为阶码（exponent），它的作用是对浮点数加权。

我们先介绍单精度浮点格式，它用 32 位来表示浮点数，划分规则如下（如图 2 的上部分）：

  • 1 个单独的符号位 \(s\) 直接编码符号 \(s\) 。
  • 8 位阶码字段 \(\text{exp} = e_7 \cdots e_1 e_0\) 编码阶码 \(E\) （编码规则后文会介绍）。
  • 23 位小数字段 \(\text{frac} = f_{22} \cdots f_1 f_0\) 编码尾数 \(M\) （编码规则后文会介绍）。

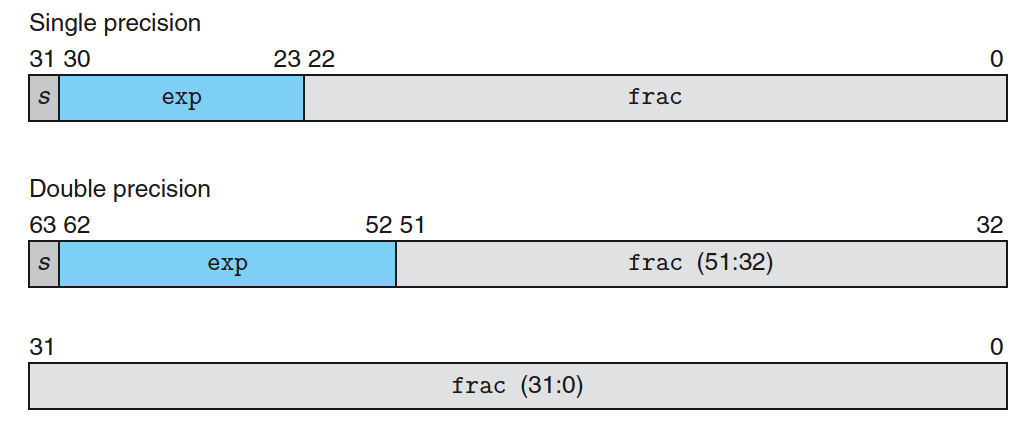
floating_point_number_ieee.png

Figure 2: IEEE 单精度和双精度浮点格式

对于双精度浮点格式，它用 64 位来表示，如果阶码字段位数记为 \(k\) ，小数字段位数记为 \(n\) ，则 \(k = 11, n = 52\) ，如图 2 的下部分。

3.1. 阶码和尾码的编码规则


根据 exp 的值，被编码的值可以分为三种不同的情况（最后一种情况有两个变种），如图 3 所示，下面针对这三种情况分别介绍阶码 \(E\) 和尾码 \(M\) 的具体编码规则。

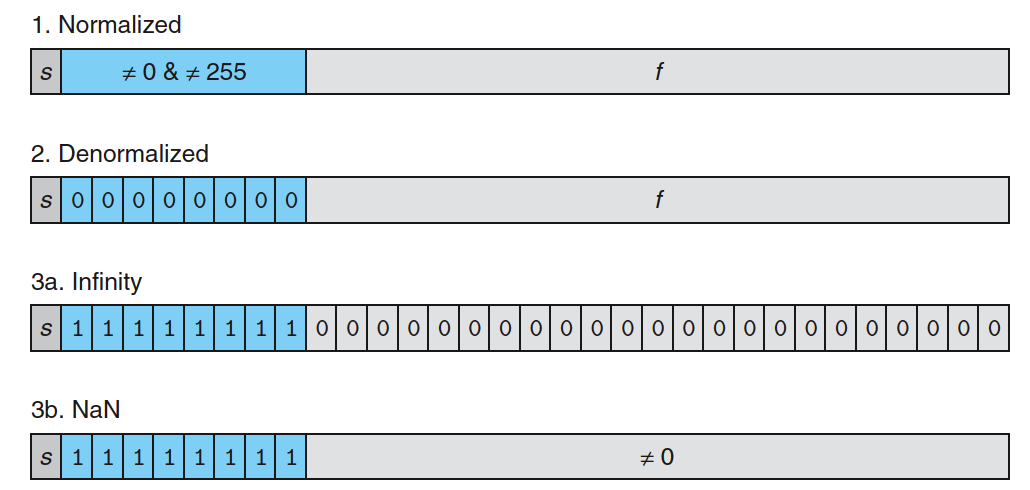
floating_point_number_ieee_float.png

Figure 3: 单精度浮点数值的分类（阶码的值决定了这个数是规格化的、非规格化的、或特殊值）

情况一：规格化的值（Normalized Values）
这是最普遍的情况。当 exp 的位模式既不全为 0，也不全为 1 时，都属于这类情况。这种情况下，阶码和尾码的编码规则定义如下：
\[\begin{align*} E &= (e_{k-1} \cdots e_1 e_0)_2 - Bias \\ M &= (1.f_{n-1} \cdots f_1 f_0)_2 \end{align*}\]

上面尾码 \(M\) 的定义说明我们约定二进制小数点在小数字段 frac 最高有效位的左边，而且是隐含的以 1 开头的（implied leading 1）表示。

\(Bias\) 是一个等于 \(2^{k-1} - 1\) 的偏置值（单精度是 127，双精度是 1023）。在单精度浮点情况下，规格化值的阶码和尾码的编码规则为：
\[\begin{align*} E &= (e_{7} \cdots e_1 e_0)_2 - 127 \\ M &= (1.f_{22} \cdots f_1 f_0)_2 \end{align*}\]

情况二：非规格化的值（Denormalized Values）
当 exp 的位模式全为 0，所表示的数就是非规格化形式。这种情况下，阶码和尾码的编码规则定义如下：
\[\begin{align*} E &= 1 - Bias \\ M &= (0.f_{n-1} \cdots f_1 f_0)_2 \end{align*}\]
上面尾码 \(M\) 的定义中并没有隐含以 1 开头，但规格化值中尾码 \(M\) 的定义是隐含以 1 开头的。在单精度浮点情况下，非规格化值的阶码和尾码的编码规则为：
\[\begin{align*} E &= 1 - 127 = -126 \\ M &= (0.f_{22} \cdots f_1 f_0)_2 \end{align*}\]

注：如果和规格化值中阶码的定义一致，阶码“应该”定义为 \(0 - Bias\) 。 之所以在非规格化值中把阶码定义为 \(1 - Bias\) ，是为了使非规格化值平滑地转换到规格化值。 下节对此有说明。

情况三：特殊值
最后一类数值是当指阶码全为 1 的时候出现的。当小数域全为 0 时，得到的值表示无穷，当 \(s=0\) 时是 \(+ \infty\) ，或者当 \(s=1\) 时是 \(- \infty\) 。当我们把两个非常大的数相乘，或者除以零时，无穷能够表示溢出的结果。当小数域为非零时，结果值被称为“NaN”，就是“不是一个数”（Not a Number）的缩写。一些运算的结果不能是实数或无穷，就会返回这样的 NaN 值，比如当计算 \(\sqrt{-1}\) 或 \(\infty - \infty\) 时。在某些应用中，表示未初始化的数据时，它们也很有用处。

3.2. 数字示例


图 4 展示了假定的 8 位浮点格式的示例，其中有 \(k=4\) 的阶码位和 \(n=3\) 的小数位。偏置量 \(Bias = 2^{4-1} -1=7\) 。图被分成了三个区域，用来描述三类数字。不同的列给出了阶码字段是如何编码阶码 \(E\) 的，小数字段是如何编码尾数 \(M\) 的，以及它们一起是如何形成要表示的值 \(V=2 ^E \times M\) 的。

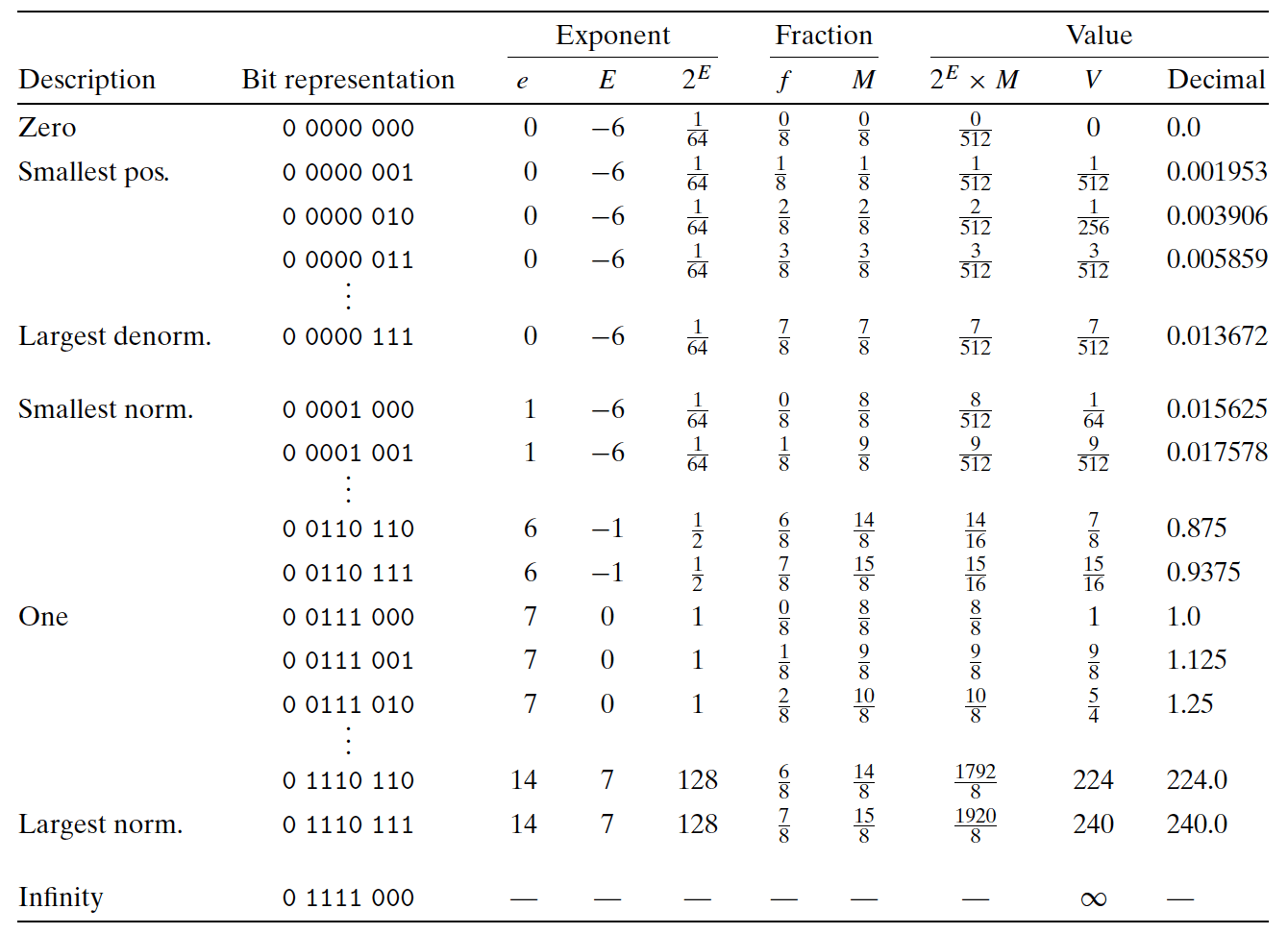
floating_point_number_float8_example.gif

Figure 4: 8 位浮点格式的非负值示例

从 0 自身开始，最靠近 0 的是非规格化数。这种格式的非规格化数的 \(E= 1-7=-6\) , 得到权 \(2^E = \frac{1}{64}\) 。小数 \(f\) 的值的范围是 \(0, \frac{1}{8}, \cdots, \frac{7}{8}\) ，从而得到数 \(V\) 的范围是 \(0 \sim \frac{1}{64} \times \frac{7}{8} = \frac{7}{512}\) 。

可以观察到最大非规格化数 \(\frac{7}{512}\) 和最小规格化数 \(\frac{8}{512}\) 之间的平滑转变。这种平滑性归功于我们对非规格化数的 \(E\) 的定义。通过将 E 定义为 \(1-Bias\) ，而不是 \(-Bias\) ，我们可以补偿非规格化数的尾数没有隐含的开头的 1 这一事实。

当增大阶码时，我们成功地得到更大的规格化值，通过 1.0 后得到最大的规格化数。这个数具有阶码 \(E= 7\) , 得到一个权 \(2^E = 128\) 。小数等于 \(\frac{7}{8}\) 得到尾数 \(M=\frac{15}{8}\) 。因此，最大的规格化数是 \(V=128 \times \frac{15}{8} = 240\) 。超出这个值就会溢出到 \(+ \infty\) 。按照同样的算法， 我们容易得到单精度浮点数所表示的最大的规格化数的比特位可表示为 \(0 \; 11111110 \; 11111111111111111111111_2\) ，按照规格化值其阶码和尾码的编码规则可以得到对应十进制数约为 \(3.4028234664 \times 10^{38}\) ，超出这个值的单精度浮点数就会溢出到 \(+ \infty\) 。

这种表示具有一个有趣的属性， 假如我们将图 4 中的值的位表达式解释为无符号整数，它们就是按升序排列的，就像它们表示的浮点数一样。这不是偶然的——IEEE 如此设计格式就是为了浮点数能够使用整数排序函数来进行排序，这是通过精巧地定义 Bias 来实现的。

3.3. Tips: 为什么要有 Bias

The exponent does not have a sign; instead an exponent bias is subtracted from it (127 for single and 1023 for double precision). This, and the bit sequence, allows floating-point numbers to be compared and sorted correctly even when interpreting them as integers.

上面内容摘自：https://floating-point-gui.de/formats/fp/ ，关于为什么可以使用整数排序函数来对浮点数进行排序的细节可以参考上一节的例子。

4. 舍入（向偶数舍入）

因为表示方法限制了浮点数的范围和精度，浮点运算只能近似地表示实数运算。因此，对于值 \(x\) ，我们一般想用一种系统的方法，能够找到“最接近的”匹配值 \(x'\) ，它可以用期望的浮点形式表示出来。这就是舍入（rounding）运算的任务。 一个关键问题是在两个可能值的中间确定舍入方向。例如，如果我有 1.50 美元，想把它舍入到最接近的整数美元数，应该是 1 美元还是 2 美元呢？ IEEE 浮点格式定义了四种不同的舍入方式。

图 5 举例说明了应用四种舍入方式，将一个金额数舍入到最接近的整数美元数。 向偶数舍入（round-to-even），也称为向最接近的值舍入（round-to-nearest），是默认的方式 ，试图找到一个最接近的匹配值。因此，它将 1.40 美元舍入成 1 美元，而将 1.60 美元舍入成 2 美元，因为它们是最接近的整数美元值。唯一的设计决策是确定两个可能结果中间数值的舍入效果。 向偶数舍入方式采取的方法是：将数字向上或者向下舍入，使得结果的最低有效数字是偶数。 因此，这种方法将 1.5 美元和 2.5 美元都舍入成 2 美元。

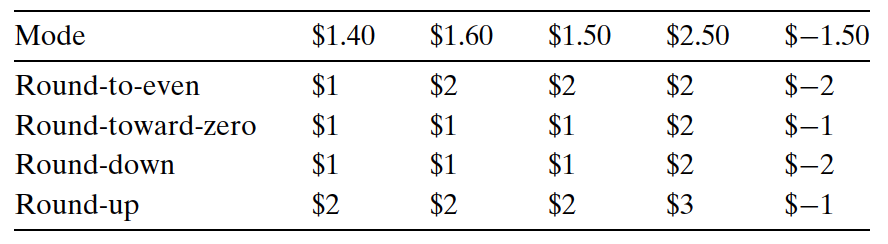
floating_point_number_rounding.png

Figure 5: 以美元为例说明舍入方式（单位为美元）

向偶数舍入最初看上去好像是个相当随意的目标——有什么理由偏向取偶数呢？为什么不始终把位于两个可表示的值中间的值都向上舍入呢？使用这种方法的一个问题就是很容易假想到这样的情景：这种方法舍入一组数值，会在计算这些值的平均数中引人统计偏差。我们采用这种方式舍入得到的一组数的平均值将比这些数本身的平均值略高一些。相反，如果我们总是把两个可表示值中间的数字向下舍入，那么舍入后的一组数的平均值将比这些数本身的平均值略低一些。 向偶数舍入的优点是在大多数现实情况中避免了这种统计偏差。 在 50% 的时间里，它将向上舍入，而在 50% 的时间里，它将向下舍入。

采用向偶数舍入方式舍入到只有两位小数，数字 1.2349999 将舍入到 1.23，数字 1.2350001 将舍入到 1.24，因为 1.2349999 和 1.2350001 都不是两个可能值的正中间值，舍入到距离最近的可能值；而数字 1.2350000（恰好在 1.23 和 1.24 中间）和 1.2450000（恰好在 1.24 和 1.25 中间）采用向偶数舍入方式则都会舍入到 1.24 ，因为 4 是偶数。

相似地， 向偶数舍入法能够运用于二进制小数。我们将最低有效位的值 0 认为是偶数，值 1 认为是奇数。 一般来说，只有对形如 \(XX \cdots XYY \cdots Y100 \cdots\) 的二进制位模式的数，这种舍入方式才有效，其中 \(X\) 和 \(Y\) 表示任意位值，最右边的 \(Y\) 是要舍入的位置。只有这种位模式表示在两个可能的结果正中间的值。例如，考虑舍入值到最近的四分之一的问题（也就是二进制小数点右边 2 位）。我们将 \(10.00011_2(2 \frac{3}{32})\) 向下舍入到 \(10.00_2(2)\) ， \(10.00110_2(2\frac{3}{16})\) 向上舍入到 \(10.01_2(2\frac{1}{4})\) ，因为这些值不是两个可能值的正中间值。我们将 \(10.11100_2(2\frac{7}{8})\) 向上舍入成 \(11.00_2(3)\) ，而 \(10.10100_2(2\frac{5}{8})\) 向下舍入成 \(10.10_2(2\frac{1}{2})\) ，因为这些值是两个可能值的中间值，并且我们倾向于使最低有效位为零。

5. 浮点运算（不满足结合率和分配率）

浮点运算会出其不意，如下面 golang 代码并不会输出 10.0，误差会累积：

package main

import "fmt"

func main() {
	var n float64 = 0
	for i := 0; i < 1000; i++ {
		n += 0.01
	}
	fmt.Println(n) // 输出 9.999999999999831，
                   // 如果 n 定义为 float 32，上一行会输出 10.0001335，其累积的误差更大
}

我们必须非常小心地使用浮点运算，因为浮点运算只有有限的范围和精度，而且 浮点运算不遵守普遍的算术属性，比如结合率和分配率。

在单精度浮点情况下，表达式 \((3.14 + 1 e^{10}) - 1 e^{10}\) 求值得到 \(0.0\) ——因为舍入，值 \(3.14\) 会丢失；而另一方面，表达式 \(3.14 + (1 e^{10} - 1 e^{10})\) 得到值 \(3.14\) 。可见，浮点运算不遵守结合率。

在单精度浮点情况下，表达式 \(1 e^{20} \times (1 e^{20} - 1 e^{20})\) 求值得到 \(0.0\) ，而表达式 \(1 e^{20} \times 1 e^{20} - 1 e^{20} \times 1 e^{20}\) 得到值 \(NaN\) 。可见，浮点运算不遵守分配率。

6. 浮点数的精度

我们知道单精度浮点数可以表示大到 \(3.4028234664 \times 10^{38}\) 的数字（参见节 3.2 ），但显然不能表示这个范围内的所有数字。 当我们说浮点数的“精度”为 \(d\) 位时，是指在浮点数本身可表示的数字范围内，所有的具有 \(d\) 位有效数字的定点数编码为浮点数比特流后，还可以重新转换回来（可恢复为和以前一样的定点数，两个转换方向都可能有舍入）。

比如，12345.67890123 有 13 位有效数字，它转换为单精度浮点数后，无法再恢复为 12345.67890123 了，这说明单精度浮点数的“精度”达不到 13 位；而 12345.67890123 转换为双精度浮点数后，还可以恢复回来，但这个例子说明双精度浮点数的“精度”可能达到 13 位（事实上，双精度浮点数的“精度”超过了 13 位）。

package main
import "fmt"
func main() {
	var a float32 = 12345.67890123
	fmt.Println(a) // 输出 12345.679，已经有舍入误差了，float32精度肯定不能达到13位

	var b float64 = 12345.67890123
	fmt.Println(b) // 输出 12345.67890123，没有舍入误差
}

关于浮点数的精度，下面直接给出结论：
1、 单精度浮点数的“精度”为 6 位有效数字 （更具体点，在其可表示范围内，所有 6 位有效数字的十进制定点数都可以安全地表达为单精度浮点数，大部分 7 位有效数字的十进制定点数可以安全地表达为单精度浮点数，少部分 8 位有效数字的十进制定点数可以安全地表达为单精度浮点数，没有一个 9 位有效数字的十进制定点数可以安全地表达为单精度浮点数）。
2、 双精度浮点数的“精度”为 15 位有效数字 （更具体点，在其可表示范围内，所有 15 位有效数字的十进制定点数都可以安全地表达为双精度浮点数，大部分 16 位有效数字的十进制定点数可以安全地表达为双精度浮点数，没有一个 17 位有效数字的十进制定点数可以安全地表达为双精度浮点数）。

关于本节内容，详情可参考：https://www.exploringbinary.com/decimal-precision-of-binary-floating-point-numbers/

7. 使用浮点数应遵循的指导原则

使用浮点数应遵循的指导原则：
1、避免数量级相差巨大的数之间的加减运算（ 如果你必须把多个相差巨大的浮点数求和，则应该先对其进行排序，然后从最小值开始把它们加起来 ）。
2、避免等量判断（浮点数的相等性判断一定不能直接使用等号，要使用类似 abs(v1 - v2) < 0.000001 这样的判断来判断浮点数是否相等）。
3、处理舍入误差问题（可以采用二进制编码的十进制变量，如 Java 中的 BigDecimal 类型避免浮点误差；或者直接变换为整形，如表示人民币金额时可以采用按分保存，这样使用整数即可）。

参见：《代码大全（第 2 版）》12.3 浮点数

8. 实例：0.2 的双精度浮点表示

通过在线转换工具（如 http://www.binaryconvert.com/result_double.html ），我们可以得到 0.2 的双精度浮点比特位为：\(0 \; 01111111100 \; 1001100110011001100110011001100110011001100110011010_2\)

下面来验证一下为什么这个比特位可以表示数字 0.2，按照节 3.1 的规则，有：

\[\begin{align*} E &= e - bias = 01111111100_2 - 1023 = 1020 - 1023 = -3 \\ M &= (1.1001100110011001100110011001100110011001100110011010)_2 \end{align*}\]

那么所编码的浮点数为：
\[\begin{align*} V &= (-1)^s \times M \times 2^E \\ &= 1 \times (1.1001100110011001100110011001100110011001100110011010)_2 \times \frac{1}{8} \end{align*}\]

下面使用工具 bc 来计算上面算子：

$ echo 'ibase=2;1.1001100110011001100110011001100110011001100110011010' | bc
1.6000000000000000888178419700125232338905334472656250
$ echo 'scale=60;1.6000000000000000888178419700125232338905334472656250/8' |bc
.200000000000000011102230246251565404236316680908203125000000

上面结果就是 64 个比特位：\(0 \; 01111111100 \; 1001100110011001100110011001100110011001100110011010_2\) 所表达的数（非常接近 0.2）。

9. 参考

本文的大部分内容直接摘自《深入理解计算机系统(原书第 2 版)》2.4 浮点数

单精度和双精度的浮点格式可仿照节 3.2 ，还可参考：
https://en.wikipedia.org/wiki/Single-precision_floating-point_format
https://en.wikipedia.org/wiki/Double-precision_floating-point_format

Author: cig01

Created: <2019-01-02 Wed>

Last updated: <2019-03-09 Sat>

Creator: Emacs 27.1 (Org mode 9.4)