GMW (A Generic MPC Protocol)

1. 简介
2. GMW (Semi-Honest MPC)
3. GMW Compiler (Malicious MPC)
4. 高效实现 GMW（Beaver Triples）
5. 参考

1. 简介

姚期智提出的混淆电路（Garbled Circuit）是一个通用的两方安全计算协议（Two-Party Computation），不过它不能简单地扩展为多方（多于两方）安全计算协议（Multi-Party Computation）。到 1990 年，D. Beaver, S. Micali and P. Rogaway 在论文 The round complexity of secure protocols 中才把姚期智的混淆电路扩展为了支持“多方”的安全计算协议，这被称为 BMR 协议。

1987 年，Oded Goldreich, Silvio Micali, Avi Wigderson 在论文 How to Play Any Mental Game 中提出了一种通用的多方安全计算协议，一般称它为 GMW 协议。GMW 协议是第一个通用的多方安全计算协议，本文将介绍它。

2. GMW (Semi-Honest MPC)

在 GMW 协议中，使用布尔逻辑电路或者算术电路来表示 MPC，如图 1 所示。本文仅介绍布尔逻辑电路，不介绍算术电路。

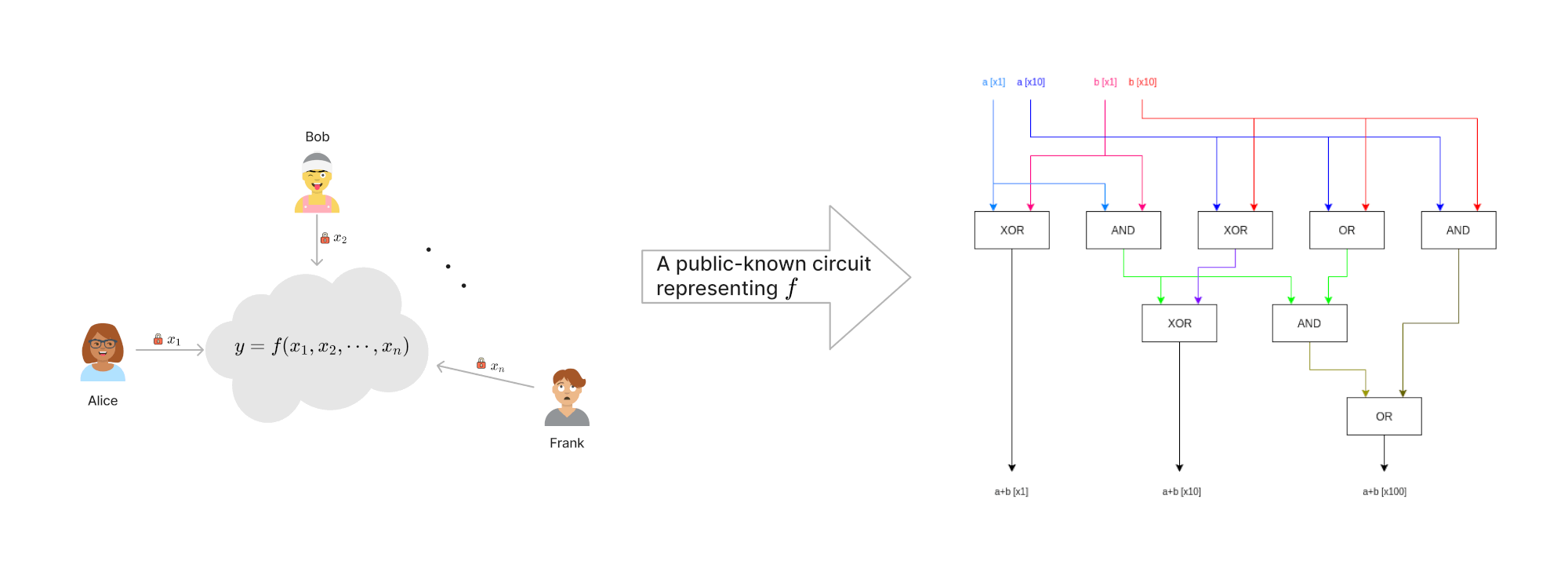
Figure 1: 左图为 MPC 示意图（输入 $x_{i}$ 是参与者 $i$ 的秘密信息，不能让其它人知道），右图是等价的布尔逻辑电路示意图

图 1 右边的布尔逻辑电路（摘自：https://vitalik.ca/general/2020/03/21/garbled.html ）是一个“two-bit 加法器”。假设 Alice 和 Bob 两个人参与这个运算，这个布尔逻辑电路有 4 个输入，其中 $a [\times 1]$ 和 $a [\times 10]$ 表示 Alice 的输入二进制数 $a$ （即左图 $x_{1}$ ）的“个位”和“十位”； $b [\times 1]$ 和 $b [\times 10]$ 表示 Bob 的输入二进制数 $b$ （即左图 $x_{2}$ ）的“个位”和“十位”。这个布尔逻辑电路有 3 个输出 $a + b [\times 1]$ 和 $a + b [\times 10]$ 和 $a + b [\times 100]$ ，分别表示结果二进制数 $a + b$ 的“个位”、“十位”和“百位”。

GMW 提出了一种方法，可以执行布尔逻辑电路，且可保证 Alice 的输入 $a$ 不泄露给 Bob；Bob 的输入 $b$ 不泄露给 Alice。 需要说明的是：对于“two-bit 加法器”来说，计算完成得到结果后，Alice 可以用结果减去她手中的秘密 $a$ 从而推算出 Bob 的秘密 $b$ 。这在协议中不算是秘密泄露，这是由电路的逻辑决定的，如果电路编码了 Hash 计算等不可反向推导的逻辑，那么就无法从结果反推输入了。

布尔逻辑电路的运算在 $F_{2}$ 中进行，每个 Gate 的输入输出都是二进制 0 或者 1，所有的运算都会有个 modulo 2 的过程，为简单起见后文中有时会省略写 modulo 2。

2.1. GMW 协议流程

GMW 协议流程如下：
第 1 步：Input-sharing Phase。各个参与者把自己输入数据（需要保密）的每一个比特位变为随机的 Additive Shares，分发给其它的参与者；
第 2 步：Gate Evaluation。电路输入线的值改为自己分配到的 shares，按照后文介绍的 Gate 执行方式来执行电路中每个 Gate；
第 3 步：Output Reconstruction。对于最后的输出 Gate，各个参与者把自己得到的 Output Share 告诉其它人。输出线上的所有 Output Share 加起来就得到最后的输出。

2.2. 第 1 步：Input-sharing Phase（参与者把输入拆分为 Additive Shares 后分发给其它人）

在 MPC 运算中，假设一共有 $n$ 个参与者，参与者 $P_{i}$ 的输入是 $x_{i}$ ，它是需要保密的。

假设 $P_{i}$ 的输入 $x_{i}$ 由 $k$ 个比特位组成： $x_{i}^{1}, x_{i}^{2}, \dots, x_{i}^{k}$ ，对每一个比特位（记为 $b$ ）进行下面操作：

把 $b$ 拆分为 Additive Shares 的形式。具体做法是：选择 $n - 1$ 个随机比特 $b_{1}, b_{2}, \dots, b_{n - 1}$ ，且定义 $b_{n} ≜ b_{1} + b_{2} + \dots + b_{n - 1} + b (\mod 2)$ ，这样一定有 $b = \sum_{i = 1}^{n} b_{i} (\mod 2)$ 。也就是说 比特位 $b$ 被拆分为了 $n$ 个加性分片（Additive Shares ），所有分片加起来会等于 $b$ ；
把 $b_{j}$ 发送给 $P_{j}$ （其中有一份是发送给自己的）。

上面过程如图 2 所示。

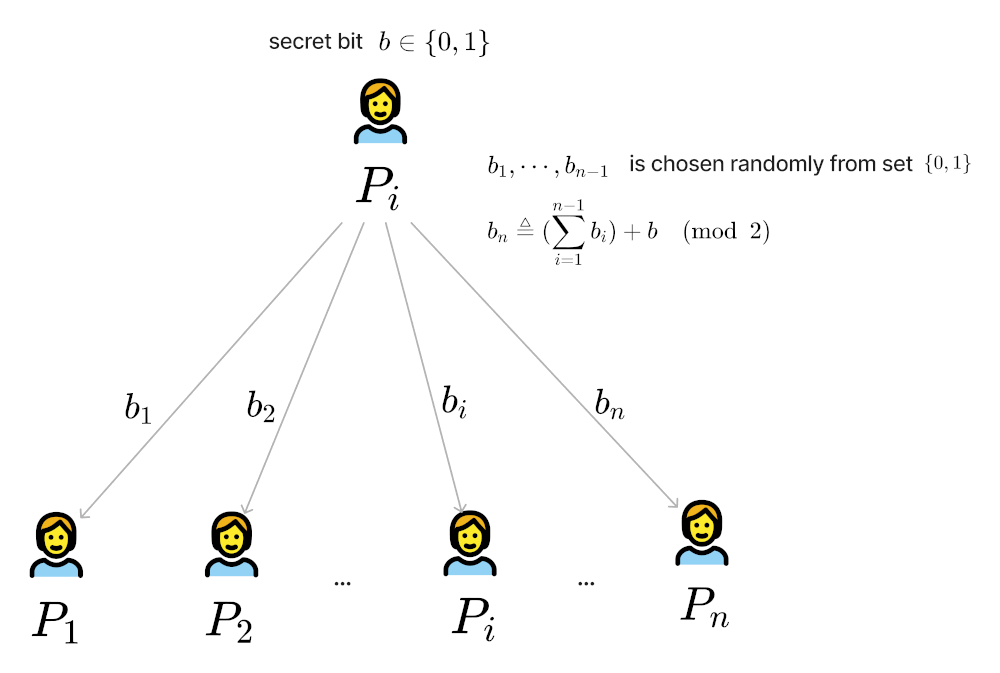
Figure 2: $P_{i}$ 把自己的秘密比特位 $b$ 拆分为 Additive Shares 后分发给其它人

假设 Alice 和 Bob 要执行图 1 右边的布尔逻辑电路，由于这是一个“two-bit 加法器”，Alice 需要进行 2 次图 2 所示的过程分别把它的 2 个输入比特位拆分为 Additive Shares 后分发给其它人；同理 Bob 也是要进行 2 次图 2 所示的过程。

2.3. 第 2 步：Gate Evaluation

下面介绍如何执行 NOT Gate 和 AND Gate。因为布尔逻辑电路的其它逻辑门都可以使用 NOT Gate 和 AND Gate 这两种逻辑门来表达（关于这个结论可参考：https://en.wikipedia.org/wiki/NAND_logic ），所以我们可以只讨论这两种逻辑门而不失一般性。

2.3.1. NOT Gate

NOT Gate 的真值表如表 1 所示，显然输入输出满足关系 $c = b + 1 (\mod 2)$

Table 1: NOT Gate 真值表
input b	ouput c
0	1
1	0

在前面介绍的第 1 步中，参与者已经把它的秘密 $b$ 拆分为 Additive Shares $b_{i}$ 后分发给其它人，即有 $b = \sum b_{i}$ 。每个参与者手头都有 $b_{i}$ ，我们需要寻找一种方法计算每个 $c_{i}$ ，使得所有 $c_{i}$ 之和等于 $b_{i}$ 之和加 $1$ ，也就是原始 NOT Gate 的真值表关系 $c = b + 1 (\mod 2)$ 需要维持住，不能被破坏。

NOT Gate 按照下面规则执行（图 3 最右图）：

$P_{1}$ 这样计算： $c_{1} ≜ b_{1} + 1 (\mod 2)$
其它参与者 $P_{i}, i = 2, 3, \dots, n$ 这样计算： $c_{i} ≜ b_{i}$

按照这个规则，容易验证 $\sum c_{i} = \sum b_{i} + 1 (\mod 2)$ 是成立的，也就是真值表关系 $c = b + 1 (\mod 2)$ 仍然成立。注：只有 $P_{1}$ 的规则和其它参与者不一样，不过选择谁是 $P_{1}$ 是不重要的，任意一个参与者执行 $P_{1}$ 的规则都行。

NOT Gate 是可以本地计算的，意思是 $P_{i}$ 计算 $c_{i}$ 时，并不需要其它参与者的配合。后面将介绍的 AND Gate 没有这么简单，需要其它参与者配置才行。

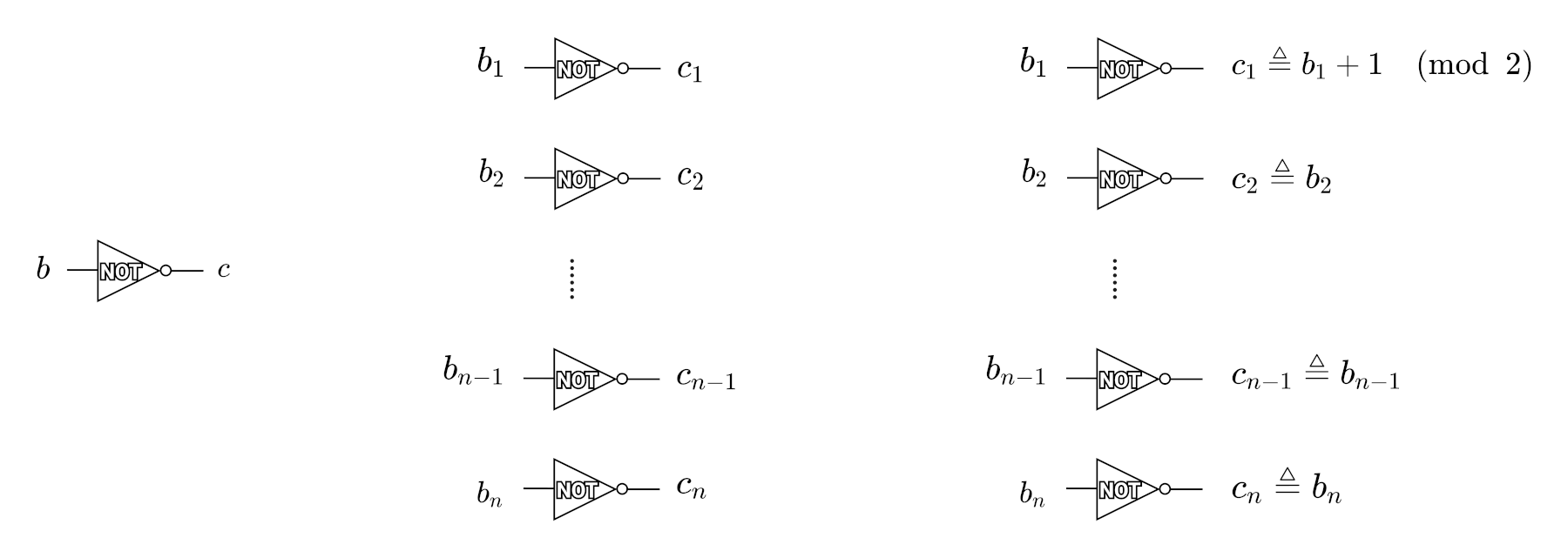
Figure 3: GMW NOT Gate

2.3.2. AND Gate

AND Gate（图 4）的真值表如表 2 所示，显然 AND Gate 相当于 $b = c d$ 。

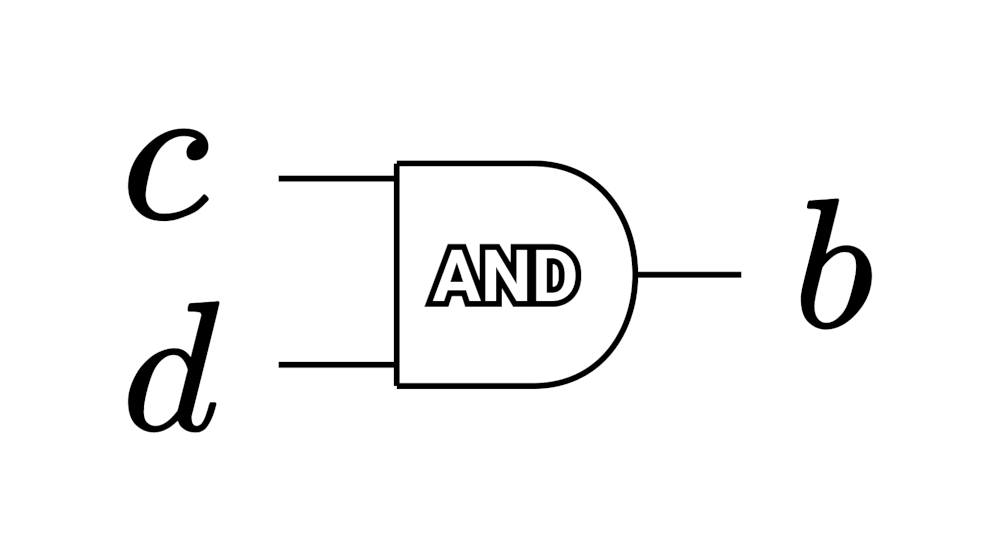
Figure 4: AND Gate

Table 2: AND Gate 真值表
input c	input d	ouput b
0	0	0
0	1	0
1	0	0
1	1	1

每个参与者手头只有 Input Shares $c_{i}, d_{i}$ ，我们需要寻找一种方法计算 Output Share $b_{i}$ ，使得 $\sum b_{i} = (\sum c_{i}) (\sum d_{i})$ 成立，也就是原始 AND Gate 的真值表关系 $b = c d$ 需要维持住，不能被破坏。

AND Gate 要麻烦一些，我们先讨论 Two-Party 的情况，然后再讨论 N-Party 的一般情况。

2.3.2.1. Two-Party Case

假设只有两个参与者 $P_{1}$ 和 $P_{2}$ 。 $P_{1}$ 手头有两个 Input Shares $c_{1}, d_{1}$ ， $P_{2}$ 手头有两个 Input Shares $c_{2}, d_{2}$ 。我们的目的是设计一种方案让 $P_{1}$ 得到 $b_{1}$ ，让 $P_{2}$ 得到 $b_{2}$ ，且它们要满足 $\sum b_{i} = (\sum c_{i}) (\sum d_{i})$ 。

AND Gate 的输出 $\begin{aligned} c d & = (c_{1} + c_{2}) (d_{1} + d_{2}) \\ = \underset{P_{1} 可以本地计算}{\underset{⏟}{c_{1} d_{1}}} + \underset{P_{1} 和 P_{2} 交换信息才能完成计算}{\underset{⏟}{c_{1} d_{2} + c_{2} d_{1}}} + \underset{P_{2} 可以本地计算}{\underset{⏟}{c_{2} d_{2}}} \end{aligned}$

我们不能简单地定义 $b_{1} ≜ c_{1} d_{1} + c_{1} d_{2}$ 和 $b_{2} ≜ c_{2} d_{1} + c_{2} d_{2}$ ，因为 $P_{1}$ 手里并没有 $d_{2}$ ，同样 $P_{2}$ 手里也没有 $d_{1}$ 。如果 $P_{1}$ 把 $d_{1}$ 告诉 $P_{2}$ ，而 $P_{2}$ 把 $d_{2}$ 告诉 $P_{1}$ 这样可行吗？这是不行的，因为这不能保证 $d$ 的隐私， $P_{1}$ 和 $P_{2}$ 通过 $d = d_{1} + d_{2}$ 就可知道 $d$ 了。

下面介绍使用 1-out-of-4 OT 协议来拆分 $c_{1} d_{2} + c_{2} d_{1}$ 为两个部分之和，使得 $P_{1}, P_{2}$ 分别可计算其它的一部分且不泄露各自的隐私。假设 $P_{1}$ 作为 1-out-of-4 OT 协议的 sender， $P_{2}$ 作为 1-out-of-4 OT 协议的 receiver。

首先 $P_{1}$ 定义下面 4 个式子 $\begin{aligned} S (0, 0) & ≜ (c_{1} \cdot 0) + (0 \cdot d_{1}) \\ S (0, 1) & ≜ (c_{1} \cdot 0) + (1 \cdot d_{1}) \\ S (1, 0) & ≜ (c_{1} \cdot 1) + (0 \cdot d_{1}) \\ S (1, 1) & ≜ (c_{1} \cdot 1) + (1 \cdot d_{1}) \end{aligned}$

$P_{1}$ 选择一个随机比特 $r \in {0, 1}$ ， $P_{1}$ 准备好 1-out-of-4 OT 协议的 4 个值 $\begin{array}{r} m_{0, 0} ≜ r + S (0, 0) \\ m_{0, 1} ≜ r + S (0, 1) \\ m_{1, 0} ≜ r + S (1, 0) \\ m_{1, 1} ≜ r + S (1, 1) \end{array}$

$P_{1}$ 把上面 4 个值发送给 $P_{2}$ 。 $P_{2}$ 从中选择 $m_{c_{2}, d_{2}}$ ，具体来说就是，如果 $c_{2} = 0, d_{2} = 0$ ，则 $P_{2}$ 选择 $m_{0, 0}$ ，如果 $c_{2} = 0, d_{2} = 1$ ，则 $P_{2}$ 选择 $m_{0, 1}$ ，如果 $c_{2} = 1, d_{2} = 0$ ，则 $P_{2}$ 选择 $m_{1, 0}$ ，如果 $c_{2} = 1, d_{2} = 1$ ，则 $P_{2}$ 选择 $m_{1, 1}$ 。

定义 $\begin{aligned} b_{1} & ≜ c_{1} d_{1} + r \\ b_{2} & ≜ c_{2} d_{2} + m_{c_{2}, d_{2}} \end{aligned}$ $P_{1}$ 计算 $b_{1}$ 时只用使用他手头的 Input Shares $c_{1}, d_{1}$ ， $P_{2}$ 计算 $b_{2}$ 时也只用使用他手头的 Input Shares $c_{2}, d_{2}$ 。

下面我们来验证一下 $b_{1} + b_{2} = (c_{1} + c_{2}) (d_{1} + d_{2})$ 是否成立。

$\begin{aligned} b_{1} + b_{2} & = c_{1} d_{1} + r + c_{2} d_{2} + m_{c_{2}, d_{2}} (\mod 2) \\ = c_{1} d_{1} + r + c_{2} d_{2} + r + S (c_{2}, d_{2}) (\mod 2) \\ = c_{1} d_{1} + c_{2} d_{2} + S (c_{2}, d_{2}) (\mod 2) \end{aligned}$

当 $c_{2} = 0, d_{2} = 0$ 时，上式为 $c_{1} d_{1} + c_{2} d_{2} = c_{1} d_{1}$ ，而直接计算 $(c_{1} + c_{2}) (d_{1} + d_{2})$ 也是这个值。
当 $c_{2} = 0, d_{2} = 1$ 时，上式为 $c_{1} d_{1} + c_{2} d_{2} + d_{1} = c_{1} d_{1} + d_{1}$ ，而直接计算 $(c_{1} + c_{2}) (d_{1} + d_{2})$ 也是这个值；
当 $c_{2} = 1, d_{2} = 0$ 时，上式为 $c_{1} d_{1} + c_{2} d_{2} + c_{1} = c_{1} d_{1} + c_{1}$ ，而直接计算 $(c_{1} + c_{2}) (d_{1} + d_{2})$ 也是这个值；
当 $c_{2} = 1, d_{2} = 1$ 时，上式为 $c_{1} d_{1} + c_{2} d_{2} + c_{1} + d_{1} = c_{1} d_{1} + 1 + c_{1} + d_{1}$ ，而直接计算 $(c_{1} + c_{2}) (d_{1} + d_{2})$ 也是这个值；

从而 $b_{1} + b_{2} = (c_{1} + c_{2}) (d_{1} + d_{2})$ 总是成立。

$P_{1}$ 和 $P_{2}$ 计算 $b_{1}, b_{2}$ 的过程可总结为图 5 所示，其中左子图是利用 1-out-of-4 OT 拆分 $c_{1} d_{2} + c_{2} d_{1}$ 为两个部分（ $r$ 和 $m_{c_{2}, d_{2}}$ ）之和。

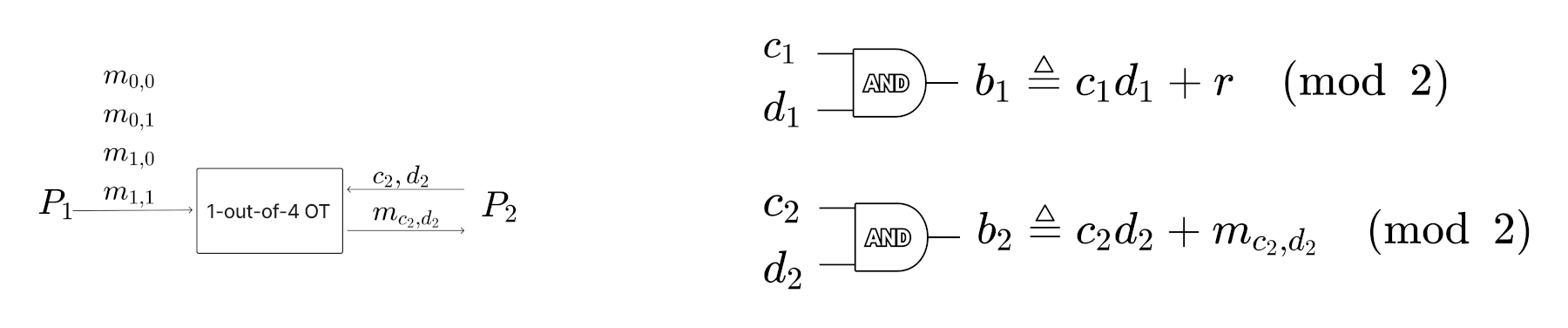
Figure 5: GMW AND Gate Two-Party Case

2.3.2.2. N-Party Case

前面介绍的是 Two-Party 的情况，容易扩展为 N-Party 的通用情况。下面以 4 个 Party 为例介绍一下 N-Party 时的思路。

假设有 4 个参与者 $P_{1}, P_{2}, P_{3}, P_{4}$ 。经过第 1 步（即 Input-sharing Phase）后， $P_{1}$ 手头有两个 Input Shares $c_{1}, d_{1}$ ， $P_{2}$ 手头有两个 Input Shares $c_{2}, d_{2}$ ， $P_{3}$ 手头有两个 Input Shares $c_{3}, d_{3}$ ， $P_{4}$ 手头有两个 Input Shares $c_{4}, d_{4}$ 。我们的目的是设计一种方案让 $P_{1}, P_{2}, P_{3}, P_{4}$ 分别得到 $b_{1}, b_{2}, b_{3}, b_{4}$ ，且它们要满足 $\sum b_{i} = (\sum c_{i}) (\sum d_{i})$ 。

$\begin{aligned} c d = & (c_{1} + c_{2} + c_{3} + c_{4}) (d_{1} + d_{2} + d_{3} + d_{4}) \\ = & c_{1} d_{1} + c_{1} d_{2} + c_{1} d_{3} + c_{1} d_{4} \\ c_{2} d_{1} + c_{2} d_{2} + c_{2} d_{3} + c_{2} d_{4} \\ c_{3} d_{1} + c_{3} d_{2} + c_{3} d_{3} + c_{3} d_{4} \\ c_{4} d_{1} + c_{4} d_{2} + c_{4} d_{3} + c_{4} d_{4} \end{aligned}$

其中 $c_{1} d_{1}$ 可由 $P_{1}$ 本地计算， $c_{2} d_{2}$ 可由 $P_{2}$ 本地计算， $c_{3} d_{3}$ 可由 $P_{3}$ 本地计算， $c_{4} d_{4}$ 可由 $P_{4}$ 本地计算。

任意两个参与者 $P_{i}, P_{j}$ 之间进行 1-out-of-4 OT 协议交换信息（和上一节介绍的相同）。 比如红色部分 $c_{1} d_{2} + c_{2} d_{1}$ 由 $P_{1}, P_{2}$ 进行一次 1-out-of-4 OT 协议可拆分为两个部分之和， $P_{1}, P_{2}$ 各取一部分（如 $r^{P_{1}, P_{2}}, m_{c_{2}, d_{2}}^{P_{1}, P_{2}}$ ）；蓝色部分 $c_{1} d_{3} + c_{3} d_{1}$ 由 $P_{1}, P_{3}$ 进行一次 1-out-of-4 OT 协议可拆分为两个部分之和， $P_{1}, P_{3}$ 各取一部分（如 $r^{P_{1}, P_{3}}, m_{c_{3}, d_{3}}^{P_{1}, P_{3}}$ ）；绿色部分 $c_{1} d_{4} + c_{4} d_{1}$ 由 $P_{1}, P_{4}$ 进行一次 1-out-of-4 OT 协议可拆分为两个部分之和， $P_{1}, P_{4}$ 各取一部分（如 $r^{P_{1}, P_{4}}, m_{c_{4}, d_{4}}^{P_{1}, P_{4}}$ ）；其它类似。4 个参与者执行一个 AND Gate 一共要进行 6 次 1-out-of-4 OT 协议。

这样， $P_{1}, P_{2}, P_{3}, P_{4}$ 的 Output Share 可分别定义为 $\begin{aligned} b_{1} & ≜ c_{1} d_{1} + r^{P_{1}, P_{2}} + r^{P_{1}, P_{3}} + r^{P_{1}, P_{4}} (\mod 2) \\ b_{2} & ≜ m_{c_{2}, d_{2}}^{P_{1}, P_{2}} + c_{2} d_{2} + r^{P_{2}, P_{3}} + r^{P_{2}, P_{4}} (\mod 2) \\ b_{3} & ≜ m_{c_{3}, d_{3}}^{P_{1}, P_{3}} + m_{c_{3}, d_{3}}^{P_{2}, P_{3}} + c_{3} d_{3} + r^{P_{3}, P_{4}} (\mod 2) \\ b_{4} & ≜ m_{c_{4}, d_{4}}^{P_{1}, P_{4}} + m_{c_{4}, d_{4}}^{P_{2}, P_{4}} + m_{c_{4}, d_{4}}^{P_{3}, P_{4}} + c_{4} d_{4} (\mod 2) \end{aligned}$

这些 Output Share 加起来会为 $c d$ 。

当参与者个数为其它数时，情况也类似，不再介绍。

2.4. 第 3 步：Output Reconstruction

当参与者执行完 Gate，得到 Gate 输出线上的 Output Share 后，如果这个 Gate 不是最后一个 Gate，则这个 Output Share 就作为后一个 Gate 的 Input Share 继续往下执行。直到执行到最后一层 Gate。

假设 3 个参与者 Alice/Bob/Carol 执行图 6 所示电路，他们的输入都只有一个比特位，分别为 a/b/c，当执行结束后，Alice/Bob/Carol 可分别得到 $y_{1}, y_{2}, y_{3}$ 。要得到最终的结果 $y$ ，Alice 需要把 $y_{1}$ 告诉其它参与者，Bob 需要把 $y_{2}$ 告诉其它参与者，Carol 需要把 $y_{3}$ 告诉其它参与者。这样，每个参与者都可以使用 $y = y_{1} + y_{2} + y_{3}$ 计算 $y$ 了。

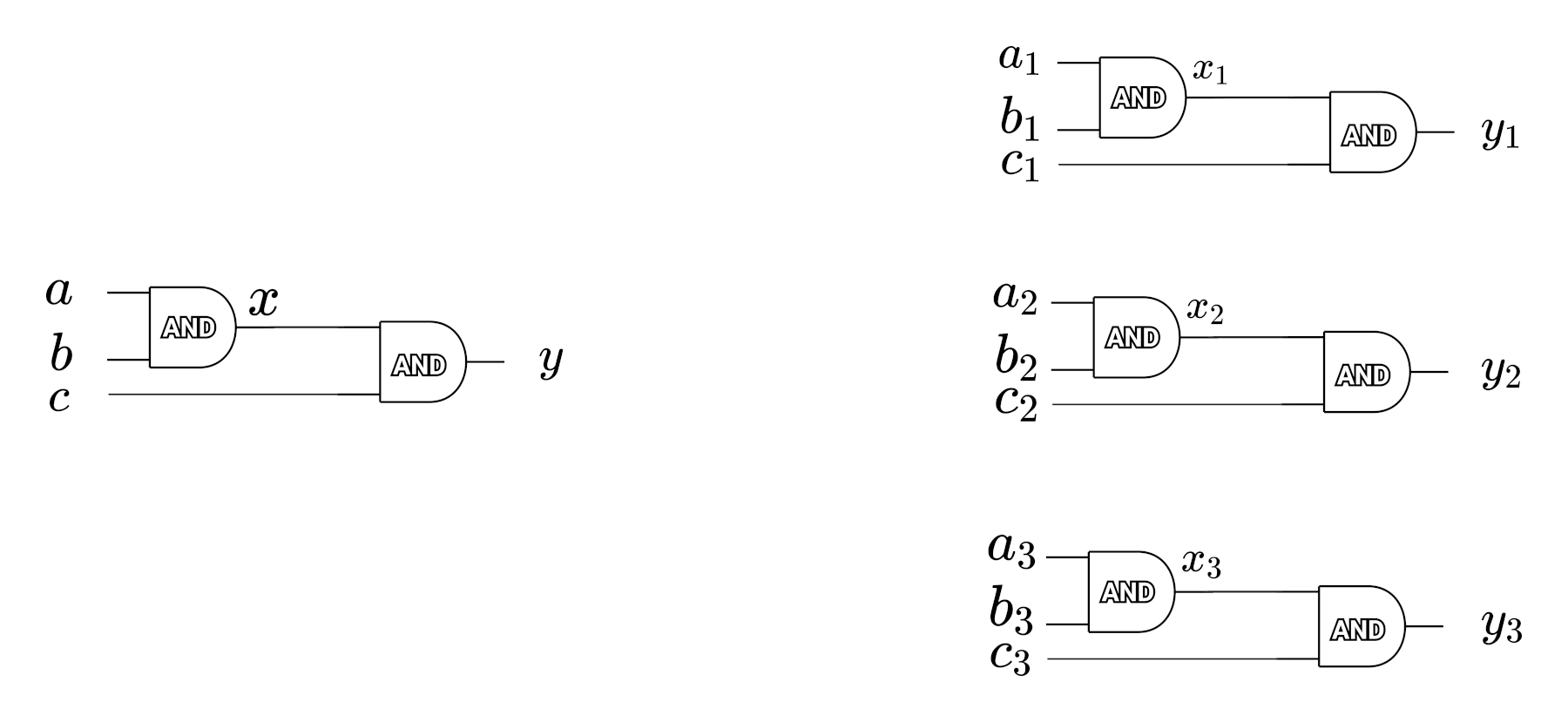
Figure 6: Alice/Bob/Carol 执行电路示意图

3. GMW Compiler (Malicious MPC)

前面介绍的 GMW 协议是基于 Semi-Honest 敌手模型，也就是假设各个参与者会忠实地执行协议，但是参与者可能保留交互时得到的信息。

GMW Compiler 是 Goldreich、Micali 和 Wigderson 提出的一种通用编译器，它可以将 Semi-Honest MPC 协议转换为 Malicious MPC 协议。 GMW Compiler 的基本思路是：使用零知识证明来确保每一步计算时参与者都不会偏离协议，从而确保了每一步计算的正确性。 比如，在执行 NOT Gate 时（参考 2.3.1）， $P_{1}$ 会计算 $c_{1} = b_{1} + 1 (\mod 2)$ ， $P_{1}$ 需要同时提供 $c_{1}$ 的一个证明，以证明 $c_{1}$ 确实是由 $b_{1} + 1 (\mod 2)$ 计算而来。

GMW Compiler 总结： 先设计一个 Semi-Honest MPC 协议，然后对每一步引入零知识证明以确保参与者忠实地执行协议，这样就把 Semi-Honest MPC 协议改造成了 Malicious MPC 协议。

4. 高效实现 GMW（Beaver Triples）

1992 年，Donald Beaver 在论文 Efficient multiparty protocols using circuit randomization 中提出了 Beaver Triples（也称 Beaver’s Multiplication Triples）。 利用它可以去掉 GMW 中的 1-out-of-4 OT 协议，由于 Beaver triples 可以提前计算，这使得 GMW 的性能大大提升。 高性能的 GMW 协议实现都会使用 Beaver Triples 进行优化。本文不介绍 Beaver Triples 的细节。

5. 参考

Course 600.641 Lecture 14: Secure Multiparty Computation: https://www.cs.jhu.edu/~susan/600.641/scribes/lecture14.pdf
Oblivious Transfer and GMW MPC: https://slideplayer.com/slide/13844223/
A pragmatic introduction to secure multi-party computation. 3.2 Goldreich-Micali-Wigderson (GMW) Protocol
A pragmatic introduction to secure multi-party computation. 6.5.1 GMW Compiler