Hidden Markov Model
Table of Contents
1. 隐马尔可夫模型简介
隐马尔可夫模型(Hidden Markov Model, HMM)是一个著名的概率模型,可应用于词性标注、语音识别、中文分词等等方面。
下面介绍一个简单的 HMM 模型例子(摘自其 wikipedia )。
Alice 和 Bob 是好朋友,他们不在一个城市,每天通过电话了解对方当天作了什么。Bob 仅仅对三种活动感兴趣(一天仅做一个活动):散步,购物,清理房间。他选择做哪件事只凭当天的天气。Alice 对于 Bob 所住的地方的天气情况并不了解,但是他知道总的趋势。在 Bob 告诉 Alice 每天所做的事情基础上,Alice 想要猜测 Bob 所在地的天气情况。
可以简单地认为天气的运行就像一个马尔可夫链。其有两个状态 “雨”和“晴”,但 Alice 是无法直接观察它们,也就是说,它们对于 Alice 是隐藏的。每天,Bob 有一定的概率进行下列活动:“散步”,“购物”,或“清理房间”。因为 Bob 会告诉 Alice 他的活动,所以这些活动就是 Alice 的观察数据。这整个系统就是一个隐马尔可夫模型。
Alice 可以通过“观察数据”(Bob 的活动)预测出最可能的“状态数据”(Bob 所在地市天气)。这是隐马尔可夫模型的主要问题之一,可以用“维特比”算法解决。
参考:
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
http://www.52nlp.cn/hmm-learn-best-practices-and-cui-johnny-blog
1.1. HMM 的正式描述
隐马尔可夫模型描述一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。 隐藏的马尔可夫链随机生成的状态的序列,称为状态序列(state sequence);每个状态生成一个观测,而由此产生的观测的随机序列,称为观察序列(observation sequence)。序列的每一个位置又可以看作是一个时刻。
隐马尔可夫模型由三个要素决定:初始状态概率分布、状态转移概率分布以及观测概率分布。
隐马尔可夫模型的形式定义如下:
设 \(Q\) 是所有可能的状态的集合, \(V\) 是所有可能的观测的集合:
\[Q= \{q_1, q_2, \cdots, q_N\}, V= \{v_1, v_2, \cdots, v_M \}\]
其中, \(N\) 是可能的状态数, \(M\) 是可能的观测数。
\(I\) 是长度为 \(T\) 的状态序列, \(O\) 是对应的观测序列。
\[I= (i_1, i_2, \cdots, i_T), O= (o_1, o_2, \cdots, o_T)\]
\(A\) 是状态转移概率矩阵:
\[A = \left[ a_{ij} \right]_{N \times N}\]
其中, \(a_{ij} = P(i_{t+1} = q_j | i_t = q_i), \, i=1,2,\cdots,N; j = 1,2,\cdots, N\) 是在时刻 \(t\) 处于状态 \(q_i\) 的条件下在时刻 \(t+1\) 转移到状态 \(q_j\) 的概率。
\(B\) 是观测概率矩阵:
\[B= \left[b_{jk}\right]_{N \times M}\]
其中, \(b_{jk} = P(o_t = v_k | i_t = q_j), \, k=1,2,\cdots,M; j=1,2,\cdots,N\) 是时刻 \(t\) 处于状态 \(q_j\) 的条件下生成观测 \(v_k\) 的概率。在不至于混淆的情况下,下文可能将 \(b_{jk}\) 记作 \(b_{q_j v_k}\) 或 \(b_{q_j \to v_k}\) ,这样更加直观。
\(\boldsymbol{\pi}\) 是初始状态概率向量:
\[\boldsymbol{\pi} = (\pi_i)\]
其中, \(\pi_i = P(i_1 = q_i), \, i=1,2,\cdots,N\) 是时刻 \(t=1\) 处于状态 \(q_i\) 的概率。
隐马尔可夫模型由初始状态概率向量 \(\boldsymbol{\pi}\) ,状态转移概率矩阵 \(A\) 和观测概率矩阵 \(B\) 决定。因此,隐马尔可夫模型参数 \(\lambda\) 可以用三元符号表示,即:
\[\lambda = (A, B, \boldsymbol{\pi})\]
\(A, B, \boldsymbol{\pi}\) 称为隐马尔可夫模型的三要素。
状态转移概率矩阵 \(A\) 与初始状态概率向量 \(\boldsymbol{\pi}\) 确定了隐藏的马尔可夫链,生成无法观测的状态序列。观测概率矩阵 \(B\) 确定了如何从状态生成观测,与状态序列综合确定了如何产生观测序列。
对于前面“Alice 预测其朋友 Bob 所在城市的天气”的例子,可以建立下面的 HMM 模型:
状态的集合(天气情况): \(Q=\{\text{‘Rainy’}, \text{‘Sunny’}\}\)
观测的集合(Bob 的活动): \(V=\{\text{‘Walk’}, \text{‘Shop’}, \text{‘Clean’} \}\)
初始状态概率向量: \(\boldsymbol{\pi} = (0.6, 0.4)\)
状态转移概率矩阵 \(A\) : \(A=\left(\begin{array}{cc} 0.7 & 0.3 \\ 0.4 & 0.6 \end{array} \right)\)
观测概率矩阵 \(B\) : \(B=\left(\begin{array}{ccc} 0.1 & 0.4 & 0.5 \\ 0.6 & 0.3 & 0.1 \end{array} \right)\)
上面模型可用图 1 表示。
Figure 1: HMM 模型示意图
1.2. HMM 的 2 个基本假设
从隐马尔可夫模型的定义知,HMM 作了 2 个基本假设:
(1) 齐次马尔可夫性假设。即假设隐藏的马尔可夫链在任意时刻 \(t\) 的状态只依赖其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 \(t\) 无关。
\[P(i_t | i_{t-1}, o_{t-1}, \cdots, i_2, o_2, i_1, o_1) = P(i_t|i_{t-1}), \, t=1,2,\cdots, T\]
(2) 观测独立性假设。即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
\[P(o_t|i_T, o_T, i_{T-1}, o_{T-1}, \cdots, i_{t+1}, o_{t+1}, i_t, i_{t-1}, o_{t-1}, \cdots, i_1,o_1)= P(o_t|i_t)\]
1.3. HMM 的 3 个基本问题
对于隐马尔可夫模型,有 3 个基本问题。
(1) 概率计算问题。已知模型 \(\lambda = (A, B, \boldsymbol{\pi})\) 和观测序列 \(O=(o_1, o_2, \cdots, o_T)\) ,计算在模型 \(\lambda\) 下观测序列 \(O\) 出现的概率 \(P(O| \lambda)\) 。如,前面例子中,Alice 和 Bob 通了三天电话后发现第一天 Bob 去 Walk 了,第二天他去 Shop 了,第三天他对房间进行了 Clean。那么这个观察序列“Walk, Shop, Clean”的总的概率是多少?
(2) 学习问题。已知观测序列 \(O=(o_1, o_2, \cdots, o_T)\) ,估计模型参数 \(\lambda = (A, B, \boldsymbol{\pi})\) 。
(3) 预测问题(又称解码问题)。已知模型 \(\lambda = (A, B, \boldsymbol{\pi})\) 和观测序列 \(O=(o_1, o_2, \cdots, o_T)\) ,求对给定观测序列条件概率 \(P(I|O)\) 最大的状态序列 \(I=(i_1^{*}, i_2^{*}, \cdots, i_T^{*})\) ,即 给定观测序列,求最有可能的对应的状态序列。 如,前面例子中,Alice 可以通过“观察数据”(Bob 的活动)预测出最可能的“状态数据”(Bob 所在地市天气)。这个问题可以通过维特比算法解决。
后面将讨论这 3 个问题。
2. 维特比算法
维特比算法(Viterbi algorithm)解决的是隐马尔可夫模型中的解码问题——通过观测序列寻找最可能的隐藏状态序列。
假设有下面 HMM,模型中“观测序列”为海藻湿度,有四种情况:{dry, dryish, damp, soggy},隐藏的“状态序列”为天气,有三种情况:{Sunny, Cloudy, Rainy}。
假设连续三天观察海藻湿度依次为:干燥(dry)、湿润(damp)、湿透(soggy),如何推断这三天最可能的天气情况?
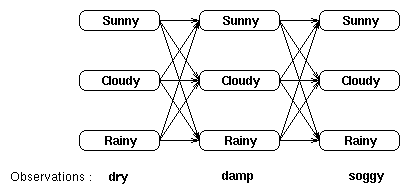
Figure 2: HMM 模型,Viterbi 算法实例
最直接的想法是穷举法:遍历所有的天气组合(27 种)。最可能的天气情况就是下面这些概率中其值最大的那个所对应的天气情况。
\[\begin{gathered} P(\text{dry}, \text{damp}, \text{soggy} \mid \text{sunny}, \text{sunny}, \text{sunny}) \\
P(\text{dry}, \text{damp}, \text{soggy} \mid \text{sunny}, \text{sunny} ,\text{cloudy}) \\
P(\text{dry}, \text{damp}, \text{soggy} \mid \text{sunny}, \text{sunny}, \text{rainy}) \\
...... \\
P(\text{dry}, \text{damp}, \text{soggy} \mid \text{rainy}, \text{rainy}, \text{rainy}) \end{gathered}\]
但是穷举效率很低,当观察序列比较长时根本不可行。
下面介绍的维特比算法利用 HMM 模型的特点加快解码的效率。
参考:
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/viterbi_algorithm/s1_pg1.html
2.1. Viterbi 算法分析
Viterbi 算法是一种动态规划算法。
定义 \(\delta_t(i)\) 是在特定的观测序列下,时刻 \(t\) 到达状态 \(i\) 的所有可能序列的概率中最大的概率,即时刻 \(t\) 到达状态 \(i\) 的“最可能的路径”的概率。
在某个固定时刻中,每一个状态,都有一个到达该状态的最可能路径。以前面介绍的“海藻湿度和天气”为例,在 \(t=3\) 时刻的 3 个状态中的每一个都有一个到达此状态的最可能路径(称为局部最佳路径),这个最可能路径可能如图 3 所示。
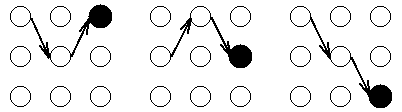
Figure 3: 每个状态都有一个到达它的“最可能路径”
特别地,如果共有 \(T\) 个观测序列,则在 \(t=T\) 时每一个状态都有一个局部最佳路径。这样可以选择这些局部最佳路径中概率最大的那条路径作为全局最佳路径,即观测序列对应的最可能的隐藏状态序列,这样 HMM 的“解码问题”得到解决。
2.1.1. 递归计算“局部最佳路径”的概率(动态规划算法)
下面将介绍如何利用 \(\delta_{t-1}(i)\) 来递归地计算 \(\delta_t(i)\) 。
先考虑 \(t=1\) 的情况。假设 \(t=1\) 时,观测数据为 \(v_1\) 。
\[\begin{gathered} \delta_1(A) = \pi(A) b_{A v_1} \\
\delta_1(B) = \pi(B) b_{B v_1} \\
\delta_1(C) = \pi(C) b_{C v_1} \end{gathered}\]
上式中, \(\pi, b\) 分别为 HMM 模型中初始状态概率向量 \(\boldsymbol{\pi}\) 和观测概率矩阵 \(B\) 中的元素。
现在考虑 \(t>1\) 的情况。假设 \(t\) 时刻,观测数据为 \(v_t\) 。
下面考虑计算 \(t\) 时刻到达状态 \(X\) ( \(X\) 可能是状态 \(A,B,C\) 中的一个)的最可能的路径,这条到达状态 \(X\) 的最可能路径将通过 \(t-1\) 时刻的状态 \(A,B,C\) 中的某一个。如图 4 所示。
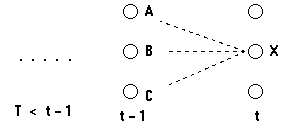
Figure 4: 通过 t-1 时刻的“局部最佳路径”计算 t 时刻的“局部最佳路径”
即有: \(t\) 时刻到达状态 \(X\) 的最可能的路径为下面路径中的一个(概率最大的那个):
\[\begin{gathered} \cdots, A, X \\
\cdots, B, X \\
\cdots, C, X \end{gathered}\]
HMM 模型中,有个齐次马尔可夫假设,即任意时刻 \(t\) 的状态只依赖其前一时刻的状态。所以我们可以这样计算 \(t\) 时刻路径末端是 \(AX\) 的最可能的路径的概率为(下式是 Viterbi 算法中最重要的递推式):
\[\footnotesize \begin{aligned} & P(t-1 \text{时刻到达状态} A \text{的最可能路径}) \times P(t-1 \text{时刻状态为} A \text{时,} t \text{时刻转移到} X) \times P(t \text{时刻状态为} X \text{时,生成观测数据} v_t) \\
= & P(t-1 \text{时刻到达状态} A \text{的最可能路径}) \times P(i_t = X | i_{t-1} = A) \times P(o_t = v_t | i_t = X) \\
= & \delta_{t-1}(A) \times a_{AX} \times b_{X v_t} \end{aligned}\]
上式中, \(a,b\) 分别为 HMM 模型中状态转移概率矩阵 \(A\) 和观测概率矩阵 \(B\) 中的元素。
类似地,可得:
\(t\) 时刻路径末端是 \(BX\) 的最可能的路径的概率为: \(\delta_{t-1}(B) \times a_{BX} \times b_{X v_t}\) 。
\(t\) 时刻路径末端是 \(CX\) 的最可能的路径的概率为: \(\delta_{t-1}(C) \times a_{CX} \times b_{X v_t}\) 。
显然, \(t\) 时刻到达状态 \(X\) 的最可能的路径的概率为前面 3 个概率中最大的那个。即有:
\[\delta(t,X) = \max_{j=\{A,B,C\}} (\delta_{t-1}(j) a_{jX} b_{X v_t}) = \max_{j=\{A,B,C\}} (\delta_{t-1}(j) a_{jX}) b_{X v_t}\]
2.1.2. 回溯得到最优路径
通过一个辅助变量,我们可以方便地回溯得到最优路径。
定义 \(\psi_t(i)\) 为在时刻 \(t\) 状态为 \(i\) 的所有单个路径 \((i_1, i_2, \cdots, i_{t-1}, i)\) 中概率最大的路径的第 \(t-1\) 个结点。 和前面的分析类似,容易得到:
\[\psi_t(i) = {\operatorname{arg} \underset{1 \le j \le N}{\max}}(\delta_{t-1}(j) a_{ji})\]
上式中, \(N\) 为总状态数, \(\operatorname{arg\,max}\) 是用来计算当括号中表达式的值最大时索引 \(j\) 对应的值。
\(\psi_t(i)\) 的计算可以和 \(\delta_t(i)\) 的计算在一趟中同时运行。
这样,如果共有 \(T\) 个观测序列,假设对应的最优路径(最可能的状态序列)为 \(i_1^{*}, i_2^{*}, \cdots, i_T^{*}\) ,则当 \(t=T\) 时,可以通过下式计算出 \(i_T^{*}\) :
\[i_T^{*} = {\operatorname{arg} \underset{1 \le j \le N}{\max}}(\delta_{T}(i))\]
得到 \(i_T^{*}\) 后,利用下式可以从后往前依次计算出 \(i_{T-1}^{*}, \cdots, i_2^{*}, i_1^{*}\) :
\[i_{t}^{*} = \psi_{t+1}(i_{t+1}^{*}), \; t=T-1,T-2,\cdots, 1\]
至此,我们得到了最终的“解码序列”。
2.1.3. Viterbi 算法的形式描述
Viterbi 算法的完整分析在前面已经介绍了。下面把 Viterbi 算法总结如下:
输入:HMM 模型参数 \(\lambda = (A, B, \boldsymbol{\pi})\) 和观测 \(O= (o_1, o_2, \cdots, o_T)\)
输出:最有可能的对应状态序列(最优路径) \(I^{*} = (i_1^{*}, i_2^{*}, \cdots, i_T^{*})\)
Viterbi 算法步骤:
(1) 初始化:
\[\begin{gathered} \delta_1(i) = \pi_i b_{i o_1}, \; 1 \le i \le N \\
\psi_1(i) = 0, \; 1 \le i \le N \end{gathered}\]
(2) 递归求解当 \(t=2,3, \cdots, T\) 时的 \(\delta_t(i)\) 和 \(\psi_t(i)\) :
\[\begin{gathered} \delta_t(i) = \max_{1 \le j \le N} (\delta_{t-1}(j) a_{ji}) b_{i o_t}, \; 1 \le i \le N \\
\psi_t(i) = {\operatorname{arg} \underset{1 \le j \le N}{\max}}(\delta_{t-1}(j) a_{ji}) \end{gathered}\]
(3) 上面的计算结束后,求最优路径的概率 \(P^{*}\) (在这里不是必要)和最优路径最后一个状态 \(i_T^{*}\) :
\[\begin{gathered} P^{*} = \max_{1 \le i \le N} (\delta_T(i)) \\
i_T^{*} = {\operatorname{arg} \underset{1 \le j \le N}{\max}}(\delta_T(i)) \end{gathered}\]
(4) 回溯得到最优路径,依次求 \(i_{T-1}^{*}, i_{T-2}^{*}, \cdots, i_1\)
\[i_{t}^{*} = \psi_{t+1}(i_{t+1}^{*}), \; t=T-1,T-2,\cdots, 1\]
2.2. Viterbi 算法实例
以“Alice 预测其朋友 Bob 所在城市的天气”为例,其对应的 HMM 模型如图 1 所示,为方便查看,重复如图 5 所示。
Figure 5: HMM 模型示意图
假设 Alice 观测到 Bob 连续三天的行动分别为:‘Walk’, ‘Shop’, ‘Clean’,请推测 Bob 所在城市这三天最可能的天气情况。
直接使用 Viterbi 算法即可,计算过程如下:
(1) 初始化
在 \(t=1\) 时,观测数据为‘Walk’。对于每一个状态 \(i, \;(i=1,2)\) (代表‘Rainy’和‘Sunny’)分别计算 \(\delta_1(i)\) :
\[\begin{gathered} \delta_1(1) = \pi_{Rainy} b_{Rainy \to Walk} = \pi_1 b_{11} = 0.6 \times 0.1 = 0.06 \\
\delta_1(2) = \pi_{Sunny} b_{Sunny \to Walk} = \pi_2 b_{21} = 0.4 \times 0.6 = 0.24 \end{gathered}\]
上式中, \(\delta_1(1)\) 表示状态为‘Rainy’,观测为‘Walk’的概率;\(\delta_1(2)\) 表示状态为‘Sunny’,观测为‘Walk’的概率。
同时,记 \(\psi_1(1) = \psi_1(2) = 0\)
(2) 求解当 \(t=2,3\) 时的 \(\delta_t(i)\) 和 \(\psi_t(i)\) 。
当 \(t=2\) 时,观测数据为‘Shop’。对于每一个状态 \(i, \;(i=1,2)\) 分别计算 \(\delta_1(i)\) :
\[\begin{gathered} \delta_2(1) = \max_{1 \le j \le 2} (\delta_{1}(j) a_{j \to Rainy}) b_{Rainy \to Shop} = \max_{1 \le j \le 2} (\delta_{1}(j) a_{j1}) b_{12} = \max\{0.06 \times 0.7, \, 0.24 \times 0.4 \} \times 0.4 = 0.0384 \\
\delta_2(2) = \max_{1 \le j \le 2} (\delta_{1}(j) a_{j \to Sunny}) b_{Sunny \to Shop} = \max_{1 \le j \le 2} (\delta_{1}(j) a_{j2}) b_{22} = \max\{0.06 \times 0.3, \, 0.24 \times 0.6 \} \times 0.3 = 0.0432 \end{gathered}\]
上式中, \(\delta_2(1)\) 为时刻 \(t=2\) 时,到达状态‘Rainy’的所有可能序列的概率中最大的概率,\(\delta_2(2)\) 为时刻 \(t=2\) 时,到达状态‘Sunny’的所有可能序列的概率中最大的概率。
上面两条概率最大路径,分别记录路径上的前一个状态:
\[\begin{gathered} \psi_2(1) = 2 \\
\psi_2(2) = 2 \end{gathered}\]
类似地,当 \(t=3\) 时,可求得:
\[\begin{gathered} \delta_3(1) = \max_{1 \le j \le 2} (\delta_{2}(j) a_{j \to Rainy}) b_{Rainy \to Clean} = \max\{0.0384 \times 0.7, 0.0432 \times 0.4 \} \times 0.5 = 0.01344 \\
\delta_3(2) = \max_{1 \le j \le 2} (\delta_{2}(j) a_{j \to Sunny}) b_{Sunny \to Clean} = \max\{0.0384 \times 0.3, 0.0432 \times 0.6 \} \times 0.1 = 0.002592 \end{gathered}\]
“到达某状态最可能路径”的前一个状态:
\[\begin{gathered} \psi_3(1) = 1 \\
\psi_3(2) = 2 \end{gathered}\]
(3) 结束,求最优路径的最后一个状态(下式中 \(T=3,N=2\) ):
\[i_T^{*} = {\operatorname{arg} \underset{1 \le j \le N}{\max}}(\delta_T(i)) = 1\]
即最后一个状态为‘Rainy’
(4) 回溯求最优路径。公式为 \(i_{t}^{*} = \psi_{t+1}(i_{t+1}^{*})\)
\[\begin{gathered} i_2^{*} = \psi_3(1) = 1 = Rainy \\
i_1^{*} = \psi_2(1) = 2 = Sunny \end{gathered}\]
所以,最后得到的最优路径为:‘Sunny’, ‘Rainy’, ‘Rainy’。求解过程如图 6 所示。
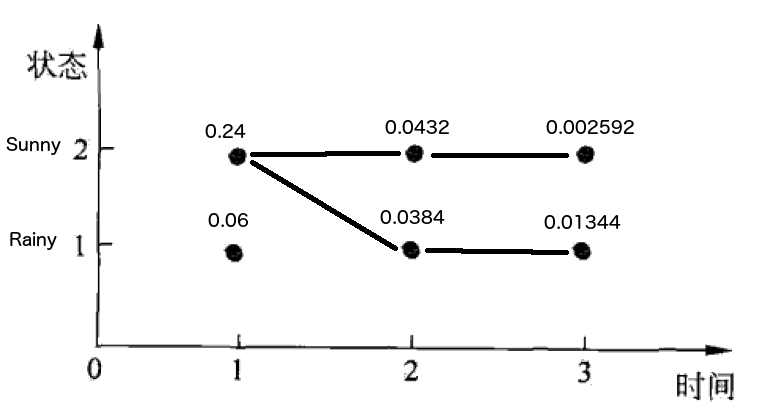
Figure 6: “最优路径”求解过程
说明 1:‘Walk’, ‘Shop’, ‘Clean’解码成了:‘Sunny’, ‘Rainy’, ‘Rainy’。但如果只进行了前两次观察‘Walk’, ‘Shop’,从上图容易知道(因为 0.0432 大于 0.0384),对应的最优路径为:‘Sunny’, ‘Sunny’(而不是‘Sunny’, ‘Rainy’)。
说明 2:上图中的路径记录着 \(\psi_t(i)\) 的值(“到达某状态最可能路径”的前一个状态),它用于算法结束时,回溯得到最优路径。当状态数和时间比较多时,可更形像地展示最后回溯得到最优路径的过程,如图 7 所示。
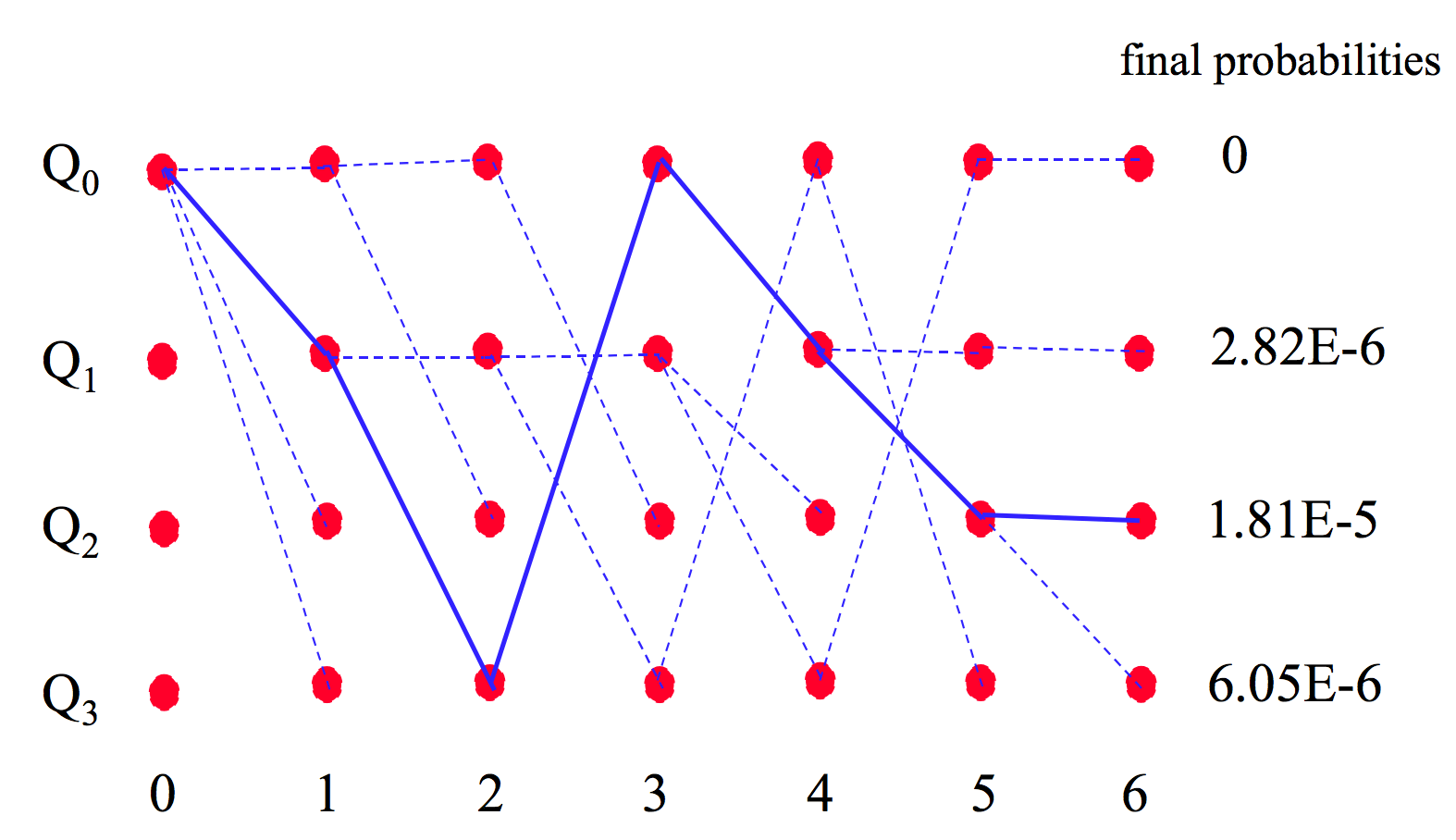
Figure 7: 回溯得到“最优路径”(摘自:http://ee163.caltech.edu/old/2005/handouts/viterbi.pdf)
2.3. Viterbi 算法实现
下面的代码摘自(可以从这个链接找到完整的测试程序):http://www.kanungo.com/software/software.html#umdhmm
/* Viterbi algorithm
* http://www.kanungo.com/software/software.html#umdhmm
*/
typedef struct {
int N; /* number of states; Q={1,2,...,N} */
int M; /* number of observation symbols; V={1,2,...,M}*/
double **A; /* A[1..N][1..N]. a[i][j] is the transition prob
of going from state i at time t to state j
at time t+1 */
double **B; /* B[1..N][1..M]. b[j][k] is the probability of
of observing symbol k in state j */
double *pi; /* pi[1..N] pi[i] is the initial state distribution. */
} HMM;
void Viterbi(HMM *phmm, int T, int *O, double **delta, int **psi,
int *q, double *pprob)
{
int i, j; /* state indices */
int t; /* time index */
int maxvalind;
double maxval, val;
/* 1. Initialization */
for (i = 1; i <= phmm->N; i++) {
delta[1][i] = phmm->pi[i] * (phmm->B[i][O[1]]);
psi[1][i] = 0;
}
/* 2. Recursion */
for (t = 2; t <= T; t++) {
for (j = 1; j <= phmm->N; j++) {
maxval = 0.0;
maxvalind = 1;
for (i = 1; i <= phmm->N; i++) {
val = delta[t-1][i]*(phmm->A[i][j]);
if (val > maxval) {
maxval = val;
maxvalind = i;
}
}
delta[t][j] = maxval*(phmm->B[j][O[t]]);
psi[t][j] = maxvalind;
}
}
/* 3. Termination */
*pprob = 0.0;
q[T] = 1;
for (i = 1; i <= phmm->N; i++) {
if (delta[T][i] > *pprob) {
*pprob = delta[T][i];
q[T] = i;
}
}
/* 4. Path (state sequence) backtracking */
for (t = T - 1; t >= 1; t--)
q[t] = psi[t+1][q[t+1]];
}
3. 概率计算算法
已知 HMM 模型 \(\lambda = (A, B, \boldsymbol{\pi})\) 和观测序列 \(O=(o_1, o_2, \cdots, o_T)\) ,如何计算在模型 \(\lambda\) 下观测序列 \(O\) 出现的概率 \(P(O| \lambda)\) 呢?
最直接的方法是按概率公式直接计算,通过列举所有可能的长度为 \(T\) 的状态序列 \(I=(i_1, i_2, \cdots, i_T)\) ,求各个状态序列 \(I\) 与观测序列 \(O=(o_1, o_2, \cdots, o_T)\) 的联合概率 \(P(O,I \mid \lambda)\) ,然后对所有可能的状态序列求和,得到 \(P(O \mid \lambda)\) 。但是这种直接计算的办法其计算量太大,不可行。
下面介绍 Forward–backward algorithm ,用“前向算法”或“后向算法”可以有效地计算观测序列的概率。
参考:
《统计学习方法,李航著》第 10 章 隐马尔可夫模型
3.1. 前向算法(动态规划算法)
和 Viterbi 算法类似,前向算法也是一种动态规划算法。
首先定义“前向概率”:HMM 模型 \(\lambda\) 中,到时刻 \(t\) 时,观测序列为 \(o_1, o_2, \cdots, o_t\) 且状态为 \(q_i\) 的概率就是 前向概率 ,记作:
\[\alpha_t(i) = P(o_1, o_2, \cdots, o_t, i_t = q_i \mid \lambda)\]
前向算法描述如下(如果理解了 Viterbi 算法,那么前向算法也比较好理解):
(1) 初值( \(N\) 为状态集的大小)
\[\alpha_1 (i) = \pi_i b_{i \to o_1}, \; i = 1,2, \cdots, N\]
(2) 递推,对于 \(t=2,3, \cdots, T\)
\[\alpha_{t+1}(i) = \left[\sum_{j=1}^{N}\alpha_t(j) a_{ji} \right] b_{i \to o_{t+1}}, \; i = 1,2, \cdots, N\]
上面递归式可以用图 8 解释:
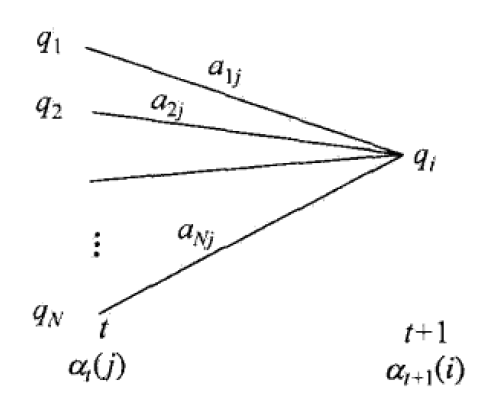
Figure 8: 前向算法中递归求解前向概率
(3) 终止
\[P(O \mid \lambda) = \sum_{i=1}^{N}\alpha_T(i)\]
参考:
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/forward_algorithm/s1_pg1.html
http://www.52nlp.cn/hmm-learn-best-practices-five-forward-algorithm-1
4. 学习算法
已知观测序列 \(O=(o_1, o_2, \cdots, o_T)\) ,估计模型参数 \(\lambda = (A, B, \boldsymbol{\pi})\) 。这就是学习算法的用途。
Baum–Welch algorithm 是著名的 HMM 学习算法。这里不做介绍。
参考:《统计学习方法,李航著》10.3 学习算法
