K-means
Table of Contents
1. K-means 简介
K-means 是一种简单的聚类算法,属于无监督学习算法(Unsupervised learning)。
给定样本集 \(D = \{\boldsymbol{x_1}, \boldsymbol{x_2}, \cdots, \boldsymbol{x_m} \}\) ,K-means 的目标是:把 \(m\) 个样本点划分到 \(k\) (由用户提供 \(k\) 值)个类簇中,使得簇划分 \(\mathcal{C} = \{C_1, C_2, \cdots, C_k \}\) 使下面的平方误差最小:
\[E = \sum_{i=1}^{k}\sum_{\boldsymbol{x} \in C_i} \Vert \boldsymbol{x} - \boldsymbol{\mu_i}\Vert^2\]
其中 \(\boldsymbol{\mu_i} = \frac{1}{\vert C_i \vert} \sum\limits_{\boldsymbol{x} \in C_i} \boldsymbol{x}\) 是簇 \(C_i\) 的均值向量。上式中,距离度量采用的是欧氏距离,不过,你也可以采用其它距离。从上式看, \(E\) 值越小意味着簇内样本的相似度越高。
不过,最小化 \(E\) 并不容易,找到它的最优解需要考察样本集 \(D\) 所有可能的簇划分,这是一个 NP 难问题。 K-means 算法采用了贪心策略,通过迭代优化来近似求解最小化 \(E\) 对应的簇划分。
1.1. K-means 算法与 K-NN 算法
K-means 算法与 K-NN(K 近邻)算法没太多关系,K-means 是一种聚类算法(无监督学习),而 K-NN 是一种分类算法(有监督学习)。
两种算法中“K”含义是不同的:
在 K-means 算法中“K”是含义是样本可以分为 K 个类簇;在 K-NN 算法中“K”的含义是给定一个待分类样本 \(\boldsymbol{x}\), 要给它分类,就从样本数据集中,在 \(\boldsymbol{x}\) 附近找离它最近的 K 个数据点,这 K 个数据点,类别 \(c\) 占的个数最多,就把 \(\boldsymbol{x}\) 分到 \(c\) 类中。
K-means 算法与 K-NN 算法的相同点:它们都包含计算样本点之间距离的过程,都可以采用多种距离计算公式。
2. K-means 算法描述
K-means 算法如图 1 所示。

Figure 1: K-means 算法
其中,第 1 行对均值向量进行初始化,在第 4-8 行与第 9-16 行依次对当前簇划分及均值向量迭代更新,若迭代更新后聚类结果保持不变,则将当前簇划分结果返回。
3. K-means 算法实例
下面以图 2 所示的西瓜相关数据集为例来演示 K-means 算法的学习过程。
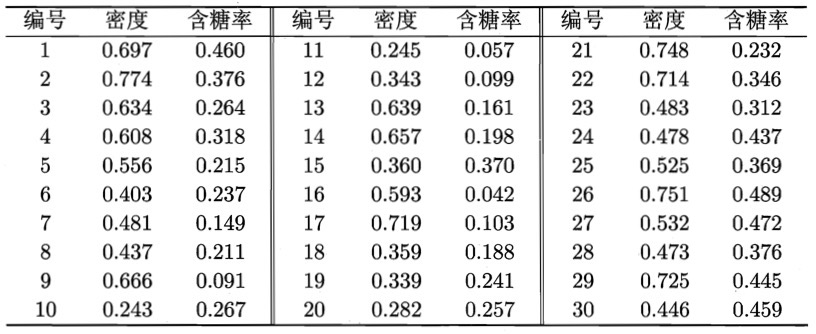
Figure 2: 西瓜数据集
为方便叙述,我们将编号为 \(i\) 的样本称为 \(\boldsymbol{x_i}\) ,这是一个包含“密度”与“含糖率”两个属性值的二维向量。
假定聚类簇数 \(k=3\) ,算法开始时随机选取三个样本 \(\boldsymbol{x_6}, \boldsymbol{x_{12}}, \boldsymbol{x_{27}}\) 作为初始均值向量,即:
\[\begin{aligned}
\boldsymbol{\mu_1} & = (0.403, 0.237) \\
\boldsymbol{\mu_2} & = (0.343, 0.099) \\
\boldsymbol{\mu_3} & = (0.532, 0.472) \\
\end{aligned}\]
考察样本 \(\boldsymbol{x_1}=(0.697, 0.460)\) ,它与当前均值向量 \(\boldsymbol{\mu_1}, \boldsymbol{\mu_2}, \boldsymbol{\mu_3}\) 的距离分别为 0.369,0.506,0.166,因此 \(\boldsymbol{x_1}\) 将被划入簇 \(C_3\) 中。类似地,对数据集中的所有样本考察一遍后,可得当前簇划分为:
\[\begin{aligned} C_1 &= \{ \boldsymbol{x_5}, \boldsymbol{x_6}, \boldsymbol{x_7}, \boldsymbol{x_8}, \boldsymbol{x_9}, \boldsymbol{x_{10}}, \boldsymbol{x_{13}}, \boldsymbol{x_{14}}, \boldsymbol{x_{15}}, \boldsymbol{x_{17}}, \boldsymbol{x_{18}}, \boldsymbol{x_{19}}, \boldsymbol{x_{20}}, \boldsymbol{x_{23}} \}\\
C_2 &= \{ \boldsymbol{x_{11}}, \boldsymbol{x_{12}}, \boldsymbol{x_{16}} \} \\
C_3 &= \{ \boldsymbol{x_1}, \boldsymbol{x_2}, \boldsymbol{x_3}, \boldsymbol{x_4}, \boldsymbol{x_{21}}, \boldsymbol{x_{22}}, \boldsymbol{x_{24}}, \boldsymbol{x_{25}}, \boldsymbol{x_{26}}, \boldsymbol{x_{27}}, \boldsymbol{x_{28}}, \boldsymbol{x_{29}}, \boldsymbol{x_{30}} \} \\
\end{aligned}\]
于是,可从 \(C_1,C_2,C_3\) 分别求出新的均值向量:
\[\begin{aligned}
\boldsymbol{\mu_1}' & = (0.473, 0.214) \\
\boldsymbol{\mu_2}' & = (0.394, 0.066) \\
\boldsymbol{\mu_3}' & = (0.623, 0.388) \\
\end{aligned}\]
更新当前均值向量后,不断重复上述过程,如图 3 所示,第五轮迭代产生的结果与第四轮迭代相同,于是算法停止,得到最终的簇划分。
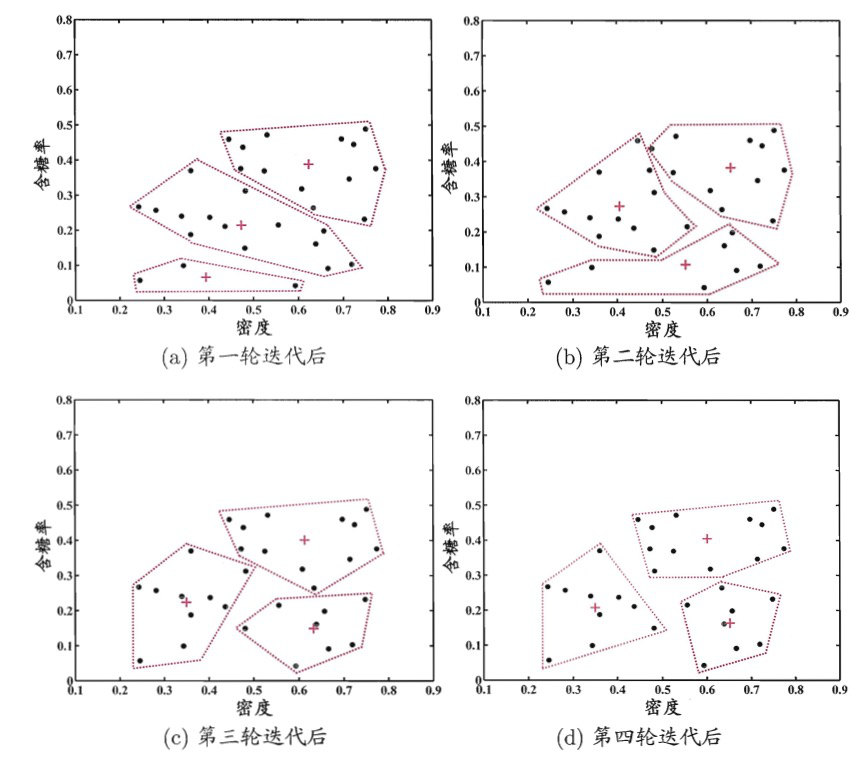
Figure 3: 西瓜数据集上 K-means 算法在各轮迭代后的结果。样本点和均值向量分别用“•”和“+”表示,红色虚线显示出簇划分
4. K-means 算法的不足
K-means 算法有下面的不足:
1、类簇个数 \(k\) 需要事先给定,但很多时候,事先不知道给定数据集分成多少个类别才合适。
2、需要人为地确定初始聚类中心(前面算法描述中是随机地选择初始聚类中心),不同的初始聚类中心可能导致完全不同的聚类结果。
关于第 2 点不足可以使用 K-means++ 算法来解决,这里不介绍 K-means++算法。
5. 参考
本文主要摘自:《机器学习,周志华,2016》,9.4.1 k均值算法