Kalman Filter
Table of Contents
1. 自动控制简介
自动控制是工程科学的一个分支,是指在没有人直接参与的情况下,利用外加的设备或装置,使机器、设备或生产过程的某个工作状态或参数自动地按照预定的规律运行。它 利用反馈原理的对动态系统的自动影响,以使得输出值接近我们想要的值 。
自动控制理论发展经历了经典控制理论,和现代控制理论。
经典控制理论中的 Wiener Filter 是一种频域方法,它要求存储全部历史数据,计算量和存储量很大,不便于实时应用。
现代控制理论中的 Kalman Filter 是一种时域方法,它具有递推形式,便于在计算机上实现,计算量和存储量相对较小。
2. Kalman 滤波器简介
卡尔曼滤波器(Kalman Filter)以其发明人 Rudolf E. Kálmán 命名。Kálmán 引入了状态变量,提出了控制系统的状态空间模型(State-space model)。
参考:
http://www.cs.unc.edu/~welch/kalman/
https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2
2.1. 状态空间模型
参考:
Modern Control Systems, 12th, by Richard C. Dorf, Robert H. Bishop, Chapter 3 State Variable Models
https://en.wikipedia.org/wiki/State-space_representation
2.1.1. 状态变量
所谓状态变量就是可以完全确定和表示系统未来行为的变量。 系统的状态变量刻画了系统的动态行为特性。
通常,状态变量是电压、电流、速度、位置、压力、温度以及其他类似的物理量。
2.1.2. 状态方程
系统状态及其变化规律可由状态变量 \((x_1, x_2, \cdots, x_n)\) 的一阶微分方程组描述,称为状态微分方程(简称状态方程)。设系统的控制信号为 \(\boldsymbol{u} = (u_1, u_2, \cdots, u_m)\) (系统的控制信号是已知的,如 steering angle, throttle setting, braking force 等等),则微分方程组可写为:
\[\begin{cases}
\dot{x_1} = a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n + b_{11}u_1 + \cdots + b_{1m}u_m \\
\dot{x_2} = a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n + b_{21}u_1 + \cdots + b_{2m}u_m \\
\vdots \\
\dot{x_n} = a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n + b_{n1}u_1 + \cdots + b_{nm}u_m \\
\end{cases}\]
其中, \(\dot{x_i}= \frac{dx_i}{dt}\) 。上面方程组可写为如下向量方程形式:
\[\dot{\boldsymbol{x}} = \mathbf{A}\boldsymbol{x} + \mathbf{B}\boldsymbol{u}\]
上式就是系统的状态方程。
2.2. Kalman 滤波器适应的基本动态系统模型
Kalman Filter 假设 \(k\) 时刻系统的真实状态从 \(k-1\) 时刻演化而来,满足下面离散随机差分方程:
\[\boldsymbol{x_k} = \mathbf{F_k}\boldsymbol{x_{k-1}} + \mathbf{B_k}\boldsymbol{u_{k}} + \boldsymbol{w_{k}}\]
系统的测量方程为:
\[\boldsymbol{z_k} = \mathbf{H_k}\boldsymbol{x_{k}} + \boldsymbol{v_k}\]
说明 1:系统离散随机差分方程中, \(\boldsymbol{x_k}\) 是 \(k\) 时刻系统的状态(如速度等), \(\boldsymbol{u_{k}}\) 是 \(k\) 时刻对系统的控制量(如方向盘转角等)。 \(\mathbf{F_k}\) 和 \(\mathbf{B_k}\) 是系统参数, \(\mathbf{F_k}\) 称为状态转移矩阵, \(\mathbf{B_k}\) 称为输入输出矩阵。 \(\boldsymbol{w_{k}}\) 是过程噪声,假设其服从正态分布 \(p(\boldsymbol{w_k}) \sim N(0, \mathbf{Q})\) 。
说明 2:系统测量方程中, \(\boldsymbol{z_k}\) 是 \(k\) 时刻系统状态的测量值(用传感器等直接或间接测量系统的状态), \(\mathbf{H_k}\) 称为测量矩阵(如果系统的所有状态都可以直接测量得到,则测量矩阵就是单位矩阵)。 \(\boldsymbol{v_{k}}\) 是测试噪声,假设其服从正态分布 \(p(\boldsymbol{v_k}) \sim N(0, \mathbf{R})\) 。
卡尔曼滤波建立在隐马尔可夫模型(hidden Markov model)上。其基本动态系统可以用一个马尔可夫链表示,该马尔可夫链建立在一个被高斯噪声(即正态分布的噪声)干扰的线性算子上的。
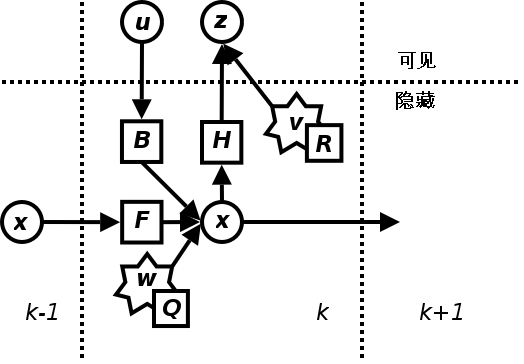
Figure 1: 卡尔曼滤波器的模型
说明 1:上图中圆圈代表向量,方块代表矩阵,星号代表高斯噪声,其协方差矩阵在右下方标出。图片摘自https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2
说明 2:实际上,很多真实世界的动态系统都并不确切地符合这个模型;但是由于卡尔曼滤波器被设计在有噪声的情况下工作,一个近似的符合已经可以使这个滤波器非常有用了。
2.3. Kalman 滤波器应用
Kalman 滤波器的应用非常广泛,比如雷达系统,机器人导航等等。近年来也应用于计算机图像处理领域,例如人脸识别,图像分割,图像边缘检测等等。
参考:
https://en.wikipedia.org/wiki/Kalman_filter#Applications
3. Kalman 滤波器算法
卡尔曼滤波是一种递推的估计,即只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值,因此不需要记录观测或者估计的历史信息。卡尔曼滤波器与大多数滤波器不同之处,在于它是一种纯粹的时域滤波器,它不需要像低通滤波器等频域滤波器那样,需要在频域设计再转换到时域实现。
卡尔曼滤波的原理多少有些复杂,但它的核心内容仅是 5 个公式。尽管公式的推导比较麻烦,但结合现代的计算机,实现卡尔曼滤波器并不难。
参考:
Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation: https://www.cl.cam.ac.uk/~rmf25/papers/Understanding%20the%20Basis%20of%20the%20Kalman%20Filter.pdf
An Introduction to the Kalman Filter: http://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf
An Introduction to the Kalman Filter (chinese): http://www.cs.unc.edu/~welch/kalman/media/pdf/kalman_intro_chinese.pdf
3.1. 2 个阶段,5个公式
卡尔曼滤波包括两个阶段:预测和更新(即校正);在估计阶段,滤波器应用上一状态的估计做出对当前状态的估计。在更新阶段,滤波器利用在当前状态的观测值优化预测阶段的预测值,以获的一个更精确的当前状态的估计。
离散卡尔曼滤波器算法 5 个公式如下(仅结出结论,不推导):
\[\begin{array}{cc}
\text{离散卡尔曼滤波器时间更新方程(预测阶段的 2 个公式)} & \text{离散卡尔曼滤波器状态更新方程(校正阶段的 3 个公式)} \\
\hline \\
\boldsymbol{\hat{x}_{k}^{-}} = \mathbf{F} \boldsymbol{\hat{x}_{k-1}} + \mathbf{B} \boldsymbol{\hat{u}_{k-1}} & \mathbf{K}_{k} = \mathbf{P}^{-}_{k} \mathbf{H}^{\mathsf{T}} (\mathbf{H} \mathbf{P}^{-}_{k} \mathbf{H}^{\mathsf{T}} + \mathbf{R})^{-1} \\
\mathbf{P}^{-}_{k} = \mathbf{F} \mathbf{P}_{k-1} \mathbf{F}^{\mathsf{T}} + \mathbf{Q} & \boldsymbol{\hat{x}_{k}} = \boldsymbol{\hat{x}_{k}^{-}} + \mathbf{K}_{k} (\boldsymbol{z_k} - \mathbf{H} \boldsymbol{\hat{x}_{k}^{-}}) \\
& \mathbf{P}_{k} = (\mathbf{I} - \mathbf{K}_{k} \mathbf{H}) \mathbf{P}^{-}_{k} \\
\end{array}\]
说明 1:上面式子中符号 \({}^-\) 表示“先验”, \(\hat{}\) 表示“估计”。
说明 2: \(\mathbf{F}, \mathbf{B}, \mathbf{Q}, \mathbf{H}, \mathbf{R}\) 为系统的参数,系统模型建立好后是已知的。
说明 3: \(\mathbf{K}\) 称为卡尔曼增益(Kalman Gain)。 \(\mathbf{P}\) 是误差协方差。编程实现时可以认为是“中间变量”。
说明 4: \(\boldsymbol{\hat{x}_{k}} = \boldsymbol{\hat{x}_{k}^{-}} + \mathbf{K}_{k} (\boldsymbol{z_k} - \mathbf{H} \boldsymbol{\hat{x}_{k}^{-}})\) 中 \(\boldsymbol{\hat{x}_{k}}\) 是想要得到的估计值, \(\boldsymbol{\hat{x}_{k}^{-}}\) 是通过系统状态方程得到的理论预测值, \(\boldsymbol{z_k}\) 是系统的测量值。
说明 5:尽管没有介绍这些公式的推导,由这 5 个公式,我们可以直接编程实现卡尔曼滤波器了。
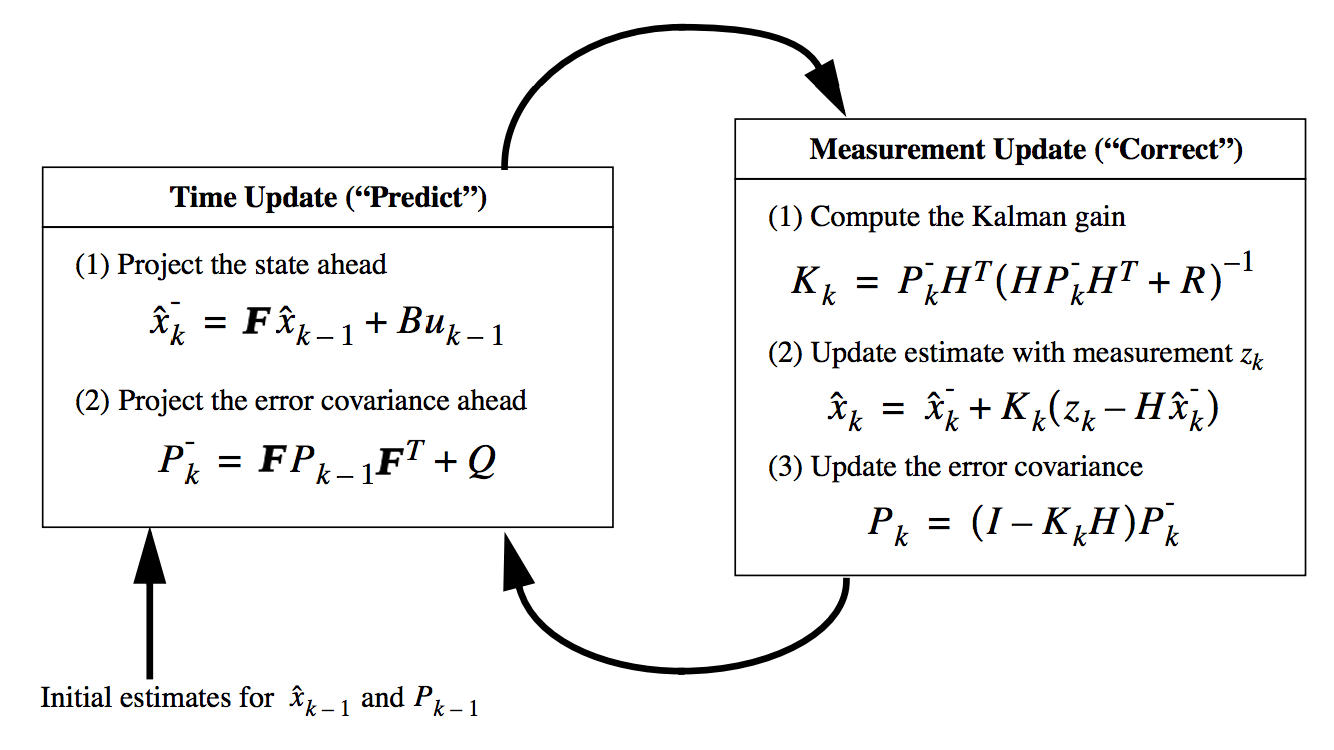
Figure 2: 卡尔曼滤波器的完整计算过程
4. Kalman 滤波器实例
有一辆质量为 \(m\) 的小车,受力 \(f_t\) ,沿着 \(r\) 方向做匀加速直线运动。已知小车在 \(t - \Delta t\) 时刻的位移是 \(s(t-1)\) ,此时的速度为 \(v(t-1)\) ,如何估计在 \(t\) 时刻的位移 \(s(t)\) 和速度 \(v(t)\) 呢?
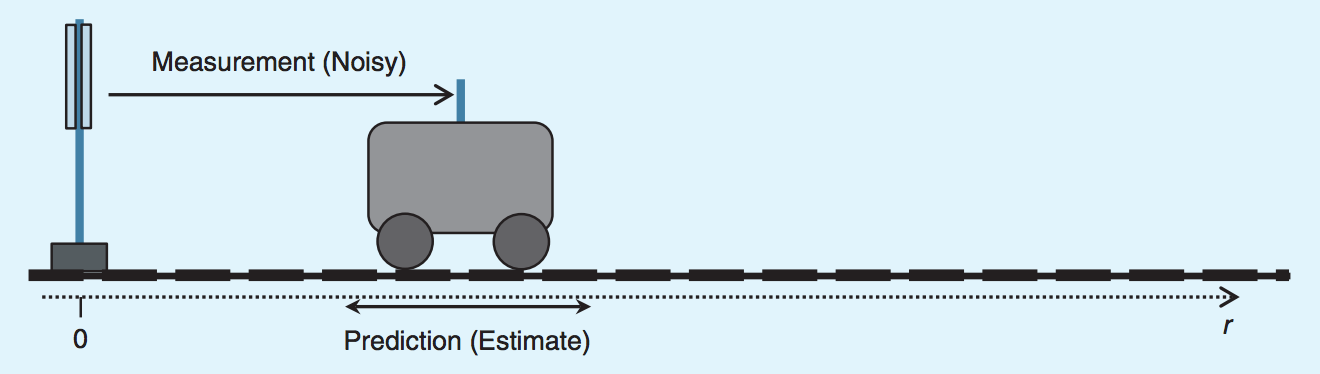
Figure 3: 小车沿 r 方向作加速运动
4.1. 建立状态空间模型
由牛顿第二定律,我们知道其加速度为 \(\frac{f_t}{m}\) ,这可以看作是系统的控制信号,即有: \(u_t = \frac{f_t}{m}\)
由力学知识有:
\[\begin{gathered} s(t) = s(t-1) + v(t-1) \Delta t + \frac{1}{2} \frac{f_t}{m} (\Delta t)^2 \\
v(t) = v(t-1) + \frac{f_t}{m} \Delta t \end{gathered}\]
如果我们把位置和速度看作是系统的“状态变量”,上面两式又可写为:
\[\left( \begin{array}{c} s_t \\ v_t \end{array} \right) = \left( \begin{array}{cc} 1 & \Delta t \\ 0 & 1 \end{array} \right) \left( \begin{array}{c} s_{t-1} \\ v_{t-1} \end{array} \right) + \left( \begin{array}{c} \frac{(\Delta t)^2}{2} \\ \Delta t \end{array} \right)^2 \frac{f_t}{m}\]
上式就是系统的状态方程。显然,系统的参数 \(\mathbf{F_t}, \mathbf{B_t}\) 分别为:
\[\mathbf{F_t} = \left( \begin{array}{cc} 1 & \Delta t \\ 0 & 1 \end{array} \right), \mathbf{B_t} = \left( \begin{array}{c} \frac{(\Delta t)^2}{2} \\ \Delta t \end{array} \right)^2\]
4.2. 用 Kalman Filter 进行估计
系统状态方程为:
\[\boldsymbol{x_k} = \mathbf{F_k}\boldsymbol{x_{k-1}} + \mathbf{B_k}\boldsymbol{u_{k}} + \boldsymbol{w_{k}}\]
系统的测量方程为:
\[\boldsymbol{z_k} = \mathbf{H_k}\boldsymbol{x_{k}} + \boldsymbol{v_k}\]
由系统的状态方程可以得到一个理论预测值(前面例子用牛顿第二定律得到),而通过实际测量(如速度传感器等)可以得到一个测量值。这两个值都存在噪声(误差)。
怎么通过这两个值来估计实际值呢?Kalman 滤波器就是来完成这个工作的。
Kalman 滤波器算法的第 4 个公式告诉我们可以这样得到一个比较好的估计值: \(\boldsymbol{\hat{x}_{k}} = \boldsymbol{\hat{x}_{k}^{-}} + \mathbf{K}_{k} (\boldsymbol{z_k} - \mathbf{H} \boldsymbol{\hat{x}_{k}^{-}})\) 中 \(\boldsymbol{\hat{x}_{k}}\) 是想要得到的估计值, \(\boldsymbol{\hat{x}_{k}^{-}}\) 是通过系统状态方程得到的理论预测值, \(\boldsymbol{z_k}\) 是系统的测量值。
式子 \(\boldsymbol{\hat{x}_{k}} = \boldsymbol{\hat{x}_{k}^{-}} + \mathbf{K}_{k} (\boldsymbol{z_k} - \mathbf{H} \boldsymbol{\hat{x}_{k}^{-}})\) 可直观地理解为 卡尔曼增益 \(\mathbf{K}_{k}\) 决定了理论预测值和实际测量值在估计值中的比重 。
如果状态变量能直接通过传感器测量,则测量矩阵就是单位矩阵,即 \(\mathbf{H} = \mathbf{I}\) 。
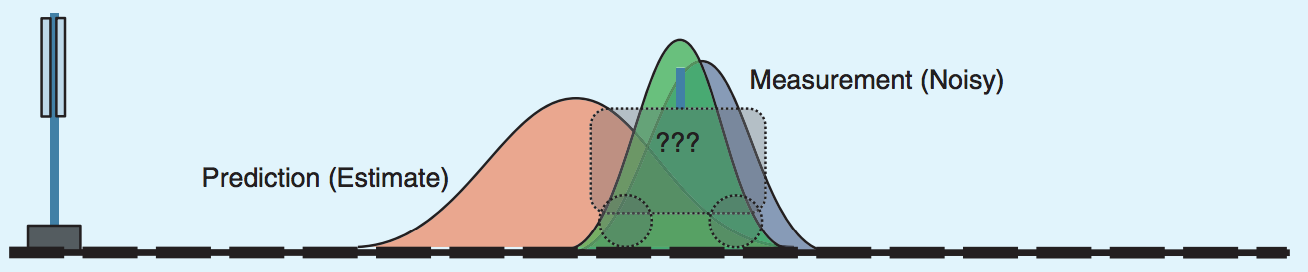
Figure 4: 如何利用“理论预测值”和“测量值”得到“估计值”
参考:
https://www.cl.cam.ac.uk/~rmf25/papers/Understanding%20the%20Basis%20of%20the%20Kalman%20Filter.pdf
4.3. 为什么使用“Filter”这个词
在前面介绍的例子中,Kalman Filter 的作用是“去除测量数据中的噪声”,这在随机过程理论中称为滤波问题(Filtering problem)。
参考:https://en.wikipedia.org/wiki/Filtering_problem_(stochastic_processes)
4.4. 再看“卡尔曼增益(Kalman Gain)”
Kalman Filter 算法中,卡尔曼增益决定了系统状态变量“测量值”在系统状态变量“估计值”中的所占比重。
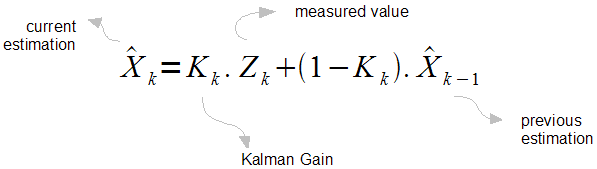
Figure 5: 卡尔曼增益决定了“测量值”在“估计值”中的所占比重
说明:上面式子对原始公式作了很多简化,它假设测量矩阵为单位矩阵,假设先验值 \(\boldsymbol{\hat{x}_{k}^{-}}\) 等于上一次的估计值 \(\boldsymbol{\hat{x}_{k-1}}\) 。
参考:Kalman Filter For Dummies: http://bilgin.esme.org/BitsAndBytes/KalmanFilterforDummies
5. Kalman 滤波器算法演示实例
考虑的一个元件的电压测试例子:假设电压是恒定不变的,电压测量仪的测量噪声 \(R=0.1 V\) ,下面是测量 10 次的结果:
| TIMS (ms) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| VALUE (V) | 0.39 | 0.50 | 0.48 | 0.29 | 0.25 | 0.32 | 0.34 | 0.48 | 0.41 | 0.45 |
下面将演示用 Kalman 滤波器算法对电压进行估计。
参考:Kalman Filter For Dummies: http://bilgin.esme.org/BitsAndBytes/KalmanFilterforDummies
5.1. 建立状态空间模型
系统的状态变量只有一个(即电压),所以状态空间模型中的各个矩阵都简化成了单个数。由于假设电压是不变的,所以 \(\mathbf{F}=1\) ;又由于系统没有控制量,所以 \(\boldsymbol{u_{k}}=0\) 。系统状态变量电压是直接测量得到的,所以 \(\mathbf{H}=1\) 。
系统的状态方程为:
\[\boldsymbol{x_k} = \mathbf{F_k}\boldsymbol{x_{k-1}} + \mathbf{B_k}\boldsymbol{u_{k}} + \boldsymbol{w_{k}} = \boldsymbol{x_{k-1}} + \boldsymbol{w_{k}}\]
系统的测量方程为:
\[\boldsymbol{z_k} = \mathbf{H_k}\boldsymbol{x_{k}} + \boldsymbol{v_k} = \boldsymbol{x_{k}} + \boldsymbol{v_k}\]
由于假设电压恒定不变,可假设 \(Q=0\) ;题中已知测量噪声 \(R=0.1 V\) 。
5.2. 应用 Kalman 滤波器算法
利用前面的状态空间模型,代入系统的参数,Kalman 滤波器算法的 5 个公式如下:
\[\begin{array}{cc}
\text{Time Update (prediction)} & \text{Measurement Update (correction)} \\
\hline \\
\hat{x}_{k}^{-} = \hat{x}_{k-1} & K_k = \frac{P^{-}_{k}}{P^{-}_{k} + 0.1} \\
P_{k}^{-} = P_{k-1} & \hat{x}_{k} = \hat{x}_{k}^{-} + K_k (z_k - \hat{x}_{k}^{-}) \\
& P_{k} = (1 - K_k) P^{-}_{k} \\
\end{array}\]
5.3. 演示 Kalman 滤波器算法的迭代过程(很易编程实现)
开始迭代前,需要给 \(x\) 和 \(p\) 设定一个初值,这里假设它们的初值分别为 0 和 1。
下面将演示电压估计 \(\hat{x}_k\) 的迭代求解过程。
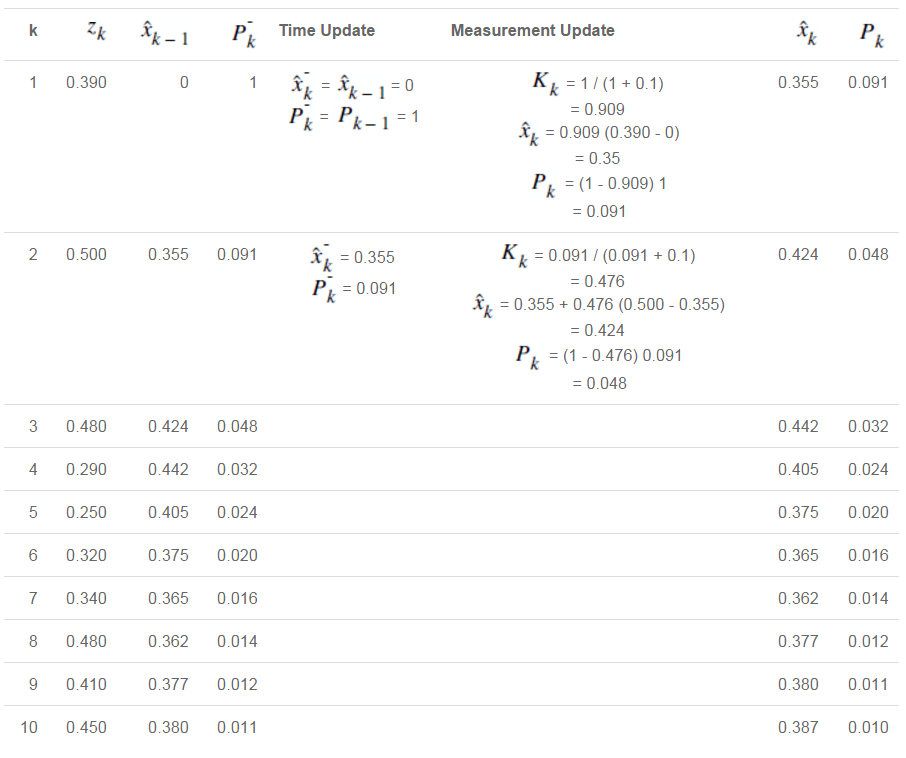
Figure 6: Kalman 滤波器算法迭代过程
通过上面迭代求得的电压估计 \(\hat{x}_k\) 如下图所示:
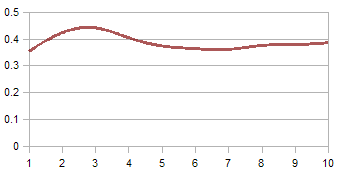
Figure 7: Kalman 滤波器算法对电压的估计
6. Extended Kalman Filter(EKF)
卡尔曼滤波器估计一个用线性随机差分方程描述的离散时间过程的状态变量。
Extended Kalman Filter 考虑的场景是被估计的过程和(或)观测变量与过程的关系是 非线性的 。也就是系统的状态空间模型为:
\[\begin{gathered} \boldsymbol{x_k} = f(\boldsymbol{x_{k-1}} , \boldsymbol{u_{k}} ) + \boldsymbol{w_{k}} \\
\boldsymbol{z_k} = h(\boldsymbol{x_{k}}) + \boldsymbol{v_k} \end{gathered}\]
这里不详细介绍 EKF,更多资料可参考:https://en.wikipedia.org/wiki/Extended_Kalman_filter