Kernel Method
Table of Contents
1. Kernel Method 简介
Kernel Method 常应用于支持向量机中。Kernel Method 是一种通用的方法,它还可以用在感知器(Kernel Perceptron),主成分分析(Kernel PCA)等其他算法中。
本文主要讨论 Kernel Method 在感知器中的应用(在支持向量机中的应用也差不多,为简单起见本文不讨论支持向量机)。
参考:
Kernel Methods for Pattern Analysis (中文版名为《模式分析的核方法》)
Kernel Methods in Computer Vision by Christoph H. Lampert: http://pub.ist.ac.at/~chl/papers/lampert-fnt2009.pdf
Pattern Recognition And Machine Learning, Chapter 6 Kernel Methods
An Introduction to Support Vector Machines and Other Kernel-based Learning Methods
2. 从“让感知器支持线性不可分数据”说起
我们知道,对于感知器,仅当训练数据线性可分时才适合。如何让感知器能对线性不可分数据进行分类呢?
图 1 是线性不可分数据的简单例子。
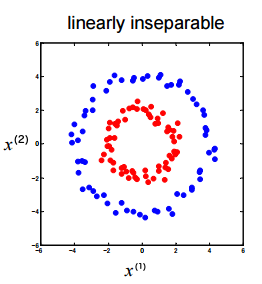
Figure 1: 线性不可分训练数据集
如何把红色和蓝色的点分开呢?请看下文分解。
2.1. 用“特征映射”处理线性不可分数据
处理前面线性不可分数据一种可行的办法是:把每个训练数据的特征 \(x^{(1)}, x^{(2)}\) 分别变为新的特征 \(y^{(1)} = {x^{(1)}}^2, y^{(2)} = {x^{(2)}}^2\) ,即做下面的特征映射(坐标变换):
\[\left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \left( \begin{array}{c} {x^{(1)}}^2 \\ {x^{(2)}}^2 \end{array} \right)\]
在新的特征空间里,训练数据是线性可分的,如图 2 所示。
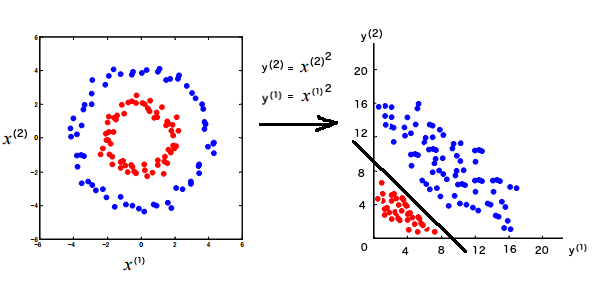
Figure 2: 把线性不可分训练数据集“映射”到线性可分的特征空间
假设在新特征空间里我们求得感知器为: \(f = sign ( y^{(1)} + y^{(2)} - 9 )\) ,则可以得到原始空间中的感知器为: \(f = sign \left( {x^{(1)}}^2 + {x^{(2)}}^2- 9 \right)\) ,这样达到了感知器处理线性不可分数据的目的。
说明 1:由于训练数据集的特征比较少,可以直观地画出来,从而帮助我们很快地找到一个方法映射到线性可分的空间。当特征比较多,无法直接展示训练数据的规律时,我们可能需要做各种尝试才能找到一个合适的特征映射方法。
说明 2:在上面例子中,把直角坐标转换为极坐标,也可以得到一个线性可分的特征空间。如图 3 所示。
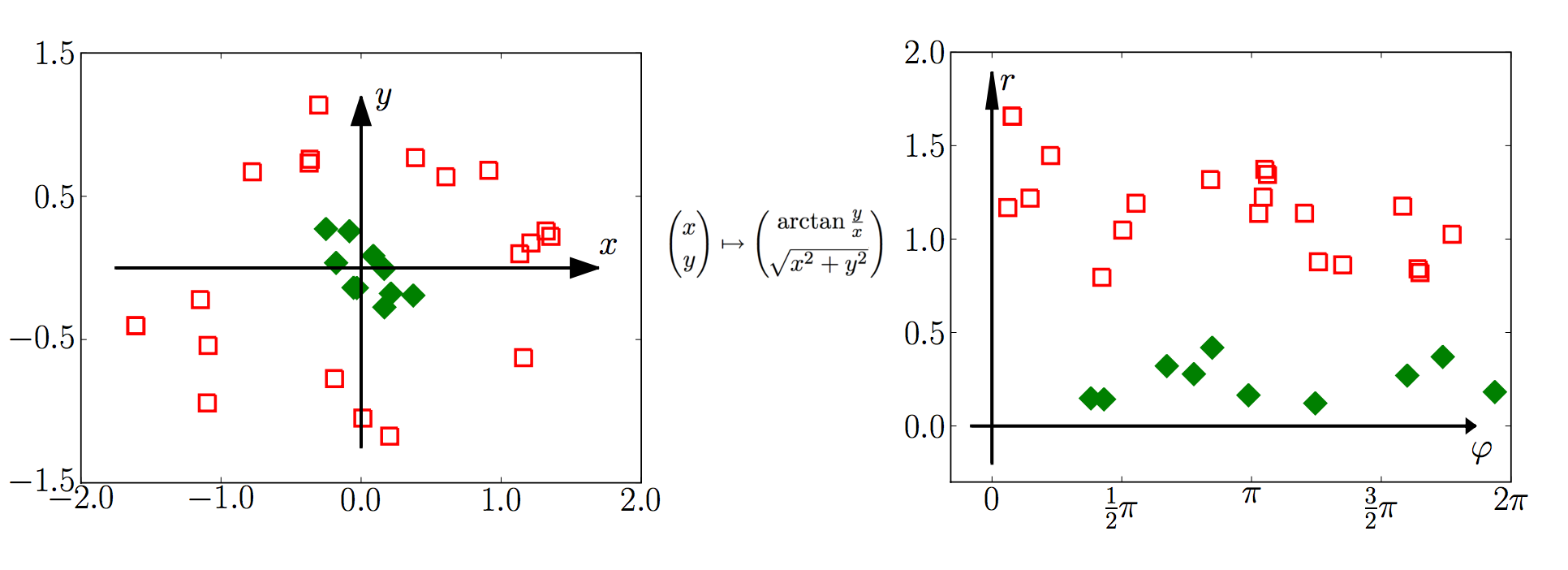
Figure 3: “映射”到线性可分的特征空间(图片来源http://pub.ist.ac.at/~chl/papers/lampert-fnt2009.pdf)
2.2. 考虑一个“特别的”特征映射
现在考虑下面的特征映射:
\[\boldsymbol{x} = \left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \phi(\boldsymbol{x}) = \left( \begin{array}{c} {x^{(1)}}^2 \\ {x^{(2)}}^2 \\ \sqrt{2}x^{(1)} x^{(2)} \end{array} \right) = \left( \begin{array}{c} z^{(1)} \\ z^{(2)} \\ z^{(3)} \end{array} \right)\]
新的特征空间是一个三维空间,如图 4 所示。其中为什么 \(x^{(1)} x^{(2)}\) 前面有一个系数 \(\sqrt{2}\) 呢?看起来有些“特别”,后面将解释这样做的原因。不过,增加一个系数(仅仅相当于伸缩坐标轴 \(z^{(3)}\) )并不会改变数据的线性可分性。
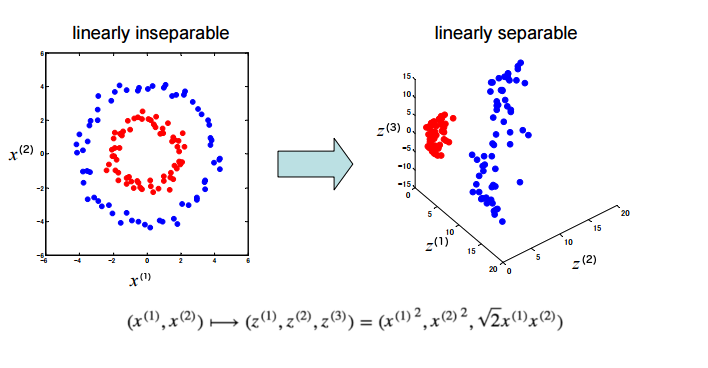
Figure 4: “映射”到线性可分的特征空间(图片来源:http://www.ism.ac.jp/~fukumizu/Kyushu2008/Kernel_intro_1.pdf)
在新的特征空间,数据是线性可分的,我们当然可以利用“感知器算法的原始形式”求得新空间中的感知器模型。但这里介绍的重点是“感知器算法的对偶形式”,我们会发现在这个“特别的”特征空间中应用“感知器算法的对偶形式”可以简化计算!详情请看下文分解。
2.2.1. “感知器算法的对偶形式”可以简化运算
感知器算法的对偶形式中(参见附录),训练数据过程中,当 \(y_i(\sum_{j=1}^{N} \alpha_j y_j \langle \boldsymbol{x_j}, \boldsymbol{x_i} \rangle + b) \le 0\) 时(即它是一个错误分类点),迭代更新参数。可以发现训练数据仅以“内积”的形式(即 \(\langle \boldsymbol{x_j}, \boldsymbol{x_i} \rangle\) )出现。
假设原空间(又称输入空间)的两个训练数据为 \(\boldsymbol{u}, \boldsymbol{v}\) ,映射到新的特征空间后变为: \(\phi(\boldsymbol{u}), \phi(\boldsymbol{v})\) 。
我们在新特征空间里应用感知器算法的对偶形式。有:
\[\begin{aligned} \langle \phi(\boldsymbol{u}), \phi(\boldsymbol{v}) \rangle & = \left \langle \left ({u^{(1)}}^2, {u^{(2)}}^2, \sqrt{2} u^{(1)} u^{(2)} \right)^{\mathsf{T}}, \left ({v^{(1)}}^2, {v^{(2)}}^2, \sqrt{2}v^{(1)} v^{(2)} \right)^{\mathsf{T}} \right \rangle \\
& = {u^{(1)}}^2 {v^{(1)}}^2 + {u^{(2)}}^2 {v^{(2)}}^2 + 2 u^{(1)} u^{(2)} v^{(1)} v^{(2)} \\
& = \left(u^{(1)} v^{(1)} + u^{(2)} v^{(2)} \right)^2 \\
& = \left \langle \boldsymbol{u}, \boldsymbol{v} \right \rangle^2 \\
\end{aligned}\]
上式意味着:我们在新特征空间里训练感知器,测试 \(y_i(\sum_{j=1}^{N} \alpha_j y_j \langle \phi(\boldsymbol{x_j}), \phi(\boldsymbol{x_i}) \rangle + b) \le 0\) 时,直接测试 \(y_i(\sum_{j=1}^{N} \alpha_j y_j \langle \boldsymbol{x_j}, \boldsymbol{x_i} \rangle^2 + b) \le 0\) 即可, 根本不用真正计算训练数据在新特征空间里对应的值,也不用在新特征空间中进行内积计算!直接利用原输入空间的数据间内积(Gram 矩阵,一般可提前准备好)即可,减少了很多计算量。
说明:做特征映射时,如果 \(x^{(1)} x^{(2)}\) 前面没有系数 \(\sqrt{2}\) ,即采用这样的映射 \(\left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \left( \begin{array}{c} {x^{(1)}}^2 \\ {x^{(2)}}^2 \\ x^{(1)} x^{(2)} \end{array} \right)\) ,则我们无法把 \(\langle \phi(\boldsymbol{u}), \phi(\boldsymbol{v}) \rangle\) 化简为 \(\left \langle \boldsymbol{u}, \boldsymbol{v} \right \rangle^2\) ,如果采用感知器算法的对偶形式,则迭代更新参数时,只能老老实实地先计算训练数据在新特征空间里对应的值,再计算它们内积。
3. 核函数(Kernel Function)
前面已经介绍了很多简单的背景知识,现在可以介绍核函数(Kernel Function)了。
设 \(\mathcal{X}\) 是输入空间(欧氏空间的子集 \(\mathbb{R}^n\) 或离散集合),又设 \(\mathcal{H}\) 为特征空间(希尔伯特空间),如果存在一个从 \(\mathcal{X}\) 到 \(\mathcal{H}\) 映射:
\[\phi(\boldsymbol{x}) : \mathcal{X} \mapsto \mathcal{H}\]
使得对所有 \(\boldsymbol{u},\boldsymbol{v} \in \mathcal{X}\) ,函数 \(K(\boldsymbol{u},\boldsymbol{v})\) 满足条件:
\[K(\boldsymbol{u},\boldsymbol{v}) = \langle \phi(\boldsymbol{u}), \phi(\boldsymbol{v}) \rangle\]
则称 \(K(\boldsymbol{u},\boldsymbol{v})\) 为 核函数 ,称 \(\phi(\boldsymbol{x})\) 为映射函数。
用一句话概括核函数就是:A function that takes as its inputs vectors in the original space and returns the dot product of the vectors in the feature space is called a kernel function.
前面介绍过的映射函数和核函数如表 1 所示。
| 映射函数 \(\phi(\boldsymbol{x})\) | 对应的核函数 \(K(\boldsymbol{u},\boldsymbol{v}) = \langle \phi(\boldsymbol{u}), \phi(\boldsymbol{v}) \rangle\) | 说明 |
|---|---|---|
| \(\left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \left( \begin{array}{c} {x^{(1)}}^2 \\ {x^{(2)}}^2 \end{array} \right)\) | \(K(\boldsymbol{u},\boldsymbol{v}) = {u^{(1)}}^2 {v^{(1)}}^2 + {u^{(2)}}^2 {v^{(2)}}^2\) | |
| \(\left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \left( \begin{array}{c} {x^{(1)}}^2 \\ {x^{(2)}}^2 \\ \sqrt{2}x^{(1)} x^{(2)} \end{array} \right)\) | \(K(\boldsymbol{u},\boldsymbol{v}) = \left \langle \boldsymbol{u}, \boldsymbol{v} \right \rangle^2\) | 后文将说明这个核函数还可能对应其它的映射函数 |
| \(\left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \left( \begin{array}{c} {x^{(1)}}^2 \\ {x^{(2)}}^2 \\ x^{(1)} x^{(2)} \end{array} \right)\) | \(K(\boldsymbol{u},\boldsymbol{v}) = {u^{(1)}}^2 {v^{(1)}}^2 + {u^{(2)}}^2 {v^{(2)}}^2 + u^{(1)} u^{(2)} v^{(1)} v^{(2)}\) | 映射关系和上一个类似,但核函数计算速度没上一个快 |
3.1. 核函数可能对应多种映射关系
前面提到过,核函数 \(K(\boldsymbol{u},\boldsymbol{v}) = \left \langle \boldsymbol{u}, \boldsymbol{v} \right \rangle^2\) 对应的映射关系为:
\[\boldsymbol{x} = \left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \phi(\boldsymbol{x}) = \left( \begin{array}{c} {x^{(1)}}^2 \\ {x^{(2)}}^2 \\ \sqrt{2}x^{(1)} x^{(2)} \end{array} \right)\]
但如果按下面方式映射到另外一个三维空间:
\[\boldsymbol{x} = \left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \phi(\boldsymbol{x}) = \left( \begin{array}{c} \frac{1}{\sqrt{2}} ( {x^{(1)}}^2 - {x^{(2)}}^2 ) \\ \frac{2}{\sqrt{2}} x^{(1)} x^{(2)} \\ \frac{1}{\sqrt{2}} ( {x^{(1)}}^2 + {x^{(2)}}^2 ) \end{array} \right)\]
我们容易验证: \(K(\boldsymbol{u},\boldsymbol{v}) = \langle \phi(\boldsymbol{u}), \phi(\boldsymbol{v}) \rangle = \left \langle \boldsymbol{u}, \boldsymbol{v} \right \rangle^2\) 同样成立。
又如,按下面方式映射到一个四维空间:
\[\boldsymbol{x} = \left( \begin{array}{c} x^{(1)} \\ x^{(2)} \end{array} \right) \mapsto \phi(\boldsymbol{x}) = \left( \begin{array}{c} {x^{(1)}}^2 \\ x^{(1)} x^{(2)} \\ x^{(1)} x^{(2)} \\ {x^{(2)}}^2 \end{array} \right)\]
同样,我们容易验证: \(K(\boldsymbol{u},\boldsymbol{v}) = \langle \phi(\boldsymbol{u}), \phi(\boldsymbol{v}) \rangle = \left \langle \boldsymbol{u}, \boldsymbol{v} \right \rangle^2\) 也成立。
这说明: 确定核函数后,并不能唯一确定映射关系。
3.2. 核技巧(Kernel trick)
核技巧(Kernel trick)的意思是:在学习与预测时只定义核函数 \(K(\boldsymbol{u},\boldsymbol{v})\) ,而不显式地定义特征映射函数 \(\phi\) 和新特征空间。
如果不显式地定义映射函数,那么怎么知道某个函数是核函数呢?可以不关心这个问题,因为在实际应用时,我们一般选择一些已知的核函数。
3.3. 核函数的充要条件
设 \(K: \mathcal{X} \times \mathcal{X} \to \mathbb{R}\) 是对称函数,则 \(K\) 为(正定)核函数的充要条件是对任意 \(\boldsymbol{x_i}, \boldsymbol{x_j} \in \mathcal{X}, i,j=1,2,\cdots,m\) , \(K\) 对应的 Gram 矩阵 \(\left[K(\boldsymbol{x_i}, \boldsymbol{x_j}) \right]_{m \times m}\) 是半正定矩阵。
说明:按上面充要条件,如果要验证一个具体函数是核函数需要对任意输入集 \(\{\boldsymbol{x_1}, \boldsymbol{x_2}, \cdots, \boldsymbol{x_m} \}\) 验证 \(K\) 对应的 Gram 矩阵是否为半正定矩阵。但要证明一个具体函数不是核函数,则只需要找到一个反例即可。
实例:判断函数 \(K(\boldsymbol{u}, \boldsymbol{v}) = \begin{cases} 1 & \text{if} \; \Vert \boldsymbol{u}, \boldsymbol{v} \Vert^2 \le 1 \\ 0 & \text{otherwise} \end{cases}\) 是否为核函数。
假设 \(\mathcal{X} =\mathbb{R}\) ,我们取 3 个点: \(x_1 = 1, x_2 = 2, x_3 = 3\) ,则对应的 Gram 矩阵为:
\[K = \left( \begin{array}{ccc}
1 & 1 & 0 \\
1 & 1 & 1 \\
0 & 1 & 1 \\
\end{array} \right)\]
这个矩阵的 3 个特征值分别为 \((\sqrt{2} - 1)^{-1}, 1, (1 - \sqrt{2})\) ,显然它不是半正定矩阵(因为半正定矩阵的所有特征值大于等于 0),从而 \(K\) 不是核函数。
这例子摘自:
An Introduction to Machine Learning, L3: Perceptron and Kernels: http://alex.smola.org/teaching/pune2007/pune_3.pdf
3.3.1. 从已知的核函数构造加复杂的核函数
如果 \(\kappa_1\) 和 \(\kappa_2\) 是定义在 \(\mathcal{X} \times \mathcal{X}\) 上的核函数, \(\mathcal{X} \subseteq \mathbb{R}^n, a \in \mathbb{R}^{+}\) , \(f(\cdot)\) 是 \(\mathcal{X}\) 上的一个实值函数,则下面函数都是核函数:
(1) \(\kappa (\boldsymbol{u}, \boldsymbol{v}) = \kappa_1 (\boldsymbol{u}, \boldsymbol{v}) + \kappa_2 (\boldsymbol{u}, \boldsymbol{v})\)
(2) \(\kappa (\boldsymbol{u}, \boldsymbol{v}) = a \kappa_1 (\boldsymbol{u}, \boldsymbol{v})\)
(3) \(\kappa (\boldsymbol{u}, \boldsymbol{v}) = \kappa_1 (\boldsymbol{u}, \boldsymbol{v}) \kappa_2 (\boldsymbol{u}, \boldsymbol{v})\)
(4) \(\kappa (\boldsymbol{u}, \boldsymbol{v}) = f(\boldsymbol{u}) f(\boldsymbol{v})\)
3.4. 常用的核函数
| 常用的核 | 核函数 | 说明 |
|---|---|---|
| 线性核 | \(K(\boldsymbol{u},\boldsymbol{v}) = \langle \boldsymbol{u},\boldsymbol{v} \rangle\) | 线性核只是为了统一形式,它只能处理线性可分数据 |
| 多项式核 | \(K(\boldsymbol{u},\boldsymbol{v}) = \left (\langle \boldsymbol{u},\boldsymbol{v} \rangle + c \right)^d\) | |
| Gaussian 核 | \(K(\boldsymbol{u},\boldsymbol{v}) = \exp \left( - \dfrac{\Vert \boldsymbol{u} - \boldsymbol{v} \Vert^2}{2 \sigma^2} \right)\) | 高斯核是最常用的核,也常写为 \(\exp \left( - \gamma \Vert \boldsymbol{u} - \boldsymbol{v} \Vert^2 \right)\) 形式,它是一种径向基核函数(Radial Basis Function, RBF) |
| Laplacian 核 | \(K(\boldsymbol{u},\boldsymbol{v}) = \exp \left( - \dfrac{\Vert \boldsymbol{u} - \boldsymbol{v} \Vert}{\sigma} \right)\) | 也是一种径向基核函数 |
| Sigmoid 核 | \(K(\boldsymbol{u},\boldsymbol{v}) = \tanh \left ( \eta \langle \boldsymbol{u},\boldsymbol{v} \rangle + \theta \right)\) |
注:高斯核中 \(\Vert \boldsymbol{u} - \boldsymbol{v} \Vert^2 = \langle \boldsymbol{u} - \boldsymbol{v}, \boldsymbol{u} - \boldsymbol{v}\rangle = \langle \boldsymbol{u}, \boldsymbol{u}\rangle + \langle \boldsymbol{v}, \boldsymbol{v}\rangle - 2 \langle \boldsymbol{u}, \boldsymbol{v}\rangle\)
3.4.1. Gaussian 核相当于映射到无穷维空间
Gaussian 核是最常用的核函数,它相当于把输入空间映射到无穷维空间。
我们知道, \(e^x = \sum_{n=0}^{\infty} \dfrac{x^n}{n!}\) ,所以核 \(\exp \left( \frac{\langle \boldsymbol{u},\boldsymbol{v} \rangle}{\sigma^2} \right) = \sum_{n=0}^{\infty} \dfrac{\langle \boldsymbol{u},\boldsymbol{v} \rangle^n}{\sigma^{2n} n!}\) ,故这个核函数可看作是映射到无穷维空间。而高斯核可以看作是把核 \(\exp \left( \frac{\langle \boldsymbol{u},\boldsymbol{v} \rangle}{\sigma^2} \right)\) 规范化而得到的:
\[\begin{aligned} \dfrac{\exp(\langle \boldsymbol{u},\boldsymbol{v} \rangle / \sigma^2)}{\sqrt{ \exp(\Vert \boldsymbol{u} \Vert^2 / \sigma^2) \exp(\Vert \boldsymbol{v} \Vert^2 / \sigma^2) }} & = \exp \left( \dfrac{\langle \boldsymbol{u},\boldsymbol{v} \rangle}{\sigma^2} - \dfrac{\langle \boldsymbol{u},\boldsymbol{u} \rangle}{2 \sigma^2 } - \dfrac{\langle \boldsymbol{v},\boldsymbol{v} \rangle}{2 \sigma^2} \right) \\
& = \exp \left( - \dfrac{\Vert \boldsymbol{u} - \boldsymbol{v} \Vert^2}{2 \sigma^2} \right)
\end{aligned}\]
当 \(\sigma\) 取较大值(或者 RBF 表示形式中的参数 \(\gamma\) 取较小值)时,高次特征上的权重会降低,这近似于一个低维的子空间;当 \(\sigma\) 取较小值(或者 RBF 表示形式中的参数 \(\gamma\) 取较大值)时,可以将任意的数据映射为线性可分的空间(这可能会导致严重的过拟合问题)。通过调整参数,高斯核具有很大的灵活性。
图 5 是在支持向量机中应用高斯核的实例。
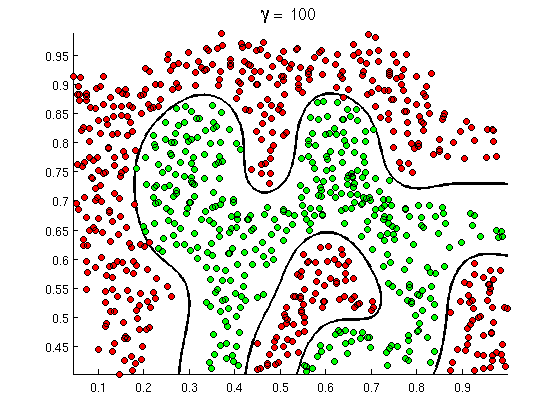
Figure 5: 支持向量机中应用高斯核
3.5. 为什么使用 Kernel Function
不使用 Kernel Function,使用特征映射,我们也可以让感知器支持线性不可分数据。为什么还要使用 Kernel Function 呢?
原因一:Speed. 用 Kernel Function 速度更快。
因为我们根本不用真正计算训练数据在新特征空间里对应的值,这减少了“特征映射”计算成本。当新特征空间的维数很高时,用 Kernel Function 的计算优势更加明显。
不过,这要求模型的训练算法中只使用训练数据的内积形式(即 Gram 矩阵)。在感知器的对偶形式、支持向量机的对偶形式中都满足这个要求。只有这样,才能在“新特征空间”里应用对应算法时直接把内积形式替换为核函数(参见核函数定义)。
原因二:Flexibility. 用 Kernel Function 更加灵活。
我们根本不需要知道 Kernel Function 背后所隐藏的特征映射是什么(Kernel trick),直接尝试那些常用的核函数直到找到一个合适的即可。
参考:
Kernel Methods in Computer Vision by Christoph H. Lampert: http://pub.ist.ac.at/~chl/papers/lampert-fnt2009.pdf
3.6. 核函数不是万能的
当训练数据非常多,且维数也很大时,Kernel 方法并不适用(太慢)!
4. 附录
4.1. 附录:感知器算法的对偶形式
感知器学习算法的对偶形式 描述如下(直接给出结论,推导过程略):
感知器模型:
\[\begin{aligned} f(\boldsymbol{x}) & = sign \left(\langle \boldsymbol{w}, \boldsymbol{x} \rangle + b \right) \\
& = sign \left( \left \langle \sum_{i=1}^{N} \alpha_i y_i \boldsymbol{x_i}, \boldsymbol{x} \right \rangle + b \right) \\
& = sign \left(\sum_{i=1}^{N} \alpha_i y_i \langle \boldsymbol{x_i}, \boldsymbol{x} \rangle + b \right) \\
\end{aligned}\]
输入:线性可分的训练数据集 \(T= \{(\boldsymbol{x_1}, y_1), (\boldsymbol{x_2}, y_2), \cdots, (\boldsymbol{x_N}, y_N)\}\) ,其中 \(\boldsymbol{x_i} \in \mathbb{R}^n, y_i \in \{+1, -1\}, \; i = 1,2, \cdots, N\) ,学习率 \(\mu (0< \mu \le 1)\)
输出:感知器模型参数 \(\boldsymbol{\alpha} = (\alpha_1, \alpha_2, \cdots, \alpha_N)^{\mathsf{T}} ,b\)
\(\boldsymbol{\alpha},b\) 的求解过程如下:
(1) \(\boldsymbol{\alpha} = (\alpha_1, \alpha_2, \cdots, \alpha_N)^{\mathsf{T}} \leftarrow (0,0,\cdots,0)^{\mathsf{T}} ,b \leftarrow 0\)
(2) 在训练数据集中选取数据 \((\boldsymbol{x_i}, y_i)\)
(3) 如果 \(y_i(\sum_{j=1}^{N} \alpha_j y_j \langle \boldsymbol{x_j}, \boldsymbol{x_i} \rangle + b) \le 0\) (即它是一个错误分类点),则按下面方法更新 \(\alpha_i,b\) :
\[\begin{cases}
\alpha_i \leftarrow \alpha_i + \mu \\
b \leftarrow b + \mu y_i
\end{cases}\]
(4) 转至(2),直到没有错误分类点。
4.1.1. 对 Perceptron 应用核函数
这里总结一下(知识点前面都介绍过了)如何对感知器算法的对偶形式应用核方法。
决策函数可写为:
\[\begin{aligned} f(\boldsymbol{x}) & = sign \left(\sum_{i=1}^{N} \alpha_i y_i \langle \phi(\boldsymbol{x_i}), \phi(\boldsymbol{x}) \rangle + b \right) \\
& = sign \left(\sum_{i=1}^{N} \alpha_i y_i {\color{red}{K(\boldsymbol{x_i},\boldsymbol{x})}} + b \right) \\
\end{aligned}\]
训练时,错误分类点的判断可以写为:
\[y_i \left (\sum_{j=1}^{N} \alpha_j y_j {\color{red}{K(\boldsymbol{x_j},\boldsymbol{x_i})}} + b \right) \le 0\]
说明:相当于在映射后的特征空间中应用感知器算法的对偶形式。