k-NN (k-Nearest Neighbor)
Table of Contents
1. k 近邻简介
k 近邻法(k-Nearest Neighbor, k-NN)是一种基本的分类和回归方法。这里主要讨论分类问题中的 k 近邻法。
k-NN 算法的思想很简单: 给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的 k 个实例,这 k 个实例的多数属于某个类,就把该输入实例分为这个类。 如果用于回归模型,则可以把最近 k 个实例的平均值作为输出结果。
图 1 (图片摘自k-NN wikipedia)是 k-NN 算法的实例。
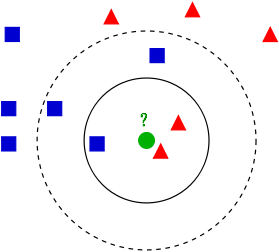
Figure 1: k-NN 实例(当 k 取 3 时,绿色圆点划分到红三角形一类;当 k 取 5 时,绿色圆点划分到蓝方块一类)
k-NN 算法有两个基本问题需要确定:(1)如何选择 k 值;(2)如何度量距离。
参考:统计学习方法,李航著,第 3 章,k近邻法
1.1. k 值的选择
k 值的选择会对 k 近邻法的结果产生重大影响。
如果选择较小的 k 值,就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说,k值的减小就意味着整体模型变得复杂,容易发生过拟合;
如果选择较大的 k 值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且 k 值的增大就意味着整体的模型变得简单。
如果 k=N,那么无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的累,模型过于简单,忽略了训练实例中大量有用信息,是不可取的。
在实际应用中,k值一般取一个比较小的数值。 例如采用交叉验证法(简单来说,就是一部分样本做训练集,一部分做测试集)来选择最优的 k 值。
参考:统计学习方法,李航著,3.2.3,k 值的选择
1.2. 距离度量
特征空间中两个实例点的距离是两个实例点相似程序的反映。k近邻模型的特征空间一般是 \(n\) 维实数向量空间 \(\mathbb{R}^n\) ,使用的距离是欧氏距离(Euclidean distance),但也可以是其他距离,如曼哈顿距离(Manhattan Distance)等等。其它一些距离度量方法可参考:机器学习中的相似性度量
2. k 近邻的实现:kd-tree
实现 k 近邻法时,主要考虑的问题是如何对训练数据进行快速 k 近邻搜索。这点在特征空间的维数大及训练数据容量大时尤其必要。
k 近邻法的最简单实现是线性扫描,这时要计算输入实例与每一个训练实例的距离,当训练集很大时,计算非常耗时,这种方法是不可行的。为了提高 k 近邻搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数。具体方法有很多,这里介绍一种称为 kd-tree 的方法。
2.1. 构造 kd-tree
kd-tree 是一种对 k 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd-tree 是二叉树,构造 kd-tree 相当于不断地用垂直于坐标轴的超平面将 k 维空间切分,构成一系列的 k 维超矩形区域。
kd-tree 的构造方法描述如下:构造根结点,使根结点对应于 k 维空间中包含所有实例点的超矩形区域;通过下面的递归方法,不断地对 k 维空间进行划分,生成子结点。在超矩形区域(结点)上选择一个坐标轴和在此坐标轴上的一个切分点,确定一个超平面,这个超平面通过选定的切分点并垂直于选定的坐标轴,将当前超矩形区域且分为左右两个子区域(子结点);这时,实例点被分到两个子区域。这个过程直到子区域内没有实例点时终止(终止时的结点即为叶结点)。在此过程中,将实例保存到相应的结点上。
关于切分点的选择通常有多种方法,最常用的是一种方法是:对于所有的样本点,统计它们在每个维上的方差,挑选出方差中的最大值,对应的维数记为 split 维。数据方差最大表明沿该维度数据点分散得比较开,这个方向上进行数据分割可以获得最好的分辨率,然后再将所有实例点按其第 split 维的值进行排序,位于正中间的那个实例点选为切分点。通常,依次选择坐标轴对空间切分,选择训练实例点在选定的坐标轴上的中位数为切分点,这样得到的 kd-tree 是平衡的,但是平衡的 kd-tree 搜索时未必是效率最优的结构。
2.1.1. kd-tree 构造实例
给定一个二维空间的数据集: \(T=\{(2,3)^{\mathsf{T}}, (5,4)^{\mathsf{T}}, (9,6)^{\mathsf{T}}, (4,7)^{\mathsf{T}}, (8,1)^{\mathsf{T}}, (7,2)^{\mathsf{T}} \}\) ,请构造一个平衡 kd-tree。
解:根结点对应包含数据集 \(T\) 的矩形,选择 \(x^{(1)}\) 轴,6个数据点的 \(x^{(1)}\) 坐标的中位数是 7,以平面 \(x^{(1)} = 7\) 将空间分为左、右两个子矩形(子结点);接着,左矩形以 \(x^{(2)}=4\) (4是左矩形 \(x^{(2)}\) 轴中位数切分点)分为两个子矩形,右矩形以 \(x^{(2)}=6\) (6是右矩形 \(x^{(2)}\) 轴中位数切分点)分为两个子矩形,如此递归,最后得到如图 2 所示的特征空间划分和如图 3 所示的 kd-tree。
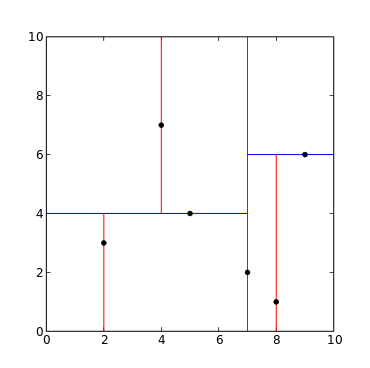
Figure 2: 特征空间划分
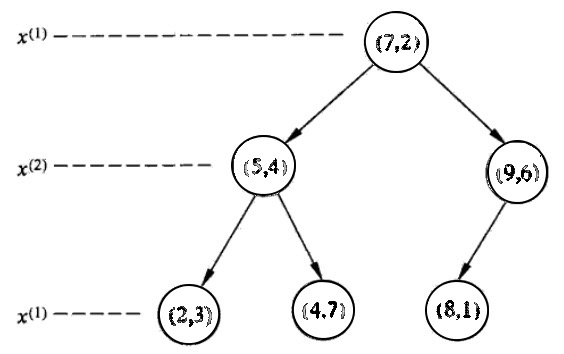
Figure 3: kd-tree 示例
2.2. 搜索 kd-tree
kd-tree 构造出来后,如何在 kd-tree 中找到输入数据点的 k 近邻呢?这时,我们仅考虑 \(k=1\) 即最近邻的情况。
2.2.1. 跳过某些结点的检查
这里,先不介绍完整的 kd-tree 搜索算法。通过一个简单来直观了解下 kd-tree 搜索时可以跳过某些结点的检查。
假设,从训练数据构造出来的 kd-tree 如图 4 所示。
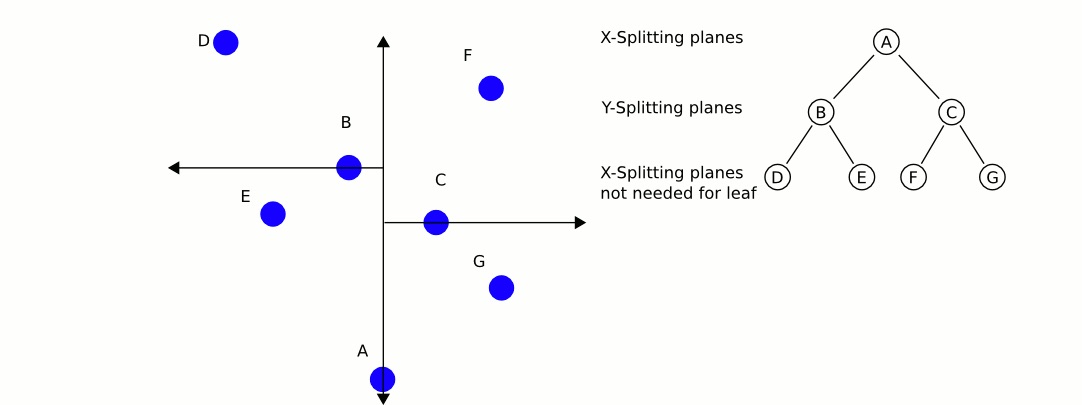
Figure 4: 给定 kd-tree
给定一个输入点(如图 5 中斜十字叉的中心点),如何找到它的最近邻呢?
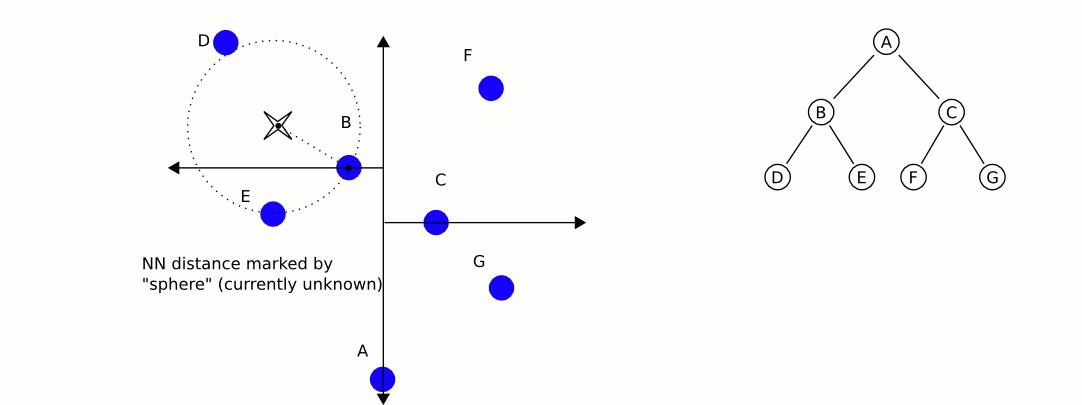
Figure 5: 给定输入点,寻找其最近邻
从 kd-tree 的根结点开始(如图 6 所示),考查它的两个子结点(如图 7 所示,先考查左子结点 B)。
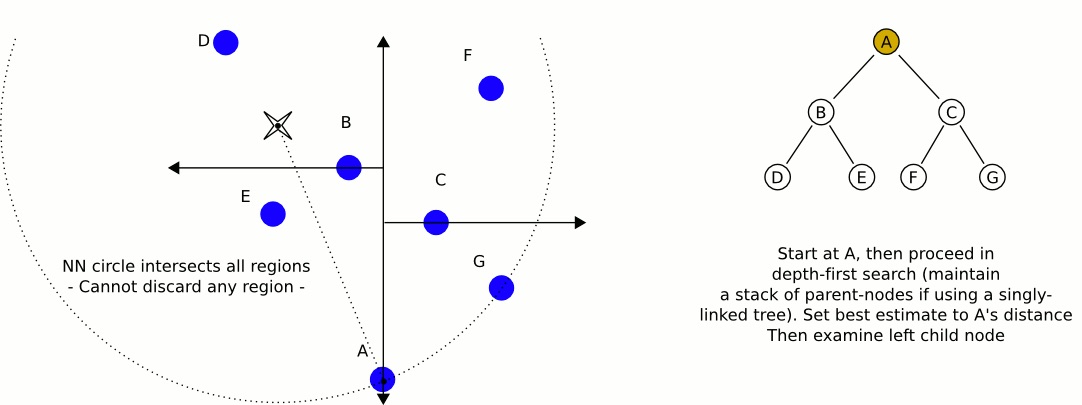
Figure 6: 先检查 kd-tree 根结点
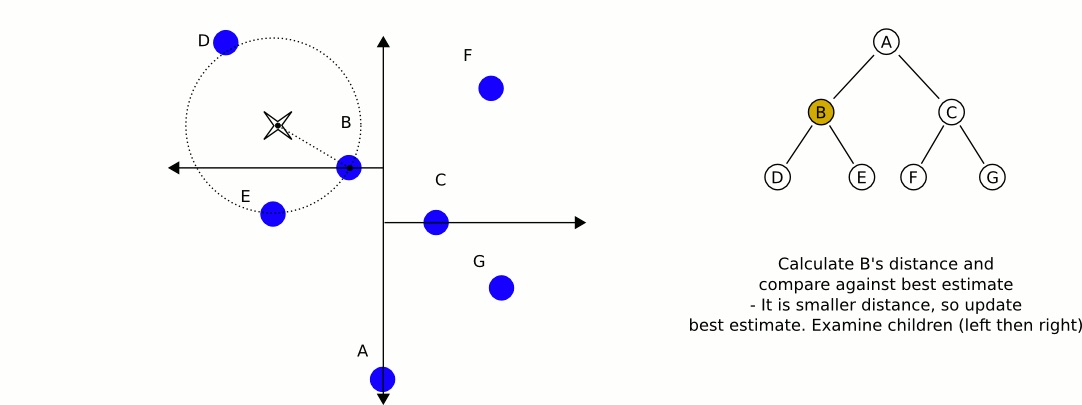
Figure 7: 检查 kd-tree 根结点的左子结点
在考查左子结点 B 时,发现以输入点为圆心,“输入点到结点 B 的距离”为半径的圆和图中的垂直线没有相交,如图 8 所示。这说明 右子结点 C 及其子结点(即垂直线右边的那些结点)根本不用检查,它们不会是输入点的最近邻点。 如图 9 所示。
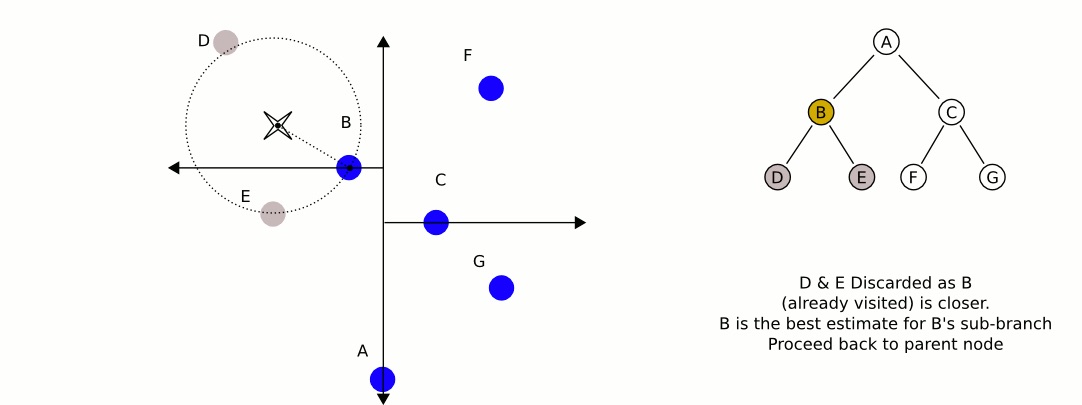
Figure 8: 以输入点为圆心,“输入点到结点 B 的距离”为半径的圆和图中的垂直线没有相交
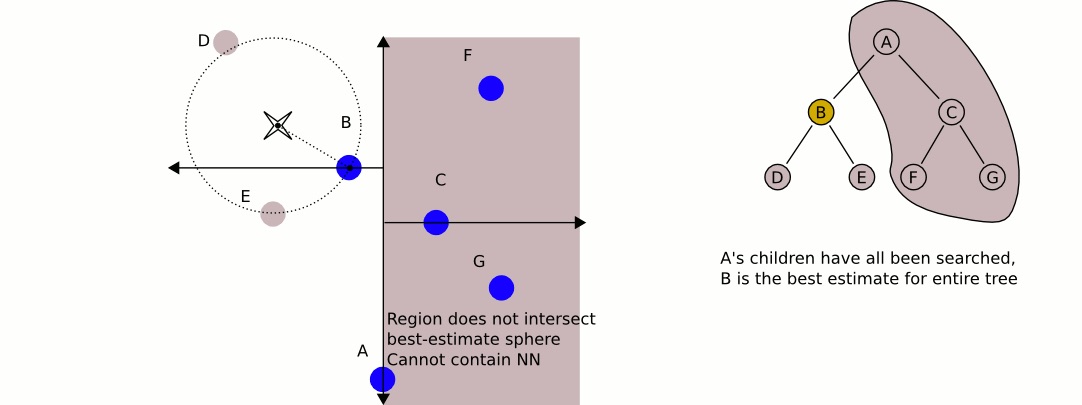
Figure 9: 跳过对右子结点 C 及其子结点的检查,它们不会是输入点的最近邻点
注:这个例子摘自 kd-tree Wikipedia
2.2.2. 最近邻搜索算法
输入:已构造的 kd-tree,目标点 \(\boldsymbol{x}\) ;
输出: \(\boldsymbol{x}\) 的最近邻。
算法步骤如下:
(1)在 kd-tree 中找出包含目标点 \(\boldsymbol{x}\) 的叶结点:从根结点出发,递归地向下搜索 kd-tree。若目标点 \(\boldsymbol{x}\) 当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子结点,直到子结点为叶结点为止。
(2)以此叶结点为“当前最近点”。
(3)递归地向上回溯,在每个结点进行以下操作:
(3.1)如果该结点保存的实例点比当前最近点距离目标点更近,则更新“当前最近点”为当前结点。
(3.2)当前最近点一定存在于该结点一个子结点对应的区域,检查子结点的父结点的另一子结点对应的区域是否有更近的点。具体做法是,检查另一子结点对应的区域是否以目标点位球心,以目标点与“当前最近点”间的距离为半径的圆或超球体相交:如果相交,可能在另一个子结点对应的区域内存在距目标点更近的点,移动到另一个子结点,接着,继续递归地进行最近邻搜索;如果不相交,向上回溯。
(4)当回退到根结点时,搜索结束,最后的“当前最近点”即为 \(\boldsymbol{x}\) 的最近邻点。
下文将通过两个例子来说明 kd-tree 的搜索过程。这两个例子摘自《图像局部不变性特征与描述, 王永明、王贵锦》7.1.2,最近邻查询算法。
2.2.2.1. 最近邻搜索实例一
已知 kd-tree 为图 3 所示,求输入数据点 \((2.1, 3.1)\) 的最近邻点(下面使用 \((x,y)\) 代替前面的表示 \((x^{(1)},x^{(2)})\) )。
第一步:二叉搜索过程。从根结点开始,找到叶结点 \((2, 3)\) 作为输入数据点的“当前最近点”,不过,它不一定就是最近邻(这个例子中它确实是最近邻,下一节的例子中二叉搜索找到的点不是最近邻)。
第二步:回溯查找过程。上一步得到 \((2, 3)\) 为查询点的“当前最近点”之后,回溯到其父节点 \((5, 4)\) ,并判断在该父节点的其他子节点空间中是否有离查询点更近的数据点。以 \((2.1, 3.1)\) 为圆心,以 \((2.1, 3.1)\) 到 \((2, 3)\) 的距离为半径画圆,如图 10 所示。可发现该圆和超平面 \(y = 4\) 不相交,因此不用进入 \((5, 4)\) 结点右子空间中(图 10 中灰色区域)去搜索。这步回溯结束后,“当前最近点”依然是 \((2, 3)\) 。
再进一步回溯到到 \((7,2)\) ,以 \((2.1, 3.1)\) 为圆心,以\((2.1, 3.1)\) 到 \((2, 3)\) 的距离为半径的圆显然也不会与 \(x = 7\) 超平面相交,因此,不用进入 \((7,2)\) 右子空间进行查找。至此,搜索路径中的节点已经全部回溯完。得到的最近邻点为 \((2, 3)\) 。
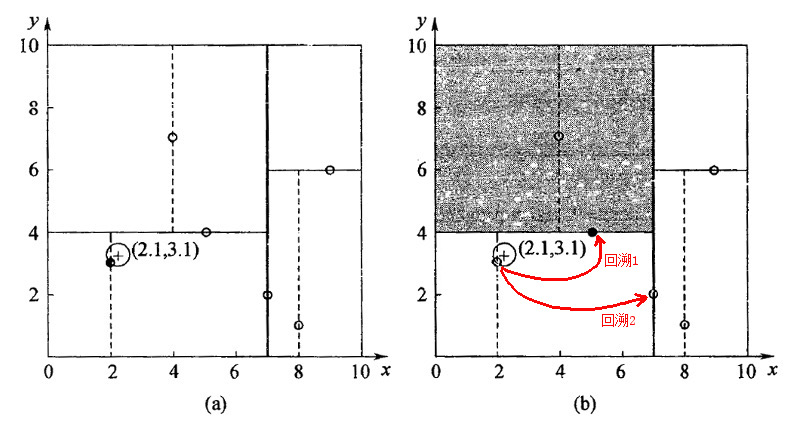
Figure 10: 对 \((2.1, 3.1)\) 进行最近邻查询的过程
2.2.2.2. 最近邻搜索实例二
已知 kd-tree 为图 3 所示,求输入数据点 \((2, 4.5)\) 的最近邻点。
第一步:二叉搜索过程。沿查询路径 \((7,2) \to (5,4) \to (4,7)\) ,得到叶结点 \((4,7)\) 为“当前最近点”。
第二步:回溯查找过程。从叶结点 \((4,7)\) 回溯到 \((5,4)\) 后,发现 \((5,4)\) 离输入数据点 \((2, 4.5)\) 更近。以 \((2, 4.5)\) 为圆心并经过 \((5,4)\) 的圆和分割超平面 \(y=4\) 相交,所以必须考察灰色区域,即考察 \((5,4)\) 的右子结点。发现,结点 \((2,3)\) 是更好的“当前最近点”。以 \((2, 4.5)\) 为圆心并经过 \((2,3)\) 的圆不和 \(x=7\) 相交,不用考察 \(x=7\) 右边的结点。搜索路径回溯结束。得到的最近邻点为 \((2, 3)\) 。
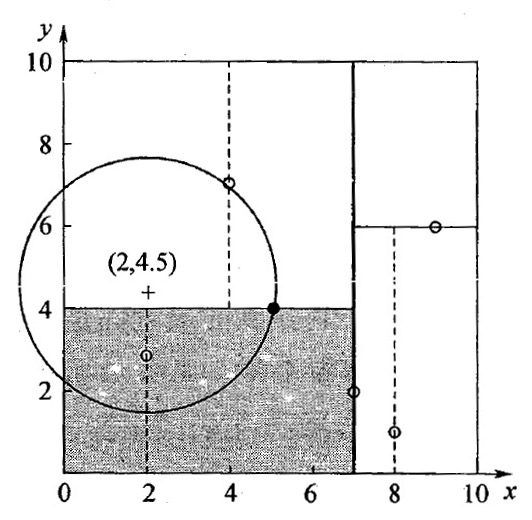
Figure 11: 对 \((2, 4.5)\) 进行最近邻查询的过程
2.2.3. 训练数据的分布会影响搜索性能
一般来讲,最近邻搜索只用检测几个叶子结点,如图 12 所示。
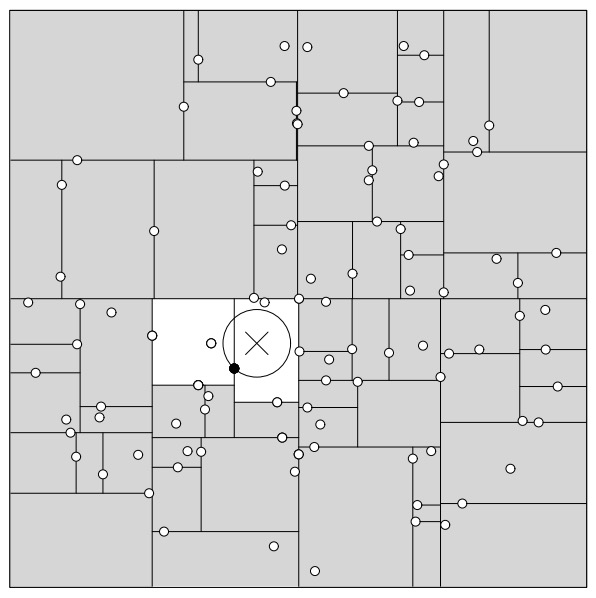
Figure 12: Generally during a nearest neighbour search only a few leaf nodes need to be inspected
但也会遇到几乎要遍历所有的结点的情况,如图 13 所示。
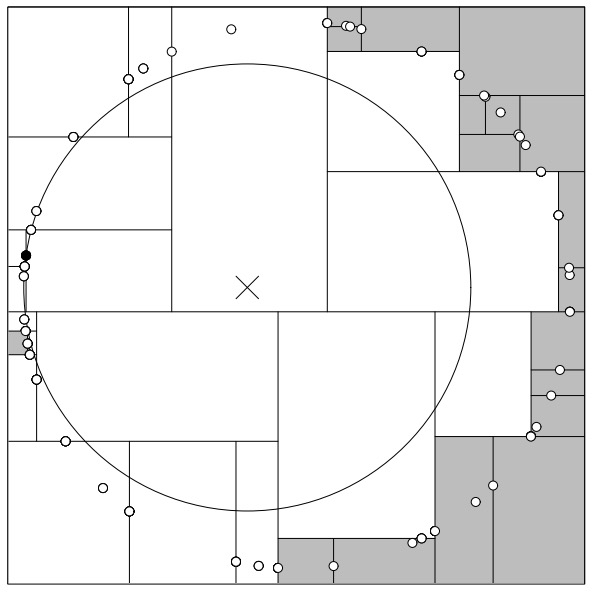
Figure 13: A bad distribution which forces almost all nodes to be inspected
参考:An intoductory tutorial on kd-trees, by Andrew W. Moore
2.3. kd-tree 的适应情况
kd-tree 适用于训练实例数远大于空间维数时的 k 近邻搜索。当空间维数接近训练实例数时,它的效率会迅速下降,几乎接近线性扫描。
2.4. kd-tree 搜索算法优化:BBF (Best Bin First)
kd-tree 在维度较小时的查找效率很高,然而当 kd-tree 用于对高维数据进行索引和查找时,查找效率会随着维度的增加而迅速下降。 使用标准的 kd-tree 时,数据集的维数一般不应超过 20。
不过,我们常常处理的数据都具有高维的特点,例如在图像检索和识别中,每张图像通常用一个几百维的向量来表示,每个特征点的局部特征用一个高维向量来表征(例如:128 维的 SIFT 特征)。为此,人们提出了一些 kd-tree搜索的改进算法,如BBF (Best Bin First),该算法能够实现近似k近邻的快速搜索,在保证一定查找精度的前提下使得查找速度较快。
这里不介绍BBF,可以参考《图像局部不变性特征与描述, 王永明、王贵锦》7.1.3,改进kd-tree最近邻查询。