Linear Least Squares
Table of Contents
1. 最小二乘法的历史
1801 年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过 40 天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。时年 24 岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于 1809 年他的著作《天体运动论》中,而法国科学家勒让德于 1806 年独立发现“最小二乘法”,但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。
摘自:https://zh.wikipedia.org/wiki/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95
2. 最小二乘法简介
最小二乘法常常用来做“曲线拟合”。 有一些实验数据,且已知实验数据近似满足的函数关系(但参数未知),最小二乘法常常用来估计函数关系式中的未知参数。
下面两个实例摘自:《高等数学》第九章,第十节,最小二乘法
2.1. 最小二乘法实例 1
为了测定刀具的磨损速度,每隔一小时,测量一次刀具的厚度(单位为 mm),得到下面的实验数据:
| 时间 \(t_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 刀具厚度 \(y_i\) | 27.0 | 26.8 | 26.5 | 26.3 | 26.1 | 25.7 | 25.3 | 24.8 |
已知时间 \(t\) 和刀具厚度满足经验公式 \(f(t) = at + b\) ,如何确定参数 \(a,b\) 呢?
我们可以选取这样的 \(a,b\) ,使得 \(f(t) = at + b\) 在 \(t_0, t_1, \cdots, t_7\) 处的函数值与实验数据 \(y_0, y_1, \cdots, y_7\) 相差都很小。即设法使 \(\sum_{i=0}^{7} | y_i - f(t_i) |\) 最小。但绝对值的计算不方便,最小二乘法放弃了绝对值运算,而是采用平方运算。 最小二乘法采用的策略是选取 \(a,b\) 使得下式最小:
\[M = \sum_{i=0}^{7} [y_i - (at_i +b )]^2\]
这是一个求函数极值问题(上式中 \(a,b\) 看作未知数,而 \(t_i,y_i\) 是已知的),利用微分学中求函数极值的知识可得, \(a,b\) 可从下面方程组中求得:
\[\begin{cases}
\dfrac{\partial M}{\partial a} = -2 \sum\limits_{i=0}^{7} [ y_i - (at_i + b) ] t_i = 0 \\
\dfrac{\partial M}{\partial b} = -2 \sum\limits_{i=0}^{7} [ y_i - (at_i + b)] = 0 \\
\end{cases}\]
通过上面方程组,可以求得: \(a = -0.3036, b = 27.125\) ,所以得到的经验公式为:
\[y= f(t) = - 0.3036 t + 27.125\]
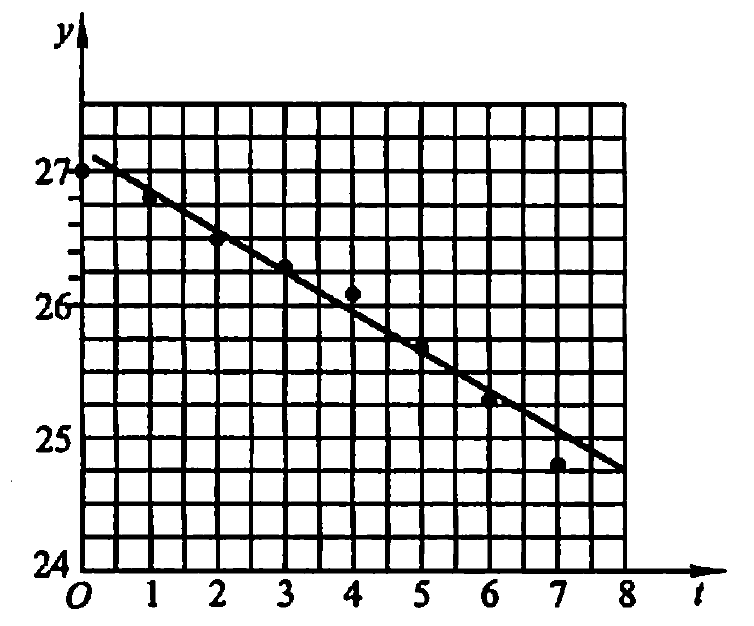
Figure 1: 刀具磨损速度
函数值 \(f(t_i)\) 和实测值 \(y_i\) 有一定的偏差,如表 2 所示。
| \(t_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 实测的 \(y_i\) | 27.0 | 26.8 | 26.5 | 26.3 | 26.1 | 25.7 | 25.3 | 24.8 |
| 算得的 \(f(t_i)\) | 27.125 | 26.821 | 26.518 | 26.214 | 25.911 | 25.607 | 25.303 | 25.000 |
| 偏差 | - 0.123 | -0.021 | -0.018 | 0.086 | 0.189 | 0.093 | -0.003 | -0.200 |
偏差的平方和 \(M=0.108165\) ,它的大小在一定程序上反映了用经验公式来近似表达原来函数关系的近似程序的好坏。
总结: 最小二乘法的核心思想就是保证“数据偏差的平方和”最小。
2.2. 最小二乘法实例 2
在研究某分子化学反应速度时,得到表 3 所示数据。
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \(\tau_i\) | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| \(y_i\) | 57.6 | 41.9 | 31.0 | 22.7 | 16.6 | 12.2 | 8.9 | 6.5 |
其中 \(\tau\) 表示从实验开始算起的时间, \(y\) 表示时刻 \(\tau\) 反应物的量。由化学反应速度的理论知道,它们满足经验公式 \(y = k e^{m \tau}\) ,如何用最小二乘法确实未知参数 \(k,m\) ?
对经验公式两边取常用对数后,得到 \(\lg y = (m \cdot \lg e) \tau + \lg k\) ,该式是 \(\lg y\) 关于 \(\tau\) 的线性函数。可以和前面例子采用同样的方法,最后求得: \(y = 78.78 e^{-0.1036 \tau}\)
详细过程可参考:《高等数学》第九章,第十节,最小二乘法
3. 推广到多变量的情况(OLS)
上面介绍的例子,是只有一个变量的情况。可以把最小二乘法推广到多变量的情况,即 OLS(Ordinary Least Squares)。
假设有 \(n\) 条实验数据,实验数据满足下面经验公式:
\[f(\boldsymbol{t}) = b_0 + b_1 t_1 + \cdots + b_q t_q\]
下面将利用这 \(n\) 条实验数据来估计参数 \(\boldsymbol{b}\) 。
每一条实验数据的误差分别为:
\[\begin{gathered}y_1 - (b_0 + b_1 t_{11} + \cdots + b_q t_{1q}) \\
y_2 - (b_0 + b_1 t_{21} + \cdots + b_q t_{2q}) \\
\vdots \\
y_n - (b_0 + b_1 t_{n1} + \cdots + b_q t_{nq}) \end{gathered}\]
把 \(\left( \begin{array}{ccc} 1 & t_{11} & \cdots & t_{1q} \\ 1 & t_{21} & \cdots & t_{2q} \\ \vdots \\ 1 & t_{n1} & \cdots & t_{nq} \end{array} \right)\) 记作数据矩阵 \(\mathbf{A}\) (它在实验数据中已给出,是已知的),观测值 \(y_i\) 记为向量 \(\boldsymbol{y}\) (它也是已知的)。那么,“误差的平方和”记为 \(Q\) ,有:
\[Q = \sum_{i=1}^{n} (y_i - (b_0 + \sum_{j=1}^{q}t_{ij} b_j))^2 = (\boldsymbol{y} - \mathbf{A} \boldsymbol{b})^{\mathsf{T}} (\boldsymbol{y} - \mathbf{A} \boldsymbol{b}) = \Vert \boldsymbol{y} - \mathbf{A} \boldsymbol{b} \Vert^2\]
上式中,符号 \(\Vert \cdot \Vert\) 为向量的范数,即 \(\Vert \boldsymbol{x} \Vert = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2}\) 。
\(Q\) 取最小值时,对应的 \(\boldsymbol{b}\) 就是我们所要求的经验公式的参数 \(\boldsymbol{b}\) 的估计值。即:
\[\hat{\boldsymbol{b}} = \operatorname{arg} \underset{\boldsymbol{b}}{\min} Q = \operatorname{arg} \underset{\boldsymbol{b}}{\min} \Vert \boldsymbol{y} - \mathbf{A} \boldsymbol{b} \Vert^2\]
求函数极值问题可以利用微分学中知识求得, \(\hat{\boldsymbol{b}}\) 满足下面方程组(下式是对向量 \(\boldsymbol{b}\) 的每个分量求偏导数,所以这里说“方程组”):
\[\left. \frac{\partial Q}{\partial \boldsymbol{b}} \right|_{\boldsymbol{b} = \hat{\boldsymbol{b}}} = 0\]
由上式可以得:
\[\begin{aligned} \left. \frac{\partial Q}{\partial \boldsymbol{b}} \right|_{\boldsymbol{b} = \hat{\boldsymbol{b}}} & = \left. \frac{\partial}{\partial \boldsymbol{b}} \left( (\boldsymbol{y} - \mathbf{A} \boldsymbol{b})^{\mathsf{T}} (\boldsymbol{y} - \mathbf{A} \boldsymbol{b}) \right)\right|_{\boldsymbol{b} = \hat{\boldsymbol{b}}} \\
& = \left. \frac{\partial}{\partial \boldsymbol{b}} \left((\boldsymbol{y}^{\mathsf{T}} - \boldsymbol{b}^{\mathsf{T}} \mathbf{A}^{\mathsf{T}} ) (\boldsymbol{y} - \mathbf{A} \boldsymbol{b}) \right)\right|_{\boldsymbol{b} = \hat{\boldsymbol{b}}} \\
& = \left. \frac{\partial}{\partial \boldsymbol{b}} \left( \boldsymbol{y}^\mathsf{T} \boldsymbol{y} - \boldsymbol{b}^\mathsf{T} \mathbf{A}^\mathsf{T} \boldsymbol{y} - \boldsymbol{y}^\mathsf{T} \mathbf{A} \boldsymbol{b} + \boldsymbol{b}^\mathsf{T} \mathbf{A}^\mathsf{T} \mathbf{A} \boldsymbol{b} \right)\right|_{\boldsymbol{b} = \hat{\boldsymbol{b}}} \\
& = -2 \mathbf{A}^\mathsf{T} \boldsymbol{y} + 2 \mathbf{A}^\mathsf{T} \mathbf{A} \hat{\boldsymbol{b}} \\
& = 0 \end{aligned}\]
假设 \(\mathbf{A}^\mathsf{T} \mathbf{A}\) 可逆,从上式可得:
\[\hat{\boldsymbol{b}} = (\mathbf{A}^\mathsf{T} \mathbf{A})^{-1} \mathbf{A}^\mathsf{T} \boldsymbol{y}\]
上式就是线性最小二乘法的解(即对参数的估计)。
说明:在上式中, \((\mathbf{A}^\mathsf{T} \mathbf{A})^{-1} \mathbf{A}^\mathsf{T}\) 是 \(\mathbf{A}\) 的 pseudo-inverse 矩阵,可以记作 \(\mathbf{A}^{+}\) ;如果 \(\mathbf{A}^\mathsf{T} \mathbf{A}\) 不可逆,可以用其他方式定义 \(\mathbf{A}^{+}\) (这里不详述),所以最小二乘法的解可以记作:
\[\hat{\boldsymbol{b}} = \mathbf{A}^{+} \boldsymbol{y}\]
参考:
https://en.wikipedia.org/wiki/Linear_least_squares_(mathematics)
4. Ridge, Lasso, ElasticNet
我们用线性最小二乘法求得已有数据所满足的关系后(模型参数),往往用这个模型来对新的数据进行估计。如前面例子中,求得刀具的厚度随时间的关系后,我们就可以估计刀具在其它时间(如 8 小时后)的厚度了。
不过,有的时候会出现“过拟合”的情况,即模型对已有数据拟合得非常好(损失函数“数据偏差的平方和”很小),但是对新数据的预测却不准确。
为避免过拟合现象,人们改进损失函数,把模型复杂度也考虑在内,这种方法被称为“正则化(Regularization)”。
线性回归模型可记为:
\[y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_q x_{iq}\]
或者写为向量形式:
\[y_i = \boldsymbol{\beta} \cdot \boldsymbol{x_i}\]
不同正则化方式对应的损失函数如表 4 所示。
| 线性回归类型 | 损失函数 |
|---|---|
| OLS | \(\sum_{i=1}^N (y_i - \boldsymbol{\beta} \cdot \boldsymbol{x_i})^2\) |
| Ridge Regression | \(\sum_{i=1}^N (y_i - \boldsymbol{\beta} \cdot \boldsymbol{x_i})^2 + \lambda \sum_{j=1}^q ( \beta_j )^2\) |
| LASSO Regression | \(\sum_{i=1}^N (y_i - \boldsymbol{\beta} \cdot \boldsymbol{x_i})^2 + \lambda \sum_{j=1}^q \vert \beta_j \vert\) |
| Elastic Net Regression | \(\sum_{i=1}^N (y_i - \boldsymbol{\beta} \cdot \boldsymbol{x_i})^2 + \lambda_1 \sum_{j=1}^q \vert \beta_j \vert + \lambda_2 \sum_{j=1}^q ( \beta_j )^2\) |
注 1:一般使用交叉验证(Cross validation)的办法来寻找合适的 \(\lambda\) 值。
注 2:LASSO 是“Least Absolute Shrinkage and Selection Operator”的缩写,它有一个重要的性质在于它更容易产生稀疏解(即得到的 \(\beta_i\) 中有很多为零),这起到了特征选择的效果。