Markov Decision Process (MDP)
Table of Contents
1. Markov Decision Processes 简介
Markov decision processes (MDPs) provide a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker.
1.1. 一个例子
假设一个智能体(Agent)在图 1 中所示的 \(4 \times 3\) 环境中。从初始状态(标为 START)开始,它在每个时间步必须选择一个行动。在智能体到达一个标有 \(+1\) 或者 \(-1\) 的目标状态时与环境的交互终止。在每一个位置,可用的行动包括:Up、Down、Left、Right。目前我们假设环境是完全可观察的,因而智能体总是知道自己所在的位置。
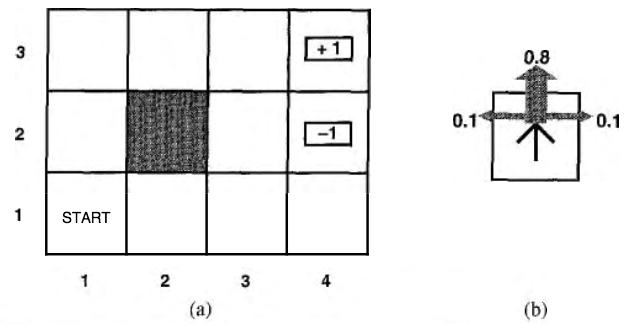
Figure 1: (a) 一个简单的 \(4 \times 3\) 环境,(b) 这个环境的转移模型示意图
如果环境是确定的,得到一个解很容易:[Up, Up, Right, Right, Right]。不幸的是,由于行动是不可靠的(比如对机器人的控制不可能完全精确),所以环境不一定沿着这个解发展。图 1 (b) 是一个环境转移模型的示意,每步行动以 \(0.8\) 的概率达到预期效果,以 \(0.1\) 的概率分别向垂直于预期方向的两个方向移动。此外,如果智能体撞到墙(如图 1 (a) 中黑色模块)后会停在原地。两个终止状态分别有 \(+1\) 和 \(-1\) 的回报,其他所有状态有 \(-0.04\) 的回报。现在智能体要解决的问题是如何得到最大的回报,对应的策略就是最优策略。
我们用 \(T(s, a, s')\) 表示当在状态 \(s\) 中完成行动 \(a\) 时,到达状态 \(s'\) 的概率。这里假设这些转换具有马尔可夫性,即从状态 \(s\) 到 \(s'\) 的概率只取决于 \(s\) ,而不取决于之前的状态历史。规定在每个状态 \(s\) 中,智能体得到一个可正可负的但肯定有限的回报 \(R(s)\) 。在上面例子中,除了终止状态外(它们的回报分别是 \(+1\) 和 \(-1\) ),其它状态的回报都是 \(-0.04\) 。这里,我们简单地使用“累加回报”来表示一个“状态序列的效用值”。例如,智能体用了 10 步到达 \(+1\) 状态,那么这个状态序列的效用值是 \(+1 + 10 \times (-0.04) = 0.6\) 。
对于完全可观察的环境,马尔可夫决策过程可表示为:
1、初始状态: \(s_0\)
2、转移模型: \(T(s, a, s')\)
3、回报函数: \(R(s)\)
那么,上面问题的解是什么样的?显然任何固定的行动序列都无法解决这个问题,这是因为智能体可能最后移动到非目标的其他状态。因此, MDP 问题的解必须指定在智能体可能到达的任何状态下,智能体应当采取什么行动。这种类型的解称为策略(policy)。 通常我们用 \(\pi\) 来表示策略,用 \(\pi(s)\) 表示策略 \(\pi\) 下处于状态 \(s\) 时的推荐行动。如果智能体有完备的策略,那么无论任何行动的结果如何,智能体总是知道下一步该做什么。
策略 \(\pi\) 并不是一个简单的状态序列,它表示的是在所有可能状态下的下一步行动。最优策略一般用 \(\pi^*\) 表示。
图 2 (a)是对于非终止状态中 \(R(s) = -0.04\) 的随机环境的一个最优策略。
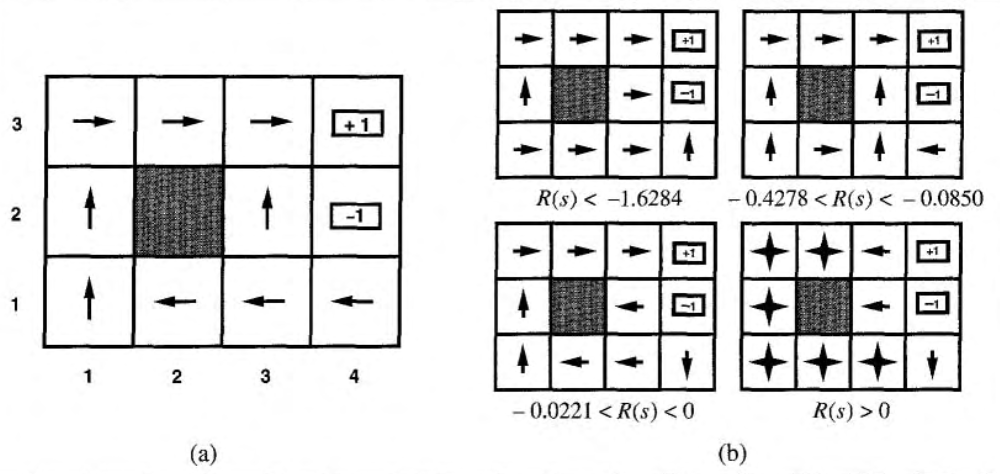
Figure 2: (a) 是对于非终止状态中 \(R(s) = -0.04\) 的随机环境的一个最优策略,(b) 对于不同的 \(R(s)\) 对应的最优策略。
图 2 (a)是对于图 1 环境的一个最优策略。注意,因为多走一步的代价与偶然结束在状态 \((4, 2)\) 中的惩罚相比是相当小的,所以状态 \((3,1)\) 的最优策略是谨慎的:策略建议绕一个远道,而不走可能进入状态 \((4, 2)\) 的近道,即当处于 \((3,1)\) 时我们往左走,而不往上走。当非终止状态 \(R(s) < -1.6284\) 时,智能体觉得“生活太痛苦”,于是直奔最近的出口,即使出口的价值是 \(-1\) ;当非终止状态 \(-0.4278 < R(s) < -0.0850\) 时,智能体觉得“生活很不愉快”,选择通往 \(+1\) 状态的最近路径,并愿意冒偶然落进 \(-1\) 状态的风险,如当处于 \((3,1)\) 时智能体往上走,而不往左走;当非终止状态 \(-0.0221 < R(s) < 0\) 时,智能体觉得“生活只是有些沉闷”,最优策略选择根本不冒险。最后,如果非终止状态 \(R(s) > 0\) ,则智能体觉得“生活令人愉快”,智能体会躲避所有的出口。
参考:
http://lanbing510.info/2015/11/17/Master-Reinforcement-Learning-MDP.html
http://lanbing510.info/2018/07/16/DQN.html
http://lanbing510.info/2018/07/17/DQN.html
1.2. “累加回报”和“折扣回报”
状态序列的效用值有两种表示:“累加回报(Addictive Reward/Cumulated Reward)”和“折扣回报(Discounted Reward)”。
累加回报(前面例子采用的就是累加回报):状态序列 \([s_0, s_1, s_2, \cdots]\) 的效用值为:
\[V([s_0, s_1, s_2, \cdots]) = R(s_0) + R(s_1) + R(s_2) + \cdots\]
折扣回报:状态序列 \([s_0, s_1, s_2, \cdots]\) 的效用值为:
\[V([s_0, s_1, s_2, \cdots]) = R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \cdots\]
其中,折扣因子 \(\gamma\) 是一个介于 \(0\) 和 \(1\) 之间的数,它描述了智能体对于当前回报与未来回报相比的偏好。当 \(\gamma\) 接近于 \(0\) 时,遥远未来的回报被认为无关紧要。而当 \(\gamma\) 是 \(1\) 时,折扣回报就和累加回报完全等价,所以累加回报是折扣回报的一个特例。
当采用折扣回报时,我们的目标就是使回报期望值最大:
\[E[R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \cdots]\]
设 \(\pi^*\) 为最优策略,则:
\[\begin{aligned} \pi^* & = \operatorname{arg} \underset{\pi}{\max} E[R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \cdots \mid \pi, s_0 = s] \\
& = \operatorname{arg} \underset{\pi}{\max} E \left[\sum_{t=0}^{\infty} \gamma^t R(s_t) \mid \pi, s_0=s \right] \\
\end{aligned}\]
1.3. 用 MDP 对“给西瓜浇水问题”进行建模
我们考虑一下如何种西瓜。种瓜有许多步骤,从一开始的选种,到定期浇水、施肥、除草、杀虫,经过一段时间才能收获西瓜。通常要等到收获后,我们才知道种出的瓜好不好。若将得到好瓜作为辛勤种瓜劳动的奖赏,则在种瓜过程中当我们执行某个操作(例如,施肥)时, 并不能立即获得这个最终奖赏,甚至难以判断当前操作对最终奖赏的影响,仅能得到一个当前反馈(例如,瓜苗看起来更健壮了)。我们需多次种瓜,在种瓜过程中不断摸索,然后才能总结出较好的种瓜策略。这个过程抽象出来,就是“强化学习”(reinforcement learning)。强化学习任务通常用马尔可夫决策过程来描述。
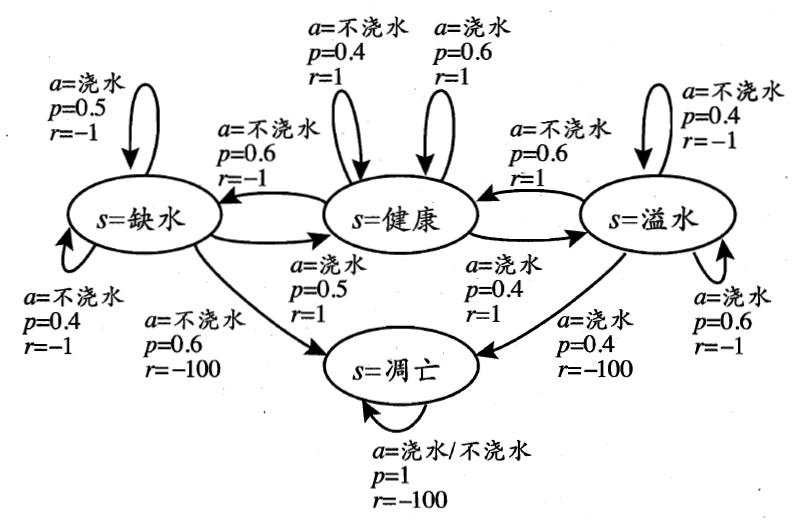
Figure 3: “给西瓜浇水问题”的马尔可夫决策过程
图 3 给出了一个简单的例子:给西瓜浇水的马尔可夫决策过程。该任务中只有四个状态(健康、缺水、溢水、凋亡)和两个动作(浇水、不浇水),在每一个步转移后,若状态是保持瓜苗健康则获得奖赏 \(1\) ,瓜苗缺水或溢水奖赏为 \(-1\) ,这时通过浇水或不浇水可以恢复健康状态,当瓜苗凋亡时奖赏是最小值 \(-100\) ,且无法恢复。图中箭头表示状态转移,箭头旁的 \(a,p,r\) 分别表示导致状态转移的动作、转移概率以及返回的奖赏。容易看出,最优策略在“健康”状态选择动作“浇水”、在“溢水”状态选择动作“不浇水”、在“缺水”状态选择动作“浇水”、在“凋亡”状态可选择任意动作。
本节的例子摘自:机器学习,周志华,第 16 章,强化学习
2. 求解 MDP
2.1. Value iteration (a.k.a. dynamic programming)
2.1.1. 状态的效用值
在节 1.2 中已经介绍过“状态的效用值是通过状态序列的效用值来定义的”,这里把它描述得更加正式一些。
粗略地说, 一个状态的效用值就是“可能跟随它出现的所有状态序列”的期望效用值。 显然,状态序列取决于执行的策略,在策略 \(\pi\) 下,我们定义下式为状态 \(s\) 的效用值:
\[V^{\pi}(s) = E[R(s_0) + \gamma R(s_1) + \gamma^2 R(s_2) + \cdots \mid \pi, s_0 = s]\]
上式也称为 策略 \(\pi\) 的值函数(Value Function)。 当智能体执行最优策略 \(\pi^*\) 时对应的效用值 \(V^{\pi^*}(s)\) 就是状态 \(s\) 的真正效用值(后面提到的状态效用值均指状态的真正效用值)。
可以证明,最优策略对应的值函数 \(V^{\pi^*}(s)\) 满足贝尔曼等式(Bellman Equation):
如果回报函数 \(R(s)\) 和行动相关,它应该记为 \(R(s,a)\) ,从而贝尔曼等式应该写为:
上式中, \(A\) 表示动作集合,例如前面例子中表示 Up、Down、Left、Righ; \(p(s' \mid s, a)\) 表示当在状态 \(s\) 中完成行动 \(a\) 时,到达状态 \(s'\) 的概率,也就是前面的记号 \(T(s, a, s')\) ; \(S\) 表示状态集合,例如前面例子中 \(4 \times 3\) 的每个环境 \(\{(i,j) \mid i = 1,2,3,4, j=1,2,3\}\)
注 1:贝尔曼是动态规划(Dynamic Programming)的创始人。
注 2:贝尔曼等式表明:一个状态的效用值是“转移到下一个状态的回报加上下一个状态效用值”的最大值。
注 3:这里不证明为什么 \(V^{\pi^*}(s)\) 会满足贝尔曼等式,感兴趣的读者可以参考:Markov Decision Processes in Artificial Intelligence, 1.5.2.2 Optimality equations
一旦我们求得了所有状态 \(s\) 的效用值,则最优策略就是:
\[\pi^*(s) = \operatorname{arg} \underset{a \in A}{\max} \left( R(s, a) + \gamma \sum_{s' \in S} p(s' \mid s, a) V^{\pi^*}(s') \right)\]
2.1.2. 求解状态效用值(求解贝尔曼等式)
贝尔曼等式是求解 MDP 的基础。如果有 \(n\) 个可能的状态,那么就有 \(n\) 个贝尔曼等式,每个状态一个等式。比如,节 1.1 所示例子中,状态 \((1,1)\) 处的贝尔曼等式为:
其它每个状态也都有一个相应的贝尔曼等式。这 \(n\) 个等式包含了 \(n\) 个未知量(即状态效用值)。我们希望可以同时求解出这 \(n\) 个等式组成的方程组,从而得到所有状态效用值。利用线性代数相关知识可以快速地求解线性方程组,但它不适用于求解贝尔曼等式组成的方程组,因为这些等式是非线性的(其中的“max”运算不是线性运算)。
下面介绍使用“迭代法”求解贝尔曼等式组成的方程组。从任意的初始值开始,我们算出等式右边的值,再把它代入到左边——这相当于 根据它们的邻接状态的效用值来更新每个状态的效用值。如此重复直到达到一种均衡(即各个状态效用值不再变化)。
设 \(V_{n}(s)\) 为状态 \(s\) 在第 \(n\) 次迭代中的效用值,那么贝尔曼更新的迭代步骤为:
\[V_{n+1} (s) = \max_{a \in A} \left( R(s, a) + \gamma \sum_{s' \in S} p(s' \mid s, a)V_{n}(s') \right)\]
注:多次应用贝尔曼更新,它一定会达到均衡,而且均衡时的效用值一定是贝尔曼方程组的唯一解。这里不证明为什么会这样,感兴趣的读者可以参考:《人工智能:一种现代方法(第二版)》17.2.3 价值迭代的收敛。
图 4 是对节 1.1 所示例子进行贝尔曼更新的实例(图片摘自http://mas.cs.umass.edu/classes/cs683/lectures-2010/Lec13_MDP2-F2010-4up.pdf)。
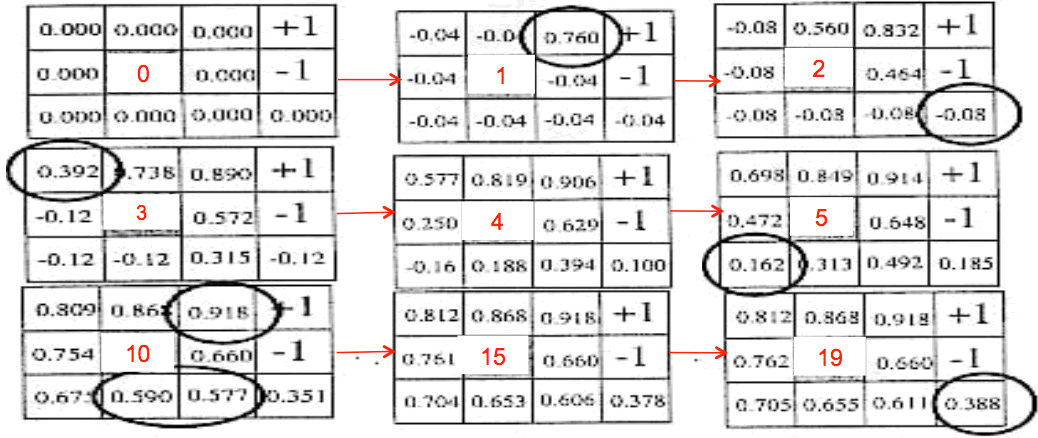
Figure 4: 贝尔曼更新的迭代实例(红色数字为迭代次数)
2.1.3. 求解最优策略
前面介绍过,一旦我们求得了所有状态 \(s\) 的效用值,则最优策略就是:
\[\pi^*(s) = \operatorname{arg} \underset{a \in A}{\max} \left( R(s, a) + \gamma \sum_{s' \in S} p(s' \mid s, a) V^{\pi^*}(s') \right)\]
如,在上节中我们求得了节 1.1 所示例子的状态效用值为图 5 所示。
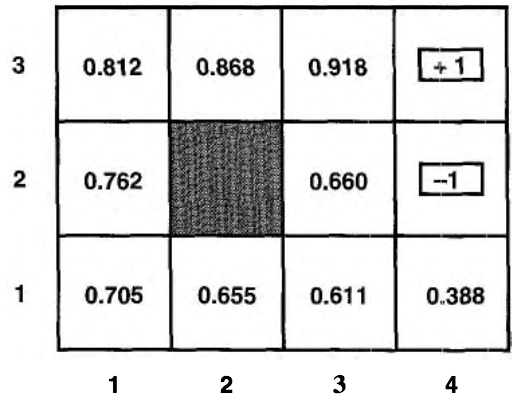
Figure 5: 状态效用值
那么当状态为 \((1,1)\) 时,采用最优策略时的行动是什么呢?我们把状态效用值(图 5 的结论)代入下式:
可知,当状态为 \((1,1)\) 时最优策略的行动为 Up。
2.1.4. 总结:价值迭代算法
前面完整地介绍了价值迭代算法的细节,可总结为图 6 所示(摘自 Markov Decision Processes in Artificial Intelligence, 1.6.2.2 The value iteration algorithm),这个图中 \(r(s,a)\) 就是前面介绍的 \(R(s,a)\) 。

Figure 6: 使用“价值迭代”算法求解 MDP 问题的最优策略
2.2. Policy iteration
策略迭代是求解 MDP 的一种通用框架,思想比较简单。
策略迭代算法从某个初始策略 \(\pi_0\) 开始,交替执行下面的两个步骤:
(1) 策略评价(Policy Evaluation):给定策略 \(\pi_n\) ,计算在这个策略下每个状态的效用值 \(V_n(s)\)
(2) 策略改进(Policy Improvement):已知状态效用值,计算新策略 \(\pi_{n+1} = \operatorname{arg} \underset{a \in A}{\max} \left( R(s, a) + \gamma \sum_{s' \in S} p(s' \mid s, a) V_{n}(s') \right)\)
当上面两个步骤没有产生效用值的改变(或策略的改变)时,算法终止。
“策略迭代”算法如图 7 所示,这个图中 \(r(s,a)\) 就是前面介绍的 \(R(s,a)\) 。

Figure 7: 使用“策略迭代”算法求解 MDP 问题的最优策略
给定策略 \(\pi_n\) ,计算在这个策略下每个状态的效用值 \(V_n(s)\) 要比求解标准贝尔曼等式组成的方程组(价值迭代中就是这样做的)要简单得多,因为策略固定后每个状态中的行动也就固定了:
\[V_n(s) = R(s, \pi_n(s)) + \gamma \sum_{s' \in S} p(s' \mid s, \pi_n(s)) V_{n}(s')\]
假设 \(\pi_n\) 是图 2 (a)所示策略,那么 \(\pi_n(1,1) = Up, \pi_n(1,2) = Up, \cdots\) ,代入上面公式(设 \(\gamma = 1\) )后得到这个策略下每个状态的效用值为:
\[\begin{aligned} V_n(1,1) &= -0.04 + 0.8 V_n(1,2) + 0.1 V_n(1,1) + 0.1 V(2,1)\\
V_n(1,2) &= -0.04 + 0.8 V_n(1,3) + 0.2 V_n(1,2) \\
& \cdots \end{aligned}\]
可以看到上面式子中没有贝尔曼等式中的“max”运行算,它们是普通的线性方程组!采用标准的线性代数方法可以在 \(O(N^3)\) ( \(N\) 为状态数)时间内求解出在某策略下每个状态的效用值。
2.2.1. Value iteration VS. Policy iteration
对于小的状态空间,策略迭代一般能够更快的收敛;但对于状态规模很大的 MDP,策略迭代中求每个状态的效用值 \(O(N^3)\) 的时间复杂度仍然让人望而却步。 策略迭代中“先进行策略评价,再进行策略改进”的这种思想在环境未知的强化学习中应用广泛。
价值迭代(动态规划思想)要求在一个完全已知的环境模型中,这在现实中很少存在。
3. 参考
《人工智能:一种现代方法》第 17 章 制定复杂决策
Markov Decision Processes in Artificial Intelligence