Back Propagation Neural Networks
Table of Contents
1. 反向传播算法和 BP 网络简介
“误差反向传播算法(Error Back Propagation)”的提出,使得多层感知器的模型中神经元的参数的计算变得简单可行。
误差反向传播算法简称反向传播算法(即 BP 算法)。反向传播算法于 1986 年由 David E. Rumelhart 和 James L. McClelland 发表于书籍 Parallel Distributed Processing 中。使用反向传播算法的多层感知器又称为 BP 神经网络 。
BP 算法是一个迭代算法,它的基本思想为:(1) 先计算每一层的状态和激活值,直到最后一层(即信号是前向传播的);(2) 计算每一层的误差,误差的计算过程是从最后一层向前推进的(这就是反向传播算法名字的由来);(3) 更新参数(目标是误差变小),迭代前面两个步骤,直到满足停止准则(比如相邻两次迭代的误差的差别很小)。
参考:Parallel Distributed Processing (1986, by David E. Rumelhart, James L. McClelland), Chapter 8 Learning Internal Representations by Error Propagation: http://psych.stanford.edu/~jlm/papers/PDP/Volume%201/Chap8_PDP86.pdf
本文的记号说明:
- \(n_{l}\) 表示第 \(l\) 层神经元的个数;
- \(f(\cdot)\) 表示神经元的激活函数;
- \(W^{(l)} \in \mathbb{R}^{n_l \times n_{l-1}}\) 表示第 \(l-1\) 层到第 \(l\) 层的权重矩阵;
- \(w^{(l)}_{ij}\) 是权重矩阵 \(W^{(l)}\) 中的元素,表示第 \(l-1\) 层第 \(j\) 个神经元到第 \(l\) 层第 \(i\) 个神经元的连接的权重(注意标号的顺序);
- \(\boldsymbol{b}^{(l)} = (b_1^{(l)}, b_2^{(l)}, \cdots, b_{n_l}^{(l)})^{\mathsf{T}} \in \mathbb{R}^{n_l}\) 表示 \(l-1\) 层到第 \(l\) 层的偏置;
- \(\boldsymbol{z}^{(l)} = (z_1^{(l)}, z_2^{(l)}, \cdots, z_{n_l}^{(l)})^{\mathsf{T}} \in \mathbb{R}^{n_l}\) 表示 \(l\) 层神经元的状态;
- \(\boldsymbol{a}^{(l)} = (a_1^{(l)}, a_2^{(l)}, \cdots, a_{n_l}^{(l)})^{\mathsf{T}} \in \mathbb{R}^{n_l}\) 表示 \(l\) 层神经元的激活值(即输出值)。
关于记号的特别注意 :不同的文献所采用的记号可能不同,这将导致不同文献的公式结论可能不同。如 Andrew Ng的教程 中用 \(W^{(l)}\) 表示的是第 \(l\) 层到第 \(l+1\) 层的权重矩阵。又如,本文用“下标”来标记一个向量的不同分量,而有一些资料却用“上标”来标记向量的不同分量。
下面以三层感知器(即只含有一个隐藏层的多层感知器)为例介绍“反向传播算法(BP 算法)”。
三层感知器如图 1 所示。例子中,输入数据 \(\boldsymbol{x} = (x_1, x_2, x_3)^{\mathsf{T}}\) 是 3 维的(对于第一层,可以认为 \(a^{(1)}_i = x_i\) ),唯一的隐藏层有 3 个节点,输出数据是 2 维的。

Figure 1: 三层感知器实例
2. 信息前向传播
显然,图 1 所示神经网络的第 2 层神经元的状态及激活值可以通过下面的计算得到:
\[\begin{aligned} z^{(2)}_1 &= w^{(2)}_{11} x_1 + w^{(2)}_{12} x_2 + w^{(2)}_{13} x_3 + b^{(2)}_1 \\
z^{(2)}_2 &= w^{(2)}_{21} x_1 + w^{(2)}_{22} x_2 + w^{(2)}_{23} x_3 + b^{(2)}_2 \\
z^{(2)}_3 &= w^{(2)}_{31} x_1 + w^{(2)}_{32} x_2 + w^{(2)}_{33} x_3 + b^{(2)}_3 \\
a^{(2)}_1 &= f(z^{(2)}_1) \\
a^{(2)}_2 &= f(z^{(2)}_2) \\
a^{(2)}_3 &= f(z^{(2)}_3)\end{aligned}\]
类似地,第 3 层神经元的状态及激活值可以通过下面的计算得到:
\[\begin{aligned} z^{(3)}_1 &= w^{(3)}_{11} a^{(2)}_1 + w^{(3)}_{12} a^{(2)}_2 + w^{(3)}_{13} a^{(2)}_3 + b^{(3)}_1 \\
z^{(3)}_2 &= w^{(3)}_{21} a^{(2)}_1 + w^{(3)}_{22} a^{(2)}_2 + w^{(3)}_{23} a^{(2)}_3 + b^{(3)}_2 \\
a^{(3)}_1 &= f(z^{(3)}_1) \\
a^{(3)}_2 &= f(z^{(3)}_2) \end{aligned}\]
可总结出,第 \(l \; (2 \le l \le L)\) 层神经元的状态及激活值为(下面式子是向量表示形式):
\[\begin{aligned} \boldsymbol{z}^{(l)} &= W^{(l)} \boldsymbol{a}^{(l-1)} + \boldsymbol{b}^{(l)} \\
\boldsymbol{a}^{(l)} &= f(\boldsymbol{z}^{(l)})\end{aligned}\]
对于 \(L\) 层感知器,网络的最终输出为 \(\boldsymbol{a}^{(L)}\) 。前馈神经网络中信息的前向传递过程如下:
\[\boldsymbol{x} = \boldsymbol{a}^{(1)} \to \boldsymbol{z}^{(2)} \to \cdots \to \boldsymbol{a}^{(L-1)} \to \boldsymbol{z}^{(L)} \to \boldsymbol{a}^{(L)} = \boldsymbol{y}\]
3. 误差反向传播
“信息前向传播”讲的是已知各个神经元的参数后,如何得到神经网络的输出。但怎么得到各个神经元的参数呢?“误差反向传播”算法解决的就是这个问题。
假设训练数据为 \(\{ (\boldsymbol{x}^{(1)}, \boldsymbol{y}^{(1)}), (\boldsymbol{x}^{(2)}, \boldsymbol{y}^{(2)}), \cdots, (\boldsymbol{x}^{(i)}, \boldsymbol{y}^{(i)}), \cdots, (\boldsymbol{x}^{(N)}, \boldsymbol{y}^{(N)}) \}\) ,即共有 \(N\) 个。又假设输出数据为 \(n_L\) 维的,即 \(\boldsymbol{y}^{(i)} = (y_1^{(i)}, \cdots, y_{n_L}^{(i)})^{\mathsf{T}}\) 。
对某一个训练数据 \((\boldsymbol{x}^{(i)}, \boldsymbol{y}^{(i)})\) 来说,其代价函数可写为:
\[\begin{aligned} E_{(i)} &= \frac{1}{2} \Vert \boldsymbol{y}^{(i)} - \boldsymbol{o}^{(i)} \Vert \\
&= \frac{1}{2} \sum_{k=1}^{n_L} (y_k^{(i)} - o_k^{(i)})^2 \end{aligned}\]
说明 1: \(\boldsymbol{y}^{(i)}\) 为期望的输出(是训练数据给出的已知值), \(\boldsymbol{o}^{(i)}\) 为神经网络对输入 \(\boldsymbol{x}^{(i)}\) 产生的实际输出。
说明 2:代价函数中的系数 \(\frac{1}{2}\) 显然不是必要的,它的存在仅仅是为了后续计算时更方便。
说明 3:以图 1 所示神经网络为例, \(n_L=2, \boldsymbol{y}^{(i)}= (y_1^{(i)}, y_2^{(i)})^{\mathsf{T}}\) ,从而有 \(E_{(i)} = \frac{1}{2} (y_1^{(i)} - a^{(3)}_1)^2 + \frac{1}{2} (y_2^{(i)} - a^{(3)}_2)^2\) ,如果展开到隐藏层,则有 \(E_{(i)} = \frac{1}{2} (y_1^{(i)} - f(w^{(3)}_{11} a^{(2)}_1 + w^{(3)}_{12} a^{(2)}_2 + w^{(3)}_{13} a^{(2)}_3 + b^{(3)}_1))^2 + \frac{1}{2} (y_2^{(i)} - f(w^{(3)}_{21} a^{(2)}_1 + w^{(3)}_{22} a^{(2)}_2 + w^{(3)}_{23} a^{(2)}_3 + b^{(3)}_2))^2\) ,还可以进一步展开到输入层(替换掉 \(a^{(2)}_1, a^{(2)}_2, a^{(2)}_3\) 即可),最后可得: 代价函数 \(E_{(i)}\) 仅和权重矩阵 \(W^{(l)}\) 和偏置向量 \(\boldsymbol{b}^{(l)}\) 相关,调整权重和偏置可以减少或增大代价(误差)。
显然,所有训练数据的总体(平均)代价可写为:
\[E_{total} = \frac{1}{N} \sum_{i=1}^{N} E_{(i)}\]
我们是目标就是调整权重和偏置使总体代价(误差)变小,求得总体代价取最小值时对应的各个神经元的参数(即权重和偏置)。
如果采用梯度下降法(这里其实是“批量梯度下降法”,除此外还可以采用“随机梯度下降法”),可以用下面公式更新参数 \(w_{ij}^{(l)}, b_i^{(l)}, 2 \le l \le L\) :
\[\begin{aligned} W^{(l)} &= W^{(l)} - \mu \frac{\partial E_{total}}{\partial W^{(l)}} \\
&= W^{(l)} - \frac{\mu}{N} \sum_{i=1}^{N} \frac{\partial E_{(i)}}{\partial W^{(l)}} \\
\boldsymbol{b}^{(l)} &= \boldsymbol{b}^{(l)} - \mu \frac{\partial E_{total}}{\partial \boldsymbol{b}^{(l)}} \\
&= \boldsymbol{b}^{(l)} - \frac{\mu}{N} \sum_{i=1}^{N} \frac{\partial E_{(i)}}{\boldsymbol{b}^{(l)}} \\
\end{aligned}\]
由上面公式知,只需求得每一个训练数据的代价函数 \(E_{(i)}\) 对参数的偏导数 \(\frac{\partial E_{(i)}}{\partial W^{(l)}}, \frac{\partial E_{(i)}}{\boldsymbol{b}^{(l)}}\) 即可得到参数的迭代更新公式。
为简单起见,在下文的推导中,我们去掉 \(E_{(i)}\) 的下标,直接记为 \(E\) (要理解它是单个训练数据的误差)。
下面将介绍用“反向传播算法”求解单个训练数据误差对参数的偏导数 \(\frac{\partial E}{\partial W^{(l)}}\) 和 \(\frac{\partial E}{\partial \boldsymbol{b}^{(l)}}\) 的过程。我们求解一个简单的情况:图 1 所示神经网络,最后再归纳出通用公式。
参考:
How the backpropagation algorithm works: http://neuralnetworksanddeeplearning.com/chap2.html
Backpropagation Algorithm: http://deeplearning.stanford.edu/wiki/index.php/Backpropagation_Algorithm
3.1. 输出层的权重参数更新
把 \(E\) 展开到隐藏层,有:
\[\begin{aligned} E &= \frac{1}{2} \Vert \boldsymbol{y} - \boldsymbol{o} \Vert \\
&= \frac{1}{2} \Vert \boldsymbol{y} - \boldsymbol{a}^{(3)} \Vert \\
&= \frac{1}{2} \left((y_1 - a_1^{(3)})^2 + (y_2 - a_2^{(3)})^2 \right) \\
&= \frac{1}{2} \left((y_1 - f(z_1^{(3)}))^2 + (y_2 - f(z_2^{(3)}))^2 \right) \\
&= \frac{1}{2} \left((y_1 - f(w^{(3)}_{11} a^{(2)}_1 + w^{(3)}_{12} a^{(2)}_2 + w^{(3)}_{13} a^{(2)}_3 + b^{(3)}_1))^2 + (y_2 - f(w^{(3)}_{21} a^{(2)}_1 + w^{(3)}_{22} a^{(2)}_2 + w^{(3)}_{23} a^{(2)}_3 + b^{(3)}_2))^2 \right) \end{aligned}\]
由求导的链式法则,对“输出层神经元的权重参数”求偏导,有:
\[\begin{aligned} \frac{\partial E}{\partial w^{(3)}_{11}} &= \frac{1}{2} \cdot 2 (y_1 - a_1^{(3)})(- \frac{\partial a_1^{(3)}}{\partial w^{(3)}_{11}}) \\
&= - (y_1 - a_1^{(3)}) f'(z_1^{(3)}) \frac{\partial z_1^{(3)}}{\partial w^{(3)}_{11}} \\
&= - (y_1 - a_1^{(3)}) f'(z_1^{(3)}) a_1^{(2)} \end{aligned}\]
如果我们把 \(\frac{\partial E}{\partial z_i^{(l)}}\) 记为 \(\delta_i^{(l)}\) ,即规定下面定义:
\[\delta_i^{(l)} \equiv \frac{\partial E}{\partial z_i^{(l)}}\]
则 \(\frac{\partial E}{\partial w^{(3)}_{11}}\) 显然可以写为:
\[\begin{aligned} \frac{\partial E}{\partial w^{(3)}_{11}} &= \frac{\partial E}{\partial z_1^{(3)}} \frac{\partial z_1^{(3)}}{\partial w^{(3)}_{11}} \\
&= \delta_1^{(3)} a_1^{(2)} \end{aligned}\]
其中: \(\delta_1^{(3)} = \frac{\partial E}{\partial z_1^{(3)}} = \frac{\partial E}{\partial a_1^{(3)}} \frac{\partial a_1^{(3)}}{\partial z_1^{(3)}} = - (y_1 - a_1^{(3)}) f'(z_1^{(3)})\)
对于输出层神经元的其它权重参数,同样可求得:
\[\begin{aligned} \frac{\partial E}{\partial w^{(3)}_{12}} = \delta_1^{(3)} a_2^{(2)} \\
\frac{\partial E}{\partial w^{(3)}_{13}} = \delta_1^{(3)} a_3^{(2)} \\
\frac{\partial E}{\partial w^{(3)}_{21}} = \delta_2^{(3)} a_1^{(2)} \\
\frac{\partial E}{\partial w^{(3)}_{22}} = \delta_2^{(3)} a_2^{(2)} \\
\frac{\partial E}{\partial w^{(3)}_{23}} = \delta_2^{(3)} a_3^{(2)} \\
\end{aligned}\]
其中, \(\delta_2^{(3)} = -(y_2 - a_2^{(3)}) f'(z_2^{(3)})\)
说明: 之所以要引入记号 \(\delta_i^{(l)}\) ,除了它能简化 \(\frac{\partial E}{\partial w^{(l)}_{ij}}\) 和 \(\frac{\partial E}{\partial b^{(l)}_i}\) 的表达形式外;更重要的是我们可以通过 \(\delta_i^{(l+1)}\) 来求解 \(\delta_i^{(l)}\) (后文将说明),这样可以充分利用之前计算过的结果来加快整个计算过程。
推广到一般情况,假设神经网络共 \(L\) 层,则:
\[\begin{aligned} & \delta_i^{(L)} = - (y_i - a_i^{(L)}) f'(z_i^{(L)}) && (1 \le i \le n_L) \\
& \frac{\partial E}{\partial w^{(L)}_{ij}} = \delta_i^{(L)} a_j^{(L-1)} && (1 \le i \le n_L, 1 \le j \le n_{L-1}) \end{aligned}\]
如果把上面两式表达为矩阵(向量)形式,则为:
\[\begin{aligned} & \boldsymbol{\delta}^{(L)} = - (\boldsymbol{y} - \boldsymbol{a}^{(L)}) \odot f'(\boldsymbol{z}^{(L)}) \\
& \nabla_{W^{(L)}} E = \boldsymbol{\delta}^{(L)} (\boldsymbol{a}^{(L-1)})^{\mathsf{T}} \\
\end{aligned}\]
注:符号 \(\odot\) 表示 Element-wise Product Operator,又称作 Hadamard product 。规则简单,把对应位置的元素分别相乘即可。如:
\[\left( \begin{array}{cc}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{array} \right) \odot \left( \begin{array}{cc}
b_{11} & b_{12} \\
b_{21} & b_{22} \\
b_{31} & b_{32}
\end{array} \right) = \left( \begin{array}{cc}
a_{11}b_{11} & a_{12}b_{12} \\
a_{21}b_{21} & a_{22}b_{22} \\
a_{31}b_{31} & a_{32}b_{32}
\end{array} \right)\]
向量式子 \(\boldsymbol{\delta}^{(L)} = - (\boldsymbol{y} - \boldsymbol{a}^{(L)}) \odot f'(\boldsymbol{z}^{(L)})\) 在前面的例子中,表达的就是这两个式子:
\[\begin{aligned} \delta_1^{(3)} = - (y_1 - a_1^{(3)}) f'(z_1^{(3)}) \\
\delta_2^{(3)} = -(y_2 - a_2^{(3)}) f'(z_2^{(3)})
\end{aligned}\]
3.2. 隐藏层的权重参数更新
对“隐藏层神经元的权重参数”求偏导,利用 \(\delta_i^{(l)}\) 的定义,有:
\[\begin{aligned} \frac{\partial E}{\partial w^{(l)}_{ij}} &= \frac{\partial E}{\partial z_i^{(l)}} \frac{\partial z_i^{(l)}}{\partial w^{(l)}_{ij}} \\
&= \delta_i^{(l)} \frac{\partial z_i^{(l)}}{\partial w^{(l)}_{ij}} \\
&= \delta_i^{(l)} a_j^{(l-1)} \\
\end{aligned}\]
其中 \(\delta_i^{(l)}, 2 \le l \le L-1\) 的推导如下:
\[\begin{aligned} \delta_i^{(l)} & \equiv \frac{\partial E}{\partial z_i^{(l)}} \\
&= \sum_{j=1}^{n_{l+1}} \frac{\partial E}{\partial z_j^{(l+1)}} \frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}} \\
&= \sum_{j=1}^{n_{l+1}} \delta_j^{(l+1)} \frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}} \\
\end{aligned}\]
上面式子中为什么有 \(\frac{\partial E}{\partial z_i^{(l)}} = \sum_{j=1}^{n_{l+1}} \frac{\partial E}{\partial z_j^{(l+1)}} \frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}\) 呢?其实利用的仅是“函数之和的求导法则”及“求导的链式法则”。如果把 \(E\) 从后往前展开,当展开到 \(l+1\) 层时, \(E\) 可看作是 \(\boldsymbol{z}^{(l+1)}\) 的函数;如果再往前展开一层到 \(l\) 层, \(E\) 可看作是 \(\boldsymbol{z}^{(l)}\) 的函数。 \(E\) 对 \(l\) 层的某个 \(z_i^{(l)}\) 求导时, 由于 \(l+1\) 层的每个神经元都和 \(z_i^{(l)}\) 所在神经元有连接,所以在函数 \(E\) 中,自变量 \(z_i^{(l)}\) 出现了 \(n_{l+1}\) 次,出现的每一次对应一个 \(z_j^{(l+1)}, 1 \le j \le n_{l+1}\) ,从而由“函数之和的求导法则”及“求导的链式法则”有:
\[\begin{aligned} \frac{\partial E}{\partial z_i^{(l)}} &= \frac{\partial E}{\partial z_1^{(l+1)}} \frac{\partial z_1^{(l+1)}}{\partial z_i^{(l)}} + \frac{\partial E}{\partial z_2^{(l+1)}} \frac{\partial z_2^{(l+1)}}{\partial z_i^{(l)}} + \cdots + \frac{\partial E}{\partial z_{n_{l+1}}^{(l+1)}} \frac{\partial z_{n_{l+1}}^{(l+1)}}{\partial z_i^{(l)}} \\
&= \sum_{j=1}^{n_{l+1}} \frac{\partial E}{\partial z_j^{(l+1)}} \frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}} \\
\end{aligned}\]
上面的推导过程可以从图 2 中更清楚地展示出来。
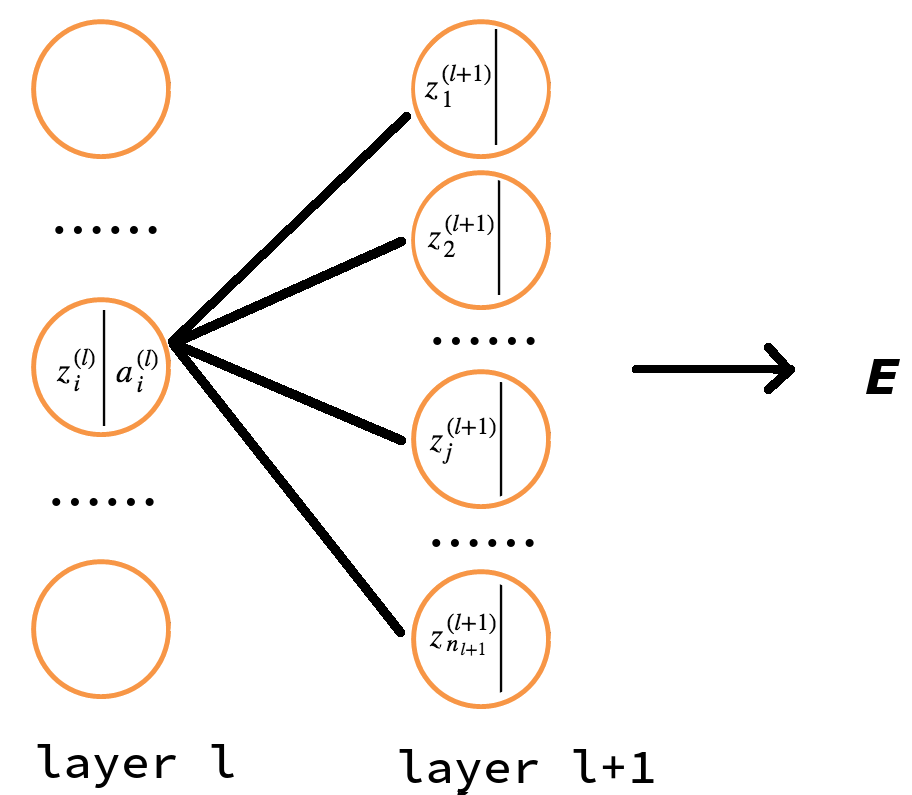
Figure 2: 由 \(\boldsymbol{\delta}^{(l+1)}\) 求 \(\delta_i^{(l)}\)
看一个简单的特例,如在图 1 所示神经网络中,有 \(\frac{\partial E}{\partial z_1^{(2)}} = \sum_{j=1}^{2} \frac{\partial E}{\partial z_j^{(3)}} \frac{\partial z_j^{(3)}}{\partial z_1^{(2)}}\)
由于 \(z_j^{(l+1)} = \sum_{i=1}^{n_l} w_{ji}^{(l+1)} a_i^{(l)} + b_j^{(l+1)} = \sum_{i=1}^{n_l} w_{ji}^{(l+1)} f(z_i^{(l)}) + b_j^{(l+1)}\) ,所以有 \(\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}} = \frac{\partial z_j^{(l+1)}}{\partial a_i^{(l)}} \frac{\partial a_i^{(l)}}{\partial z_i^{(l)}} = w_{ji}^{(l+1)} f'(z_i^{(l)})\) ,代入到前面计算的 \(\delta_i^{(l)}\) 式中,从而有:
\[\begin{aligned} {\color{red}{\delta_i^{(l)}}} &= \sum_{j=1}^{n_{l+1}} \delta_j^{(l+1)} w_{ji}^{(l+1)} f'(z_i^{(l)}) \\
&= {\color{red}{\left( \sum_{j=1}^{n_{l+1}} \delta_j^{(l+1)} w_{ji}^{(l+1)} \right) f'(z_i^{(l)})}} \\
\end{aligned}\]
上式是 BP 算法最核心的公式。它利用 \(l+1\) 层的 \(\boldsymbol{\delta}^{(l+1)}\) 来计算 \(l\) 层的 \(\boldsymbol{\delta}^{(l)}\) ,这就是“误差反向传播算法”名字的由来。 如果把它表达为矩阵(向量)形式,则为:
\[\boldsymbol{\delta}^{(l)} = \left((W^{(l+1)})^{\mathsf{T}} \boldsymbol{\delta}^{(l+1)} \right) \odot f'(\boldsymbol{z}^{(l)})\]
利用上面推导出来的隐藏层通用公式,对于图 1 所示神经网络,有:
\[\begin{gathered} \frac{\partial E}{\partial w^{(2)}_{11}} = \left(\delta_1^{(3)} w^{(3)}_{11} + \delta_2^{(3)} w^{(3)}_{21} \right) f'(z_1^{(2)}) a_1^{(1)} \\
\frac{\partial E}{\partial w^{(2)}_{12}} = \left(\delta_1^{(3)} w^{(3)}_{11} + \delta_2^{(3)} w^{(3)}_{21} \right) f'(z_1^{(2)}) a_2^{(1)} \\
\frac{\partial E}{\partial w^{(2)}_{13}} = \left(\delta_1^{(3)} w^{(3)}_{11} + \delta_2^{(3)} w^{(3)}_{21} \right) f'(z_1^{(2)}) a_3^{(1)} \\
\frac{\partial E}{\partial w^{(2)}_{21}} = \left(\delta_1^{(3)} w^{(3)}_{12} + \delta_2^{(3)} w^{(3)}_{22} \right) f'(z_2^{(2)}) a_1^{(1)} \\
\frac{\partial E}{\partial w^{(2)}_{22}} = \left(\delta_1^{(3)} w^{(3)}_{12} + \delta_2^{(3)} w^{(3)}_{22} \right) f'(z_2^{(2)}) a_2^{(1)} \\
\frac{\partial E}{\partial w^{(2)}_{23}} = \left(\delta_1^{(3)} w^{(3)}_{12} + \delta_2^{(3)} w^{(3)}_{22} \right) f'(z_2^{(2)}) a_3^{(1)} \\
\frac{\partial E}{\partial w^{(2)}_{31}} = \left(\delta_1^{(3)} w^{(3)}_{13} + \delta_2^{(3)} w^{(3)}_{23} \right) f'(z_3^{(2)}) a_1^{(1)} \\
\frac{\partial E}{\partial w^{(2)}_{32}} = \left(\delta_1^{(3)} w^{(3)}_{13} + \delta_2^{(3)} w^{(3)}_{23} \right) f'(z_3^{(2)}) a_2^{(1)} \\
\frac{\partial E}{\partial w^{(2)}_{33}} = \left(\delta_1^{(3)} w^{(3)}_{13} + \delta_2^{(3)} w^{(3)}_{23} \right) f'(z_3^{(2)}) a_3^{(1)} \\
\end{gathered}\]
通过把 \(E\) 继续展开到输入层可以验证上面这些式子:
\[\tiny \begin{aligned}
E\! &= \frac{1}{2} \Vert \boldsymbol{y} - \boldsymbol{o} \Vert \\
&= \frac{1}{2} \Vert \boldsymbol{y} - \boldsymbol{a}^{(3)} \Vert \\
&= \frac{1}{2} \left((y_1 - a_1^{(3)})^2 + (y_2 - a_2^{(3)})^2 \right) \\
&= \frac{1}{2} \left((y_1 - f(z_1^{(3)}))^2 + (y_2 - f(z_2^{(3)}))^2 \right) \\
&= \frac{1}{2} \left((y_1 - f(w^{(3)}_{11} a^{(2)}_1 + w^{(3)}_{12} a^{(2)}_2 + w^{(3)}_{13} a^{(2)}_3 + b^{(3)}_1))^2 + (y_2 - f(w^{(3)}_{21} a^{(2)}_1 + w^{(3)}_{22} a^{(2)}_2 + w^{(3)}_{23} a^{(2)}_3 + b^{(3)}_2))^2 \right) \\
&= \frac{1}{2} \left((y_1 - f(w^{(3)}_{11} f(z^{(2)}_1) + w^{(3)}_{12} f(z^{(2)}_2) + w^{(3)}_{13} f(z^{(2)}_3) + b^{(3)}_1))^2 + (y_2 - f(w^{(3)}_{21} f(z^{(2)}_1) + w^{(3)}_{22} f(z^{(2)}_2) + w^{(3)}_{23} f(z^{(2)}_3) + b^{(3)}_2))^2 \right) \\
&= \frac{1}{2}\! \left(y_1\! -\! f\! \left(w^{(3)}_{11} f( {\color{red}{w^{(2)}_{11}}} a^{(1)}_1 + w^{(2)}_{12} a^{(1)}_2 + w^{(2)}_{13} a^{(1)}_3 + b^{(2)}_1) + w^{(3)}_{12} f(w^{(2)}_{21} a^{(1)}_1 + w^{(2)}_{22} a^{(1)}_2 + w^{(2)}_{23} a^{(1)}_3 + b^{(2)}_2)\! +\! w^{(3)}_{13} f(w^{(2)}_{31} a^{(1)}_1 + w^{(2)}_{32} a^{(1)}_2 + w^{(2)}_{33} a^{(1)}_3 + b^{(2)}_3) + b^{(3)}_1 \right)\! \right)^2 \\
& \; + \frac{1}{2}\! \left(y_2\! -\! f\! \left(w^{(3)}_{21} f( {\color{red}{w^{(2)}_{11}}} a^{(1)}_1 + w^{(2)}_{12} a^{(1)}_2 + w^{(2)}_{13} a^{(1)}_3 + b^{(2)}_1) + w^{(3)}_{22} f(w^{(2)}_{21} a^{(1)}_1 + w^{(2)}_{22} a^{(1)}_2 + w^{(2)}_{23} a^{(1)}_3 + b^{(2)}_2)\! +\! w^{(3)}_{23} f(w^{(2)}_{31} a^{(1)}_1 + w^{(2)}_{32} a^{(1)}_2 + w^{(2)}_{33} a^{(1)}_3 + b^{(2)}_3) + b^{(3)}_2 \right)\! \right)^2
\end{aligned}\]
上式中, \(a^{(1)}_i = x_i\) ,也就是某个训练数据的第 \(i\) 个维度,可参考图 1 中的表示。
3.3. 输出层和隐藏层的偏置参数更新
\[\begin{aligned} \frac{\partial E}{\partial b_i^{(l)}} &= \frac{\partial E}{\partial z_i^{(l)}} \frac{\partial z_i^{(l)}}{ b_i^{(l)}} \\
&= \delta_i^{(l)} \end{aligned}\]
对应的矩阵(向量)形式为:
\[\nabla_{b^{(l)}} E = \boldsymbol{\delta}^l\]
3.4. BP 算法四个核心公式
前面已经完整地介绍了误差反向传播算法,可总结为下面四个公式:
这四个公式可以写成对应的矩阵(向量)形式:
或者表示为:
3.5. BP 算法计算某个训练数据的代价函数对参数的偏导数
BP 算法四个核心公式就是求某个训练数据的代价函数对参数的偏导数,它的具体应用步骤总结如下:
第一步,初始化参数 \(W, \boldsymbol{b}\) 。
一般地,把 \(w_{ij}^{(l)}, b_i^{(l)}, 2 \le l \le L\) 初始化为一个很小的,接近于零的随机值。
注意:不要把 \(w_{ij}^{(l)}, b_i^{(l)}, 2 \le l \le L\) 全部初始化为零或者相同的其它值,这会导致对于所有 \(i\) , \(w_{ij}^{(l)}\) 都会取相同的值。
第二步,利用下面的“前向传播”公式计算每层的状态和激活值:
\[\begin{aligned} \boldsymbol{z}^{(l)} &= W^{(l)} \boldsymbol{a}^{(l-1)} + \boldsymbol{b}^{(l)} \\
\boldsymbol{a}^{(l)} &= f(\boldsymbol{z}^{(l)})\end{aligned}\]
第三步,计算 \(\boldsymbol{\delta}^{(l)}\)
首先,利用下面公式计算输出层的 \(\boldsymbol{\delta}^{(L)}\)
\[\delta_i^{(L)} = - (y_i - a_i^{(L)}) f'(z_i^{(L)}), \quad (1 \le i \le n_L)\]
其中, \(y_i\) 是期望的输出(这是训练数据给出的已知值), \(a_i^{(L)}\) 是神经网络对训练数据产生的实际输出。
然后,利用下面公式从第 \(L-1\) 层到第 2 层依次计算隐藏层的 \(\boldsymbol{\delta}^{(l)}, (l = L-1, L-2, L-3, \cdots, 2)\)
\[\delta_i^{(l)} = \left( \sum_{j=1}^{n_{l+1}} \delta_j^{(l+1)} w_{ji}^{(l+1)} \right) f'(z_i^{(l)}), \quad (1 \le i \le n_l)\]
第四步,按下面公式求这个训练数据的代价函数对参数的偏导数:
\[\begin{align*}
& \frac{\partial E}{\partial w^{(l)}_{ij}} = \delta_i^{(l)} a_j^{(l-1)} \\
& \frac{\partial E}{\partial b_i^{(l)}} = \delta_i^{(l)} \\
\end{align*}\]
工程实现中注意事项:
在前面传播的过程中,我们已经计算出了所有的 \(a_i^{(l)}\) ,反向传播过程中的 \(f'(z_i^{(l)})\) 可以直接利用 \(a_i^{(l)}\) 来计算。
假设使用的激活函数为 \(f(x) = \frac{1}{1 + e^{-x}}\) ,则 \(f'(x) = -2 \times \frac{1}{(1+e^{-x})^2} \times e^{-x} \times (-1) = \frac{2e^{-x}}{(1+e^{-x})^2}\) ,容易验证它又等于 \(f(x)(1-f(x))\) ,因此: \(f'(z_i^{(l)}) = a_i^{(l)} (1 - a_i^{(l)})\)
3.5.1. 反向传播中偏导数计算实例
3.6. BP 算法总结:用“批量梯度下降”算法更新参数
“批量梯度下降”算法更新参数的总结如下:
(1) 用 BP 算法四个核心公式求得每一个训练数据的代价函数对参数的偏导数;
(2) 按下面公式更新参数:
\[\begin{aligned} W^{(l)} &= W^{(l)} - \frac{\mu}{N} \sum_{i=1}^{N} \frac{\partial E_{(i)}}{\partial W^{(l)}} \\
\boldsymbol{b}^{(l)} &= \boldsymbol{b}^{(l)} - \frac{\mu}{N} \sum_{i=1}^{N} \frac{\partial E_{(i)}}{\boldsymbol{b}^{(l)}} \\
\end{aligned}\]
(3) 迭代执行第(1),(2)步,直到满足停止准则(比如相邻两次迭代的误差的差别很小,或者直接限制迭代的次数)。
说明:每对参数进行一次更新都要遍历整个训练数据集,当训练数据集不大时这不是问题,当训练数据集非常巨大时,可以采用“随机梯度下降法”(每次仅使用一个训练数据来更新参数)。
4. 梯度消失问题及其解决办法
前面介绍过,误差反向传播有下面迭代公式:
\[\delta_i^{(l)} = \left( \sum_{j=1}^{n_{l+1}} \delta_j^{(l+1)} w_{ji}^{(l+1)} \right) f'(z_i^{(l)})\]
其中用到了激活函数 \(f(x)\) 的导数。误差从输出层反向传播时,在每一层都要乘以激活函数 \(f(x)\) 的导数。
如果我们使用 \(\sigma(x)\) 或 \(\tanh(x)\) 作为激活函数,则其导数为:
\[\begin{aligned} \sigma'(x) &= \sigma(x) (1 - \sigma(x)) \in [0, 0.25] \\
\tanh'(x) &= 1 - (\tanh(x))^2 \in [0, 1] \end{aligned}\]
可以看到,它们的导数的值域都会小于 1。这样,误差经过每一层传递都会不断地衰减。 当网络导数比较多时,梯度不断地衰减,甚至消失,这使得整个网络很难训练。这就是梯度消失问题(Vanishing gradient problem)。
减轻梯度消失问题的一个方法是使用线性激活函数(比如 rectifier 函数)或近似线性函数(比如 softplus 函数)。这样,激活函数的导数为 1,误差可以很好地传播,训练速度会提高。
参考:
神经网络与深度学习讲义(邱锡鹏)