NumPy
Table of Contents
1. NumPy 简介
NumPy (Numeric Python) is the fundamental package for scientific computing with Python.
NumPy 是一个运行速度非常快的数学库,主要用于数组计算。它可以让你在 Python 中使用向量和数学矩阵,以及许多用 C 语言实现的底层函数,你还可以体验到很好的运行效率。
参考:
http://www.numpy.org/
https://docs.scipy.org/doc/numpy/user/quickstart.html
NumPy Reference
http://old.sebug.net/paper/books/scipydoc/numpy_intro.html
2. NumPy 基础:ndarray
NumPy 中定义的最重要的对象是称为 ndarray 的 N 维数组类型,它是相同类型元素的集合。
下面是创建 2 维数组(大小为 2x3)和 3 维数组(大小为 2x3x4)的简单例子:
>>> import numpy as np
>>> x = np.array([[1, 2, 3], [4, 5, 6]])
>>> type(x)
<type 'numpy.ndarray'>
>>> x.shape
(2, 3)
>>> y = np.array([[[ 0, 1, 2, 3],
[ 3, 4, 5, 6],
[ 6, 7, 8, 9]],
[[18, 19, 20, 21],
[21, 22, 23, 24],
[24, 25, 26, 27]]])
>>> y.shape
(2, 3, 4)
2.1. ndarray 常见属性
表 1 是 ndarray 的常见属性。
| ndarray 属性 | 描述 |
|---|---|
| ndim | 数组维度。前面例子中 x.ndim=2 |
| shape | 形状,即多少行和列。前面例子中 x.shape=(2, 3) |
| size | 元素个数。前面例子中 x.size=6 |
| dtype | 元素类型。前面例子中 x.dtype=dtype('int64') |
| itemsize | 每一个条目所占的字节。前面例子中 x.itemsize=8 |
| nbytes | 所有元素占的字节。前面例子中 x.nbytes=48 |
2.1.1. ndarray 内存布局
ndarray 数组在内存中是连续内存块。有两种策略来组织多维数据:一种是 column-major order(Fortran 和 Matlab 采用这种策略),另一种是 row-major order(C 语言中采用这种策略)。如图 1 (摘自 Guide to NumPy, 2.3.1 Contiguous Memory Layout)所示。
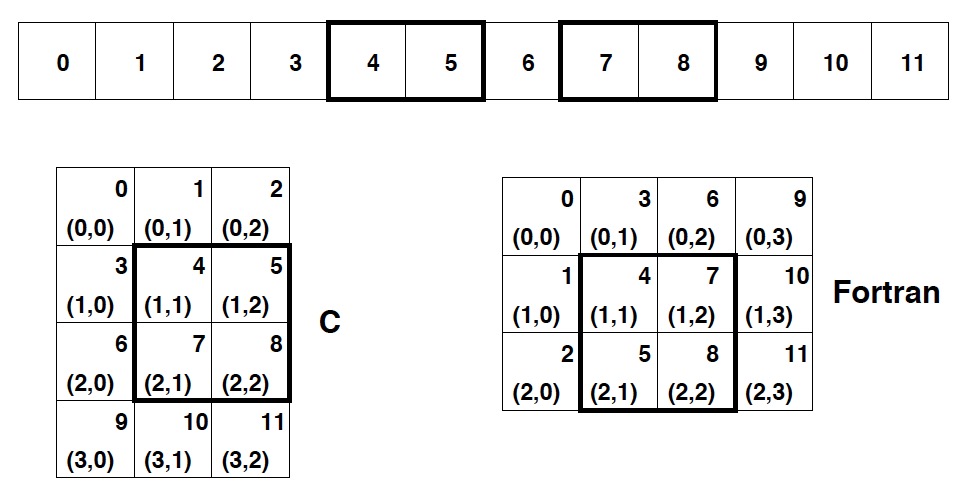
Figure 1: Options for memory layout of a 2-dimensional array
ndarray 既支持 C 风格的内存布局,也支持 Fortran 风格的内存布局。 默认为 C 风格,进行转置操作后变为 Fortran 风格的内存布局。
>>> x = np.array([[1, 2, 3], [4, 5, 6]]) >>> x.flags C_CONTIGUOUS : True # 表明x使用的是C风格的内存布局 F_CONTIGUOUS : False OWNDATA : True WRITEABLE : True ALIGNED : True UPDATEIFCOPY : False >>> y = x.transpose() >>> y.flags C_CONTIGUOUS : False F_CONTIGUOUS : True # 表明y使用的是Fortran风格的内存布局 OWNDATA : False WRITEABLE : True ALIGNED : True UPDATEIFCOPY : False
对于一维数组,显然既是 C 风格,又是 Fortran 风格的内存布局。
>>> x = np.array([0, 1, 2]) # 一维数组,显然既是C风格,又是Fortran风格的内存布局 >>> x.flags C_CONTIGUOUS : True F_CONTIGUOUS : True OWNDATA : True WRITEABLE : True ALIGNED : True UPDATEIFCOPY : False
2.2. 创建 ndarray
表 2 是创建 ndarray 的一些函数。
| 创建 ndarray 的函数 | 说明 |
|---|---|
| array | 创建 ndarray |
| empty | 创建未初始化的 ndarray |
| zeros | 创建全为 0 的 ndarray |
| ones | 创建全为 1 的 ndarray |
| full | 创建全为指定元素的 ndarray |
| identity | 创建单位矩阵 |
| eye | 创建对角线(可指定哪个对角线)为 1,其它元素为 0 的二维数组 |
| arange | 基于开始值、终值和步长来创建一维数组 |
| linspace | 基于开始值、终值和元素个数来创建一维数组 |
| logspace | 和 linspace 类似,对数刻度上均匀分布的一维数据 |
| frombuffer | 从 buffer 创建数组 |
| fromstring | 从 string 序列中创建数组 |
| fromfunction | 从函数创建数组 |
| fromfile | 基于 tofile 命令保存的文件创建 ndarray |
| load | 基于 save 命令保存的文件创建 ndarray |
| loadtxt | 基于 csv 文本文件内容创建 ndarray |
参考:https://docs.scipy.org/doc/numpy/reference/routines.array-creation.html
2.2.1. 基于 CSV 文件创建 ndarray(loadtxt 实例)
假设“1.txt”内容如下。
$ cat 1.txt 0, 1, 2 3, 4, 5
使用 loadtxt 可以把文本文件中的数据加载为 ndarray。如:
>>> import numpy as np
>>> x = np.loadtxt("1.txt", delimiter=",") # 指定分隔符为逗号,默认使用空格为分隔符
>>> x
array([[ 0., 1., 2.],
[ 3., 4., 5.]])
2.3. 存取元素(Indexing & Slicing)
数组元素的存取方法和 Python 的标准方法相同,如:
>>> a = np.arange(10) >>> a array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) >>> a[4] # 用整数作为下标可以获取数组中的某个元素 4 >>> a[1:3] # 用范围作为下标获取数组的一个切片,含头(a[1])不含尾(a[3]) array([1, 2]) >>> a[:3] # 省略开始下标,表示从a[0]开始 array([0, 1, 2]) >>> a[:-2] # 下标可以使用负数,表示从数组后往前数 array([0, 1, 2, 3, 4, 5, 6, 7]) >>> a[0:5:2] # 开始下标0,结束下标5,步长2 array([0, 2, 4])
和 Python 的列表序列不同, NumPy 中通过“下标范围”获取的新的数组是原始数组的一个视图。也就是说它与原始数组共享同一块数据空间:
>>> a array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) >>> b=a[1:3] # 通过“下标范围”获取的新的数组是原始数组的一个视图 >>> b[0]=99 # 修改了b[0] >>> a array([ 0, 99, 2, 3, 4, 5, 6, 7, 8, 9]) # a也被修改了
2.3.1. 多维数组
多维数组有多个轴,所以它的下标需要用多个值来表示,NumPy 中采用组元(tuple)表示数组的下标,也就是用逗号分开多个轴的索引。请看下面实例:
>>> import numpy as np
>>> x = np.array([[ 0, 1, 2, 3, 4, 5],
... [10, 11, 12, 13, 14, 15],
... [20, 21, 22, 23, 24, 25],
... [30, 31, 32, 33, 34, 35],
... [40, 41, 42, 43, 44, 45],
... [50, 51, 52, 53, 54, 55]])
>>>
>>> x[0]
array([0, 1, 2, 3, 4, 5])
>>> x[1]
array([10, 11, 12, 13, 14, 15])
>>> x[1, 4] # 逗号分开。逗号前是0轴索引,逗号后是1轴索引。
14
>>> x[0, 2:5] # 逗号分开。逗号前是0轴索引,逗号后是1轴索引。
array([2, 3, 4])
>>> x[1, 2:5] # 逗号分开。逗号前是0轴索引,逗号后是1轴索引。
array([12, 13, 14])
>>> x[:, 2]
array([ 2, 12, 22, 32, 42, 52])
>>> x[1:4, 2:6] # 逗号分开。逗号前是0轴索引,逗号后是1轴索引。
array([[12, 13, 14, 15],
[22, 23, 24, 25],
[32, 33, 34, 35]])
>>> x[1:, 2:6] # 逗号分开。逗号前是0轴索引,逗号后是1轴索引。
array([[12, 13, 14, 15],
[22, 23, 24, 25],
[32, 33, 34, 35],
[42, 43, 44, 45],
[52, 53, 54, 55]])
下面是设置子多维数组元素为同一个数字的例子:
>>> x[1:4, 2:6] = [[100, 100, 100, 100], [100, 100, 100, 100], [100, 100, 100, 100]]
>>> x[1:4, 2:6]
array([[100, 100, 100, 100],
[100, 100, 100, 100],
[100, 100, 100, 100]])
当然没必要像上面这么繁琐,使用“Broadcast”(后文有介绍)可以更加简单:
>>> x[1:4, 2:6] = 100 # 发生Broadcast
>>> x[1:4, 2:6]
array([[100, 100, 100, 100],
[100, 100, 100, 100],
[100, 100, 100, 100]])
>>> x[1:4, 2:6] = [100, 100, 100, 100] # 发生Broadcast
>>> x[1:4, 2:6]
array([[100, 100, 100, 100],
[100, 100, 100, 100],
[100, 100, 100, 100]])
>>> x[1:4, 2:6] = [1, 2, 3, 4] # 发生Broadcast
>>> x[1:4, 2:6]
array([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
2.3.2. 高级索引:整数序列索引
可以使用“整数序列”对数组元素进行存取,这时将使用整数序列中的每个元素作为下标,整数序列可以是 Python 中的列表或者 NumPy 中的数组。 使用整数序列作为下标获得的数组不和原始数组共享数据空间。 例如:
>>> import numpy as np >>> x = np.array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0]) >>> y = x[[0, 2, 3]] # 使用整数序列 [0, 2, 3] 对数组元素进行存取,相当于以序列中每个元素作为下标进行索引。 >>> y array([9, 7, 6]) >>> y[0] = 1111 # 使用整数序列作为下标获得的数组y和原数组x不共享空间。修改y,不会影响到x。 >>> y array([1111, 7, 6]) >>> x array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
下面是多维数组中,使用整数序列索引的例子:
>>> import numpy as np
>>> x = np.array([[ 0, 1, 2, 3, 4, 5],
... [10, 11, 12, 13, 14, 15],
... [20, 21, 22, 23, 24, 25],
... [30, 31, 32, 33, 34, 35],
... [40, 41, 42, 43, 44, 45],
... [50, 51, 52, 53, 54, 55]])
>>>
>>> x[2, [1,2,3,5]] # 第0轴是一个数,第1轴是整数序列 [1,2,3,5]
array([21, 22, 23, 25])
>>> x[2:, [1,2,3,5]] # 第0轴是一个范围,第1轴是整数序列 [1,2,3,5]
array([[21, 22, 23, 25],
[31, 32, 33, 35],
[41, 42, 43, 45],
[51, 52, 53, 55]])
2.3.3. 高级索引:布尔数组索引
当使用布尔数组 b 作为下标存取数组 x 中的元素时,将收集数组 x 中所有在数组 b 中对应下标为 True 的元素。 使用布尔数组作为下标获得的数组不和原始数组共享数据空间。 注意这种方式只对应于 NumPy 中的布尔数组,不能使用 Python 中的布尔列表。
>>> import numpy as np >>> x = np.array([4, 3, 2, 1, 0]) >>> x[np.array([True, False, False, True])] # 使用布尔数组 np.array([True, False, False, True]) 作为索引,收集数组x中对应下标为True的元素 array([4, 1]) >>> x[[True, False, True, False, False]] # 如果使用布尔列表 [True, False, True, False, False] 作为索引,则把True当作1, False当作0,按照整数序列方式获取x中的元素 array([3, 4, 3, 4, 4])
NumPy 布尔数组一般不是手工产生,而是使用布尔运算的 Universal Function 函数产生。如:
>>> x = np.random.rand(10) # 产生长度为10,元素值在(0,1)区间内的随机数的数组
>>> x
array([ 0.31405475, 0.25280231, 0.08440324, 0.27874072, 0.81103738,
0.19872166, 0.62412707, 0.62278573, 0.94702961, 0.18089782])
>>> x > 0.5 # > 是Universal Function函数,返回布尔数组
array([False, False, False, False, True, False, True, True, True, False], dtype=bool)
>>> x[x > 0.5] # 使用x>0.5返回的布尔数组收集x中的元素,因此得到的结果是x中所有大于0.5的元素的数组
array([ 0.81103738, 0.62412707, 0.62278573, 0.94702961])
2.4. Shape manipulation
表 3 总结了 ndarray 形状操作的相关函数。
| Shape manipulation function | Description |
|---|---|
| ndarray.reshape(shape[, order]) | Returns an array containing the same data with a new shape. |
| ndarray.resize(new_shape[, refcheck]) | Change shape and size of array in-place. |
| ndarray.transpose(*axes) | Returns a view of the array with axes transposed. |
| ndarray.swapaxes(axis1, axis2) | Return a view of the array with axis1 and axis2 interchanged. |
| ndarray.flatten([order]) | Return a copy of the array collapsed into one dimension. |
| ndarray.ravel([order]) | Return a flattened array. |
| ndarray.squeeze([axis]) | Remove single-dimensional entries from the shape of a. |
参考:
https://docs.scipy.org/doc/numpy/user/quickstart.html#shape-manipulation
https://docs.scipy.org/doc/numpy/reference/arrays.ndarray.html#shape-manipulation
2.4.1. reshape 实例
下面是 reshape 的使用实例:
>>> import numpy as np
>>> x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
>>> x.reshape(2, 4)
array([[1, 2, 3, 4],
[5, 6, 7, 8]])
>>> x.reshape(4, 2)
array([[1, 2],
[3, 4],
[5, 6],
[7, 8]])
>>> x.reshape(2, 2, 2)
array([[[1, 2],
[3, 4]],
[[5, 6],
[7, 8]]])
3. Array Calculation
表 4 中是数组计算的相关函数。它们中的大部分函数接受参数 axis:
(1) 如果省略参数 axis,则表示对整个数组进行操作;
(2) 如果提供了参数 axis,则表示在对应坐标轴上进行操作。
>>> x = np.array([[1, 2, 3], [4, 5, 6]]) >>> x.sum() # 省略了axis,对所有元素求和 21 >>> x.sum(0) array([5, 7, 9]) # 5=1+4, 7=2+5, 9=3+6 >>> x.sum(1) array([ 6, 15]) # 6=1+2+3, 15=4+5+6 >>> x.min() # 省略了axis,在所有元素中找最小元素 1 >>> x.min(0) array([1, 2, 3]) >>> x.min(1) array([1, 4])
| Calculation 函数 | 说明 |
|---|---|
| ndarray.argmax([axis, out]) | Return indices of the maximum values along the given axis. |
| ndarray.min([axis, out, keepdims]) | Return the minimum along a given axis. |
| ndarray.argmin([axis, out]) | Return indices of the minimum values along the given axis of a. |
| ndarray.ptp([axis, out]) | Peak to peak (maximum - minimum) value along a given axis. |
| ndarray.clip([min, max, out]) | Return an array whose values are limited to [min, max]. |
| ndarray.conj() | Complex-conjugate all elements. |
| ndarray.round([decimals, out]) | Return a with each element rounded to the given number of decimals. |
| ndarray.trace([offset, axis1, axis2, dtype, out]) | Return the sum along diagonals of the array. |
| ndarray.sum([axis, dtype, out, keepdims]) | Return the sum of the array elements over the given axis. |
| ndarray.cumsum([axis, dtype, out]) | Return the cumulative sum of the elements along the given axis. |
| ndarray.mean([axis, dtype, out, keepdims]) | Returns the average of the array elements along given axis. |
| ndarray.var([axis, dtype, out, ddof, keepdims]) | Returns the variance of the array elements, along given axis. |
| ndarray.std([axis, dtype, out, ddof, keepdims]) | Returns the standard deviation of the array elements along given axis. |
| ndarray.prod([axis, dtype, out, keepdims]) | Return the product of the array elements over the given axis |
| ndarray.cumprod([axis, dtype, out]) | Return the cumulative product of the elements along the given axis. |
| ndarray.all([axis, out, keepdims]) | Returns True if all elements evaluate to True. |
| ndarray.any([axis, out, keepdims]) | Returns True if any of the elements of a evaluate to True. |
参考:https://docs.scipy.org/doc/numpy/reference/arrays.ndarray.html#calculation
4. Universal Function (对每个元素进行操作的函数)
Universal Function(简写为 ufunc)是一种能对数组的每个元素进行操作的函数。 NumPy 内置的许多 ufunc 函数都是在 C 语言级别实现的,它们的计算速度非常快。
下面是 ufunc numpy.sin 的例子:
>>> import numpy as np
>>> x = np.linspace(0, 2*np.pi, 9)
>>> y = np.sin(x) # numpy.sin 是 ufunc ,它对数组每个元素进行操作
>>> y
array([ 0.00000000e+00, 7.07106781e-01, 1.00000000e+00,
7.07106781e-01, 1.22464680e-16, -7.07106781e-01,
-1.00000000e+00, -7.07106781e-01, -2.44929360e-16])
下面是 ufunc numpy.add 的例子:
>>> import numpy as np
>>> x = np.array([[1, 2, 3],
... [4, 5, 6]])
>>> y = np.array([[11, 12, 13],
... [14, 15, 16]])
>>> np.add(x, y) # numpy.add 是 ufunc
array([[12, 14, 16],
[18, 20, 22]])
>>> x+y # 由于Python的操作符重载功能,np.add(x, y)可以简单地写为x+y
array([[12, 14, 16],
[18, 20, 22]])
4.1. Broadcasting
当我们使用 ufunc 函数对两个数组进行计算时,ufunc 函数会对这两个数组的对应元素进行计算,因此它要求这两个数组有相同的大小(shape 相同)。如果两个数组的 shape 不同的话,会进行广播(broadcasting)处理。
这里不详细介绍广播规则。下面是一个广播的实例:
>>> import numpy as np
>>> a = np.array([[ 0.0, 0.0, 0.0],
[ 10.0, 10.0, 10.0],
[ 20.0, 20.0, 20.0],
[ 30.0, 30.0, 30.0]])
>>> b = np.array([1.0, 2.0, 3.0])
>>> a+b # a和b的形状不一样,会进行广播(broadcasting)处理
array([[ 1., 2., 3.],
[ 11., 12., 13.],
[ 21., 22., 23.],
[ 31., 32., 33.]])
参考:
http://old.sebug.net/paper/books/scipydoc/numpy_intro.html#id6
https://www.tutorialspoint.com/numpy/numpy_broadcasting.htm
https://docs.scipy.org/doc/numpy/reference/ufuncs.html#broadcasting
5. Matrix
在 NumPy 中的 matrix 是 array 的子类,它所以继承了 array 的所有特性并且有自己独特的地方。比如使用 matrix 时, * 是矩阵乘法;而使用 array 时, * 是 ufunc(每个对应元素相乘)。
>>> import numpy as np
>>> a = np.matrix('1 2; 3 4') # 创建matrix。注:np.matrix 可以简写为 np.mat
>>> a
matrix([[1, 2],
[3, 4]])
>>> a.T # a的转置矩阵
matrix([[1, 3],
[2, 4]])
>>> a.I # a的逆矩阵
matrix([[-2. , 1. ],
[ 1.5, -0.5]])
参考:
https://docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.html