Principal Component Analysis (PCA)
Table of Contents
1. PCA 简介
真实的训练数据可能存在着冗余的维度,或者强关联的维度可以合并。如:
1、拿到一个汽车的样本,里面既有以“千米/小时”度量的最大速度特征,也有“英里/小时”的最大速度特征,显然这两个特征有一个多余。
2、拿到一个数学系的本科生期末考试成绩单,里面有三列,一列是对数学的兴趣程度,一列是复习时间,还有一列是考试成绩。我们知道要学好数学,需要有浓厚的兴趣,所以第二项与第一项强相关,第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢?
主成分分析(Principal Component Analysis, PCA)常用于 降低数据集的维度,挑选主要特征,可降低算法的计算开销。
PCA 的基本思想是 将 \(n\) 维特征映射到 \(k \; (k < n)\) 维上,这 \(k\) 维是全新的正交特征。这 \(k\) 维特征称为主元,是重新构造出来的 \(k\) 维特征,而不是简单地从 \(n\) 维特征中去除其余 \(n-k\) 维特征。
参考:
主成分分析(Principal components analysis)-最大方差解释:http://www.cnblogs.com/jerrylead/archive/2011/04/18/2020209.html
2. PCA 基本原理及步骤
PCA 的基本步骤如下:
(1) 对所有训练数据都减去均值。
(2) 计算协方差矩阵
(3) 计算协方差矩阵的特征值和特征向量
(4) 将特征值从大到小排序,保留最前面的 \(k\) 个特征值对应的特征向量
(5) 将数据转换到上述 \(k\) 个特征向量构建的新空间中,得到最后降维的数据。
PCA 的基本原理如下:
对一个 \(n \times n\) 的对称矩阵进行分解,我们可以求出它的特征值和特征向量,就会产生 \(n\) 个 \(n\) 维的正交基,每个正交基会对应一个特征值。然后把矩阵投影到这 \(n\) 个基上,此时特征值的模就表示矩阵在该基的投影长度。 特征值越大,说明矩阵在对应的特征向量上的方差越大,样本点越分散,越容易区分,信息量也就越多。因此,特征值最大的对应的特征向量方向上所包含的信息量就越多,如果某几个特征值很小,那么就说明在该方向的信息量非常少,我们就可以删除小特征值对应方向的数据,只保留大特征值方向对应的数据,这样做以后数据量减小,但有用的信息量都保留下来了。
也就是说,在 PCA 中,我们对数据的坐标进行了旋转,该旋转的过程取决于数据本身。第一条坐标轴转到覆盖数据的最大方差(数据最分散)位置。数据的最大方差给出了数据的最重要的信息。在选择了覆盖数据最大差异性的坐标轴之后,我们选择第二条坐标轴,该坐标轴和第一条坐标轴正交,这就是覆盖数据次大差异性的坐标轴。
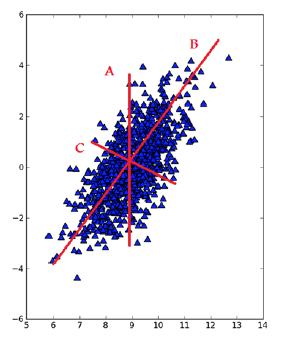
Figure 1: 直线 B 是数据集中差异化最大的方向,选择它为第一坐标轴;和 B 正交的 C 是第二条坐标轴
在 PCA 中,我们仅保留前面比较大的 \(k\) 个特征值对应的特征向量(这相当于对数据进行了降维)。
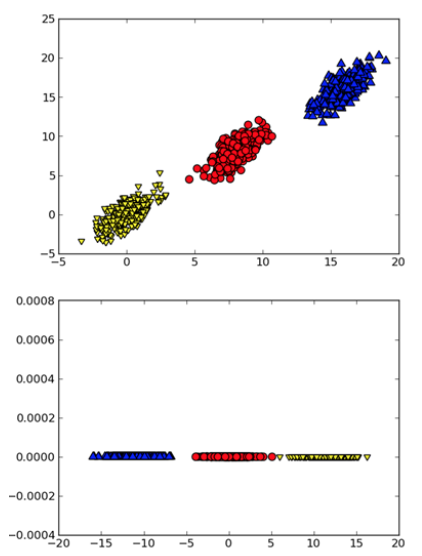
Figure 2: 二维空间的 3 个类别。应用 PCA 可对数据降维(本例中可以删除一个维度),从而分类更容易处理
参考:
机器学习实战,13.2 节 PCA
PCA 主成分分析 Python 实现:http://blog.csdn.net/Dream_angel_Z/article/details/50760130
2.1. PCA 简单实例
为简单起见,下面例子中我们仅考虑二维数据,数据如图 3 所示。

Figure 3: 原始数据(共二维)
通过简单的观察,我们可以发现数据的二个维度是“强相关的”,可以去掉一个维度,为了演示 PCA 的应用过程,我们将按照 PCA 的基本步骤一步一步进行说明。
第一步,对所有训练数据都减去均值。 这里维度 x 的均值为 1.81,维度 y 的均值为 1.91。所有数据都减去均值后得到如图 4 所示数据。
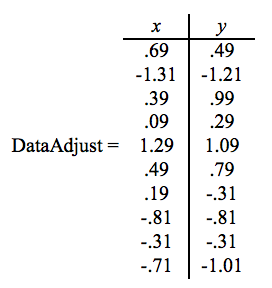
Figure 4: 所有数据都减去均值后的数据
第二步,计算协方差矩阵。
\[cov = \begin{pmatrix} 0.616555556 & 0.615444444 \\ 0.615444444 & 0.716555556 \\ \end{pmatrix}\]
协方差的绝对值越大,两者对彼此的影响越大。
第三步,计算协方差矩阵的特征值和特征向量。
\[eigenvalues = \begin{pmatrix} 0.0490833989 \\ 1.28402771 \\ \end{pmatrix}\]
\[eigenvectors = \begin{pmatrix} eig_1 & eig_2 \end{pmatrix} = \begin{pmatrix} -0.735178656 & -0.677873399 \\ 0.677873399 & -0.735178656 \\ \end{pmatrix}\]
这里的特征向量已归一化为单位向量。特征值 0.0490833989 对应特征向量为 \((-0.735178656, 0.677873399)^\mathsf{T}\) ,特征值 1.28402771 对应特征向量为 \((-0.677873399, -0.735178656)^\mathsf{T}\) 。
第四步,将特征值从大到小排序,保留最前面的 \(k\) 个特征值对应的特征向量。 这里只有两个特征值,我们保留较大的那个特征值(即 1.28402771),及其对应特征向量 \((-0.677873399, -0.735178656)^\mathsf{T}\) 。
第五步,将数据转换到上述 \(k\) 个特征向量构建的新空间中,得到最后降维的数据。 将数据投影到选取的特征向量上。
\[FinalData_{m \times k} = DataAdjust_{m \times n} \times EigenVectors_{n \times k}\]
对于这个例子,有:
\[\begin{aligned} FinalData & = \begin{pmatrix} 0.69 & 0.49 \\ -1.31 & -1.21 \\ 0.39 & 0.99 \\ 0.09 & 0.29 \\ 1.29 & 1.09 \\ 0.49 & 0.79 \\ 0.19 & -1.31 \\ -1.81 & -0.81 \\ -0.31 & -0.31 \\ -0.71 & -1.01 \end{pmatrix} \begin{pmatrix} -0.677873399 \\ -0.735178656 \end{pmatrix} \\
& = \begin{pmatrix} -0.827970186 \\ 1.77758033 \\ -0.992197494 \\ -0.274210416 \\ -1.67580142 \\ -0.912949103 \\ 0.0991094375 \\ 1.14457216 \\ 0.438046137 \\ 1.22382056 \end{pmatrix} \\
\end{aligned}\]
至此,通过 PCA 已经把数据从二维降到了一维。
这个例子摘自:
A tutorial on Principal Components Analysis: http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf
2.2. 更多例子
PCA 的更多例子可参考下面资料:
《机器实习实战》13.3 示例:利用 PCA 对半导体制造数据降维
《机器学习:实用案例解析》第 8 章 PCA:构建股票市场指数
3. PCA 的特点
PCA 技术的一个很大的优点是,它是完全无参数限制的。在 PCA 的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。