Prime Number
Table of Contents
1. 素数简介
大于 1 的自然数中,除了 1 和该数自身外,无法被其他自然数整除的数(也就是说只有 1 和该数本身两个因数),被称为素数(Prime Number),也称质数。 那些大于 1 的自然数中不是素数的数,被称为合数(Composite Number)。1 既不是素数,也不是合数。
图 1(摘自:https://www.math-salamanders.com/prime-numbers-chart.html) 中黄色背景的数是 100 以内的素数。
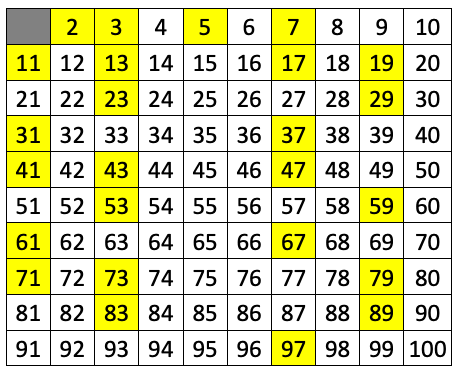
Figure 1: 100 以内的素数(共 25 个)
古希腊数学家欧几里得(Euclid)于公元前 300 年前后证明了素数有无限个,参见 Euclid's theorem 。
目前,关于素数的一些问题,如哥德巴赫猜想(每个大于 2 的偶数可表示成两个素数之和)及孪生素数猜想(存在无穷多对相差 2 的素数)等还没有得到解决。
1.1. 素数生成算法
尽管有一些公式可以直接生成素数(Formula for primes),但它们都很低效。一般来说,要生成素数,采用的办法是先随机生成一个数,然后测试它是否是素数,如果它不是素数,则再随机生成另一个数,再测试它是否是素数,这个过程一直继续,直接找到素数为止。
2. 素性测试
2.1. 试除法(Trial Division)
记被测试的自然数为 \(n\) ,逐一测试 \([2,\sqrt{n}]\) 之间的整数,如果它们都不能整除 \(n\) ,则 \(n\) 是素数。
为什么测试 \([2,\sqrt{n}]\) 中的数就够了,而没有必要测试 \([2, n-1]\) 中的所有整数呢?假设 \(n\) 不是素数,可分解为 \(n = pq\) ,那么 \(p,q\) 中至少有一个数会小于等于 \(\sqrt{n}\) ,因为如果 \(p,q\) 都大于 \(\sqrt{n}\) 的话,那它们的乘积一定会大于 \(n\) ,显然产生了矛盾。
2.2. 费马素性测试
费马素性测试是利用费马小定理进行素数检验的方法。在介绍它之前,让我们先了解一下费马小定理。
2.2.1. 费马小定理
费马小定理: 如果 \(p\) 是素数, \(a\) 是整数,则 \(a^p - a\) 是 \(p\) 的倍数。 这个定理可表示为: \[a^{p} - a \equiv 0{\pmod {p}}\] 或者表示为: \[a^{p} \equiv a {\pmod {p}}\] 比如, \(a = 2, p = 7\) ,则 \(a^p - a = 2^7 - 2 = 126 = 7 \times 18\) ,显然 \(126\) 是 \(7\) 的倍数。又如, \(a = 14, p = 7\) ,则 \(a^p - a = 14^7 - 14 = 105413490 = 7 \times 15059070\) ,显然 \(105413490\) 是 \(7\) 的倍数。
需要说明的是: 费马小定理的逆叙述是不成立的,即假设 \(a^p - a\) 是 \(p\) 的倍数, \(p\) 不一定是素数。 比如, \(2^{341} - 2\) 是 \(341\) 的倍数,但 \(341 = 11 \times 31\) ,显然不是素数。
2.2.2. 费马小定理另一种表述
对于素数 \(p\) ,如果 \(a\) 不是 \(p\) 的倍数(注:由于 \(p\) 本身就是素数,这相当于说 \(a\) 和 \(p\) 互素,即满足 \(\gcd(a,p)=1\) ),则下式一定成立: \[a^{p-1} \equiv 1{\pmod {p}}\] 这是费马小定理另一种表述。比如, \(a = 2, p = 7\) ,它们显然满足 \(\gcd(a,p)=1\) ,计算上面式子的左边 \(a^{p-1} = 2^{7-1} = 64 = 7 \times 9 + 1\) ,显然它除以素数 \(p\) 确实余 \(1\) 。又比如, \(a = 3, p = 7\) ,它们显然满足 \(\gcd(a,p)=1\) ,计算上面式子的左边 \(a^{p-1} = 3^{7-1} = 729 = 7 \times 104 + 1\) ,显然它除以素数 \(p\) 确实余 \(1\) 。只要 \(a\) 不是素数 \(p\) 的倍数,上式都会成立。
2.2.3. 费马素性测试算法
利用费马小定理可以检验一个数 \(n\) 是否是素数,算法如下:
- 在范围 \([1, n-1]\) 中随机选择 \(a\) ,这显然会满足费马小定理另一种表述的要求 \(\gcd(a,n)=1\) ;
- 测试 \(a^{n-1} \equiv 1{\pmod {n}}\) 是否成立;
- 如果不成立,则 \(n\) 一定不是素数,即 \(n\) 是合数;
- 如果成立,则 \(n\) 可能是素数(不能直接确定 \(n\) 就是素数,因为费马小定理的逆叙述是不成立的)。
- 如果不成立,则 \(n\) 一定不是素数,即 \(n\) 是合数;
如果重复运行上面算法 \(k\) 次,每次的结果都是 \(n\) 可能是素数,则我们认为 \(n\) 极有可能是素数,称为 Probably Prime。
注:很多资料会把 \(a\) 的选择范围调整为 \([2, n-2]\) ,这是因为 \(a=1\) 或者 \(a=n-1\) 时,不管等待测试的数 \(n\) 是合数还是素数,费马素性测试一定都会通过。所以,没有必要选择 \(a=1\) 或者 \(a=n-1\) 进行费马素性测试。
2.2.4. 费马素性测试算法的缺点
一般来说,增加测试次数 \(k\) ,可以提高费马素性测试算法的正确率。但是,也有一些数可以通过任意次数的费马素性测试,但它却不是素数。
比如, \(561=3\times 11\times 17\) 不是素数,但不管随机选择的 \(a\) 是什么数,它都可以通过费马素性测试,这类数被称为卡迈克尔数(Carmichael Number),也称为“费马伪素数”。 由于 Carmichael Number 的存在,我们在应用时不能只采用费马素性测试算法来判断某个数是否是素数。
2.3. Miller-Rabin 测试
Miller-Rabin 测试是另一种素性测试算法,它也利用了费马素性测试的思想。
设 \(n\) 是奇数(注:素数除 \(2\) 外都是奇数),则 \(n-1\) 是偶数,对一个偶数来说,我们总可以写为一个偶数 \(2^s\) 和一个奇数 \(d\) 相乘的形式,从而有: \[n - 1 = 2^s \cdot d,~\text{with}~d~\text{odd}.\]
利用上面结论,结合费马小定理,有下面的推导: \begin{array}{rl}
a^{n-1} ≡ 1 \bmod n &\Longleftrightarrow a^{2^s d} - 1 ≡ 0 \bmod n \\
&\Longleftrightarrow (a^{2^{s-1} d} + 1) (a^{2^{s-1} d} - 1) ≡ 0 \bmod n \\
&\Longleftrightarrow (a^{2^{s-1} d} + 1) (a^{2^{s-2} d} + 1) (a^{2^{s-2} d} - 1) ≡ 0 \bmod n \\
&\quad\vdots \\
&\Longleftrightarrow (a^{2^{s-1} d} + 1) (a^{2^{s-2} d} + 1) ⋯ (a^{d} + 1) (a^{d} - 1) ≡ 0 \bmod n \\
\end{array}
上面最后一个式子表明, 如果 \(n\) 是素数,则 \((a^{2^{s-1} d} + 1), (a^{2^{s-2} d} + 1), \cdots, (a^{d} + 1), (a^{d} - 1)\) 这些数中一定存在某个数它是 \(n\) 的倍数(即模 \(n\) 余 \(0\) )。如果这些数全都不是 \(n\) 的倍数,则 \(n\) 一定不是素数。这就是 Miller-Rabin 测试的思路。
具体来说,Miller-Rabin 测试算法如下:
- 把 \(n-1\) 拆分为 \(2^s \cdot d\) 的形式;
- 在 \([2,n-2]\) 范围中随机选择 \(a\) ,为什么是这个范围,请参见 2.2.3 ;
- 测试下面这些式子是否成立:
- \(a^d \equiv 1 \bmod n\)
- \(a^d \equiv n-1 \bmod n\)
- \(a^{2 \cdot d} \equiv n - 1 \bmod n\)
- \(a^{2^2 \cdot d} \equiv n - 1 \bmod n\)
- \(a^{2^3 \cdot d} \equiv n - 1 \bmod n\)
- \(\cdots \cdots\)
- \(a^{2^{(s-1)} \cdot d} \equiv n - 1 \bmod n\)
- \(a^d \equiv 1 \bmod n\)
- 如果上面的式子中有一个成立,则认为 \(n\) 是 Probably Prime;如果上面这些式子都不成立,则 \(n\) 一定不是素数。
和费马素性测试类似,Miller-Rabin 测试也需要执行 \(k\) 次(如果待测试的数 \(n\) 的比特位为 512 或者 1024,NIST 建议设置 \(k=5\) )来提高 Probably Prime 的正确性。
我们知道,费马素性测试中,存在卡迈克尔数(Carmichael Number)会使费马素性测试失效;在 Miller-Rabin 测试中目前还没有发现存在这样的数使 Miller-Rabin 测试失效,也就是说只要多选择几次 \(a\) ,合数无法通过 Miller-Rabin 测试。
2.3.1. Miller-Rabin 测试伪代码
Miller-Rabin 测试算法的伪代码如下:
Input #1: n > 2, an odd integer to be tested for primality
Input #2: k, the number of rounds of testing to perform
Output: "composite" if n is found to be composite, "probably prime" otherwise
let s > 0 and d odd > 0 such that n − 1 = 2^s * d # by factoring out powers of 2 from n − 1
repeat k times:
a ← random(2, n − 2)
t ← a^d mod n
if t = 1 then
return "probably prime"
repeat s times:
if t = n - 1 then
return "probably prime"
t ← t^2 mod n
return "composite"
2.3.2. Miller-Rabin 测试实例
假设 \(n=221\) ,我们对它进行 Miller-Rabin 测试。
- 首先,我们把 \(n-1\) 写为 \(2^s \cdot d\) 的形式,有 \(220=2^2 \times 55\) ,所以 \(s=2, d=55\) 。
- 随机选择 \(a = 174\) ,我们计算:
- \(a^d \bmod n = 174^{55} \bmod 221 = 47\) ,它不等于 \(1\) ,也不等于 \(n-1\) ;
- \(a^{2^1 d} \bmod n = 174^{110} \bmod 221 = 220\) ,它等于 \(n-1\) 。
- \(a^d \bmod n = 174^{55} \bmod 221 = 47\) ,它不等于 \(1\) ,也不等于 \(n-1\) ;
- 我们发现上面的 3 个检测(第 1 个式子要和 \(1, n-1\) 两个数进行相等比较,后续式子只用和 \(n-1\) 进行相等比较),有一个成立,所以 \(221\) 暂时通过了一轮的 Miller-Rabin 测试;
- 再随机选择另一个 \(a\) ,比如 \(a=137\) ,我们计算:
- \(a^d \bmod n = 137^{55} \bmod 221 = 188\) ,它不等于 \(1\) ,也不等于 \(n-1\) ;
- \(a^{2^1 d} \bmod n = 137^{110} \bmod 221 = 205\) ,它不等于 \(n-1\) 。
- \(a^d \bmod n = 137^{55} \bmod 221 = 188\) ,它不等于 \(1\) ,也不等于 \(n-1\) ;
- 我们发现当 \(a=137\) 时,上面的 3 个检测一个也不成立。所以,我们得到结论: \(n=221\) 不是素数,事实上 \(221 = 13 \times 17\) 。
2.4. 其它素性测试算法
还有其它的一些素性测试算法,如 Baillie-PSW。和 Miller-Rabin 类似,Baillie–PSW 也是一种概率性算法,也就是说,它只是很大的概率(不是百分百)得到正确的结果。
2002 年,Manindra Agrawal,Neeraj Kayal,Nitin Saxena 提出了首个可在多项式时间内运行的确定性素性测试算法(简称为 AKS 算法),也就是说使用 AKS 算法判断某个数是素数的话,则它百分百是素数。不过,AKS 算法并没有 Miller-Rabin 算法快,因此它并未代替古老的概率性算法。
还有其它的一些素性测试算法,可参考 Taxonomy and Practical Evaluation of Primality Testing 。
3. 素数的分布
我们在使用 Miller-Rabin 测试算法或其他概率性素数测试算法时,发现一个素数之前会测试多少个整数呢? 由素数定理(Prime number theorem)可知,在整数 \(n\) 附近的素数分布情况为:平均每 \(\ln(n)\) 个整数中有一个素数。这样,平均而言,在找到一个素数之前,我们需要测试约 \(\ln(n)\) 个整数。 因为除整数 2 外所有偶数肯定不是素数,因此需测试的整数个数可减半,为 \(0.5\times\ln(n)\) 。例如,若要找 \(2^{200}\) 附近的素数,则约需 \(0.5\ln(2^{200}) = 69\) 次测试。然而,这只是平均值。在数轴上的某些位置,素数非常密集;而在其他有些位置,素数非常稀疏。
4. 参考
本文主要参考下面资料:
- https://en.wikipedia.org/wiki/Fermat%27s_little_theorem
- https://en.wikipedia.org/wiki/Miller%E2%80%93Rabin_primality_test
- 密码编码学与网络安全——原理与实践(第七版),2.6.3 素数的分布