Probability Theory
Table of Contents
- 1. 概率论简介
- 2. 随机变量及其分布
- 3. 多维随机变量及其分布
- 4. 随机变量的数字特征
- 5. 大数定律和中心极限定理
- 6. 数理统计基本概念
- 7. 参数估计
- 8. 随机过程(Stochastic Process)和随机场(Random Field)
- 9. 马尔可夫链(Markov Chain)
- 10. 平稳随机过程
1. 概率论简介
Probability theory is the branch of mathematics concerned with probability, the analysis of random phenomena.
在个别的试验中其结果呈现出不确定性,但在大量重试验中其结果具有统计规律的现象,我们称之为随机现象。
我们是通过研究随机试验来研究随机现象的。什么是随机试验呢?请看下文。
参考:本文很多内容摘自《概率论与数理统计(第四版),浙江大学 盛骤等编》
1.1. Laplace 评概率论
Probability theory is nothing but common sense reduced to calculation. -- by Laplace
1.2. 随机试验、样本空间、事件
在概率论中具有下面三个特点的试验称为 随机试验 :
- 可以在相同的条件下重复地进行;
- 每次试验的可能结果不止一个,并且能事先知道试验的所有可能结果(这些所有可能的结果所组成的集合称为 样本空间 );
- 进行一次试验之前不能确定哪一个结果会出现。
样本空间 \(S\) 的一个子集,称为随机事件,简称 事件(event) 。
样本空间 \(S\) 是自身的子集,在每次试验中它总是发生的, \(S\) 称为必然事件。
“连续掷一个硬币两次,正反面的出现情况”是一个随机试验。样本空间可表示为: \(S=\{HH, HT, TH, TT \}\) , \(H\) 表示正面, \(T\) 表示反面。“两次出现同一面”是一个事件,可表示为: \(A=\{ HH, TT\}\) 。
1.3. 什么是概率
1933 年,俄国数学家 Andrei N. Kolmogorov 建立了概率论的公理化体 (Probability axioms),给出了“概率”的严格定义。
设 \(E\) 是随机试验, \(S\) 是它的样本空间,对于 \(E\) 的每一个事件 \(A\) 赋予一个实数,记为 \(P(A)\) ,如果集合函数 \(P( \cdot )\) 满足下面三个条件:
- 非负性:对于每一个事件 \(A\) ,有 \(P(A) \ge 0\)
- 规范性:对于必然事件 \(S\) ,有 \(P(S) =1\)
- 可列可加性:设 \(A_{1}, A_{2}, \cdots\) 是两两互不相容的事件,即对于 \(A_{i}A_{i} = \emptyset, i \ne j\) ,有 \(P(A_1 \cup A_2 \cup \cdots) = P(A_1) + P(A_2) + \cdots\)
则称 \(P(A)\) 是事件 \(A\) 的 概率 。
1.4. 条件概率
设 \(A,B\) 是两个事件,事件 \(A\) 已经发生的条件下事件 \(B\) 发生的概率称为 条件概率 ,记为 \(P(B|A)\) ,且有:
\[P(B|A) = \frac{P(AB)}{P(A)}\]
例:将一枚硬币抛掷两次,观察其出现正反面的情况( \(H\) 表示正面, \(T\) 表示反面)。设事件 \(A\) 为“至少有一次为 \(H\) ”,事件 \(B\) 为“两次掷出同一面”。求事件 \(A\) 已经发生的条件下事件 \(B\) 发生的概率。
解法一:样本空间为 \(S= \{HH, HT, TH, TT\}\) ,事件 \(A= \{HH, HT, TH\}\) ,事件 \(B= \{HH, TT\}\) 。显然有 \(P(A) = \frac{3}{4}, P(AB) = \frac{1}{4}\) ,从而 \(P(B|A) = \frac{P(AB)}{P(A)} = \frac{1}{3}\)
解法二:这个问题也从条件概率的含义直接求得。由于事件 \(A\) 已经发生,所以 \(TT\) 不可能发生。 \(A\) 中的 3 个元素,仅有 \(HH \in B\) ,于是事件 \(A\) 已经发生的条件下事件 \(B\) 发生的概率 \(P(B|A) = \frac{1}{3}\)
1.4.1. Product Rule(即乘法公式)
由条件概率知,设 \(P(A) >0\) ,则有:
\[P(AB) = P(B|A)P(A)\]
上式称为 Product Rule ,或 Chain Rule 或乘法公式。
可以推广到 \(n\) 个事件的情况。例如:设 \(A,B,C\) 为事件,且 \(P(AB) >0\) ,则有:
\[P(ABC) = P(C|AB)P(B|A)P(A)\]
1.4.2. Law of Total Probability(即全概率公式)
先介绍样本空间的划分的定义。
设 \(S\) 为试验 \(E\) 的样本空间, \(B_1, B_2, \cdots, B_n\) 为 \(E\) 的一组事件,若:
(1) \(B_i B_j = \emptyset, i \neq j, i,j = 1,2,\cdots, n\)
(2) \(B_1 \cup B_2 \cup \cdots \cup B_n = S\)
则称 \(B_1, B_2, \cdots, B_n\) 为样本空间 \(S\) 的一个划分。
显然,如果 \(B_1, B_2, \cdots, B_n\) 是样本空间的一个划分,则每次试验中,事件 \(B_1, B_2, \cdots, B_n\) 中“必有”且“仅有”一个会发生。
定理 :设试验 \(E\) 的样本空间为 \(S\) , \(A\) 为 \(E\) 的事件, \(B_1, B_2, \cdots, B_n\) 为 \(S\) 的一个划分,且 \(P(B_i) >0 ,i = 1,2,\cdots,n\) 则:
\[\begin{aligned} P(A) &= P(A|B_1)P(B_1) + P(A|B_2)P(B_2) + \cdots + P(A|B_n)P(B_n) \\
&= \sum_{i=1}^{n} P(A|B_i)P(B_i) \end{aligned}\]
上式称为 全概率公式(Law of Total Probability) 。
全概率公式的意义在于,很多实际问题中 \(P(A)\) 不易直接求得,但却容易找到 \(S\) 的一个划分 \(B_1, B_2, \cdots, B_n\) ,且 \(P(B_i)\) 和 \((A|B_i)\) 或为已知,或容易求得,那么根据全概率公式就可以求出 \(P(A)\) 。
1.4.2.1. Law of Total Probability(连续型随机变量的情况)
后文将介绍连续型随机变量,这里先直接给出连续型随机变量下的全概率公式。
\[\begin{aligned}f_X(x) & = \int_{y} f(x,y) \, \mathrm{d}y \\
& = \int_{y} f_{X|Y}(x \mid y) \cdot f_Y(y) \, \mathrm{d}y \end{aligned}\]
1.4.3. 贝叶斯公式
下面就是著名的 贝叶斯公式 :
\[P(B|A) = \frac{P(A|B)P(B)}{P(A)}\]
贝叶斯公式的更一般性描述如下:设试验 \(E\) 的样本空间为 \(S\) , \(A\) 为 \(E\) 的事件, \(B_1, B_2, \cdots, B_n\) 为 \(S\) 的一个划分,且 \(P(A) > 0, \, P(B_i) >0 ,i = 1,2,\cdots,n\) 则:
\[P(B_i|A) = \frac{P(A|B_i) P(B_i)}{\sum_{j=1}^{n} P(A|B_j)P(B_j)}\]
1.4.3.1. 贝叶斯公式应用实例
例:对以往数据分析结果表明,当机器调整得良好时,产品的合格率为 98%,而当机器发生某种故障时,其合格率为 55%,每天早上机器开动时,机器调整良好的概率为 95%。试求已知某日早上第一件产品是合格品时,机器调整良好的概率是多少?
解:设 \(A\) 为事件“产品合格”, \(B\) 为事件“机器调整良好”。已知 \(P(A|B) = 0.98, P(A|\overline{B}) = 0.55, P(B) = 0.95, P(\overline{B}) = 0.05\) ,所求的概率为 \(P(B|A)\) ,由贝叶斯公式,得
\[P(B|A) = \frac{0.98 \times 0.95}{0.98 \times 0.95 + 0.55 \times 0.05} = 0.97\]
这就是说,当生产出第一件产品是合格品时,此时机器调整良好的概率为 97%。
说明:这里概率 \(P(B)=0.95\) 是由以往的数据分析得到的,叫做 先验概率(Priori Probability) ,而在得到信息(即生产出的第一件产品是合格品)之后再重新加以修正的概率(即 \(P(B|A)=0.97\) )叫做 后验概率(Posteriori Probability) 。
1.4.3.2. 再看“贝叶斯公式”
贝叶斯公式可换一个写法:
\[P(B|A) = \frac{P(A|B)}{P(A)} P(B)\]
其中, \(\frac{P(A|B)}{P(A)}\) 又称为标准似然度(可能大于等于或小于 1)。故贝叶斯公式就是:
\[\text{后验概率} = \text{标准似然度} * \text{先验概率}\]
这是贝叶斯推断的含义:先假定一个“先验概率”,得到一些信息后可能增强也可能削弱“先验概率”,从而得到更接近事实的“后验概率”。
1.4.4. 用贝叶斯公式推测“事件的主要原因”
贝叶斯公式可以帮助我们确定结果(例如事件 \(A\) )已经发生条件下,寻找各“原因(例如事件 \(B_i\) )”发生的条件概率,从而确定结果发生的主要原因。
\[\begin{aligned} P(B_i|A) &= \frac{P(A|B_i) P(B_i)}{P(A)} \\
& \propto P(A|B_i) P(B_i) \end{aligned}\]
上式中,如果 \(P(B_k|A)\) 的概率在 \(P(B_i|A), i=1,2, \cdots,n\) 中最大(每个 \(P(B_i|A)\) 都包含相同的因子 \(P(A)\) ,可以都不计算这个因子),则可以认为事件 \(B_k\) 就是事件 \(A\) 发生的主要原因。
1.5. 随机事件的独立性
设 \(A,B\) 是两个事件,如果满足下面等式:
\[P(AB) = P(A)P(B)\]
则称 事件 \(A,B\) 相互独立。
如果 \(A,B\) 相互独立,则有 \(P(A \mid B) = P(A)\) 。证明如下:
\[\begin{aligned}P(A \mid B) &= \frac{P(AB)}{P(B)} \\
&= \frac{P(A)P(B)}{P(B)} \\
&= P(A) \end{aligned}\]
2. 随机变量及其分布
2.1. 随机变量
设随机试验的样本空间为 \(S=\{e\}\) , \(X=X(e)\) 是定义在样本空间 \(S\) 上的实值单值函数。称 \(X=X(e)\) 为随机变量。
后文将介绍两种常见随机变量:离散型随机变量和连续型随机变量。
2.2. 随机变量的分布函数(Cumulative distribution function, CDF)
设 \(X\) 是一个随机变量, \(x\) 是任意实数,下面函数是 \(X\) 的概率累积分布函数(简称分布函数):
\[F(x)=P\{X \le x\}, -\infty < x < \infty\]
若已知 \(X\) 的分布函数,就可以知道 \(X\) 落在任一区间 \((x_{1}, x_{2}]\) 上的概率为 \(P\{x_{1} < X \le x_{2}\} = P\{X \le x_{2}\} - P\{X \le x_{1}\} = F(x_{2}) - F(x_{1})\) ,从这个意义上说, 分布函数完整地描述了随机变量的统计规律性。
分布函数有下面基本性质:
- 非降性。如果 \(x_{1} < x_{2}\) ,则 \(F(x_{1}) \le F(x_{2})\)
- 有界性。 \(0 \le F(x) \le 1\) 且 \(F(-\infty)=0, F(\infty) =1\)
- 右连续性。 \(F(x) = F(x+0)\)
2.3. 离散型随机变量及其“概率质量函数”(Probability mess function, pmf)
如果随机变量的全部可能取到的值是“有限个”或“可列无限个”,则这种随机变量称为离散型随机变量。后文将介绍三种重要的离散型随机变量。
如果离散型随机变量 \(X\) 的所有可能取值为 \(x_{k} \; (k=1,2, \cdots)\) ,则称 \(P(X=x_{k}) = p_{k}\) 为随机变量 \(X\) 的概率质量函数 (Probability mess function, pmf)。 概率质量函数又称分布律。
分布律有下面性质:
- \(p_{k} \ge 0\)
- \(\sum_{k=1}^{\infty}p_{k} = 1\)
2.3.1. (0-1)分布(又称 Bernoulli distribution)
设随机变量 \(X\) 只可能取 0 和 1 两个值,它的分布律为
\[P\{X=k\} = p^{k}(1-p)^{1-k}, k=0,1 \quad (0 < p < 1)\]
则称 \(X\) 服从 以 \(p\) 为参数的(0-1)分布或两点分布或 Bernoulli distribution 。
(0-1)分布的分布律也可写为:
\[\begin{array}{c|cc}
X & 0 & 1 \\
\hline
p_{k} & 1-p & p \\
\end{array}
\]
2.3.1.1. (0-1)分布实例
如果随机试验的样本空间只包含两个元素,即 \(S=\{e_{1}, e_{2}\}\) ,则总能在 \(S\) 上定义一个服从(0-1)分布的随机变量。
如“抛硬币”试验可以用(0-1)分布的随机变量来描述。
2.3.2. 二项分布(它是(0-1)分布的更通用形式)
如果试验 \(E\) 只有两个可能结果: \(A\) 及 \(\overline{A}\) ,设 \(P(A)=p \; (0 < p < 1)\) ,则有 \(P(\overline{A}) = 1-p\) ,我们称 \(E\) 为伯努利试验(Bernoulli Experiment)。
设随机变量 \(X\) 表示 \(n\) 次独立的伯努利试验中事件 \(A\) 发生的次数。
可以计算出随机变量 \(X\) 的分布律为(具体的计算过程可参考《概率论与数理统计(第四版),浙江大学 盛骤等编》):
\[P\{X=k\} = {n \choose k} p^{k}(1-p)^{n-k}, k = 0,1,2, \cdots, n.\]
我们说随机变量 \(X\) 服从 参数为 \(n,p\) 的二项分布 (其名字来源于 \({n \choose k}\) 是二项系数)。
特别地,当 \(n=1\) 时,二项分布可简化为: \(P\{X=k\} = p^{k}(1-p)^{1-k}, k=0,1 \quad (0 < p < 1)\) ,这就是前面介绍过的(0-1)分布。
2.3.3. 泊松分布(Poisson distribution)
设随机变量 \(X\) 所有可能的取值为 \(0,1,2, \cdots\) ,而取各个值的概率为:
\[P\{X=k\} = \frac{\lambda^{k}e^{-\lambda}}{k!}, k=0,1,2, \cdots \quad (\lambda > 0)\]
则称 \(X\) 服从参数为 λ 的泊松分布(Poisson distribution)。
2.3.3.1. 泊松分布实例
泊松分布是概率论中的重要分布,具有泊松分布的随机变量在实际应用中有很多。如一年发生的闪电的数量,某医院一天的急诊病人数量,某地区一个时间段内发生的交通事故的次数等都服从泊松分布。
2.3.3.2. 泊松分布和二项分布区别
二项分布中 \(n\) 是确定的;而泊松分布的统计次数可能大到无法计数,或本来就不确定。
2.4. 连续型随机变量及其“概率密度函数”(Probability density function, pdf)
如果对于随机变量 \(X\) 的分布函数 \(F(x)\) ,存在非负函数 \(f(x)\) ,使对于任意实数 \(x\) 有:
\[F(x) = \int_{-\infty}^{x}f(t)dt\]
则称 \(X\) 为连续型随机变量,其中函数 \(f(x)\) 称为 \(X\) 的概率密度函数(Probability density function, pdf),简称概率密度。
由上面的定义可知,概率密度函数 \(f(x)\) 具有以下性质:
- \(f(x) \ge 0\)
- \(\int_{-\infty}^{\infty}f(x)dx = 1\)
- 对于任意实数 \(x_{1},x_{2} \; (x_{1} \le x_{2})\) 有: \(P\{x_{1} < X \le x_{2}\} = F(x_{2}) - F(x_{1}) = \int_{x_{1}}^{x_{2}}f(x)dx\)
- 若 \(f(x)\) 在点 \(x\) 处连续,则有 \(F'(x) = f(x)\)
对于连续型随机变量 \(X\) ,它取任一个指定值的概率均为 0,所以在计算连续型随机变量落在某一区间的概率时,可以不区分区间是开区间还是闭区间或半开半闭区间。
后文将介绍几种重要的连续型随机变量。
2.4.1. 均匀分布
若连续型随机变量 \(X\) 具有概率密度:
\[f(x)= \begin{cases}
\frac{1}{b-a} & a \le x \le b \\
0 & \text{otherwise}
\end{cases}\]
则称 \(X\) 在区间 \([a,b]\) 上服从均匀分布(Uniform distribution)。
2.4.2. 指数分布
若连续型随机变量 \(X\) 具有概率密度:
\[f(x)= \begin{cases}
\lambda e^{-\lambda x} & x \ge 0 \\
0 & \text{otherwise}
\end{cases}\]
则称 \(X\) 服从参数为 \(\lambda (\lambda > 0)\) 的指数分布(Exponential distribution)。
2.4.2.1. 指数分布重要特点——无记忆性
指数分布有下面重要的性质:
\[P\{X > s +t \; | \; X > s\} = P\{X > t\}\]
这称为无记忆性。
如果 \(X\) 是某一元件的寿命,那么无记忆性表明,已知元件已经使用了 \(s\) 小时,它总共使用至少 \(s+t\) 小时的条件概率,与从开始使用时算起它使用至少 \(t\) 小时的概率相等。
2.4.3. 正态分布(又称高斯分布)
若连续型随机变量 \(X\) 的概率密度为:
\[f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} \quad (-\infty < x < \infty)\]
则称 \(X\) 服从参数为 \(\mu,\sigma(\sigma > 0)\) 的正态分布(Normal distribution),常记为 \(X \sim {\mathcal {N}}(\mu ,\,\sigma ^{2})\) 。正态分布又称高斯分布。
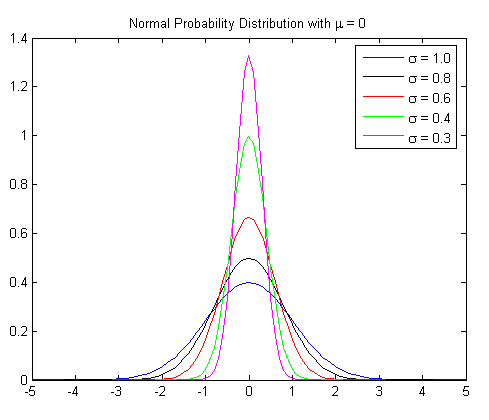
Figure 1: 正态分布概率密度(摘自:https://explorable.com/normal-probability-distribution)
特别地,当 \(\mu=0, \sigma=1\) 时,称正态分布为标准正态分布。标准正态分布的概率密度为:
\[\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}}{2}}\]
2.5. 随机变量的函数的分布
在实践中,我们有时对随机变量的函数更感兴趣。比如,我们可以测量圆轴截面的直径 \(d\) ,而关心的却是截面面积 \(A=\frac{1}{4}\pi d^2\) 。这里,随机变量 \(A\) 是随机变量 \(d\) 的函数。
例:设随机变量 \(X\) 具有概率密度 \(f_X(x), - \infty < x < \infty\) ,求 \(Y=X^2\) 的概率密度。
解:分别记 \(X,Y\) 的分布函数为 \(F_X(x), F_Y(y)\) 。
由于 \(Y=X^2 \ge 0\) ,所以当 \(y \le 0\) 时,有 \(F_Y(y) = 0\) ;当 \(y>0\) 时,有:
\[\begin{aligned} F_Y(y) &= P\{ Y \le y \} \\
&= P\{ X^2 \le y \} \\
&= P\{ - \sqrt{y} \le X \le \sqrt{y} \} \\
&= F_X(\sqrt{y}) - F_X(- \sqrt{y}) \\
\end{aligned}\]
将 \(F_Y(y)\) 关于 \(y\) 求导数,即得 \(Y\) 的概率密度为:
\[f_Y(y) = \begin{cases}
\frac{1}{2\sqrt{y}} \left[f_X(\sqrt{y}) + f_X(-\sqrt{y}) \right], & y>0 \\
0, & y \le 0
\end{cases}\]
一般地,可以用和上面类似的方法求连续型随机变量的函数的概率密度。
2.6. 其它随机变量
对于随机变量,并不是说除了离散型随机变量就是连续型随机变量。 还有一些随机变量既不是离散型随机变量,又不是连续型随机变量。
如:
概率密度函数 f(x)=1/4, 当 x 在[0,1]范围中;f(x)=3/4, 当 x 在[2,3]范围中。
这个分段函数是非离散型的,但又不是连续的。所以它既不是离散型随机变量,又不是连续型随机变量。
3. 多维随机变量及其分布
设随机试验的样本空间为 \(S=\{e\}\) ,且 \(X=X(e)\) 和 \(Y=Y(e)\) 是定义在 \(S\) 上的随机变量,由它们构成的一个向量 \((X,Y)\) 叫做 二维随机向量 ,又称为 二维随机变量 。二维随机变量 \((X,Y)\) 的性质不仅与 \(X\) 和 \(Y\) 有关,而且依赖于这两个随机变量的相互关系。
3.1. 联合分布
定义:设 \((X,Y)\) 是二维随机变量,对于任意实数 \(x,y\) ,二元函数:
\[F(x,y) = P\{(X \le x) \cap (Y \le y)\} \stackrel{\text{记为}}{=} P\{ X \le x, Y \le y \}\]
称为二维随机变量 \((X,Y)\) 的分布函数,或称为 随机变量 \(X\) 和 \(Y\) 的联合分布函数 。
3.1.1. 二维离散型随机变量的联合分布律
如果二维随机变量 \((X,Y)\) 全部可能取到的值是有限对或可列无限多对,则称 \((X,Y)\) 为二维离散型随机变量。
设二维离散型随机变量 \((X,Y)\) 所有可能取值为 \(x_i,y_i, \; i,j = 1,2, \cdots\) ,记 \(P\{ X=x_i, Y=y_i\} = p_{ij}, \; i,j = 1,2, \cdots\) ,由概率的定义有:
\[p_{ij} \ge 0, \; \sum_{i=1}^{\infty}\sum_{j=1}^{\infty} p_{ij} = 1\]
我们称 \(P\{ X=x_i, Y=y_i\} = p_{ij}, \; i,j = 1,2, \cdots\) 为二维离散型随机变量 \((X,Y)\) 的分布律,或称 离散型随机变量 \(X\) 和 \(Y\) 的联合分布律 。
我们可以用表格来表示二维离散型随机变量的联合分布律,如:
\[\begin{array}{c|ccccc}
Y \backslash X & x_1 & x_2 & \cdots & x_i & \cdots \\
\hline
y_1 & p_{11} & p_{21} & \cdots & p_{i1} & \cdots \\
y_2 & p_{12} & p_{22} & \cdots & p_{i2} & \cdots \\
\vdots & \vdots & \vdots & & \vdots & \\
y_j & p_{1j} & p_{2j} & \cdots & p_{ij} & \cdots \\
\vdots & \vdots & \vdots & & \vdots & \\
\end{array}\]
由联合分布函数定义知,离散型随机变量 \(X\) 和 \(Y\) 的联合分布函数为:
\[F(x,y) = \sum_{x_i \le x}\sum_{y_j \le y} p_{ij}\]
其中,和式是对一切满足 \(x_i \le x , y_j \le y\) 的 \(i,j\) 来求和的。
3.1.2. 二维连续型随机变量的联合概率密度
设二维随机变量 \((X,Y)\) 的分布函数为 \(F(x,y)\) ,如果存在非负函数 \(f(x,y)\) 使对于任意 \(x,y\) 有:
\[F(x,y) = \int_{-\infty}^y \int_{-\infty}^{x} f(u,v) \,\mathrm{d}u\mathrm{d}v\]
则称 \((X,Y)\) 是二维连续型随机变量,其中函数 \(f(x,y)\) 称为二维连续型随机变量的概率密度,或称为 连续型随机变量 \(X\) 和 \(Y\) 的联合概率密度 。
3.2. 边缘分布
二维随机变量 \((X,Y)\) 关于 \(X\) 的 边缘分布函数(Marginal distribution) 定义为:
\[F_X(x) = P\{X \le x \} = P\{X \le x, Y < \infty \} = F(x,\infty)\]
同样,关于 \(Y\) 的边缘分布函数定义为:
\[F_Y(y) = F(\infty, y)\]
可以认为,边缘分布是随机变量 \(X\) 和 \(Y\) 各自的分布。
3.2.1. 二维离散型随机变量的边缘分布律(“边缘”名字由来)
容易得到二维离散型随机变量 \((X,Y)\) 关于 \(X\) 的边缘分布律为:
\[p_{i \cdot} = \sum_{j=1}^{\infty}p_{ij} = P\{X=x_i\}, \; i = 1,2,\cdots\]
同样,关于 \(Y\) 的边缘分布律为:
\[p_{\cdot j} = \sum_{i=1}^{\infty}p_{ij} = P\{Y=y_i\}, \; y = 1,2,\cdots\]
说明:记号 \(p_{i \cdot}\) 中的 \(\cdot\) 表示 \(p_{ij}\) 关于 \(j\) 求和后得到的;同样, \(p_{\cdot j}\) 是由 \(p_{ij}\) 关于 \(i\) 求和后得到的。
边缘分布律实例:
设随机变量 \(X\) 在 1,2,3,4 四个整数中等可能地取一个值,另一个随机变量 \(Y\) 在“1 到 X 的整数”中等可能地取一整数值,求 \((X,Y)\) 的边缘分布律。
解:先求 \((X,Y)\) 的联合分布律,再求其边缘分布律。容易得到:
\[\begin{array}{c|cccc|c}
Y \backslash X & 1 & 2 & 3 & 4 & p_{\cdot j}=P\{ Y=j \} \\
\hline
1 & \frac{1}{4} & \frac{1}{8} & \frac{1}{12} & \frac{1}{16} & \frac{25}{48} \\
2 & 0 & \frac{1}{8} & \frac{1}{12} & \frac{1}{16} & \frac{13}{48} \\
3 & 0 & 0 & \frac{1}{12} & \frac{1}{16} & \frac{7}{48} \\
4 & 0 & 0 & 0 & \frac{1}{16} & \frac{1}{16} \\
\hline
p_{i \cdot} = P\{ X = i \} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & 1 \\
\end{array}\]
我们常常将边缘分布律写在联合分布律表格的边缘上,这就是“边缘”二字的由来。
3.2.2. 二维连续型随机变量的边缘概率密度
容易得到二维连续型随机变量 \((X,Y)\) 关于 \(X\) 的边缘概率密度为:
\[f_X(x) = \int_{-\infty}^{\infty} f(x,y) \, \mathrm{d}y = \int_{y} f(x,y) \, \mathrm{d}y\]
同样,关于 \(Y\) 的边缘概率密度为:
\[f_Y(y) = \int_{-\infty}^{\infty} f(x,y) \, \mathrm{d}x = \int_{x} f(x,y) \, \mathrm{d}x\]
3.3. 条件分布
3.3.1. 二维离散型随机变量的条件分布律
对于固定的 \(j\) ,若 \(P\{Y=y_j\} > 0\) ,则称
\[P\{X=x_i \mid Y=y_j\} = \frac{P\{X=x_i , Y=y_j\}}{P\{Y=y_j\}} = \frac{p_{ij}}{p_{\cdot j}}, \; i = 1,2, \cdots\]
为 在 \(Y=y_j\) 条件下随机变量 \(X\) 的条件分布律 。
同样,对于固定的 \(j\) ,若 \(P\{X=x_i\} > 0\) ,则称
\[P\{Y=y_i \mid X=x_i\} = \frac{P\{X=x_i , Y=y_j\}}{P\{X=x_i\}} = \frac{p_{ij}}{p_{i \cdot}}, \; j = 1,2, \cdots\]
为 在 \(X=x_i\) 条件下随机变量 \(Y\) 的条件分布律 。
3.3.2. 二维连续型随机变量的条件概率密度
设二维连续型随机变量 \((X,Y)\) 的概率密度为 \(f(x,y)\) ,关于 \(Y\) 的边缘概率密度为 \(f_Y(y)\) 。若对于固定的 \(y, \; f_Y(y) > 0\) ,则称 \(\frac{f(x,y)}{f_Y(y)}\) 为在 \(Y=y\) 的条件下 \(X\) 的条件概率密度,记为 \(f_{X|Y}(x \mid y)\) ,即有:
\[f_{X|Y}(x \mid y) = \frac{f(x,y)}{f_Y(y)}\]
同样,在 \(X=x\) 的条件下 \(Y\) 的条件概率密度定义为:
\[f_{Y|X}(y \mid x) = \frac{f(x,y)}{f_X(x)}\]
3.4. 相互独立的随机变量
随机变量相互独立是概率论中非常重要的概念,它是随机事件相互独立的推广。
如果二维随机变量 \((X,Y)\) ,有:
\[P\{X \le x, Y \le y\} = P\{X \le x\} P\{Y \le y\}\]
则称随机变量 \(X\) 和 \(Y\) 相互独立。
显然, 如果随机变量 \((X,Y)\) 相互独立,则联合分布可由边缘分布唯一确定。
3.4.1. 离散型随机变量相互独立
设 \((X,Y)\) 为二维离散型随机变量,随机变量 \(X\) 和 \(Y\) 相互独立等价于对于 \((X,Y)\) 的所有可能取值 \((x_i,y_j)\) 都有:
\[P\{X=x_i, Y=y_j\} = P\{X=x_i\} P\{Y=y_j\}\]
3.4.2. 连续型随机变量相互独立
设 \((X,Y)\) 为二维连续型随机变量, \(f(x,y), f_X(x), f_Y(y)\) 分别为 \((X,Y)\) 的概率密度和边缘概率密度,则随机变量 \(X\) 和 \(Y\) 相互独立等价于:
\[f(x,y) = f_X(x) f_Y(y)\]
在平面上几乎处处成立(“几乎处处成立”在此的含义是:在平面上除去“面积”为零的集合以外,处处成立)。
3.5. 两个随机变量的函数的分布
本节讨论两个随机变量的函数的分布。
3.5.1. Z=X+Y 的分布
设 \((X,Y)\) 是二维连续型随机变量,它具有概率密度 \(f(x,y)\) ,则 \(Z=X+Y\) 仍为连续型随机变量,其概率密度为:
\[f_{X+Y}(z) = \int_{- \infty}^{\infty} f(z-y,y) \, \mathrm{d} y\]
或者:
\[f_{X+Y}(z) = \int_{- \infty}^{\infty} f(x,z-x) \, \mathrm{d} x\]
进一步,如果 \(X\) 和 \(Y\) 相互独立,记 \((X,Y)\) 关于 \(X,Y\) 的边缘密度分别为 \(f_X(x),f_Y(y)\) ,则上面式子还可以写为:
\[f_{X+Y}(z) = \int_{- \infty}^{\infty} f_X(z-y)f_Y(y) \, \mathrm{d} y\]
或者:
\[f_{X+Y}(z) = \int_{- \infty}^{\infty} f_X(x)f_Y(z-x) \, \mathrm{d} x\]
其证明略。
例:设 \(X\) 和 \(Y\) 是两个相互独立的随机变量,它们都服从 \(N(0,1)\) 分布,其概率密度为:
\[\begin{gathered} f_X(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2}, \quad -\infty < x < \infty \\
f_Y(y) = \frac{1}{\sqrt{2\pi}} e^{-y^2/2}, \quad -\infty < y < \infty \end{gathered}\]
求 \(Z=X+Y\) 的概率密度。
解:由前面给出的结论有:
\[\begin{aligned} f_Z(z) &= \int_{- \infty}^{\infty} f_X(x)f_Y(z-x) \, \mathrm{d} x \\
&= \frac{1}{2\pi} \int_{- \infty}^{\infty} e^{-\frac{x^2}{2}} \cdot e^{-\frac{(z-x)^2}{2}} \, \mathrm{d} x \\
&= \frac{1}{2\pi} e^{-\frac{z^2}{4}} \int_{- \infty}^{\infty} e^{-(x- \frac{z}{2})^2} \, \mathrm{d} x \\
\end{aligned}\]
令 \(t=x-\frac{z}{2}\) ,得:
\[f_Z(z) = \frac{1}{2\pi} e^{-\frac{z^2}{4}} \int_{- \infty}^{\infty} e^{-t^2} \, \mathrm{d} t = \frac{1}{2\pi} e^{-\frac{z^2}{4}} \sqrt{\pi} = \frac{1}{2\sqrt{\pi}} e^{-\frac{z^2}{4}}\]
即 \(Z\) 服从 \(N(0,2)\) 分布。
更一般地, 若 \(X_i \sim N(\mu_i, \sigma_i^2) \; (n=1,2,\cdots,n)\) ,且它们相互独立,则它们的和 \(Z=X_1+X_2+ \cdots + X_n\) 仍然服从正态分布,且有 \(Z \sim N(\mu_1 + \mu_2 + \cdots + \mu_n, \sigma_1^2 + \sigma_2^2 + \cdots + \sigma_n^2)\) 。
3.5.2. Z=Y/X 和 Z=XY 的分布
设 \((X,Y)\) 是二维连续型随机变量,它具有概率密度 \(f(x,y)\) ,则 \(Z=\frac{Y}{X}, \, Z=XY\) 仍为连续型随机变量,其概率密度为:
\[\begin{aligned} f_{Y/X}(z) & = \int_{- \infty}^{\infty} \vert x \vert \, f(x,xz) \, \mathrm{d} x \\
f_{XY}(z) & = \int_{- \infty}^{\infty} \frac{1}{\vert x \vert} \, f(x,\frac{z}{x}) \, \mathrm{d} x \end{aligned}\]
进一步,如果 \(X\) 和 \(Y\) 相互独立,记 \((X,Y)\) 关于 \(X,Y\) 的边缘密度分别为 \(f_X(x),f_Y(y)\) ,则上面式子还可以写为:
\[\begin{aligned} f_{Y/X}(z) & = \int_{- \infty}^{\infty} \vert x \vert \, f_X(x)f_Y(xz) \, \mathrm{d} x \\
f_{XY}(z) & = \int_{- \infty}^{\infty} \frac{1}{\vert x \vert} \, f_X(x)f_Y(\frac{z}{x}) \, \mathrm{d} x \end{aligned}\]
其证明略。
4. 随机变量的数字特征
4.1. 数学期望(Expectation)
设离散型随机变量 \(X\) 的分布律(概率质量函数)为: \(P\{X=x_k\} = p_k \quad (k=1,2, \cdots)\) ,如果级数 \(\sum_{i}^{\infty}x_{k}p_{k}\) 绝对收敛,则称它为随机变量 \(X\) 的数学期望,记为 \(E(X)\) 。即离散型随机变量有数学期望:
\[E(X)=\sum_{i}^{\infty}x_{k}p_{k}\]
设连续型随机变量 \(X\) 的概率密度函数为 \(f(x)\) ,如果积分 \(\int_{-\infty}^{\infty} xf(x)dx\) 绝对收敛,则称它为随机变量 \(X\) 的数字期望,记为 \(E(X)\) 。即连续型随机变量的数学期望:
\[E(X)=\int_{-\infty}^{\infty} xf(x)dx\]
数学期望简称期望,又称均值。
数学期望具有下面几个重要性质:
(1) 设 \(C\) 是常数,则 \(E(C)=C\) 。
(2) 设 \(X\) 是随机变量, \(C\) 是常数,则:
\[E(CX) = C E(X)\]
(3) 设 \(X,Y\) 是两个随机变量,则:
\[E(X+Y) = E(X) + E(Y)\]
(4) 如果 \(X,Y\) 是相互独立的随机变量,则:
\[E(XY) = E(X) E(Y)\]
4.1.1. 随机变量函数的期望
定理(证明略):设 \(Y\) 是随机变量 \(X\) 的函数,满足 \(Y=g(X)\) ,其中 \(g\) 是连续函数。则:
(1) 如果 \(X\) 是离散型随机变量,它的分布律为 \(P \{ X=x_k \} = p_k, k=1,2,\cdots\) ,如果 \(\sum_{k=1}^{\infty}g(x_k)p_k\) 绝对收敛,则:
\[E(Y) = E[g(X)] = \sum_{k=1}^{\infty}g(x_k)p_k\]
(2) 如果 \(X\) 是连续型随机变量,它的概率密码为 \(f(x)\) ,如果 \(\int_{- \infty}^{\infty}g(x)f(x) \, \mathrm{d}x\) 绝对收敛,则:
\[E(Y) = E[g(X)] = \int_{- \infty}^{\infty}g(x)f(x) \, \mathrm{d}x\]
4.2. 方差(Variance)和标准差(Standard deviation)
先从例子说起。假设一批灯泡平均寿命为 \(E(X)=1000\) 小时。要评价这批灯泡的好坏,我们还想知道灯泡寿命 \(X\) 和它的均值(即 1000 小时)的偏离程度。若偏离程度越小,说明质量越稳定。
如何描述和均值偏离程度呢?容易想到 \(E[|X-E(X)|]\) ,但绝对值的运算不方便。通常我们用 \(E[(X-E(X))^2]\) 来度量随机变量 \(X\) 与其均值的偏离程序。
设 \(X\) 是一个随机变量,若 \(E[(X-E(X))^2]\) 存在,则称它为 \(X\) 的方差(Variance),记为 \(D(X)\) 或者 \(Var(X)\) 。即方差为:
\[D(X)=Var(X)=E[(X-E(X))^2]\]
由方差的定义知,方差是随机变量 \(X\) 的函数 \(g(X) = (X-E(X))^2\) 的数学期望。所以,对于离散型随机变量,设 \(X\) 的分布律为 \(P\{X=x_k\} = p_k, k = 1,2,\cdots\) ,有:
\[D(X) = \sum_{k=1}^{\infty}[x_k - E(X)]^2 p_k\]
对于连续型随机变量,设 \(X\) 的概率密度为 \(f(x)\) ,有:
\[D(X) = \int_{- \infty}^{\infty}[x - E(X)]^2 f(x) dx\]
方差的平方根称为标准差(Standard deviation)或者均方差。记为 \(\sigma(X)\) 。即标准差为:
\[\sigma(X)=\sqrt{D(X)}=\sqrt{Var(X)}\]
方差具有下面几个重要性质:
(1) 设 \(C\) 是常数,则 \(D(C)=0\) 。
(2) 设 \(X\) 是随机变量, \(C\) 是常数,则:
\[\begin{aligned} D(CX) = C^2 D(X) \\
D(X+C) = D(X) \end{aligned}\]
(3) 设 \(X,Y\) 是两个随机变量,则:
\[D(X+Y) = D(X) + D(Y) + 2 E\{ (X-E(X)) (Y-E(Y)) \}\]
特别地,如果 \(X,Y\) 相互独立,则:
\[D(X+Y) = D(X) + D(Y)\]
4.3. 协方差(Covariance)与相关系数(Correlation coefficient)
对于二维随机变量 \((X,Y)\) ,我们除了讨论 \(X\) 和 \(Y\) 的数学期望和方差以外,还需要描述 \(X\) 和 \(Y\) 之间相互关系的数学特征。
量 \(E[(X-E(X))(Y-E(Y))]\) 称为随机变量 \(X\) 与 \(Y\) 的协方差(Covariance),记为 \(Cov(X,Y)\) 。即随机变量 \(X\) 和 \(Y\) 的协方差为:
\[Cov(X,Y) = E[(X-E(X))(Y-E(Y))]\]
由上面定义知: \(Cov(X,Y)=Cov(Y,X)\) 且 \(Cov(X,X) = Var(X)\)
随机变量 \(X\) 和 \(Y\) 的相关系数(Correlation coefficient)的定义为:
\[\rho_{XY} = \frac{Cov(X,Y)}{\sigma(X)\sigma(Y)}=\frac{Cov(X,Y)}{\sqrt{Var(X)}\sqrt{Var(Y)}}\]
可以认为相关系数是“归一化”的协方差。相关系数的大小在-1 和 1 之间变化,即有 \(|\rho_{XY}| \le 1\) 。
当 \(\rho_{XY} = 0\) 时,称随机变量 \(X\) 和 \(Y\) 不相关。当 \(|\rho_{XY}| = 1\) 时,说明随机变量 \(X\) 和 \(Y\) 之间存在线性关系。
4.4. 协方差矩阵(Covariance matrix)
定义二维随机变量 \((X,Y)\) 的协方差矩阵(Covariance matrix)为:
\[C=\left( \begin{array}{cc}
Cov(X,X) & Cov(X,Y) \\
Cov(Y,X) & Cov(Y,Y) \end{array} \right)=\left( \begin{array}{cc}
Var(X) & Cov(X,Y) \\
Cov(X,Y) & Var(Y) \end{array} \right)\]
推广到 \(n\) 维随机变量 \((X_1, X_2, \cdots, X_n)\) 的情况,其协方差矩阵为:
\[C=\left( \begin{array}{cccc}
Cov(X_1,X_1) & Cov(X_1,X_2) & \cdots & Cov(X_1, X_n)\\
Cov(X_2,X_1) & Cov(X_2,X_2) & \cdots & Cov(X_2, X_n)\\
\vdots & \vdots & &\vdots \\
Cov(X_n,X_1) & Cov(X_n,X_2) & \cdots & Cov(X_n, X_n)\\
\end{array} \right)\]
由于 \(Cov(X,Y)=Cov(Y,X)\) ,所以上面矩阵是一个对称矩阵。
一般地, \(n\) 维随机变量的分布是不知道的,或者太复杂,所以实际应用中协方差矩阵就显得很重要了。
4.4.1. n 维正态随机变量的概率密度
正态分布是最重要的分布。我们从二维正态随机变量的概率密度开发,介绍 \(n\) 维正态随机变量的概率密度。
二维正态随机变量 \((X_1, X_2)\) 的概率密度,其定义为:
\[f(x_1, x_2) = \frac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} \exp \left\{ - \frac{1}{2(1-\rho^2)} \left[\frac{(x_1 - \mu_1)^2}{\sigma_1} -2\rho \frac{(x_1 - \mu_1)(x_2 - \mu_2)}{\sigma_1 \sigma_2} + \frac{(x_2 - \mu_2)^2}{\sigma_2} \right] \right\}\]
其中, \(\mu_1, \mu_2, \sigma_1 > 0, \sigma_2 > 0, \vert \rho \vert < 1\) 是常数。现在将上式中花括号内的式子写为矩阵的形式,为此引入列向量:
\[\boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}, \; \boldsymbol{\mu} = \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\]
\((X_1, X_2)\) 的协方差矩阵(其中矩阵元素 \(c_{ij} = Cov(X_i, X_j)\) )为:
\[\Sigma = \begin{bmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{bmatrix} = \begin{bmatrix} \sigma_2^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_1^2 \end{bmatrix}\]
它的列行式 \(\det \Sigma = \sigma_1^2 \sigma_2^2 (1-\rho^2)\) , \(\Sigma\) 的逆矩阵为:
\[\Sigma^{-1} = \frac{1}{\det \Sigma} \begin{bmatrix} \sigma_2^2 & - \rho \sigma_1 \sigma_2 \\ - \rho \sigma_1 \sigma_2 & \sigma_1^2 \end{bmatrix}\]
经过计算可知:
\[\begin{aligned} (\boldsymbol{x} - \boldsymbol{\mu})^{\mathsf{T}} \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) & = \frac{1}{\det \Sigma} \begin{bmatrix} x_1 - \mu_1 & x_2 - \mu_2 \end{bmatrix} \begin{bmatrix} \sigma_2^2 & - \rho \sigma_1 \sigma_2 \\ - \rho \sigma_1 \sigma_2 & \sigma_1^2 \end{bmatrix} \begin{bmatrix} x_1 - \mu_1 \\ x_2 - \mu_2 \end{bmatrix} \\ \\
& = \frac{1}{1-\rho^2} \left[\frac{(x_1 - \mu_1)^2}{\sigma_1} -2\rho \frac{(x_1 - \mu_1)(x_2 - \mu_2)}{\sigma_1 \sigma_2} + \frac{(x_2 - \mu_2)^2}{\sigma_2} \right]
\end{aligned}\]
从而, \((X_1, X_2)\) 的概率密度还可以写为:
\[f(x_1, x_2) = \frac{1}{(2\pi)^{2/2} (\det \Sigma)^{1/2}} \exp \left\{ - \frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^{\mathsf{T}} \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right\}\]
其中,矩阵 \(\Sigma\) 是 \((X_1,X_2)\) 的协方差矩阵,它是一个正定对称矩阵。
这个定义可以推广到 \(n\) 维正态随机变量。
4.4.1.1. n 维正态随机变量及其性质
记:
\[\boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}, \; \boldsymbol{\mu} = \begin{bmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_n \end{bmatrix} = \begin{bmatrix} E(X_1) \\ E(X_2) \\ \vdots \\ E(X_n) \end{bmatrix}\]
\(n\) 维正态随机变量 \((X_1,X_2, \cdots, X_n)\) 的概率密度的定义为:
\[\begin{aligned} f(x_1,x_2, \cdots, x_n) &= \frac{1}{(2\pi)^{n/2} (\det \Sigma)^{1/2}} \exp \left\{ - \frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^{\mathsf{T}} \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right\} \\
&= \det(2\pi \Sigma)^{-\frac{1}{2}} \exp \left\{ - \frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^{\mathsf{T}} \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right\} \\
\end{aligned}\]
其中: \(\Sigma\) 是 \((X_1,X_2, \cdots, X_n)\) 的协方差矩阵。
\(n\) 维正态随机变量具有以下四条重要性质(这里不证明):
(1) \(n\) 维正态随机变量 \((X_1,X_2, \cdots, X_n)\) 的每一个分量 \(X_i, i=1,2,\cdots,n\) 都是正态随机变量;反之,若 \(X_i, i=1,2,\cdots,n\) 都是正态随机变量,且相互独立,则 \((X_1,X_2, \cdots, X_n)\) 是 \(n\) 维正态随机变量。
(2) \(n\) 维随机变量 \((X_1,X_2, \cdots, X_n)\) 服从 \(n\) 维正态分布的充要条件是 \(X_1,X_2, \cdots, X_n\) 的任意的线性组合:
\[l_1X_1 + l_2X_2 + \cdots + l_n X_n\]
服从一维正态分布(其中 \(l_1,l_2,\cdots,l_n\) 不全为零)。
(3) 若 \((X_1,X_2, \cdots, X_n)\) 服从 \(n\) 维正态分布,设 \(Y_1,Y_2, \cdots, Y_m\) 分别是 \(X_1,X_2, \cdots, X_n\) 的非零线性组合,则 \((Y_1,Y_2, \cdots, Y_m)\) 是 \(m\) 维正态分布随机变量。
(4) 设 \((X_1,X_2, \cdots, X_n)\) 服从 \(n\) 维正态分布,则 “ \(X_1,X_2, \cdots, X_n\) 相互独立”和“ \(X_1,X_2, \cdots, X_n\) 两两不相关”是等价的。
4.5. 矩(Moment)和矩生成函数(Moment-generating function)
4.5.1. 矩(Moment)
设 \(X\) 是随机变量,如果
\[E(X^k), \quad k=1,2,\cdots\]
存在,则称它为 \(X\) 的 \(k\) 阶原点矩,简称 \(k\) 阶矩(Moment)。
设 \(X\) 是随机变量,如果
\[E[(X - E(X))^k ], \quad k=1,2,\cdots\]
存在,则称它为 \(X\) 的 \(k\) 阶中心矩 ,一般记为 \(\mu_k\) 。
4.5.1.1. 标准矩(Standardized moment)、偏度(Skewness)和峰度(Kurtosis)
标准矩(Standardized moment)是经过标准化后的中心矩, \(k\) 阶标准矩 的定义如下:
\[\frac{\mu_k}{\sigma^k}\]
其中, \(\mu_k\) 是\(k\) 阶中心矩;而 \(\sigma^k\) 是标准差的 \(k\) 次方,即 \(\sigma^k = \left( \sqrt{E[(X - E(X))^2]} \right)^k\) 。故 \(k\) 阶标准矩又可写为:
\[\frac{\mu_k}{\sigma^k} = \frac{E[(X - E(X))^k ]}{\left( E[(X - E(X))^2] \right)^{k/2}}\]
其中,3阶标准矩又称为 偏度(Skewness) ,可用来描述概率分布的不对称性;4阶标准矩又称为 峰度(Kurtosis) ,可用来描述分布的中心聚集程度。
4.5.2. 矩生成函数(Moment-generating function)
随机变量 \(X\) 的概率密度函数为 \(f(x)\) ,则它的 矩生成函数(Moment-generating function) 定义为:
\[M_X(t) := E \left[ e^{tX}\right] = \int_{-\infty}^{\infty} e^{tx} f(x) \, \mathrm{d} x, \qquad t \in \mathbb{R}\]
矩生成函数仅当上式中积分收敛时存在(也就是说,矩生成函数可能不存在)。矩生成函数又称矩母函数。
由于:
\[e^{tX} = 1 + tX + \frac{t^2 X^2}{2!} + \frac{t^3 X^3}{3!} + \cdots + \frac{t^n X^n}{n!} + \cdots\]
从而有:
\[\begin{aligned} M_X(t) = E \left[ e^{tX}\right] & = 1 + t E(X) + \frac{t^2 E(X^2)}{2!} + \frac{t^3 E(X^3)}{3!} + \cdots + \frac{t^n E(X^n)}{n!} + \cdots \\
& = 1 + tm_1 + \frac{t^2 m_2}{2!} + \frac{t^3 m_3}{3!} + \cdots + \frac{t^n m_n}{n!} + \cdots
\end{aligned}\]
其中, \(m_n\) 表示的是 \(X\) 的 \(n\) 阶矩(即 \(E(X^n)\) )。
由上式可知, \(\left. M_X'(t) \right|_{t=0} = M_X'(0) = E(X)\) 。一般地, 通过矩生成函数可以生成 \(X\) 的各阶矩 :
\[m_n = E(X^n) = M_X^{(n)}(0) = \frac{\mathrm{d}^n M_X}{\mathrm{d} t^n}(0)\]
这就是 \(M_X(t)\) 被称为矩生成函数的原因。
参考:https://en.wikipedia.org/wiki/Moment-generating_function#Calculations_of_moments
4.5.2.1. 矩生成函数和分布函数相互唯一确定
矩生成函数有个重要性质: 如果矩生成函数存在,则矩生成函数和分布函数相互唯一确定。 也就是说,如果两个随机变量的矩生成函数相同,则它们的分布函数一定也相同;如果分布函数相同,则矩生成函数也相同(如果矩生成函数存在的话)。
5. 大数定律和中心极限定理
5.1. 大数定律
大数定理(Law of large numbers)解决了“为什么可以用频率当概率的估计”这个很基本问题。
大数定律有多种数学表述,这里仅介绍伯努利大数定律。
伯努利大数定律:设 \(f_A\) 是 \(n\) 次独立重复试验中事件 \(A\) 发生的次数, \(p\) 是事件 \(A\) 在每次试验中发生的概率,则对于任意正数 \(\varepsilon > 0\) ,有
\[\lim_{n \to \infty}P\left\{\left|\frac{f_A}{n} - p\right| < \varepsilon \right\} =1\]
大数定律表述了这样一种事实:在相同条件下,随着随机试验次数的增多,频率越来越接近于概率。
5.2. 中心极限定理
中心极限定理(Central limit theorem)指出 大量的独立随机变量之和近似于正态分布。
很多人做过抛硬币的实验。
| 试验者 | 试验次数 | 正面朝上次数 | 正面朝上频率 |
|---|---|---|---|
| 德摩根 | 4092 | 2048 | 50.05% |
| 蒲丰 | 4040 | 2048 | 50.69% |
| 费勒 | 10000 | 4979 | 49.79% |
| 皮尔逊 | 24000 | 12012 | 50.05% |
| 罗曼洛夫斯基 | 80640 | 39699 | 49.23% |
大数定理能够说明:当试验的次数非常非常大(接近无穷)时,正面朝上频率会非常非常接近正面朝上的概率。
中心极限定理能够说明:如果很多人都进行抛硬币试验,正面朝上的频率会服从正态分布。
6. 数理统计基本概念
在实践中,我们研究的随机变量的分布往往是未知的,通过对所研究的随机变量进行重复独立的观察,得到许多观察值,对这些数据进行分析,从而对所研究的随机变量的分布作出推断。
6.1. 总体、样本
在数理统计中,我们将研究对象的全体称为 总体 ,而组成总体的每一个基本元素称为个体。
设 \(X\) 是具有分布函数 \(F\) 的随机变量,若 \(X_1, X_2, \cdots, X_n\) 是具有同一分布函数 \(F\) 的、相互独立的随机变量,则称 \(X_1, X_2, \cdots, X_n\) 为从分布函数 \(F\) (或总体 \(X\) )得到的容量为 \(n\) 的简单随机样本,简称 样本 ,它们的观察值 \(x_1, x_2, \cdots, x_n\) 称为 样本值 。取得样本的过程称为 抽样 。
可以将样本看成是一个随机向量,写成 \((X_1, X_2, \cdots, X_n)\) ,此时样本值相应地写成 \((x_1, x_2, \cdots, x_n)\) 。由定义知:若总体 \(X\) 的分布函数为 \(F(x)\) ,则样本 \(X_1, X_2, \cdots, X_n\) 相互独立,且它们的分布函数都是 \(F\) ,从而 \((X_1, X_2, \cdots, X_n)\) 的分布函数(即 \(X_1, X_2, \cdots, X_n\) 的联合分布函数)为:
\[F^{*}(x_1, x_2, \cdots, x_n) = P \{X_1 \le x_1, X_2 \le x_2, \cdots, X_n \le x_n \} = \prod_{i=1}^{n}P \{X_i \le x_i \} = \prod_{i=1}^{n} F(x_i)\]
又若 \(X\) 具有概率密度 \(f\) ,则 \((X_1, X_2, \cdots, X_n)\) 的概率密度为:
\[f^{*}(x_1, x_2, \cdots, x_n) = \prod_{i=1}^{n} f(x_i)\]
6.1.1. 抽样方法简介
可以把抽样(Sampling)方法分为两大类:
- 概率抽样(Probability Sampling)
- 又称随机抽样。 总体中,每个观察单位都有被抽中的可能,任何一个对象被抽中的概率是已知的或可计算的。
- 非概率抽样(Non-probability Sampling)
- 又称非随机抽样。 总体中,每个观察单位被抽中的概率是未知的或无法计算的。 抽样时不是遵循随机原则,而是按照研究人员的主观经验或其它条件来抽取样本的一种抽样方法。比如偶遇抽样(Accidental Sampling),判断抽样(Judgmental Sampling),配额抽样(Quota Sampling),滚雪球抽样(Snowball Sampling),应答推动抽样(Respond-driven Sampling)等等。非概率抽样失去了大数定律的存在基础,也就无法确定抽样误差,无法正确地说明样本的统计值在多大程度上适合于总体。
6.1.2. 常用概率抽样方法(系统抽样、分层抽样、整群抽样等)
常用概率抽样方法有:
(1) 简单随机抽样(Simple Random Sampling):将调查的抽样框中的全部观察单位进行编号,用抽签或随机数字等方法在抽样框中随机抽取部分观察单位组成样本。
优点:操作简单,均数、率及相应的标准误计算简单。
缺点:总体较大时,难以一一编号。
(2) 系统抽样(Systematic Sampling):又称机械抽样、等距抽样。先将总体的观察单位按某一顺序号分成 n 个部分,再从第一部分随机抽取第 k 号观察单位,依次用相等间距从每一部分各抽取一个观察单位组成样本。
优点:易于理解,简便易行。
缺点:总体有周期或增减趋势时,易产生偏性。
(3) 整群抽样(Cluster Sampling):先将总体分成若干群体,再随机抽取几个群组成样本,群内全部调查。
优点:便于组织,节省经费。
缺点:当样本含量一定时,抽样误差一般大于简单随机抽样的误差。
(4) 分层抽样(Stratified Sampling):将总体样本按其属性特征分成若干类型或层,然后在类型或层中随机抽取样本单位,合起来组成样本。
优点:样本代表性好,抽样误差减少。
缺点:如果分层变量选择不当,层内变异度较大,层间均数相近,分层抽样就失去了意义。
(5) 多阶段抽样(Multistage Sampling):前述的四种基本抽样方法都是通过一次抽样产生一个完整的样本,称为单阶段抽样。将整个抽样过程分为若干阶段来进行,各阶段可采用相同或不同的抽样方法。
参考:
卫生统计学,常用抽样方法:http://58.20.53.45/files/files_upload/content/material_240/content/010/file_2.htm
百度文库,常用的抽样方法:http://wenku.baidu.com/view/067fb8fe700abb68a982fb85.html
6.2. 统计量
设 \(X_1, X_2, \cdots, X_n\) 是来自总体 \(X\) 的一个样本, \(g(X_1, X_2, \cdots, X_n)\) 是 \(X_1, X_2, \cdots, X_n\) 的函数,若 \(g\) 中不含有未知参数,则称 \(g(X_1, X_2, \cdots, X_n)\) 为一个 统计量 。
统计量是随机变量的函数,它也是随机变量。
6.2.1. 常用统计量
下面列出几个常用的统计量。设 \(X_1, X_2, \cdots, X_n\) 是来自总体 \(X\) 的一个样本。
- 样本均值
- \[\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_i\]
- 样本方差
- \[S^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2 = \frac{1}{n-1} (\sum_{i=1}^{n} X_i^2 - n \overline{X})\]
- 样本标准差
- \[S=\sqrt{S^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2}\]
- 样本 \(k\) 阶(原点)矩
- \[A_k = \frac{1}{n} \sum_{i=1}^{n}X_i^k, \quad k=1,2,\cdots\]
- 样本 \(k\) 阶中心矩
- \[B_k = \frac{1}{n} \sum_{i=1}^{n} \left( X_i - \overline{X}\right)^k, \quad k=1,2,\cdots\]
将样本观察值 \(x_1, x_2, \cdots, x_n\) 代入上述各式,得到 统计值 ,以相应的小写字母表示。即它们的观察值分别为:
\[\overline{x} = \frac{1}{n} \sum_{i=1}^{n} x_i\]
\[s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \overline{x})^2 = \frac{1}{n-1} (\sum_{i=1}^{n} x_i^2 - n \overline{x})\]
\[s=\sqrt{s^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \overline{x})^2}\]
这些观察值仍然分别称为样本均值、样本方差、样本标准差等等。
6.2.1.1. 样本方差是除以 n-1,而不除以 n
有上面的定义中,为什么样本方差是除以 n-1,而不除以 n?
因为样本方差 \(\frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2\) 是总体方差的无偏估计,而统计量 \(\frac{1}{n} \sum_{i=1}^{n} (X_i - \overline{X})^2\) 不是总体方差的无偏估计。
6.2.2. 经验分布函数(Empirical distribution function)
下面介绍一个与总体分布函数 \(F(x)\) 相关的统计量:经验分布函数。
设 \(X_1, X_2, \cdots, X_n\) 是总体 \(F\) 的一个样本,用 $S(x) 表示 \(X_1, X_2, \cdots, X_n\) 中不大于 \(x\) 的随机变量的个数。定义 经验分布函数(Empirical distribution function) \(F_n(x)\) 为:
\[F_n(x) = \frac{1}{n}S(x), \quad -\infty < x < \infty\]
对于一个样本值,那么经验分布函数 \(F_n(x)\) 的观察值(仍用 \(F_n(x)\) 表示)很容易得到。例如,设总体 \(F\) 具有一个样本值 1,2,3,则经验分布函数 \(F_3(x)\) 的观察值为:
\[F_3(x) = \begin{cases} 0, & \text{if} \, x < 1 \\
\frac{1}{3}, & \text{if} \, 1 \le x < 2 \\
\frac{2}{3}, & \text{if} \, 2 \le x < 3 \\
1, & \text{if} \, x \ge 3 \\
\end{cases}\]
又假设总体 \(F\) 具有一个样本值 1,1,2,则经验分布函数 \(F_3(x)\) 的观察值为:
\[F_3(x) = \begin{cases} 0, & \text{if} \, x < 1 \\
\frac{2}{3}, & \text{if} \, 1 \le x < 2 \\
1, & \text{if} \, x \ge 2 \\
\end{cases}\]
一般,设 \(x_1, x_2, \cdots, x_n\) 是总体 \(F\) 的一个容量为 \(n\) 的样本值,先将它们按从小到大的次序排列,并重新编号,设为:
\[x_{(1)} \le x_{(2)} \le \cdots \le x_{(n)}\]
则,经验分布函数 \(F_n(x)\) 的观察值为:
\[F_n(x) = \begin{cases} 0, & \text{if} \, x < x_{(1)} \\
\frac{k}{n}, & \text{if} \, x_{(k)} \le x < x_{(k+1)} \\
1, & \text{if} \, x \ge x_{(n)} \\
\end{cases}\]
经验分布函数的图示如下。
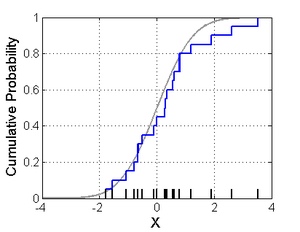
Figure 2: 经验分布函数(蓝色折线),图片摘自https://en.wikipedia.org/wiki/Empirical_distribution_function
Glivenko 在 1933 年证明了, 当 \(n \to \infty\) 时,经验分布函数 \(F_n(x)\) 以概率 1 一致收敛于总体分布函数 \(F(x)\) 。 所以,当样本容量充分大时,任一个观察值 \(F_n(x)\) 和总体分布函数 \(F(x)\) 的差别将很小。
6.3. 抽样分布(统计学三大分布)
统计量的分布称为抽样分布(Sampling distribution)。
\(\chi^2\) 分布 、\(t\) 分布 、\(F\) 分布 是统计学的三大分布,在数理统计中有着广泛的应用。
下面是 \(\chi^2\) 分布定义。
设 \(X_1, X_2, \cdots, X_n\) 是来自总体 \(N(0,1)\) 的样本,则称统计量
\[\chi^2 = X_1^2 + X_2^2 + \cdots + X_n^2\]
服从自由度为 \(n\) 的 \(\chi^2\) 分布,记为 \(\chi^2 \sim \chi^2(n)\) 。这里,自由度是指上式右端包含的独立变量的个数。
7. 参数估计
7.1. 点估计
设总体 \(X\) 的分布函数的形式已经,但它的一个或多个参数未知,借助于总体 \(X\) 的一个样本来估计总体未知参数的问题称为参数的 点估计 问题。
点估计问题的一般提法如下:设总体 \(X\) 的分布函数 \(F(x; \theta)\) 的形式为已知, \(\theta\) 为待估参数。 \(X_1, X_2, \cdots, X_n\) 是 \(X\) 的一个样本, \(x_1, x_2, \cdots, x_n\) 是相应的一个样本值。点估计问题就是要构造一个适当的统计量 \(\hat{\theta}(X_1, X_2, \cdots, X_n)\) ,用它的观察值 \(\hat{\theta}(x_1, x_2, \cdots, x_n)\) 作为未知参数 \(\theta\) 的近似值。我们称 \(\hat{\theta}(X_1, X+2, \cdots, X_n)\) 为 \(\theta\) 的 估计量 ,称 \(\hat{\theta}(x_1, x_2, \cdots, x_n)\) 为 \(\theta\) 的 估计值 。
在不致混淆的情况下估计量和估计值都可称为估计,并都简记为 \(\hat{\theta}\) 。由于估计量是样本的函数,因此 对于不同的样本值, \(\theta\) 的估计值一般是不同的。
7.1.1. 最大似然估计
若总体 \(X\) 属于离散型随机变量,其分布律 \(P \{ X=x \} = p(x;\theta), \theta \in \Theta\) 的形式为已知, \(\theta\) 为待估参数, \(\Theta\) 是 \(\theta\) 可能取值的范围。设 \(X_1, X_2, \cdots, X_n\) 是来自 \(X\) 的样本,则样本分布函数( \(X_1, X_2, \cdots, X_n\) 的联合分布律)为:
\[\prod_{i=1}^{n} p(x_i; \theta)\]
设 \(x_1, x_2, \cdots, x_n\) 是样本的一个观察值,易知取到观察值 \(x_1, x_2, \cdots, x_n\) 的概率,亦即事件 \(\{X_1 = x_1, X_2 = x_2, \cdots, X_n = x_n\}\) 的概率为:
\[L(\theta) = \prod_{i=1}^{n} p(x_i; \theta), \, \theta \in \Theta\]
上式中, \(x_1, x_2, \cdots, x_n\) 是已知的样本值,它们都是常数。 \(L(\theta)\) 称为样本的 似然函数 ,它是未知参数 \(\theta\) 的函数。
最大似然估计基于以下直观的想法:既然已经取到样本值 \(x_1, x_2, \cdots, x_n\) 了,则表明取到这一样本值的概率 \(L(\theta)\) 比较大。如果已知当 \(\theta = \theta_0 \in \Theta\) 时使 \(L(\theta)\) 取很大值,而 \(\Theta\) 中的其他 \(\theta\) 的值使 \(L(\theta)\) 取很小值,我们自然认为取 \(\theta_0\) 作为未知参数 \(\theta\) 的估计值较为合理。
最大似然估计法: 固定样本观察值 \(x_1, x_2, \cdots, x_n\) ,在 \(\theta\) 取值的可能范围 \(\Theta\) 内选择使似然函数 \(L(\theta)\) 达到最大时的参数值 \(\hat{\theta}\) 作为参数 \(\theta\) 的估计值。
类似地,若总体 \(X\) 属于连续型随机变量,其概率密度 \(f(x; \theta), \theta \in \Theta\) 的形式已知,参数 \(\theta\) 未知。样本的似然函数可以写为:
\[L(\theta) = \prod_{i=1}^{n} f(x_i; \theta)\]
利用微分学中求函数最大值的知识可以求解 \(\hat{\theta}\) 。
很多情况下 \(p(x; \theta)\) 和 \(f(x; \theta)\) 关于 \(\theta\) 可微,这时 \(\hat{\theta}\) 可以从下面方程中求得:
\[\frac{d}{d \theta} L(\theta) = 0\]
由于 \(L(\theta)\) 和 \(\ln L(\theta)\) 在同一 \(\theta\) 处取得极值,因此, \(\theta\) 的最大似然估计 \(\hat{\theta}\) 了可以从下面方程中求得:
\[\frac{d}{d \theta} \ln L(\theta) = 0\]
上面这个方程称为对数似然方程,求解对数似然方程往往比直接求解似然方程更方便。
如果分布函数中含有多个未知参数 \(\theta_1, \theta_2, \cdots, \theta_k\) ,则它们的最大似然估计可以从下面方程组中求得:
\[\frac{\partial}{\partial \theta_i} L = 0, \, i = 1,2,\cdots,k\]
多个参数的最大似然估计也可以从下面的对数似然方程组中求得:
\[\frac{\partial}{\partial \theta_i} \ln L = 0, \, i = 1,2,\cdots,k\]
7.1.1.1. 实例——求解最大似然估计
设 \(X \sim N(\mu, \sigma^2)\) ,其中参数 \(\mu, \sigma^2\) 未知,已知 \(x_1, x_2, \cdots, x_n\) 是来自 \(X\) 的一个样本观察值。求 \(\mu, \sigma^2\) 的最大似然估计值。
解: \(X\) 的概率密度为:
\[f(x;\mu, \sigma^2) = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}}\]
所以,似然函数为:
\[L(\mu, \sigma^2) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x_i-\mu)^{2}}{2\sigma^{2}}} = (2\pi)^{-n/2} (\sigma^2)^{-n/2} e^{-\frac{\sum_{i=1}^{n}(x_i-\mu)^{2}}{2\sigma^{2}}}\]
对数似然函数为:
\[\ln L = - \frac{n}{2} \ln (2\pi) - \frac{n}{2} \ln \sigma^{2} - \frac{1}{2 \sigma^{2}} \sum_{i=1}^{n} (x_i - \mu)^2\]
考虑下面对数似然方程组:
\[\begin{cases}
\frac{\partial}{\partial \mu} \ln L = \frac{1}{\sigma^2} (\sum\limits_{i=1}^{n} x_i - n \mu) = 0 \\
\frac{\partial}{\partial \sigma^2} \ln L = - \frac{n}{2 \sigma^2} + \frac{1}{2 (\sigma^2)^2} \sum\limits_{i=1}^{n} (x_i - \mu)^2 = 0
\end{cases}\]
求解前一式得: \(\hat{\mu} = \frac{1}{n} \sum\limits_{i=1}^{n} x_i = \overline{x}\) ,代入后一式得: \(\hat{\sigma}^2 = \frac{1}{n} \sum\limits_{i=1}^{n} (x_i - \overline{x})^2\)
8. 随机过程(Stochastic Process)和随机场(Random Field)
随机过程(Stochastic process, or random process)的研究对象是随时间演变的随机现象。
随机过程定义:
设 \(T\) 是一个无限实数集,我们把依赖于参数 \(t \in T\) 的一族(无限多个)随机变量称为 随机过程 ,记为 \(\{X(t), t \in T\}\) ,其中 \(T\) 称为参数集。对每一个 \(t \in T\) , \(X(t)\) 是一随机变量。
我们常把 \(t\) 看作时间,称 \(X(t)\) 为时刻 \(t\) 时 随机过程的状态 。其中参数 \(t\) 通常解释为时间,但它也可以表示其他的量,如序号、距离等等。对于一切 \(t \in T\) , \(X(t)\) 的所有可能取值的全体称为 随机过程的状态空间 。
样本函数定义:
对随机过程 \(\{X(t), t \in T\}\) 进行一次试验(即在 \(T\) 上进行一次全程观测),其结果是 \(t\) 的函数,记为 \(x(t), t \in T\) ,称它为随机过程的一个 样本函数 或样本曲线。
8.1. 随机过程实例
随机过程实例一:
电子元件由于内部微观粒子的随机热骚动所引起的端电压称为热噪声电压,它在任一确定时刻 \(t\) 的值是一随机变量,记为 \(V(t)\) ,不同时刻对应不同的随机变量,所以热噪声电压随时间变化的过程可以描述为一个随机过程。
在相同条件下,对某种电子元件多次测量热噪声电压,可得到一些样本函数(样本曲线),如:
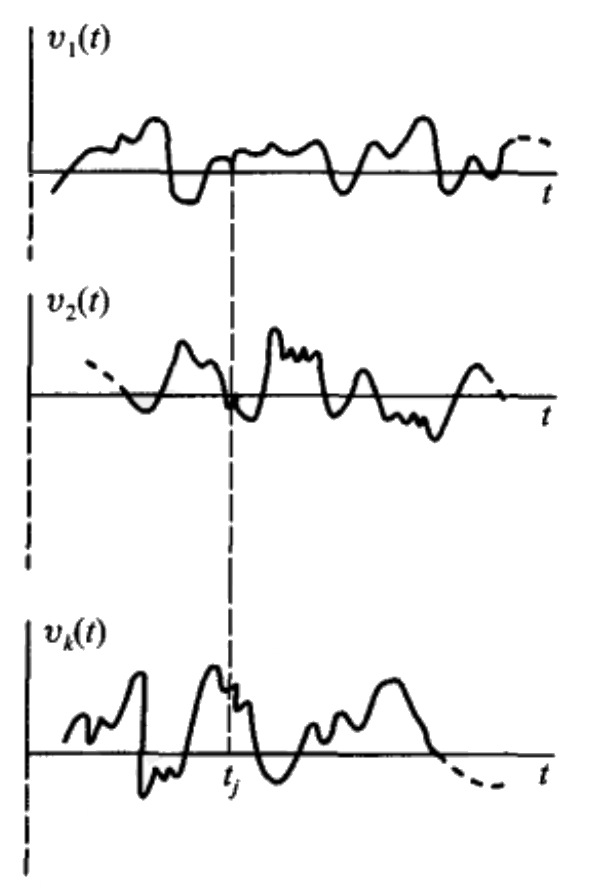
Figure 3: 某电子元件热噪声电压的样本曲线
随机过程实例二:
设某城市的 120 急救电话台可接收用户的呼叫,以 \(X(t)\) 表示时间间隔 \((0,t]\) 内接到的呼叫次数,它是一个随机变量,且对于不同的 \(t \ge 0\) , \(X(t)\) 是不同的随机变量。于是, \(\{X(t), t \ge 0 \}\) 是一随机过程,且它的状态空间是 \(\{0, 1, 2, \cdots\}\) 。
8.2. 随机过程分类
随机过程可以按照在任一时刻的 状态 是连续型随机变量或离散型随机变量而分为 连续型随机过程 和 离散型随机过程 。
如,前面介绍的热噪声电压就是连续型随机过程的例子,而急救电话台则是离散型随机过程的例子。
随机过程还可以按照 时间 (参数)是连续或离散进行分类。当时间集 \(T\) 是离散集合,例如 \(T= \{0,1,2, \cdots\}\) ,称 \(\{X(t), t \in T \}\) 为 离散参数随机过程 或 随机序列 ;当时间集 \(T\) 为有限区间(或无限区间)时,则称 \(\{X(t), t \in T \}\) 为 连续参数随机过程 。
8.3. 随机过程的数学特征
给定随机过程 \(\{X(t), t \in T\}\) ,固定 \(t \in T\) , \(X(t)\) 是一随机变量,它的均值一般与 \(t\) 有关,记为:
\[\mu_X(t) = E[X(t)]\]
我们称 \(\mu_X(t)\) 为随机过程 \(\{X(t), t \in T\}\) 的 均值函数 。均值函数 \(\mu_X(t)\) 表示了随机过程 \(\{X(t), t \in T\}\) 的所有样本函数的摆动中心。
随机过程 \(\{X(t), t \in T\}\) 的方差函数定义为:
\[\sigma_X^2(t) = D[X(t)] = E\{[X(t) - \mu_X(t)]^2\}\]
方差函数的平方根 \(\sigma_X(t)\) 称为随机过程 \(\{X(t), t \in T\}\) 的标准差函数。标准差函数表示随机过程 \(\{X(t), t \in T\}\) 在时刻 \(t\) 对于均值 \(\mu_X(t)\) 的平均偏离程序。如:
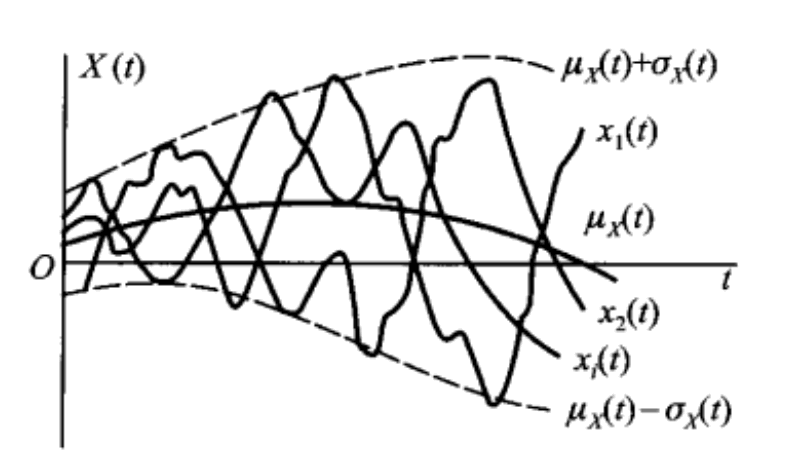
Figure 4: 随机过程的均值函数和标准差函数
8.4. 随机场(Random Field)
A random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors.
随机场是随机过程在空间域上的推广。随机过程的基本参数是时间变量 \(t\) ,而随机场的基本参数是位置向量 \(\boldsymbol{u}\) 。尽管随机场的参数集可以同时包含位置向量和时间变量,但实际实用中,一般只考虑仅包含位置向量的随机场,并记作 \(\{X(\boldsymbol{u}), \boldsymbol{u} \in D \subset \mathbb{R}^n\}\)
9. 马尔可夫链(Markov Chain)
在物理学中,很多确定性现象具有如下演变规律:时刻 \(t_0\) 时系统所处的状态,可以决定系统在时刻 \(t>t_0\) 所处的状态,而无需借助于 \(t_0\) 以前系统所处状态的历史资料。如微分方程初值问题所描绘的物理过程就属于这类确定性现象。
把上述规律延伸到随机现象,可以引入以下的 马尔可夫性 或 无后效性 :过程在时刻 \(t_0\) 所处的状态为已知的条件下,过程在时刻 \(t>t_0\) 所处状态的条件分布与过程在时刻 \(t_0\) 之前所处的状态无关。
9.1. 马尔可夫过程和马尔可夫链
下面用分布函数来正式表述马尔可夫性和马尔可夫过程。
设随机过程 \(\{X(t), t \in T \}\) 的状态空间为 \(I\) ,如果对时间 \(t\) 的任意 \(n\) 个数值 \(t_1 < t_2 < \cdots < t_n, t_i \in T\) 在条件 \(X(t_i) = x_i, x_i \in I, i = 1, 2, \cdots, n-1\) 下, \(X(t_n)\) 的条件分布函数恰好等于在条件 \(X(t_{n-1} = x_{n-1}\) 下 \(X(t_n)\) 的条件分布函数,即有:
\[P\{ X(t_n) \le x_n \mid X(t_1) = x_1, X(t_2) = x_2, \cdots, X(t_{n-1}) = x_{n-1} \} \\
= P\{ X(t_n) \le x_n \mid X(t_{n-1}) = x_{n-1} \}\]
则称随机过程 \(\{X(t), t \in T \}\) 具有马尔可夫性或无后效性,并称此过程为 马尔可夫过程 。
如果马尔可夫过程的时间和状态空间都是离散的,则称它为马尔可夫链(Markov Chain)。
10. 平稳随机过程
如果随机过程的统计特性不随时间的推移而变化,则称为 平稳随机过程 。
严格地说,如果对于任意 \(t_1, t_2, \cdots, t_n \in T\) 和任意实数 \(h\) ,当 \(t_1 + h, t_2 + h, \cdots, t_n + h \in T\) 时, \(n\) 维随机变量
\[(X(t_1), T(t_2), \cdots, X(t_n))\]
和
\[(X(t_1 + h), T(t_2 + h), \cdots, X(t_n + h))\]
具有相同的分布函数,则称随机过程 \(\{X(t), t \in T\}\) 具有平稳性,并称此过程为 平稳随机过程 ,或简称 平稳过程 。
平稳过程的参数集 \(T\) 一般为 \((- \infty, + \infty), [0, + \infty), \{0, \pm 1, \pm2, \cdots\}, \{0, 1, 2, \cdots\}\) 。当定义在离散参数集上时,也称过程为 平稳随机序列 ,或 平稳时间序列 。
10.1. 平稳随机过程实例
在实际问题中,确定过程的分布函数,并用它来判定其平稳性,一般是很难的。但是,对于一个被研究的随机过程,如果前后的环境和主要条件都不随时间的推移而变化,则一般就可以认为是平稳的。
如,强震阶段的地震波幅、船舶的颠簸过程、照明电网中电压的波动过程以及各种噪声和干扰等待在工程上都被认为是平稳的。