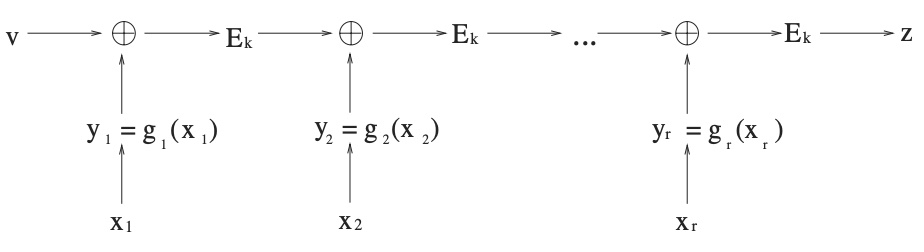Ring Signature

1. Ring Signature
2. 其它类型的 Ring Signature
- 2.1. Linkable Ring Signature
- 2.2. Traceable Ring Signature

1. Ring Signature

环签名（Ring Signature）是一种特殊的签名：一个签名者可以代表一个签名集体进行签名，别人不知道到底是哪个签名者进行的签名。比如：一个签名集体共有 A、B、C 三个参与者，其中任意一个参与者可以生成签名，别人只知道这个签名是由 A、B、C 中某个参与者生成的，但却不知道具体是哪一个参与者生成的签名。

环签名是 Ron Rivest, Adi Shamir, and Yael Tauman Kalai 于 2001 年在论文 How to Leak a Secret 中提出的。

1.1. Ring Signature VS. Group Signature

环签名和群签名（Group Signature）有点像，都是某个人代表一个集体进行签名。不过，群签名中有个“Group Manager”的角色，Group Manager 有能力查看一个签名到底是谁创建的，而且他还可以把某人加入到签名集体中，或者把已经加入到签名集体中的参与者剔除出签名集体。

关于 Ring Signature 和 Group Signature 的区别，总结一句话就是：

A ring signature scheme can be considered as a group signature scheme without a group manager.

1.2. Ring Signature 流程

设待签名的消息为 \(m\) ，签名集体有 \(r\) 个成员，每个成员的公钥分别为 \((P_1, P_2, \cdots, P_r)\) ，设这次生成签名的成员的编号为 \(s\) （显然 \(1 \le s \le r\) ）， \(E_k(m)\) 是一种使用密钥 \(k\) 对消息 \(m\) 进行加密的对称加密算法。

1.2.1. Ring Signature 签名

Ring Signature 生成签名数据的流程：

令 \(k=hash(m)\) 作为对称加密算法的密钥。
选择一个随机数 \(v\) 。
选择 \(r-1\) 个随机数 \(x_1, \cdots, x_i, \cdots, x_r\) ，其中 \(i \neq s\) 。并且计算 \(r-1\) 个值： \[y_i = g_i(x_i)\] 这里 \(g_i\) 是一个 trap-door 函数（陷门函数），也就是说已知 \(x_i\) 求 \(y_i\) 很容易，但已知 \(y_i\) 反向求 \(x_i\) 则很难（这个“很难”是指不掌握额外机密信息情况下很难，如果掌握额外机密信息则也可以很容易）。
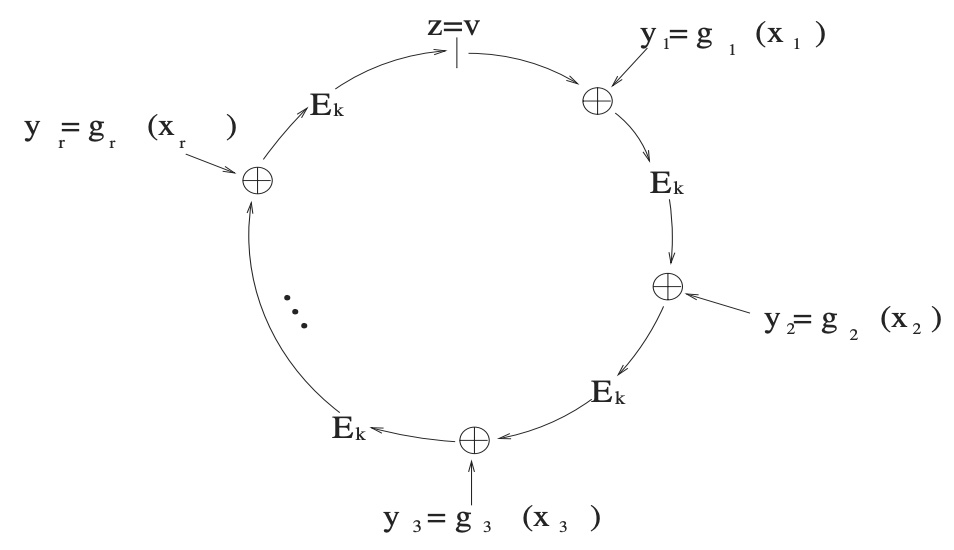
求解 \(y_s\) 。定义 Combining Function 为 \(C_{k,v}(y_{1},y_{2},\dots ,y_{r}) \triangleq E_{k}(y_{r}\oplus E_{k}(y_{r-1}\oplus E_{k}(\dots \oplus E_{k}(y_{1}\oplus v)\dots )))\) ，求解下面式子（称为 Ring Equation）： \[C_{k,v}(y_{1},y_{2},\dots ,y_{r}) = v\] 中的未知数 \(y_s\) 。上面式子中，右边 \(v\) 是已知的，左边的 \(r\) 个 \(y\) 中，有 \(r-1\) 个已知的（上一步计算而来），只有一个 \(y_s\) 是未知的。
求解 \(x_s\) 。本次签名者 \(s\) ，利用它的私钥（即公钥 \(P_s\) 所对应的私钥），计算出满足 \(y_s = g_s(x_s)\) 的 \(x_s\) ，由于 \(g\) 是陷门函数，只有掌握了额外机密信息（即签名人 \(s\) 的私钥）的人才容易反向计算出 \(x_s\) 。
签名数据就是下面 \(2r+1\) 元组： \[(P_1, P_2, \cdots, P_r; v; \underbrace{x_1,x_2, \cdots, x_r}_{\text{仅一个值}x_s\text{不是随机产生的}})\]

1.2.2. Ring Signature 验证

Ring Signature 校验签名数据的流程：

计算 \(y_i=g_i(x_i)\) ，其中 \(1 \le i \le r\) ，得到 \(y_1, \cdots,\cdots, y_r\) 。
计算 \(k = hash(m)\) 。
验证 \[C_{k,v}(y_{1},y_{2},\dots ,y_{r}) = v\] 是否成立，如果成立就是合法签名；不成立就是非法签名。

1.2.3. Combining Function 和 Ring Equation

节 1.2.1 中提到了 Combining Function \(C_{k,v}\) ，可以形象地用图 1（摘自原论文）来表示，其中 \(v\) 是初始向量，而 \(k\) 是对称加密算法的密钥。

Figure 1: An illustration of the proposed combining function

Ring Equation 表示的意思是经过 Combining Function 处理后，其结果回到原点，即等于初始向量 \(v\) ，可形象地理解为形成了一个环，如图 2（摘自原论文）所示。

Figure 2: Ring Equation

1.3. RSA-based Ring Signatures

下面基于 RSA 算法，介绍一个具体的环签名实例。

设待签名的消息为 \(m\) ，签名集体有 \(3\) 个成员，每个成员的公钥分别为 \(P_1=(n, e_1), P_2=(n, e_2), P_3=(n, e_3)\) ，设这次由第 \(2\) 个成员（公钥为 \(P_2\) ）来生成签名，对称加密函数为 \(E_k(m) \triangleq m \oplus k\) ，陷门函数 \(g_i(x) \triangleq x^{e_i} \bmod n\) 。

第 \(2\) 个成员生成签名的流程：

令 \(k=hash(m)\) 作为对称加密算法的密钥。
选择一个随机数 \(v\) 。
选择 \(2\) 个随机数 \(x_1, x_3\) ，计算 \(y_1=g_1(x_1), y_3=g_3(x_3)\) 。
由 \(C_{k,v}(y_1, y_2, y_3) = y_3 \oplus ( y_2 \oplus ( \underbrace{y_1 \oplus v \oplus k}_{E_k(y_1 \oplus v)}) \oplus k) \oplus k = v\) ，计算出 \(y_2\) 。
由 \(P_2\) 对应的私钥计算出 \(y_2 = x_2^{e_2} \bmod n\) 的 \(x_2\) ，也就是利用 RSA 私钥计算出密文 \(y_2\) 所对应明文 \(x_2\) 。
签名数据就是下面 \(7\) 元组： \[(P_1, P_2, P_3; v; x_1, x_2, x_3)\]

1.4. Rabin-based Ring Signatures

原论文中还介绍了基于 Rabin 算法的环签名，这里不介绍。

2. 其它类型的 Ring Signature

2.1. Linkable Ring Signature

可链接环签名（Linkable Ring Signature）是一种特殊的环签名，它可以确定两个签名是否是同一个签名人生成（但不能确定具体哪一个签名人）。也就是说“可链接环签名”可以发现某用户是否做了两次签名，它可用于匿名电子投票系统中防止重复投票。

Linkable Ring Signature 在 Monero 中有用到，可参考：

2.2. Traceable Ring Signature

可追踪环签名（Traceable Ring Signature）是一种特殊的环签名，它可以确定生成了两次或以上签名的某个签名人的身份，它可用于匿名电子投票系统中防止重复投票。