Motion Model
Table of Contents
1. Motion Model
回顾一下,用于状态估计的贝叶斯滤波公式如下:
\[bel(x_t) = \eta \, \underbrace{p(z_t \mid x_t)}_{\text{Sensor Model}} \int \underbrace{p(x_t \mid x_{t-1}, u_t)}_{\text{Motion Model}} bel(x_{t-1}) \, \mathrm{d} x_{t-1}\]
其中,系统的控制量模型(Motion Model)和传感器模型(Measurement Model, or Sensor Model)需要提前建立好。
这里我们要讨论的模型是 Motion Model: \(p(x_t \mid x_{t-1}, u_t)\) ,即已知机器人上一个位置 \(x_{t-1}\) ,和当前控制量 \(u_t\) ,计算当前位置 \(x_t\) 的概率分布。
参考:
本文主要摘自:Probabilistic Robotics, by Sebastian Thrun, 5 Robot Motion
http://ais.informatik.uni-freiburg.de/teaching/ss15/robotics/slides/06-motion-models.pdf
1.1. 机器人位姿建模
怎么表达机器人的位姿(Pose)呢?在三维空间中,可以用 6 维向量来表示,其中 3 个元素为欧拉空间的坐标,另外 3 个元素分别是和三个坐标轴的夹角(roll, pitch, yaw)。这里我们仅考虑二维平面的情况,这时可以用 3 维向量来表示机器人的位姿:
\[\begin{pmatrix} x \\ y \\ \theta \end{pmatrix}\]
其中, \(x,y\) 为坐标, \(\theta\) 为机器人方向和 \(x\) 轴正方向的夹角。
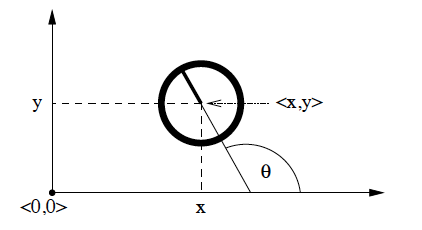
Figure 1: Robot Pose in 2D
在这里,我们贝叶斯滤波框架进行状态估计的状态 \(x_t\) 就是机器人位姿 \((x \; y \; \theta)^{\mathsf{T}}\) 。
注意:不要把状态 \(x_t\) 和坐标 \(x\) 混淆了,坐标 \(x\) 仅是状态 \(x_t\) 的一个分量。
1.1.1. Location 和 Bearing
在位姿 \(\begin{pmatrix} x \\ y \\ \theta \end{pmatrix}\) 中, \(\begin{pmatrix} x \\ y \end{pmatrix}\) 称为 Location,而 \(\theta\) 称为 Bearing 或者 Heading Direction。
2. Velocity Motion Model (Dead Reckoning)
Velocity Motion Model 假设机器人的控制量可以用两个速度(线速度 \(v_t\) 和角速度 \(\omega_t\) )来表达,即:
\[u_t = \begin{pmatrix} v_t \\ \omega_t \end{pmatrix}\]
2.1. Velocity Motion Model 抽样算法
对于粒子滤波器来说,不需要使用它的解析解,我们只需要得到 Motion Model 的样本即可。用图 2 所示算法可以得到 \(p(x_t \mid x_{t-1}, u_t)\) 的样本。

Figure 2: Algorithm for sampling poses \(x_{t} = (x' \; y' \; \theta')^{\mathsf{T}}\) from a pose \(x_{t-1} = (x \; y \; \theta)^{\mathsf{T}}\) and a control \(u_t = (v \; \omega)^{\mathsf{T}}\)
说明:函数 \(\text{sample}(b^2)\) 是均值为零,方差为 \(b^2\) 的正态分布或三角分布的抽样函数。通常可以用图 3 所示方法之一来实现 \(\text{sample}(b^2)\) 函数。

Figure 3: Algorithm for sampling from (approximate) normal and triangular distributions with zero mean and variance \(b^2\)
2.1.1. Velocity Motion Model 抽样算法的推导(航迹推算,Dead Reckoning)
首先,考虑没有误差时的理想情况。
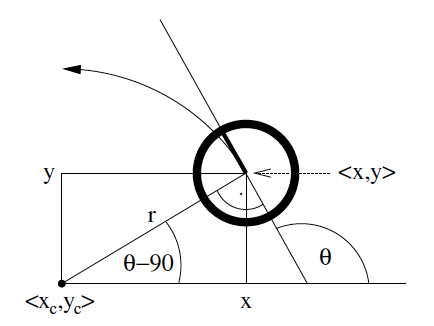
Figure 4: Velocity Motion Model
已知位姿 \(x_{t-1} = (x \; y \; \theta)^{\mathsf{T}}\) 以及线速度 \(v_t\) 和角速度 \(\omega_t\) ,经过很短的一段时间 \(\Delta t\) ,我们可以推导出机器人的新位姿。
当角速度 \(\omega_t\) 不为零时,机器人绕圆运动,圆的半径可以这样计算: \(r = \left| \frac{v}{\omega} \right|\) (当角速度为零时,是直线运动,可以认为它绕无穷大的圆运动)。圆心的坐标可以这样计算:
\[\begin{aligned} x_c & = x - \frac{v}{\omega} \sin \theta \\
y_c & = y + \frac{v}{\omega} \cos \theta \\
\end{aligned}\]
经过时间 \(\Delta t\) 后,机器人和圆心连线所转过的角位移 \(\Delta \theta\) 为:
\[\Delta \theta = \omega \Delta t\]
从而机器人的新位姿为:
\[\begin{aligned} \begin{pmatrix} x' \\ y' \\ \theta' \end{pmatrix} & = \begin{pmatrix} x_c + r \sin(\theta + \Delta \theta) \\ y_c - r \cos(\theta + \Delta \theta) \\ \theta + \Delta \theta \end{pmatrix} \\
& = \begin{pmatrix} x_c + \frac{v}{\omega} \sin(\theta + \omega \Delta t) \\ y_c - \frac{v}{\omega} \cos(\theta + \omega \Delta t) \\ \theta + \omega \Delta t \end{pmatrix} \\
\end{aligned}\]
把前面计算的圆心坐标代入上式,可得机器人的新位姿为:
\[\begin{pmatrix} x' \\ y' \\ \theta' \end{pmatrix} = \begin{pmatrix} x \\ y \\ \theta \end{pmatrix} + \begin{pmatrix} -\frac{v}{\omega} \sin\theta + \frac{v}{\omega} \sin(\theta + \omega \Delta t) \\ \frac{v}{\omega} \cos\theta - \frac{v}{\omega} \cos(\theta + \omega \Delta t) \\ \omega \Delta t \end{pmatrix}\]
现在,我们考虑有误差的情况。
现实中,我们无法知道真实的线速度和角速度,我们得到的值和真实值之间会有误差。假设我们得到的线速度为 \(v\) ,角速度为 \(\omega\) ,真实的线速度和角速度可以这样表达:
\[\begin{pmatrix} \hat{v} \\ \hat{\omega} \end{pmatrix} = \begin{pmatrix} v \\ \omega \end{pmatrix} + \begin{pmatrix} \varepsilon_{\alpha_1 v^2 + \alpha_2 \omega^2} \\ \varepsilon_{\alpha_3 v^2 + \alpha_4 \omega^2} \end{pmatrix}\]
其中,参数 \(\alpha_1, \cdots, \alpha_4\) 是与机器人相关的误差参数,如果机器人越精确,则这些误差应该设置得越小。 \(\varepsilon_{b^2}\) 是均值为零,方差为 \(b^2\) 的正态分布(也可以用三角形分布来替代)。
相应地,机器人的新位姿为:
\[\begin{pmatrix} x' \\ y' \\ \theta' \end{pmatrix} = \begin{pmatrix} x \\ y \\ \theta \end{pmatrix} + \begin{pmatrix} -\frac{\hat{v}}{\hat{\omega}} \sin\theta + \frac{\hat{v}}{\hat{\omega}} \sin(\theta + \hat{\omega} \Delta t) \\ \frac{\hat{v}}{\hat{\omega}} \cos\theta - \frac{\hat{v}}{\hat{\omega}} \cos(\theta + \hat{\omega} \Delta t) \\ \hat{\omega} \Delta t \end{pmatrix}\]
其实,前面推导中隐含假设 \(\Delta t\) 内速度是不变的(这时轨迹会是圆),但这个假设并不准确。为了使模型更准确,我们一般还要 假设机器人在到达最终位置后,还会有额外的方向旋转。 即:
\[\theta' = \theta + \hat{\omega} \Delta t + \hat{\gamma} \Delta t\]
其中, \(\hat{\gamma} = \varepsilon_{\alpha_5 v^2 + \alpha_6 \omega^2}\) ,参数 \(\alpha_5, \alpha_6\) 也是与机器人相关的参数。
至此,图 2 所示 Velocity Motion Model 抽样算法已经推导完毕。
2.2. Velocity Motion Model 解析形式解
这里直接给出 Velocity Motion Model 中 \(p(x_t \mid x_{t-1}, u_t)\) 的求解公式(后文将推导它),如图 5 所示。

Figure 5: Algorithm for computing \(p(x_t \mid x_{t-1}, u_t)\) based on velocity information \((v \; \omega)^{\mathsf{T}}\). Here we assume \(x_{t-1} = (x \; y \; \theta)^{\mathsf{T}}\), \(x_{t} = (x' \; y' \; \theta')^{\mathsf{T}}\), \(u_t = (v \; \omega)^{\mathsf{T}}\)
说明 1: \(\alpha_1, \alpha_2, \cdots, \alpha_6\) 为机器人相关的误差参数。
说明 2:The function prob(a, b) computes the probability of its argument a under a zero-centered distribution with variance b. 通常可以用图 6 所示方法之一来实现 prob(a,b)函数。

Figure 6: Algorithms for computing densities of a zero-centered normal distribution and the triangular distribution with variance b.
2.2.1. Velocity Motion Model 解析形式解推导
如何得到 Velocity Motion Model 解析形式解呢?如果系统没有误差,则非常简单。由前面的推导可知当新的位姿为 \(\begin{pmatrix} x' \\ y' \\ \theta' \end{pmatrix} = \begin{pmatrix} x \\ y \\ \theta \end{pmatrix} + \begin{pmatrix} -\frac{v}{\omega} \sin\theta + \frac{v}{\omega} \sin(\theta + \omega \Delta t) \\ \frac{v}{\omega} \cos\theta - \frac{v}{\omega} \cos(\theta + \omega \Delta t) \\ \omega \Delta t \end{pmatrix}\) 时概率 \(p(x_t \mid x_{t-1}, u_t)\) 为 1,其它情况概率 \(p(x_t \mid x_{t-1}, u_t)\) 为 0。
真实系统是有误差的,这时我们的思路是: 既然线速度、角速度是有误差的,我们将先利用其它信息求解出它们的一个理论估计值,再和测量值一起对误差进行建模。
线速度、角速度的估计值为:
\[\begin{pmatrix} \hat{v} \\ \hat{\omega} \end{pmatrix} = \begin{pmatrix} \frac{\Delta \text{dist}}{\Delta t} \\ \frac{\Delta \theta}{\Delta t} \end{pmatrix}\]
其中, \(\Delta \text{dist}\) 是 \(\Delta t\) 时间内圆弧上的弧线长。弧线长可以这样求解: \(\Delta \text{dist} = r^{*} \Delta \theta\) 。
至此,要求解线速度、角速度的估计值只用求解圆的半径 \(r^{*}\) 以及转向角的变化 \(\Delta \theta\) 。
下面通过求解圆心坐标(最终目的是求解线速度、角速度的理论估计值,不能利用线速度、角速度的测量值)来求解圆的半径 \(r^{*}\) 以及转向角的变化 \(\Delta \theta\) 。
假设圆心为 \((x^* \; y^*)^{\mathsf{T}}\) ,由于圆心连线和运行初始方向垂直,有:
\[\begin{pmatrix} x^* \\ y^* \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} -\lambda \sin\theta \\ \lambda \cos \theta \end{pmatrix}\]
又由于圆心在点 \((x \; y)^{\mathsf{T}}\) 和点 \((x' \; y')^{\mathsf{T}}\) 所确定线段的中垂线上,所以有:
\[\begin{pmatrix} x^* \\ y^* \end{pmatrix} = \begin{pmatrix} \frac{x+x'}{2} + \mu (y-y') \\ \frac{y+y'}{2} + \mu(x' - x) \end{pmatrix}\]
联立上面两个等式,可以求得:
\[\mu = \frac{1}{2} \frac{(x-x') \cos\theta + (y-y')\sin\theta}{(y-y')\cos\theta - (x-x')\sin\theta}\]
从而,圆心坐标 \((x^* \; y^*)^{\mathsf{T}}\) 为:
\[\begin{pmatrix} x^* \\ y^* \end{pmatrix} = \begin{pmatrix} \frac{x+x'}{2} + \frac{1}{2} \frac{(x-x') \cos\theta + (y-y')\sin\theta}{(y-y')\cos\theta - (x-x')\sin\theta} (y-y') \\ \frac{y+y'}{2} + \frac{1}{2} \frac{(x-x') \cos\theta + (y-y')\sin\theta}{(y-y')\cos\theta - (x-x')\sin\theta} (x'-x) \end{pmatrix}\]
从而,圆的半径 \(r^*\) 为:
\[r^* = \sqrt{(x-x^*)^2 + (y-y^*)^2} = \sqrt{(x'-x^*)^2 + (y' - y^*)^2}\]
转向角变化 \(\Delta \theta\) 为:
\[\Delta \theta = \text{atan2}(y' - y^*, x'-x^*) - \text{atan2}(y-y^*, x-x^*)\]
至此,线速度、角速度的估计值 \(\begin{pmatrix} \hat{v} \\ \hat{\omega} \end{pmatrix}\) 已经可以求出。
误差:
\[\begin{aligned} v_{err} &= v - \hat{v} \\
\omega_{err} &= \omega - \hat{\omega} \\
\end{aligned}\]
和推导抽样算法时类似,对额外的方向旋转也建立误差:
\[\gamma_{err} = \hat{\gamma} = \frac{\theta' - \theta}{\Delta t} - \hat{\omega}\]
理想情况下,上面 3 个误差都为 0。现实中,我们假设它们相互独立,服从均值为零的正态分布。 \(p(x_t \mid x_{t-1}, u_t)\) 是这三个误差分布的乘积。
\[p(x_t \mid x_{t-1}, u_t) = \text{prob}(v- \hat{v}, \alpha_1 v^2 + \alpha_2 \omega^2) \cdot \text{prob}(\omega- \hat{\omega}, \alpha_3 v^2 + \alpha_4 \omega^2) \cdot \text{prob}(\hat{\gamma}, \alpha_5 v^2 + \alpha_6 \omega^2)\]
其中, \(\text{prob}(a,b)\) 表示使参数 \(a\) 的均值为 0,方差为 \(b\) 的概率分布。
至此,图 5 所示 Velocity Motion Model 算法已经推导完毕。
2.3. 推导线速度和角速度
有时,机器人的线速度和角速度并不能直接得到。如果要使用 Velocity Motion Model,我们需要从其它控制量中推导出它们。
2.3.1. “两轮差分驱动”推导线速度和角速度
考虑两轮机器人(为了稳定性,一般是三个轮,但后面那个轮一般不配置动力),如图 7 所示。
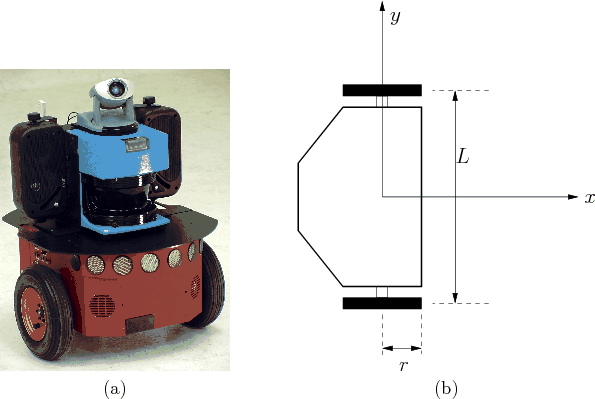
Figure 7: Differential Driven Wheeled Mobile Robot
设左轮和右轮速度分别为: \(v_l, v_r\) ,左轮和右轮的间距为 \(l\) ,如图 8 所示。下面来推导出线速度 \(v\) 和角速度 \(\omega\) 。
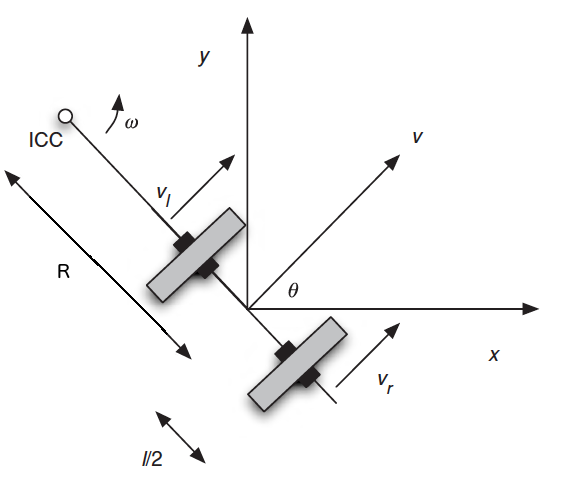
Figure 8: Differential Drive
注:图中 ICC 是瞬时曲率中心(Instantaneous Center of Curvature)的缩写,也就是运动时弧线对应的圆心位置。
显然左轮和右轮具有相同的角速度和瞬时曲率中心,从而有:
\[\begin{aligned} \omega (R + l/2) &= v_r \\
\omega (R - l/2) &= v_l \end{aligned}\]
由上面两式,可得:
\[\begin{aligned} R &= \frac{l(v_r + v_l)}{2(v_r - v_l)} \\
\omega &= \frac{v_r - v_l}{l} \end{aligned}\]
进一步,可得线速度 \(v = R \cdot \omega = \frac{v_r + v_l}{2}\)
参考:
Computational Principles of Mobile Robotics, 2nd, 3.1.5 Wheeled Mobile Robots
http://planning.cs.uiuc.edu/node659.html
2.3.2. “Car-like Mobile Robot”推导线速度和角速度
Car-like Mobile Robot 有两个控制量:油门(Accelerator)和方向盘(Steering Wheel)。假设前后轮距离为 \(L\) ,前进速度为 \(\varsigma\) ,前进方向和车主方向的夹角为 \(\varphi\) ,如图 9 所示。
可知(推导略),线速度和角速度分别为:
\[\begin{aligned} v_t &= \varsigma_t \cos(\varphi_t) \\
\omega_t &= \frac{\varsigma_t}{L} \sin(\varphi_t) \end{aligned}\]
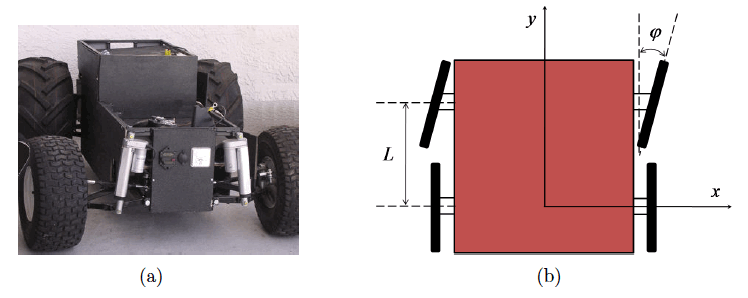
Figure 9: Car-like Mobile Robot
参考:Self-adaptive Markov Localization for Single-Robot and Multi-Robot Systems
3. Odometry Motion Model (Wheel Encoders)
Odometry Motion Model 是另外一个运动模型。这个模型假设机器人的控制量可以用它“已经经过的轨迹信息(Odometry)”来表达,即:
\[u_t = \begin{pmatrix} \bar{x}_{t-1} \\ \bar{x}_{t} \end{pmatrix}\]
说明 1:上面式子中的字母上方有一个横线(如 \(\bar{x}_{t-1}\) )表示 这个位姿信息是基于机器人内部坐标系,它和全局坐标系的关系未知。 后面介绍中 \(\bar{x}_{t-1}\) 用 \(( \bar{x} \; \bar{y} \; \bar{\theta} )^{\mathsf{T}}\) 来表示, \(\bar{x}_{t}\) 用 \(( \bar{x}' \; \bar{y}' \; \bar{\theta}' )^{\mathsf{T}}\) 来表示。
说明 2:显然轨迹信息(Odometry)应该是测量值,而不是控制量。为什么把它当做控制量呢?
Technically, odometric information are sensor measurements, not controls. To model odometry as measurements, the resulting Bayes filter would have to include the actual velocity as state variables—which increases the dimension of the state space. To keep the state space small, it is therefore common to consider odometry data as if it were control signals.
Odometry Motion Model 的主要思路是: 利用 \(\begin{pmatrix} \bar{x}_{t-1} \\ \bar{x}_{t} \end{pmatrix}\) 计算出 \(\begin{pmatrix} \delta_{\text{rot1}} \\ \delta_{\text{trans}} \\ \delta_{\text{rot2}} \end{pmatrix}\) (这个向量三个分量的含义如图 10 所示),再利用这三个量在不同坐标系中会不变的特征从而推导出机器人在全局坐标系中的位置。
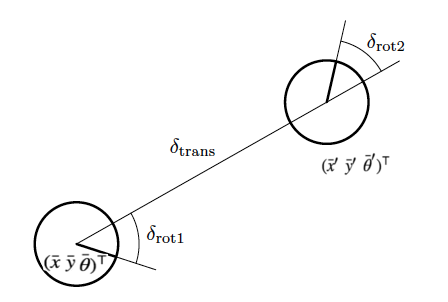
Figure 10: Odometry Motion Model
下面介绍利用 \(\begin{pmatrix} \bar{x}_{t-1} \\ \bar{x}_{t} \end{pmatrix}\) 推导 \(\begin{pmatrix} \delta_{\text{rot1}} \\ \delta_{\text{trans}} \\ \delta_{\text{rot2}} \end{pmatrix}\) 的过程。
假设机器人从 \(\bar{x}_{t-1} = ( \bar{x} \; \bar{y} \; \bar{\theta} )^{\mathsf{T}}\) 移动到了 \(\bar{x}_{t} = ( \bar{x}' \; \bar{y}' \; \bar{\theta}' )^{\mathsf{T}}\) ,则:
\[\begin{aligned}
\delta_{\text{rot1}} &= \text{atan2}(\bar{y}' - \bar{y}, \bar{x}' - \bar{x}) - \bar{\theta} \\
\delta_{\text{trans}} &= \sqrt{(\bar{x}' - \bar{x})^2 + (\bar{y}' - \bar{y})^2} \\
\delta_{\text{rot2}} &= \bar{\theta}' - \bar{\theta} - \delta_{\text{rot1}}
\end{aligned}\]
这三个量在不同坐标系中显然是不变的。假设系统没有误差,在全局坐标系中,机器人从 \(x_{t-1} = ( x \; y \; \theta )^{\mathsf{T}}\) 移动到 \(x_{t} = ( x' \; y' \; \theta' )^{\mathsf{T}}\) ,则 \(x_{t}\) 可以这样计算(这是因为线段 \(\delta_{\text{trans}}\) 在全局坐标系中的方向会为 \(\theta + \delta_{\text{rot1}}\) ):
\[\begin{pmatrix} x' \\ y' \\ \theta' \end{pmatrix} = \begin{pmatrix} x \\ y \\ \theta \end{pmatrix} + \begin{pmatrix} \delta_{\text{trans}} \cos(\theta + \delta_{\text{rot1}}) \\ \delta_{\text{trans}} \sin(\theta + \delta_{\text{rot1}}) \\ \delta_{\text{rot1}} + \delta_{\text{rot2}} \end{pmatrix}\]
有了上面的基本分析,我们容易得到 Odometry Motion Model 抽样算法和解析形式解。
3.1. Odometry Motion Model 抽样算法和解析形式解
Odometry Motion Model 抽样算法如图 11 所示,解析形式解如图 12 所示。
上节中,已经对 Odometry Motion Model 进行了基本分析,容易得到 Odometry Motion Model 抽样算法和解析形式解,这里不再推导它们。可以参考 Velocity Motion Model 的推导过程。

Figure 11: Algorithm for sampling from \(p(x_t \mid u_t, x_{t−1})\) based on odometry information.

Figure 12: Algorithm for computing \(p(x_t \mid u_t, x_{t−1})\) based on odometry information.
说明 1:式中 \(\alpha_1, \cdots, \alpha_4\) 是与机器人相关的误差参数,如果机器人越精确,则这些误差应该设置得越小。
说明 2:式中 \(x_{t-1} = (x \; y \; \theta)^{\mathsf{T}}, \; x_{t} = ( x' \; y' \; \theta' )^{\mathsf{T}}, \; u_{t} = (\bar{x}_{t-1} \; \bar{x}_t)^{\mathsf{T}}, \; \bar{x}_{t-1} = ( \bar{x} \; \bar{y} \; \bar{\theta} )^{\mathsf{T}}, \; \bar{x}_{t} = ( \bar{x}' \; \bar{y}' \; \bar{\theta}' )^{\mathsf{T}}\)
3.2. Odometry Model Vs. Velocity Model
一般地,Odometry Model 比 Velocity Model 更加精确,当机器人装备有Wheel Encoders时,一般采用 Odometry Model。 但 Odometry Model 使用的轨迹(Odometry)信息仅当机器人已经移动后才能得到,所以它不能用于 motion planning.
4. Map-based Motion Model
前面讨论的是 \(p(x_t \mid u_t, x_{t-1})\) ,没有考虑地图,很多时候我们是已知地图的,地图能提供额外的信息,如机器人不可能处于被物体占据的位置中。如果考虑地图(地图常用 \(m\) 表示),则 Motion Model 可以表达为:
\[p(x_t \mid u_t, x_{t-1}, m)\]
上式就称为 Map-based Motion Model,它比不使用地图的模型能提供更准确的信息。但直接计算上式是很困难的。
一般采用下面式子来近似地计算 \(p(x_t \mid u_t, x_{t-1}, m)\) :
\[p(x_t \mid u_t, x_{t-1}, m) = \eta p(x_t \mid m) p(x_t \mid u_t, x_{t-1}\]
上式并不是一个严格的公式,它仅是做很多假设后的近似公式。它的含义是把 Map-based Motion Model 分解为了 \(p(x_t \mid m)\) 和不带地图信息的 Motion Model。对于Occupancy map来说, \(p(x_t \mid m) = 0\) 表示机器人不会移动到已经被占用的单元中。