RSA Encryption and Signature Example
Table of Contents
1. RSA 算法基本过程
RSA 算法的密钥由公钥 \((e,n)\) 和私钥 \((d,n)\) 组成,其加密和解密过程如下:
- 已经明文为 P,则用公钥加密的过程(设对应密文为 C)为: \(C = P^e (\bmod n)\) 。
- 假设密文为 C,则用私钥解密的过程(设对应明文为 P)为: \(P = C^d (\bmod n)\) 。
其中, \(e,d,n\) 都为正整数, \(e\) 称为 public exponent(一般取固定值为 65537), \(d\) 称为 private exponent, \(n\) 称为模数(modulus)。 当我们说 RSA 密钥的大小(长度)时,是指模数 \(n\) 表示为二进制时的位数。例如 2048 位的 RSA 密钥,那么其模数 \(n\) 为 2048 比特位(即 256 字节)。
2. RSA 密钥对生成
2.1. 用 OpenSSL 生成 RSA 公钥和私钥对
使用工具 openssl 可以生成 RSA 公钥和私钥对。
第 1 步,生成 RSA 密钥文件(包含了私钥和公钥)。下面是生成 1024 位(128 字节)RSA 密钥的例子:
$ openssl genpkey -algorithm RSA -out private_key.pem -pkeyopt rsa_keygen_bits:1024 $ cat private_key.pem -----BEGIN PRIVATE KEY----- MIICdwIBADANBgkqhkiG9w0BAQEFAASCAmEwggJdAgEAAoGBAKnBUcwS5azsWao5 XYFr2uy9yTlU/gMy+oXFDaxxu1qCQ/LDA+cBO6FnPRPRZ7BAfYKp1LAAe7Z9wYsn wEkVFXIzuQMob1L6wrr9czWDtu3pviEwt9vJbKLktzH4TW8HCNDE67P8j4xapaSV cUPlMwz8bMiCj9mf1fLnQygEhcU7AgMBAAECgYBsT1t4YOpIPfkr4jQl+oIRoTn9 qZv0wJcVuNfzmhFXO1xNTV51CtVYMz3GIksNKuip8OAyd+x3UJ+nwPIv7xLh46Pf 7+mFUVIpDE+jGk31iKVNqU1VkU/oxkc8+5ofJezOv+k83g/oNH8lQNyUQQMn+gKE GXWv8zKul07+c1AZqQJBANi9EulszCJbFG9g4QWGfXLUa31/eYRUi0E98JDamm+K Lq1YoWgIPvDlElUMAN1luhTdztlYPH7Ys7lfaOUoMtUCQQDIgXXQyfyc794OVW7Z cLejNtXeWejsgL0YnBbX7/OTcro70WqVxdCJN90uYQGWK+GhZrDCCCblxXsdno4N GX/PAkEA12BD+8wOqpFBpFBsK9ZysPpfeo2DTrnIy+NmPDvPPcneCopJkpynFzE7 X2IXNesR2Ax2scqaCx8CsdIa5aVlpQJBAMVo2SOpS0ME07+PE+WYGeXjXmxeX3tD QWqSe9c9U7cvtPaiN+ugaLJBQ06fid1d9PdhUNSpDAscBRxjeH6jRXcCQEPknb1E hnNuu1eCCW5r0JrKmuHqo+JOmaMAV3P2HbZMxzpLaAmzs1b7j18crF2/xEOe2+dS +CSnOxCJk76UKaM= -----END PRIVATE KEY-----
第 2 步,查看 RSA 的公钥和私钥。
$ openssl rsa -text -in private_key.pem
Private-Key: (1024 bit)
modulus:
00:a9:c1:51:cc:12:e5:ac:ec:59:aa:39:5d:81:6b:
da:ec:bd:c9:39:54:fe:03:32:fa:85:c5:0d:ac:71:
bb:5a:82:43:f2:c3:03:e7:01:3b:a1:67:3d:13:d1:
67:b0:40:7d:82:a9:d4:b0:00:7b:b6:7d:c1:8b:27:
c0:49:15:15:72:33:b9:03:28:6f:52:fa:c2:ba:fd:
73:35:83:b6:ed:e9:be:21:30:b7:db:c9:6c:a2:e4:
b7:31:f8:4d:6f:07:08:d0:c4:eb:b3:fc:8f:8c:5a:
a5:a4:95:71:43:e5:33:0c:fc:6c:c8:82:8f:d9:9f:
d5:f2:e7:43:28:04:85:c5:3b
publicExponent: 65537 (0x10001)
privateExponent:
6c:4f:5b:78:60:ea:48:3d:f9:2b:e2:34:25:fa:82:
11:a1:39:fd:a9:9b:f4:c0:97:15:b8:d7:f3:9a:11:
57:3b:5c:4d:4d:5e:75:0a:d5:58:33:3d:c6:22:4b:
0d:2a:e8:a9:f0:e0:32:77:ec:77:50:9f:a7:c0:f2:
2f:ef:12:e1:e3:a3:df:ef:e9:85:51:52:29:0c:4f:
a3:1a:4d:f5:88:a5:4d:a9:4d:55:91:4f:e8:c6:47:
3c:fb:9a:1f:25:ec:ce:bf:e9:3c:de:0f:e8:34:7f:
25:40:dc:94:41:03:27:fa:02:84:19:75:af:f3:32:
ae:97:4e:fe:73:50:19:a9
......
从上面的输出中可知,RSA 公钥和私钥分别为(16 进制表示):
modulus=0x00a9c151cc12e5acec59aa395d816bdaecbdc93954fe0332fa85c50dac71bb5a8243f2c303e7013ba1673d13d167b0407d82a9d4b0007bb67dc18b27c04915157233b903286f52fac2bafd733583b6ede9be2130b7dbc96ca2e4b731f84d6f0708d0c4ebb3fc8f8c5aa5a4957143e5330cfc6cc8828fd99fd5f2e743280485c53b public exponent=0x10001 private exponent=0x6c4f5b7860ea483df92be23425fa8211a139fda99bf4c09715b8d7f39a11573b5c4d4d5e750ad558333dc6224b0d2ae8a9f0e03277ec77509fa7c0f22fef12e1e3a3dfefe9855152290c4fa31a4df588a54da94d55914fe8c6473cfb9a1f25eccebfe93cde0fe8347f2540dc94410327fa02841975aff332ae974efe735019a9
表示为对应的 10 进制,则为:
modulus=119206123292429371819908502167652190639725838417146837988211741054499347946286206953095566584657419999929226143391551082623221293842603113214182283348140165334909652082918891282099079263751160881533261378364698327507127995624737240734885279425387071955714448998303237443877039001189363998284524113886771004731 public exponent=65537 private exponent=76057861139095994364244228727899909236006163440697545363337869481268447356057764983805958721599249542961084443687042564046111332560667244137678443905007554506646354491362036790233381549836292285545365335064324815925298557929704945487609269035117636304672897796747055609045520946344630094728384669160475466153
注:可以用 python 进行 16 进制和 10 进制的相互转换。python 中 int 函数可以把 16 进行转换为 10 进制,如:
$ python -c 'print(int("00a9c151cc12e5acec59aa395d816bdaecbdc93954fe0332fa85c50dac71bb5a8243f2c303e7013ba1673d13d167b0407d82a9d4b0007bb67dc18b27c04915157233b903286f52fac2bafd733583b6ede9be2130b7dbc96ca2e4b731f84d6f0708d0c4ebb3fc8f8c5aa5a4957143e5330cfc6cc8828fd99fd5f2e743280485c53b", 16))'
119206123292429371819908502167652190639725838417146837988211741054499347946286206953095566584657419999929226143391551082623221293842603113214182283348140165334909652082918891282099079263751160881533261378364698327507127995624737240734885279425387071955714448998303237443877039001189363998284524113886771004731
python 中 hex 函数可以把 10 进行转换为 16 进制,如:
$ python -c 'print(hex(119206123292429371819908502167652190639725838417146837988211741054499347946286206953095566584657419999929226143391551082623221293842603113214182283348140165334909652082918891282099079263751160881533261378364698327507127995624737240734885279425387071955714448998303237443877039001189363998284524113886771004731))' 0xa9c151cc12e5acec59aa395d816bdaecbdc93954fe0332fa85c50dac71bb5a8243f2c303e7013ba1673d13d167b0407d82a9d4b0007bb67dc18b27c04915157233b903286f52fac2bafd733583b6ede9be2130b7dbc96ca2e4b731f84d6f0708d0c4ebb3fc8f8c5aa5a4957143e5330cfc6cc8828fd99fd5f2e743280485c53bL
2.2. 用 Java 生成 RSA 公钥和私钥对
下面 Java 程序可以产生一对 RSA 公钥和私钥对。
// file TestRSAKeyGen.java
import java.math.BigInteger;
import java.security.Key;
import java.security.KeyFactory;
import java.security.KeyPair;
import java.security.KeyPairGenerator;
import java.security.spec.RSAPrivateKeySpec;
import java.security.spec.RSAPublicKeySpec;
public class TestRSAKeyGen {
public static void main(String[] args) throws Exception {
generateKeys();
}
public static void generateKeys() throws Exception {
KeyPairGenerator kpg = KeyPairGenerator.getInstance("RSA");
kpg.initialize(1024);
KeyPair kp = kpg.genKeyPair();
Key publicKey = kp.getPublic();
Key privateKey = kp.getPrivate();
KeyFactory fact = KeyFactory.getInstance("RSA");
RSAPublicKeySpec pub = (RSAPublicKeySpec) fact.getKeySpec(publicKey, RSAPublicKeySpec.class);
RSAPrivateKeySpec priv = (RSAPrivateKeySpec) fact.getKeySpec(privateKey, RSAPrivateKeySpec.class);
BigInteger modules = pub.getModulus(); // same as priv.getModulus()
BigInteger publicExponent = pub.getPublicExponent();
BigInteger privateExponent = priv.getPrivateExponent();
System.out.println("Key Modulus: " + modules);
System.out.println("Public key Exponent: " + publicExponent);
System.out.println("Private key Exponent: " + privateExponent);
System.out.println("----------");
System.out.println("Key Modulus(HEX): " + modules.toString(16));
System.out.println("Public key Exponent(HEX): " + publicExponent.toString(16));
System.out.println("Private key Exponent(HEX): " + privateExponent.toString(16));
}
}
运行上面 Java 程序,可得到类似于下面的输出(public exponent 和前面用 openssl 工具生成的相同,都为 65537):
Key Modulus: 94622928382447445977163483618337096783921099210771238401957889119242480132322701475349180775948649634108628756798953966261504018646185704007168335936577899984313085074149012356458062681731023954414819411913645143083191029141028904201648862988915953382209115160443578274978688221191187420161336328436795293237 Public key Exponent: 65537 Private key Exponent: 1150715991284474639421995154551088181283627814379429589489302800372861996512827762574626502257214607906748510294471311032095132564215786595262419148594726196399789527479449550760519801678321978065864767408841267007776622347827205762616030258710633385020327025460194991520123250134721636455838553350234158589 ---------- Key Modulus(HEX): 86bf5da74f8964395782582314ea7cc92e760211fc0336dad681d317ec7044f0bd8d0fc31572d2e3bcf6d79bcd3185d96db683c4f9bcb1520e5ca4de7994f3f8613443f610485a4fb2ab20cb0990f867a0f1f617e2939cc073d29eef910d7be2ae749e7ec620db87066bca7cc82e22462e72fc169bf747ff6f6835cae26fbe35 Public key Exponent(HEX): 10001 Private key Exponent(HEX): 1a3802311bf8cfd7987f7446df3b012ce42d7219adbfb25cc2806062b74ee11b36c6cbda59c20de6e24de5861b5717844724cc5ef7790fc7b7a3af30dad770e10b07c2d28b292f59152aaa125ec4851bb35e27710fb7030a84a22b870c4423c5e40e970dffbeb17592655459453f81f1fd3a79a69b03390baa92c6c3f27b5fd
3. RSA 加解密
3.1. 两种填充方案
为了对抗攻击,一般会在使用 RSA 加密算法前,会先对明文填充一些随机数字。在 PKCS #1: RSA Cryptography Specifications(RFC8017)中定义了 RSA 用作加密算法时的两种填充方案:
- RSAES-OAEP (Optimal Asymmetric Encryption Padding)
- RSAES-PKCS1-v1_5
其中,RSAES-PKCS1-v1_5 填充方案已经不是很安全了(它在是目前使用最广泛的方式,它也是 Sun JDK 中默认的填充方案,后文将介绍它),在新的应用中推荐使用 RSAES-OAEP 填充方案(不过,本文不打算介绍它)。
3.2. RSAES-OAEP
本文不介绍。
3.3. RSAES-PKCS1-v1_5(即 PKCS1Padding)
RSAES-PKCS1-v1_5 填充方法也称 PKCS1Padding,下面将对它进行简单地描述。
使用 PKCS1Padding 填充方案的 RSA 加密过程为:
(1) 设原始待加密明文为 D,加密前先在 D 前面填充 4 个部分内容(填充后数据记为 EB, Encryption-block):
第 1 部分占 1 字节,内容为 0x00;
第 2 部分占 1 字节,内容为 0x02;
第 3 部分是 Padding string,它是随机数据,但不能包含 0x00,且为安全起见至少填充 8 个字节,随机数据越多越好,最多可以是多少呢?最多可以 把 EB 填充为和密钥大小相同的字节数(如当密钥大小为 1024 位时,填充 EB 为 1024/8=128 字节) ,这时因为 RSA 算法要求加密前数字(EB 对应数字)要比模数 n 小,否则无法正确解密,由于 EB 的第一个字节为 0x00,这保证了当 EB 和 n 具有相同字节数时 EB 会比模数 n 小;
第 4 部分占 1 字节,内容为 0x00。
即,填充后的数据可表示为:
\[\text{EB = }\overbrace{\text{0x00 || 0x02 ||} \underbrace{\text{Padding string}}_{\text{随机数据,至少 8 字节}} \text{|| 0x00 || D}}^{\text{和密钥大小相同的字节数}}\]
(2) 由于 RSA 算法是对整数(而不是字符串)进行的运算,需要把 EB 转换为整数表示。
(3) 对 EB 对应的整数表示作为输入明文,应用 RSA 加密公式,即可得到密文整数。
(4) 把密文整数转换为十六进制字符串表示(这就是最终的密文),是步骤(2)的逆过程。
对应的解密过程为:
(1) 把密文转换为对应整数表示。
(2) 把上一步得到的整数,应用 RSA 解密公式,即可得一个解密后的整数。
(3) 把解密后的整数转换为十六进制字符串表示,是步骤(1)的逆过程。
(4) 去掉上一步得到的十六进制字符串中前面的填充内容(即去掉 \(\text{0x00 || 0x02 || Padding string || 0x00}\) ,由于在加密前填充时要求 Padding string 不能包含 0x00,所以不会有歧义),得到的结果就是最终的明文。
说明:后文将通过实例详细介绍上面这些步骤。
3.4. PKCS1Padding 加解密演示
已知 RSA 密钥(1024 位,即 128 字节)为:
modulus=0x00a9c151cc12e5acec59aa395d816bdaecbdc93954fe0332fa85c50dac71bb5a8243f2c303e7013ba1673d13d167b0407d82a9d4b0007bb67dc18b27c04915157233b903286f52fac2bafd733583b6ede9be2130b7dbc96ca2e4b731f84d6f0708d0c4ebb3fc8f8c5aa5a4957143e5330cfc6cc8828fd99fd5f2e743280485c53b public exponent=0x10001 private exponent=0x6c4f5b7860ea483df92be23425fa8211a139fda99bf4c09715b8d7f39a11573b5c4d4d5e750ad558333dc6224b0d2ae8a9f0e03277ec77509fa7c0f22fef12e1e3a3dfefe9855152290c4fa31a4df588a54da94d55914fe8c6473cfb9a1f25eccebfe93cde0fe8347f2540dc94410327fa02841975aff332ae974efe735019a9
请详细说明使用“PKCS1Padding”填充方案,对字符串“RSA_123”进行加密和解密的过程。
3.4.1. PKCS1Padding 加密步骤演示
加密过程如下:
(1) 求填充后的数据 EB。EB 和密钥大小相同,也为 128 字节,由于原始待加密明文仅占 7 个字节(0x5253415F313233),所以 \(\text{0x00 || 0x02 || Padding string || 0x00}\) 应该占 121 字节,随机数据 Padding string 应该占 118 字节。这个例子中使用下面随机数据(当然你可以使用其它随机数据):
E0EF89D66C103C5F64C2DD7A9F51D0D583D5B725BF9E5DCB8BA75C86B035CECD736A5813554D28BB490DBCBE8ABB7E06F5D92DEEC761069A4F9CCFEB4FCC1C4755FA7BE099EB3D3B2F7B9F9980DA2DBAF8768887018F915EECFBE6F016FE5A596C3756C0E168CF6CAA67FCABC8EE29043790DEDCF397
从而最终得到 EB 为:
0002E0EF89D66C103C5F64C2DD7A9F51D0D583D5B725BF9E5DCB8BA75C86B035CECD736A5813554D28BB490DBCBE8ABB7E06F5D92DEEC761069A4F9CCFEB4FCC1C4755FA7BE099EB3D3B2F7B9F9980DA2DBAF8768887018F915EECFBE6F016FE5A596C3756C0E168CF6CAA67FCABC8EE29043790DEDCF397005253415F313233
(2) 把 EB 转换为对应整数表示。
直接看成是 16 进制数字即可。
0x0002E0EF89D66C103C5F64C2DD7A9F51D0D583D5B725BF9E5DCB8BA75C86B035CECD736A5813554D28BB490DBCBE8ABB7E06F5D92DEEC761069A4F9CCFEB4FCC1C4755FA7BE099EB3D3B2F7B9F9980DA2DBAF8768887018F915EECFBE6F016FE5A596C3756C0E168CF6CAA67FCABC8EE29043790DEDCF397005253415F313233
(3) 对上一步得到的整数(记为 P),应用 RSA 加密公式,即可得到密文整数(记为 C)。
用 python 程序计算如下:
#!/usr/bin/python P=0x0002E0EF89D66C103C5F64C2DD7A9F51D0D583D5B725BF9E5DCB8BA75C86B035CECD736A5813554D28BB490DBCBE8ABB7E06F5D92DEEC761069A4F9CCFEB4FCC1C4755FA7BE099EB3D3B2F7B9F9980DA2DBAF8768887018F915EECFBE6F016FE5A596C3756C0E168CF6CAA67FCABC8EE29043790DEDCF397005253415F313233 e=0x10001; n=0x00a9c151cc12e5acec59aa395d816bdaecbdc93954fe0332fa85c50dac71bb5a8243f2c303e7013ba1673d13d167b0407d82a9d4b0007bb67dc18b27c04915157233b903286f52fac2bafd733583b6ede9be2130b7dbc96ca2e4b731f84d6f0708d0c4ebb3fc8f8c5aa5a4957143e5330cfc6cc8828fd99fd5f2e743280485c53b; C=pow(P, e, n); ## same as C = (P ** e) % n; but more efficient print(C);
运行上面程序,得:
C=63250045914524029747616996741402377154382297912689338492817568185286579087160673183858118373701750694038461083525729041748061840999183976781099184573733726985516251833208328490882684067260154678117013801850363394774942848724244481996240262074567658308499142551417541787388651319389599160948632828987328495986
(4) 把密文整数转换为十六进制字符串表示。
$ python -c 'print(hex(63250045914524029747616996741402377154382297912689338492817568185286579087160673183858118373701750694038461083525729041748061840999183976781099184573733726985516251833208328490882684067260154678117013801850363394774942848724244481996240262074567658308499142551417541787388651319389599160948632828987328495986))' 0x5a1230ac0cabc2b3349bb1885a6daa873aed196082290ba8bc37ec25d64daa64f267d51c9aab948dd0690d52ceeb5dc2d843e7d6c83c218a1d9fb82c1b392863fc926507b2736f81535a18e772542a5158a34b7d54feab480633eae9f015f67b2d087f8bfe3be3e5bb363d1b2a48101d67914a0056dd76ec436f393372990172L
所以,密文为:
5a1230ac0cabc2b3349bb1885a6daa873aed196082290ba8bc37ec25d64daa64f267d51c9aab948dd0690d52ceeb5dc2d843e7d6c83c218a1d9fb82c1b392863fc926507b2736f81535a18e772542a5158a34b7d54feab480633eae9f015f67b2d087f8bfe3be3e5bb363d1b2a48101d67914a0056dd76ec436f393372990172
3.4.2. PKCS1Padding 解密步骤演示
本节将介绍如何利用前面给出的私钥对下面密文进行解密。
5a1230ac0cabc2b3349bb1885a6daa873aed196082290ba8bc37ec25d64daa64f267d51c9aab948dd0690d52ceeb5dc2d843e7d6c83c218a1d9fb82c1b392863fc926507b2736f81535a18e772542a5158a34b7d54feab480633eae9f015f67b2d087f8bfe3be3e5bb363d1b2a48101d67914a0056dd76ec436f393372990172
(1) 把密文转换为对应整数表示,整数的十六进制表示为:
0x5a1230ac0cabc2b3349bb1885a6daa873aed196082290ba8bc37ec25d64daa64f267d51c9aab948dd0690d52ceeb5dc2d843e7d6c83c218a1d9fb82c1b392863fc926507b2736f81535a18e772542a5158a34b7d54feab480633eae9f015f67b2d087f8bfe3be3e5bb363d1b2a48101d67914a0056dd76ec436f393372990172
(2) 应用 RSA 解密公式。
用 python 程序计算如下:
#!/usr/bin/python C=0x5a1230ac0cabc2b3349bb1885a6daa873aed196082290ba8bc37ec25d64daa64f267d51c9aab948dd0690d52ceeb5dc2d843e7d6c83c218a1d9fb82c1b392863fc926507b2736f81535a18e772542a5158a34b7d54feab480633eae9f015f67b2d087f8bfe3be3e5bb363d1b2a48101d67914a0056dd76ec436f393372990172 d=0x6c4f5b7860ea483df92be23425fa8211a139fda99bf4c09715b8d7f39a11573b5c4d4d5e750ad558333dc6224b0d2ae8a9f0e03277ec77509fa7c0f22fef12e1e3a3dfefe9855152290c4fa31a4df588a54da94d55914fe8c6473cfb9a1f25eccebfe93cde0fe8347f2540dc94410327fa02841975aff332ae974efe735019a9 n=0x00a9c151cc12e5acec59aa395d816bdaecbdc93954fe0332fa85c50dac71bb5a8243f2c303e7013ba1673d13d167b0407d82a9d4b0007bb67dc18b27c04915157233b903286f52fac2bafd733583b6ede9be2130b7dbc96ca2e4b731f84d6f0708d0c4ebb3fc8f8c5aa5a4957143e5330cfc6cc8828fd99fd5f2e743280485c53b; P=pow(C, d, n); ## same as P = (C ** d) % n; but more efficient print(P);
运行上面程序,得:
P=7896329422618699107281053387726396496733905004702396851703143372858419433868516222850771517642682918935866181916299222276127844526511045477372655265529503324103683332059225015289169165520670664592878372189493472266017572100723122716251888502461249402248181409428731819987469167607605339862327359895056947
(3) 把解密后的整数转换为十六进制字符串表示。
可用下面 python 程序实现:
$ python -c 'print(hex(7896329422618699107281053387726396496733905004702396851703143372858419433868516222850771517642682918935866181916299222276127844526511045477372655265529503324103683332059225015289169165520670664592878372189493472266017572100723122716251888502461249402248181409428731819987469167607605339862327359895056947))' 0x2e0ef89d66c103c5f64c2dd7a9f51d0d583d5b725bf9e5dcb8ba75c86b035cecd736a5813554d28bb490dbcbe8abb7e06f5d92deec761069a4f9ccfeb4fcc1c4755fa7be099eb3d3b2f7b9f9980da2dbaf8768887018f915eecfbe6f016fe5a596c3756c0e168cf6caa67fcabc8ee29043790dedcf397005253415f313233L
python 的 hex 函数输出时,默认去掉了前导的 0,如果加上省略的前导 0,则可得解密后整数的字符串表示为:
0002e0ef89d66c103c5f64c2dd7a9f51d0d583d5b725bf9e5dcb8ba75c86b035cecd736a5813554d28bb490dbcbe8abb7e06f5d92deec761069a4f9ccfeb4fcc1c4755fa7be099eb3d3b2f7b9f9980da2dbaf8768887018f915eecfbe6f016fe5a596c3756c0e168cf6caa67fcabc8ee29043790dedcf397005253415f313233
(4) 去掉填充内容,得到原始数据。
上面明文前面包含填充数据 \(\text{0x00 || 0x02 || Padding string || 0x00}\) (Padding string 不含 0x00),去掉它们,可得最终的明文为:
5253415f313233
“5253415f313233”对应的 ASCII 码就是“RSA_123”。
3.4.3. Tips:相同密钥,同一明文每次加密后将得到不同密文
前面例子中,使用的随机数据为:
E0EF89D66C103C5F64C2DD7A9F51D0D583D5B725BF9E5DCB8BA75C86B035CECD736A5813554D28BB490DBCBE8ABB7E06F5D92DEEC761069A4F9CCFEB4FCC1C4755FA7BE099EB3D3B2F7B9F9980DA2DBAF8768887018F915EECFBE6F016FE5A596C3756C0E168CF6CAA67FCABC8EE29043790DEDCF397
显然,如果填充其他不同的随机数据,则 RSA 密文会不一样。但这不会影响最终的解密数据,因为得到最终解密数据前会去掉填充的数据。后文的例子将再次说明这点。
3.4.4. Tips:待加密文本过大时需要切割
由前面的计算过程可知, 对于 1024 位(128 字节)的密钥,仅支持加密最大 128-(3+8)=117 个字节的数据 ,因为其中填充数据 \(\text{0x00 || 0x02 || Padding string || 0x00}\) 至少占 3+8 个字节。如果带加密数据过长,则要提前分割后再加密。
3.5. 不填充(Nopadding,不安全)
也可以采用不填充随机数据的方案,其加解密过程和采用 PKCS1Padding 填充方案的加解密过程非常类似。区别在于:加密时把填充的数据 \(\text{0x00 || 0x02 || Padding string || 0x00}\) 全部换为 0x00(可以认为在前面填充 0x00);而解密时不用去掉前置的填充数据。
不过,需要注意的是,用 Nopadding 方案来加密二进制数据(非文本数据)时,如果二进制数据以多个 0x00 打头,解密后无法得知原始数据中打头的 0x00 有多少个了。
显然,Nopadding 方式,同一明文用同一密钥每次加密后得到的密文是相同的。
3.6. RSA 加解密的 Sun JDK 实现
Sun JDK 中默认采用的 RSA 填充方案是就是 RSAES-PKCS1-v1_5,如:
Cipher.getInstance("RSA"); // Sun JDK中,是下一行的简写。
Cipher.getInstance("RSA/ECB/PKCS1Padding", "SunJCE"); // 注:SunJCE中这个名字“RSA/ECB/PKCS1Padding”取得不好,“RSA/None/PKCS1Padding”可能更合适,因为它并不能自动处理过长的数据,你得提前分割。
Java 中 RSA 加解密算法采用 PKCS1Padding 或 Nopadding 方案的实例:
import java.math.BigInteger;
import java.security.KeyFactory;
import java.security.PrivateKey;
import java.security.PublicKey;
import java.security.spec.RSAPrivateKeySpec;
import java.security.spec.RSAPublicKeySpec;
import java.util.Arrays;
import javax.crypto.Cipher;
public class RSATest {
private static final String ALGORITHOM = "RSA";
private static final String CIPHER_PROVIDER = "SunJCE";
private static final String TRANSFORMATION_Nopadding = "RSA/ECB/NOPADDING";
private static final String TRANSFORMATION_PKCS1Paddiing = "RSA/ECB/PKCS1Padding";
private static final String STRING_TO_ENCRYPT = "RSA_123";
private static final String CHAR_ENCODING = "UTF-8";
private static final String KEY_MODULUS_HEX =
"00a9c151cc12e5acec59aa395d816bdaecbdc93954fe0332fa85c50dac71bb5a8243f2c303e7013b"
+ "a1673d13d167b0407d82a9d4b0007bb67dc18b27c04915157233b903286f52fac2bafd733583b6ed"
+ "e9be2130b7dbc96ca2e4b731f84d6f0708d0c4ebb3fc8f8c5aa5a4957143e5330cfc6cc8828fd99f"
+ "d5f2e743280485c53b";
private static final String KEY_PUBLIC_EXPONENT_HEX = "10001";
private static final String KEY_PRIVATE_EXPONENT_HEX =
"6c4f5b7860ea483df92be23425fa8211a139fda99bf4c09715b8d7f39a11573b5c4d4d5e750ad558"
+ "333dc6224b0d2ae8a9f0e03277ec77509fa7c0f22fef12e1e3a3dfefe9855152290c4fa31a4df588"
+ "a54da94d55914fe8c6473cfb9a1f25eccebfe93cde0fe8347f2540dc94410327fa02841975aff332"
+ "ae974efe735019a9";
public static void main(String[] args) throws Exception {
PublicKey pubKey = getRSAPublicKey(new BigInteger(KEY_MODULUS_HEX, 16), new BigInteger(KEY_PUBLIC_EXPONENT_HEX, 16));
PrivateKey privKey = getRSAPrivateKey(new BigInteger(KEY_MODULUS_HEX, 16), new BigInteger(KEY_PRIVATE_EXPONENT_HEX, 16));
System.out.println("____Begin test RSA with Pkcs1padding, the plain text is: " + STRING_TO_ENCRYPT);
testEncryptDecryptPkcs1padding(pubKey, privKey, STRING_TO_ENCRYPT);
testEncryptDecryptPkcs1padding(pubKey, privKey, STRING_TO_ENCRYPT);
System.out.println("____Begin test RSA with Nopadding, the plain text is: " + STRING_TO_ENCRYPT);
testEncryptDecryptNopadding(pubKey, privKey, STRING_TO_ENCRYPT);
testEncryptDecryptNopadding(pubKey, privKey, STRING_TO_ENCRYPT);
}
public static void testEncryptDecryptPkcs1padding(PublicKey pubKey, PrivateKey privKey, String plainText) throws Exception {
// 开始加密
byte[] cipherData = encryptPkcs1padding(pubKey, plainText.getBytes(CHAR_ENCODING));
// 输出密文
System.out.print("Data after encryption(HEX String): ");
dumpByteArrayToHex(cipherData);
// 开始解密
byte[] decryptedData = decryptPkcs1padding(privKey, cipherData);
// 输出解密后的明文(HEX String形式)
System.out.print("Data after decryption(HEX String): ");
dumpByteArrayToHex(decryptedData);
// 输出解密后的明文
String decryptedString = new String(decryptedData, CHAR_ENCODING);
System.out.println("Data after decryption: " + decryptedString);
}
public static void testEncryptDecryptNopadding(PublicKey pubKey, PrivateKey privKey, String plainText) throws Exception {
// 开始加密
byte[] cipherData = encryptNopadding(pubKey, plainText.getBytes(CHAR_ENCODING));
// 输出密文
System.out.print("Data after encryption(HEX String): ");
dumpByteArrayToHex(cipherData);
// 开始解密
byte[] decryptedData = decryptNopadding(privKey, cipherData);
// 输出解密后的明文(HEX String形式)
System.out.print("Data after decryption(HEX String): ");
dumpByteArrayToHex(decryptedData);
// 输出解密后的明文
String decryptedString = new String(decryptedData, CHAR_ENCODING);
System.out.println("Data after decryption: " + decryptedString);
}
public static PublicKey getRSAPublicKey(BigInteger modulus, BigInteger publicExp) throws Exception {
KeyFactory fact = KeyFactory.getInstance(ALGORITHOM);
RSAPublicKeySpec publicKeySpec = new RSAPublicKeySpec(modulus, publicExp);
return fact.generatePublic(publicKeySpec);
}
public static PrivateKey getRSAPrivateKey(BigInteger modulus, BigInteger privateExp) throws Exception {
KeyFactory fact = KeyFactory.getInstance(ALGORITHOM);
RSAPrivateKeySpec privateKeySpec = new RSAPrivateKeySpec(modulus, privateExp);
return fact.generatePrivate(privateKeySpec);
}
public static byte[] encryptPkcs1padding(PublicKey publicKey, byte[] data) throws Exception {
Cipher ci = Cipher.getInstance(TRANSFORMATION_PKCS1Paddiing, CIPHER_PROVIDER);
ci.init(Cipher.ENCRYPT_MODE, publicKey);
return ci.doFinal(data);
}
public static byte[] decryptPkcs1padding(PrivateKey privateKey, byte[] data) throws Exception {
Cipher ci = Cipher.getInstance(TRANSFORMATION_PKCS1Paddiing, CIPHER_PROVIDER);
ci.init(Cipher.DECRYPT_MODE, privateKey);
return ci.doFinal(data);
}
public static byte[] encryptNopadding(PublicKey publicKey, byte[] data) throws Exception {
Cipher ci = Cipher.getInstance(TRANSFORMATION_Nopadding, CIPHER_PROVIDER);
ci.init(Cipher.ENCRYPT_MODE, publicKey);
return ci.doFinal(data);
}
public static byte[] decryptNopadding(PrivateKey privateKey, byte[] data) throws Exception {
Cipher ci = Cipher.getInstance(TRANSFORMATION_Nopadding, CIPHER_PROVIDER);
ci.init(Cipher.DECRYPT_MODE, privateKey);
byte[] decryptedData = ci.doFinal(data);
// 对Nopadding方式的密文进行解密后(即ci.doFinal(data);)返回的数组中有很多前导0x00,这里仅是对文本数据加解密,应该去掉前导0x00。
int i = 0;
while (i < decryptedData.length && decryptedData[i] == 0) {
i++;
}
return Arrays.copyOfRange(decryptedData, i, decryptedData.length);
}
private static void dumpByteArrayToHex(byte[] bytes) {
System.out.println(javax.xml.bind.DatatypeConverter.printHexBinary(bytes));
}
}
上面程序运行的一个可能结果:
____Begin test RSA with Pkcs1padding, the plain text is: RSA_123 Data after encryption(HEX String): 2B432DF85F0B412082FEDB59382B57CFAA418972204B922369CE109C3192EC3CA9BBBE2A5EF23C3774925BB41D11052116A976D55A4D776023F9A30A8714AE4E551E8EEB5A442DF61768CB9E71F81B30C4939FC6AA6194DA192194AF24AEAD74DA56AA9C8E12FA46354AD39F6E5113E48EC0FE7E0033172CCC157B122DB8F54E Data after decryption(HEX String): 5253415F313233 Data after decryption: RSA_123 Data after encryption(HEX String): 4A4F06DE1CCFE3B91227EAE34AAC4EFCD6F25D37044859DB138316A6B8D4D61CD1D26FD81394FCB324E83821DD936A87D3322DEFC7D7DDEA81235C95DD486D0AC9F93E90AFFA37E82EFF356763EF8A80AF93EEA9AA06FF30A10BC1FE8AAB613DE89CCE5DAD26CF10631CD28B5973CCE48598C41FE6975A349870E01CAC052BAF Data after decryption(HEX String): 5253415F313233 Data after decryption: RSA_123 ____Begin test RSA with Nopadding, the plain text is: RSA_123 Data after encryption(HEX String): A597CAEA2962531E088E18D2F4591AA98D3E14D418FBF574AF434159F423DCCA04410E492439FBADB44C3A83F08F5EAB1D7A1FB65C4C1906627470C3A01C59BD1FE28D467AF61FCFEAF120E6EFDD1460D85564ACA42FE45FC6D96C8D6E8800362871D7869239AB5D2B4E9BF9EAA910583EEF35A587D7849E38C9CDD8B0C09532 Data after decryption(HEX String): 5253415F313233 Data after decryption: RSA_123 Data after encryption(HEX String): A597CAEA2962531E088E18D2F4591AA98D3E14D418FBF574AF434159F423DCCA04410E492439FBADB44C3A83F08F5EAB1D7A1FB65C4C1906627470C3A01C59BD1FE28D467AF61FCFEAF120E6EFDD1460D85564ACA42FE45FC6D96C8D6E8800362871D7869239AB5D2B4E9BF9EAA910583EEF35A587D7849E38C9CDD8B0C09532 Data after decryption(HEX String): 5253415F313233 Data after decryption: RSA_123
从上面结果中,可知,采用填充方式后,相同密钥每次对明文加密后得到的密文是不同的;而 Nopadding 方式,则总得到相同的密文。
参考:
Java Cryptography Architecture Oracle Providers Documentation for Java Platform Standard Edition 7
4. RSA-KEM
当需要加密大量数据时,基于性能考虑,我们一般不会直接使用 RSA 加密。一般采用的方式是先随机生成一个 256-bit AES 密钥,使用 AES 加密大量数据,而使用 RSAES-OAEP 对 AES 密钥进行加密。接收方收到 AES 密文和数据密文后,先使用 RSAES-OAEP 解密出 AES 密钥,再用 AES 密钥解密数据密文。
上面过程的其实就是如何使用 RSAES-OAEP 协商出一个对称加密算法的密钥。
RSA-KEM 是另一种使用 RSA 算法协商对称加密算法密钥的方案,它在 ISO/IEC 18033-2:2006 中被标准化。 这里的 KEM 是 Key Encapsulation Mechanism 的缩写。
下面通过例子介绍一下使用 RSAES-OAEP 和使用 RSA-KEM 协商对称加密算法密钥的区别。
Bob 使用 RSAES-OAEP 想和 Alice 协商一个 256 bit AES 密钥 \(M\) ,其方法如下:
- Bob 随机产生 256-bit AES 密钥 \(M\) ;
- Bob 使用 OAEP 机制把 256 bit 的 \(M\) 变为一个大整数 \(m\) ,满足 \(1 < m < n\) ;
- Bob 使用 Alice 公钥 \((e,n)\) 对 \(m\) 进行加密,密文为 \(c \equiv m^e \bmod n\),把密文 \(c\) 发送给 Alice;
- Alice 使用自己的私钥 \((d,n)\) 对密文解密,得到明文 \(m \equiv c^d \bmod n\) ;
- Alice 去掉 OAEP 中引入的 Padding 数据,得到 \(M\) 。
Bob 使用 RSA-KEM 想和 Alice 协商一个 256 bit AES 密钥 \(M\) ,其方法如下:
- Bob 随机产生 \(m\) ,满足 \(1 < m < n\) ;
- Bob 使用 KDF 函数(或者密码学安全的 Hash 函数)推导出 AES 密钥 \(M=KDF(m)\) ;
- Bob 使用 Alice 公钥 \((e,n)\) 对 \(m\) 进行加密,密文为 \(c \equiv m^e \bmod n\) ,把密文 \(c\) 发送给 Alice;
- Alice 使用自己的私钥 \((d,n)\) 对密文解密,得到明文 \(m \equiv c^d \bmod n\) ;
- Alice 使用和 Bob 一样的 KDF 函数(或者密码学安全的 Hash 函数),推导 AES 密钥 \(M=KDF(m)\) 。
使用 RSA-KEM 的好处是:RSA-KEM 通过引入 KDF 去掉了 RSAES-OAEP 中复杂的 Padding 机制。
参考:https://crypto.stackexchange.com/questions/83470/where-is-rsa-kem-used-as-of-2020
5. RSA 签名
RSA 的签名过程其实使用的就是它的加解密方法。在 RSA 加解密算法中,使用公钥加密数据,使用私钥解密数据,即 \(D(E(P)) = P\) ,其中 E 是加密过程,D 是解密过程,P 是明文数据。RSA 算法有一个特性就是“先使用私钥解密数据,再使用公钥加密数据”也可以得到原始数据,即 \(E(D(P)) = P\) 。用 RSA 进行数字签名正是利用了 RSA 的这个特点。
5.1. 两种签名方案
在 PKCS #1: RSA Cryptography Specifications(RFC8017)中定义了 RSA 用作签名时的两种填充方案:
- RSASSA-PSS (RSA Signature Scheme with Appendix - Probabilistic Signature Scheme)
- RSASSA-PKCS1-v1_5
其中,RSASSA-PKCS1-v1_5 已经不再推荐使用,仅在对旧应用程序做兼容时才使用。新应用程序应该使用 RSASSA-PSS。
5.2. RSASSA-PSS 介绍
RSASSA-PSS 如图 1 所示,详情可参考:https://datatracker.ietf.org/doc/html/rfc8017#section-8.1
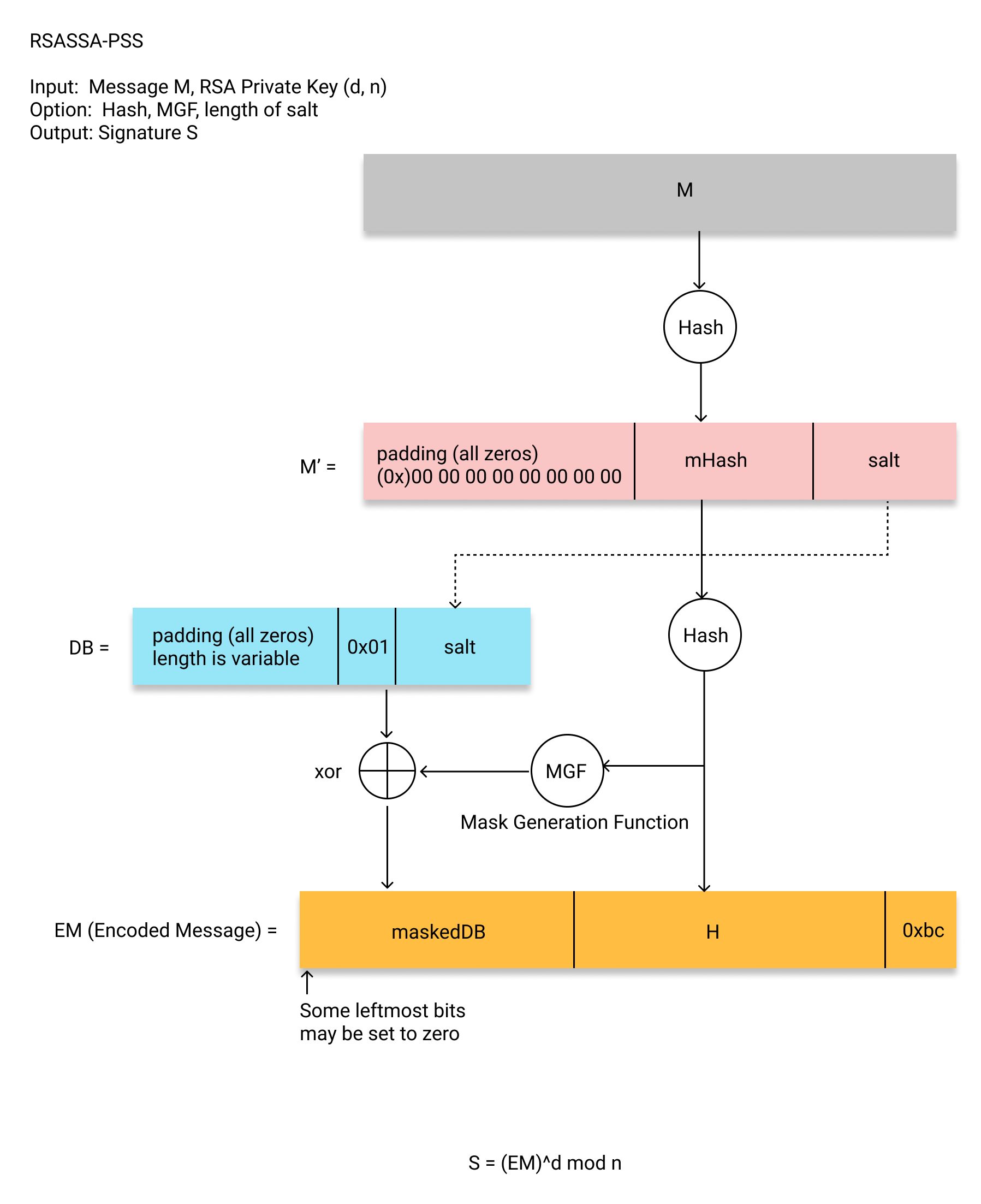
Figure 1: RSASSA-PSS 图示(原始消息 M 经过一些操作后变为了 EM,再对 EM 使用私钥进行 RSA“解密”操作)
5.3. RSASSA-PSS 实例(Python)
下面 RSASSA-PSS 签名方案的实例(Python 实现):
#!/usr/bin/env python3
# pip3 install pycryptodome
from Crypto.Signature import pss
from Crypto.Hash import SHA256
from Crypto.PublicKey import RSA
# 生成 key
key = RSA.generate(2048)
# 下面私钥和公钥可以直接保存到 pem 文件中
private_key = key.export_key()
public_key = key.publickey().export_key()
# 待签名数据
message = b'To be signed'
# 使用私钥进行签名
key = RSA.import_key(private_key)
h = SHA256.new(message)
signature = pss.new(key).sign(h)
# 使用公钥验证签名
key = RSA.import_key(public_key)
h = SHA256.new(message)
verifier = pss.new(key)
try:
verifier.verify(h, signature)
print("The signature is valid.")
except (ValueError, TypeError):
print("The signature is invalid.")