Schnorr Threshold Signature (Stinson and Strobl's 2001 paper)
Table of Contents
1. 论文介绍
2001 年,D.R. Stinson and R.Strobl 在论文 Provably Secure Distributed Schnorr Signatures and a (t,n) Threshold Scheme for Implicit Certificates 中提出了一种 Schnorr 门限签名方案,本文将介绍它。
2. 基础知识
2.1. Schnorr 签名
设椭圆曲线定义在有限素数域 \(\mathbb{F}_{p}\) 上,椭圆曲线的 Generator 为 \(G\) ,用户的私钥和公钥分别为 \((x, Y)\) ,记待签名的消息为 \(m\) ,则 Schnorr 签名过程如下:
- 随机选择 \(e \in \mathbb{Z}_p\)
- 计算 \(V= eG\)
- 计算 \(\sigma = e + h(m, V) x \bmod p\)
- 输出签名 \((V, \sigma)\)
签名验证时,如果 \((V, \sigma)\) 满足下面等式则通过验证: \[\sigma G = V + h(m,V) Y\]
2.2. Shamir's Secret Sharing
如何把秘密值 \(s \in \mathbb{Z}_p\) 分散保管到 \(n\) 个参与者中,且至少需要其中 \(t\) 个参与者才能恢复出秘密值 \(s\) 。
Shamir 给出的方案是,由可信任的第 3 方(称为 Dealer)随机生成一个满足条件 \(f(0)=s\) 的 \(t-1\) 次多项式,为第 \(i\) 个参与者分配的 Shared Key 为: \[s_i = f(i), \; 1 \le i \le n\]
使用拉格朗日插值公式,由点 \((1, s_1), (2, s_2), \cdots, (n, s_n)\) 中任意的 \(t\) 个点(这 \(t\) 个点的横坐标组成的集合记为 \(P\) )可以重建出多项式 \(f(x)\) : \[f(x) = \sum_{i \in P} s_i w_i(x), \;\; \text{where} \; w_i(x) = \prod_{j \in P, j \ne i}\frac{x-j}{i-j} \bmod p\]
由于 \(s = f(0)\) ,所以 \(s\) 还可以写为: \[s=\sum_{i \in P}s_iw_i, \;\; \text{where} \; w_i = w_i(0) = \prod_{j \in P, j \ne i}\frac{j}{j-i} \bmod p\]
2.3. Feldman's VSS
为了防止 Shamir 方案中的 Dealer 做恶(比如分配给参与者的 shared key 是随便给的,并不满足相关约束),Feldman 提出了另一种方案。
Dealer 随机选择多项式 \[f(x) = s + a_1 x + a_2 x^2 + \cdots + a_t x^t\] 这里 \(s\) 是秘密值, \(f(i)\) 通过加密通道分配给参与者 \(P_i\) 。
Dealer 同时公开下面信息(被称为 Commitment)
每个参与者 \(P_i\) 验证自己收到的 \(f(i)\) 是否满足 \[f(i)G = C_0 + C_1 i + C_2 i^2 + \cdots + C_t i^t\] 或者写为 \[s_i G = sG + \sum_{j=1}^{t-1} a_j i^j G\] 如果满足则说明 Dealer 没有做恶。
3. 协议介绍
3.1. DKG
论文 Provably Secure Distributed Schnorr Signatures and a (t,n) Threshold Scheme for Implicit Certificates 中没有提出新的 Distributed Key Generation(DKG)协议,它直接使用了 1999 年 Rosario Gennaro, Stanislaw Jarecki, Hugo Krawczyk, and Tal Rabin 在论文 Secure Distributed Key Generation for Discrete-Log Based Cryptosystems 中提出的 DKG 协议,简称 GJKR99 协议,图 1 是 GJKR99 协议 的总结。
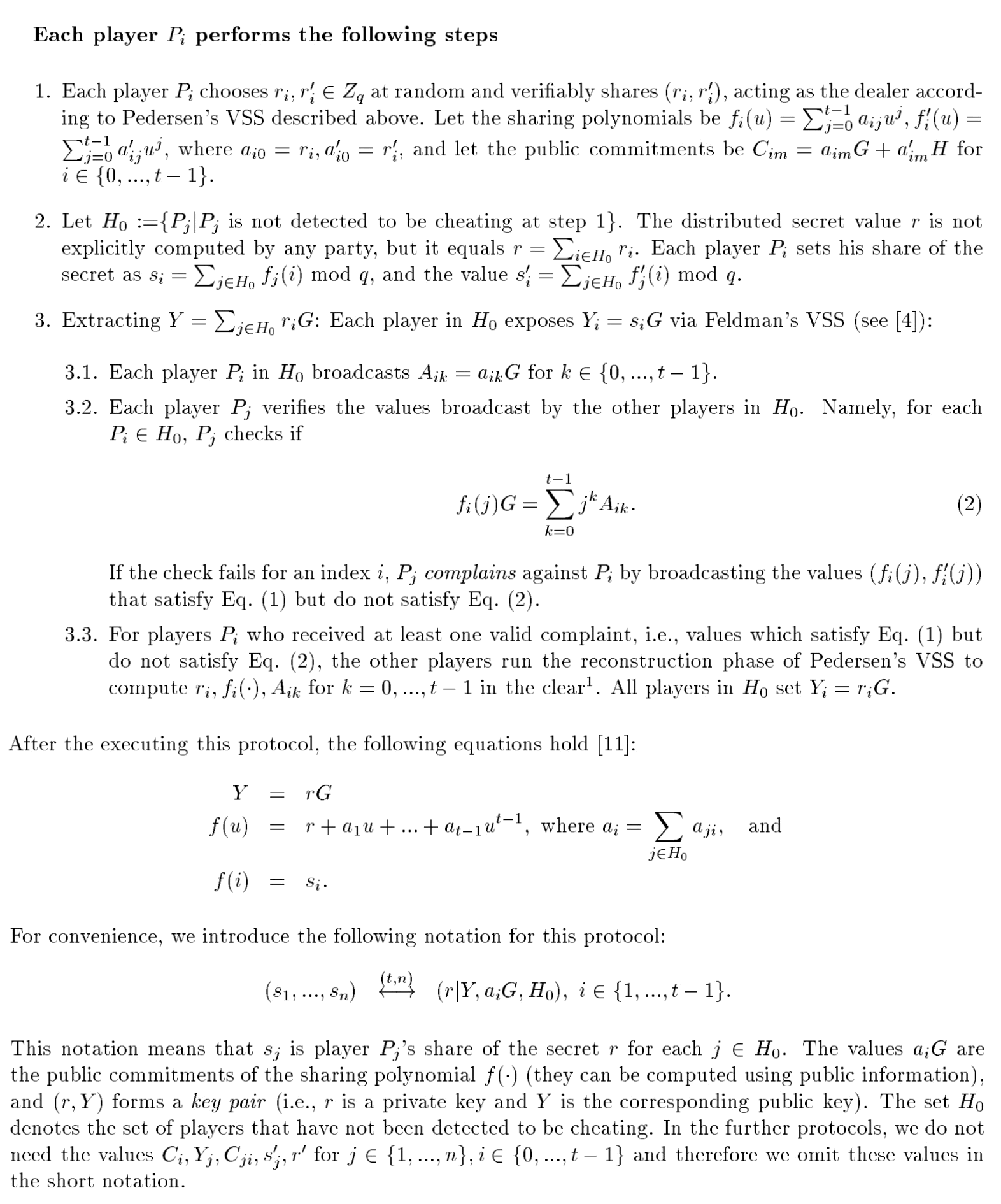
Figure 1: GJKR99 DKG
这里简单交待一下记号 \[(s_1,\cdots,s_n) \overset{(t,n)}{\longleftrightarrow} (r|Y, a_iG, H_0), i \in \{1, \cdots, t-1\}\] 的含义:秘密值 \(r\) 分散保存到 \(n\) 个参与者,每个人得到的 shared key 为 \(s_i\) ,\(H_0\) 是诚实的参与者集合,每个参与者可以得到的公开信息有:公钥 \(Y\) 及 Feldman Commitment \(a_i G\) ,其中 \(a_i\) 就是多项式 \(f(x) = r + a_1 x + \cdots + a_{t-1}x^{t-1}\) 的各个系数,这个多项式满足 \(f(i) = s_i\) 。
3.2. 门限签名过程
介绍签名前,先要进行 DKG,假设采用节 3.1 所示的协议得到的 DKG 结果为: \[(\alpha_1,\cdots,\alpha_n) \overset{(t,n)}{\longleftrightarrow} (x|Y, b_iG, H_0), i \in \{1, \cdots, t-1\}\] 也就是说真正的私钥是 \(x\) ,公钥是 \(Y\) ,每个参与都得到的 shared key 为 \((\alpha_1,\cdots,\alpha_n)\) 。
论文 Provably Secure Distributed Schnorr Signatures and a (t,n) Threshold Scheme for Implicit Certificates 中的门限签名协议如图 2 所示。
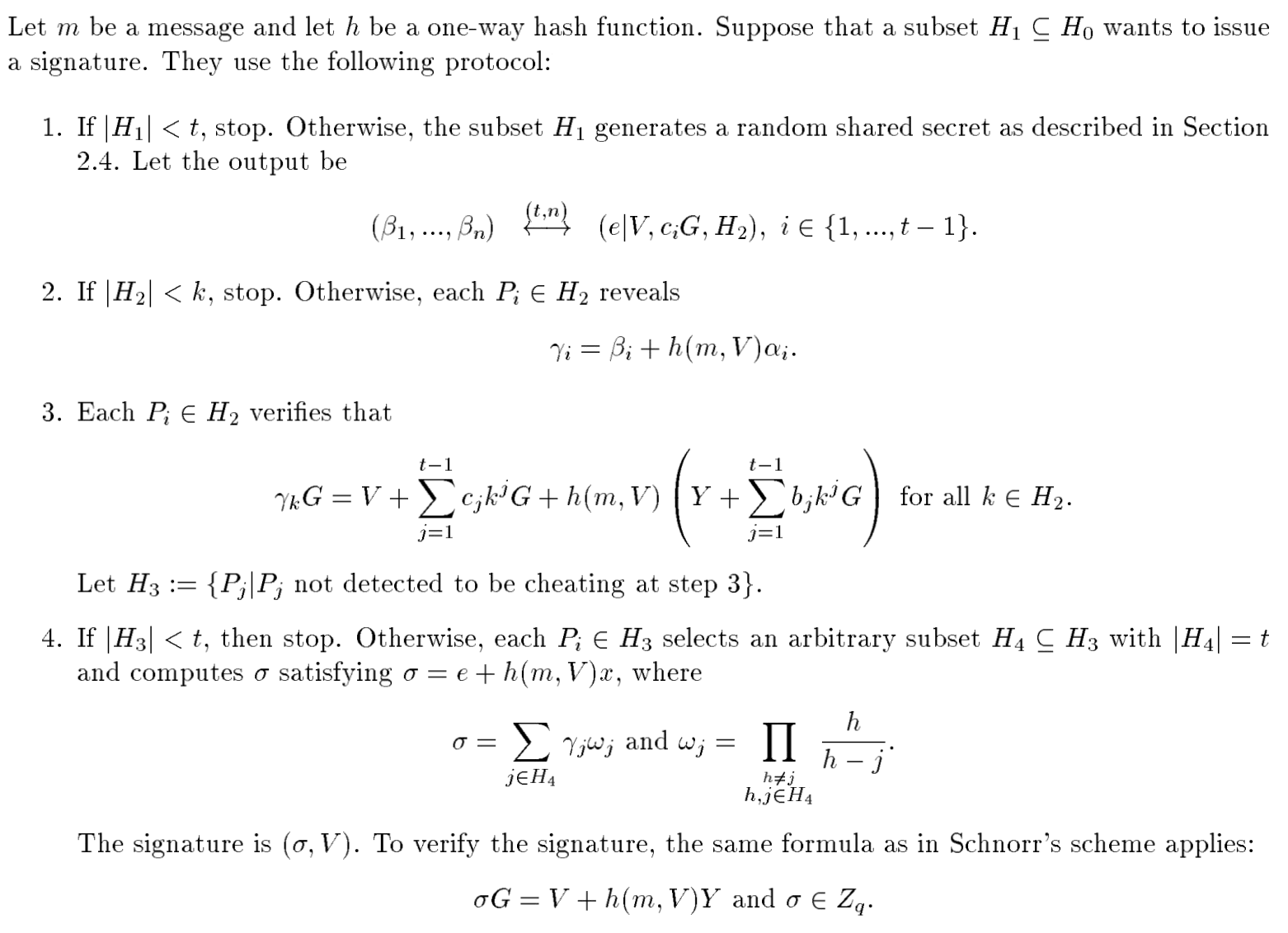
Figure 2: Signature Issuing Protocol
下面简单说明一下每个步骤。
第 1 步,采用 DKG 相同的协议(参见节 3.1)把随机数 \(e\) 分散到集合 \(H_1\) 的所有参与者中,每个参与者得到的 Shared Key 是 \(\beta_i\) 。
第 2 步,上一步的诚实参与者 \(P_i \in H_2\) 公布 \[\gamma_i = \beta_i + h(m,V) \alpha_i\] 其中, \(V=eG\) , \(\alpha_i\) 是 DKG 结束后每个参与者得到的 Shared Key。
第 3 步,每个 \(P_i \in H_2\) 验证下式是否成立 \[\gamma_k G = V + \sum_{j=1}^{t-1} c_j k^j G + h(m,V)\left(Y + \sum_{j=1}^{t-1}b_j k_j G \right) \; \text{for all} \; k \in H_2\] 如果成立,则 \(P_k\) 就是这一步的诚实参与者。这个式子为什么应该成立呢?下面是推导过程:
关于为什么 \(\beta_k G = V + \sum_{j=1}^{t-1}c_j k^j G,\; \alpha_k G = Y + \sum_{j=1}^{t-1}b_j k^j G\) ,可参考节 2.3 。
第 4 步,上一步的诚实参与者中,取 \(t\) 个组成集合 \(H_4\) ,计算 \[\sigma = \sum_{j \in H_4} \gamma_j w_j \; \text{and} \; w_j = \prod_{\;h \ne j\\ h,j \in H_4} \frac{h}{h-j}\] 签名输出就是 \((V, \sigma)\) 。我们知道,在标准的 Schnorr 签名中(参考节 2.1), \(\sigma = e + h(m,V)x\) ,为什么它会等于这里的 \(\sum_{j \in H_4} \gamma_j w_j\) 呢?下面来推导一下:
关于为什么 \(e= \sum \beta_j w_j,\; x = \sum \alpha_j w_j\) ,可参考节 2.2 。
3.2.1. 4 Rounds
上面介绍的门限签名过程至少需要参与者进行 4 轮的数据交换,其中签名过程中的 DKG 占据了 3 轮。
This construction requires at minimum four rounds for each signing operation (assuming no participant misbehaves): three rounds to perform the DKG, and one round to distribute signature shares and compute the group signature.