Statistics Simulation (Monte Carlo Sampling)
Table of Contents
1. Simulation 简介
Statistical simulations are used to estimate features of distributions such as means of functions, quantiles, and other features that we cannot compute in closed form.
Simulation is a technique that can be used to help shed light on how a complicated system works even if detailed analysis is unavailable.
统计模拟(Statistical Simulations)往往又称为蒙特卡罗方法(Monte Carlo Method, or Monte Carlo Simulation, or Monte Carlo Sampling)。
20 世纪 40 年代,在冯·诺伊曼,斯塔尼斯拉夫·乌拉姆(Stanislaw Ulam)和尼古拉斯·梅特罗波利斯(Nicholas Metropolis)在洛斯阿拉莫斯国家实验室为核武器计划工作时,发明了蒙特卡罗方法。因为乌拉姆的叔叔经常在蒙特卡罗赌场输钱得名,而蒙特卡罗方法正是以概率为基础的方法。
统计模拟中有个重要问题: 已知一个概率分布(不一定有解析表达式),如何用计算机生成它的样本。
参考:
Simulation, Sheldon M Ross, 5th, 2013(本文主要参考)
Pattern Recognition and Machine Learning, Chapter 11 Sampling Methods
2. 生成随机数
生成随机数并不是一件简单的事情。历史上人们提出了各种得到随机数的方法,如冯诺伊曼提出的——“平方取中法”(即:取前面的随机数的平方,并抽取中部的数字),但都有弊端。
2.1. 线性同余法
一种流行的随机数(满足均匀分布)生成方法是:线性同余法(Linear Congruential)。
线性同余求随机数的方法如下:
首先选择 4 个魔术整数:
\[\begin{aligned} & m,\, 0 < m \quad – \; \text{the “modulus”} \\
& a,\, 0 < a < m \quad – \; \text{the “multiplier”} \\
& c,\, 0 \leq c< m \quad – \; \text{the “increment”} \\
& X_{0},\,0 \leq X_{0} < m \quad – \; \text{the “seed” or “start value”} \end{aligned}\]
然后通过下式:
\[X_{n+1} = \left(a X_n + c\right) \mod m, \quad n \ge 0\]
得到 随机数序列 ,这个序列称为线性同余序列。
这个线性同余序列并不总是随机的,例如当 \(m=10\) 和 \(X_0 = a = c = 7\) 时,得到的序列是:
\[7,6,9,0,7,6,9,0,\cdots\]
参考:计算机程序设计艺术——第 2 卷 半数值算法(第 3 版),第 3 章随机数,3.2 节生成一致随机数
2.2. 其它随机数生成算法
目前,在编程语言中使用最广的随机数生成算法是 Mersenne Twister。此外,在 List of Random Number Generators 中列出很多随机数生成算法。
3. 利用随机数计算积分
想要计算下面的积分:
\[\theta = \int_0^1 g(x) \, \mathrm{d}x\]
如果定积分可以解析求出,则可直接求出;定积分不能解析求出时,可以利用随机数来近似计算。
假设 \(U\) 是 \((0,1)\) 上的均匀分布,即它的概率分布为:
\[f(x) = \begin{cases} 1, \, 0 < x < 1 \\
0, \, \text{otherwise} \end{cases}\]
则:
\[E[g(U)] = \int_{- \infty}^{\infty} f(x) g(x) \, \mathrm{d} x = \int_0^1 g(x) \, \mathrm{d}x\]
从而我们可以这样计算 \(\theta\) :
\[\theta = E[g(U)]\]
如果 \(U_1, \cdots, U_k\) 是 \((0,1)\) 上的相互独立随机变量,那么随机变量 \(g(U_1), \cdots, g(U_k)\) 也相互独立,由“强大数定理”可知:
\[\sum_{i=1}^k \frac{g(U_i)}{k} \to E[g(U)] \quad \text{when} \; k \to \infty\]
这样,我们生成大量 \((0,1)\) 上随机数 \(u_i \; (1 \le i \le k)\) 后,有:
\[\theta = \int_0^1 g(x) \, \mathrm{d}x \approx \sum_{i=1}^k \frac{g(u_i)}{k}\]
如果定积分上下界为其它情况(如 \(\int_a^b g(x) \, \mathrm{d}x\) 或 \(\int_0^{\infty} g(x) \, \mathrm{d}x\) )时,我们可以想办法把它转换为前面介绍的下界为 0,上界为 1 的情况。
参考:Simulation, Sheldon M Ross, 5th, 3.2 Using Random Numbers to Evaluate Integrals
3.1. 计算圆周率
我们知道, \(\pi = \int_0^1 \sqrt{1 - x^2} \, \mathrm{d}x\) ,按照前面介绍的用随机数计算积分的知识,我们可以用随机数来计算圆周率 \(\pi\) 。具体过程略。
4. 生成离散型随机变量
4.1. 逆变换抽样
如何产生随机数,满足下面的分布律呢?
\[P\{X=x_i\} = p_i, \quad i = 0,1,\cdots, \quad \sum_{i}p_i =1\]
逆变换抽样(Inverse transform sampling)的方法如下:
首先产生 \((0,1)\) 上的随机数 \(U\) ,然后按下面方法产生 \(X\) :
\[X = \begin{cases} x_0 \quad \text{if} \; U < p_0 \\
x_1 \quad \text{if} \; p_0 \le U < p_0 + p_1\\
\vdots \\
x_i \quad \text{if} \; \sum_{k=0}^{i-1}p_k \le U < \sum_{k=0}^{i}p_k \\
\vdots \\
\end{cases}\]
证明如下: \(U\) 是 \((0,1)\) 上满均匀分布,对于 \(0 < a < b <1, \, p\{a \le U < b\} = b-a\) ,所以有:
\[p\{ X = x_i \} = p \left\{ \sum_{k=0}^{i-1}p_k \le U < \sum_{k=0}^{i} p_k \right\} = p_i\]
从而 \(X\) 满足所要求的分布律。
4.1.1. 实例:利用逆变换抽样生成离散型随机变量
实例:生成具有如下概率分布的随机变量 \(X\) :
\[p_1 = 0.20, \quad p_2 = 0.15, \quad p_3 = 0.25, \quad p_4 = 0.40 \quad \text{where} \; p_i = P\{ X=i \} \]
用逆变换抽样的算法如下:
首先产生一个 \((0,1)\) 上的随机数 \(U\) ,然后:
如果 \(U < 0.10\) 则令 \(X=1\) 并停止;
如果 \(U < 0.35\) 则令 \(X=2\) 并停止;
如果 \(U < 0.60\) 则令 \(X=3\) 并停止;
其他情况,令 \(X=4\) 。
4.2. 拒绝(Rejection)抽样
略。和后文“生成连续型随机变量”中“拒绝抽样”的描述基本类似。
5. 生成连续型随机变量
5.1. 逆变换抽样
设 \(U\) 是 \((0,1)\) 上满足均匀分布的随机变量。如果某个分布函数 \(F\) 是连续的,且随机变量 \(X\) 由下式定义:
\[X = F^{-1}(U)\]
则随机变量 \(X\) 满足分布函数 \(F\) 。
注:按反函数定义, \(x = F^{-1}(u)\) 表示满足 \(u = F(x)\) 。
证明如下:记 \(F_X\) 为 \(X\) 的分布函数,则由分布函数的定义有:
\[\begin{aligned} F_X(x) & = P \{ X \le x \} \\
& = P \{ F^{-1}(U) \le x \}
\end{aligned}\]
由于 \(F\) 是一个分布函数,从而它是单调递增函数,所以 \(a \le b\) 等价于 \(F(a) \le F(b)\) ,利用这个结论有:
\[\begin{aligned} F_X(x) & = P \{ F^{-1}(U) \le x \} \\
& = P \{ F(F^{-1}(U)) \le F(x) \} \\
& = P \{ U \le F(x) \} \\
& = F(x) \qquad \qquad \text{since U is uniform (0,1)} \end{aligned}\]
证明毕。
5.1.1. 实例:利用逆变换抽样生成连续型随机变量
实例:生成具有如下概率密度函数的随机变量 \(X\) :
\[f(x) = \begin{cases} 8x & \text{if} \, 0 \le x < 0.25 \\
\frac{8}{3} - \frac{8}{3}x & \text{if} \, 0.25 \le x < 1 \\
0 & \text{otherwise}
\end{cases}\]
用逆变换抽样(Inverse transform sampling)的方法如下:
首先,由概率密度函数求得对应的分布函数:
\[\begin{aligned} F(x) & = \int_{-\infty}^x f(t) \, \mathrm{d} x \\
& = \begin{cases} 0 & \text{if} \, x < 0 \\
4x^2 & \text{if} \, 0 \le x < 0.25 \\
\frac{8}{3} x - \frac{4}{3} x^2 - \frac{1}{3} & \text{if} \, 0.25 \le x \le 1 \\
1 & \text{if} \, x > 1 \end{cases}
\end{aligned}\]
然后,生成 \((0,1)\) 上的随机数 \(U\) ,利用上面分布函数的反函数可得 \(X\) 的一个样本值:
\[X = F^{-1}(U) = \begin{cases} \frac{\sqrt{U}}{2} & \text{if} \, 0 \le U < 0.25 \\
1 - \frac{\sqrt{3(1-U)}}{2} & \text{if} \, 0.25 \le U \le 1 \\
\end{cases}\]
摘自:
Sampling Methods, by Patrick Lam: http://www.people.fas.harvard.edu/~plam/teaching/methods/sampling/sampling.pdf
5.2. 拒绝(Rejection)抽样
使用逆变换抽样时需要知道随机变量的分布函数,还需要求它的反函数。有时分布函数或其反函数很难求得。
这里介绍另外一种抽样方法:拒绝抽样(Rejection sampling),又称为接受-拒绝抽样、舍选抽样法。
拒绝抽样的基本思想是: 我们想要对分布 \(p(x)\) 进行抽样,由于某些原因(如不能求出分布函数反函数)无法使用逆变换抽样。这时我们先产生另一个容易抽样的分布 \(q(x)\) 的样本,再用某种办法去掉一些样本,从而使得剩下的样本就是所求分布 \(p(x)\) 的样本。
例如,要产生单位圆内的随机点。用拒绝抽样思想可以这样做:首先,先产生一个点 \((x,y)\) ,其中 \(x\) 和 \(y\) 是 \((-1,1)\) 内的随机数;然后,验证 \(x^2 + y^2 \le 1\) 是否成立,如果成立就接受,如果不成立就拒绝;重复这个过程直到被接受的样本点数量达到要求。如图 1 所示。
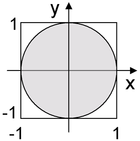
Figure 1: 拒绝抽样基本原理介绍(要采样单位圆,先采样外围正方形)
拒绝抽样算法的正式描述如下:
要对概率分布为 \(p(x)\) 进行模拟。我们先找到一个容易模拟的概率分布设为 \(q(x)\) ,寻找一个常数 \(c\) ,满足下式:
\[p(x) \le c q(x) \quad \text{for all} \; x\]
拒绝抽样的步骤如下:
步骤 1:生成随机变量 \(Y\) 满足概率分布 \(q\)
步骤 2:生成 \((0,1)\) 内的随机数 \(U\)
步骤 3:测试下式:
\[U \le \frac{p(Y)}{c q(Y)}\]
如果上式成立,则设 \(X=Y\) (这就是“接受”),如果上式不成立则跳转到步骤 1(这就是“拒绝”)。如图 2 所示。
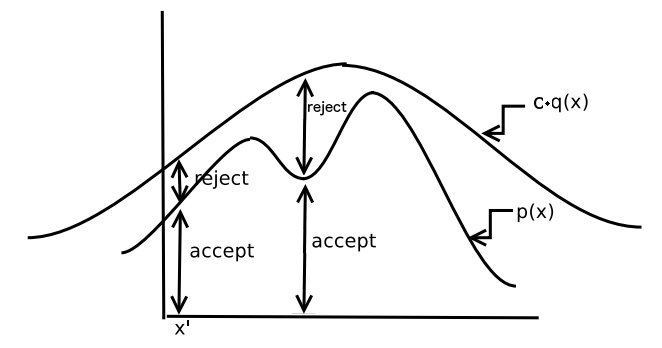
Figure 2: 拒绝抽样,图片改编自 Monte Carlo Sampling, by Michael I. Jordan
显然,要产生一个样本值可能要迭代多次。
定理(证明略):
(1) 生成的随机变量 \(X\) 会满足概率分布 \(p\)
(2) 生成一个样本值,平均需要迭代的次数为 \(c\) (所以, 我们最好选择最小的 \(c\) 来提高抽样效率 )
这里省略严格的证明。直观地看, \(cq(x)\) 会“盖住” \(p(x)\) , \(cq(x)\) 和 \(p(x)\) 更加“接近”的位置相对被接受的概率高。
5.2.1. 拒绝抽样实例 1
随机变量 \(X\) 的概率密度如下:
\[f(x) = 20x(1-x)^3, \; 0 < x < 1\]
请用拒绝抽样方法来生成它的样本。
我们考虑一个更简单的随机变量: \((0,1)\) 上的随机数,即满足:
\[g(x) = 1, \; 0 < x < 1\]
然后,寻找一个最小的常数 \(c\) 满足 \(f(x)/g(x) \le c\) ,这可以通过微积分对函数求极值的知识来求得,即求下式的最大值:
\[\frac{f(x)}{g(x)} = 20x(1-x)^3\]
用求导法,得上式在 \(x=\frac{1}{4}\) 时取得最大值,这时有:
\[\frac{f(x)}{g(x)} \le 20 \left( \frac{1}{4} \right) \left( \frac{3}{4} \right)^3 = \frac{135}{64} \equiv c\]
从而:
\[\frac{f(x)}{cg(x)} = \frac{256}{27} x (1-x)^3\]
对于这个问题,拒绝抽样的步骤如下:
第 1 步,生成两个 \((0,1)\) 上的随机数 \(U_1, U_2\)
第 2 步,如果 \(U_2 \le \frac{256}{27} U_1 (1-U_1)^3\) 成立,则 \(X=U_1\) ;如果不成立,则回到第 1 步接着执行。
说明:这个问题中,产生一个随机变量样本值的上面算法的平均迭代次数为 \(c=\frac{135}{64} \approx 2.11\)
5.2.2. 拒绝抽样实例 2:产生 Gamma 分布样本
实例:请生成下面 Gamma 分布的样本:
\[f(x) = K x^{1/2} e^{-x}, x > 0\]
上式中 \(K= 1/\Gamma(\frac{3}{2}) = 2 / \sqrt{\pi}\)
Gamma 分布的分布函数不便于直接求反函数,故不方便直接用逆变换抽样。可以用拒绝抽样法,思路是先产生 Exponential 分布(可以直接用逆变换抽样可对指数分布进行抽样)的样本。
详细过程略。可参考 Simulation, Sheldon M Ross, 5th, 5.2 The Rejection Method
5.2.3. 拒绝抽样缺点及 Adaptive rejection sampling
如果使用的 \(q(x)\) 和 \(c\) 不合适(概率密度和 \(p(x)\) 不相近),则被拒绝的点会很多,从而产生样本值的效率会很低。
Adaptive rejection sampling 可以克服上述的拒绝抽样缺点,具体介绍略。
5.3. Sampling Importance Resampling (SIR)
问题:模拟具有概率密度函数为 \(f(x)\) 的随机变量 \(X\) 。
先回顾一下使用拒绝抽样的办法,基本思路为:先产生另外一个服从分布 \(g(y)\) 的随机变量 \(Y\) 的样本,再找一个常数 \(C > 0\) 满足 \(\frac{f(y)}{C g(y)} \le 1\) ,再以概率 \(\frac{f(y)}{C g(y)}\) 接受 \(Y\) ,若未接受就重复前面过程。常数 \(C\) 是生成一个样本值时程序需要迭代的平均次数。
但是,很多时候拒绝抽样中的常数 \(C\) 很难计算出来,这时不得不使用一个很大的 \(C\) 来满足 \(\frac{f(y)}{C g(y)} \le 1\) ,这会导致抽样效率非常低。这时需要其它的抽样方法。
SIR 方法和拒绝抽样类似,但它并不需要计算拒绝抽样中的常数 \(C\) 。 请看下节。
5.3.1. SIR 算法步骤
假设问题是:模拟具有概率密度函数为 \(f(x)\) 的随机变量 \(X\) 。
SIR 算法步骤如下:
(1) 寻找另外一个容易抽样的概率函数为 \(g(x)\) 的随机变量 \(Y\) ,模拟随机变量 \(Y\) 产生 \(N\) 个样本值,并记为:
\[\{y_1, y_2, \cdots, y_N \}\]
(2) 定义权重 \(w_i, i=1,2,\cdots,N\) 为:
\[w_i = \frac{f(y_i)}{g(y_i)}\]
(3) 模拟随机变量 \(X\) ,使其满足:
\[P\{ X = y_j \} = \frac{w_j}{\sum_{i=1}^{N}w_i}, \quad j = 1,2,\cdots,N\]
那么,当 \(N\) 充分大时,按上面方法产生的随机变量 \(X\) 具有概率函数 \(f\) (证明略)。
说明 1:上面过程中,步骤(3)称为 “重抽样(Resample)” ,因为它是在步骤(1)产生的样本集合中再次进行抽样。
说明 2:在步骤(2)中计算 \(w_i = \frac{f(y_i)}{g(y_i)}\) 时, \(f(y_i)\) 和 \(g(y_i)\) 中的常数因子可以省略。假设 \(f(y_i) = C_1 f_0(y_i), g(y_i) = C_2 g_0(y_i)\) ,其中 \(C_1,C_2\) 为常数,则 \(w_i\) 可以这样计算 \(w_i = \frac{f_0(y_i)}{g_0(y_i)}\) ,这是因为常数因子会同时出现在步骤(3)的分子和分母中,不会影响步骤(3)的计算结果。所以,我们也可以把 \(w_i\) 记为:
\[\begin{aligned} w_i &= \eta \frac{f(y_i)}{g(y_i)} \\
& \propto \frac{f(y_i)}{g(y_i)} \end{aligned}\]
说明 3:上面描述中,一般 \(f(x)\) 称为 target 分布,\(g(x)\) 一般称为 proposal 分布。
5.3.1.1. SIR 算法图示
假设想要模拟的随机变量概率函数如图 3 所示。
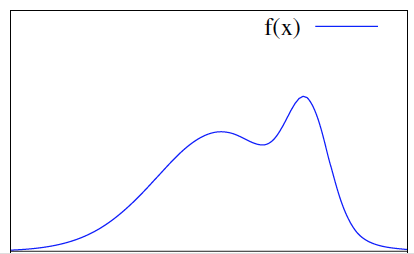
Figure 3: target 分布
SIR 算法的第一步是先从另外一个概率函数中抽样,假设样本为 \(\{y_1, y_2, \cdots, y_N \}\) 。如图 4 所示。
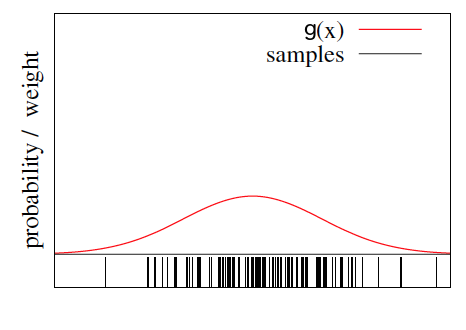
Figure 4: 寻找一个 proposal 分布,并抽样(下方的竖线为样本)
SIR 算法的第二步是计算第一步中每个样本的权重 \(w_i = \frac{f(y_i)}{g(y_i)}\)
SIR 算法的第三步是对第一步中产生的样本进行“重抽样”,其规则是使 \(y_i\) 的概率满足 \(\frac{w_j}{\sum_{i=1}^{N}w_i}\) 。如图 5 所示。
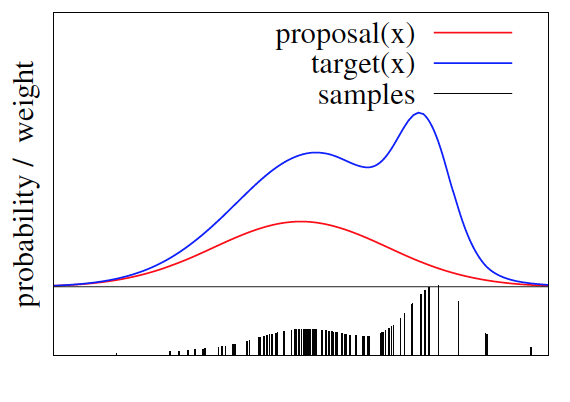
Figure 5: 对 proposal 分布中的样本进行“重抽样”(下方竖线的长度表示这个样本被抽中的概率)
说明: SIR 算法中第一步产生了 \(N\) 个样本,如果第三步中抽取样本的个数也是 \(N\) ,则一般是“放回抽样”,这样有一些概率小的样本很可能不会被抽中,而概率大的样本会被抽中好多次。
注:这几个图片摘自:“Robotic Mapping and Exploration, 2009”
5.3.2. SIR 算法实例
下面是用 R 语言实现 SIR 算法的一个例子。
假设需要模拟的随机变量概率密度为: \(f(x) = \frac{1}{c} h(x)\) ,其中 \(c\) 为未知的常数, \(h(x) = e^{0.4*(x-0.4)^2 - 0.08*x^4}\) 。尽管 \(f(x)\) 中有未知常数 \(c\) ,我们也可以用 SIR 算法对 \(f(x)\) 进行抽样。
# SIR example
k <- function(x, a=.4, b=.08){exp(a*(x-a)^2 - b*x^4)} # k(x)本身不是概率密度函数,它是概率密度函数f(x)乘以某个未知常数
x <- seq(-4, 4, 0.1)
g <- function(x){rep.int(0.125,length(x))} # g(x)为proposal分布,这里是(-4,4)上的均匀分布
N <- 1000
x.g <- runif( N, -4, 4 ) # 第1步,对g(x)进行抽样
ww <- k(x.g) / g(x.g) # 第2步,计算每个样本的权重
qq <- ww / sum(ww)
x.acc <- sample(x.g, prob=qq, replace=T) # # 第3步,resample
pdf(file="myplot_SIR.pdf")
par(mfrow=c(2,2), mar=c(2,2,1,1))
plot(x,k(x),type="l")
plot(x,g(x),type="l")
barplot(table(round(x.acc,1))/length(x.acc))
上面程序生成的 myplot_SIR.pdf 如图 6 所示。
Figure 6: SIR 抽样(左上角是目标分布乘以某个常数,右上角是 proposal 分布,左下角是目标分布的样本)
注:这个例子比较简单,也可以用拒绝抽样的方法。
参考:http://people.math.aau.dk/~kkb/Undervisning/Bayes14/sorenh/docs/sampling-notes.pdf
5.4. 实例:模拟标准正态分布
标准正态分布的分布函数的反函数不能显式地求出,故不能用逆变换法产生标准正态分布的随机变量。
下面介绍利用中心极限定理来模拟标准正态分布。
设 \(U_i \sim U(0,1), \quad i = 1,2,\cdots,n\) 且它们相互独立。由于 \(E(U_i) = 1/2, D(U_i) = 1/12\) ,则中心极限定理知,当 \(n\) 较大时近似有:
\[Z = \frac{\sum_{i=1}^{n} - \frac{n}{2}}{\sqrt{n} \sqrt{\frac{1}{12}}} \sim N(0,1)\]
取 \(n = 12\) 得: \(Z=\sum_{i=1}^{12} U_i - 6 \sim N(0,1)\)
也就是说,只需产生 12 个 \((0,1)\) 之间的随机数,将它们加起来,再减去 6,即可近似得到标准正态分布的样本值了。
如何得到一般正态分布的样本值呢?设 \(X \sim N(\mu, \sigma^2), Z \sim N(0,1)\) ,利用关系式 \(X= \mu + \sigma Z\) 就能得到一般正态分布随机变量 \(X\) 的样本值。
参考:《概率论与数理统计(第四版),浙江大学》参读材料 随机变量样本值的产生
除上面方法外,还可以使用极坐标变换(又称 Box-Muller变换 )或 Ziggurat algorithm 算法(属于拒绝抽样)对正态分布进行模拟。
6. 统计模拟基本步骤和控制模拟精度
要用统计模拟方法(即蒙特卡罗)方法求解实际问题时,一般遵循下面 基本步骤:
(1) 根据实际问题构造一个概率统计模型,把“原始问题的解”转化为模型中随机变量的某个特征(往往是随机变量的均值)。
(2) 根据所建模型中各个随机变量的分布,在计算机上进行模拟,抽取足够多(到底多少次应该由模拟精度决定)的随机数,对相关特征进行统计。
(3) 分析模拟结果,给出所求解的估计。
(4) 分析模拟精度。如有必要,改进模拟过程来提高精度。
很多时候,我们都会 把实际问题 \(\theta\) 转换为某个随机变量的均值。 这样对随机变量产生 \(k\) 个样本值后,可以用 \(\sum_{i=1}^{k}X_i/k\) 来估计总体的均值(即原问题的解 \(\theta\) )。
如,前面介绍的求解积分 \(\theta = \int_0^1 g(x) \, \mathrm{d}x\) ,可转换为求解随机变量 \(U \sim U(0,1)\) 的函数(也是随机变量) \(g(U)\) 的均值,即 \(\theta = E[g(U)]\) 。
6.1. 估计总体均值,控制模拟精度
把实际问题 \(\theta\) 转换为求随机变量的均值后。首先生成随机变量样本,然后可以用样本均值 \(\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_i\) 作为总体均值的估计(可以证明样本均值是总体均值的无偏估计)。
假设 \(X_1, \cdots, X_n\) 是相互独立的具有相同分布的随机变量,它们的均值和方差(都是未知的)分别为 \(\theta, \sigma^2\) ,即有 \(\theta = E(X) = E(X_i), \sigma^2 = Var(X) = Var(X_i)\) 。我们用“样本均值”来估计“总体均值”有多准确呢?考虑估计的均方误差(Mean squared error):
\[\begin{aligned} MSE_{\overline{X}} & = E \left[(\overline{X} - \theta)^2 \right] \\
& = E \left[(\overline{X} - E(\overline{X}))^2 \right] \\
& = Var \left (\overline{X} \right) \\
& = Var \left(\frac{1}{n}\sum_{i=1}^{n} X_i \right) \\
& = \frac{1}{n^2} Var \left(\sum_{i=1}^{n} X_i \right) \qquad \text{(by independence)}\\
& = \frac{1}{n^2} \sum_{i=1}^{n}Var(X_i) \\
& = \frac{\sigma^2}{n}
\end{aligned}\]
上式越小时,用“样本均值”来估计“总体均值”越准确。
从另一方面来看,如果把样本均值 \(\overline{X}\) 看作随机变量,那么由上面的计算知 随机变量 \(\overline{X}\) 的方差为 \(\frac{\sigma^2}{n}\) 。这个方差 \(\frac{\sigma^2}{n}\) (或标准差 \(\frac{\sigma}{\sqrt{n}}\) )越小时,意味着样本均值 \(\overline{X}\) 越稳定(变化很小),显然这时用“样本均值”来估计“总体均值”越准确。
不过要注意 \(\sigma^2\) 是总体方差,它是未知的。可以用样本方差 \(S^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2 = \frac{1}{n-1} (\sum_{i=1}^{n} X_i^2 - n \overline{X})\) 来估计总体方差 \(\sigma^2\) 。
所以, 当估计的标准误差(即估计均方误差的开方) \(\frac{S}{\sqrt{n}}\) (其中 \(S\) 为样本标准差)比较小时,用“样本均值”来估计“总体均值”是比较准确的。
6.1.1. 何时可以停止产生新数据
用“样本均值”来估计“总体均值”时,样本值的数量当然是越多越好。但产生更多的样本值意味更程序运行更长的时间,何时可以停止产生新数据呢?
结合前面的分析,我们可以采用下面的方法来确定何时可以停止产生新数据。
第 1 步,选择一个合适的值 \(d\) 作为估计量的标准误差。
第 2 步,产生至少 100 个数据。
第 3 步,继续产生新数据,直到 \(k\) 个数据时 \(\frac{S_k}{\sqrt{k}} < d\) 成立就可以停止,其中 \(S_k\) 是这 \(k\) 个数据确定的样本标准差(即 \(S_k=\sqrt{S_k^2} = \sqrt{\frac{1}{k-1} \sum_{i=1}^{k} (X_i - \overline{X})^2}\) )。
第 4 步,总体均值 \(\theta\) 的估计量就是样本均值 \(\overline{X} = \sum_{i=1}^{k}X_i/k\) 。
说明 1:在第 3 步中,每次产生一个新数据,都要计算 \(S_k\) 并验算 \(\frac{S_k}{\sqrt{k}} < d\) 是否成立。在编程实现时为了更快速度,可以采用迭代的方式来计算 \(S_k\) ,这样可以利用 \(S_j\) 快速计算 \(S_{j+1}\) ,具体迭代公式(证明略)如下:
\[\begin{gathered} \overline{X}_0 = 0, S_1^2 = 0 \\
\overline{X}_{j+1} = \overline{X}_{j} + \frac{X_{j+1} - \overline{X}_{j} }{j+1} \\
S_{j+1}^2 = \left( 1 - \frac{1}{j} \right) S_j^2 + (j+1) \left(\overline{X}_{j+1} - \overline{X}_{j} \right)^2 \\
\end{gathered}\]
说明 2:如果随机变量的方差是期望的函数(如Bernoulli distribution),这时可以调整上面算法。因为在推导上面算法时用样本方差 \(S^2\) 来估计总体方差 \(\sigma^2\) ,而对于 Bernoulli distribution 来说没有必要用样本方差估计总体方差。因为:
\[X_i = \begin{cases} 1 \quad \text{with probability p} \\
0 \quad \text{with probability 1-p} \\
\end{cases}\]
Bernoulli distribution 的均值为 \(p\) ,方差为 \(p(1-p)\) 。
我们直接用 \(\overline{X}_{n}(1 - \overline{X}_{n})\) 来估计总体方差 \(\sigma^2\) 即可。
所以,对于估计 Bernoulli distribution 的期望,其算法为:
第 1 步,选择一个合适的值 \(d\) 作为估计量的标准误差。
第 2 步,产生至少 100 个数据。
第 3 步,继续产生新数据,直到 \(k\) 个数据时 \(\sqrt{\frac{\overline{X}_k (1- \overline{X}_k)}{k}} < d\) 成立就可以停止。
第 4 步,Bernoulli distribution 的期望为样本均值 \(\overline{X}_k = \sum_{i=1}^{k}X_i/k\) 。
6.2. 总体均值的区间估计
前面介绍中,用样本均值 \(\overline{X}\) 作为总体均值 \(\theta\) 的估计,这是点估计。有时我们想根据样本均值 \(\overline{X}\) 构造一个合适区间来覆盖总体均值 \(\theta\) ,这是区间估计。这里不详细介绍区间估计。
7. 方差减少(精度改进)技术
在前面介绍中,我们知道建模时,一般先把实际问题 \(\theta\) 转换为某个随机变量的均值。这样对随机变量产生 \(k\) 个样本值后,可以用样本均值 \(\overline{X} = \sum_{i=1}^{k}X_i/k\) 来估计总体的均值 \(\theta\) 。估计的标准误差 \(\frac{S}{\sqrt{n}}\) 越小,估计越准确。
显然当样本个数 \(n\) 越大时,估计会越准确,但样本个数 \(n\) 越大意味着计算会越多。 是否可以改进模拟方法使得对于同样的样本数 \(n\) ,估计的标准误差 \(\frac{S}{\sqrt{n}}\) 会更小呢? 答案是肯定的,这就是本节讨论的内容。
7.1. 对偶变量法(Antithetic Variables)
假设我们对 \(\theta = E(X)\) 的估计感兴趣,模拟产生 \(X\) 的样本后,用样本均值对它进行估计。
把样本均值看作随机变量,那么它的方差(假设仅产生了两个独立同分布的随机变量 \(X_1,X_2\) )为:
\[Var(\overline{X}) = Var \left( \frac{X_1 + X_2}{2} \right) = \frac{1}{4} \left[Var(X_1) + Var(X_2) + 2 Cov(X_1,X_2) \right]\]
如果 \(X_1,X_2\) 是负相关的,那么它们的协方差 \(Cov(X_1,X_2)\) 会为负,从而 \(Var \left( \frac{X_1 + X_2}{2} \right)\) 会减小。也就是估计的精度会提高。
上面就是“对偶变量法”的基本原理。
7.1.1. 对偶变量法实例
估计 \(\theta = \int_0^1 e^x \, \mathrm{d}x\) 。
容易知道 \(E[e^U] = \int_0^1 e^x \, \mathrm{d}x\) (其中 \(U \sim U(0,1)\) ),即求随机变量 \(e^U\) 的均值即可估计 \(\theta\) 。
说明:容易精确计算出结果为 \(\theta = e -1\) ,在这里我们仅仅是通过该例子来说明对偶变量法可以提高模拟精度。
(1)如果产生相互独立的两个随机数 \(U_1,U_2\) ,则样本均值的方差(也就是估计的均方误差)为:
\[Var\left( \frac{e^{U_1} + e^{U_2}}{2} \right) = \frac{Var(e^U)}{2}\]
其中, \(Var(e^U) = E[e^{2U}] - (E[e^U])^2 = \int_0^1 e^{2x} \, \mathrm{d}x - (e-1)^2 = 0.2420\) ,所以:
\[Var\left( \frac{e^{U_1} + e^{U_2}}{2} \right) = \frac{0.2420}{2} = 0.1210\]
(2)如果使用对偶变量 \(U, 1-U\) ,容易验证 \(Cov(e^U, e^{1-U}) = E[e^Ue^{1-U}] - E[e^U]E[e^{1-U}] = e - (e-1)^2 = -0.2342\) ,则样本均值的方差(也就是估计的均方误差)为:
\[Var\left( \frac{e^{U} + e^{1 - U}}{2} \right) = \frac{Var(e^U)}{2} + \frac{Cov(e^U, e^{1-U})}{2} = 0.0039\]
由此可知,使用对偶变量时,样本均值的方差减少了: \((0.1210-0.0039)/0.1210 = 96.7 \%\)
7.2. 重要性抽样法(Importance Sampling)
7.2.1. 回顾积分计算的简单模拟方法
先回顾一下前面介绍的用模拟方法计算积分的知识。比如,要计算下面积分:
\[\theta = \int_0^1 g(x) \, \mathrm{d}x\]
解决办法:假设 \(U\) 是 \((0,1)\) 上的均匀分布,即它的概率分布为:
\[f(x) = \begin{cases} 1, \, 0 < x < 1 \\
0, \, \text{otherwise} \end{cases}\]
则:
\[E[g(U)] = \int_{- \infty}^{\infty} f(x) g(x) \, \mathrm{d} x = \int_0^1 g(x) \, \mathrm{d}x\]
从而我们把积分的计算转换成为求随机变量函数(仍是随机变量) \(g(U)\) 的均值问题。随机变量的均值(总体均值)问题可以通过模拟生成一些样本,利用样本均值来对总体均值进行估计,即用 \(\sum_{i=1}^k \frac{g(U_i)}{k}\) 估计 \(E[g(U)]\) 。
7.2.2. 重要性抽样法基本思想
上节介绍的方法有个缺点: 如果不同随机数 \(U\) 对应的 \(g(U)\) 相差很大,则“样本均值”的方差会比较大(估计值不稳定),这时用“样本均值”做估计值是不合适的。当然我们可以通过增加样本数来使方差减小(估计值变稳定),重要性抽样法提供了另外的方法来使估计值变稳定(方差减小)。
重要性抽样法的思想是:模拟具有概率密度函数 \(f(x)\) 的随机变量 \(X\) ,设 \(Y=\frac{g(X)}{f(X)}\) ,这时由随机变量函数期望的性质可得:
\[E(Y) = \int \frac{g(x)}{f(x)} f(x) \, \mathrm{d}x = \int g(x) \, \mathrm{d}x\]
所以,我们通过模拟生成 \(Y\) 的样本,利用 \(Y\) 的样本均值即可估计原始问题 \(\int g(x) \, \mathrm{d}x\) 。其中, 函数 \(f(x)\) 称为 重要性概率密度函数(importance density function),或简称重要性函数。选择重要性概率密度函数 \(f(x)\) 的一个要求是当 \(g(x) > 0\) 时 \(f(x) > 0\) (此时 \(f(x)\) 不能等于 0,否则上式不成立);另一个要求是 \(Y=\frac{g(X)}{f(X)}\) 的方差要小(这是重要性抽样法具有价值的关键所在),从而在模拟时可以更快地得到一个稳定的估计值。
说明:上节介绍的简单模拟方法其实就是重要性抽样法中重要性概率密度函数为均匀分布时特例。
7.2.2.1. 重要性抽样法实例
计算积分 \(\int_0^1 \frac{e^{-x}}{1+x^2} \, \mathrm{d}x\) 。
分别选择下面 5 个概率密度函数作为重要性函数:
\[\begin{aligned} f_0(x) &= 1, \quad 0 < x < 1 \\
f_1(x) &= e^{-x}, \quad 0 < x < \infty \\
f_2(x) &= (1+x^2)^{-1}/\pi, \quad - \infty < x < \infty \\
f_3(x) &= e^{-x}/(1-e^{-1}), \quad 0 < x < 1 \\
f_4(x) &= 4(1+x^2)^{-1}/\pi, \quad 0 < x < 1 \\
\end{aligned}\]
上面每一个概率密度函数当 \(\frac{e^{-x}}{1+x^2} > 0\) 时都会大于 0,且容易用逆变换抽样对它们进行模拟。
详细过程略。都进行 10000 次模拟,选择不同概率密度函数作为重要性函数的模拟结果如表 1 所示。
| j | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| \(\overline{Y}\) | 0.5185 | 0.5110 | 0.5128 | 0.5224 | 0.5211 |
| \(\sigma\) | 0.2440 | 0.4217 | 0.9312 | 0.0973 | 0.1409 |
从测试的结果看, \(f_3(x)\) 对应的估计标准差最小为 0.0973,可以认为把 0.5224 作为待求积分的估计值最可信。
参考:Probability and Statistics, by Morris H. DeGroot, 4th Edition, Example 12.4.1
8. Markov Chain Monte Carlo (MCMC)
前面介绍了很多抽样方法,但在处理复杂的、高维的分布时前面的方法难以实施。Markov Chain Monte Carlo(MCMC)是解决这类方法的有效方法。如贝叶斯统计推断中后验分布可能非常复杂,在计算上非常困难,这时 MCMC 方法就有用武之地了。
下面先介绍马尔可夫链的相关知识。
8.1. 马尔可夫链基本知识
己知现在,将来只与现在相关,而与过去无关,这个性质称为马尔可夫性,或称无后效性。具有马尔可夫性的随机过程称为马尔可夫过程。如果马尔可夫过程的时间和状态空间都是离散的,则称它为马尔可夫链。马尔可夫链满足:
\[P\{ X_{n+1} = j \mid {\color{red}{X_n = i}}, X_{n-1} = i_{n-1}, \cdots, X_0 = i_0 \} = P\{X_{n+1} = j \mid {\color{red}{X_n = i}} \}\]
上式体现了无后效性(即下一个状态只和当前状态相关,而和以前的状态无关)。
其中, \(X\) 的所有可能取值称为马尔可夫链的状态空间,记为 \(I\) ,即 \(i_0, i_1, \cdots, i_{n-1}, i, j \in I\) 。
8.1.1. 马尔可夫链和极限分布
下面例子摘自:http://www.aw-bc.com/greenwell/markov.pdf
在社会学中,人按其收入可分为下层(lower-class),中层(middle-class)和上层(upper-class)这三个阶层。社会学发现“当前这一代的所在阶层”严重影响着“下一代的阶层”。下表是父代和子代阶层转移的概率矩阵如图 7 所示。
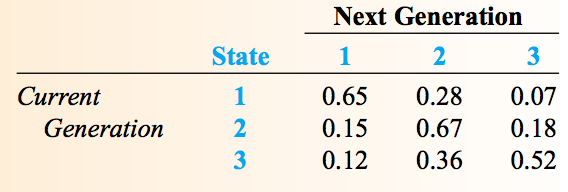
Figure 7: 阶层转移概率(用数字 1,2,3 分别表示下中上三个阶层)
也可以记为矩阵的形式,如:
\[P = \begin{bmatrix}
0.65 & 0.28 & 0.07 \\
0.15 & 0.67 & 0.18 \\
0.12 & 0.36 & 0.52 \\
\end{bmatrix}\]
一般,我们用 \(p_{ij}\) 表示从状态 \(i\) 转移到状态 \(j\) 的概率。
这个转移概率矩阵很有用。比如,我们可以利用转移概率矩阵计算“已知父亲为上层,孙子为中层的概率”。计算过程如图 8 所示。
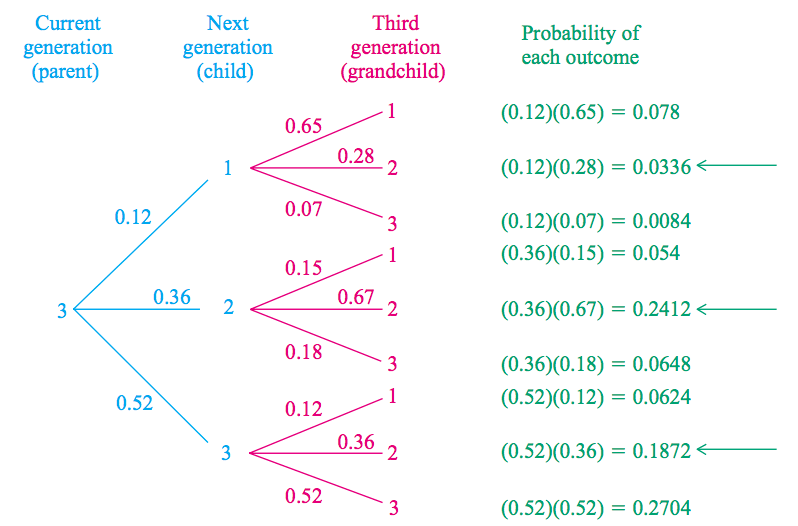
Figure 8: 已知父亲为上层,孙子为中层的概率
已知父亲为上层,孙子为中层的概率为: \(p_{31} \cdot p_{12} + p_{32} \cdot p_{22} + p_{33} \cdot p_{32} = 0.0336 + 0.2412 + 0.1872 = 0.4620\) 。
一般地,假设上一代“下中上”三个阶层的比例为概率分布向量 \(\boldsymbol{\pi_{n-1}} = [\pi_{n-1}(1),\pi_{n-1}(2),\pi_{n-1}(3)]\) ,则这一代“下中上”三个阶层的比例将为: \(\boldsymbol{\pi_{n}} = \boldsymbol{\pi_{n-1}} P\) 。
下面我们将会观察到一个有趣的现象——不管初始时“下中上”三个阶层的所占比例是多少,经过多次迭代后,处于“下中上”三个阶层的比例会稳定不变。
例如,“下中上”三个阶层初始比例为概率分布向量 \(\boldsymbol{\pi_0} = [0.210,0.680,0,110]\) ,多次迭代后的比例为(由于有舍入误差,有时比例和会不为 1)图 9 所示。
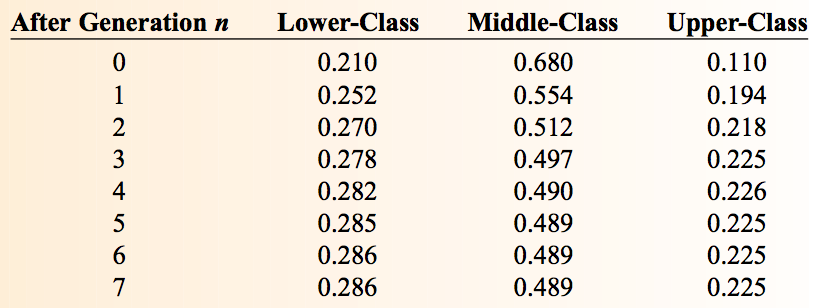
Figure 9: 初始比例为[0.210,0.680,0,110],第 6 代开始后稳定不变
又如,“下中上”三个阶层初始比例为概率分布向量 \(\boldsymbol{\pi_0} = [0.75,0.15,0,1]\) ,多次迭代后的比例为图 10 所示。
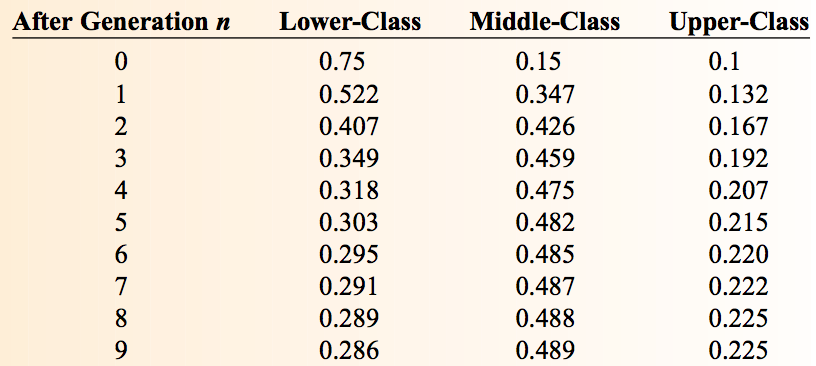
Figure 10: 初始比例为[0.75,0.15,0,1],第 9 代开始后稳定不变
最终的概率分布不仅收敛,而且和初始概率分布无关。初始概率分布不同时,都收敛到同一个概率分布 \(\boldsymbol{\pi} =[0.286,0.489,0.225]\) 。 最后收敛到的这个分布称为马尔可夫链的极限分布。
但并不是所有的马尔可夫链都存在极限分布。比如转移概率矩阵为:
\[P = \begin{bmatrix}
0 & 1/2 & 0 & 1/2 \\
1/2 & 0 & 1/2 & 0 \\
0 & 1/2 & 0 & 1/2 \\
1/2 & 0 & 1/2 & 0 \\
\end{bmatrix}\]
的马尔可夫链不会收敛,不存在极限分布。
8.1.2. 遍历性和极限分布存在定理
满足什么条件时,马尔可夫链存在极限分布呢?
定理:
设马尔可夫链的状态空间为 \(I=\{a_1, a_2, \cdots, a_N\}\) , \(P\) 为马尔可夫链的转移概率矩阵(矩阵中元素用 \(p_{ij}\) 表示)。记 \(p_{ij}(n)\) 为从状态 \(i\) 经过 \(n\) 次转移到达状态 \(j\) 的概率。如果存在正整数 \(m\) ,使对任意 \(a_i,a_j \in I\) ,都有:
\[p_{ij}(m) > 0, \quad i,j=1,2,\cdots,N\]
则称此马尔可夫链具有 遍历性 ,且极限分布(又称平稳分布)存在。且极限分布 \(\boldsymbol{\pi} = [\pi_1,\pi_2,\cdots,\pi_N]\) 可以从下面方程组中求得:
\[\begin{cases}
& \pi_j = \sum_{i=1}^{N} \pi_i p_{ij}, \quad j=1,2,\cdots,N \\
& \pi_j > 0, \quad j=1,2,\cdots,N \\
& \sum_{j=1}^{N}\pi_j = 1 \\
\end{cases}\]
这个定理的证明略。
由这个定理知,要证明马尔可夫链是遍历的,只需要找一正整数 \(m\) ,使 \(m\) 步转移概率矩阵 \(P^m\) 中无零元素(全部大于零)。
8.2. MCMC 基本思想:由极限分布,构造马尔可夫链进行抽样
假设初始概率分布为 \(\boldsymbol{\pi_0}\) ,且到第 \(n\) 步后马尔可夫链收敛到极限分布 \(\boldsymbol{\pi}\) 。如果在马尔可夫链的状态空间中做状态转移,记 \(X_i\) 的概率分布为 \(\boldsymbol{\pi_i}\) ,如 \(X_0\) 满足概率分布 \(\boldsymbol{\pi_0}\) ,\(X_1\) 满足概率分布 \(\boldsymbol{\pi_1}\) ,从 \(n\) 开始, \(X_i, i \ge n\) 满足概率分布 \(\boldsymbol{\pi}\) ,即有:
\[\begin{aligned}
X_0 & \sim \boldsymbol{\pi_0} \\
X_1 & \sim \boldsymbol{\pi_1} \\
& \cdots \\
X_{n-1} & \sim \boldsymbol{\pi_{n-1}} \\
X_n & \sim \boldsymbol{\pi} \qquad \text{概率分布从这步开始稳定} \\
X_{n+1} & \sim \boldsymbol{\pi} \\
& \cdots \\
\end{aligned}\]
显然, 如果马尔可夫链从 \(n\) 步开始稳定,则观察值 \(x_n,x_{n+1}, \cdots\) 就是服从马尔可夫链的极限分布 \(\boldsymbol{\pi}\) 的样本值。
如果要生成概率分布 \(\pi(x)\) 的样本值,我们可以把 \(\pi(x)\) 看作是某一个马尔可夫链的极限分布。这样,马尔可夫链稳定后的观察值就是概率分布 \(\pi(x)\) 的样本值,从而完成了对 \(\pi(x)\) 的抽样。这就是 MCMC 的基本思想。
如前面例子中,人处于“下中上”三个阶层的极限分布为 \(\boldsymbol{\pi} =[0.286,0.489,0.225]\) 。如果要生成这个概率分布的样本,则只需要在对应马尔可夫链上做状态转移,稳定后的状态观察值就是极限分布的样本值。
现在的关键问题是如何由一个极限分布得到对应马尔可夫链呢?请看下文。
8.3. Metropolis-Hastings
定理(细致平稳条件,Detail Balance Condition):当非周期性的马尔可夫链的概率转移矩阵 \(P\) 和某个分布 \(\boldsymbol{\pi}\) 满足:
\[\pi(i) p_{ij} = \pi(j) p_{ji}, \quad \text{for all} \; i,j\]
时,那么分布 \(\boldsymbol{\pi}\) 就是该马尔可夫链的平稳分布(极限分布)。
说明 1:马尔可夫链的概率转移矩阵保存的是条件概率,所以 \(\pi(i) p_{ij} = \pi(j) p_{ji}\) 常常也写为 \(\pi(i) p(j \mid i) = \pi(j) p_(i \mid j)\)
说明 2:利用细致平稳条件,我们可以验证一个分布是否为马尔可夫链的平稳分布。
说明 3:还是考虑前面例子,人处于“下中上”三个阶层的极限分布为 \(\boldsymbol{\pi} = [0.286,0.489,0.225]\) 。容易验证这个极限分布确实是马尔可夫链 \(P = \begin{bmatrix} 0.65 & 0.28 & 0.07 \\ 0.15 & 0.67 & 0.18 \\ 0.12 & 0.36 & 0.52 \end{bmatrix}\) 的平稳分布。
下面我们将利用“细致平稳条件”来构造一个马尔可夫链,使它的平稳分布为 \(\pi(x)\) ,这样在马尔可夫链上的状态转移(稳定后)就是平稳分布 \(\pi(x)\) 的样本点。
首先,借助另一个已知的马尔可夫链 \(Q\) 。当然,一般情况下有:
\[\pi(i) q(j \mid i) \ne \pi(j) q(i \mid j)\]
细致平稳条件不成立,从而 \(\pi(x)\) 不是马尔可夫链 \(Q\) 的平稳分布。我们对上式进行改造,使得细致平稳条件成立。如,引入 \(\alpha(i,j), \alpha(j, i)\) ,希望下式成立:
\[\pi(i) q(j \mid i) \alpha(i,j) = \pi(j) q(i \mid j) \alpha(j,i)\]
也就是希望下式成立:
\[\frac{\alpha(i,j)}{\alpha(j,i)} = \frac{\pi(j) q(j \mid i)}{\pi(i) q(i \mid j)}\]
显然,如果定义 \(\alpha(i,j) = \pi(j) q(j \mid i), \, \alpha(j,i) = \pi(i) q(i \mid j)\) 则上式是成立的。即有:
\[\pi(i) \underbrace{q(j \mid i) \alpha(i,j)}_{Q'(i \to j)} = \pi(j) \underbrace{q(i \mid j) \alpha(j,i)}_{Q'(j \to i)}\]
所以,新马尔可夫链 \(Q'\) 的平稳分布为 \(\pi(x)\) 。这样在新马尔可夫链 \(Q'\) 上的状态转移(稳定后)就是平稳分布 \(\pi(x)\) 的样本点。
由上面分析知,新马尔可夫链 \(Q'\) 从 \(i\) 到 \(j\) 的转移概率为: \(q(j \mid i) \alpha(i,j)\) 。 我们可以这样理解 \(q(j \mid i) \alpha(i,j)\) :以概率 \(q(j \mid i)\) 从 \(i\) 转移到 \(j\) ,以概率 \(\alpha(i,j)\) 接受这个转移( \(\alpha(i,j)\) 又称为接受率)。
综上所述,我们得到了一个抽样算法:
(1) 寻找另一个辅助的概率分布(称为建议分布) \(q(y \mid x)\) ,初始化马尔可夫链 \(X_0 = x_0\) 。
(2) 对 \(t=0,1,2,\cdots\) ,用下面方法迭代进行抽样。
(2.1) 记 \(t\) 时刻状态为 \(X_t = x_t\) ,从建议分布中抽样得到样本 \(y\) ,即 \(y \sim q(x \mid x_t)\) 。
(2.2) 产生一个(0,1)之间的随机数 \(u\) 。
(2.3) 如果 \(u < \alpha(x_t, y) = \pi(y)q(x_t \mid y)\) ,则接受转移 \(x_t \to y\) ,即 \(X_{t+1} = y\) ;否则不接受转移,即 \(X_{t+1} = x_t\) 。
这样,得到的样本 \(X\) 经过一定迭代次数后达到稳定状态,这时它就符合概率分布 \(\pi(x)\) 。
8.3.1. Metropolis-Hastings 算法
前面抽样算法可以工作,但如果接受率 \(\alpha(i,j)\) 比较小,则采样时马尔可夫链容易原地踏步,拒绝大量的跳转,这使得马尔可夫链遍历整个状态空间要花费太长的时间,收敛到平稳分布 \(\pi(x)\) 的速度太慢。下面我们将提高想办法提高接受率。
如果 \(\alpha(i,j)=0.1, \alpha(j,i)=0.2\) ,此时的细致平稳条件为:
\[\pi(i) q(j \mid i) \times 0.1 = \pi(j) q(i \mid j) \times 0.2\]
显然, \(\alpha(i,j)\) 和 \(\alpha(j,i)\) 同比例放大,使得两数中最大的一个放大到 1 时,细致平稳条件仍然会满足。如把上式两边扩大 5 倍,有:
\[\pi(i) q(j \mid i) \times 0.5 = \pi(j) q(i \mid j) \times 1\]
“两数中最大的一个放大到 1”用公式表达就是:
\[\alpha(i,j) = \min\left\{1, \frac{\pi(j)q(i \mid j)}{\pi(i)q(j \mid i)} \right\}\]
这就是 Metropolis-Hastings算法 。
(1) 寻找另一个辅助的概率分布(称为建议分布) \(q(y \mid x)\) ,初始化马尔可夫链 \(X_0 = x_0\) 。
(2) 对 \(t=0,1,2,\cdots\) ,用下面方法迭代进行抽样。
(2.1) 记 \(t\) 时刻状态为 \(X_t = x_t\) ,从建议分布中抽样得到样本 \(y\) ,即 \(y \sim q(x \mid x_t)\) 。
(2.2) 产生一个(0,1)之间的随机数 \(u\) 。
(2.3) 如果 \(u < \alpha(x_t, y) = \min\left\{1, \frac{\pi(y)q(x_t \mid y)}{\pi(x_t)q(y \mid x_t)} \right\}\) ,则接受转移 \(x_t \to y\) ,即 \(X_{t+1} = y\) ;否则不接受转移,即 \(X_{t+1} = x_t\) 。
这样,得到的样本 \(X\) 经过一定迭代次数后达到稳定状态,这时它就符合概率分布 \(\pi(x)\) 。
说明 1:Metropolis-Hastings 算法得到的样本并不独立,但是我们所要求的是得到的样本符合给定的概率分布,并不要求独立。
说明 2:Metropolis-Hastings 算法中的“接受”和拒绝抽样或 SIR 中的“接受”不是同一回事。Metropolis-Hastings 算法中的“接受”是指接受这个状态转移(如果不接受则意味着采用当前状态作为下一个状态,不管“接受”还是“不接受”都得到了一个样本值),而拒绝抽样或 SIR 中的“接受”是指接受样本值(如果不接受则意味着相关程序还要运行一次才可能得到一个样本值)。
说明 3:对于高维空间的 \(\pi(\boldsymbol{x})\) ,如果满足细致平稳条件
\[\pi(\boldsymbol{x})Q′(\boldsymbol{x} \to \boldsymbol{y})=\pi(\boldsymbol{y})Q′(\boldsymbol{y} \to \boldsymbol{x})\]
以上的 Metropolis-Hastings 算法一样有效。
参考:http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/
8.3.2. Metropolis-Hastings 算法实例
这里采用前面介绍 SIR 算法时所使用的实例。
假设需要模拟的随机变量概率密度为: \(f(x) = \frac{1}{c} h(x)\) ,其中 \(c\) 为未知的常数, \(h(x) = e^{0.4*(x-0.4)^2 - 0.08*x^4}\) 。
k <- function(x, a=.4, b=.08){exp(a*(x-a)^2 - b*x^4)} # k(x)本身不是概率密度函数,它是概率密度函数f(x)乘以某个未知常数
x <- seq(-4, 4, 0.1)
N <- 100000
x.acc5 <- rep.int(NA, N)
u <- runif(N)
acc.count <- 0
std <- 0.05 ## Spread of proposal distribution
xc <- 0; ## Starting value
for (ii in 1:N){
xp <- rnorm(1, mean=xc, sd=std) ## proposal distribution
alpha <- min(1, (k(xp)/k(xc)) * (dnorm(xc, mean=xp,sd=std)/dnorm(xp, mean=xc,sd=std)))
x.acc5[ii] <- xc <- ifelse(u[ii] < alpha, xp, xc)
}
pdf(file="myplot_MH.pdf")
par(mfrow=c(2,2), mar=c(2,2,1,1))
plot(x,k(x),type="l")
barplot(table(round(x.acc5,1))/length(x.acc5))
上面程序生成的 myplot_MH.pdf 如图 11 所示。
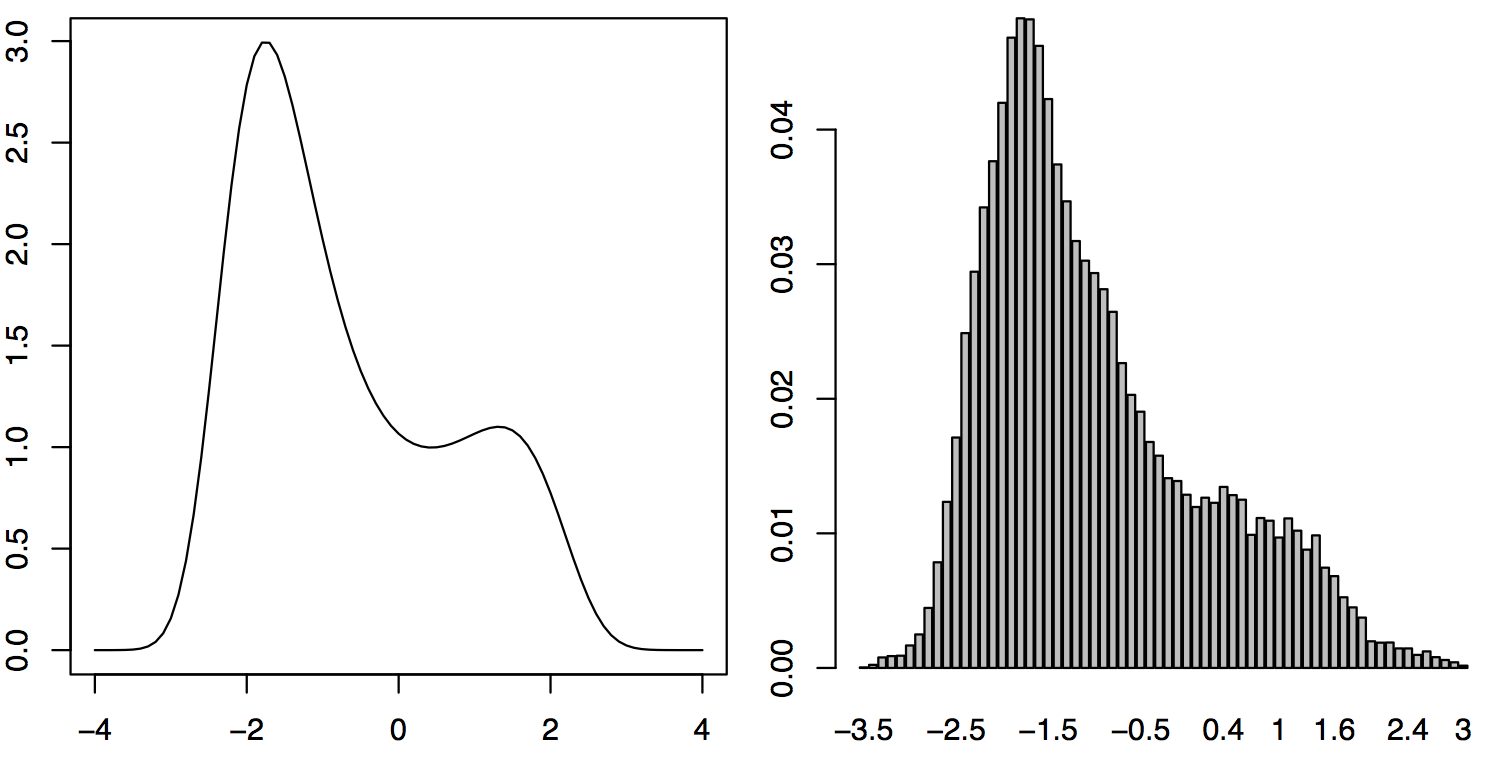
Figure 11: Metropolis-Hastings 算法实例
参考:http://people.math.aau.dk/~kkb/Undervisning/Bayes14/sorenh/docs/sampling-notes.pdf
8.4. Gibbs Sampling(每次对一个变量维度抽样)
当状态很多或维度比较高时,Metropolis-Hastings 算法的接受率不高仍然是个问题(因为接受率不高会导致收敛到平稳分布的速度会很慢)。从 \(i\) 转移到 \(j\) 时,接受率是否可能一直为 1 呢?这是可以做到的。
Gibbls 抽样将高维的抽样转化为多个一维的抽样,每次沿着垂直于某个变量维度的轴走(即每次只对一个变量维度进行抽样)。 Gibbls 抽样在抽样过程中没有拒绝。
二维 Gibbls 抽样算法如下:
(1) 随机初始化 \(X_0 = x_0, Y_0 = y_0\)
(2) 对 \(t=0,1,2.\cdots\) ,按下面方式循环抽样
\[\begin{aligned} y_{t+1} \sim \pi(y \mid x_t) \\
x_{t+1} \sim \pi(x \mid y_{t+1}) \\
\end{aligned}\]
得到的样本 \((x_0,y_0), (x_0,y_1), (x_1,y_1), (x_1,y_2),(x_2,y_2), \cdots\) 经过一定迭代次数后达到稳定状态,这时它就符合概率分布 \(\pi(x,y)\)
说明:Gibbs 抽样和 Metropolis-Hastings 抽样一样,得到样本并不独立,但是我们所要求的是得到的样本符合给定的概率分布,并不要求独立。
参考:
LDA-math-MCMC 和 Gibbs Sampling, by 靳志辉
随机模拟的基本思想和常用采样方法(sampling)
