Unconstrained Optimization (Derivative-based methods)

1. 无约束最优化简介
2. Steepest Descent Method
- 2.1. 最速下降法总结
- 2.2. 最速下降法应用实例
3. Newton's Method
4. Quasi-Newton Method

1. 无约束最优化简介

无约束最优化（Unconstrained Optimization）问题表示如下：
$min_{x \in R^{n}} f (x)$
即求 $f (x)$ 取极小值时对应的 $x$ 值。

无约束最优化问题的解法（方法）可以分为两大类：“Derivative-based optimization”和“Derivative-free optimization”（比如 Pattern search, Powell's method 等等）。不过，“Derivative-free optimization”方法的收敛速度一般比较慢，本文不介绍它们。本文的重点是介绍“基于导数”的无约束最优化方法。

参考：
本文主要摘自：最优化理论与算法(第 2 版), 陈宝林

2. Steepest Descent Method

考虑无约束最优化问题： $min_{x \in R^{n}} f (x)$ ，其中函数 $f (x)$ 是 $R^{n}$ 上具有一阶连续偏导数的函数。

梯度下降法(Gradient Descent)是一种迭代算法，选取适当的初值后，不断迭代更新 $x$ 的值，进行目标函数的极小化，直到收敛。梯度下降法背后的原理是“负梯度方向是使函数值下降最快的方向”，梯度下降法的更新公式为：
$x_{k + 1} = x_{k} - λ \nabla f (x_{k})$
其中， $x_{k}$ 为第 $k$ 次迭代时 $x$ 的值， $λ$ 是大于零的实数，称为步长。

有很多设置步长 $λ$ 的方法。下面介绍的最速下降法(Steepest Descent)是其中的一种（注：有时我们提到梯度下降法时，指的就是最速下降法）。

2.1. 最速下降法总结

最速下降法每次迭代时都采用不同的 $λ$ 。记 $d_{k} \overset{def}{=} - \nabla f (x_{k})$ ，迭代公式可写为：
$x_{k + 1} = x_{k} + λ_{k} d_{k}$
其中 $d_{k}$ 是从 $x_{k}$ 出发的搜索方向， $λ_{k}$ 是从 $x_{k}$ 出发沿方向 $d_{k}$ 进行一维搜索（也称“线搜索”，也就是单变量函数极小化问题）得到的步长，即 $λ_{k}$ 满足：
$f (x_{k} + λ_{k} d_{k}) = min_{λ \geq 0} f (x_{k} + λ d_{k})$
也就是：
$λ_{k} = \arg min_{λ \geq 0} f (x_{k} + λ d_{k})$

最速下降法计算步骤：
(1) 给定初始点 $x_{1} \in R^{n}$ ，允许误差 $ε$ ，置 $k = 1$ 。
(2) 计算搜索方向 $d_{k} = - \nabla f (x_{k})$
(3) 如果 $‖ \nabla f (x_{k}) ‖ \leq ε$ ，则停止迭代，返回 $x_{k}$ 作为 $f (x)$ 极小点；否则，从 $x_{k}$ 出发，沿 $d_{k}$ 进行一维搜索，求 $λ_{k}$ ，即：
$λ_{k} = \arg min_{λ \geq 0} f (x_{k} + λ d_{k})$
(4) 令 $x_{k + 1} = x_{k} + λ_{k} d_{k}$ ，转到步骤(2)。

2.2. 最速下降法应用实例

用最速下降法求解下面优化问题（精度 $ε = \frac{1}{10}$ ）：
$min 2 x^{2} + y^{2}$
解：记 $x = (x, y)^{T}$ ，目标函数的 $f (x)$ 的梯度为：
$\nabla f (x) = [\begin{matrix} 4 x \\ 2 y \end{matrix}]$
取初值点 $x_{1} = (1, 1)^{T}$ 。
第 1 次迭代。 计算搜索方向 $d_{1}$ ：
$d_{1} = - \nabla f (x_{1}) = [\begin{matrix} - 4 \\ - 2 \end{matrix}]$
由于 $‖ \nabla f (x_{1}) ‖ = \sqrt{16 + 4} = 2 \sqrt{5} > \frac{1}{10}$ ，所以要接着迭代计算。
从 $x_{1}$ 出发，沿 $d_{1}$ 进行一维搜索，求 $λ_{1}$ ，方法如下：
$min_{λ \geq 0} φ (λ) \overset{def}{=} f (x_{1} + λ d_{1})$
由于：
$x_{1} + λ d_{1} = [\begin{matrix} 1 \\ 1 \end{matrix}] + λ [\begin{matrix} - 4 \\ - 2 \end{matrix}] = [\begin{matrix} 1 - 4 λ \\ 1 - 2 λ \end{matrix}]$
所以：
$φ (λ) = 2 (1 - 4 λ)^{2} + (1 - 2 λ)^{2}$
令：
$φ^{'} (λ) = - 16 (1 - 4 λ) - 4 (1 - 2 λ) = 0$
上式解得的值即为 $λ_{1}$ ：
$λ_{1} = \frac{5}{8}$
由迭代公式有：
$x_{2} = x_{1} + λ_{1} d_{1} = [\begin{matrix} - \frac{1}{9} \\ \frac{4}{9} \end{matrix}]$
第 2 次迭代。 计算搜索方向 $d_{2}$ ：
$d_{2} = - \nabla f (x_{2}) = [\begin{matrix} \frac{4}{9} \\ - \frac{8}{9} \end{matrix}]$
由于 $‖ \nabla f (x_{2}) ‖ = \sqrt{(\frac{4}{9})^{2} + (- \frac{8}{9})^{2}} = \frac{4}{5} \sqrt{5} > \frac{1}{10}$ ，所以要接着迭代计算。
从 $x_{2}$ 出发，沿 $d_{2}$ 进行一维搜索，求 $λ_{2}$ ，方法如下：
$min_{λ \geq 0} φ (λ) \overset{def}{=} f (x_{2} + λ d_{2})$
由于：
$x_{2} + λ d_{2} = [\begin{matrix} - \frac{1}{9} \\ \frac{4}{9} \end{matrix}] + λ [\begin{matrix} \frac{4}{9} \\ - \frac{8}{9} \end{matrix}] = [\begin{matrix} - \frac{1}{9} + \frac{4}{9} λ \\ \frac{4}{9} - \frac{8}{9} λ \end{matrix}]$
所以：
$φ (λ) = \frac{2}{81} (- 1 + 4 λ)^{2} + \frac{16}{81} (1 - 2 λ)^{2}$
令：
$φ^{'} (λ) = \frac{16}{81} (- 1 + 4 λ) - \frac{64}{81} (1 - 2 λ) = 0$
上式解得的值即为 $λ_{2}$ ：
$λ_{2} = \frac{5}{12}$
由迭代公式有：
$x_{3} = x_{2} + λ_{2} d_{2} = \frac{2}{27} [\begin{matrix} 1 \\ 1 \end{matrix}]$
第 3 次迭代。 其过程类似，直接给出结果：
$\begin{aligned} d_{3} & = - \nabla f (x_{3}) = \frac{4}{27} [\begin{array}{c} - 2 \\ - 1 \end{array}] \\ ‖ \nabla f (x_{3}) ‖ & = \frac{4}{27} \sqrt{5} > \frac{1}{10} \\ λ_{3} & = \frac{5}{18} \end{aligned}$
从而有：
$x_{4} = x_{3} + λ_{3} d_{3} = \frac{2}{243} [\begin{matrix} - 1 \\ 4 \end{matrix}]$
这时 $‖ \nabla f (x_{4}) ‖ = \frac{8}{243} \sqrt{5} < \frac{1}{10}$ ，已经满足精度要求，停止迭代，得到近似解：
$[\begin{matrix} x \\ y \end{matrix}] = \frac{2}{243} [\begin{matrix} - 1 \\ 4 \end{matrix}]$
实际上，这个问题的最优解为： $(0, 0)^{T}$

3. Newton's Method

在数学中，有两个地方会提到牛顿方法：在微积分领域中，牛顿方法用于求解方程的根；在最优化理论中，牛顿方法用于求解无约束最优化问题。这里介绍的是后者。

参考：https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization

3.1. 一维情况

为简单起见，先介绍牛顿方法求解一维情况下无约束最优化问题（即单变量的极小化问题）。

考虑问题：
$min_{x \in R} f (x)$
假设 $x_{k}$ 是 $f (x)$ 的极小点的一个估计。我们把 $f (x)$ 在 $x_{k}$ 点处展开为 Taylor 级数，并取二阶近似：
$f (x) \approx φ (x) \overset{def}{=} f (x_{k}) + f^{'} (x_{k}) (x - x_{k}) + \frac{1}{2} f^{″} (x_{k}) (x - x_{k})^{2}$

为了求 $φ (x)$ 的驻点(Stationary point)，令 $φ^{'} (x) = 0$ ，有： $φ^{'} (x) = f^{'} (x_{k}) + f^{″} (x_{k}) (x - x_{k}) = 0$ 从而有： $x = x_{k} - \frac{f^{'} (x_{k})}{f^{″} (x_{k})}$ 把求得的 $φ (x)$ 驻点记为 $x_{k + 1}$ ，即有： $x_{k + 1} = x_{k} - \frac{f^{'} (x_{k})}{f^{″} (x_{k})} (单变量时牛顿法迭代公式)$ 由于在点 $x_{k}$ 附近 $f (x) \approx φ (x)$ ，因此可用函数 $φ (x)$ 的极小点作为目标函数 $f (x)$ 的极小点的估计。如果 $x_{k}$ 是 $f (x)$ 的极小点的一个估计，那么利用上式求得的 $x_{k + 1}$ 是极小点的一个进一步的估计，经过很多次迭代后，一般会收敛于极值点。

3.2. 多维情况

前面介绍了单变量极小化问题的牛顿法，这里推广到一般无约束问题的牛顿法。
设 $f (x)$ 是二次可微实函数， $x \in R^{n}$ 。又设 $x_{k}$ 是 $f (x)$ 的极小点的一个估计。我们把 $f (x)$ 在 $x_{k}$ 点处展开为 Taylor 级数，并取二阶近似：
$f (x) \approx φ (x) \overset{def}{=} f (x_{k}) + \nabla f (x_{k})^{T} (x - x_{k}) + \frac{1}{2} (x - x_{k})^{T} \nabla^{2} f (x_{k}) (x - x_{k})$
为了求 $φ (x)$ 的驻点(Stationary point)，令 $\nabla φ (x) = 0$ ，有：
$\nabla φ (x) = \nabla f (x_{k}) + \nabla^{2} f (x_{k}) (x - x_{k}) = 0$
设 $\nabla^{2} f (x_{k})$ 可逆（其逆矩阵记为 $\nabla^{2} f (x_{k})^{- 1}$ ），从而有：
$x = x_{k} - \nabla^{2} f (x_{k})^{- 1} \nabla f (x_{k})$
把求得的 $φ (x)$ 驻点记为 $x_{k + 1}$ ，即有： $x_{k + 1} = x_{k} - \nabla^{2} f (x_{k})^{- 1} \nabla f (x_{k}) (牛顿法迭代公式)$
经过上面公式多次迭代后，得到的序列 $x_{1}, x_{2}, \dots, x_{k}, x_{k + 1}, \dots$ ，在适当条件下，会收敛于极值点。

3.3. 牛顿法应用实例

用牛顿法求解下列问题：
$min (x - 1)^{4} + y^{2}$
解：记 $x = (x, y)^{T}$ ，目标函数 $f (x)$ 的梯度和 Hessian 矩阵分别为：
$\begin{aligned} \nabla f (x) & = [\begin{array}{c} 4 (x - 1)^{3} \\ 2 y \end{array}] \\ \nabla^{2} f (x) & = [\begin{array}{cc} 12 (x - 1)^{2} & 0 \\ 0 & 2 \end{array}] \end{aligned}$
取初值点 $x_{1} = (0, 1)^{T}$ 。
第 1 次迭代：
$\begin{aligned} \nabla f (x_{1}) & = [\begin{array}{c} - 4 \\ 2 \end{array}] \\ \nabla^{2} f (x_{1}) & = [\begin{array}{cc} 12 & 0 \\ 0 & 2 \end{array}] \end{aligned}$
由牛顿法迭代公式有：
$x_{2} = x_{1} - \nabla^{2} f (x_{1})^{- 1} \nabla f (x_{1}) = [\begin{matrix} 0 \\ 1 \end{matrix}] - {[\begin{array}{cc} 12 & 0 \\ 0 & 2 \end{array}]}^{- 1} [\begin{matrix} - 4 \\ 2 \end{matrix}] = [\begin{matrix} \frac{1}{3} \\ 0 \end{matrix}]$
第 2 次迭代：
$\begin{aligned} \nabla f (x_{2}) & = [\begin{array}{c} - \frac{32}{27} \\ 0 \end{array}] \\ \nabla^{2} f (x_{2}) & = [\begin{array}{cc} \frac{48}{9} & 0 \\ 0 & 2 \end{array}] \end{aligned}$
由牛顿法迭代公式有：
$x_{3} = x_{2} - \nabla^{2} f (x_{2})^{- 1} \nabla f (x_{2}) = [\begin{matrix} \frac{1}{3} \\ 0 \end{matrix}] - {[\begin{array}{cc} \frac{48}{9} & 0 \\ 0 & 2 \end{array}]}^{- 1} [\begin{matrix} - \frac{32}{27} \\ 0 \end{matrix}] = [\begin{matrix} \frac{5}{9} \\ 0 \end{matrix}]$
继续迭代下去，得到：
$x_{4} = [\begin{matrix} \frac{19}{27} \\ 0 \end{matrix}], x_{5} = [\begin{matrix} \frac{65}{81} \\ 0 \end{matrix}], \dots$
这个问题的最优解为 $x^{*} = (1, 0)^{T}$ 。从迭代进展情况看，牛顿法收敛比较快。

3.4. 牛顿法优缺点

牛顿方法的优点是 收敛速度很快 ，经过较少的迭代次数即可接近极小值点。

牛顿方法的缺点：
(1) 需要计算 $\nabla^{2} f (x_{k})^{- 1}$ ，它的计算量过程比较复杂。为此，人们提出了拟牛顿法（寻找更容易计算的矩阵来近似 $\nabla^{2} f (x_{k})^{- 1}$ ），后文将介绍它。
(2) 运用牛顿法时，牛顿方向 $d_{k} \overset{def}{=} - \nabla^{2} f (x_{k})^{- 1} \nabla f (x_{k})$ 不一定是下降方向，经迭代，目标函数值可能上升。此外，即使目标函数值下降，得到的点 $x_{k + 1}$ 也不一定是沿牛顿方向的最好点或极小点。为此，人们提出了阻尼牛顿法，后文将介绍它。
(3) 运用牛顿法时，初始点的选择十分重要。如果初始点远离极小点，牛顿法可能不收敛。如优化问题 $min x^{4} + x y + (1 + y)^{2}$ ，当取初始点为 $(0, 0)^{T}$ 时，用原始牛顿法或者阻尼牛顿法都不会收敛。人们提出了一些修正算法来确保从任意初始点开始迭代都能得到极小值点，本文不介绍这些修正算法。参考《最优化理论与算法(第 2 版), 陈宝林》10.2.3 节

3.5. 阻尼牛顿法(Damped Newton's Method)

阻尼牛顿法与原始牛顿法的区别在于增加了沿牛顿方向的一维搜索，阻尼牛顿法的迭代公式为：
$x_{k + 1} = x_{k} - λ_{k} \nabla^{2} f (x_{k})^{- 1} \nabla f (x_{k}) (阻尼牛顿法迭代公式)$ 其中 $λ_{k}$ 是由一维搜索得到的步长。记牛顿方向 $d_{k} \overset{def}{=} - \nabla^{2} f (x_{k})^{- 1} \nabla f (x_{k})$ ，则 $λ_{k}$ 由下式求得：
$f (x_{k} + λ_{k} d_{k}) = min_{λ \geq 0} f (x_{k} + λ d_{k})$
由于阻尼牛顿法含有一维搜索，因此 每次迭代时目标函数值一般会有所下降（绝不会上升）。

阻尼牛顿法是对原始牛顿法非常小的一个改进。 有时，当我们提到牛顿法时，就是指阻尼牛顿法。

4. Quasi-Newton Method

4.1. 动机

运用牛顿法（阻尼牛顿法）时，需要 计算目标函数的 Hessian 矩阵的逆矩阵，这个计算过程比较复杂。

$x_{k + 1} = x_{k} - λ_{k} \underset{\begin{matrix} 这是 Hessian 矩阵的逆矩阵 \\ 拟牛顿法思路： \\ 寻找易计算的矩阵来近似它 \end{matrix}}{\underset{⏟}{\nabla^{2} f (x_{k})^{- 1}}} \nabla f (x_{k}) (阻尼牛顿法迭代公式)$

为了解决这个问题，人们提出了拟牛顿法(Quasi-Newton Method)，其基本思想是 用不包含二阶导数的矩阵来近似牛顿法中的 Hessian 矩阵的逆矩阵。 由于构造近似矩阵的方法不同，因而出现了不同的拟牛顿法。

4.2. 拟牛顿条件

为了构造 $\nabla^{2} f (x_{k})^{- 1}$ 的近似矩阵，我们先分析 $\nabla^{2} f (x_{k})^{- 1}$ 和一阶导数的关系。
设在第 $k$ 次迭代后，得到点 $x_{k + 1}$ ，我们将目标函数 $f (x)$ 在点 $x_{k + 1}$ 处展开为 Taylor 级数，并取二阶近似，有：
$f (x) \approx f (x_{k + 1}) + \nabla f (x_{k + 1})^{T} (x - x_{k + 1}) + \frac{1}{2} (x - x_{k + 1})^{T} \nabla^{2} f (x_{k + 1}) (x - x_{k + 1})$
对上式两个求偏导有：
$\nabla f (x) \approx \nabla f (x_{k + 1}) + \nabla^{2} f (x_{k + 1}) (x - x_{k + 1})$
令 $x = x_{k}$ ，则：
$\nabla f (x_{k}) \approx \nabla f (x_{k + 1}) + \nabla^{2} f (x_{k + 1}) (x_{k} - x_{k + 1})$
定义下面两个符号：
$\begin{aligned} Δ x_{k} & \overset{def}{=} x_{k + 1} - x_{k} \\ y_{k} & \overset{def}{=} \nabla f (x_{k + 1}) - \nabla f (x_{k}) \end{aligned}$
前面的式子可写为：
$y_{k} \approx \nabla^{2} f (x_{k + 1}) Δ x_{k}$
设矩阵 $\nabla^{2} f (x_{k + 1})$ 可逆，则：
$Δ x_{k} \approx \nabla^{2} f (x_{k + 1})^{- 1} y_{k}$
这样，计算出 $Δ x_{k}$ 和 $y_{k}$ 后，可以根据上式估计在 $x_{k + 1}$ 处的 $\nabla^{2} f (x_{k + 1})^{- 1}$ 。因此，为了用不包含二阶导数的矩阵（记为 $H_{k + 1}$ ）取代牛顿法中的 $\nabla^{2} f (x_{k + 1})^{- 1}$ ，有理由令 $H_{k + 1}$ 满足： $Δ x_{k} = H_{k + 1} y_{k} (拟牛顿条件)$ 上式称为 拟牛顿条件，满足这个条件的 $H_{k + 1}$ 都可以作为 $\nabla^{2} f (x_{k + 1})^{- 1}$ 的近似代替。

4.3. Davidon-Fletcher-Powell (DFP)

DFP(Davidon-Fletcher-Powell)著名的拟牛顿法，它由 William C. Davidon 首先提出，后来被 Roger Fletcher 和 Michael J. D. Powell 改进。

DFP 方法采用下面公式（这里直接给出结论，不推导）迭代计算拟牛顿条件中的 $H_{k + 1}$ （即 $\nabla^{2} f (x_{k + 1})^{- 1}$ 的近似）： $H_{k + 1} = H_{k} + \frac{Δ x_{k} Δ x_{k}^{T}}{Δ x_{k}^{T} y_{k}} - \frac{H_{k} y_{k} y_{k}^{T} H_{k}}{y_{k}^{T} H_{k} y_{k}} (DFP formula)$ 初始时， $H_{1}$ 通常选择 $n$ 阶单位矩阵 $I$ 。上面的公式中，只用到了一阶偏导数信息，并不需要二阶偏导数相关信息。

4.3.1. DFP 算法总结

输入：目标函数 $f (x)$ ，精度 $ε$
输出： $f (x)$ 的极小点 $x^{*}$ 。

DFP 方法计算步骤如下：
(1) 选定初始点 $x_{1} \in R^{n}$
(2) 置 $H_{1} = I_{n}$ （单位矩阵），计算出在 $x_{1}$ 处的梯度 $\nabla f (x_{1})$ 。如果 $‖ \nabla f (x_{1}) ‖ < ε$ ，则停止计算，极小点 $x^{*}$ 的近似值就是初始点 $x_{1}$ ；否则，置 $k = 1$ ，接着执行下面步骤。
(3) 令 $d_{k} = - H_{k} \nabla f (x_{k})$
(4) 求步长 $λ_{k}$ （阻尼牛顿法中的步长），使它满足：
$f (x_{k} + λ_{k} d_{k}) = min_{λ \geq 0} f (x_{k} + λ d_{k})$
(5) 置 $x_{k + 1} = x_{k} + λ_{k} d_{k}$
(6) 计算 $\nabla f (x_{k + 1})$ ，如果 $‖ \nabla f (x_{k + 1}) ‖ < ε$ ，则停止迭代，得到近似解 $x^{*} = x_{k + 1}$ ；否则，令 $Δ x_{k} = x_{k + 1} - x_{k}, y_{k} = \nabla f (x_{k + 1}) - \nabla f (x_{k})$ ，按下式计算 $H_{k + 1}$ ： $H_{k + 1} = H_{k} + \frac{Δ x_{k} Δ x_{k}^{T}}{Δ x_{k}^{T} y_{k}} - \frac{H_{k} y_{k} y_{k}^{T} H_{k}}{y_{k}^{T} H_{k} y_{k}} (DFP formula)$
(7) 置 $k = k + 1$ ，返回步骤(3)

4.3.2. DFP 算法应用实例

用 DFP 方法求解下列问题：
$min 2 x^{2} + y^{2} - 4 x + 2$
解：记 $x = (x, y)^{T}$ ，目标函数 $f (x)$ 的梯度为：
$\nabla f (x) = [\begin{matrix} 4 (x - 1) \\ 2 y \end{matrix}]$
初始点 $x_{1}$ 和初始矩阵 $H_{1}$ 分别取为：
$x_{1} = [\begin{matrix} 2 \\ 1 \end{matrix}], H_{1} = [\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}]$
第 1 次迭代，在点 $x_{1}$ 处的梯度：
$\nabla f (x_{1}) = [\begin{matrix} 4 \\ 2 \end{matrix}]$
令搜索方向：
$d_{1} = - H_{1} \nabla f (x_{1}) = [\begin{matrix} - 4 \\ - 2 \end{matrix}]$
求 $λ_{1}$ ，即从 $x_{1}$ 出发沿 $d_{1}$ 作一维搜索，即求解：
$f (x_{1} + λ_{1} d_{1}) = min_{λ \geq 0} f (x_{1} + λ d_{1})$
得到 $λ_{1} = \frac{5}{18}$ 。令
$x_{2} = x_{1} + λ_{1} d_{1} = [\begin{matrix} 2 \\ 1 \end{matrix}] + \frac{5}{18} [\begin{matrix} - 4 \\ - 2 \end{matrix}] = [\begin{matrix} \frac{8}{9} \\ \frac{4}{9} \end{matrix}]$
计算 $\nabla f (x_{2})$ ：
$\nabla f (x_{2}) = [\begin{matrix} 4 (\frac{8}{9} - 1) \\ 2 \cdot \frac{4}{9} \end{matrix}] = [\begin{matrix} - \frac{4}{9} \\ \frac{8}{9} \end{matrix}]$
第 2 次迭代。
$\begin{aligned} Δ x_{1} & = x_{2} - x_{1} = [\begin{array}{c} - \frac{10}{9} \\ - \frac{5}{9} \end{array}] \\ y_{1} & = \nabla f (x_{2}) - \nabla f (x_{1}) = [\begin{array}{c} - \frac{40}{9} \\ - \frac{10}{9} \end{array}] \end{aligned}$
计算矩阵：
$\begin{aligned} H_{2} & = H_{1} + \frac{Δ x_{1} Δ x_{1}^{T}}{Δ x_{1}^{T} y_{1}} - \frac{H_{1} y_{1} y_{1}^{T} H_{1}}{y_{1}^{T} H_{1} y_{1}} \\ = [\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}] + \frac{1}{18} [\begin{array}{cc} 4 & 2 \\ 2 & 1 \end{array}] - \frac{1}{17} [\begin{array}{cc} 16 & 4 \\ 4 & 1 \end{array}] \\ = \frac{1}{306} [\begin{array}{cc} 86 & - 38 \\ - 38 & 305 \end{array}] \end{aligned}$
令：
$d_{2} = - H_{2} \nabla f (x_{2}) = - \frac{1}{306} [\begin{array}{cc} 86 & - 38 \\ - 38 & 305 \end{array}] [\begin{matrix} - \frac{4}{9} \\ \frac{8}{9} \end{matrix}] = \frac{12}{51} [\begin{matrix} 1 \\ - 4 \end{matrix}]$
求 $λ_{2}$ ，即从 $x_{2}$ 出发沿 $d_{2}$ 作一维搜索，即求解：
$f (x_{2} + λ_{2} d_{2}) = min_{λ \geq 0} f (x_{2} + λ d_{2})$
得到 $λ_{2} = \frac{17}{36}$ 。令
$x_{3} = x_{2} + λ_{2} d_{2} = [\begin{matrix} \frac{8}{9} \\ \frac{4}{9} \end{matrix}] + \frac{17}{36} \cdot \frac{12}{51} [\begin{matrix} 1 \\ - 4 \end{matrix}] = [\begin{matrix} 1 \\ 0 \end{matrix}]$
这时有：
$\nabla f (x_{3}) = [\begin{matrix} 0 \\ 0 \end{matrix}]$
驻点为零的点就是极值点。因此得到的最优解为：
$(x, y) = (1, 0)$

4.4. Broyden-Fletcher-Goldfarb-Shanno (BFGS)

BFGS(Broyden–Fletcher–Goldfarb–Shanno)方法另一种拟牛顿法。

BFGS 方法采用下面公式（这里直接给出结论，不推导）迭代计算拟牛顿条件中的 $H_{k + 1}$ （即 $\nabla^{2} f (x_{k + 1})^{- 1}$ 的近似）： $H_{k + 1} = (I - \frac{Δ x_{k} y_{k}^{T}}{y_{k}^{T} Δ x_{k}}) H_{k} (I - \frac{y_{k} x_{k}^{T}}{y_{k}^{T} Δ x_{k}}) + \frac{Δ x_{k} Δ x_{k}^{T}}{y_{k}^{T} Δ x_{k}} (BFGS formula)$

BFGS 算法和 DFP 算法的具体步骤是一样的，仅仅只是计算 $H_{k + 1}$ 的迭代公式不同。 数值计算经验表明，使用 BFGS 公式比使用 DFP 公式还要快，目前 BFGS 方法得到广泛应用。

4.4.1. BFGS 公式和 DFP 公式的关系

在 BFGS 公式和 DFP 公式中， $H_{k + 1}$ 是 $\nabla^{2} f (x_{k + 1})^{- 1}$ 的近似，如果记 $B_{k + 1}$ 为 $\nabla^{2} f (x_{k + 1})$ 的近似，则有图 1 (摘自 https://en.wikipedia.org/wiki/Quasi-Newton_method )所示结论。有时， BFGS 公式也称为 DFP 公式的对偶公式。

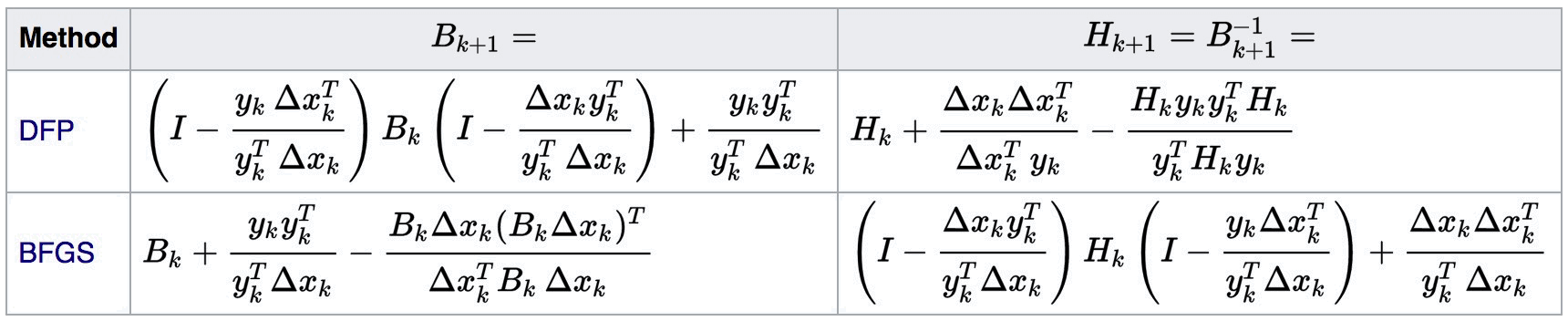
Figure 1: BFGS 公式和 DFP 公式的关系

4.4.2. Limited-memory BFGS (L-BFGS)

假设原始优化问题 $f (x)$ 有 $n$ 个变量（ $x$ 为 $n$ 维向量），则在 BFGS 公式中， $H_{k}$ 的规模为 $n \times n$ ，当 $n$ 很大时，存储这个 $n \times n$ 矩阵会很占计算机资源，Limited-memory BFGS (L-BFGS)是在受限内存时的一种 BFGS 近似算法。

4.4.3. 使用 SciPy 库进行最优化

Python 的 SciPy 库实现了常见的最优化算法，参考：https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html

下面是使用 BFGS 算法求解最优化问题 $min (x - 1)^{4} + y^{2}$ （这个问题我们在节 3.3 中求解过）的演示：

>>> from scipy import optimize
>>> def f(x):
...     return (x[0] - 1)**4 + x[1]**2
...
>>> optimize.minimize(f, [0, 0], method='BFGS')
   status: 0
  success: True
     njev: 15
     nfev: 60
 hess_inv: array([[  1.04206844e+03,   1.26935227e+00],
       [  1.26935227e+00,   5.33941376e-01]])
      fun: 1.0776982563563174e-09
        x: array([  1.00570151e+00,  -4.58021983e-06])
  message: 'Optimization terminated successfully.'
      jac: array([  7.41364167e-07,  -9.14553849e-06])

上面输出中，倒数第 3 行就是求得的极小值点：

        x: array([  1.00570151e+00,  -4.58021983e-06])