zk-SNARK, Pinocchio
Table of Contents
1. 零知识证明简介
零知识证明(Zero-knowledge proof),由 Shafi Goldwasser(2012 年图灵奖获得者)、Silvio Micali(2012 年图灵奖获得者)及 Charles Rackoff(1993 年哥德尔奖获得者) 在 1989 年发表的论文“The Knowledge Complexity of Interactive Proof-Systems”(可简称 GMR89)中提出。它指的是 证明者(prover)能够在不向验证者(verifier)提供任何有用的信息的情况下,使验证者(verifier)相信某个论断是正确的。
顾名思义,零知识证明就是既能充分证明自己是某种权益的合法拥有者,又不把有关的信息泄露出去——即给外界的“知识”为“零”。其实,零知识证明并不是什么新东西,早在 16 世纪的文艺复兴时期,意大利有两位数学家为竞争一元三次方程求根公式发现者的桂冠,就采用了零知识证明的方法。当时,数学家塔尔塔里雅和菲奥都宣称自己掌握了这个求根公式,为了证明自己没有说谎,又不把公式的具体内容公布出来(可能在当时数学公式也是一种技术秘密),他们摆开了擂台:双方各出 30 个一元三次方程给对方解,谁能全部解出,就说明谁掌握了这个公式。比赛结果显示,塔尔塔里雅解出了菲奥出的全部 30 个方程,而菲奥一个也解不出。于是人们相信塔尔塔里雅是一元三次方程求根公式的真正发现者,虽然当时除了塔尔塔里雅外,谁也不知道这个公式到底是个什么样子。摘自:https://baike.baidu.com/item/%E9%9B%B6%E7%9F%A5%E8%AF%86%E8%AF%81%E6%98%8E
1.1. 零知识证明协议的 3 个性质
在任意的「零知识证明」系统中,都有一个证明者(prover)在不泄漏任何额外信息的前提下要让验证者(verifier)确信某些陈述(Statement)是正确的。零知识证明协议应当满足下面三个性质:
- 完备性(Completeness):只要「陈述」是正确的,prover 就可以让 verifier 确信;也就是说 verifier 无法欺骗 prover;
- 可靠性(Soundness):如果「陈述」是错误的,那么作弊的 prover 就没有办法让 verifier 相信;也就是说 prover 无法欺骗 verifier;
- 零知识(Zero-knowledge):协议的交互仅仅揭露「陈述」是否正确而不泄漏任何其它的信息。
1.2. 零知识证明应用场景
下面是零知识证明的一些应用场景。
1、证明关于隐私数据的声明:
- 一个人 A 的银行账户金额多于 X;
- 去年,一家银行未与实体 Y 进行交易;
- 在不暴露全部 DNA 数据的前提下匹配 DNA;
- 一个人的信用评分高于 Z。
2、匿名认证:
- 在不揭露身份的情况下(比如登录密码),证明请求者 R 有权访问网站的受限区域;
- 证明一个人来自一组被允许的国家/地区列表中的某个国家/地区,但不暴露具体是哪个;
- 证明一个人持有地铁月票,而不透露卡号。
3、匿名支付:
- 付款完全脱离任何一种身份;
- 纳税而不透露收入。
4、外包计算:
- 将昂贵的计算外包,并在不重新执行的情况下验证结果是否正确;它打开了一种零信任计算的类别;
- 改进区块链模型,从所有节点做同样的计算,到只需一方计算然后其它节点进行验证。
2. 证明的媒介
先不要去管零知识,非交互性,其形式和适用性等,我们从尝试证明一些简单的东西开始。
假设有个长度为 10 的位数组,现在要向 verifier 证明这样一个陈述:所有的位都被设置为 1。
\[b=[?,?,?,?,?,?,?,?,?,?]\]
verifier 只能一次检查(读取)一位。为了验证这个陈述,我们以某种任意的顺序读取元素并检查其是否确实等于 1 。如果第一次抽样检查的结果是 1,就设置「陈述」的可信度为 10%,否则,如果等于 0,就说明「陈述」是错误的。验证者继续进行下一轮验证,直到获得足够的可信度为止。假如在一些场景下要信任 prover 需要至少 50% 的可信度,那就意味着必须执行 5 次校验。但假如在其它一些场景下需要 95% 的可信度,就需要检查所有的元素。很明显这个证明协议的缺点是必须要根据元素的数量进行检查,如果我们处理数百万个元素的数组,这么做是不现实的。
2.1. 引入多项式
现在我们来看一下由数学方程式表示的多项式,它可以被画成坐标系上的一条曲线,如图 1 所示。
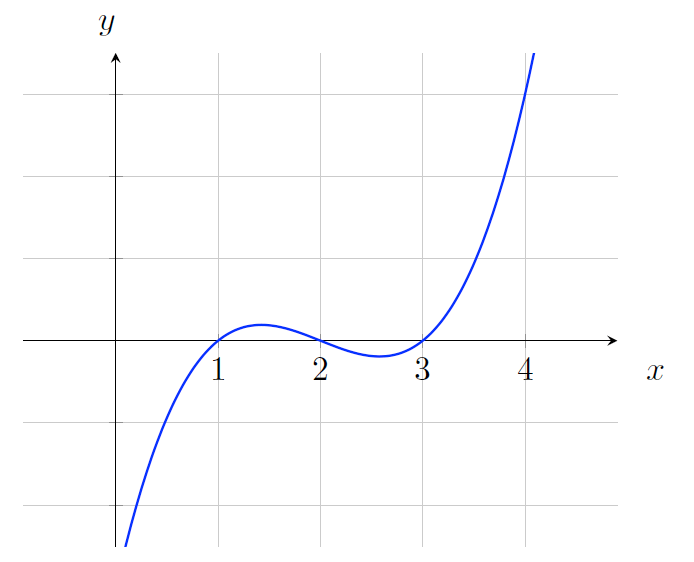
Figure 1: \(f(x) = x^3 - 6x^2 + 11x - 6\)
图 1 中曲线对应的多项式为: \(f(x) = x^3 - 6x^2 + 11x - 6\) 。多项式的阶数 \(d\) 就是 \(x\) 的最大指数,这个多项式的阶数是 \(d=3\) 。
多项式有一个非常好的特性,就是 如果我们有两个阶为 \(d\) 的不相等多项式,它们相交的点数不会超过 \(d\) 。 例如,修改一下原来的多项式为 \(x^3 - 6b^2 + 10x - 5\) ,并在图上用绿色标出,如图 2 所示。
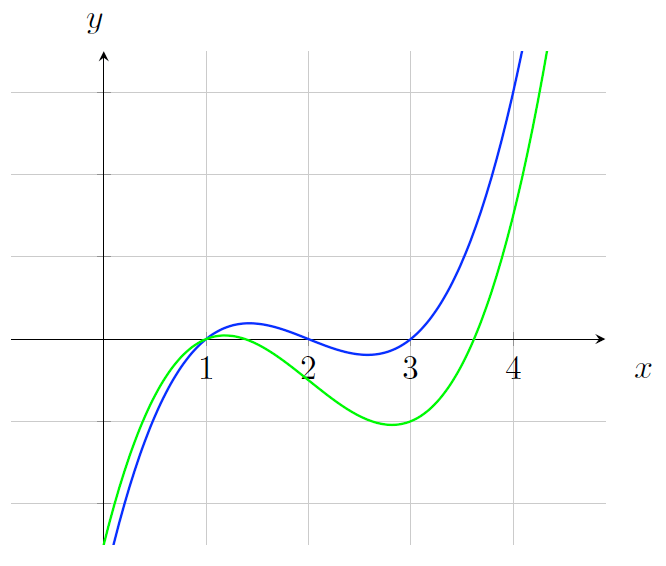
Figure 2: 两个 3 阶多项式,它们的交点最多有 3 个
在 \(x\) 可以选择的所有值中,最多只有 3 个值(即多项式的阶数)能够使上面两个多项式相等,其它的值都是不相等的。
代数的基本原理告诉我们, 对于一个阶数为 \(d\) 的多项式最多有 \(d\) 个解。 这个结论和前面说的“如果我们有两个阶为 \(d\) 的不相等多项式,它们相交的点数不会超过 \(d\) ”表达的是同一个意思。
事实上, 我们不可能找到两条不同的曲线,它们会在某段区域内重合(它们只会相交于一些点)。
2.2. 证明 prover 知道某个多项式
如果一个 prover 声称他知道 verifier 也知道的某个多项式(比如 3 阶多项式 \(f(x) = x^3 - 6x^2 + 11x - 6\) )。 那么 verifier 怎么证明 prover 没有说谎呢?prover 可以直接公布出多项式,verifier 验证一下即可,但这直接泄露了多项式本身,已经不是零知识证明了。
在不泄露多项式的前提下,我们可以采用下面的简单协议:
- 在一个较大的范围内(如 \(1\) 到 \(10^{77}\) ),verifier 选择一个随机值 \(x\) 并在本地计算多项式结果;
- verifier 将 \(x\) 值给到 prover,并让他计算相关的多项式结果;
- prover 代入 \(x\) 到多项式计算并将结果给到 verifier;
- verifier 检查本地的计算结果和 prover 的计算结果是否相等,如果相等那就说明 prover 的陈述具有较高的可信度。
上面的证明过程为什么可行呢?会不会出现 prover 并不知道多项式 \(f(x) = x^3 - 6x^2 + 11x - 6\) ,他知道的是另外一个多项式,而恰好同一个 \(x\) 两个式项式算出的值一样呢?出现这种情况的可能性很小。
上一节介绍过, 如果我们有两个阶为 \(d\) 的不相等多项式,它们相交的点数不会超过 \(d\) 。 也就是说,假设 prover 不知道 \(f(x) = x^3 - 6x^2 + 11x - 6\) 的情况下,拿另外一个 3 阶多项式作弊,能那么作弊成功的 \(x\) 值最多只有 3 个,由于 \(x\) 是由 verifier 在一个较大的范围( \(1\) 到 \(10^{77}\) )中随机选择的,所以作弊成功的可能性几乎为零(假设选择随机值时只选择 \(1\) 到 \(10^{77}\) 内的整数,那么作弊成功的概率不会超过 \(\frac{3}{10^{77}}\) )。当然如果 prover 不拿 3 阶多项式作弊,而是拿一个更高阶的多项式,那么作弊成功的概率会增加。
2.3. Schwartz-Zippel 定理
Schwartz-Zippel 定理:在有限域 \(\mathbb{F}\) 上,给定一个 \(n\) 元 \(d\) 次多项式 \(f(x_1, x_2, \cdots, x_n)\) ,对于 \(\mathbb{F}\) 的某个子集 \(S\) ,我们从中随机挑选 \(n\) 值给每个变量赋值,那么这个多项式等于零的概率小于等于: \[\frac{d}{|S|}\] 其实,上一节中已经介绍过了 Schwartz-Zippel 定理,只是没有把它形式化而已。两个 3 阶多项式相等,就是一个 3 阶多项式为零。上一节中提到 \(x\) 在 \(1\) 到 \(10^{77}\) 中取随机整数时,两个 3 阶多项式恰好相等的概率不超过 \(\frac{3}{10^{77}}\) ,这表达的就是 Schwartz-Zippel 定理的特殊情况。
3. 因式分解
如果一个 prover 声称他知道一个 3 阶多项式 \(p(x)\) ,其中两个根分别为 \(x=1, x=2\) 。 那么 verifier 怎么证明 prover 没有说谎呢?
我们先了解一下因式分解。代数的基本定理表明了任意的一个多项式只要它有解,就可以将它分解成线性多项式(即阶数为 1 的多项式)的乘积,因此,我们可以把任意有效的多项式看成是其因式的乘积:
\[(x-a_0)(x-a_1)\cdots(x-a_n) = 0\]
例如,多项式 \(x^3-3x^2+2x\) 可分解为:
\[x^3-3x^2+2x = (x-0)(x-1)(x-2)\]
也就是说这个多项式的解就是 \(0,1,2\) 。
我们再回到前面的问题,prover 宣称他知道一个阶数为 3,其中两个根分别为 1 和 2 的多项式,也就是说这个多项式的形式为:
\[(x-1)(x-2)\,\cdot\, ...\]
如果 prover 想要在不揭示多项式的前提下证明他的多项式确实有这两个根,那么他就需要去证明他的多项式 \(p(x)\) 是 \(t(x) = (x- 1)(x- 2)\) (也称为目标多项式)和另一个多项式 \(h(x)\) 的乘积,即:
\[p(x) = t(x)\cdot h(x)\]
为了简化起见,后面我们会用多项式的字母变量来代替计算结果值,例如: \(p = p(r)\) 。
3.1. 证明 prover 知道的 d 阶多项式包含指定因子
我们可以使用下面检查协议来证明 prover 没有说谎(即 prover 知道的 3 阶多项式 \(p(x)\) 的两个根分别为 1 和 2 ):
- verifier 挑选一个随机值 \(r\) ,计算 \(t = t(r)\) ,将 \(r\) 发送给 prover;
- prover 计算 \(h(x) = p(x) / t(x)\) ,并对 \(p(r)\) 和 \(h(r)\) 进行求值,将计算结果 \(p, h\) 提供给 verifier;
- verifier 验证 \(p = t\cdot h\) ,如果这个等式成立相等,就意味着 \(t(x)\) 是 \(p(x)\) 的因式。
实践一下,假设 prover 声明他知道的 3 阶多项式为 \(p(x) = (x-1)(x-2)x\) ,用下面的例子来执行这个协议:
- verifier 选一个随机数 23,并计算 \(t = t(23) = (23 - 1)(23 - 2) = 462\) ,然后将 23 发给 prover;
- prover 计算 \(h(x) = p(x) / t(x) = x\) , 并对 \(p(r)\) 和 \(h(r)\) 进行求值, \(p = p(23) = 10626, h = h(23) = 23\) ,将 \(p\) 和 \(h\) 提供给 verifier;
- verifier 再验证 \(p= t \cdot h\) ,即 \(10626 = 462 \cdot 23\) ,这显然是正确的,这样陈述就被证明了。
3.2. 证明协议中存在的问题
- prover 可能并不知道他所声称的 \(p(x)\) ,他可以先算一下 \(t = t(r)\) ,然后随便选择一个数 \(h\) ,由此计算出 \(p = t\cdot h\) 。因为等式是成立的,所以也能通过 verifier 的校验。比如,prover 计算出来 \(t = t(23)=462\) 后,随便选择一个数,如 \(h=123\) ,由此计算出 \(p = t \cdot h = 462 \cdot 123 = 56826\) ,将 \(p\) 和 \(h\) 提供给 verifier,这也会通过 verifier 的验证。
- 因为 prover 知道随机点 \(x = r\) ,他可以构造出一个任意的多项式,这个任意多项式与 \(t(r) \cdot h(r)\) 在 \(x=r\) 处有共同点。比如,prover 知道 verifier 发送给他的值为 23 后,随便找一个包含 \((x-23)\) 因子的多项式,例如 \(p'(x)=(x-23)^2\) , 去验证上面协议,照样可以通过验证。
- 在前面的「陈述」中,prover 声称他知道一个特定阶数的多项式,但现在的协议对阶数并没有明确的要求。因而 prover 完全可以拿一个满足因式校验的更高阶数的多项式来欺骗 verifier。比如,尽管要证明 prover 声称知道的 \(p(x) = (x-1)(x-2)x = x^3 - 3x^2 + 2x\) ,但在上面协议中,prover 使用另外一个更高阶数多项式,如 \(p'(x) = (x-1)(x-2)x^3 = x^5 - 3x^4 + 2x^3\) 去验证上面协议,照样可以通过验证。
4. 模糊计算
在节 3.2 中提到的前 2 个问题是由于暴露了原始值(例子中的随机数 23)而导致的,也就是 prover 知道了 \(r\) 和 \(t(r)\) 。但如果 verifier 给出的这个值像放在黑盒里一样不可见的话就完美了,也就是一个人即使不破坏协议,也依然能在这些模糊的值上面完成计算。
如何在不暴露原始值前提下,还进行验证呢?请看下文。
4.1. 同态加密
同态加密(Homomorphic encryption)可以解决前面提到的“原始值暴露”的问题。 同态加密允许在密文上进行算术运算,进行算术运算时不用先解密出原文。
同态加密关注的是数据处理安全。同态加密提供了一种对加密数据进行处理的功能。我们举个实际生活中的例子(这个例子摘自 https://www.zhihu.com/question/27645858/answer/37598506 )。有个叫 Alice 的用户买到了一大块金子,她想让工人把这块金子打造成一个项链。但是工人在打造的过程中有可能会偷金子啊,毕竟就是一克金子也值很多钱。因此能不能有一种方法,让工人可以对金块进行加工,但是不能得到任何金子?
当然有办法啦,Alice 可以这么做:
- Alice 将金子锁在一个密闭的盒子里面,这个盒子安装了一个手套。
- 工人可以带着这个手套,对盒子内部的金子进行处理。但是盒子是锁着的,所以工人不仅拿不到金块,连处理过程中掉下的任何金子都拿不到。
- 加工完成后。Alice 拿回这个盒子,把锁打开,就得到了金子。
这个过程如图 3 所示。
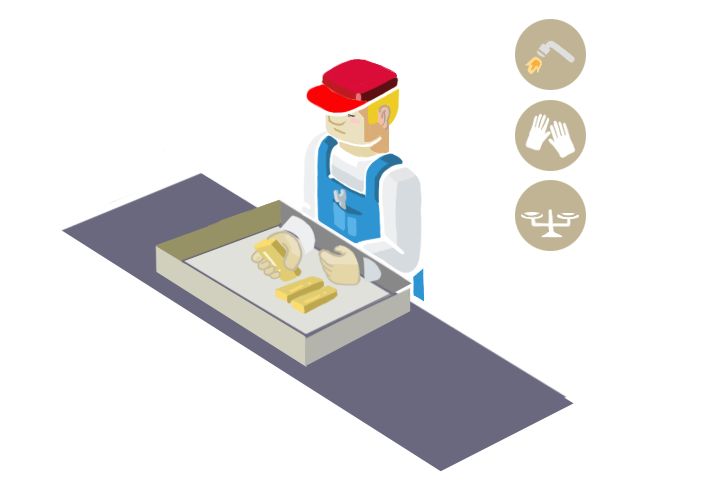
Figure 3: 同态加密类比:工人不直接接触金子的情况下加工金子
同态加密的思路是选择一个基础的(基数需要具有某些特定的属性)的自然数 \(g\) (比如 5),然后我们以要加密的值为指数对 \(g\) 进行求幂。例如,如果我们要对 3 进行加密:
\[5^3 =125\]
这里 125 就是 3 对应的密文。如果我们想要对原数据(被加密值)乘 2,我们可以以 2 为指数来对这个密文进行计算:
\[125^2 = 15625 = (5^3)^2 =5^{2 \times 3} = 5^6\]
我们不仅可以用 2 来乘以一个未知的值并保持密文的有效性,还可以通过密文相乘来使两个原数据相加,例如原数据上的 \(3+2\) 运算,对应密文上的操作就是它们的加密值相乘:
\[5^3 \cdot 5^2 = 5^{3+2} = 5^5= 3125\]
不过由于基数 5 是公开的,很容易就可以找到被加密的数字。只要将密文一直除以 5,直到结果为 1,那么做除法的次数也就是被加密值的数。如密文 \(125\) 除以 5,重复 3 次就是结果 1,重复除法次数就是原数据,这泄露了原数据 3。 为了把基数 g 和原数据(上面例子中的 3)的关系切断,更好地保护原数据,我们在同态加密中引入「模运算」。
先看几个模运算的例子(对 7 取模):
引入模运算后,告诉你加密后的值,就很难知道指数(原值)是多少了。比如,告诉你加密后的值为 6,那么 3,9,15 都满足条件,就无法知道原值到底是多少了。
引入模运算后,前面介绍的性质没变:
上面第 2/3 个式子的含义是: 对加密后的值取 \(n\) 次幂,相当于对原数据乘以数字 \(n\) 后再加密;两个加密后的值相乘,相当于对原数据相加后再加密。
我们来明确地说明一下加密函数:
\[E(v)=g^v \pmod m\]
这里 \(v\) 就是我们要加密的值。
4.1.1. 同态加密的限制
对于上面介绍的同态加密,有个限制: 给你两个加密值,我们没有办法通过加密值上的运算来实现“原数据的相乘”。
前面介绍的 \(\text{multiplication:} \quad (5^3)^2 = 5^{3 \times 2} = 1 \pmod 7\) ,其中原数据相乘 \(3 \times 2\) 中的数字 \(2\) 在加密值上运算时,是以明文 \(2\) 的形式直接参与运算,而不是以它的加密形式 \(5^2\) 参与运算的,所以这个计算过程中只涉及了一个加密值(即 \(5^3\) )。
在节 6.1 中将介绍如何处理这个问题。
4.2. 新的验证协议
有了同态加密后,对于在节 3 中提到的证明问题,可以为它重新设计一个验证协议了,在这个验证协议中,不会暴露原始的随机数了。
在介绍新验证协议之前,先介绍一下已知在 \(x\) 处 \(x, x^2, x^3\) 的加密值为 \(E(x), E(x^2), E(x^3)\) ,如何计算多项式 \(p(x) = x^3 - 3x^2 + 2x\) 的加密计算结果。
现在我们更新一下节 3 中设计的证明协议。
prover 声称他知道一个 \(d\) 阶多项式 \(p(x)=c_d x^d + \cdots + c_1 x^1 + c_0 x^0\) ,这个多项式包含因子 \(t(x)\) (这个多项式前面介绍过,称为目标多项式)。那么 verifier 怎么证明 prover 没有说谎呢?
验证过程如下(在下面的写法中把 \(E(v)=g^v \pmod m\) 直接省写为了 \(E(v)=g^v\) )。
第一步,verifier 进行下面操作:
- 取一个随机数 \(s\) ,也称为秘密值;
- 分别计算 \(i\) 取值为 \(0,1,\cdots, d\) 时 \(s^i\) 的加密结果,即 \(E(s^i) = g^{s^i}\) ;
- 代入 \(s\) 计算未加密的目标多项式 \(t(s)\) ;
- 将第 2 步计算出来的加密值 \(g^{s^0}, g^{s^1}, g^{s^2}, \cdots, g^{s^d}\) 提供给 prover。
第二步,prover 进行下面操作:
- 计算多项式 \(h(x) = p(x)/t(x)\) ;
- 使用加密值 \(g^{s^0}, g^{s^1}, g^{s^2}, \cdots, g^{s^d}\) 和 prover 所已知的 \(p(x)\) 的系数 \(c_0, c_1, \cdots, c_d\) 计算出 \(p(x)\) 的加密值,采用式子 \(E(p(s)) = g^{p(s)} = (g^{s^d})^{c_d} \cdots (g^{s^1})^{c_1} \cdot (g^{s^0})^{c_0}\) 即可,其结果记为 \(g^p\) ;
- 使用和上一步相同的方法计算出 \(h(s)\) 的加密值 \(E(h(s))\) ,记为 \(g^h\) ;
- 把上两步的结果 \(g^p\) 和 \(g^h\) 提供给 verifier。
最后,verifier 进行下面验证:
- 在加密空间中,校验 \(g^p = \left(g^h\right)^{t(s)} = g^{t(s) \cdot h}\) 是否成立。如果成立,则说明 \(p = t(s) \cdot h\) ,从而 prover 所知道的多项式 \(p(x)\) 有很大的可能性确实具有因子 \(t(x)\) 。
在这个证明协议中,prover 并不知道跟秘密值 \(s\) 相关的任何信息,这就使得他很难提出不合法但是能够匹配验证的计算结果(节 3.2 中提到的前 2 个问题得到了解决)。
尽管这个协议中对 prover 作弊的手段进行了限制,但 prover 依然可以在实际根本不使用 verifier 所提供的加密值进行计算,而是通过其它的方式来伪造证明。也就是说,在 prover 提交给 verifier 的两个值 \(g^p\) 和 \(g^h\) 时,并不是按照协议规定的方式计算出来的,而是 prover 用其它方式得到的只要满足条件 \(z_p = (z_h)^{t(s)}\) 的 \(z_p, z_h\) ,如果 prover 用 \(z_p, z_h\) 来分别伪造 \(g^p\) 和 \(g^h\) ,下一步 verifier 验证时,照样可以通过验证。为了堵住这个漏洞,请看节 4.3 的内容。
4.2.1. 具体实例
我们以节 3 提到的证明问题为例,即 prover 声称他知道一个 3 阶多项式(假设为 \(p(x)= x^3 - 3x^2 + 2x\) ),有因子 \(t(x) = (x-1)(x-2)\) ,演示一下上面的过程。
设加密函数为 \(E(v) = 5^v \pmod 7\)
第一步,verifier 进行下面操作:
- 取一个随机数 \(s=23\) ,也称为秘密值;
- 分别计算 \(i\) 取值为 \(0,1,\cdots, d\) 时 \(s^i\) 的加密结果,即 \(g^{s^1} = 5^{23} \pmod 7 = 3, g^{s^2} = 5^{23^2} \pmod 7 = 5, g^{s^3} = 5^{23^3} \pmod 7 = 3\) ;
- 代入 \(s\) 计算未加密的目标多项式 \(t(s)=t(23)=(23-1)(23-2)= 462\) ;
- 将第 2 步计算出来的加密值 \(g^{s^1}=3, g^{s^2}=5, g^{s^3}=3\) 提供给 prover。
第二步,prover 进行下面操作:
- 计算多项式 \(h(x) = p(x)/t(x) = x\) ;
- 使用加密值 \(g^{s^1}, g^{s^2}, g^{s^3}\) 和 prover 所已知的 \(p(x)\) 的系数 \(c_1=2, c_2=-3, c_3=1\) 计算出 \(p(x)\) 的加密值,采用式子 \(E(p(s)) = g^{p(s)} = (g^{s^d})^{c_d} \cdots (g^{s^1})^{c_1} \cdot (g^{s^0})^{c_0}\) 即可,其结果记为 \(g^p = 3^1 \cdot 5^{-3} \cdot 3^2 \pmod 7 = 27/125 \pmod 7 = 1\) ;
- 使用和上一步相同的方法计算出 \(h(s)\) 的加密值 \(E(h(s))\) ,记为 \(g^h = 3^1 \pmod 7 = 3\) ;
- 把上两步的结果 \(g^p=1\) 和 \(g^h=3\) 提供给 verifier。
最后,verifier 验证 \(g^p = (g^h)^{t(s)}\) ,即 \(1 = 3^{462} \mod 7\) ,这个式子是成立的,验证通过。
上面过程中涉及了分数取模,即 \(27/125 \pmod 7 = 1\) ,可参考:
https://stackoverflow.com/questions/32418693/modular-arithmetic-using-fractions
https://math.stackexchange.com/questions/586595/finding-modular-of-a-fraction
4.3. 限制多项式(Knowledge-of-Exponent Assumption)
上一节的验证协议中有个漏洞:prover 可能使用另外的值 \(z_p, z_h\) 来伪造 \(g^p\) 和 \(g^h\) 。我们需要想办法确保 prover 给出的值( \(g^p\) 和 \(g^h\) )就是通过 verifier 提供给 prover 的加密值 \(g^{s^0}, g^{s^1}, g^{s^2}, \cdots, g^{s^d}\) 计算而来。
我们看一个由一个变量和一个系数组成的一阶多项式的简单例子,对应的 \(s\) 的加密值为 \(E(s) = g^s\) 。这里我们要做的就是确保 prover 是拿 \(g^s\) (而不是其他值)与系数 \(c\) 做同态相乘的。所以结果一定是这个形式:
\[\left(g^s \right)^c\]
通过 Knowledge-of-Exponent Assumption(简称 KEA)方法可以实现上面的目标。 后文将描述 KEA。
4.3.1. 限制对某个值只能进行指数取模运算
Alice 有一个值 \(a\) ,她提供给 Bob,要求 Bob 只对值 \(a\) 进行指数取模运算后返回计算结果。
1、为了确保上面这一点,Alice 进行下面操作:
1.1、选择一个随机数 \(\alpha\)
1.2、计算 \(a' = a^{\alpha} \pmod n\)
1.3、提供一个元组 \((a, a')\) 给 Bob,然后让他对 \((a, a')\) 两个值执行相同的指数运算,返回结果元组 \((b, b')\)
2、因为 Bob 无法从元组 \((a, a')\) 中提取 \(\alpha\) 值,通过暴力破解也难以实现,那就可以推断 Bob 生成有效元组的唯一方法就是执行下面的步骤:
2.1、选择一个值 \(c\)
2.2、计算 \(b=(a)^c \pmod n\) 和 \(b' = (a')^c \pmod n\)
2.3、回复 \((b,b')\) 给 Alice
3、有了回复的元组 \((b,b')\) 和 \(\alpha\) ,Alice 验证等式: \((b)^{\alpha} = b' \pmod n\)
最后一步,如果 Alice 验证 \((b)^{\alpha} = b' \pmod n\) 成立,则说明 Bob 对 \(a\) 和 \(a'\) 采用了相同的指数进行计算。
注:在上面协议中,随机数 \(\alpha\) 只有 Alice 知道(Bob 不知道),而 \(c\) 值只有 Bob 知道(Alice 不知道)。
上面介绍的 KEA 方法可表示为:
Alice Bob
(a, a^\alpha mod n) ----希望 Bob 对这两个值只进行指数取模运算---->
黑盒子
<----- 运算后返回 (b, b') -------
如果 Alice 验证 b^\alpha = b' mod n 成立,则数 b 确实是由 Bob 对 a 进行「指数取模」运算而来。
我们把 \(a \overset{\alpha \; \text{shift}}{\longrightarrow} a^\alpha \pmod n\) 称作是 \(\alpha\) shift,这两个数分别进行指数取模运算后,得到的结果也会满足 \(\alpha\) shift,即 \(b \overset{\alpha \; \text{shift}}{\longrightarrow} b'\) ;反过来,如果两个结果值满足 \(\alpha\) shift,那么 \(b\) 一定是从 \(a\) (而不是其他值)经过指数取模运算(而不是其它运算)而来。
在同态加密中,求幂是对被加密值进行乘法运算。我们可以应用这个结构到一个简单的系数多项式 \(f(x) = c \cdot x\) 的例子中:
- verifier 选择随机数 \(s, \alpha\) ,把值 \((g^s, g^{\alpha s})\) 提供给 prover;
- prover 代入系数 \(c\) 计算 \(((g^s)^c, (g^{\alpha s})^c) = (g^{cs}, g^{\alpha c s})\) ,把结果 \((g^{cs}, g^{\alpha c s})\) 返回给 verifier;
- verifier 验证 \((g^{cs})^\alpha = g^{\alpha c s}\) ,如果成立说明 prover 是对 \(s\) (而不是其它值)进行指数取模运算。
4.3.2. 扩展 KEA 到多项式
现在我们可以扩展这种单项式上的 KEA 方法到多项式上。对于阶数为 \(d\) 的多项式:
1、verifier 选择随机数 \(s, \alpha\) ,把加密值 \(g^{s^0}, g^{s^1}, \cdots, g^{s^d}\) 和它们的 \(\alpha\) shift 值 \(g^{\alpha s^0}, g^{\alpha s^1}, \cdots, g^{\alpha s^d}\) 提供给 prover;
2、prover 进行下面操作:
2.1、使用 verifer 提供的加密值,计算 \(g^{p(s)} = \left(g^{s^0}\right)^{c_0} \cdot \left(g^{s^1}\right)^{c_1} \cdots \left(g^{s^d}\right)^{c_d} = g^{c_0 s^0 + c_1 s^1 + \cdots + c_d s^d}\)
2.2、使用 verifer 提供的加密值的 \(\alpha\) shift 值,计算 \(g^{\alpha p(s)} = \left(g^{\alpha s^0}\right)^{c_0} \cdot \left(g^{\alpha s^1}\right)^{c_1} \cdots \left(g^{\alpha s^d}\right)^{c_d} = g^{\alpha(c_0 s^0 + c_1 s^1 + \cdots + c_d s^d)}\)
2.3、把上面两步的结果作为 \(g^p, g^{p'}\) ,提供给 verifier
3、验证 \((g^p)^{\alpha} = g^{p'}\)
以前面介绍过的多项式 \(p(x) = x^3 - 3 x^2 + 2x\) 为例,演示一下上面的过程。
1、verifier 选择随机数 \(s, \alpha\) ,把加密值 \(g^{s^1}, g^{s^2}, g^{s^3}\) 和它们的 \(\alpha\) shift 值 \(g^{\alpha s^1}, g^{\alpha s^2}, g^{\alpha s^3}\) 提供给 prover;
2、prover 进行下面计算,把结果返回给 verifier:
3、verifier 验证 \((g^p)^{\alpha} = g^{p'}\)
现在我们就可以确保 prover 是用 verifier 提供的加密值(而不是其它值)做指数取模运算(而不是其它运算)了,因为别的方法不能够保证 prover 返回给 verifier 的两个值 \((g^p, g^{p'})\) 也满足 \(\alpha\) shift。
把上面的 KEA 过程结合到节 4.2 介绍的协议中,我们就有了一个比较健壮的协议了。
5. 零知识
KEA 过程结合到节 4.2 介绍的协议后(参见上节),prover 提供了 3 个值 \(g^p, g^{p'}, g^h\) 给 verifier,verifier 使用这些数据验证下面两个等式:
如果上面第一个式子通过验证说明 \(p(x)\) 有因子 \(t(x)\) ,而第二个式子通过验证则说明 prover 确实是用 verifier 提供的加密值做指数取模运算。
现在的问题是,我们担心 verifier 能够从 prover 提供的数据 \(g^p, g^{p'}, g^h\) 中提取未知多项式 \(p(x)\) 的相关信息。零知识证明的关键就是 prover 所知道的信息(这里指多项式 \(p(x)\) )不能泄露出来。
如何使得两个校验依然有效,同时又保证没有知识能被提取?我们可以使用随机值 \(\delta\) (这个值只有 prover 知道)来“变换”这些值,也就是说,prover 不直接提供 \(g^p, g^{p'}, g^h\) 给 verifier,而是提供下面 3 个值:
\[(g^p)^\delta, (g^{p'})^\delta, (g^h)^\delta\]
verifier 收到这 3 个值后,同样可以采用前面的方式进行验证:
由于这种方式实现零知识是如此简单,这种方式也被称为“无成本的”零知识。
借助这个“无成本的”技巧,就可以轻松实现零知识了。但是这里实现零知识的方法和实际中的 Pinocchio 协议(参考节 7.12),还有 Groth16 方案略有不同。
6. 非交互式(Non-Interactivity)
到现在为止,我们已经讲完了一个交互式的零知识方案。但为什么我们还需要有非交互式(Non-Interactive Zero-Knowledge, NIZK)呢?因为交互式证明只对原始的 verifier 有效,其他任何人(其他的 verifier)都不能够信任这个证明,因为:
- verifier 可以和 prover 串通,告诉他秘密参数 \(s, \alpha\) ,有了这些参数 prover 就可以伪造证明;
- verifier 也可以使用同样的方法自己伪造证明;
- verifier 必须保存 \(\alpha\) 和 \(t(s)\) 直到所有相关证明被验证完毕,这就带来了一个可能造成秘密参数泄漏的额外攻击面。
我们需要一个可以被重复使用,公开,可信,又不会被滥用的秘密参数。
我们先来思考一下在构造出秘密值 \(\alpha, t(s)\) 之后如何保证它的安全性。我们可以对其进行同态加密。但是节 4.1.1 中提到,我们使用的同态加密并不支持“加密空间中实现原数据相乘”,但验证时我们需要验证原数据 \(t(s)\) 和 \(h\) 相乘,以及原数据 \(p\) 和 \(\alpha\) 的相乘。所以我们需要想办法在加密空间中实现原数据相乘。
下一节将解决这个问题。
6.1. 加密空间中实现原数据相乘(Elliptic Curve Pairings)
Cryptographic pairings (bilinear map) 是一个数学结构,记为函数 \(e(g^*, g^*)\) ,它给定一个数据集中的两个加密的输入(即 \(g^a, g^b\) ),可以将他们确定性地映射到另一组不同的输出数据集上的它们的乘积,即 \(e(g^a, g^b) = e(g, g)^{ab}\) ,如图 4 所示。
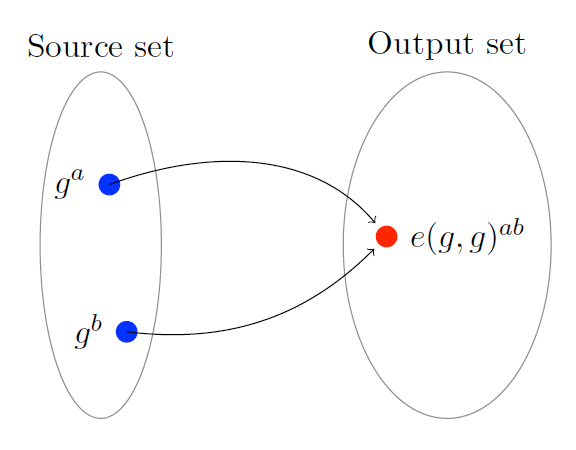
Figure 4: Cryptographic pairings
因为源数据集和输出数据集是不同的,所以一个配对的结果不能用做其他配对计算的输入。我们可以将输出集(也称为“目标集”)视为“不同的宇宙”。因而我们不能用另一个加密值乘以结果,而且配对这个名称本身也表明了,我们一次只能将两个加密值相乘。 注:乍一眼看过去,这个限制可能会阻碍相关功能的实现,但在 zk-SNARK 中这反而是保证安全模式的最重要性质,参见节 6.4。
在某种意义上,这个类似于一个哈希函数,他将所有可能的输入值映射到输出值的集合中的一个元素上,而且这个过程是不可逆的。
配对函数 \(e(g,g)\) 可以初步地(严格来说是不对的)类比成“交换”每一个输出的基数和指数的操作,使得基数 \(g\) 在交换过程中被修改成了指数的方式,即 \(g^a \to a^\mathbf{g}\) (注:这是两个不同的 g,所以使用了不同的字体)。“被转换”的两个输入一起被修改了,这样原始值 \(a\) 和 \(b\) 就在同一个指数下相乘了,即:
\[e(g^a, g^b) = a^{\mathbf{g}} \cdot b^{\mathbf{g}} = (ab)^{\mathbf{g}} \qquad \text{(注:这仅是个类比,是不对的)}\]
因为基数在“转换”中被修改了,所以在另一个配对中不能再使用这个结果 \((ab)^{\mathbf{g}}\) ,也就是说 \(e((ab)^{\mathbf{g}}, g^{c})\) 并不会构造出想要的加密乘积 \(abc\) 。
配对的核心性质可以表示成下面的等式:
\[e(g^a, g^b) = e(g^b, g^a) = e(g^{ab}, g^1) = e(g^1, g^{ab}) = e(g^1, g^a)^b = e(g^1, g^1)^{ab} = \cdots\]
严格来说,一个 Cryptographic pairing 的结果是在目标集的一个不同生成元 \(\mathbf{g}\) 下对原始值乘积的加密,即 \(e(g^a, g^b) = \mathbf{g}^{ab}\) 。 因而它具备同态加密的性质,也就是说我们可以把多个 Cryptographic pairing 的加密乘积放到一起:
\[e(g^a, g^b) \cdot e(g^c, g^d) = \mathbf{g}^{ab} \cdot \mathbf{g}^{cd} = \mathbf{g}^{ab+cd}= e(g,g)^{ab+cd}\]
Cryptographic pairing 利用“椭圆曲线”来实现上面性质,也可称“Elliptic Curve Pairings”。
关于 Cryptographic pairings 的更多知识,可参考 Pairings for beginners, by Craig Costello 。
6.2. 可信任参与方的 Setup
有了 Cryptographic pairing,我们现在就准备去设置安全公开且可复用的参数了。假定一下我们让一个诚实的参与方来生成秘密值 \(s\) 和 \(\alpha\) 。 一旦 \(\alpha\) 和所有必要的 \(s\) 的幂及其对应的 \(\alpha\) 变换被加密了(即生成 \(g^{\alpha}, g^{s^i}, g^{\alpha s^i}, i = 0,1,\cdots,d\) ),那么原始数据就必须要被删除。
注:Zcash 团队在论文 A multi-party protocol for constructing the public parameters of the Pinocchio zk-SNARK 中提出了 MPC 协议来进行“可信任参与方的 Setup”。
这些参数通常被称为 common reference string 或者 CRS。CRS 生成后,任何的 prover 和任何的 verifier 都可以使用它来构造非交互式的零知识证明协议。CRS 的优化版本将包含目标多项式的加密值 \(g^{t(s)}\) ,尽管这个值并不重要。
CRS 可分成两组( \(i = 0,1,\cdots,d\) ):
- proving key(也被称为 evaluation key): \((g^{s^i}, g^{\alpha s^i})\)
- verification key: \((g^{t(s)}, g^{\alpha})\)
只要能够乘以加密值,verifier 就可以在协议的最后一步验证多项式了。有了 verification key,verifier 就可以处理从 prover 那里得到的加密多项式的值 \(g^p, g^h, g^{p'}\) ,进行下面两个校验即可:
- 在加密空间中校验 \(p = t \cdot h\) ,即校验 :
\[e(g^p, g^1) = e(g^t, g^h)\]
- 校验多项式的限制:
\[e(g^p, g^{\alpha}) = e(g^{p'}, g^1)\]
6.3. 信任任意一个参与者
可信任参与方的 Setup 很有效率,但众多 CRS 用户也必须要相信生成者确实删除了 \(\alpha\) 和 \(s\) ,不过我们没有办法证明生成者删除了它们。因而很有必要去最小化或者消除这种信任。否则一个不诚实的参与方就可以构造假证明而不被发现。
一种解决办法就是由多个参与方使用前面小节中介绍的数学工具来生成一个组合式 CRS,这样这些参与方就都不知道“秘密”了。 下面是一个实现方案,我们假设有三个参与者 Alice,Bob 和 Carol ,对应为 A,B 和 C,其中 \(i = 1, 2, \cdots, d\) :
- Alice 选择随机数 \(s_A\) 和 \(\alpha_A\) ,然后公开她的 CRS: \((g^{s_A^i}, g^{\alpha_A}, g^{\alpha_A s_A^i})\)
- Bob 选择他的随机数 \(s_B\) 和 \(\alpha_B\) ,然后通过同态乘法结合 Alice 的 CRS: \(((g^{s_A^i})^{s_B^i}, (g^{\alpha_A})^{\alpha_B}, (g^{\alpha_A s_A^i})^{\alpha_B s_B^i}) = (g^{(s_A s_B)^i}, g^{\alpha_A \alpha_B}, g^{\alpha_A \alpha_B (s_A s_B)^i})\) 然后公开两方 Alice-Bob 的 CRS 结果: \((g^{s_{AB}^i}, g^{\alpha_{AB}}, g^{\alpha_{AB} s_{AB}^i})\)
- Carol 用她的随机数 \(s_C\) 和 \(\alpha_C\) 做同样的事: \(((g^{s_{AB}^i})^{s_C^i}, (g^{\alpha_{AB}})^{\alpha_C}, (g^{\alpha_{AB} s_{AB}^i})^{\alpha_C s_C^i}) = (g^{(s_A s_B s_C)^i}, g^{\alpha_A \alpha_B \alpha_C}, g^{\alpha_A \alpha_B \alpha_C (s_A s_B s_C)^i})\) 然后公开 Alice-Bob-Carol 的 CRS 结果: \((g^{s_{ABC}^i}, g^{\alpha_{ABC}}, g^{\alpha_{ABC} s_{ABC}^i})\)
这个协议最后我们就获得了一个混合的 \(s^i = s_A^i s_B^i s_C^i\) 和 \(\alpha = \alpha_A \alpha_B \alpha_C\) 。除非他们串谋,否则参与者们互相之间并不知道其他人的秘密参数。实际上,一个参与者必须要和其它所有的参与者串谋才能得到 \(s\) 和 \(\alpha\) ,这样在所有的参与者中只要有一个是诚实的,就没有办法伪造证明。
有一个问题是如何验证参与者在生成 CRS 时用的随机数值是一致的(有效的),因为攻击者可以生成多个不同的随机数 \(s_1, s_2, \cdots\) 和 \(\alpha_1, \alpha_2, \cdots\) ,然后代入这些不同的随机数去执行 \(s\) 的不同次幂计算(或提供随机数作为一个 CRS 的扩充),从而导致 CRS 无效或者不可用。
庆幸的是,因为我们可以使用配对来乘以加密值,所以我们就可以从第一个参数开始逐一执行一致性校验,并且确保了每个参数都源于前一个。
- 我们用 \(s\) 的 1 次幂作为标准来校验每一个其它次幂的值与之是否保持一致: \(e(g^{s^i}, g) = \left.e(g^{s^1}, g^{s^{i-1}}) \right|_{i \in 2, 3, \cdots, d}\) 。例如:对于 2 次幂这样验证: \(e(g^{s^2}, g) = e(g^{s^1}, g^{s^{1}}) \Rightarrow e(g, g)^{s^2} = e(g, g)^{s^{1+1}}\) ;对于 3 次幂这样验证: \(e(g^{s^3}, g) = e(g^{s^1}, g^{s^{2}}) \Rightarrow e(g, g)^{s^3} = e(g, g)^{s^{1+2}}\)
- 我们现在再验证一下前面步骤中 \(\alpha\) 变换后的值是否正确: \(e(g^{s^i}, g^{\alpha}) = \left.e(g^{\alpha s^i}, g) \right|_{i \in [d]}\) 。记号 \([d]\) 表示 \(1, 2, \cdots, d\) ,后文将大量使用这个记号。例如:对于 3 次幂这样验证: \(e(g^{s^3}, g^{\alpha}) = e(g^{\alpha s^3}, g) \Rightarrow e(g,g)^{s^3 \cdot \alpha} = e(g,g)^{\alpha s^3}\)
当我们在验证每一个参与者秘密参数的一致性时,要注意参与者生成 CRS 的过程并没有强制后一个参与者(就是我们例子中的 Bob 和 Carol)都要使用前面已经公开的 CRS。因而如果一个攻击者是链上的最后一个参与者,他可以像链上的第一个参与者一样忽略前面的 CRS 随便构造一个有效的 CRS,这样他就变成了唯一一个知道秘密 \(s\) 和 \(\alpha\) 的人。
为了解决这个问题,我们可以额外再要求除了第一个以外的每一个参与者去加密然后公开他的参数。例如,Bob 同时还要公开:
\[\left.(g^{s_B^i}, g^{\alpha_B}, g^{\alpha_B s_B^i}) \right|_{i \in [d]}\]
这样,为了确认 Bob 的 CRS 确实是乘以了 Alice 的参数后获得的,验证下面式子即可:
类似的方法,Carol 也可证明她的 CRS 是乘以了 Alice-Bob 的 CRS 后正常获得的。
这是一个健壮的 CRS 设置模式,它并不完全依赖于单个参与者。事实上,即使其它所有的参与者都串谋了,只要有一个参与者是诚实的,他能够删除并且永远不共享它的秘密参数,这个 CRS 就是有效的。
6.4. 多项式的 SNARK
到目前为止,我们已经介绍了多项式的 SNARK (Succinct Non-Interactive Argument of Knowledge) 协议。
为简洁起见,我们将使用大括号来表示由旁边的下标填充的一组元素,例如: \(\{s^i\}_{i \in [d]}\) 表示集合 \(s^1, s^2, \cdots, s^d\)
这里再重复一下所要证明的问题。 prover 声称他知道一个 \(d\) 阶多项式 \(p(x)=c_d x^d + \cdots + c_1 x^1 + c_0 x^0\) ,这个多项式包含因子 \(t(x)\) (称为目标多项式)。 通过下面步骤可证明 prover 没有说谎。
- Setup
- 挑选随机值 \(s, \alpha\)
- 计算加密值 \(g^{\alpha}, \{g^{s^i}\}_{i \in [d]}, \{g^{\alpha s^i}\}_{i \in {0, \cdots, d}}\)
- 生成 proving key: \((\{g^{s^i}\}_{i \in [d]}, \{g^{\alpha s^i}\}_{i \in {0, \cdots, d}})\)
- 生成 verification key: \((g^{\alpha}, g^{t(s)})\)
- 挑选随机值 \(s, \alpha\)
- Proving
- 求多项式 \(h(x) = p(x) / t(x)\)
- 使用 \(\{g^{s^i}\}_{i \in [d]}\) 计算多项式 \(g^{p(s)}\) 和 \(g^{h(s)}\) 的值
- 使用 \(\{g^{\alpha s^i}\}_{i \in [d]}\) 计算多项式 \(g^{\alpha p(s)}\) 的值
- 选择随机数 \(\delta\)
- 构造 \((g^{\delta p(s)}, g^{\delta h(s), g^{\delta \alpha p(s)}})\) ,它们被称为“提供的证明”,简记为 \((g^p, g^h, g^{p'})\)
- 求多项式 \(h(x) = p(x) / t(x)\)
- Verification
- 验证多项式约束: \(e(g^{p'}, g) = e(g^p, g^{\alpha})\)
- 验证多项式系数: \(e(g^p, g) = e(g^{t(s)}, g^h)\)
- 验证多项式约束: \(e(g^{p'}, g) = e(g^p, g^{\alpha})\)
6.4.1. 安全的关键:Cryptographic pairing 结果不能复用
如果 Cryptographic pairing 的结果有可能在其它类似的乘法协议中被复用,那么这里就完全没有安全性可言了,因为这样的话 prover 就可以构造:
\[g^{p'} = e(g^p, g^{\alpha})\]
这样也可以通过“多项式约束”的检查:
\[e(e(g^p, g^{\alpha}), g) = e(g^p, g^{\alpha})\]
6.5. 结论
我们用 zk-SNARK 协议来解决多项式问题的知识,不过这是一个有局限的例子。因为大家可以说 prover 只要用另外一个有界的多项式去乘以 \(t(x)\) 就可以很容易得构造出一个能够通过测试的多项式 \(p(x)\) ,并且这种结构也是有效的。
verifier 知道 prover 有一个有效的多项式,但是并不知道是哪一个。我们可以利用多项式的其他性质添加额外的证明,如:被多个多项式整除,是某个多项式的平方等等。
下面总结一下这篇文章中是如何一步一步解决了下面的几个问题:
- 保证 prover 的证明是按照规则正确构造的 ——> KEA
- 保证知识的零知性 ——> “无成本的” \(\delta\) 变换
- 可复用证明 ——> 非交互式
- 非交互中如何设置安全公开且可复用的参数 ——> 参数加密,verifier 借助密码配对进行验证
- 保证参数的生成者不泄密 ——> 多方的 Setup
至此,一个用来证明多项式知识的完整的 zk-SNARK 协议就构造出来了,不过现在的协议在通用性上依然还有很多限制,后面的文章将继续介绍如何构造通用的 zk-SNARK。
7. 通用的零知识证明
前面我们已经理顺了一个 zk-SNARK 简单方案的思路,它包含了 zk-SNARK 大部分内在机制,现在我们继续完善方案,使它能执行零知识程序。
7.1. 计算
Algorithm 1: Operation depends on an input
————————————————————————————————————————————————————————————————————
function calc(w, a, b)
if w then
return a × b
else
return a + b
end if
end function
看起来这段程序和我们协议里面的多项式并没有什么关系。我们现在就 需要找到一种方式来将程序转换成多项式。 第一步是将程序转换成数学语言,这个相对简单一些,声明可以表达成下面的形式(假定 \(w\) 是 0 或 1):
\[f(w, a, b) = w(a \times b) + (1 - w)(a + b)\]
执行 \(calc(1, 4, 2)\) 和对 \(f(1, 4, 2)\) 求值都可以得到相同的结果:8。如果执行 \(calc(0, 4, 2)\) 和 \(f(0,4,2)\) 也都能够得到 6。其实 我们可以用这种方法表达任何形式的有限程序。
接下来(上面的例子)需要我们证明的是,对于表达式 \(f(w,a,b)\) ,输入为 \((1, 4, 2)\) 时输出为 8,换句话说,我们要校验多项式:
\[w(a \times b)+(1-w)(a+b) = 8\]
7.2. 单个运算符
尽管已经将程序转换成了由数学语言表达的一般计算形式,我们还是需要再把它翻译成多项式。我们先来仔细研究一下计算的本质。任何计算的内核都是由以下形式的基本运算组成的:
\[\text{左操作数} \quad \text{运算操作符} \quad \text{右操作数} \quad = \text{输出}\]
两个操作数(即值)与一个运算符(即 +,-,×,÷)放在一起执行运算。例如操作数是 2 和 3,运算符为乘,那么运算出来就是 \(2 \times 3 = 6\) 。由于任何复杂的计算(或者程序)都是由一系列这样的基本运算组成的,所以首先我们需要知道在多项式中单个运算是怎么表示的。
7.2.1. 关联多项式和算术运算
我们先来看一下如何将多项式和算术运算关联起来。例如有两个多项式 \(f(x)\) 和 \(g(x)\) ,尝试将他们相乘使得 \(h(x) = f(x) \times g(x)\) ,在任意一个 \(x = r\) 处 \(h(x)\) 的计算结果都是 \(f(r)\) 和 \(g(r)\) 的乘积。再看一下多项式 \(f(x) = 2x^2 - 9x+ 10\) 和 \(g(x) = - 4x^2 + 15x - 9\) ,它们如图 5 所示。
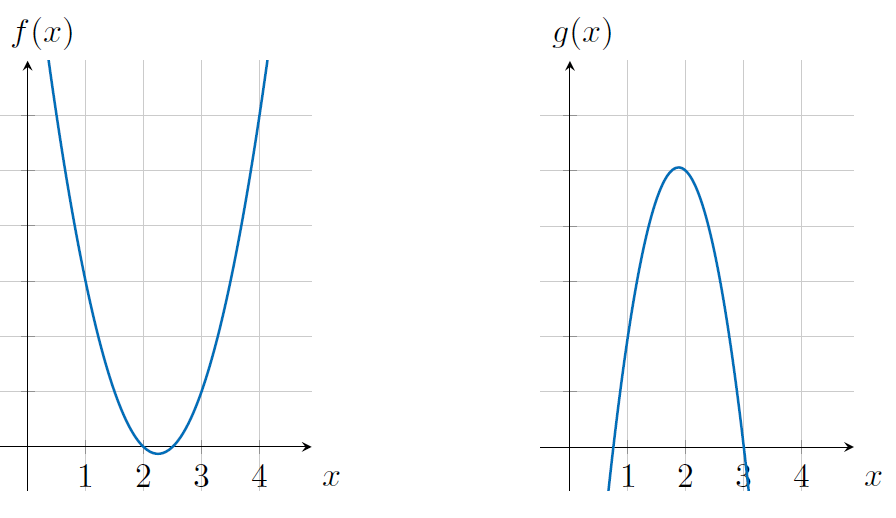
Figure 5: \(f(x)\) 和 \(g(x)\)
当 \(x = 1\) 时 \(f(1) = 2 - 9 + 10 = 3, g(1) = - 4 + 15 - 9 = 2\) 。把两个多项式相乘: \(h(x) = f(x) \times g(x) = - 8x^4 + 66x^3 - 193x^2 + 231x - 90\) ,当 \(x=1\) 时, \(f(x) \times g(x)\) 结果为: \(h(1) = -8 + 66 - 193 + 231 - 90 = 6\) ,如图 6 所示,也就是说当 x = 1 时, \(h(x)\) 就是 \(f(x)\) 和 \(g(x)\) 相乘的结果, \(x\) 取其它值的时候也一样。
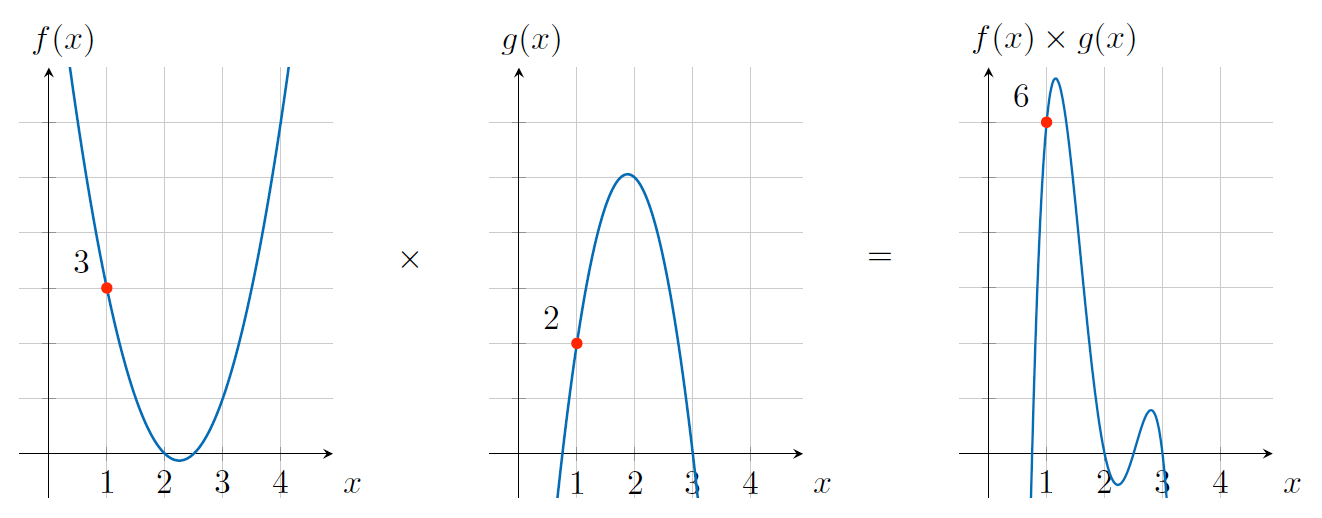
Figure 6: \(f(x) \times g(x)\)
同样地,如果我们将 \(f(x)\) 和 \(g(x)\) 相加,在 \(x=1\) 处的计算结果就是 5,如图 7 所示。 \(x\) 取其它值时,多项式相加的计算结果也是将两者多项式的值加在一起的结果,例如你可以验证一下 \(x=2, x=3\) 处的结果。
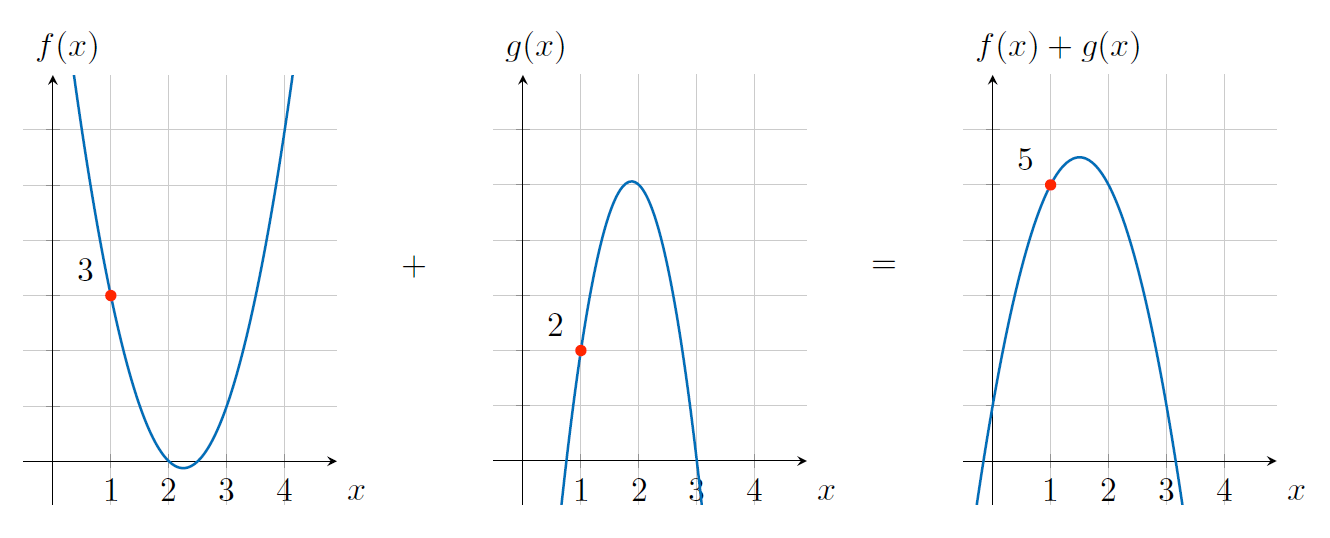
Figure 7: \(f(x) + g(x)\)
如果我们可以将操作数的值表示为多项式(我们也确实可以这么做),那么利用算术属性,我们就能够得到操作数的计算结果了。
7.3. 限制运算
如果一个 prover 声称知道某两个数字的乘积,verifier 要怎样去验证呢?为了证明单个计算的正确性,我们就 必须首先确保所提供的操作数的输出(结果)的正确性。 我们再来看一下运算的形式:
\[\text{左操作数} \quad \text{运算操作符} \quad \text{右操作数} \quad = \text{输出}\]
类似地,我们也可以将其表示为一个运算多项式:
\[l(x) \quad \text{运算操作符} \quad r(x) \quad = o(x)\]
在一些选定的取值 \(x = a\) 处的运算:
- \(l(x)\) :表示(运算结果为)左操作数
- \(r(x)\) :表示(运算结果为)右操作数
- \(o(x)\) :表示运算结果(输出)
因而在计算过程中如果操作数和结果都可以用多项式的形式正确地表示出来,那么 \(l(a) \;operator\; r(a) = o(a)\) 就能够成立。也就是说假如输出多项式 \(o(x)\) 所代表的值是由运算符在操作数多项式 \(l(x)\) 和 \(r(x)\) 上进行某种运算得出的正确结果,那么我们把输出多项式 \(o(x)\) 放到等式的左边就能够得到: \(l(a) \;operator\; r(a) - o(a) = 0\) ,这也就表明了当取值为 \(a\) 时多项式 \(l(x) \;operator\; r(x) - o(x)\) 计算结果为 0 。那么只要多项式是有效的,运算多项式就一定有一个根 \(a\) 。因此,根据前面的基础这个多项式里面一定包含因式 \((x-a)\) ,这就是我们要证明的目标多项式,即 \(t(x) = x - a\) 。
例如,我们来看一个运算: \(3 \times 2 = 6\) 。可以用一个简单的多项式表示它: \(l(x) = 3x, r(x) = 2x, o(x) = 6x\) ,取 \(a=1\) 进行计算,即 \(l(1) = 3; r(1) = 2; o(1) = 6\) ,如图 8 所示。
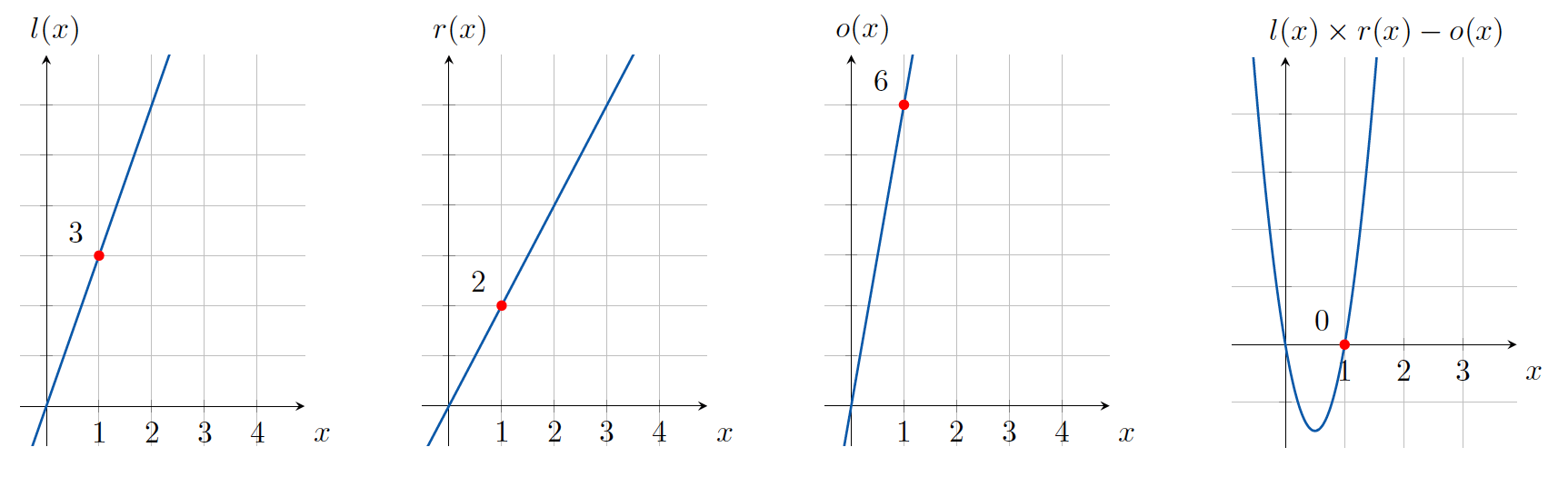
Figure 8: \(l(x) \times r(x) - o(x)\)
\(l(x) \times r(x) - o(x) = 2x \times 3x - 6x = 6x^2 - 6x = 6x(x-1)\) ,显然 \(l(x) \times r(x) - o(x)\) 是有因子 \(x-1\) 的。
因而如果 prover 用 \(l(x), r(x), o(x)\) 这些多项式来代替 \(p(x)\) ,因为它们依然可以被 \(t(x)\) 整除,所以 verifier 就可以认为它们是有效的。相反,如果 prover 尝试用 4 来代替输出值去欺骗 verifier ,即 \(o(x) = 4x\) ,那么运算多项式就变成了 \(6x^2 - 4x = 0\) ,如图 9 所示。
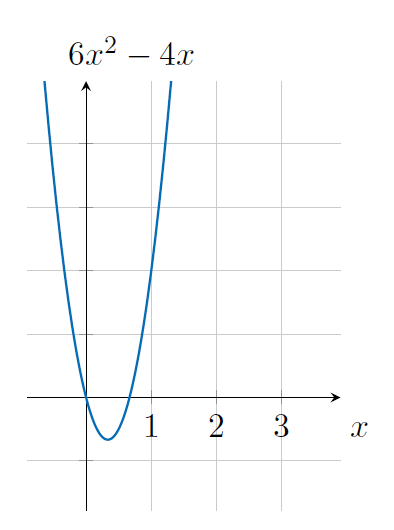
Figure 9: \(6x^2 - 4x\)
图 9 中这个多项式并没有 \(x=1\) 的解,因而 \(l(x) \times r(x) - o(x)\) 就不能被 \(t(x)\) 整除。因而 verifier 不会接受 4 这个计算结果。
7.4. 运算的证明
现在我们来修改一下最新协议使它支持单个乘法计算的证明。在节 6.4 中,我们已经有证明多项式 \(p(x)\) 的知识了,只不过现在要计算的是三个多项式 \(l(x), r(x), o(x)\) 。我们可以定义 \(p(x) = l(x) \times r(x) - o(x)\) ,但这里存在两个争议点。首先,在我们的协议中证明阶段是不能做加密值乘法计算的(即 \(l(s) \times r(s)\) ),因为配对只能用一次,这个要用在校验多项式的约束上。第二,这里给 prover 留下了一个可以修改多项式结构但依然保留有效因式 \(t(x)\) 的机会,例如可以令 \(p(x) = l(x)\) 或者 \(p(x) = l(x) - r(x)\) 甚至是 \(p(x) = l(x) \times r(x) + o(x)\) ,只要这里的 \(p(x)\) 还保留着根 \(a\) 就可以了。这个修改本质上是让证明的内容变成了别的声明,所以这样是不行的。
所以 prover 必须要分别提供多项式 \(l(s), r(s), o(s)\) 值的证明,即协议必须修改要证明的多项式的知识。verifier 在加密空间中要验证的是 \(l(s) \times r(s) – o(s) = t(s)h(s)\) 。verifier 可以使用密码学配对来执行乘法,但还有一个小问题就是做减法( \(– o(x)\) )是非常昂贵的计算(这需要去找到一个 \(g^{o(s)}\) 的逆向转换),这里我们可以把 \(o(x)\) 移到等式右边来: \(l(x)r(x) = t(x)h(x) + o(x)\) 。在加密空间中,verifier 的验证就可以转换成:
保持 setup 阶段(参见节 6.4)不变,协议更新为:
- Proving
- 计算多项式 \(h(x) = \frac{l(x) \times r(x) - o(x)}{t(x)}\)
- 使用 \(\{g^{s^i}\}_{i \in [d]}\) 计算多项式 \(g^{l(s)}, g^{r(s)}, g^{o(s)}, g^{h(s)}\) 的值
- 使用 \(\{g^{\alpha s^i}\}_{i \in [d]}\) 计算多项式 \(g^{\alpha l(s)}, g^{\alpha r(s)}, g^{\alpha o(s)}\) 的值
- 构造 \((g^{l(s)}, g^{r(s)}, g^{o(s)}, g^{h(s)}, g^{\alpha l(s)}, g^{\alpha r(s)}, g^{\alpha o(s)})\) ,它们被称为“提供的证明”,简记为 \((g^l, g^r, g^o, g^h, g^{l'}, g^{r'}, g^{o'})\)
- 计算多项式 \(h(x) = \frac{l(x) \times r(x) - o(x)}{t(x)}\)
- Verification
- 验证多项式约束:\(e(g^{l'}, g) = e(g^l, g^{\alpha}), \quad e(g^{r'}, g) = e(g^r, g^{\alpha}), \quad e(g^{o'}, g) = e(g^o, g^{\alpha})\)
- 验证运算的有效性: \(e(g^l, g^r) = e(g^{t(s)}, g^h) \cdot e(g^o, g)\)
- 验证多项式约束:\(e(g^{l'}, g) = e(g^l, g^{\alpha}), \quad e(g^{r'}, g) = e(g^r, g^{\alpha}), \quad e(g^{o'}, g) = e(g^o, g^{\alpha})\)
这个协议就能够证明两个值相乘的计算结果是正确的了。
你可能注意到了在这个新的协议中我们放弃了零知识部分(即没有引入节 6.4 中用于实现零知识的随机数 \(\delta\) )。这么做是为了简化协议的变换。后面的章节(节 7.12)我们会再变回零知识。
7.5. 多个运算
现在我们已经能够证明单个算术运算了,但是要怎么扩展到多个运算上呢(这是我们的最终目标)?我们来尝试一下增加一个基本运算。想一想计算 \(a \times b \times c\) 乘积的需求,在基本操作模型中,这代表着两个操作:
前面的讨论中我们通过对运算符多项式在任意 \(x\) 处,例如 \(x=1\) ,计算一个对应值,来表示一个操作数或者结果。有了这个性质的多项式并不会约束我们在不同 \(x\) 取值处用多项式来表示其他值。如图 10 中的 \(x=2\) 。
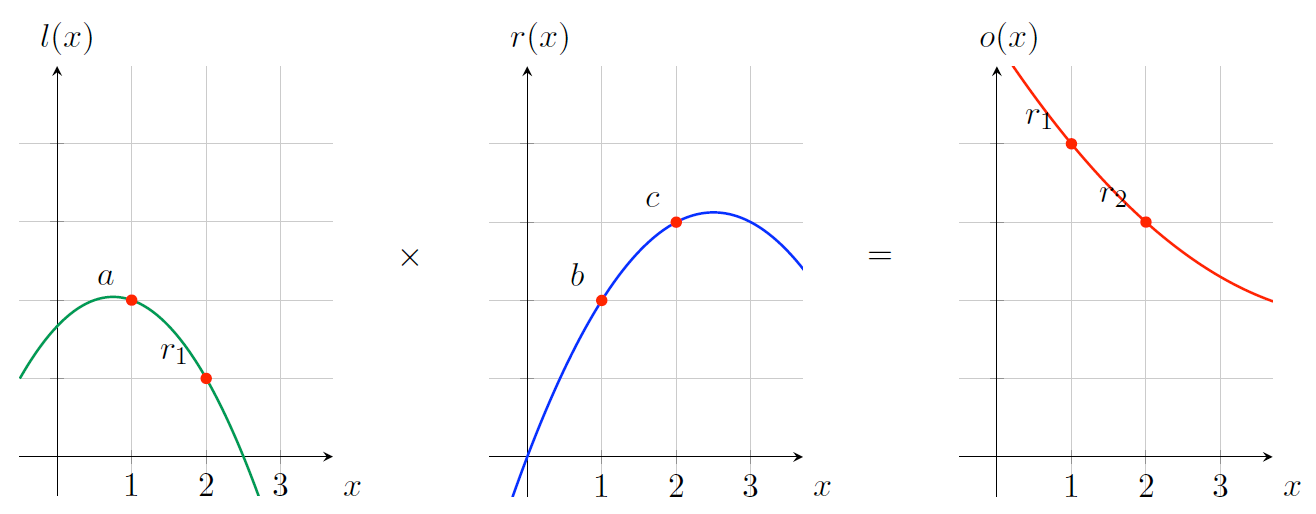
Figure 10: 一次同时执行两个运算 \(l(1) \times r(1), l(2) \times r(2)\)
这种独立性允许我们一次同时执行两个运算并且又不会把这两者搞乱。这个多项式算术的结果就变成了图 11 所示。
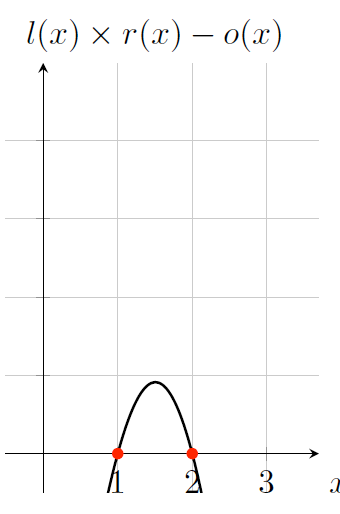
Figure 11: \(l(x) \times r(x) - o(x)\)
可以看出这个多项式有两个根 \(x=1, x=2\) 。因而也就是两次计算都被正确执行了。
我们再来看一个有三个乘法运算的例子 \(2 \times 1 \times 3 \times 2\) ,它按照下面的步骤执行:
我们要把它们表示为操作数多项式, 对于由 \(x \in \{1, 2, 3\}\) 所表示的计算, \(l(x)\) 相应的值等于 2,2 和 6。即通过点 \((1, 2), (2, 2), (3, 6)\) ,同样的 \(r(x)\) 通过点 \((1, 1),(2, 3),(3,2)\) ,\(o(x)\) 通过点 \((1, 2), (2, 6), (3, 12)\) 。
现在是问题是, 我们要怎么找到经过这些点的多项式呢? 对于任何包含超过一个点的例子,就必须要使用特定的数学方法了。
7.5.1. 多项式插值
为了构造操作数和输出多项式,我们需要一种方法来用给定的一组点去构造一个能经过所有这些点的弯曲多项式,这叫插值。有几种不同的方法可以算出这个多项式:
- 一组未知方程
- 牛顿多项式
- Neville 算法
- 拉格朗日多项式
- 快速傅里叶变换
我们以第一个方法为例。这个方法的思路是存在一个系数未知,阶数至多为 \(n\) 的特定的多项式 \(p(x)\) 能够经过给定的 \(n+1\) 个点,对于每个点 \(\{(x_i, y_i)\}_{i \in [n+1]}\) 来说,多项式在 \(x_i\) 处的计算结果都等于 \(y_i\) ,即对于所有的 \(i\) , \(p(x_i) = y_i\) 。在我们的例子中,三个点就可以变成一个用以下形式所表示的阶数为 2 的多项式:
\[ax^2 + bx + c = y\]
我们先来看一下如何求得 \(l(x)\) 多项式:
\[\begin{cases} l(1) = 2 \\ l(2) = 2 \\ l(3) = 6 \end{cases} \Rightarrow \begin{cases} a(1)^2 + b \cdot 1 + c = 2 \\ a(2)^2 + b \cdot 2 + c = 2 \\ a(3)^2 + b \cdot 3 + c = 6 \end{cases} \Rightarrow \begin{cases} a = 2 \\ b = -6 \\ c = 6 \end{cases}\]
因而“左操作数多项式”就是:
\[l(x) = 2x^2 - 6x + 6\]
我们用相同的方式可以计算得到:
\[r(x) = \frac{-3x^2 + 13x - 8}{2}; \quad o(x) = x^2 + x\]
7.5.2. 含有多个运算的多项式
现在我们有了代表三个运算的操作数多项式,再进一步看一下怎么去校验每个计算的正确性。回到 verifier 寻找等式 \(l(x) \cdot r(x) - o(x) = t(x)h(x)\) 的过程。在这个例子中,因为计算是在点 \(x \in \{1, 2, 3\}\) 处被表示出来的,所以目标多项式在这些点处的计算结果必须为 0,换句话说, \(t(x)\) 的根必须是 1,2 和 3,它的基本形式如图 12 所示。
Figure 12: \(t(x)\) 的基本形式
结合上一节得到的 \(l(x), r(x), o(x)\) ,可以得到:
\[h(x) = \frac{l(x) \times r(x) - o(x)}{t(x)} = \frac{-3x^4 + 22x^3 - 56x^2 + 63x - 24 - (x^2 + x)}{(x-1)(x-2)(x-3)} = -3x + 4\]
把 \(h(x)\) (往往是其加密值)提供给 verifier 后,verifier 验证 \(l(x) \times r(x) = t(x)h(x) + o(x)\) ,这就是我们要证明的内容。
7.6. 变量多项式
有了前文介绍的方法来解决证明多个计算多项式的问题,我们就可以一次证明多个运算(如上百万个甚至更多)了,但是这个方案还有一个关键的缺点。
如果证明中执行的“程序”在不同运算中使用了相同的变量作为操作数或输出, 例如:
这里 \(a\) 代表两个运算中的左操作符多项式,如图 13 所示。
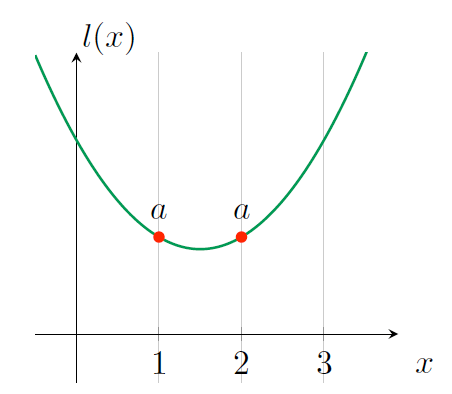
Figure 13: \(l(x)\) 经过点 \((1, a), (2, a)\)
然而,因为我们的协议中是允许 prover 为多项式设置任何系数的,所以他可以不受限制地为不同计算(即,用一些 \(x\) 表示的多项式)中的 \(a\) 设置不同的值,如图 14 所示。
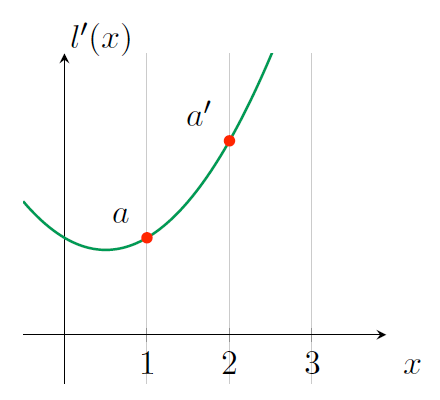
Figure 14: \(l'(x)\)
这个自由打破了一致性,有空间允许 prover 能去证明了一些并非 verifier 感兴趣的其它无关的程序执行。因而我们 必须要确保每一个变量(assignment)在所有运算中出现的地方都只有一个取值。
注意:文中的“变量”与常规的计算机科学中变量的定义不同,这里的变量是不可改变的而且每次执行都只赋值一次。请务必注意这里“变量”的含义,它是程序中的变量,但是却又不能改,这不是很矛盾吗?其实,这里变量是指本文开头的示例伪代码中的那些不会被修改的变量。在 zkSNARK 论文中,这个“变量”其实有一个对应的名词叫做 assignment,是算术电路的“赋值”。而所有的 assignments 是一个算术电路可满足性问题的解,包含了算术电路的输入值以及电路运算过程中输出的中间结果值。
7.6.1. 单个变量的操作数多项式
我们来看一个简单的例子(就是当前的例子),在左操作符多项式 \(l(x)\) 表示的所有左操作数中只包含一个变量(即 \(a\) )。我们要找出是否有可以确保这个多项式在每一个运算中 \(a\) 都相同的方法。prover 可以设置不同值是因为他可以任意控制 \(x\) 的每个次幂的系数。因而如果这些系数是固定的,就可以解决问题了。
我们来仔细看看包含相等值的多项式。例如检查一下图 15 中的两个多项式,他们分别都表示了有两个相等值对应的运算(即在 \(x=1\) 和 \(x=2\) 处),这里第一个多项式的值为 1,第二个多项式的值为 2。
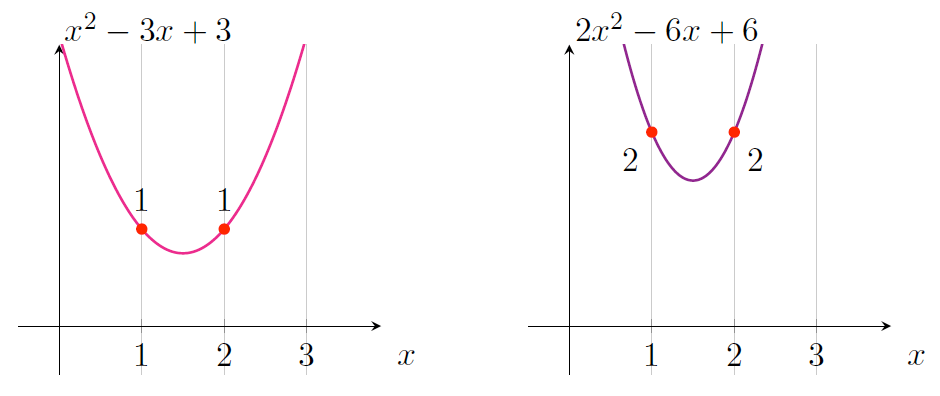
Figure 15: \(x=1\) 和 \(x=2\) 处相等
注意每个多项式中相应的系数是成比例的,也就是第二个多项式的系数是第一个的两倍大,即:
\[2x^2-6x+6=2 \times (x^2 -3x+3)\]
那么由于多项式的算术性质,如果我们想要同时地改变多项式中所有的值我们就需要改变它的比例,如果我们用一个数字乘以多项式,那么在每一个可能的 \(x\) 处的计算结果也要和相同的数字相乘(即,等比例变换)。为了验证这一点,我们尝试用 3 或者其它数字来乘第一个多项式。
因此, 如果 verifier 需要在所有计算中强制 prover 设置相同的值,他就要限制 prover 只能修改比例而不是单个系数。
所以怎么保持系数比例不变呢?对于这个问题我们可以先思考一下在左运算多项式中我们提供的证明是什么。是 \(l(x)\) 在一些秘密值 \(s\) 处的加密值: \(g^{l(s)}\) ,即,一个被加密了的数。我们已经从节 4.3 中知道了怎样通过一个 \(\alpha\) 变换去限制 prover 只能使用 verifier 提供的 \(s\) 的幂做计算,来使得单个运算能够满足同态乘法。
和限制单个求幂值相似,verfier 可以一次限制完整的多项式。我们知道,限制单个求幂值时,提供单独的加密 \(g^{s^1}, g^{s^2}, \cdots, g^{s^d}\) 及其 \(\alpha\) 变换 \(g^{\alpha s^1}, g^{\alpha s^2}, \cdots, g^{\alpha s^d}\) 即可;要一次限制完整的多项式时,可以使用下面协议:
- Setup
- 使用对应的系数构造相应的操作符多项式 \(l(x)\)
- 选择随机数 \(\alpha\) 和 \(s\)
- 使用加密的 \(l(s)\) 和它的“变换” \((g^{l(s)}, g^{\alpha l(s)})\) 来设置 proving key
- 设置 verification key: \((g^{\alpha})\)
- 使用对应的系数构造相应的操作符多项式 \(l(x)\)
- Proving
- 对于操作数值 \(v\)
- 乘以操作数多项式: \((g^{l(s)})^v\)
- 乘以变换后的操作数多项式: \((g^{\alpha l(s)})^v\)
- 乘以操作数多项式: \((g^{l(s)})^v\)
- 根据上面的计算,构造 \((g^{v l(s)}, g^{v \alpha l(s)})\) ,它们被称为“提供的证明”,简记为 \((g^l, g^{l'})\)
- 对于操作数值 \(v\)
- Verification
- 验证比例: \(e(g^{l'}, g) = e(g^l, g^{\alpha})\)
- 验证比例: \(e(g^{l'}, g) = e(g^l, g^{\alpha})\)
prover 需要返回同样的 \(\alpha\) 变换关系,因为无法从 proving key 中恢复出 \(\alpha\) ,所以保持这个变换的唯一方法就是用同一个值去分别乘以这两个加密值: \(g^{l(s)}\) 和 \(g^{\alpha l(s)}\) 。这个 prover 就无法修改 \(l(x)\) 的单个系数了,例如如果多项式为 \(l(x) = ax^2 + bx + c\) ,prover 只可以用一个值 \(v\) 去修改整个多项式: \(v \cdot (ax^2 + bx + c) = v \cdot ax^2 + v \cdot bx+ v \cdot c\) ,而不能单独修改某个系数。
有了这个协议后,怎么去构造满足要求(即经过点 \((1,a), (2,a)\) )的操作数多项式 \(l(x)\) 呢?由于任何整数都可以通过乘以 1 得到它本身,所以多项式中对应的每个计算结果都应该为 1,如图 16 所示。
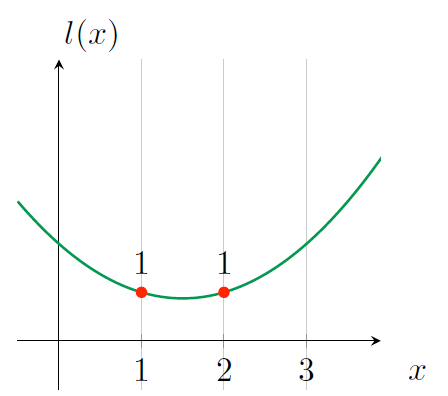
Figure 16: \(l(x)\) 经过 \((1,1), (2,1)\)
然后再让 prover 在其上”分配“一个值 \(a\) ,如图 17 所示。
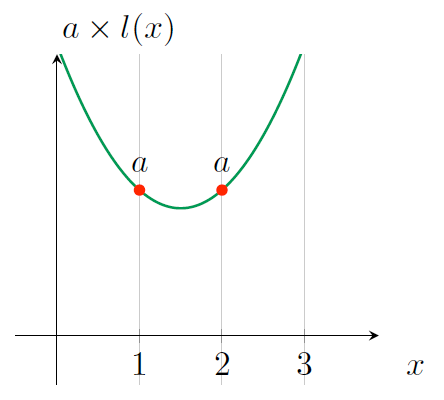
Figure 17: \(a \times l(x)\)
7.6.1.1. 存在的问题
上节的协议中,由于 verification key 包含了加密了的 \(\alpha\) ,所以可以用多项式加(或者减)任意一个值 \(v'\) ,即:
因而可以修改多项式使其超出 verifier 的预期以及证明一个不同的声明,在节 7.9.3 我们将会解决掉这个问题。
7.6.2. 多变量的操作数多项式
通过前面的介绍,我们已经解决了“证明中执行的程序在不同运算中使用了相同的变量 \(a\) 作为操作数或输出”。但是,如果左操作数中再多一个值 \(d\) 要怎么做呢,如图 18 所示。
Figure 18: 左操作数为 \(a,a,d\)
假如我们还使用相同的方法,我们无法分别地为每一个变量设置值,并且让这些变量乘到一起去。也就是说这个受限的多项式只能支持一个变量的情况。我们可以把操作数多项式 \(l(x)\) 分成操作数的变量多项式 \(l_a(x)\) 和 \(l_d(x)\) 。
这与上一节的方法一致,变量 \(a\) 和 \(d\) 可以被赋值并分别进行约束,然后加在一起就可以表示所有的左操作数变量了。因为我们将操作数的变量多项式加在了一起,所以我们就要能够确保在每次计算中相加后的结果只表示所有操作符多项式中的一个。
有了这个算术性质我们就可以逐一构造操作数变量多项式了,这样如果变量多项式在一个对应运算中被用做操作数,那么这一项就置为 1,否则就置为 0。0 跟任何值相乘结果都是零,当把他们相加在一起的时候也就可以忽略掉这一项。在我们的例子中这些变量多项式必须满足以下计算:
如图 19 所示。
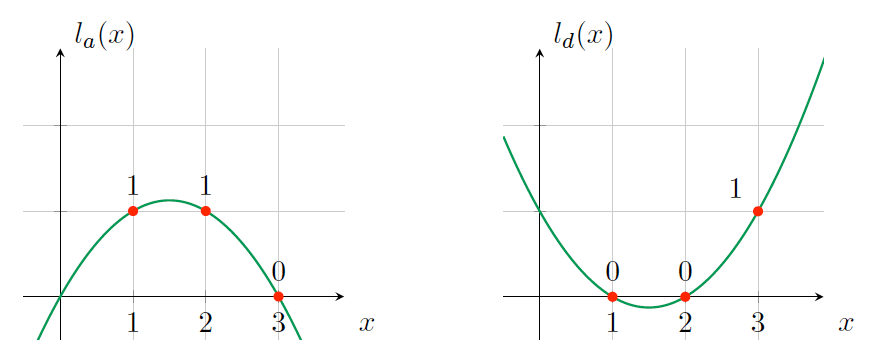
Figure 19: \(l_a(x), l_d(x)\)
于是我们就可以将每个变量分开设置值,然后把他们加在一起来计算出操作数多项式,例如当 \(a = 3, d = 2\) 时,如图 20 所示。
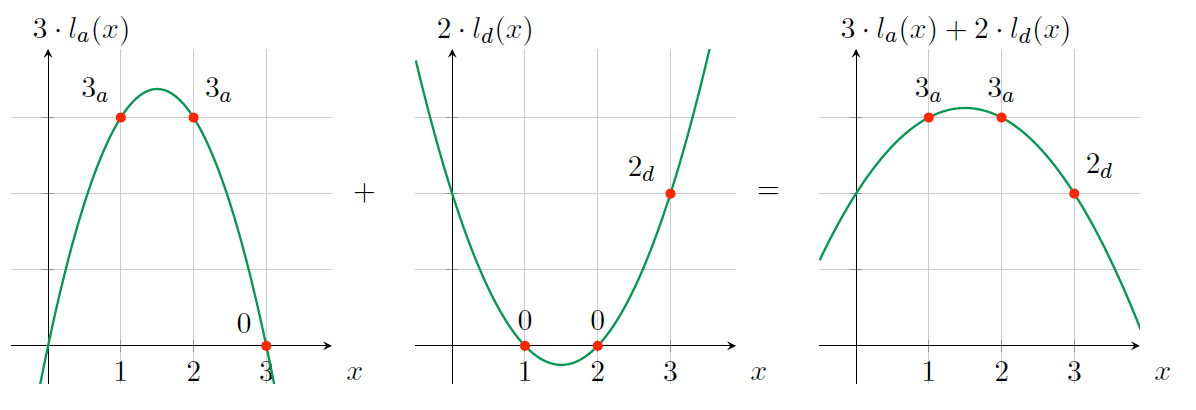
Figure 20: \(3 l_a(x) + 2 l_d(x)\)
注意:我们在一个值的后面使用下标表示它代表的变量,如, \(3_a\) 是一个用 3 实例化的变量 \(a\) 。
现在起我们用大写字母来表示这个复杂的操作符多项式,即:
\[L(x) = al_a(x) + dl_d(x)\]
计算结果为 \(L\) ,也就是 \(L=L(s)\) 。仅当每一个操作数的变量多项式是由 verifier 约束的,结果才有效,与左多项式相关的交互应该相应得更改为:
- Setup
- 构造 \(l_a(x), l_d(x)\) 使得它能够在对应的 “计算 x” 处为 1,在其他地方为 0
- 选择随机数 \(s, \alpha\)
- 计算并加密未赋值的变量多项式: \(g^{l_a(s)}, g^{l_d(s)}\)
- 计算变换后的这些多项式: \(g^{\alpha l_a(s)}, g^{\alpha l_d(s)}\)
- 上面得到的值组成 proving key: \((g^{l_a(s)}, g^{l_d(s)}, g^{\alpha l_a(s)}, g^{\alpha l_d(s)})\)
- 设置 verification key: \((g^{\alpha})\)
- 构造 \(l_a(x), l_d(x)\) 使得它能够在对应的 “计算 x” 处为 1,在其他地方为 0
- Proving
- 为变量多项式赋值 \(a\) 和 \(d\) : \((g^{l_a(s)})^a, (g^{l_d(s)})^d\)
- 对变换后的变量多项式做同样的赋值: \((g^{\alpha l_a(s)})^a, (g^{\alpha l_d(s)})^d\)
- 把所有赋值好的变量多项式加起来变成操作数多项式的形式: \(g^{L(s)} = g^{a l_a(s)} \cdot g^{d l_d(s)} = g^{al_a(s) + dl_d(s)}\)
- 和上类似,计算一个 \(\alpha\) 变换版本: \(g^{\alpha L(s)} = g^{a \alpha l_a(s)} \cdot g^{d \alpha l_d(s)} = g^{\alpha (al_a(s) + dl_d(s))}\)
- 提供左操作数的有效证明: \((g^{L(s)}, g^{\alpha L(s)})\) ,简记为 \((g^L, g^{L'})\)
- 为变量多项式赋值 \(a\) 和 \(d\) : \((g^{l_a(s)})^a, (g^{l_d(s)})^d\)
- Verification
- 验证提供的多项式是否是最初提供的多个未赋值的变量多项式的和: \(e(g^{L'}, g) = e(g^L, g^{\alpha})\) ,这里也就是验证了 \(\alpha a l_a(s) + \alpha d l_d(s) = \alpha \times (a l_a(s) + d l_d(s))\)
- 验证提供的多项式是否是最初提供的多个未赋值的变量多项式的和: \(e(g^{L'}, g) = e(g^L, g^{\alpha})\) ,这里也就是验证了 \(\alpha a l_a(s) + \alpha d l_d(s) = \alpha \times (a l_a(s) + d l_d(s))\)
注意: \(L(s)\) 和 \(\alpha L(s)\) 代表所有的变量多项式并且由于 \(\alpha\) 只用在计算变量多项式中,所以 prover 没有别的选择只能在 setup 提供的原始加密值和变换后的加密值上赋予相同的系数做计算。
结果,prover :
- 除了“分配”值外,不能再修改它们的系数进而来修改变量多项式 了,因为 prover 只拿到了这些多项式的加密值,也因为 s 必要次幂的加密值不能与它们的 \(\alpha\) 变换值一起使用。
- 不能通过另一个多项式相加去提供一个结果因为这样 α-比例关系将会被破坏掉。
- 不能通过与其他的一些多项式 \(u(x)\) 相乘来修改操作数多项式,这样可能会使得修改后的值不成比例因为在预配对空间中无法进行加密乘法。
不过尽管 prover 被限制了多项式的使用,他还有拥有一些可允许范围内的自由度:
- 当 prover 决定不加入一些变量多项式 \(l_i(x)\) 来构造操作符多项式 \(L(x)\) 时依然是可以接受的,因为这和为它分配值为 0 是一样的: \(g^{al_a(x)} = g^{ala(x)+0l_d(x)}\)
- 如果 prover 添加同一个变量多项式多次也是可以接受的因为这和一次分配多个值的和是一样的: \(g^{al_a(x)} \cdot g^{al_a(x)} \cdot g^{al_a(x)} = g^{3al_a(x)}\)
这些方法在右操作数和输出操作数 \(R(x), O(x)\) 上也同样适用。
7.7. Construction Properties(结构性质)
上文中的修改额外带来了一些其它有用的性质。
7.7.1. 常量系数
在上文的构造中,我们通过对“未赋值的变量多项式”的计算得到 0 或者 1 ,以此表示在运算中是否要用到这个变量。自然地想,我们也可以使用其它系数值,包括负数值,因为我们可以插值计算出经过任何必要的点(前提是没有两个计算使用了同一个 \(x\) )的多项式。如下是这种运算的一些例子:
现在我们的程序就可以使用常量系数了,例如:
Algorithm 2: Constant coefficients
—————————————————————————————————————————————————————
function calc(w, a, b)
if w then
return 3a × b
else
return 5a × 2b
end if
end function
在 setup 阶段这些系数类似于 0 或者 1 将被“硬编码”进去,之后就不能再修改了。现在我们将运算形式修改为:
\[{\color{green}{c_a \cdot a}} \times {\color{blue}{c_b \cdot b}} = {\color{red}{c_r \cdot r}}\]
或者更正式地,对于变量 \(v_i \in \{v_1, v_2, \cdots, v_n\}\) :
\[{\color{green}{c_l \cdot v_l}} \times {\color{blue}{c_r \cdot v_r}} = {\color{red}{c_o \cdot v_o}}\]
其中下标 \(l,r,o\) 表示变量在运算中的位置。
注意:在不同的运算和操作数/输出中,同一个变量的常量系数可以是不同的。
7.7.2. 没有成本的做加法
看一下这个新结构,很显然在多项式的表示中,每一个不同 \(x\) 所要代表的操作数都是所有操作数变量多项式的总和,其中只有一个被用到的变量是非零值而其它都为 0,图 21 很好得表达了这个意思。
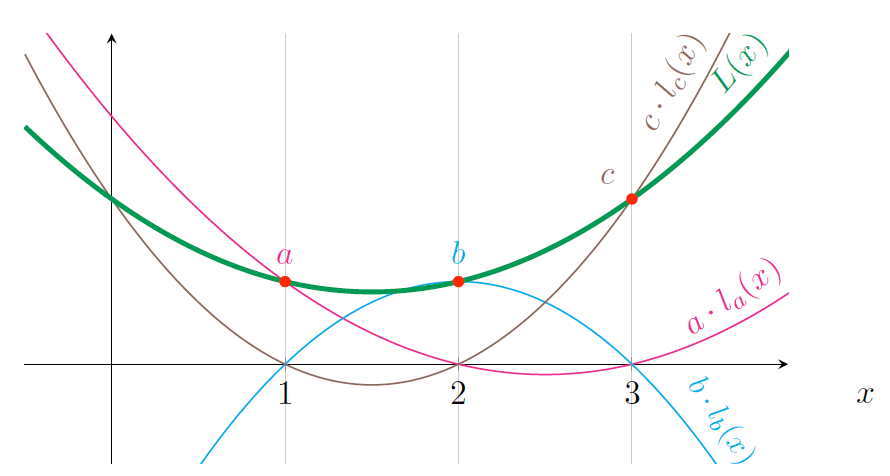
Figure 21: 加法
我们可以利用这一个结构,加任何数量必要的变量 到每一个运算的操作符/输出中。例如在第一个运算中,我们可以首先做加法 \(a+c\) ,然后就只需要用别的操作数与之相乘了,即 \((a + c) \times b = r\) ,可以表示为图 22 所示。
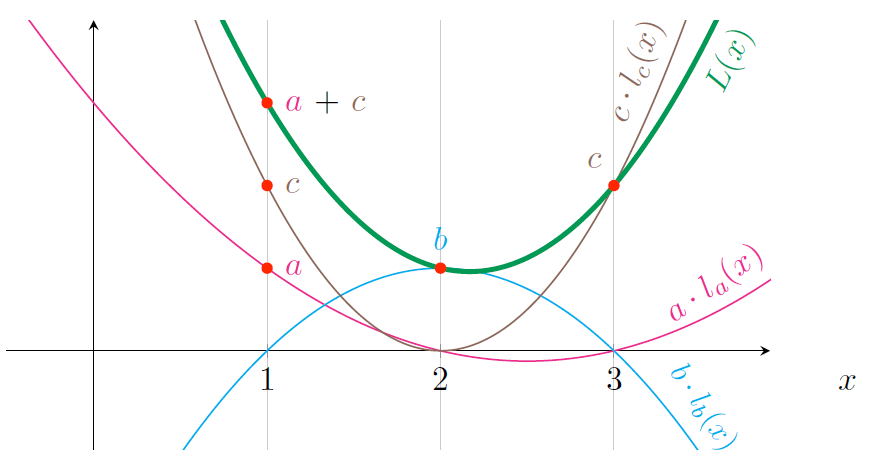
Figure 22: 先加后乘
因而也可以将这些变量中任意个,对它们先乘以任意的系数再一并加入到一起作为单个操作数中,以此来根据相应程序的需要构造一个操作数值。这个特性实际上就允许将运算结构改为:
\[(c_{l,a} \cdot a + c_{l,b} \cdot b + \cdots) \times (c_{r,a} \cdot a + c_{r,b} \cdot b + \cdots) = (c_{o,a} \cdot a + c_{o,b} \cdot b + \cdots)\]
或者使用更正式一些的表示,使用变量 \(v_i \in \{v_1, v_2, \cdots, v_n \}\) 和操作数变量系数 \(c_{l,i} \in \{c_{l,1}, c_{l,2}, \cdots, c_{l,n}\}, c_{r,i} \in \{c_{r,1}, c_{r,2}, \cdots, c_{r,n}\}, c_{o,i} \in \{c_{o,1}, c_{o,2}, \cdots, c_{o,n}\}\) ,上面的式子就是:
\[{\color{green}{\sum_{i=1}^{n} c_{l,i} \cdot v_i}} \times {\color{blue}{\sum_{i=1}^{n} c_{r,i} \cdot v_i}} = {\color{red}{\sum_{i=1}^{n} c_{o,i} \cdot v_i}}\]
7.7.3. 加法,减法和除法
到目前为止,我们一直专注于乘法操作。但是为了能够执行通用计算,真实环境下的程序也需要加法,减法和除法。
7.7.3.1. 加法
在前面的章节中,我们已经确定了可以在单个操作数的内容中将变量加起来,然后和另一个操作数相乘,即 \((3a + b) \times d = r\) ,但是如果我们只是想做加法,没有乘法,例如一个程序中需要做 \(a + b\) 的计算,我们可以按照下面的方式来表示:
\[{\color{green}{(a+b)}} \times {\color{blue}{1}} = {\color{red}{r}}\]
7.7.3.2. 减法
减法与加法几乎一致,唯一的不同就是负系数, \(a-b\) 也就是:
\[{\color{green}{(a + -1 \cdot b)}} \times {\color{blue}{1}} = {\color{red}{r}}\]
7.7.3.3. 除法
如果我们检查除法运算 \(\frac{factor}{divisor} = result\) ,可以看到除法的结果是就是我们要得到一个结果值使其乘以 divisor 能够得到 factor。所以我们也可以用乘法来表示出同一个意思: \(divisor \times result = factor\) 。这样就是说如果我们想要去证明除法运算 \(a / b= r\) ,我们就可以把它表示为:
\[{\color{green}{b}} \times {\color{blue}{r}} = {\color{red}{a}}\]
7.7.3.4. 总结
运算的结构也称为“约束” ,因为多项式结构代表的运算,并非是为了计算出结果,而是在 prover 已经知晓的变量赋值的情况下,检验这个运算的过程是否正确。
算术电路的目的是为了实现“计算的验证”,而非“计算的过程”。
7.8. 计算示例
有了前面的基础后,我们可以将节 7.1 的程序转换成一组运算,然后再转换成多项式的形式。我们先来考虑一下算法的数学形式(用变量 \(v\) 表示运算结果):
\[w \times (a \times b) + (1 - w) \times (a + b) = v\]
这里有三个乘法,但是由于运算结构只支持一个乘法操作,所以这里至少就要做三次运算。但是,我们可以将它简化为:
进行简化后,现在只需要两个乘法。这种运算的完整形式就是:
我们还要再增加一条约束使 \(w\) 必须为二进制数(参见节 7.1):
\[3: \quad \quad {\color{green}{1 \cdot w}} \times {\color{blue}{1 \cdot w}} = {\color{red}{1 \cdot w}}\]
上面限制了 \(w\) 为 0 或者为 1。
现在一共有 5 个变量,其中 2 个左操作符( \(a,w\) ), 4 个右操作符( \(b,m,a,w\) )和 5 个输出( \(m,v,a,b,w\) )。
我们把多项式里变量的系数当作是另一个多项式的函数值,为了方便,假设这些系数是取点 \(x=1,2,3\) 时的函数值。
也就是上面约束可写为:
如果这个多项式在计算的操作数或者输出中没有被用到的话系数就置为 0:
显然进行这样的赋值可以满足前面的要求。
从而 \(t(x)\) 就是 \(t(x) = (x – 1)(x –2)(x –3)\) ,它必须确保这三个运算都能被正确计算。
接下来,根据前面的等式我们利用多项式插值法来找到每个变量多项式:
绘制出来如图 23 所示。
Figure 23: 示意图
我们准备通过多项式去证明计算,首先,选择函数的输入值,例如: \(w = 1, a = 3, b= 2\) 。其次,计算过程中的中间变量值为:
操作符多项式为:
然后,我们把所有计算结果中的值赋值到“变量多项式”中,然后相加得到操作数或者输出多项式的形式:
如图 24 所示。
Figure 24: 前一个示意图的实例化
把它们相加成对应运算中的操作数和输出值,如图 25 所示。
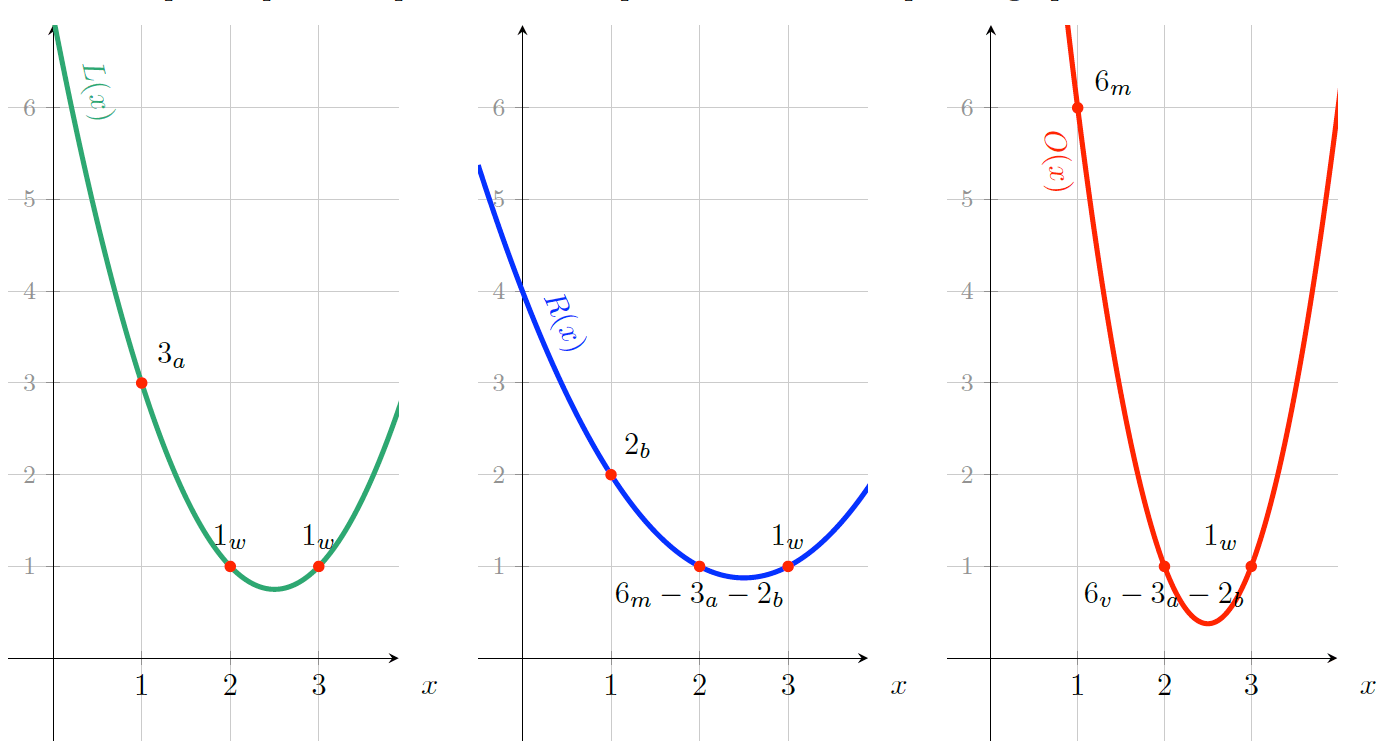
Figure 25: \(L(x), R(x), O(x)\)
我们需要去证明 \(L(x) \times R(x) – O(x) = t(x)h(x)\) ,因而我们先找出 \(h(x)\) :
\[h(x) = \frac{L(x) \times R(x) - O(x)}{t(x)} = \frac{\frac{1}{2}x^4 - 5 x^3 + \frac{35}{2} x^2 - 25 x + 12}{(x-1)(x-2)(x-3)} = \frac{1}{2}x - 2\]
\(L(x) \times R(x), O(x), L(x) \times R(x) - O(x)\) 如图 26 所示。
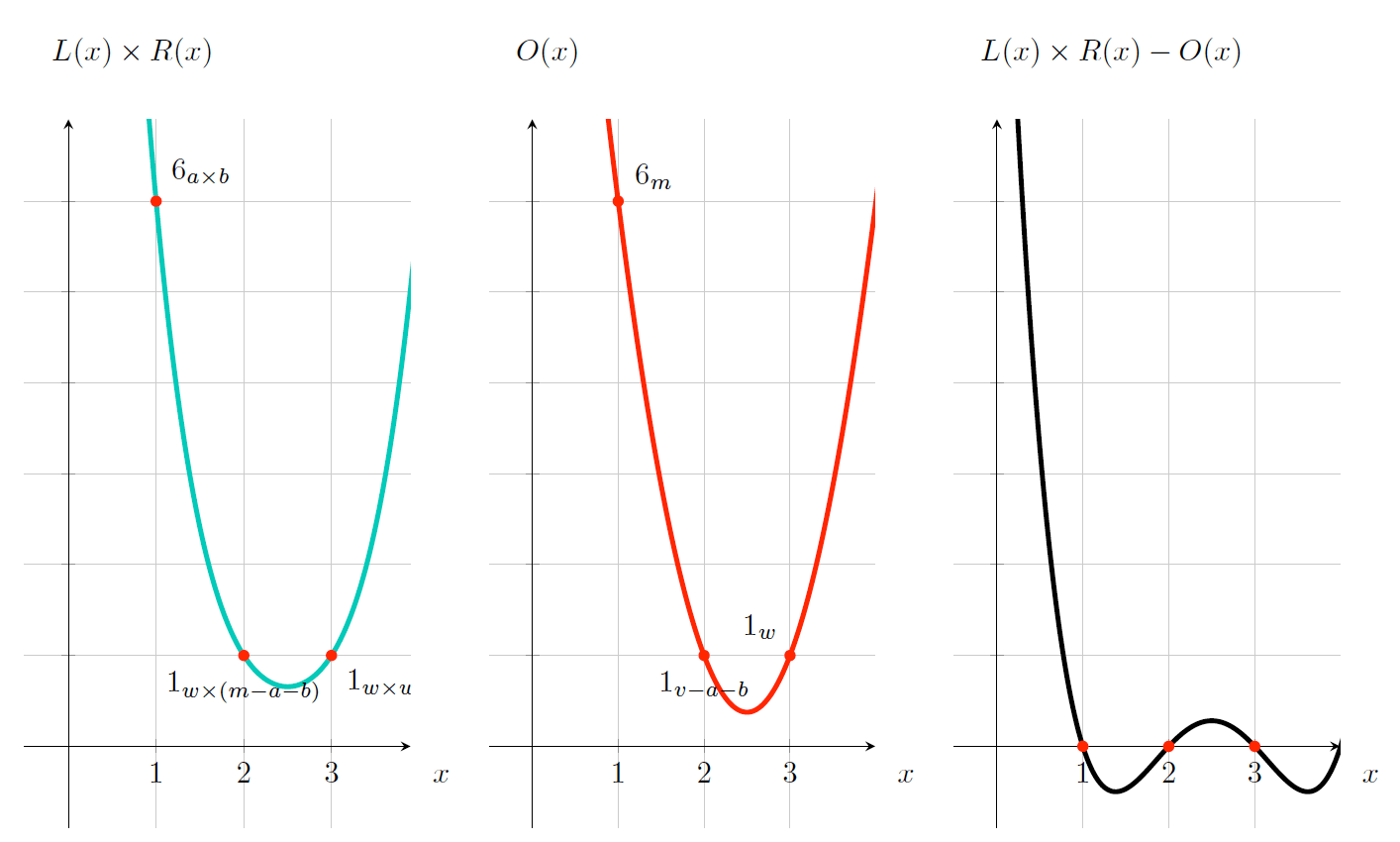
Figure 26: \(L(x) \times R(x) - O(x)\)
这里很明显多项式 \(L(x) \times R(x) – O(x)\) 的解为 \(x=1, x=2, x=3\) ,因而 \(t(x)\) 是它的因式,假如使用了和它不一致的变量值,情况就不是这样了。
这就是一组能够正确计算的变量值,如何在多项式层面上证明出来的。下面 prover 还要再继续处理协议的密码学部分。
7.9. 可验证的计算协议
我们基于节 6.4 中介绍的协议做了很多重要的修改使它变得更通用,我们再来看一下它现在的定义。假定函数 \(f(*)\) 是要证明的问题中的计算结果,其中操作数的数量为 \(d\) ,变量的数量 \(n\) ,以及它们对应的系数为: \(\{c_{L,i,j}, c_{R,i,j}, c_{O,i,j} \}_{i\in \{i, \cdots, n\}, j \in \{1, \cdots, d\}}\)
- Setup
- 为左操作数 \({l_i(x)}_{i \in \{1,\cdots,n\}}\) 构造变量多项式,然后对于所有 \(j \in \{1,\cdots, d\}\) 的运算都算出其对应的系数,即 \(l_i(j) = c_{L,i,j}\) ,对右操作数和输出也做同样的事情。
- 挑选随机值 \(s, \alpha\)
- 计算 \(t(x) = (x-1)(x-2)\cdots (x-d)\) 及其结果 \(g^{t(s)}\)
- 计算 proving key: \((\{g^{s^k} \}_{k \in [d]}, \{g^{l_i{s}}, g^{r_i{s}}, g^{o_i{s}}, g^{\alpha l_i{s}}, g^{\alpha r_i{s}}, g^{\alpha o_i{s}}\})\)
- 计算 verification key: \((g^{t(s)}, g^{\alpha})\)
- 为左操作数 \({l_i(x)}_{i \in \{1,\cdots,n\}}\) 构造变量多项式,然后对于所有 \(j \in \{1,\cdots, d\}\) 的运算都算出其对应的系数,即 \(l_i(j) = c_{L,i,j}\) ,对右操作数和输出也做同样的事情。
- Proving
- 计算函数 \(f(*)\) 以此计算相应的变量 \(\{v_i\}_{i \in \{1, \cdots, n\}}\)
- 计算 \(h(x) = \frac{L(x) \times R(x) - O(x)}{t(x)}\) ,其中 \(L(x) = \sum_{}^{} v_i \cdot l_i(x)\) , \(R(x), O(x)\) 与之相似。
- 给变量赋值并对操作数多项式求和: \[g^{L(s)} = (g^{l_1(s)})^{v_1} \cdots (g^{l_n(s)})^{v_n}, g^{R(s)} = \prod_{i=1}^n (g^{r_i(s)})^{v_i}, g^{O(s)} = \prod_{i=1}^n (g^{o_i(s)})^{v_i}\]
- 对 \(\alpha\) 变换后的多项式赋值: \[g^{\alpha L(s)} = \prod_{i=1}^n (g^{\alpha l_i(s)})^{v_i}, g^{\alpha R(s)} = \prod_{i=1}^n (g^{\alpha r_i(s)})^{v_i}, g^{\alpha O(s)} = \prod_{i=1}^n (g^{\alpha o_i(s)})^{v_i}\]
- 使用 \(s\) 的幂加密值: \(\{g^{s^k}\}_{k \in [d]}\) 计算加密值 \(g^{h(s)}\)
- 生成证明: \((g^{L(s)}, g^{R(s)}, g^{O(s)}, g^{\alpha L(s)}, g^{\alpha R(s)}, g^{\alpha O(s)}, g^{h(s)})\) ,简记为 \((g^L, g^R, g^O, g^{L'}, g^{R'}, g^{O'}, g^h)\)
- 计算函数 \(f(*)\) 以此计算相应的变量 \(\{v_i\}_{i \in \{1, \cdots, n\}}\)
- Verification
- 检查变量多项式约束: \[e(g^L, g^{\alpha}) = e(g^{L'}, g), e(g^R, g^{\alpha}) = e(g^{R'}, g), e(g^O, g^{\alpha}) = e(g^{O'}, g)\]
- 验证计算有效性: \[e(g^L, g^R) = e(g^t, g^h) \cdot e(g^O, g)\]
- 检查变量多项式约束: \[e(g^L, g^{\alpha}) = e(g^{L'}, g), e(g^R, g^{\alpha}) = e(g^{R'}, g), e(g^O, g^{\alpha}) = e(g^{O'}, g)\]
对变量多项式 \(\{l_i(x), r_i(x), o_i(x)\}_{i \in \{1, \cdots, n\}}\) 和目标多项式 \(t(x)\) 的设置称为转换为二次算术程序(Quadratic Arithmetic Program,QAP),在节 7.8 中有转换为 QAP 的实例。
虽然协议足够健壮,可以进行常规的计算验证,但这里依然还有两个安全考虑需要去解决。
7.9.1. 操作数和输出的不可交换性(单独进行 KEA 检查)
因为在“变量多项式约束检查”中的所有操作数上我们使用了同一个 \(\alpha\) ,所以就没有办法阻止 prover 做下面的欺骗行为:
- 使用其它的操作数中的变量多项式,如 \(L′(s) = o_1(s) + r_1(s) + r_5(s) + \cdots\)
- 完全交换操作数多项式,如换成 \(O(s) \times R(s) = L(s)\)
- 复用相同的操作数多项式,即 \(L(s) \times L(s) = O(s)\)
可交换性就是指 prover 可以修改计算过程,并有效证明一些其它无关的计算结果。 防止这种行为的一个很显然的方式就是在不同的操作数上使用不同的 \(\alpha\) (也就是使用 \(\alpha_l,\alpha_r, \alpha_o\) 代替 \(\alpha\) ), 具体协议就可以修改为:
- Setup
- ......
- 选择随机数 \(\alpha_l,\alpha_r, \alpha_o\) 代替 \(\alpha\)
- 计算 proving key: \((\{g^{s^k} \}_{k \in [d]}, \{g^{l_i{s}}, g^{r_i{s}}, g^{o_i{s}}, g^{\alpha_l l_i{s}}, g^{\alpha_r r_i{s}}, g^{\alpha_o o_i{s}}\})\)
- 计算 verification key: \((g^{t(s)}, g^{\alpha_l}, g^{\alpha_r}, g^{\alpha_o})\)
- ......
- Proving
- ......
- 对 \(\alpha\) 变换后的多项式赋值: \[g^{\alpha_l L(s)} = \prod_{i=1}^n (g^{\alpha_l l_i(s)})^{v_i}, g^{\alpha_r R(s)} = \prod_{i=1}^n (g^{\alpha_r r_i(s)})^{v_i}, g^{\alpha_o O(s)} = \prod_{i=1}^n (g^{\alpha_o o_i(s)})^{v_i}\]
- ......
- Verification
- ......
- 检查变量多项式约束: \[e(g^L, g^{\alpha_l}) = e(g^{L'}, g), e(g^R, g^{\alpha_r}) = e(g^{R'}, g), e(g^O, g^{\alpha_o}) = e(g^{O'}, g)\]
- ......
7.9.2. 跨操作数的变量一致性
对于任意的变量 \(v_i\) ,我们都必须将它的值分配到每个相应操作数中的一个与之对应的变量多项式上,即: \((g^{l_i(s)})^{v_i}, (g^{r_i(s)})^{v_i}, (g^{o_i(s)})^{v_i}\)
因为每一个操作数运算符的有效性是分开校验的,并不强制要求我们在对应的变量多项式中使用相同的变量值。这就意味着在左操作数中变量 \(v_1\) 的值可以与右操作数或输出中的变量值 \(v_1\) 不同。
我们可以通过熟悉的限制多项式的方法(也就是限制变量多项式的方法)在操作数之间强制变量值相等。如果我们能够在所有的操作数之间创造一个作为“变换的校验和”的变量多项式,那么就可以限制 prover 使其只能够赋予相同的值。verifier 可以将这些每个变量的多项式加起来,即: \(g^{l_i(s) + r_i(s) + o_i(s)}\) ,然后乘以一个额外的随机数 \(\beta\) ,即 \(g^{\beta(l_i(s) + r_i(s) + o_i(s))}\) 。提供这些变换后的多项式给 prover,与变量多项式一起给它赋上变量值:
\[(g^{l_i(s)})^{v_{L,i}}, (g^{r_i(s)})^{v_{R,i}}, (g^{o_i(s)})^{v_{O,i}}, (g^{\beta(l_i(s) + r_i(s) + o_i(s))})^{v_{\beta,i}}\]
然后加密 \(\beta\) 并把 \(g^{\beta}\) 加到 verification key 中。现在,如果所有的 \(v_i\) 值相同,即:
\[v_{L,i} = v_{R,i} = v_{O,i} = v_{\beta, i} \quad for i \in \{1, \cdots, n\}\]
则下面等式会成立:
\[e(g^{v_{L,i} \cdot l_i(s)} \cdot g^{v_{R,i} \cdot r_i(s)} \cdot g^{v_{O,i} \cdot o_i(s)}, g^{\beta}) = e(g^{v_{\beta,i} \cdot \beta(l_i(s) + r_i(s) + o_i(s))}, g)\]
尽管这个一致性校验很有用,但还是存在一定的概率 \(l(s), r(s), o(s)\) 中至少有两项要么计算值相同要么一个多项式可以被另一个整除等情况,这就允许 prover 去分解 \(v_{L,i}, v_{R,i}, v_{O,i}, v_{\beta, i}\) 这些值的关系,使得即使有至少两个不相等的值也依然能够保持等式成立,从而使下面的一致性校验失效:
\[(v_{L,i} \cdot l_i(s) + v_{R,i} \cdot r_i(s) + v_{O,i} \cdot o_i(s)) \cdot \beta = v_{\beta,i} \cdot \beta \cdot (l_i(s) + r_i(s) + o_i(s))\]
假如,一个以 \(l(x) = r(x)\) 为例的单个运算。我们用 \(w\) 来表示这两个值(即 \(w=l(s)=r(s)\) ),同时假设 \(y = o(s)\) 。上面等式看起来就是:
\[(v_L w + v_R w + v_O y) \cdot \beta = v_{\beta} \cdot \beta (w + w + y)\]
对于任意的 \(v_R, v_O\) ,如果令 \(v_{\beta} = v_O, v_L = 2 v_O - v_R\) ,则上式就是:
\[(2v_O w - v_R w + v_R w + v_O y) \cdot \beta = v_O \cdot \beta (2w + y)\]
上式是“一定成立的”,也就是说对于任意的 \(v_R, v_O\) 都能通过检验,从而这个一致性检验失效了。
缓解这种情况的一种方法是对每个操作数都使用不同的 \(\beta\) ,确保操作数的变量多项式中包含无法预测的值。以下就是修改后的协议:
- Setup
- ... 随机数 \(\beta_l, \beta_r, \beta_o\)
- 对变量一致性多项式进行计算,加密并添加到 proving key 中: \(\{g^{\beta_l l_i(s) + \beta_r r_i(s) + \beta_o o_i(s)}\}_{i \in \{1, \cdots, n\}}\)
- 把 3 个随机数加密后添加到 verification key 中: \((g^{\beta_l}, g^{\beta_r}, g^{\beta_o})\)
- ... 随机数 \(\beta_l, \beta_r, \beta_o\)
- Proving
- ... 将变量值赋给变量一致性多项式: \(g^{z_i(s)} = (g^{\beta_l l_i(s) + \beta_r r_i(s) + \beta_o o_i(s)})^{v_i} \quad for i \in \{1, \cdots, n\}\)
- 增加分配的多项式到加密空间中: \(g^{Z(s)} = \prod_{i=1}^{n} g^{z_i(s)} = g^{\beta_l L(s) + \beta_r R(s) + \beta_o O(s)}\)
- 再在证明中加入: \(g^{Z(s)}\) ,简记为 \(g^Z\)
- ... 将变量值赋给变量一致性多项式: \(g^{z_i(s)} = (g^{\beta_l l_i(s) + \beta_r r_i(s) + \beta_o o_i(s)})^{v_i} \quad for i \in \{1, \cdots, n\}\)
- Verification
- ... 校验提供的操作数多项式和“校验和”多项式之间的一致性: \(e(g^L, g^{\beta_l}) \cdot e(g^R, g^{\beta_r} \cdot e(g^O, g^{\beta_o}) =e(g^Z, g)\) ,这相当于: \(e(g,g)^{\beta_l L + \beta_r R + \beta_o O} = e(g,g)^Z\)
- ... 校验提供的操作数多项式和“校验和”多项式之间的一致性: \(e(g^L, g^{\beta_l}) \cdot e(g^R, g^{\beta_r} \cdot e(g^O, g^{\beta_o}) =e(g^Z, g)\) ,这相当于: \(e(g,g)^{\beta_l L + \beta_r R + \beta_o O} = e(g,g)^Z\)
这个构造中同一个变量值就无法乱用了,因为不同的 \(\beta\) 使得相同多项式无法兼容。
不过,这个协议存在与节 7.6.1.1 类似的缺陷,由于 \(g^{\beta_l}, g^{\beta_r}, g^{\beta_o}\) 是公开可见的,攻击者可以修改任意变量多项式的“零指数项的系数”,因为它并不依赖于 \(s\) ,即 \(g^{\beta_l s^0} = g^{\beta_l}\) 总是成立,不论 \(s\) 是何值。节 7.9.3.3 将解决这个问题。
7.9.3. 变量非延展性(Non-Malleability)和变量一致性多项式
7.9.3.1. 变量多项式的延展性
举一个和节 7.6.1.1 有关的例子,看一下下面的两个运算:
预期的结果 \(b = a\) 和 \(c = 3a\) , 再进一步就是 \(c = 3b\) 。这就是说左操作数的变量多项式的计算结果为 \(l_a(1) = 1\) 和 \(l_a(2) = 3\) 。先不管 \(l_a(x)\) 的形式, prover 都可以不按照上述的比例用另一个修改了的多项式 \(l_a'(x) = al_a(x) + 1\) 来给 \(a\) 赋值。 这样运算就变成了 \(l_a'(1) = a + 1\) 和 \(l_a'(2) = 3a + 1\) , 结果也就是 \(b = a + 1\) 和 \(c = 3a + 1\) ,其中 \(c \neq 3b\) ,这意味着 \(a\) 的取值的实际意义在不同运算中是不一样的。
但是因为 prover 已经拿到了 \(g^{\alpha_l}, g^{\beta_l}\) ,所以 它依然能够通过 Verfication 阶段校验:
- Proving
- 用分配不成比例的变量 \(a\) 来建立左操作数多项式: \(L(x)=a \cdot l_a(x)+1\)
- 按照常规的方式构造右操作数多项式和输出多项式: \(R(x) = r_1(x), O(x) = b \cdot o_b(x) + c \cdot o_c(x)\)
- 计算除数: \(h(x) = \frac{L(x) \cdot R(x) - O(x)}{t(x)}\)
- 计算加密值: \(g^{L(x)} = (g^{l_a(s)})^{a} \cdot g^1\) ,并按照常规方式计算 \(g^{R(s)}, g^{O(s)}\)
- 计算 \(\alpha\) 变换后的加密值: \(g^{\alpha L(s)} = (g^{\alpha l_a(s)})^{a} \cdot g^\alpha\) ,并按照常规方式计算 \(g^{\alpha R(s)}, g^{\alpha O(s)}\)
- 计算变量一致性多项式: \(g^{Z(s)} = \prod_{i \in \{1,a,b,c\}} (g^{\beta_l l_i(s) + \beta_r r_i(s) + \beta_o o_i(s)})^i \cdot g^{\beta^l} = g^{\beta_l(L(s) + 1) + \beta_r R(s) + \beta_o O(s)}\)
- 设置证明: \((g^{L(s)}, g^{R(s)}, g^{O(s)}, g^{\alpha_l L(s)}, g^{\alpha_r R(s)}, g^{\alpha_o O(s)}, g^{Z(s)}, g^{h(s)})\) ,简记为 \((g^L, g^R, g^O, g^{L'}, g^{R'}, g^{O'}, g^Z, g^h)\)
- 用分配不成比例的变量 \(a\) 来建立左操作数多项式: \(L(x)=a \cdot l_a(x)+1\)
- Verification
- 变量多项式约束检查: \(e(g^{L'}, g)=e(g^L, g^{\alpha}) \Rightarrow e(g^{\alpha a \cdot l_a(s) + \alpha}, g) = e(g^{a l_a(s) + 1}, g^{\alpha})\) ,和以前一样的方式检查 \(g^{R'}, g^{O'}\)
- 变量值一致性检查: \(e(g^L, g^{\alpha_l}) \cdot e(g^R, g^{\alpha_r}) \cdot e(g^O, g^{\alpha_o}) = e(g^Z, g) \Rightarrow e(g,g)^{(a \cdot l_a + 1) \beta_l + R \beta_r + O \beta_o} = e(g,g)^{\beta_l (L+1) + \beta_r R + \beta_o O}\)
- 验证计算有效性: \(e(g^L, g^R) = e(g^t, g^h) \cdot e(g^O, g)\)
- 变量多项式约束检查: \(e(g^{L'}, g)=e(g^L, g^{\alpha}) \Rightarrow e(g^{\alpha a \cdot l_a(s) + \alpha}, g) = e(g^{a l_a(s) + 1}, g^{\alpha})\) ,和以前一样的方式检查 \(g^{R'}, g^{O'}\)
7.9.3.2. 变量一致性多项式的延展性
除了上面的问题外, \(g^{\beta_l}, g^{\beta_r}, g^{\beta_o}\) 的存在允许我们在不同操作数的相同变量上使用不同的值。例如,如果我们有一个运算:
\[{\color{green}{a}} \times {\color{blue}{a}} = {\color{red}{b}}\]
可以用变量多项式表示:
尽管我们期待的输出是 \(b=a^2\) ,但我们可以设置不同的 \(a\) 值,例如:设置 \({\color{green}{a=2}}\) (左操作数中), \({\color{blue}{a=5}}\) (右操作数中),也可以通过验证(我们需要避免这种情况,在节 7.6 提到过,“变量”其实是 assignment,变量 \(a\) 同时出现了左操作数和右操作数中,那么就期望它们应该是相同的值)。过程如下:
- Proving
- ... 用 \(a=2\) 设置左操作数多项式: \(L(x) = 2l_a(x) + 10 l_b(x)\)
- 用 \(a=5\) 设置右操作数多项式: \(R(x) = 2r_a(x) + 3 + 10 r_b(x)\)
- 用 \(b=10\) 设置输出多项式: \(O(x) = 2 o_a(x) + 10 o_b(x)\)
- ... 计算加密值: \[\begin{align*} g^{L(s)} & = (g^{l_a(s)})^2 \cdot (g^{l_b(s)})^{10} = g^{2l_a(s) + 10 l_b(s)} \\ g^{R(s)} & = (g^{r_a(s)})^2 \cdot (g)^3 \cdot (g^{r_b(s)})^{10} = g^{2r_a(s) + 3 + 10 r_b(s)} \\ g^{O(s)} & = (g^{o_a(s)})^2 \cdot (g^{o_b(s)})^{10} = g^{2o_a(s) + 10 o_b(s)} \end{align*}\]
- 计算变量一致性多项式: \(g^{Z(s)} = (g^{\beta_l l_a(s) + \beta_r r_a(s) + \beta_o o_a (s)})^2 \cdot (g^{\beta_r})^3 \cdot (g^{\beta_l l_b(s) + \beta_r r_b(s) + \beta_o o_b(s)})^{10} = g^{\beta_l(2 l_a(s) + 10 l_b(s)) + \beta_r(2 r_a(s) + 3 + 10 r_b(s)) + \beta_o(2o_a(s) + 10 o_b(s))}\)
- ... 用 \(a=2\) 设置左操作数多项式: \(L(x) = 2l_a(x) + 10 l_b(x)\)
- Verification
- ... 变量值的一致性检查,会满足: \(e(g^L, g^{\beta_l}) \cdot e(g^R, g^{\beta_r}) \cdot e(g^O, g^{\beta_o}) = e(g^Z, g)\)
- ... 变量值的一致性检查,会满足: \(e(g^L, g^{\beta_l}) \cdot e(g^R, g^{\beta_r}) \cdot e(g^O, g^{\beta_o}) = e(g^Z, g)\)
注意:多项式 \(o_a(x), l_b(x), r_b(x)\) 其实可以被忽略掉的,因为这几项对于任何 \(x\) 的取值,计算结果都为 0,但是为了保持完整性我们依然要保留这几项。
这种行为会危害到协议的可靠性。很显然,加密的 \(\beta_l, \beta_r, \beta_o\) 不应该对 Prover 可见。下节将解决这个问题。
7.9.3.3. 非延展性
解决延展性问题的一个方法就是,在 setup 阶段将 verification key 中加密的 \(\beta_l, \beta_r, \beta_o\) 与随机秘密值 \(\gamma\) 相乘使其与加密值 \(Z(s)\) 不兼容: \(g^{\beta_l \gamma}, g^{\beta_r \gamma}, g^{\beta_o \gamma}\) 。这种被修饰过的加密值,能使修改加密值 \(g^{Z(s)}\) 变得不可行,因为 \(Z(s)\) 中没有 \(\gamma\) ,比如 \(g^{Z(s)} \cdot g^{v' \cdot \beta_l r} = g^{\beta_l (L(s) + v'r) + \beta_r R(s) + \beta_o O(s)}\) 。这个修改需要我们用 \(Z(s)\) 乘以 \(\gamma\) 来平衡协议中的变量值一致性校验等式。由于 \(\gamma\) 是随机值,prover 并不知道它的值,所以无法进行。
更新后的协议为:
- Setup
- ... 随机数 \(\beta_l, \beta_r, \beta_o, \gamma\)
- ... 设置 verification key: \((\cdots, g^{\beta_l \gamma}, g^{\beta_r \gamma}, g^{\beta_o \gamma}, g^{\gamma})\)
- ... 随机数 \(\beta_l, \beta_r, \beta_o, \gamma\)
- Proving ...
- Verification
- ... 变量值一致性检查应满足: \(e(g^L, g^{\beta_l \gamma}) \cdot e(g^R, g^{\beta_r \gamma}) \cdot e(g^O, g^{\beta_o \gamma}) = e(g^Z, g^{\gamma})\)
- ... 变量值一致性检查应满足: \(e(g^L, g^{\beta_l \gamma}) \cdot e(g^R, g^{\beta_r \gamma}) \cdot e(g^O, g^{\beta_o \gamma}) = e(g^Z, g^{\gamma})\)
这里很重要的一点是我们排除了变量多项式为 0-阶的例子(即 \(l_1(x) = 1x^0\) ),否则就可以从 proving key 的变量一致性多项式 \(\{g^{\beta_l l_i(s) + \beta_r r_i(s) + \beta_o o_i(s)} \}_{i \in \{1, \cdots, n\}}\) 中揭露出加了密的 β$ 值,比如当操作数/输出中的任意两项为 0 时,假设 \(l_1(x) = 1, r_1(s) = 0, o_1(s) = 0\) ,则 \(g^{\beta_l l_i(s) + \beta_r r_i(s) + \beta_o o_i(s)} = g^{\beta_l}\) ,这样 \(g^{\beta_l}\) 就被获得了。
我们同样也可以通过类似 \(\alpha\) 变换来解决变量多项式的延展性问题。但是这就没有必要了,因为对于变量多项式的任何修改,都需要被映射到变量的一致性多项式中,而一致性多项式是无法修改的。
7.9.4. 变量值一致性检查的优化
现在变量值一致性检查是有效的,但是这里在 verification key 中增加了 4 个昂贵的配对操作和 4 个新的项。文献 PGHR13 中的 Pinocchio 协议用了一个很聪明的方法优化,通过选择不同的生成元 \(g\) ,从而对每个操作数实行“移位”:
- Setup
- ... 选择随机数 \(\beta, \gamma, \rho_l, \rho_r\) ,设置 \(\rho_o = \rho_l \cdot \rho_r\)
- 设置生成元 \(g_l = g^{\rho_l}, g_r = g^{\rho_r}, g_o = g^{\rho_o}\)
- 设置 proving key: \[(\{g^{s^k}\}_{k \in [d]}, \{g_l^{l_i(s)}, g_r^{r_i(s)}, g_o^{o_i(s)}, g_l^{\alpha_l l_i(s)}, g_r^{\alpha_r r_i(s)}, g_o^{\alpha_o o_i(s)}, g_l^{\beta l_i(s)}, g_r^{\beta r_i(s)}, g_o^{\beta o_i(s)}\})\]
- 设置 verification key: \((g_o^{t(s)}, g^{\alpha_l}, g^{\alpha_r}, g^{\alpha_o}, g^{\beta \gamma}, g^{\gamma})\)
- ... 选择随机数 \(\beta, \gamma, \rho_l, \rho_r\) ,设置 \(\rho_o = \rho_l \cdot \rho_r\)
- Proving
- ... 设置变量值 \(g^{Z(s)} = \prod_{i=1}^n (g_l^{\beta l_i(s)} \cdot g_r^{\beta r_i(s)} \cdot g_o^{\beta o_i(s)})^{v_i}\)
- ... 设置变量值 \(g^{Z(s)} = \prod_{i=1}^n (g_l^{\beta l_i(s)} \cdot g_r^{\beta r_i(s)} \cdot g_o^{\beta o_i(s)})^{v_i}\)
- Verification
- 变量多项式约束检查: \(e(g_l^{L'}, g) = e(g_l^L, g^{\alpha_l})\) ,对 \(g_r^R, g_o^O\) 的检查也类似
- 变量值一致性检查: \(e(g_l^L \cdot g_r^R \cdot g_o^O, g^{\beta \gamma}) = e(g^Z, g^{\gamma})\)
- 验证计算有效性: \(e(g_l^L \cdot g_r^R) = e(g_o^t, g^h) e(g_o^O, g) \Rightarrow e(g,g)^{\rho_l \rho_r LR} = e(g,g)^{\rho_l \rho_r t h + \rho_l \rho_r O}\)
- 变量多项式约束检查: \(e(g_l^{L'}, g) = e(g_l^L, g^{\alpha_l})\) ,对 \(g_r^R, g_o^O\) 的检查也类似
生成元的这种随机化进一步增加了安全性,使得如节 7.6.1.1 中描述的可变多项式延展性无效。因为对于故意的修改,它必须要么是 \(\rho_l, \rho_r, \rho_o\) 原始值的倍数,要么就是不可直接用的加密值的倍数(假定,如上文所述我们不去处理可能曝光加密后的值的 0 阶可变多项式)。
这个优化使得 verification key 减少了两个项,并且去除了 verification 步骤中的两个配对运算。
注意:Jens Groth 在 paper Gro16 中有更进一步的改进。
7.10. 约束(R1CS)
我们的分析主要集中在“运算”的概念上。但是,协议实际上不是去做“计算”,而是“检验”输出值是否是操作数正确运算得到的结果。所以我们称之为“约束”,即 一个 verifier 约束 prover 去为预定义的“程序”提供有效值,而无论这个“程序”是什么。 多个约束组成的系统被称为“约束系统”,在我们的例子中这是一个一阶约束系统,或被称为(Rank 1 Constraint System, R1CS)。
我们也可以使用约束来确保其它的关系。例如,如果我们想要确认变量 a 的值只能为 0 或 1(即二进制数),我们可以用一个简单的约束去做这件事:
\[{\color{green}{a}} \times {\color{blue}{a}} = {\color{red}{a}}\]
我们也可以去约束 \(a\) 的值只能为 2:
\[{\color{green}{(a−2)}} \times {\color{blue}{1}} = {\color{red}{0}}\]
一个更复杂的例子是确保数字 \(a\) 是一个 4-bit 的数字(也称为半字节),换句话说可以用 4 个 bit 来表示出 \(a\) 。我们也可以称这个为“确保取值范围” 因为一个 4-bit 的数字可以代表 \(2^4\) 的组合,因而也就是从 0 到 15 范围内的 16 个数字。
因而如果 \(a\) 是一个 4-bit 的数,那么 \(a = b_3 \cdot 2^3 + b_2 \cdot 2^2 + b_1 \cdot 2^1 + b_0 \cdot 2^0\) ,其中 \(b_3, b_2, b_1, b_0\) 为布尔值。约束就可以表示为下面的形式:
并且为了确保 \(b_3, b_2, b_1, b_0\) 都是二进制数我们需要再增加 4 个约束(共 5 个约束):
更复杂的约束也可以用这种方式表示,以此来确保使用的值满足规则。
看一个通用的约束形式:
\[\sum_{i=1}^{n} c_{l,i} \cdot v_i \times \sum_{i=1}^n c_{r,i} \cdot v_i = \sum_{i=1}^n c_{o,i} \cdot v_i\]
需要注意的一点是上面的约束结构不能表示前面例子中的第 1 约束(也就是 \({\color{green}{a}} \times {\color{blue}{1}} = {\color{red}{8 \cdot b_3 + 4 \cdot b_2 + 2 \cdot b_1 + 1 \cdot b_0}}\) )。 \({\color{green}{1}}\) 通过 \({\color{blue}{c \cdot v_{one}}}\) 表达,其中 \({\color{blue}{c}}\) 可以被固定到 proving key 中,但是因为 \({\color{blue}{v_{one}}}\) 是由 prover 提供的,所以可以是任何别的值。尽管我们可以通过设置 \(c=0\) 来强制 \(c \cdot v_{one}\) 变成 0,但是在我们前面受限的构造方法中很难找到一个约束来强制 \(v_{one}\) 为 1。于是,verifier 需要有一种办法来设置 \(v_{one}\) 的值。
7.11. 公共输入和 1
如果不能根据 verifier 的输入对其进行检查,那么证明的可用性将受到限制。比如说,虽然知道 prover 将两个值相乘但是并不知道这些值或计算结果。尽管有可能在 proving key 中通过“硬编码”来进行验证一些特定的值(如,乘法运算的结果必须为 12),但这就需要针对每一个想要的“verifier 的输入”生成单独的密钥对。
因而,如果可以由 verifier 而不是 prover 为计算指定一些值(输入或者输出),包括 \(v_{one}\) ,那证明就可以变得更通用了。
首先,我们看一下要证明的值 \(g^L(s), g^R(s), g^O(s)\) 。因为这里使用了同态加密所以可以增大这些值,例如,我们可以与另一个加密的多项式相加使得值为 \(g^L(s) \cdot g^l_v(s) = g^{L(s)+l_v(s)}\) 。
这样如果我们能够在提供给 prover 的变量多项式中排除必要的一项,verifier 就可以在这一项变量多项式上设置他自己的值,并且使得检查依然能够通过。
因为 verifier 已经可以通过加入 \(\alpha\) 转换来限制 prover 选择多项式了,所以这个检查结果就很容易得到。因而当消除了它的 \(\alpha\) 和 \(\beta\) 校验和对应的项,这些可变多项式就可以从 proving key 转移到 verification key 当中去了。
协议更新为:
- Setup
- ... 将 \(n\) 个可变多项式全部分为两组:
- verifier 的 \(m+1\) 项: \(L_v(x) = l_0(x) + l_1(x) + \cdots + l_m(x)\) ,对 \(R_v(x)\) 和 \(O_v(x)\) 也做同样的计算。这里指数为 0 项为 \(v_{one} = 1\) 而保留。
- prover 的 \(n-m\) 项: \(L_p(x) = l_{m+1}(x) + \cdots + l_n(s)\) ,对 \(R_p(x)\) 和 \(O_p(x)\) 也做同样的计算。
- verifier 的 \(m+1\) 项: \(L_v(x) = l_0(x) + l_1(x) + \cdots + l_m(x)\) ,对 \(R_v(x)\) 和 \(O_v(x)\) 也做同样的计算。这里指数为 0 项为 \(v_{one} = 1\) 而保留。
- 设置 proving key: \((\{g^{s^k}\}_{k \in [d]}, \{g_l^{l_i(s)}, g_r^{r_i(s)}, g_o^{o_i(s)}, g_l^{\alpha_l l_i(s)}, g_r^{\alpha_r r_i(s)}, g_o^{\alpha_o o_i(s)}, g_l^{\beta l_i(s)} \cdot g_r^{\beta r_i(s)} \cdot g_o^{\beta o_i(s)}\}_{i \in \{m+1, \cdots, n\}})\)
- 添加到 verification key: \((\cdots, \{g_l^{l_i(s)}, g_r^{r_i(s)}, g_o^{o_i(s)} \}_{i \in \{0, \cdots, m\}})\)
- ... 将 \(n\) 个可变多项式全部分为两组:
- Proving
- ... 计算 \(h(x) = \frac{L(x) \cdot R(x) - O(x)}{t(x)}\), 其中 \(L(x) = L_v(x) + L_p(x)\) , \(R(x),O(x)\) 也类似。
- 设置证明: \((g_l^{L_p(s)}, g_r^{R_p(s)}, g_o^{O_p(s)}, g_l^{\alpha_l L_p(s)}, g_r^{\alpha_r R_p(s)}, g_o^{\alpha_o O_p(s)}, g^{Z(s)}, g^{h(s)})\)
- ... 计算 \(h(x) = \frac{L(x) \cdot R(x) - O(x)}{t(x)}\), 其中 \(L(x) = L_v(x) + L_p(x)\) , \(R(x),O(x)\) 也类似。
- Verification
- 为 verifier 的变量多项式赋值,并加 1: \(g_l^{L_v(s)} = g_l^{l_0(s)} \cdot \prod_{i=1}^m(g_l^{l_i(s)})^{v_i}\) ,对 \(g_r^{R_v(s)}, g_o^{O_v(s)}\) 做同样的计算
- 变量多项式约束检查: \(e(g_l^{L_p}, g^{\alpha_l} = e(g_l^{L_p'},g)\) ,对 \(g_r^{R_p}, g_o^{O_p}\) 做同样的检查
- 变量值一致性检查: \(e(g_l^{L_p}g_r^{R_p}g_o^{O_p}, h^{\beta \gamma}) = e(g^Z, g^{\gamma})\)
- 有效计算检查: \(e(g_l^{L_v(s)}g_l^{L_p}, g_r^{R_v(s)}g_r^{R_p}) = e(g_o^t, g^h) e(g_o^{O_v(s)} g_o^{O_p}, g)\)
- 为 verifier 的变量多项式赋值,并加 1: \(g_l^{L_v(s)} = g_l^{l_0(s)} \cdot \prod_{i=1}^m(g_l^{l_i(s)})^{v_i}\) ,对 \(g_r^{R_v(s)}, g_o^{O_v(s)}\) 做同样的计算
这实际上是 把一些变量从 prover 手中拿到 verifier 的手中,并同时保持等式相等。
7.12. 零知识计算
自从引入通用计算协议(节 7.4),我们一直放弃了零知识的性质,这是为了让协议的改进变得更简单。至此,我们已经构建了可验证的计算协议。
以前我们使用随机数 \(\delta\) 转换来构造多项式的“零知识”证明(节 5),这种方法能够使得证明与随机数无法区分: \(\delta p(s) = t(s) \cdot \delta h(s)\)
通过计算我们证明了:
\[L(s) \cdot R(s) - O(s) = t(s) h(s)\]
尽管我们可以通过用相同 \(\delta\) 乘以多项式的方法来调整解决方案,即提供随机值 \(\delta L(s), \delta R(s), \delta^2 O(s), \delta^2 h(s)\) ,这依然能够通过有效计算检查来满足配对验证:
\[e(g,g)^{\delta^2 L(s) R(s)} = e(g,g)^{\delta^2 (t(s)h(s) + O(s))}\]
但是问题是使用相同的 \(\delta\) 会妨碍安全性,因为我们在证明中分别用了以下这些值:
- 其他人可以很容易得辨认出两个不同的多项式值是否相同,如: \(g^{\delta L(s)}=g^{\delta R(s)}\) ,以此来获取一些知识
- \(L(s)\) 和 \(R(s)\) 的不同值之间潜在的微小关系可能会通过暴力破解来区分开来,例如如果 \(L(s) = 5R(s)\) ,就可以对 \(i \in \{1 \cdots N\}\) 取值反复校验 \(g^{L(s)}=(g^{R(s)})^i\) ,只需要执行 5 步就可以揭示出两者 5 倍区别的关系。同样的暴力破解也可以用在破解加密值的加法运算上,如: \(g^{L(s)}=g^{R(s)+5}\)
- 证明元素之间的其它关系也可能会被发现,例如,如果 \(e(g^{\delta L(s)}, g^{\delta R(s)}) = e(g^{\delta^2 O(s)},g)\) ,那么也就表示 \(L(x) \cdot R(x) = O(x)\) 。
从而,我们需要对每一个多项式的值“乘”上不同的随机数,例如:
\[\delta^l L(s) \cdot \delta_r R(s) - \delta_o O(s) = t(s) \cdot ( \Delta ? h(s))\]
为了解决等式右边不相等的问题,我们不必改变协议,只要修改证明的值 \(h(s)\) 即可。这里 \(\Delta\) 代表为了平衡方程另一侧的随机性而对 \(h(s)\) 做的处理, \(?\) 代表乘法运算或者加法运算(这个反过来也适应了除法和减法)。如果我们选择用乘法 (即 \(? = \times\) ) 来计算 \(\Delta\) ,也就意味着不太可能有较大的概率可以找到一个 \(\Delta\) ,因为存在随机性:
\[\Delta = \frac{\delta_l L(s) \cdot \delta_r R(s) - \delta_o O(s)}{t(s)h(s)}\]
设置 \(\delta_o = \delta_l \cdot \delta_r\) ,于是就变成了:
\[\Delta = \frac{\delta_l \delta_r(L(s) \cdot R(s) - O(s))}{t(s)h(s)} = \delta_l \delta_r\]
但是如前文所述,这个妨碍了零知识的性质,更重要的是这个结构也不再适合 verifier 的输入多项式,因为它们必须是某些 \(\delta\) 相应的倍数,这就需要额外的交互了。
我们可以尝试把随机数“加”到变量上,即:
\[(L(s) + \delta_l) \cdot (R(s) + \delta_r) - (O(s) + \delta_o) = t(s) \cdot (\Delta \times h(s))\]
从而:
\[\Delta = \frac{\overbrace{L(s)R(s) - O(s)}^{t(s)h(s)} + \delta_r L(s) + \delta_l R(s) + \delta_l \delta_r - \delta_o}{t(s)h(s)} = 1 + \frac{\delta_r L(s) + \delta_l R(s) + \delta_l \delta_r - \delta_o}{t(s)h(s)}\]
但是随机数是不可除尽的。尽管我们可以用 \(t(s)h(s)\) 去乘以每一个 \(\delta\) ,但由于我们已经用了 \(\Delta\) 乘以 \(h(s)\) , \(\Delta\) 是组成加密结果的一部分(即 \(g^{L(s)}\) 等),因此在没有使用配对(它的结果在另一个数值空间内)的情况下是不能计算出 \(g^{\Delta h(s)}\) 的。同样也不能使用 \(\{g^{s^i}\}_{i \in [d]}\) 对 \(\Delta h(x)\) 进行加密计算, \(\Delta h(x)\) 的阶将达到 \(2d\) 。并且,基于上述同样的原因也无法计算这个随机操作数多项式的值: \(g^{L(s)+ \delta_l t(s)h(s)}\) 。
于是,我们应该用加法(即 \(? = +\) )来使用 \(\Delta\) ,因为它可以同态地计算。
\[(L(s) + \delta_l) \cdot (R(s) + \delta_r) - (O(s) + \delta_o) = t(s) \cdot (\Delta + h(s))\]
从而:
\[\Delta = \frac{L(s)R(s) - O(s) + \delta_r L(s) + \delta_l R(s) + \delta_l \delta_r - \delta_o - t(s)h(s)}{t(s)} = \frac{\delta_r L(s) + \delta_l R(s) + \delta_l \delta_r - \delta_o}{t(s)}\]
由于分子中的每一项都包含某个 \(\delta\) ,我们可以让 \(\delta_l, \delta_r, \delta_o\) 每个都乘上 \(t(s)\) ,即采用下面式子实现零知识:
\[(L(s) + \delta_l t(s)) \cdot (R(s) + \delta_r t(s)) - (O(s) + \delta_o t(s)) = t(s) \cdot (\Delta + h(s))\]
从而:
\[\Delta = \frac{t(s)(L(s)R(s) - O(s) + \delta_r L(s) + \delta_l R(s) + \delta_l \delta_r t(s) - \delta_o - t(s)h(s))}{t(s)} = \delta_r L(s) + \delta_l R(s) + \delta_l \delta_r t(s) - \delta_o\]
这样就可以在加密的空间中进行“有效计算检查”了:
于是既隐藏了加密值,又使得等式可以通过有效计算检查。
\[L \cdot R - O + {\color{magenta}{t(\delta_r L + \delta_l R + \delta_l \delta_r t - \delta_o)}} = t(s)h + {\color{magenta}{t(s)(\delta_r L + \delta_l R + \delta_l \delta_r t - \delta_o)}}\]
这个结构就是统计学上的零知识,因为增加了随机数 \(\delta_l, \delta_r, \delta_o\) 。
为了使得“变量多项式限制”和“变量值一致性”检查与零知识的修改一致,就有必要去增加以下的参数到 proving key 中:
\[g_l^{t(s)}, g_r^{t(s)}, g_o^{t(s)}, g_l^{\alpha_l t(s)}, g_r^{\alpha_r t(s)}, g_o^{\alpha_o t(s)}, g_l^{\beta t(s)}, g_r^{\beta t(s)}, g_o^{\beta t(s)}\]
7.13. zk-SNARK(Pinocchio)协议总结
在这一步步的改进之后,我们得到了最终版本的 zk-SNARK (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge),这就是 Pinocchio 协议(参见 PGHR13),零知识部分是可选的,并用不同的颜色标注出来了。
zk-SNARK 协议就是:
- Setup
- 选择生成元 \(g\) 和加密配对 \(e\)
- 对于函数 \(f(u)=y\) ,假设它有 \(n\) 个变量,其中 \(m\) 个是输入或输出变量。把它转换为阶数为 \(d\) ( \(d\) 就是 operation 的个数)的多项式形式(即 QAP): \((\{l_i(x), r_i(x), o_i(x) \}_{i \in \{0, \cdots, n \}}, t(x))\)
- 选择随机数 \(s, \rho_l, \rho_r, \alpha_l, \alpha_r, \alpha_o, \beta, \gamma\)
- 设置 \(\rho_o = \rho_l \cdot \rho_r\) 和操作数生成元 \(g_l = g^{\rho_l}, g_r = g^{\rho_r}, g_o = g^{\rho_o}\)
- 设置 proving key: \[\begin{align*} (\{g^{s^k}\}_{k \in [d]}, \{g_l^{l_i(s)}, g_r^{r_i(s)}, g_o^{o_i(s)}\}_{i \in \{0, \cdots, n\}}, \\ \{g_l^{\alpha_l l_i(s)}, g_r^{\alpha_r r_i(s)}, g_o^{\alpha_o o_i(s)}, g_l^{\beta l_i(s)}, g_r^{\beta r_i(s)}, g_o^{\beta o_i(s)} \}_{i \in \{m+1, \cdots, n\}}, \\ {\color{magenta}{g_l^{t(s)}, g_r^{t(s)}, g_o^{t(s)}, g_l^{\alpha_l t(s)}, g_r^{\alpha_r t(s)}, g_o^{\alpha_o t(s)}, g_l^{\beta t(s)}, g_r^{\beta t(s)}, g_o^{\beta t(s)}}}) \end{align*}\]
- 设置 verification key: \((g^1, g_o^{t(s)}, \{g_l^{l_i(s)}, g_r^{r_i(s)}, g_o^{o_i(s)} \}_{i \in \{0, \cdots, m \}}, g^{\alpha_l}, g^{\alpha_r}, g^{\alpha_o}, g^{\gamma}, g^{\beta \gamma})\)
- 选择生成元 \(g\) 和加密配对 \(e\)
- Proving
- 代入输入值 \(u\) ,执行 \(f(u)\) 计算获取所有的中间变量值 \(\{v_i\}_{i \in \{ m+1, \cdots, n \}}\)
- 把所有未加密的变量多项式赋值给 \(L(x) = l_0(x) + \sum_{i=1}^n v_i \cdot l_i(x)\) ,并对 \(R(x)\) 和 \(O(x)\) 做同样的计算
- 选择随机数 \({\color{magenta}{\delta_l, \delta_r, \delta_o}}\)
- 计算 \(h(x) = \frac{L(x)R(x) - O(x)}{t(x)} {\color{magenta}{+ \delta_r L(x) + \delta_l R(x) + \delta_l \delta_r t(x) - \delta_o}}\)
- 将 prover 的变量值赋值给加密的可变多项式,并进行零知识的 \(\delta\) 转换 \(g_l^{L_p(s)} = {\color{magenta}{(g_l^{t(s)})^{\delta_l} \cdot}} \prod_{i=m+1}^n (g_l^{l_i(s)})^{v_i}\) ,再用同样的方式计算 \(g_r^{R_p(s)}, g_o^{O_p(s)}\)
- 为上面的 \(\alpha\) 变换赋值 \(g_l^{L_p'(s)} = {\color{magenta}{(g_l^{\alpha_l t(s)})^{\delta_l} \cdot}} \prod_{i=m+1}^n(g_l^{\alpha_l l_i(s)})^{v_i}\) ,再用同样的方式计算 \(g_r^{R_p'(s)}, g_o^{O_p'(s)}\)
- 为变量值一致性多项式赋值 \(g^{Z(s)} = {\color{magenta}{(g_l^{\beta t(s)})^{\delta_l} (g_r^{\beta t(s)})^{\delta_r} (g_o^{\beta t(s)})^{\delta_o}\cdot}} \prod_{i=m+1}^n(g_l^{\beta l_i(s)} g_r^{\beta r_i(s)} g_o^{\beta o_i(s)})^{v_i}\)
- 设置证明 \((g_l^{L_p(s)}, g_r^{R_p(s)}, g_o^{O_p(s)}, g_l^{L_p'(s)}, g_r^{R_p'(s)}, g_o^{O_p'(s)}, g^{Z(s)}, g^{h(s)})\)
- 代入输入值 \(u\) ,执行 \(f(u)\) 计算获取所有的中间变量值 \(\{v_i\}_{i \in \{ m+1, \cdots, n \}}\)
- Verification
- 把提供的证明简记为 \((g_l^{L_p}, g_r^{R_p}, g_o^{O_p}, g_l^{L_p'}, g_r^{R_p'}, g_o^{O_p'}, g^Z, g^h)\)
- 将输入/输出值赋值给 verifier 的加密多项式并加 1: \(g_l^{L_v(s)} = g_l^{l_0(s)} \cdot \prod_{n=1}^m(g_l^{l_i(s)})^{v_i}\) ,并对 \(g_r^{R_v(s)}, g_o^{O_v(s)}\) 做同样的计算
- 可变多项式约束检查: \(e(g_l^{L_p}, g^{\alpha_l}) = e(g_l^{L_p'}, g)\) ,并对 \(g_r^{R_p}, g_o^{O_p}\) 做同样的检查
- 变量值一致性检查: \(e(g_l^{L_p} g_r^{R_p} g_o^{O_p}, g^{\beta \gamma}) = e(g^Z, g^{\gamma})\)
- 有效计算的检查: \(e(g_l^{L_p}g_l^{L_v(s)}, g_r^{R_p}g_r^{R_v(s)}) = e(g_o^{t(s)}, g^h) \cdot e(g_o^{O_p} g_o^{O_v(s)}, g)\)
- 把提供的证明简记为 \((g_l^{L_p}, g_r^{R_p}, g_o^{O_p}, g_l^{L_p'}, g_r^{R_p'}, g_o^{O_p'}, g^Z, g^h)\)
上面三个过程可以分别用图 27,28,29(摘自:https://medium.com/coinmonks/hands-on-your-first-zk-application-70fe3a0c0d82 )表示。
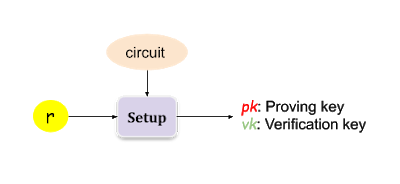
Figure 27: 第一步:Setup 过程,r 是一些随机数

Figure 28: 第二步:Prover 生成 Proof 的过程,s 是 private input(也称 witness),x 是公开的输入

Figure 29: 第三步:Verifier 进行 Verification 的过程
8. 结论
我们最终完成了一个允许证明计算的有效协议:
- 简明(Succinctly)—— 独立于计算量,证明是恒定的,小尺寸的;
- 非交互性(Non-interactive)—— 证明只要一经计算就可以在不直接与 prover 交互的前提下使任意数量的 verifier 确信;
- 可论证的知识(with Argument of Knowledge)—— 对于陈述是正确的这点有不可忽略的概率,即无法构造假证据;并且 prover 知道正确陈述的对应值(即:证据);
- 陈述有不可忽略的概率是正确的(这里指 Soundness,可靠性),即,构造假证据是不可行的;
- 零知识(zero-knowledge)—— 很“难”从证明中提取任何知识,即,它与随机数无法区分。
Pinocchio 的可靠性是 Computational Soundness。所谓的 Computational Soundness 暗含了这样的事实:如果 Prover 计算能力足够强大的话,可以破坏可靠性。
基于多项式的特殊性质,模运算,同态加密,椭圆曲线密码学,加密配对和发明者的聪明才智才使得这个协议得以实现。
这个协议证明了一个特殊有限执行机制的计算,即在一次运算中可以将几乎任意数量的变量加在一起但是只能执行一次乘法,因而就有机会优化程序以有效地利用这种特性的同时也使用这个结构最大限度地减少计算次数。
为了验证一个证明, verifier 并不需要知道所有的秘密数据,这一点很关键,这就使得任何人都可以以非交互式方式发布和使用正确构造的 verification key。这一点与只能让一个参与者确信证明的“指定 verifier”方案相反,因而它的信任是不可转移的。在 zk-SNARK 中,如果不可信或由单方生成密钥对,则可以实现这个属性。
零知识证明构造领域正在不断发展,包括引入了优化(Ben+13, Gro16, GM17),改进可更新的 proving key 和 verification key(Gro+18),以及新的构造方法(Bulletproofs Bün+17, zk-STARK Ben+18, Sonic Mal+19)。
8.1. Trusted Setup
zk-SNARK 最大的缺点在于它需要可信初始化(Trusted Setup)。可信初始化会生成参考字符串(Reference String),如果 Reference String 被泄露,那么任何人都可以生成虚假的证明。此外,Reference String 还只能被用于指定的程序,对于其他的程序,需要另外的可信初始化过程。
有两种方案来缓解上面的问题:
- Transparent Setup:可信初始化生成公共参考字符串(Common Reference String)。而 CRS 是公开的,不需要保密。不过这种方案其证明比较大,一般是 kB 量级。如 SuperSonic 和 Halo 等是采取了这种方案。
- Universal Setup:可信初始化生成了结构化参考字符串(Structure Reference String),尽管它也是需要保密的,但它有个好处是:一次生成后,所有程序都可以使用,这样不用为每个程序都进行一次 Setup 了。如 Plonk 等采取了这种方案。
参考:https://en.wikipedia.org/wiki/Zero-knowledge_proof#Zero-Knowledge_Proof_protocols
9. 参考
- Pinocchio 原始论文:Pinocchio: Nearly Practical Verifiable Computation
- Why and How zk-SNARK Works ,本文是它的中文改编(近似于翻译,但有少量取舍)
- 网上已有的 Why and How zk-SNARK Works 的中文翻译:https://learnblockchain.cn/article/287 (笔者大量参阅了该文,不过该文中的公式存在很多拼写错误,请对照原始英文论文阅读)