A* Search Algorithm
Table of Contents
1. A* 算法简介
我们知道,要计算某个点到所有其他点的最短路径长度可以使用 Dijkstra 算法。但如果用 Dijkstra 算法来求点到点的最短路径的话,它会毫无方向地向四周搜索,直到发现了目标点后即终止。
A* 算法(A* search algorithm)关注点到点的最短路径。使用 A* 算法能保证最短路径的搜索始终向着终点的方向进行,这样减少了很多不必要的计算,搜索效率更快。
参考:
人工智能:复杂问题求解的结构和策略(原书第 6 版),4.3.1 可采纳性度量
人工智能:一种现代方法(第二版),4.1.2 A* search: Minimizing the total estimated solution cost
Introduction to A* from Amit’s Thoughts on Pathfinding: http://theory.stanford.edu/~amitp/GameProgramming/AStarComparison.html
Introduction to A* from Amit’s Thoughts on Pathfinding(中文版):http://blog.csdn.net/b2b160/article/details/4057781
Introduction to A* from Red Blob Games: http://www.redblobgames.com/pathfinding/a-star/introduction.html
Implementation of A* from Red Blob Games: http://www.redblobgames.com/pathfinding/a-star/implementation.html
http://blog.csdn.net/fsdev/article/details/6849686
http://www.huhaoyu.com/A-star/
1.1. 图的表示
在介绍 A* 算法时,常常用网络地图来表示图(graph)。我们可以把网格的每一个单元看作是图的一个节点,相邻网格之间看作有一条连接两个节点的边。为了简单起见,我们假定斜线相邻单元不是直接相通的,如图 1 所示

Figure 1: 用网格地图表示图
2. 最佳优先搜索算法(Best-first search)
在介绍 A* 算法前,先介绍一下最佳优先搜索算法(Best-first search algorithm)。
最佳优先搜索是一种贪心算法,它的基本思想是:每一次都选择“它认为离目标最近”的点,不考虑从起始点到当前节点已经花费的代价。
说明:这个“它认为离目标最近”的点是通过一个估价函数(又称启发式函数)计算出来的,“它认为离目标最近”的点不一定是最短路径上的点。
2.1. 选择启发式函数
一般地,我们可以选择曼哈顿距离(Manhattan distance)作为评价函数(即启发式函数),点 \(n\) 到目标 \(goal\) 的曼哈顿距离为(其中 \(D\) 为从一个位置移动到邻近位置的最小代价):
\[h(n) = D * (\text{abs} (n.x – goal.x) + \text{abs} (n.y – goal.y))\]
我们还可以选择其它评价函数,如欧几里得距离(Euclidean distance):
\[h(n) = D * \sqrt{(n.x-goal.x)^2 + (n.y-goal.y)^2}\]
2.2. 最佳优先搜索算法伪代码
最佳优先搜索算法伪代码(摘自 wikipedia)如下:
OPEN = [initial state]
CLOSED = []
while OPEN is not empty
do
1. Remove the best node from OPEN, call it n, add it to CLOSED.
2. If n is the goal state, backtrace path to n (through recorded parents) and return path.
3. Create n's successors.
4. For each successor do:
a. If it is not in CLOSED and it is not in OPEN: evaluate it, add it to OPEN, and record its parent.
b. Otherwise, if this new path is better than previous one, change its recorded parent.
i. If it is not in OPEN add it to OPEN.
ii. Otherwise, adjust its priority in OPEN using this new evaluation.
done
说明 1:OPEN 列表用来记录可能需要搜索的节点,CLOSED 列表保存已经搜索过的节点(不会再搜索它们了)。
说明 2:由于需要把估价函数值小的节点调整到 OPEN 列表的前面位置,所以 OPEN 列表常用优先队列实现。
说明 3:上面算法是贪心算法,贪心策略是优先考虑估价函数值小的节点。
2.3. 最佳优先搜索实例(无障碍物)
2.4. 最佳优先搜索实例(有障碍物)
再考虑地图中有障碍物的情况。
这时,最佳优先搜索找到的路径很可能不是最短路径(贪心策略中没有考虑起始点到当前节点已经花费的代价),如图 4 所示。
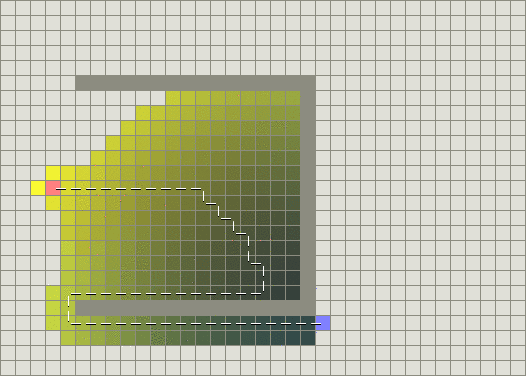
Figure 4: 最佳优先搜索(有障碍物),找到的路径不是最短路径
Dijkstra 算法尽管慢,但总可以找到最短路径,如图 5 所示。

Figure 5: Dijkstra 算法(有障碍物),尽管慢,但总可以找到最短路径
如果我们能结合“Dijkstra 算法”和“最佳优先搜索”的优点就好了,这样即可以找到最短路径,又可以避免一些不必要的搜索。这就是 A* 算法的基本思想,如图 6 所示,后方将对它进行详细描述。
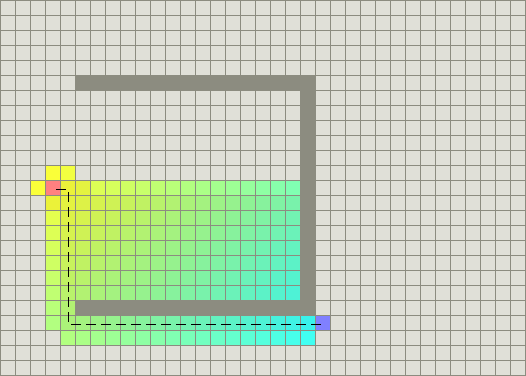
Figure 6: A*算法,结合了“Dijkstra 算法”和“最佳优先搜索”的优点
3. A* 算法描述
从概念上讲,A* 算法是简单的。
A*算法和最佳优先搜索算法类似(其伪代码和最佳优先搜索算法相同),只是换了一个估价函数。 A* 算法使用下面的估价函数(比最佳优先搜索增加了起始点到当前节点已经花费的代价)来计算节点 \(n\) 的评估值:
\[f(n) = g(n) + h(n)\]
其中, \(g(n)\) 为初始节点到节点 \(n\) 的实际代价(通过计算可确定), \(h(n)\) 是从节点 \(n\) 到目标节点的估计代价,称为启发式函数。
显然:
(1) 如果 \(h(n)=0\) ,只有 \(g(n)\) 起作用,则 A* 算法退化为 Dijkstra 算法;
(2) 如果 \(h(n)\) 远大于 \(g(n)\) ,则只有 \(h(n)\) 起作用,则 A* 算法退化成最佳优先搜索算法,不一定找到最短路径。
3.1. 什么条件下 A* 算法一定找到最短路径
如果 \(h(n)\) 小于(或等于)从节点 \(n\) 移动到目标节点的实际代价,则 A*保证能找到一条最短路径。
上面结论的证明可以参考:人工智能:复杂问题求解的结构和策略(原书第 6 版),4.7 节,习题 8
\(h(n)\) 越小,A* 搜索时扩展的结点就越多,运行就得越慢。如果 \(h(n)\) 有时比从 \(n\) 移动到目标的实际代价高,则 A*不能保证找到一条最短路径,但它运行得更快。
对于网格地图的搜索问题,使用曼哈顿距离 \(h(n) = D * (\text{abs} (n.x – goal.x) + \text{abs} (n.y – goal.y))\) 作为启发式函数,能保证 A* 算法一定找到最短路径(因为节点 \(n\) 到目标节点的曼哈顿距离小于等于从节点 \(n\) 移动到目标节点的实际代价)。
说明 1:对于网格地图的搜索问题,启发式函数也可以使用欧几里得距离,但不能使用欧几里得平方距离(由于开根号麻烦,而省略开根号运算),这会导致 \(h(n)\) 比从 \(n\) 移动到目标的实际代价高,而找到不到最短路径。
说明 2:如果 \(h(n)\) 精确地等于从 \(n\) 移动到目标的代价,则 A* 将会仅仅寻找最佳路径而不扩展别的任何结点,这会运行得非常快。尽管这不可能在所有情况下发生,你仍可以在一些特殊情况下让它们精确地相等。只要提供完美的信息,A* 会运行得很完美。
说明 3:A* 算法除了用来进行地图搜索外,还可以作为通用的启发式搜索算法来求解其它状态空间搜索问题。
3.2. 更快还是更准确
有时,我们希望得到一条好的路径即可,而不一定要找到最短路径。这时可以增加启发式函数 \(h(n)\) 的比重,从而使得 A* 算法更快。
3.3. A* 算法实例演示
3.4. A* 算法实现
下面的代码摘自:http://code.activestate.com/recipes/577457-a-star-shortest-path-algorithm/
// From: http://code.activestate.com/recipes/577457-a-star-shortest-path-algorithm/
// Astar.cpp
// http://en.wikipedia.org/wiki/A*
// Compiler: Dev-C++ 4.9.9.2
#include <iostream>
#include <iomanip>
#include <queue>
#include <string>
#include <math.h>
#include <ctime>
using namespace std;
const int n = 60; // horizontal size of the map
const int m = 30; // vertical size size of the map
static int map[n][m];
static int closed_nodes_map[n][m]; // map of closed (tried-out) nodes
static int open_nodes_map[n][m]; // map of open (not-yet-tried) nodes
static int dir_map[n][m]; // map of directions
const int dir = 8; // number of possible directions to go at any position
// if dir==4
// static int dx[dir]={1, 0, -1, 0};
// static int dy[dir]={0, 1, 0, -1};
// if dir==8
static int dx[dir] = {1, 1, 0, -1, -1, -1, 0, 1};
static int dy[dir] = {0, 1, 1, 1, 0, -1, -1, -1};
class node {
// current position
int xPos;
int yPos;
// total distance already travelled to reach the node
int level;
// priority=level+remaining distance estimate
int priority; // smaller: higher priority
public:
node(int xp, int yp, int d, int p) {
xPos = xp;
yPos = yp;
level = d;
priority = p;
}
int getxPos() const { return xPos; }
int getyPos() const { return yPos; }
int getLevel() const { return level; }
int getPriority() const { return priority; }
void updatePriority(const int &xDest, const int &yDest) {
priority = level + estimate(xDest, yDest) * 10; // A*
}
// give better priority to going strait instead of diagonally
void nextLevel(const int &i) // i: direction
{
level += (dir == 8 ? (i % 2 == 0 ? 10 : 14) : 10);
}
// Estimation function for the remaining distance to the goal.
const int &estimate(const int &xDest, const int &yDest) const {
static int xd, yd, d;
xd = xDest - xPos;
yd = yDest - yPos;
// Euclidian Distance
d = static_cast<int>(sqrt(xd * xd + yd * yd));
// Manhattan distance
// d=abs(xd)+abs(yd);
// Chebyshev distance
// d=max(abs(xd), abs(yd));
return (d);
}
};
// Determine priority (in the priority queue)
bool operator<(const node &a, const node &b) {
return a.getPriority() > b.getPriority();
}
// A-star algorithm.
// The route returned is a string of direction digits.
string pathFind(const int &xStart, const int &yStart, const int &xFinish,
const int &yFinish) {
static priority_queue<node> pq[2]; // list of open (not-yet-tried) nodes
static int pqi; // pq index
static node *n0;
static node *m0;
static int i, j, x, y, xdx, ydy;
static char c;
pqi = 0;
// reset the node maps
for (y = 0; y < m; y++) {
for (x = 0; x < n; x++) {
closed_nodes_map[x][y] = 0;
open_nodes_map[x][y] = 0;
}
}
// create the start node and push into list of open nodes
n0 = new node(xStart, yStart, 0, 0);
n0->updatePriority(xFinish, yFinish);
pq[pqi].push(*n0);
open_nodes_map[x][y] = n0->getPriority(); // mark it on the open nodes map
// A* search
while (!pq[pqi].empty()) {
// get the current node w/ the highest priority
// from the list of open nodes
n0 = new node(pq[pqi].top().getxPos(), pq[pqi].top().getyPos(),
pq[pqi].top().getLevel(), pq[pqi].top().getPriority());
x = n0->getxPos();
y = n0->getyPos();
pq[pqi].pop(); // remove the node from the open list
open_nodes_map[x][y] = 0;
// mark it on the closed nodes map
closed_nodes_map[x][y] = 1;
// quit searching when the goal state is reached
// if((*n0).estimate(xFinish, yFinish) == 0)
if (x == xFinish && y == yFinish) {
// generate the path from finish to start
// by following the directions
string path = "";
while (!(x == xStart && y == yStart)) {
j = dir_map[x][y];
c = '0' + (j + dir / 2) % dir;
path = c + path;
x += dx[j];
y += dy[j];
}
// garbage collection
delete n0;
// empty the leftover nodes
while (!pq[pqi].empty())
pq[pqi].pop();
return path;
}
// generate moves (child nodes) in all possible directions
for (i = 0; i < dir; i++) {
xdx = x + dx[i];
ydy = y + dy[i];
if (!(xdx < 0 || xdx > n - 1 || ydy < 0 || ydy > m - 1 ||
map[xdx][ydy] == 1 || closed_nodes_map[xdx][ydy] == 1)) {
// generate a child node
m0 = new node(xdx, ydy, n0->getLevel(), n0->getPriority());
m0->nextLevel(i);
m0->updatePriority(xFinish, yFinish);
// if it is not in the open list then add into that
if (open_nodes_map[xdx][ydy] == 0) {
open_nodes_map[xdx][ydy] = m0->getPriority();
pq[pqi].push(*m0);
// mark its parent node direction
dir_map[xdx][ydy] = (i + dir / 2) % dir;
} else if (open_nodes_map[xdx][ydy] > m0->getPriority()) {
// update the priority info
open_nodes_map[xdx][ydy] = m0->getPriority();
// update the parent direction info
dir_map[xdx][ydy] = (i + dir / 2) % dir;
// replace the node
// by emptying one pq to the other one
// except the node to be replaced will be ignored
// and the new node will be pushed in instead
while (!(pq[pqi].top().getxPos() == xdx &&
pq[pqi].top().getyPos() == ydy)) {
pq[1 - pqi].push(pq[pqi].top());
pq[pqi].pop();
}
pq[pqi].pop(); // remove the wanted node
// empty the larger size pq to the smaller one
if (pq[pqi].size() > pq[1 - pqi].size())
pqi = 1 - pqi;
while (!pq[pqi].empty()) {
pq[1 - pqi].push(pq[pqi].top());
pq[pqi].pop();
}
pqi = 1 - pqi;
pq[pqi].push(*m0); // add the better node instead
} else
delete m0; // garbage collection
}
}
delete n0; // garbage collection
}
return ""; // no route found
}
int main() {
srand(time(NULL));
// create empty map
for (int y = 0; y < m; y++) {
for (int x = 0; x < n; x++)
map[x][y] = 0;
}
// fillout the map matrix with a '+' pattern
for (int x = n / 8; x < n * 7 / 8; x++) {
map[x][m / 2] = 1;
}
for (int y = m / 8; y < m * 7 / 8; y++) {
map[n / 2][y] = 1;
}
// randomly select start and finish locations
int xA, yA, xB, yB;
switch (rand() % 8) {
case 0:
xA = 0;
yA = 0;
xB = n - 1;
yB = m - 1;
break;
case 1:
xA = 0;
yA = m - 1;
xB = n - 1;
yB = 0;
break;
case 2:
xA = n / 2 - 1;
yA = m / 2 - 1;
xB = n / 2 + 1;
yB = m / 2 + 1;
break;
case 3:
xA = n / 2 - 1;
yA = m / 2 + 1;
xB = n / 2 + 1;
yB = m / 2 - 1;
break;
case 4:
xA = n / 2 - 1;
yA = 0;
xB = n / 2 + 1;
yB = m - 1;
break;
case 5:
xA = n / 2 + 1;
yA = m - 1;
xB = n / 2 - 1;
yB = 0;
break;
case 6:
xA = 0;
yA = m / 2 - 1;
xB = n - 1;
yB = m / 2 + 1;
break;
case 7:
xA = n - 1;
yA = m / 2 + 1;
xB = 0;
yB = m / 2 - 1;
break;
}
cout << "Map Size (X,Y): " << n << "," << m << endl;
cout << "Start: " << xA << "," << yA << endl;
cout << "Finish: " << xB << "," << yB << endl;
// get the route
clock_t start = clock();
string route = pathFind(xA, yA, xB, yB);
if (route == "")
cout << "An empty route generated!" << endl;
clock_t end = clock();
double time_elapsed = double(end - start);
cout << "Time to calculate the route (ms): " << time_elapsed << endl;
cout << "Route:" << endl;
cout << route << endl << endl;
// follow the route on the map and display it
if (route.length() > 0) {
int j;
char c;
int x = xA;
int y = yA;
map[x][y] = 2;
for (int i = 0; i < route.length(); i++) {
c = route.at(i);
j = atoi(&c);
x = x + dx[j];
y = y + dy[j];
map[x][y] = 3;
}
map[x][y] = 4;
// display the map with the route
for (int y = 0; y < m; y++) {
for (int x = 0; x < n; x++)
if (map[x][y] == 0)
cout << ".";
else if (map[x][y] == 1)
cout << "O"; // obstacle
else if (map[x][y] == 2)
cout << "S"; // start
else if (map[x][y] == 3)
cout << "R"; // route
else if (map[x][y] == 4)
cout << "F"; // finish
cout << endl;
}
}
//getchar(); // wait for a (Enter) keypress
return (0);
}
运行上面程序,可得到类似下面的输出(其中字母 O 为障碍物,S为起点,F为终点,R为行动线路):
Map Size (X,Y): 60,30 Start: 31,29 Finish: 29,0 Time to calculate the route (ms): 9810 Route: 77777777700700777000755555555444555454454455 .............................F.............................. ..............................R............................. ...............................RRR.......................... ..............................O...RRR....................... ..............................O......RR..................... ..............................O........R.................... ..............................O.........R................... ..............................O..........RRRR............... ..............................O..............R.............. ..............................O...............R............. ..............................O................R............ ..............................O.................R........... ..............................O..................R.......... ..............................O...................R......... ..............................O....................R........ .......OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOR....... ..............................O.................RRRR........ ..............................O................R............ ..............................O...............R............. ..............................O............RRR.............. ..............................O.........RRR................. ..............................O........R.................... ..............................O.......R..................... ..............................O......R...................... ..............................O.....R....................... ..............................O....R........................ ..................................R......................... .................................R.......................... ................................R........................... ...............................S............................



