Dynamic Programming
Table of Contents
1. 动态规划简介
20 世纪 50 年代初美国数学家 Richard Bellman 等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划(Dynamic Programming)。
需要指出的是, 动态规划是用空间换时间,其空间复杂度通常比较高。
2. 动态规划解决哪类问题
和分治法一样,动态规划的整体思想是通过组合子问题的解而解决整个问题。
动态规划适合于解决同时满足下面两个条件的问题:
- 最优子结构。问题具有最优子结构是指:一个问题的最优解中包含了子问题的最优解。
- 重叠子问题。各个子问题中包含了公共的子子问题。动态规划能利用这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存下来,当再次需要计算已经计算过的子问题时,只是简单地查看一下以前保存的结果,从而获得较高的效率。
说明: 动态规划是一种优化手段,能用动态规划解决的问题一般都有一个效率不高的递归解法。
3. 动态规则的解题步骤
动态规划可按以下 4 个步骤进行:
(1)、寻找最优子结构。
(2)、利用子问题的最优解递归定义最优解的值(即先找到一个效率不高的递归解法)。
(3)、按自底向上的方式计算最优解的值。
(4)、从最后一步的最优值回溯,即可构造原始问题的最优解。
步骤(1)、(2)、(3)为动态规划的基本步骤,如果只需要得到“最优解的值”,步骤(4)可省略。如果还需要得到“最优解”则第(4)步不可省略,往往在第 3 步的计算中记录一些附加信息,使得构造一个最优解变得容易。
注 1:“最优解的值”和“最优解”的区别:
“最优解的值”是对“最优解”特征的部分描述。举例说明,最长公共子序列问题中,最长公共子序列的长度为“最优解的值”,而公共子序列具体包含哪此元素则是“最优解”。
注 2:动态规则还有一种变形方法:“top-down with memoization”。具体方法是进行到第(2)步,即找到递归解法后,把已经计算过的子问题的解保存下来(比如记录到数组或哈希表中),在递归时求解某问题时先检测是否已经计算过了,如果计算过就直接读取保存的结果以避免再次计算同样的问题,这就是 Memoization 。
4. 实例:求最长公共子序列(Longest Common Subsequence, LCS)
问题描述:请编写一个函数,输入两个字符串,求它们的最长公共子序列(最长公共子序列不一定是唯一的,求出一个即可),并打印出最长公共子序列。
例如,输入两个字符串 ABCBDAB 和 BDCABA,字符串 BCBA 和 BDAB 都是它们的最长公共子序列,则输出它们的长度 4,并打印任意一个子序列。
说明:如果字符串 1 的所有字符按其在字符串中的顺序出现在另外一个字符串 2 中,则字符串 1 称之为字符串 2 的子序列。注意,并不要求子序列(字符串 1)的字符必须连续地出现在字符串 2 中。
4.1. 问题分析
We solve the problem of finding the longest common subsequence of \(x=x_{1...m}\) and \(y=y_{1...n}\) by taking the best of the three possible cases:
- The longest common subsequence of the strings \(x_{1...m-1}\) and \(y_{1...n}\)
- The longest common subsequence of the strings \(x_{1...m}\) and \(y_{1...n-1}\)
- If \(x_{m}\) is the same as \(y_{n}\), the longest common subsequence of the strings \(x_{1...m-1}\) and \(y_{1...n-1}\), followed by the common last character.
用 \(c[i][j]\) 记录序列 \(x_{1...i}\) 和 \(y_{1...j}\) 的最长公共子序列的长度,则有递归关系:\[c[i][j] = \begin{cases} 0 & \text{if} \; i=0 \; \text{or} \; j=0 \\ c[i-1][j-1] +1 & \text{if} \; i,j>0; x_i = y_j \\ \max \{c[i][j-1], c[i-1][j] \} & \text{if} \; i,j>0; x_i \neq y_j\end{cases}\]
利用这个递归式能算出 \(c[m][n]\) ,这就是最长公共子序列的长度。
4.2. 最长公共子序列之递归解法(自顶向下)
可直接用程序求解上面的递归公式:
#include<stdio.h>
#include<string.h>
#define MAX(a,b) (((a)>(b))?(a):(b))
/* call it like this lcs_len(s, t, strlen(s)-1, strlen(t)-1) */
int lcs_len(char *s, char *t, int s_len, int t_len) {
if(s_len < 0 || t_len < 0) {
return 0;
}
if(s[s_len] == t[t_len]) {
return lcs_len(s, t, s_len-1, t_len-1)+1;
} else {
return MAX(lcs_len(s, t, s_len-1, t_len), lcs_len(s, t, s_len, t_len-1));
}
}
int main(void) {
char a[]="ABCBDAB";
char b[]="BDCABA";
printf("length: %d\n", lcs_len(a, b, strlen(a)-1, strlen(b)-1)); // 输出 length: 4
return 0;
}
上面这种递归解法的效率不高,会有过多的函数调用,而且有重复的计算。
4.3. 最长公共子序列之动态规划解法(自底向上)
前面的递归解法效率不高。下面我们设计一个表格化的、自底向上基于前面递归式的动态规化算法。其伪代码如下(摘自《算法导论(第 2 版)》):
LCS-LENGTH(X, Y)
m ← length[X]
n ← length[Y]
for i ← 1 to m
do c[i, 0] ← 0
for j ← 0 to n
do c[0, j] ← 0
for i ← 1 to m
do for j ← 1 to n
do if xi = yj then
c[i, j] ← c[i - 1, j - 1] + 1
b[i, j] ← "↖"
else if c[i - 1, j] ≥ c[i, j - 1] then
c[i, j] ← c[i - 1, j]
b[i, j] ← "↑"
else c[i, j] ← c[i, j - 1]
b[i, j] ← "←"
return c and b
上面伪代码中, \(c[i][j]\) 记录序列 \(x_{1...i}\) 和 \(y_{1...j}\) 的最长公共子序列的长度。 \(b[i][j]\) 记录着用来输出最优解的辅助信息,当 \(b[i][j]\) 等于“↖”时,意味着 \(x_i = y_j\) 是 LCS 中的一个元素,当 \(b[i][j]\) 等于“↑”时,意味着 \(x_i\) 不是 LCS 中的元素,当 \(b[i][j]\) 等于“←”时,意味着, \(y_j\) 不是 LCS 中的元素。
如果只要求最长公共子序列的长度,则可以不记录 \(b[i][j]\) 。
下面利用 \(b[i][j]\) 输出最长公共子序列。
打印最长公共子序列的伪代码如下(摘自《算法导论(第 2 版)》):
PRINT-LCS(b, X, i, j)
if i = 0 or j = 0
then return
if b[i, j] = "↖"
then PRINT-LCS(b, X, i - 1, j - 1)
print xi
else if b[i, j] = "↑"
then PRINT-LCS(b, X, i - 1, j)
else PRINT-LCS(b, X, i, j - 1)
遇到“↖”就打印出 \(x_i\) ,同时把 X、Y 都减去一个字符,再递归调用打印程序;遇到“↑”就把 X 减去一个字符,再递归调用打印程序;遇到“←”就把 Y 减去一个字符,再递归调用打印程序。
以 X=BDCABA,Y=ABCBDAB 为例,完成计算后, \(c[i][j]\) (下图中每个方格中的数字)和 \(b[i][j]\) (下图中每个方格中的小箭头)如图 1 所示:
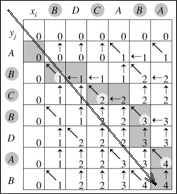
Figure 1: 动态规划实例:求解 LCS 问题
图 1 中,从左上角到右下角的大箭头表示 \(c[i][j]\) 和 \(b[i][j]\) 中元素的计算顺序。
4.3.1. 动态规划算法实现
程序中用 LCS_length 和 LCS_direction 相当于前面分析时用的数组 c 和 b。
// file LCS_DP.cpp 动态规划求解LCS问题。
#include<string.h>
#include<stdio.h>
enum Directions {kInit = 0, kLeft, kUp, kLeftUp}; // directions of LCS generation
void LCS_Print(int **LCS_direction,const char* pStr1, size_t row, size_t col);
// Get the length of two strings' LCSs, and print one of the LCSs
// Input: pStr1 - the first string
// length1 - strlen(pStr1)
// pStr2 - the second string
// length2 - strlen(pStr2)
// Output: the length of two strings' LCSs
int LCS(const char* pStr1, size_t length1, const char* pStr2, size_t length2) {
size_t i, j, lcs_length;
// initiate the length matrix
int **LCS_length;
LCS_length = new int*[length1];
for(i = 0; i < length1; ++ i)
LCS_length[i] = new int[length2];
for(i = 0; i < length1; ++ i)
for(j = 0; j < length2; ++ j)
LCS_length[i][j] = 0;
// initiate the direction matrix
int **LCS_direction;
LCS_direction = new int*[length1];
for( i = 0; i < length1; ++ i)
LCS_direction[i] = new int[length2];
for(i = 0; i < length1; ++ i)
for(j = 0; j < length2; ++ j)
LCS_direction[i][j] = kInit;
//计算LCS_length和LCS_direction。
for(i = 0; i < length1; ++ i) {
for(j = 0; j < length2; ++ j) {
if(i == 0 || j == 0) { //这是个边界的情况,应单独拿出来,否则i-1等会出界。
if(pStr1[i] == pStr2[j]) { //这个情况也得考虑。
LCS_length[i][j] = 1;
LCS_direction[i][j] = kLeftUp;
}
else
LCS_length[i][j] = 0; //可以去掉,因为前面已经全部初始为0了。
}
// a char of LCS is found,
// it comes from the left up entry in the direction matrix
else if(pStr1[i] == pStr2[j]) {
LCS_length[i][j] = LCS_length[i - 1][j - 1] + 1;
LCS_direction[i][j] = kLeftUp;
}
// it comes from the up entry in the direction matrix
else if(LCS_length[i - 1][j] > LCS_length[i][j - 1]) {
LCS_length[i][j] = LCS_length[i - 1][j];
LCS_direction[i][j] = kUp;
}
// it comes from the left entry in the direction matrix
else { //最后剩下情况是LCS_length[i - 1][j] <= LCS_length[i][j - 1]
LCS_length[i][j] = LCS_length[i][j - 1];
LCS_direction[i][j] = kLeft;
}
}
}
LCS_Print(LCS_direction, pStr1, length1 - 1, length2 - 1); //调用下面的LCS_Pring打印出所求子串。
lcs_length = LCS_length[length1 - 1][length2 - 1];
//释放二维数组空间。
for(i=0; i < length1; i++)
delete[] LCS_length[i];
delete[] LCS_length;
for(i=0; i < length1; i++)
delete[] LCS_direction[i];
delete[] LCS_direction;
return lcs_length; //返回长度。
}
// Print a LCS for two strings
// Input: LCS_direction - a 2d matrix which records the direction of
// LCS generation
// pStr1 - the first string
// row - the row index in the matrix LCS_direction
// col - the column index in the matrix LCS_direction
void LCS_Print(int **LCS_direction,
const char* pStr1,
size_t row, size_t col) {
if(pStr1 == NULL)
return;
// kLeftUp implies a char in the LCS is found
if(LCS_direction[row][col] == kLeftUp) {
if(row > 0 && col > 0)
LCS_Print(LCS_direction, pStr1, row - 1, col - 1);
// print the char
printf("%c", pStr1[row]);
}
else if(LCS_direction[row][col] == kLeft) {
// move to the left entry in the direction matrix
if(col > 0)
LCS_Print(LCS_direction, pStr1, row, col - 1);
}
else if(LCS_direction[row][col] == kUp) {
// move to the up entry in the direction matrix
if(row > 0)
LCS_Print(LCS_direction, pStr1, row - 1, col);
}
}
int main() {
char a1[]="BDCABA";
char b1[]="ABCBDAB";
printf(" length %d\n", LCS(a1, strlen(a1), b1, strlen(b1))); // 输出 BCBA length 4
char a2[] = "GCGCAATG";
char b2[] = "GCCCTAGCG";
printf(" length %d\n", LCS(a2, strlen(a2), b2, strlen(b2))); // 输出 GCCTG length 5
return 0;
}
4.4. 动态规划解法的缺点——空间复杂度高
用动态规划解决最长公共子序列问题,其空间复杂度比较高,为 \(O(mn)\) 。
如果当两个序列达到上万个节点时,内存消耗就成为了大问题。如确定一种致病基因的基本方法就是将该疾病患者的 DNA 链与健康者的 DNA 链相比较,找出其中的相同部分与不同部分,再进行分析。这种基因链的比较就可以用 LCS 算法来解决,但 DNA 序列一般都很长。所以动态规划方法不太实用。
4.5. 线性空间复杂度的 LCS 解法
针对动态规划空间复杂度高的缺陷,求解 LCS 问题有几种线性空间复杂度的其它算法,如 Hirschberg’s algorithm 和 Nakatsu algorithm 。
5. 实例:求最大子序和
问题描述:给定整数 \(A_0, A_1, \cdots, A_n\) (可能有负数),求 \(\sum_{k=i}^{j}A_k\) 的最大值(为方便起见,如果所有整数均为负数,则最大子序和为 0)。
例如:输入-2,11,-4,13,-5,-2 时,答案为 20(从 \(A_1\) 到 \(A_3\) )。
5.1. 问题分析
这是一个很有名的一个问题,在 Mark Allen Weiss 的《数据结构与算法分析——C 语言描述(原书第 2 版)》2.4.3 节中介绍了四种方法,《编程之美》2.14 节也有介绍,《编程珠玑(第二版)》第 8 章也介绍了该问题。
动态归划的思路:设 \(b[j]\) 是这些以 \(A[j]\) 结尾的众多子序列中和最大的一个,则原始问题的解就是 \(b[j], 1≤j≤n\) 中最大的一个。
5.2. 动态归划算法实现
//用动态规划算法解决最大子序和问题。
#include<iostream>
using std::cout;
using std::endl;
//返回值为子数组的最大和。
//A[]为数组,N为数组元素个数,start和end分别返回子数组开始、结束位置。
int max_sub_array(const int A[], int N, int& start, int& end) {
int b = A[0];
int sum = A[0];
int start_tmp = 0;
int end_tmp = 0; //start_tmp和end_tmp用来辅助定位start、end。
for (int j = 1; j < N; j++) {
if (b > 0) {
b = b + A[j];
end_tmp = j;
} else {
b = A[j];
start_tmp = end_tmp = j;
}
if (sum < b) {
sum = b;
start = start_tmp;
end = end_tmp;
}
}
return sum;
}
int main() {
int A[] = { -2, 11, -4, 13, -5, -2 };
int start, end;
cout << max_sub_array(A, 6, start, end) << endl;
cout << "start: A" << start << endl; // 这个例子会输出 start: A1
cout << "end: A" << end << endl; // 这个例子会输出 end: A3
}
5.3. 扩展问题:求最大子矩阵
问题描述:
给定一个 \(M \times N\) 的矩阵,请找出此矩阵的一个子矩阵,并且此矩阵的各个元素的和最大,输出这个子矩阵和最大值。
例如,在如下这个矩阵中:
0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2
拥有最大和的子矩阵为:
9 2 -4 1 -1 8
其和为 15。
POJ(北京大学程序在线评测系统)上有这个题:http://poj.org/problem?id=1050
说明:最大子矩阵问题可以看做是最大子序和问题的推广,它也是动态规划的经典实例。具体分析略。
6. 实例:求编辑距离(Edit Distance)
如何比较两个字符串的相似度呢?一种办法是计算编辑距离(Levenshtein distance, or edit distance)。
定义下面三种操作:
(1) 插入一个字符;
(2) 删除一个字符;
(3) 替换一个字符。
如果字符串 A 通过上面三个操作变成字符串 B,那么 最少的操作次数就是两个字符串的最小编辑距离(简称编辑距离)。
例如,字符串“kitten”和字符串“sitting”的编辑距离为 3(操作过程:替换 k 为 s;替换 e 为 i;在末尾插入字符 g)。
如何求解两个字符串的编辑距离呢?
参考:
Levenshtein distance Wikipedia: https://en.wikipedia.org/wiki/Levenshtein_distance
文本比较算法Ⅰ——LD 算法:http://www.cnblogs.com/grenet/archive/2010/06/01/1748448.html
6.1. 问题分析
用 ed(i,j) 表示字符串 A[0,i] 和 B[0,j] 的编辑距离。假设 A[0,i] 和 B[0,j] 的形式分别为 str1a 和 str2b 。
如果 a==b,则 ed(i,j) = ed(i-1,j-1)。
如果 a != b,则 ed(i,j) 是下面三个可能值中最小的那个:
(1) 如果 a 替换为 b 时,可使 A 变为 B,则 ed(i,j) = ed(i-1,j-1) + 1;
(2) 如果在 a 后面插入字符 d,可使 A 变为 B,则 ed(i,j) = ed(i,j-1) + 1;
(3) 如果将 a 删除,可使 A 变为 B,则 ed(i,j) = ed(i-1,j) + 1。
显然,当 i=0 时,ed(i,j) = j;当 j=0 时,ed(i,j)=i。
总结,可得编辑距离的求解公式:
\[ed(i,j) = \begin{cases} i & \text{if} \; j = 0 \\
j & \text{if} \; i = 0 \\
ed(i-1,j-1) & \text{if} \; i,j > 0; a_i = b_j \\
\min\{ed(i-1,j-1), ed(i,j-1), ed(i-1,j)\} + 1 & \text{if} \; i,j > 0; a_i \ne b_j \\
\end{cases}\]
6.2. 递归解法
用如下递归程序可直观地求解上面公式。
// len_s and len_t are the number of characters in string s and t respectively
int EditDistance(char *s, int len_s, char *t, int len_t)
{
int cost;
/* base case: empty strings */
if (len_s == 0) return len_t;
if (len_t == 0) return len_s;
/* test if last characters of the strings match */
if (s[len_s-1] == t[len_t-1]) {
return EditDistance(s, len_s - 1, t, len_t - 1);
} else {
int minimum = min(EditDistance(s, len_s - 1, t, len_t), EditDistance(s, len_s, t, len_t - 1));
return min(minimum, EditDistance(s, len_s - 1, t, len_t - 1)) + 1;
}
}
上面程序效率不高,会重复计算之前计算过的值。
6.3. 动态规划解法
递归解法效率太低,动态规则解法如下:
#include <string>
#include <iostream>
using namespace std;
int EditDistance(const string & word1, const string & word2) {
int n = word1.length();
int m = word2.length();
int dp[n+1][m+1];
for(size_t i=0; i<=n; i++){
dp[i][0] = i;
}
for(size_t j=0; j<=m; j++){
dp[0][j] = j;
}
for(size_t i=1; i<=n; i++){
for(size_t j=1; j<=m; j++){
if(word1[i-1] == word2[j-1]){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j],dp[i][j-1])) + 1;
}
}
}
return dp[n][m];
}
int main() {
string A = "GGATCGA";
string B = "GAATTCAGTTA";
cout << EditDistance(A,B) << endl; // 输出 5
}
说明,上面动态规划算法的时间复杂度为 \(O(nm)\) ,空间复杂度也为 \(O(nm)\) 。如果仅是求解编辑距离,不需要求解从字符串 A 到字符串 B 的具体转换过程,则可以对空间作进一步优化,优化过程可参考:https://en.wikipedia.org/wiki/Levenshtein_distance#Iterative_with_two_matrix_rows
7. 实例:求矩阵链乘法
给定 \(n\) 个矩阵 \(A_1, A_2, \cdots, A_n\) ,其中矩阵 \(A_i\) 的维数为 \(p_{i-1} \times p_i\) ,求矩阵链乘积 \(A_1A_2 \cdots A_n\) 的计算顺序,使得计算整个矩阵链所花的标量乘法次数最小。
说明: \(A\) 是 \(p×q\) 矩阵, \(B\) 是 \(q×r\) 矩阵,则 \(AB\) 的标量乘法次数为 \(pqr\) ,我们把 \(pqr\) 作为两个矩阵相乘所需时间的测量值。
对于矩阵链乘法 \(A_1A_2A_3A_4\) ,如果用括号来明确计算次序,则有下面 5 种方式:
\[\begin{gathered} (A_1(A_2(A_3A_4))) \\
(A_1((A_2A_3)A_4)) \\
((A_1A_2)(A_3A_4)) \\
((A_1(A_2A_3))A_4) \\
(((A_1A_2)A_3)A_4) \\
\end{gathered}\]
不同的计算顺序会导致矩阵链乘积的代价相差很大。 假如有三个矩阵: \(A_1, A_2, A_3\) ,其维数分别为 \(10×100, 100×5, 5×50\) ,如果按 \(((A_1A_2)A_3)\) 规定的次序来做乘法,求 \(A_1A_2\) 要做 10×100×5=5000 次标量乘法, \(A_1A_2\) 乘上 \(A_3\) 还要做 10×5×50=2500 次标量乘法,总共需要 7500 次标量乘法;而如果按 \((A_1(A_2A_3))\) 的次序来计算,则由同样的计算方法可知,共需要 75000 次标题乘法。由此可见,对矩阵链加括号的顺序不一样其效率也会相差很大。
矩阵链乘法问题并不是要真正进行矩阵相乘运算,我们的目标是要寻找最好的加括号方式(为更加直接,我们采用完全括号化表示),使矩阵的标量乘法次数最少。
7.1. 问题分析
这个问题,用穷举法其时间复杂度太高,我们尝试用动态规划方法求解。
(1)、寻找最优子结构。
假设 \(A_iA_{i+1} \cdots A_j\) 的最优加全部括号方案的分割点在 \(A_k\) 与 \(A_{k+1}\) 之间。那么,继续对“前缀”子链 \(A_iA_{i+1} \cdots A_k\) 进行括号化时,我们应该直接采用独立求解它时所得的最优方案。类似地,对于子链 \(A_{k+1}A_{k+2} \cdots A_j\) 我们也有相似的结论:在原问题 \(A_iA_{i+1} \cdots A_j\) 的最优括号化方案中,对子链 \(A_{k+1}A_{k+2} \cdots A_j\) 进行括号化的方法,就是它自身的最优括号化方案。
(2)、建立递归关系。
设 \(m[i][j]\) 为 \(A_iA_{i+1} \cdots A_j, (1≤i≤j≤n)\) 的加全部括号所需的标量乘法次数的最小值,则原问题的最优值为 \(m[1][n]\) 。
当 \(i = j\) 时,为单一矩阵,无需计算,因此 \(m[i][i]=0\) 。
当 \(i < j\) 时,我们假设 \(A_iA_{i+1} \cdots A_j\) 的最优加全部括号方案的分割点在 \(A_k\) 与 \(A_{k+1}\) 之间,那么 \(m[i][j]\) 就等于 \(A_iA_{i+1} \cdots A_k\) 的代价加上 \(A_{k+1}A_{k+2} \cdots A_j\) 的代价,再加上两者相乘的代价。其中两者相乘的代价为 \(p_{i-1}p_kp_j\) (设矩阵 \(A_i\) 的大小为 \(p_{i-1} \times p_{i}\) )。因此,我们得到:
\[m[i][j] = m[i][k] + m[k+1][j] + p_{i-1}p_kp_j\]
上面递归公式假设最优分割点 \(k\) 是已知的,但实际上我们是不知道的。不过, \(k\) 的取值只可能是 \(k=i, i+1, \cdots, j-1\) ,由于最优分割点必在其中,我们只需要检查所有可能情况,找到最优者即可。
综上所述,有:
\[m[i][j] = \begin{cases} 0 & \text{if} \; i=j \\ \min_{i \le k < j} \{m[i][k] + m[k+1][j] + p_{i-1}p_kp_j \} & \text{if} \; i< j \end{cases}\]
不过,上面式子中,并未提供足够的信息来构造最优解。为了有助于跟踪如何构造一个最优解,定义 \(s[i][j]\) 为使 \(m[i][j] = m[i][k] + m[k+1][j] + p_{i-1} p_kp_j\) 成立时的 \(k\) 值,也就是分裂处的值。
7.2. 动态规划算法实现
//矩阵链乘法的动态规划算法实现。
//m[i][j]和s[i][j]的下标都从1开始,这是为了和前面的描述尽量一致。
//代码参考了《计算机算法设计与分析(第3版, 王晓东编)》3.1节。
#include<iostream>
#include<iomanip> //使用setw()时需要
using std::cout;
using std::endl;
using std::setw;
#define N 6 //矩阵个数
//p为矩阵维数数组,n为矩阵个数。
void MatrixChain(int *p, int n, int m[][N + 1], int s[][N + 1]) {
for (int i = 1; i <= n; i++) {
m[i][i] = 0; //i=j时,m[i][j]为0。
}
for (int l = 2; l <= n; l++) { //子序列长度由2到n递增
for (int i = 1; i <= n - l + 1; i++) { //注意i的上限
int j = i + l - 1;
m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];
s[i][j] = i;
for (int k = i + 1; k < j; k++) {
if (m[i][j] > m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j]) { //根据递归表达式计算m[i][j]
m[i][j] = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
s[i][j] = k; //记录s[i][j]
}
}
}
}
}
//递归打印加上括号的矩阵链。
//s为保存着辅助信息的数组。i,j为矩阵链范围。
void Print_parens(int s[][N + 1], int i, int j) { //递归地构造最优解
int k = s[i][j];
if (i != j) {
if (!(i == 1 && j == N)) {
cout << "(";
}
Print_parens(s, i, k);
Print_parens(s, k + 1, j);
if (!(i == 1 && j == N)) {
cout << ")";
}
} else {
cout << "A" << i;
}
}
int main() {
int p[N + 1] = { 30, 35, 15, 5, 10, 20, 25 };
int m[N + 1][N + 1] = { 0 }; //不初赋值不会影响结果,但m的“下三角数组”会为随机数。
int s[N + 1][N + 1] = { 0 }; //不初赋值不会影响结果,但s的“下三角数组”会为随机数。
MatrixChain(p, N, m, s);
Print_parens(s, 1, N);
//打印m数组和s数组。
cout << endl << endl;
cout << "m=" << endl;
for (int i = 1; i <= N; i++) { //由于前面约定数组从1开始。
for (int j = 1; j <= N; j++) {
cout << setw(8) << m[i][j] << " ";
}
cout << endl;
}
cout << endl;
cout << "s=" << endl;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
cout << setw(8) << s[i][j] << " ";
}
cout << endl;
}
return 0;
}
上面代码的输出:
(A1(A2A3))((A4A5)A6)
m=
0 15750 7875 9375 11875 15125
0 0 2625 4375 7125 10500
0 0 0 750 2500 5375
0 0 0 0 1000 3500
0 0 0 0 0 5000
0 0 0 0 0 0
s=
0 1 1 3 3 3
0 0 2 3 3 3
0 0 0 3 3 3
0 0 0 0 4 5
0 0 0 0 0 5
0 0 0 0 0 0
7.2.1. 程序相关说明
在上面的测试代码中使用的矩阵链为:
| \(A_1\) | \(A_2\) | \(A_3\) | \(A_4\) | \(A_5\) | \(A_6\) |
|---|---|---|---|---|---|
| \(30\times35\) | \(35\times15\) | \(15\times5\) | \(5\times10\) | \(10\times20\) | \(20\times25\) |
动态规划算法 MatrixChain 计算 \(m[i][j]\) 和 \(s[i][j]\) 的先后次序如图 2 所示,它们的最终数据如图 3 所示。
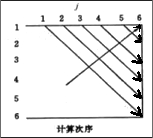
Figure 2: 求矩阵链乘法程序中数组 m 和 s 的计算次序
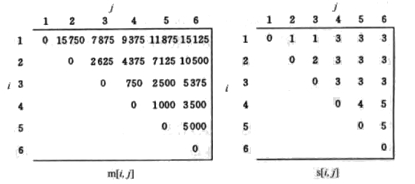
Figure 3: 求矩阵链乘法程序中数组 m 和 s 的最终结果
最终求得的最小标量乘法次数为 15125,矩阵链乘法的完全括号化方案为 \((A_1(A_2A_3))((A_4A_5)A_6)\) 。