String Searching Algorithms
Table of Contents
1. 字符串查找问题简介
字符串查找问题(又称字符串匹配问题)是指在文本串 T 中寻找指定的模式串 P。
参考:
算法导论(第 3 版),第 32 章 字符串匹配
String searching algorithm: https://en.wikipedia.org/wiki/String_searching_algorithm
Exact String Matching Algorithms: http://www-igm.univ-mlv.fr/~lecroq/string/
1.1. 本文介绍算法的时间复杂度
表 1 是后文中所介绍字符串匹配算法的时间复杂度。
| 算法 | 预处理时间 | 匹配时间(最坏情况) |
|---|---|---|
| 朴素算法 | 0 | \(O(nm)\) |
| Rabin-Karp 算法 | \(\Theta(m)\) | \(O(nm)\) |
| 有限自动机算法 | \(O(m \mid \sum \mid)\) | \(\Theta(n)\) |
| Knuth-Morris-Pratt 算法 | \(\Theta(m)\) | \(\Theta(n)\) |
说明 1:表 1 中 \(n\) 为文本串长度, \(m\) 为模式串长度, \(\mid \sum \mid\) 为输入字母表大小(如文本串和模式串仅包含小写英文字母时,输入字母表大小就是 26)。
说明 2:尽管 Rabin-Karp 算法的匹配时间(最坏情况)为 \(O(nm)\) ,但它的期望匹配时间为 \(O(n)\) 。
2. 朴素算法
Brute Force 算法,也就是蛮力算法。
//字符串匹配的Brute Force算法
//str1为文本串,str2为模式串
//返回第一个匹配的指针,找不到就返回NULL
char * BruteForce1(const char * str1, const char * str2) {
assert(str1 != NULL && str2 != NULL);
char * cp = (char *) str1;
char * s1, *s2;
while (*cp) {
s1 = cp;
s2 = (char *) str2;
while ((*s1 != NULL) && (*s2 != NULL) && (*s1 == *s2)) {
s1++;
s2++;
}
if (*s2 == NULL) {
return cp;
}
cp++;
}
return NULL;
}
也可以实现为下面形式:
//字符串匹配的Brute Force算法
//返回第一个匹配位置下标,找不到就返回-1
int BruteForce2(char const* src, int slen, char const* patn, int plen) {
int i = 0, j = 0;
while (i < slen && j < plen) {
if (src[i] == patn[j]) { //如果相同,则两者同时后移,继续比较
i++;
j++;
} else { //如果不相同,指针回溯,重新开始匹配
i = i - j + 1; //文本串退回到当次比较最开始时的位置,再后移一位
j = 0; //模式串退回到首位
}
}
if (j >= plen) {
return i - plen; //如果全部匹配成功,返回下标
} else {
return -1; //匹配不成功,返回-1
}
}
3. Rabin-Karp 算法
Rabin-Karp算法 由 Michael O. Rabin 教授(1976 年获图灵奖)和 Richard M. Karp(1985 年获图灵奖)教授于 1987 年发表,又称 Karp-Rabin 算法,简称 KR 算法。
说明:在 Go 语言的 strings 包中使用了 Rabin-Karp 算法来进行字符串的匹配。
3.1. Rabin-Karp 算法思想
Rabin-Karp 算法思想:首先设计一个 hash 函数,在文本串中每次取和模式串相同长度的子串,对其计算 hash,并和模式串的 hash 比较,如果 hash 相等(hash 不相同,两个串肯定不会相同),则用朴素的字符串匹配算法作进一步的验证,验证通过则说明找到匹配。
为了方便讨论,使用记号 \(T[i..j]\) 表示字符串 T 中下标从 \(i\) 到 \(j\) (包含 \(i\) 和 \(j\) )的子串。
3.1.1. Rolling hash
Rabin-Karp 算法之所以比朴素匹配算法要快,在于由当前文本子串 hash 值可以快速地计算后一个文本子串 hash 值:即通过 \(hash(T[j .. j+m-1])\) 可以方便计算出 \(hash(T[j+1 .. j+m])\) (假设模式串长度为 \(m\) )。 具有这个特性的 hash 函数称为 Rolling hash 。
Rabin-Karp 算法中 Rolling hash 函数定义为下面形式:
\[hash(w[0..m-1]) = w[0] a^{m-1} + w[1] a^{m-2} + \cdots + w[m-1] a^{0}\]
其中, \(a\) 为常数, \(w[0..m-1]\) 表示输入字符串“w[0]w[1]...w[m-1]”。为防止 hash 值可能太大,往往再加一个取模运算,即有 Rabin-Karp 算法中 Rolling hash 函数定义:
\[hash(w[0..m-1]) = \left(w[0] a^{m-1} + w[1] a^{m-2} + \cdots + w[m-1] a^{0} \right) \mod q\]
怎么由 \(hash(w[0..m-1])\) 快速地计算 \(hash(w[1..m])\) 呢?递推公式(这里不详细推导,推导思路是利用计算多项式的霍纳规则 Horner’s rule)为:
\[\underbrace{hash(w[1..m])}_{\text{新 hash 值}} = \left( (\underbrace{hash(w[0..m-1])}_{\text{旧 hash 值}} - \underbrace{w[0]}_{\text{旧数据中的高数位}} a^{m-1}) a + \underbrace{w[m]}_{\text{新数据中的低数位}} \right) \mod q\]
类似地,由 \(hash(w[1..m])\) 可以快速计算 \(hash(w[2..m+1])\) :
\[\underbrace{hash(w[2..m+1])}_{\text{新 hash 值}} = \left( (\underbrace{hash(w[1..m])}_{\text{旧 hash 值}} - \underbrace{w[1]}_{\text{旧数据中的高数位}} a^{m-1}) a + \underbrace{w[m+1]}_{\text{新数据中的低数位}} \right) \mod q\]
其它计算,依此类推。
3.1.2. Rabin-Karp 算法演示
图 1 演示了 Rabin-Karp 算法的工作过程。
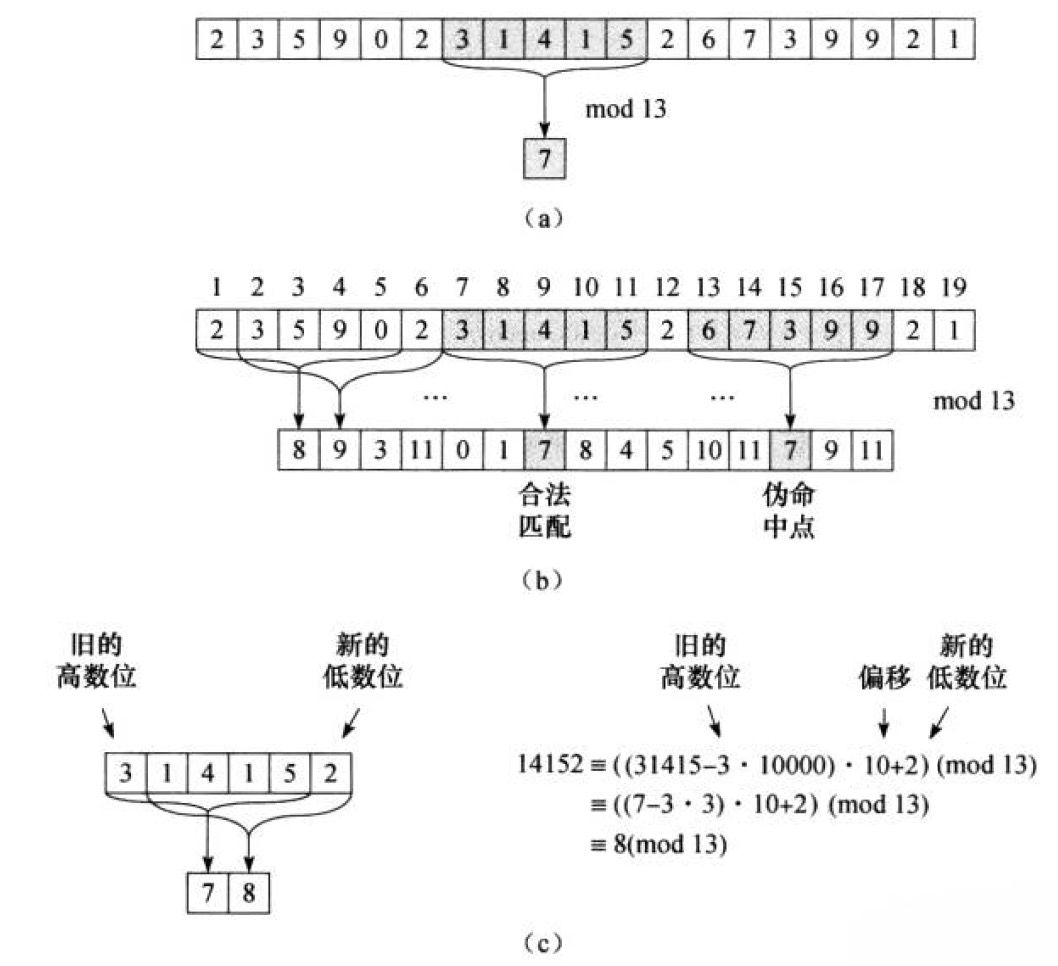
Figure 1: Rabin-Karp 算法的工作过程
在图 1 所示 Rabin-Karp 算法中,文本串为“2359023141526739921”,模式串为“31415”,使用的 Rolling hash 函数为:
\[hash=\left(w[0] \times 10^{4} + w[1] \times 10^{3} + w[2] \times 10^{2} + w[3] \times 10^{1} + w[4] \times 10^{0} \right) \mod 13\]
其中,子图(c)演示了 Rolling hash 的计算过程。
3.2. Rabin-Karp 算法实现
下面是 Rabin-Karp 算法的一个 C 语言实现。
//字符串匹配的Rabin-Karp算法实现
//代码来自http://www-igm.univ-mlv.fr/~lecroq/string/node5.html
//返回第一个匹配位置,找不到就返回NULL
//参数T为文本串指针,len1为其长度;P为模式串指针,len2为其长度。
char *Rabin_Karp(const char *T, const int len1, const char *P, const int len2) {
assert(T != NULL && P != NULL && (len1 >= len2));
int d, hashT, hashP, i, j;
/* Preprocessing */
for (d = i = 1; i < len2; ++i) { //for循环结束后,d = 2^(len2-1),当len2很大时,d可能为0。
d = (d << 1);
}
for (hashT = hashP = i = 0; i < len2; ++i) {
hashT = ((hashT << 1) + T[i]); //文本串中前len2个字符的hash值。
hashP = ((hashP << 1) + P[i]); //模式字符串的hash值。
}
/* Searching */
j = 0;
while (j <= len1 - len2) {
if (hashP == hashT) { //如果hash相同,就用朴素字符串匹配算法进一步验证
for (i = 0; i < len2; i++) {
if (P[i] != T[i + j]) {
break;
}
}
if (i == len2) {
return (char *) T + j;
}
}
hashT = ((hashT - T[j] * d) << 1) + T[j + len2]; //计算文本串中下一个len2长的子串的hash
++j;
}
return NULL;
}
使用的 Rolling hash 函数为:
\[hash(w[0..m-1]) = \left(w[0] 2^{m-1} + w[1] 2^{m-2} + \cdots + w[m-1] 2^{0} \right) \mod INT\_MAX\]
上面 C 语言实现的代码中没有显式地使用模运算,这是因为使用 INT_MAX 作为模运算的模数时,硬件对整数操作的溢出相当于模运算。
3.3. Rabin-Karp 算法时间复杂度分析
记文本串长度为 \(n\) ,模式串长度为 \(m\) 。Rabin-Karp 算法的预处理(计算模式串 hash 值及文本串第一个 hash 值)时间为 \(\Theta(m)\) 。在最坏情况下,它的匹配时间是 \(\Theta((n-m+1)m)\) ,由于 \(m\) 一般会远小于 \(n\) ,又可记为 \(O(nm)\) ,因为 Rabin-Karp 算法和朴素字符串匹配算法一样,对每个有效偏移进行显式验证,最坏情况就是所有尝试都是 hash 的伪命中点,不得不对每次尝试都用朴素字符串匹配算法做进一步验证。
当仔细地选择一个模数时,最坏情况几乎不会出现,其伪命中点会很少,Rabin-Karp 算法的期望运算时间为 \(O(n+m)\) ,由于 \(m \le n\) ,即期望运算时间为 \(O(n)\) 。
4. 利用有限自动机进行字符串匹配
用自动机进行字符串匹配非常有效: 它们只对每个文本字符检查一次,并且检查每个文本字符时所用的时间为常数。 所以,在预处理建好自动机之后进行匹配所需时间为 \(\Theta(n)\) 。
4.1. 有限自动机匹配过程(实例演示)
假设文本长度为 \(n\) ,模式长度为 \(m\) ,则自动机将会有 \(0,1, \cdots, m\) 这么多种状态(初始状态为 0,接受状态为 \(m\) )。
假设自动机已经建立好(暂时不考虑如何从模式串构造自动机),用自动机进行字符串匹配的过程如下: 从文本从左到右扫描时,对于每一个字符 \(x\) ,根据自动机当前的状态还有 \(x\) 的值可以找出自动机的下一个状态,这样一直扫描下去,当自动机状态值变为 \(m\) 时我们就可以认为在文本串中找到了一处模式串。
下面是一个简单例子,用于演示利用有限自动机进行字符串匹配的过程。
假设文本和模式只有三种字符 a,b,c(即输入字母表仅这三个字符),已知文本 T 为“abababaca”,模式 P 为“ababaca”,根据模式 P 建立的自动机如图 2 中子图(a)所示(构造过程暂不考虑,后文将介绍)。
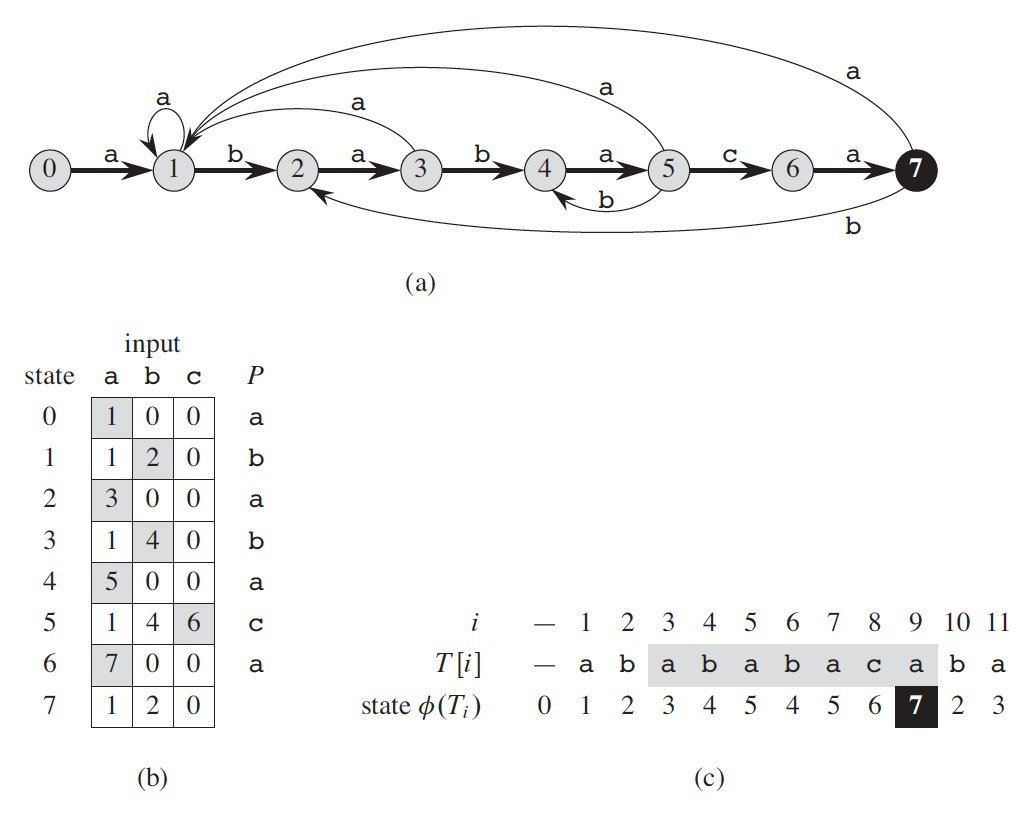
Figure 2: (a)模式 P 对应的自动机(省略了回到初始状态 0 的箭头),(b)自动机的另外表示形式(状态转换表),(c)自动机在文本 T=abababaca 上的操作
在图 2 的子图(c)中,对照自动机状态转换表(即子图(b)),一个个地扫描文本字符,扫描前状态值初始化为 0,这样在 \(i = 9\) 的时候状态值刚好变成 \(7\) (它是一个接受状态),所以找到一个匹配。
我们再看一个例子,还是图 2 中的自动机,但把文本串变为 T=cacbababaca,这时自动机在文件串上的操作过程如图 3 所示。

Figure 3: 左图为自动机对应状态转移表,右图为自动机在文本 T=cacbababaca 上的操作
匹配过程可以用下面伪代码表示:
// 自动机进行文本匹配的过程(伪代码)
Finite_Automation(T, g, m) //T为文本字符串,g为变迁函数,m为模式P的长度
{
n=strlen(T);
q=0; //q表示状态,初始为0
for i=1 to n {
q=g(q, T[i]); //通过状态转移表做状态变迁
if (q==m) { //判断是否为接受状态
print "Pattern occurs with shift" i-m //如果成功匹配,就输出初始位置
}
}
}
显然,它的匹配时间为 \(\Theta(n)\) 。
自动机的匹配过程介绍完了,现在问题只剩下如何根据给出的模式 P 计算出对应的自动机,请看下文。
4.2. 如何构造自动机
如何模式串 P 计算出对应的自动机呢?在后面的说明中还是使用上面介绍的例子,即建立模式串 P=“ababaca”的有限自动机。
假设文本长度为 \(n\) ,模式长度为 \(m\) ,则自动机将会有 \(0,1, \cdots, m\) 这么多种状态(初始状态为 0,接受状态为 \(m\) )。首先需要明白一点: 如果当前的状态值为 \(k\) ,其实说明当前文本的后缀与模式串的前缀的最大匹配长度为 \(k\) ,这时读入下一个文本字符时,即使该字符匹配,状态值也最多变成 \(k + 1\) 。
我们以“当前状态为 5,如何计算下一个状态”作为例子,来介绍自动机的构造过程。
假设当前状态为 5,则说明文本当前位置的最后 5 位为“ababa”,它就是模式串的前 5 位。要考虑下一位转移状态,我们需要考虑输入字母表(一般用 \(\sum\) 表示,这里仅为 a,b,c)中的所有字符。
(1) 如果下一位文本字符是“c”,则状态值就可以更新为 6。
(2) 如果下一位文本字符是“a”,这时我们 需要重新找到文本后缀与模式前缀的最大匹配长度。简单的寻找方法可以是令 \(k = 5 + 1=6\) (状态值最大的情况),判断文本后 \(k\) 位与模式串前 \(k\) 位是否相等,不相等的话就令 \(k = k - 1\) 后再继续找。 由于刚才文本后 5 位“ababa”其实就是模式的前 5 位,所以在构建自动机时不需要用到文本串。这个例子中,经过几次迭代测试后 \(k\) 最终为 1(只有“a”1 位相等)。
(3) 如果下一位文本字符是“b”,和上面的分析一样。这个例子中, \(k\) 为 4(模式串前 4 位和文本串后 4 位相等,都为“abab”)。
上面的分析,就是当前状态为 5 时,下一个状态值的转换情况。如图 4 所示。利用这个思路,我们可以计算出所有状态(即状态 \(0,1, \cdots, m\) ,共 \(m+1\) 个状态)的转移情况。
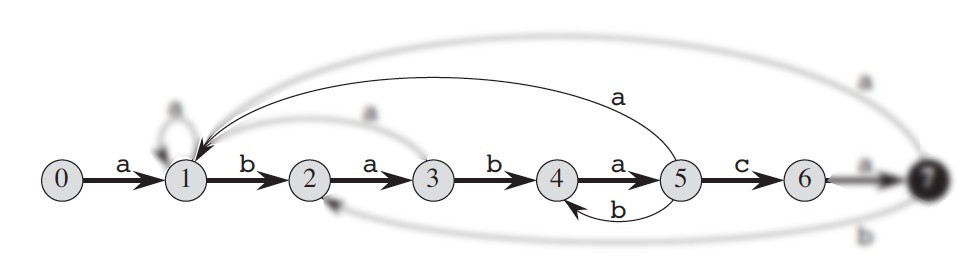
Figure 4: 当前状态为 5 时的状态转移示意图
上面介绍了自动机的构造过程,这个过程可用伪代码表示如下:
// 自动机的构造过程:根据给定模式 P[1..m] 来计算转移函数 δ
Compute_Transition_Function(P, Σ) //模式P,输入的字符表Σ
{
m=strlen(P);
for q=0 to m { //从状态0一直计算到状态m
for each character x in Σ { //枚举每个可能的输入字符
k=min(m, q+1) + 1; //k的最大可能值
repeat {
k=k-1 //重复k=k-1,直到“P的长度为k的前缀”是“P的长度为q的前缀加上字符x”的真后缀
} until (Pk is the suffix of Pq+x)
δ(q, x)=k;
}
}
return δ;
}
上面构造自动机算法的运行时间为 \(O(m^3 |\sum|)\) ,这是因为:
for q=0 to m // 消耗时间 m for each character x in Table // 消耗时间 |Σ| repeat k=k-1 // 消耗时间 m test 'Pk is the suffix of Pq+x' // 消耗时间 m
上面各个部分都是嵌套的,所以运行时间为 \(O(m^3 |\sum|)\) 。有改进的方法可以在 \(O(m |\sum|)\) 时间内根据模式串构造好自动机,这里不介绍(参考《算法导论(第 3 版)》练习 32.4-8)。
5. Knuth-Morris-Pratt 算法
Knuth-Morris-Pratt algorithm 由 D.E.Knuth 与 V.R.Pratt 和 J.H.Morris 于 1977 年发表,所以称为 KMP 算法。
我们知道,利用有限自动机进行字符串匹配时,构造自动机需要花费 \(O(m |\sum|)\) 时间。当输入字母表 \(\sum\) 和模式串长度 \(m\) 比较大时,构造自动机会花费可观时间。KMP 算法无需计算转移函数 \(\delta\) ,只用到辅助函数 \(\pi\) (称这个函数为“前缀函数”或者“失效函数”),它能在 \(\Theta(M)\) 时间内根据模式串预先计算出来,并且存储在数组 \(\pi[1..m]\) 中。数组 \(\pi\) 使得我们可以按需要“即时”地计算(从摊还意义上说)转移函数 \(\delta\) 。所以, KMP 算法的本质是构造了 DFA 并进行了模拟。
注:建议完全理解上一节内容“利用有限自动机进行字符串匹配”后,再学习 KMP 算法。
5.1. 前缀函数(真后缀的最长前缀长度)及 KMP 匹配过程
什么是模式串的前缀函数呢?
考察一下朴素算法的匹配过程。在图 5 中,T为文本串,P为模式串,匹配的字符被打上阴影且用垂直直线连接。如果发现不匹配后,则在文本串的 \(s+1\) 处进行下一轮的匹配,当然马上发会现不能匹配。
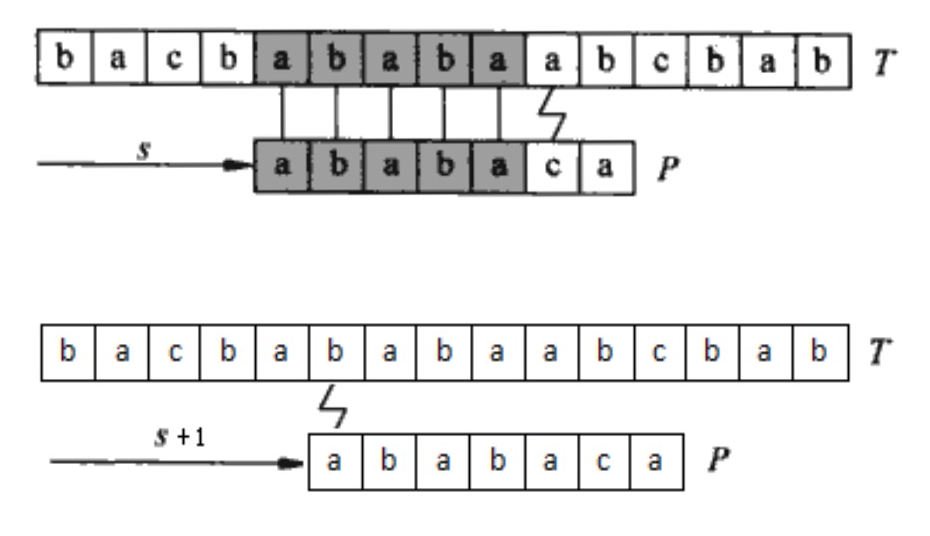
Figure 5: 朴素算法的匹配过程
其实,我们根据前面 5 个匹配字符的已有信息,可以提前知道文本串 \(s+1\) 处的匹配肯定不会成功,这样就根本用不着在 \(s+1\) 处去进行匹配,可以直接在 \(s+2\) 处匹配。更重要的是,我们还可以根据已有信息提前知道在 \(s+2\) 处匹配时,其前 3 个字符能肯定匹配上(因为在模式串的前 5 个字符构造的子串中,其前 3 个字符和后 3 个字符是相同的),也可以跳过,如图 6 所示。
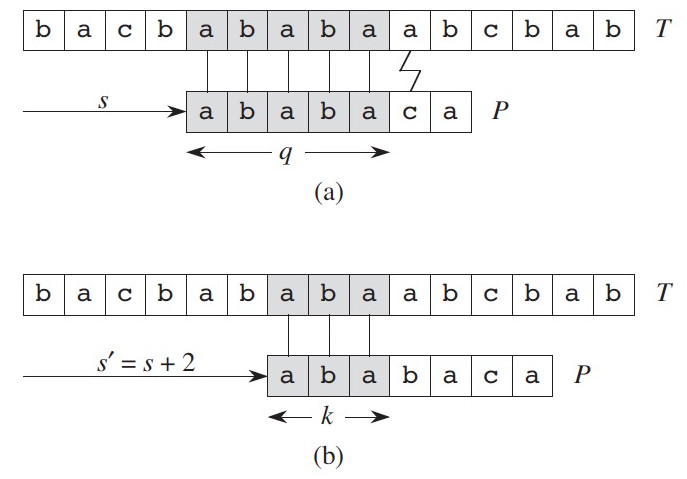
Figure 6: 前缀函数 \(\pi\) ,其中 \(\pi[5]=3\)
综上所述, 我们利用已有信息可以跳过 5 个(2+3,2 表示下一个可能的有效位移,3表示在这个有效位移上还可以进一步忽略比较的字符数)字符的比较,可以直接拿下一个文本字符和第 4 个(即 3 的后一个)模式字符进行比较。
模式串子串的“真后缀的最长前缀长度”就是当前模式串子串的前缀函数值,所有前缀函数值组成了前缀函数,一般记为 \(\pi\) ,可保存在数组中。上面例子中,模式串子串“ababa”的前缀函数值为 3,记为 \(\pi[5]=3\) (这里,约定首位下标从 1 开始,而不是从 0 开始)。
我们知道,对于朴素算法,文本串和模式串在某位失配后,文本串退回到当次比较最开始时位置的后一位进行下一次尝试,模式串从首位重新开始。
假定已经求得了前缀函数,KMP 算法的匹配过程和朴素算法非常类似,区别在于失配后如何处理:对于 KMP 算法,假设在模式串 P 的 \(k\) 位失配,如果 \(k\) 位是模式串首位,则文本串向右滑动一位后重新开始和模式串比较;如果 \(k\) 位不是模式串首位,则文本串不动(文本串不用回溯!),模式串的下一次尝试的位置是 \(P[1..k-1]\) 对应的前缀值的后面一位。 对于图 6 所示例子,失配位置是模式串第 6 位(不是模式串首位),文本串下一次尝试还是当前失配时的位置,而模式串的下一次尝试是 \(P[1..5]\) 对应的前缀值(即 3)的后一位,即第 4 个模式字符。
经过上面分析知,通过修改朴素算法失配时文本串和模式串的位移情况即可得到 KMP 算法实现。参见下文。
5.1.1. KMP 算法实现
经过前文的分析,我们可得到朴素算法和 KMP 算法的对比如下:
| 字符串匹配朴素算法 | 字符串匹配 KMP 算法 |
|
int BruteForce(char const* T, int Tlen, char const* P, int Plen) { int Tindex = 0, Pindex = 0; while (Tindex < Tlen && Pindex < Plen) { if (T[Tindex] == P[Pindex]) { Tindex++; Pindex++; } else { // 注:仅这个分支和 KMP 算法不同!! //文本串退回到当次比较最开始时的位置,再后移一位 Tindex = Tindex - Pindex + 1; //模式串退回到首位 Pindex = 0; } } if (Pindex >= Plen) { return Tindex - Plen; //如果全部匹配成功,返回下标 } else { return -1; //匹配不成功,返回-1 } } |
void getKmpPrefixFun(const char *P, int Plen, int kmpPI[]); int KMP_Match(const char *T, int Tlen, const char * P, int Plen) { int kmpPI[Plen]; //C99 标准中的变长数组 getKmpPrefixFun(P, Plen, kmpPI); //计算前缀函数,保存在 kmpPI 中 int Tindex = 0, Pindex = 0; while (Tindex < Tlen && Pindex < Plen) { if (T[Tindex] == P[Pindex]) { Tindex++; Pindex++; } else if (Pindex == 0) { //在模式串的首位失配,则把文本串后移一位 Tindex++; } else { //在模式串其他位置失配 //KMP 关键:文本串不动,模式串移动到前一位的前缀函数值处 Pindex = kmpPI[Pindex - 1]; } } if (Pindex >= Plen) { return Tindex - Plen; //如果全部匹配成功,返回下标 } else { return -1; //匹配不成功,返回-1 } } |
KMP 算法已经介绍完,只剩下如何计算前缀函数了(即如何实现函数 getKmpPrefixFun)。参见下文。
5.2. 如何计算前缀函数
以模式串“ababaca”的子串“ababa”为例。下面演示如何得到 \(\pi[5]=3\) ,进而得到所有的前缀函数值。
计算过程如下: “ababa”的真后缀(有点类似集合里真子集的概念)有Φ、“a”、“ba”、“aba”、“baba”,这些真后缀当中同时又是“ababa”的前缀的有Φ、“a”、“aba”,其中最长的前缀的长度为 3,所以 \(\pi[5]=3\) (约定首位下标从 1 开始,而不是从 0 开始)。
模式串“ababaca”的前缀有:“a”、“ab”、“aba”、“abab”、“ababa”、“ababac”、“ababaca”(不算空前缀),用上面介绍的计算方法可以求得每个前缀的“真后缀的最长前缀长度”分别为:0、0、1、2、3、0、1。所以模式串“ababaca”的完整的前缀函数 \(\pi\) 用表格表示如表 2 所示。
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| P[i] | a | b | a | b | a | c | a |
| \(\pi[i]\) | 0 | 0 | 1 | 2 | 3 | 0 | 1 |
5.2.1. 编程求解思路分析
前面已经介绍过求解前缀函数的具体步骤,这里重复如下: 把模式串的所有真后缀列出后,再找出其中同时是前缀的一部分来,再找出最长的一个算其长度。 这种思想可方便地用于手动计算前缀函数,用程序实现时我们有更快的办法。
说明:由于 C 程序中数组首元素下标为 0(而不是 1),后文中将使用 0 作为首元素下标(这和前文是不同的)。
编程求 \(\pi[i]\) 时,充分利用之前计算过的信息,如 \(\pi[i-1]\) 等。记 \(\pi[i-1]\) 为 \(j\) ,可分两种情况讨论,一种情况是 \(P[j]==P[i]\) 时,另一种是 \(P[j]!=P[i]\) 时,下面对这两种情况进行说明。
情况一: \(P[i]==P[j]\) 时,这种情况比较简单,显然有 \(\pi[i] = \pi[i-1] + 1\) ,图 7 是这种情况的一个例子。

Figure 7: \(P[i]==P[\pi(i-1)]\) 时,有 \(\pi[i] = \pi[i-1] + 1\) ,这个例子有 \(\pi[10]=4\) (对应着 \(P[0..3]==P[7..10]\) )
情况一对应的代码非常简单,为:
j = kmpPI[i - 1]; //把前一个子串对应的“真后缀的最长前缀长度”保存在j中
if(P[j] == P[i]) {
kmpPI[i] = j+1;
}
情况二: \(P[i]!=P[j]\) 时,这种情况相对复杂些。先看几个例子,如图 8,图 9,图 10 所示。
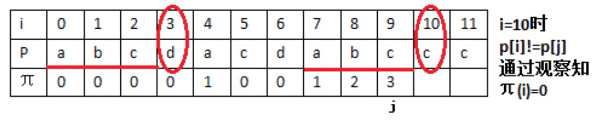
Figure 8: 模式串为“abcdacdabccc”时,有 \(\pi[10]=0\)

Figure 9: 模式串为“abcabdabcabc”时,有 \(\pi[11]=3\) (对应着 \(P[0..2]==P[9..11]\) )

Figure 10: 模式串为“abcdacdabcac”时,有 \(\pi[10]=1\) (对应着 \(P[0]==P[10]\) )
为了更好地总结出规律,我们再看一个复杂点的例子,模式串为“abcabdeabcabeabcabdeabcabc”,除最后一位,其它前缀值都已知了,现在来求最后一个前缀值 \(\pi[25]\) ,如图 11 所示。
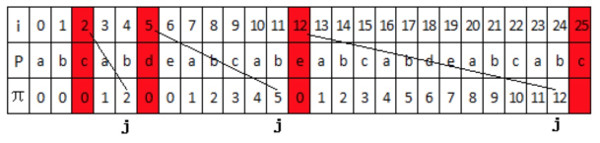
Figure 11: 模式串为“abcabdeabcabeabcabdeabcabc”时,有 \(\pi[25]=3\) (对应着 \(P[0..2]==P[23..25]\) )
图 11 中, \(\pi[25]=3\) 可通过下面几个步骤计算出来:
(1)、令 \(j=\pi[25-1]=12\) ,比较 P[j]和 P[25],发现不匹配;
(2)、令 \(j=\pi[12-1]=5\) ,比较 P[j]和 P[25],发现还是不匹配;
(3)、令 \(j=\pi[5-1]=2\) ,比较 P[j]和 P[25],这时匹配上,得 \(\pi[25]=j+1=3\) 。
另外,上面例子中如果 \(P[25]=e\) (属于情况一),则可得 \(\pi[25]=12+1=13\) ;上面例子中如果 \(P[25]=d\) ,则可得 \(\pi[25]=5+1=6\) 。
通过上面的分析,可总结出情况二对应的代码(也能处理情况一):
j = kmpPI[i - 1]; //把前一个子串对应的“真后缀的最长前缀长度”保存在j中
while (j > 0 && P[j] != P[i]) {
j = kmpPI[j - 1];
}
if (P[j] == P[i]) {
kmpPI[i] = j + 1;
} else {
kmpPI[i] = 0;
}
5.2.2. 前缀函数实现
前面已经介绍了前缀函数的求法,这里把其思路用代码完整实现如下:
//求KMP算法的前缀函数
//P为模式串,m为模式串长度,kmpPI为保存结果数组
void getKmpPrefixFun(const char *P, int Plen, int kmpPI[]) {
int i = 0;
int j = 0;
kmpPI[0] = 0; //设定kmpPI[0]为0。
for (i = 1; i < Plen; i++) { //开始求kmpPI[1]到kmpPI[m-1]
j = kmpPI[i - 1]; //把前一个子串对应的“真后缀的最长前缀长度”保存在j中
while (j > 0 && P[j] != P[i]) {
j = kmpPI[j - 1];
}
if (P[j] == P[i]) {
kmpPI[i] = j + 1;
} else {
kmpPI[i] = 0;
}
}
}
说明:代码中循环 while(j > 0 && P[j] != P[i]) 的退出有两个条件:
(1) 如果循环是由于不满足条件 P[j] != P[i] 退出,则后面一定会进入 if 语句分支;
(2) 如果循环是由于不满足条件 j > 0 而退出,后面可能进入 if 语句分支(此时真后缀的最长前缀长度为 1),也可能进入 else 分支(此时真后缀的最长前缀长度为 0)。
5.2.3. 前缀函数实现(来源于《编译原理》)
在《编译原理(第 2 版)》3.4.5 节也提到了 KMP 算法,不过书中称“前缀函数”为“失效函数”。
//求KMP算法的前缀函数,来源于《编译原理(第2版)》3.4.5节
//P为模式串,m为模式串长度,kmpPI为保存结果数组
void getKmpPrefixFun2(const char *P, int Plen, int kmpPI[]) {
int i = 0;
int j = 0;
kmpPI[0] = 0; //设定kmpPI[0]为0。
for (i = 1; i < Plen; i++) { //开始求kmpPI[1]到kmpPI[m-1]。
while (j > 0 && P[j] != P[i]) {
j = kmpPI[j - 1];
}
if (P[j] == P[i]) {
j = j + 1;
kmpPI[i] = j;
} else {
kmpPI[i] = 0;
}
}
}
说明:这个代码和前面写的 getKmpPrefixFun 其实是一样的,只是更加精简,精简后理解更困难,分析 getKmpPrefixFun 代码能更好理解前缀函数求解过程。
5.2.4. 前缀函数实现(来源于《算法导论》)
把《算法导论(第 3 版)》32.4 节中求前缀函数的伪代码实现成 C 代码,如下:
//求KMP算法的前缀函数,来源于《算法导论(第3版)》32.4节
//P为模式串,m为模式串长度,kmpPI为保存结果数组
void getKmpPrefixFun3(const char *P, int Plen, int kmpPI[]) {
int i = 0;
int j = 0;
kmpPI[0] = 0; //设定kmpPI[0]为0。
for (i = 1; i < Plen; i++) { //开始求kmpPI[1]到kmpPI[m-1]。
while (j > 0 && P[j] != P[i]) {
j = kmpPI[j - 1];
}
if (P[j] == P[i]) {
j = j + 1;
}
kmpPI[i] = j;
}
}
说明:这个代码和前面写的 getKmpPrefixFun 其实是一样的,只是更加精简,精简后理解更困难,分析 getKmpPrefixFun 代码能更好理解前缀函数求解过程。
5.3. 前缀函数(失效函数)和 DFA 关系
5.4. KMP 算法改进
下面讨论对 KMP 算法的两个小改进。
5.4.1. 改进一:前缀函数值整体向右移动一位,首位设为-1
仔细观察前面求得的前缀函数,并用前缀函数进行匹配时,我们可以发现,最后一个前缀函数值不会用到。因为根据前缀函数的定义,我们在第 \(i\) 位失配时,模式串下一次需要进行匹配的位置是第 \(i - 1\) 位的前缀函数值对应的下标位置。这样的话,在模式串的最后一位失配,只需要用到倒数第二位的前缀函数值,最后一位的前缀函数值不要用到。
改进一:把前缀函数值整体向右移动一位,并设首个前缀函数值为-1,去掉最后一个前缀函数值(因为反正用不到它),把改进后的数组记为 kmpNext。如图 14 所示。
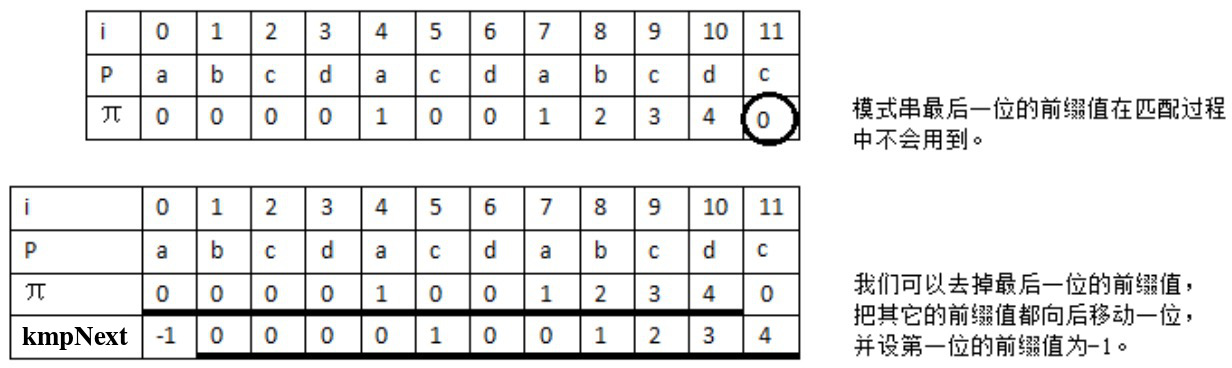
Figure 14: 把前面介绍的前缀函数值统一向右移一位,并设首位为-1
做这个改进(其实也算不上什么改进,可能叫“变种”更合适)后,可以减少了一次前缀值的计算,还可以使求前缀函数的代码更加精炼。
由于前缀数组从 PI 变为了 kmpNext,相应的匹配函数也需要调整。设失配时,文本串 T 的下标为 \(j\) ,模式串 P 的下标为 \(i\) ,则 \(kmpNext[i]\) 的含义为:
1、当 \(kmpNext[i] = -1\) 时,文本串后移一位,模式串从头开始,即进行 T[j+1]和 P[0]比较。
2、当 \(kmpNext[i] >= 0\) 时,文本串不动,模式串后移 \(i-kmpNext[i]\) 位,即进行 T[j]和 P 中的下标为 \(kmpNext[i]\) 的字符(即 \(P[kmpNext[i]]\) )的比较。
下表右边是基于前缀函数 kmpNext 的 KMP 匹配函数(左边是基于前缀函数 PI 的 KMP 匹配函数,参见节 5.1.1 ):
| 字符串匹配 KMP 算法(基于 PI 数组) | 字符串匹配 KMP 算法(基于 kmpNext 数组) |
|
void getKmpPrefixFun(const char *P, int Plen, int kmpPI[]); | void getKmpNext(const char *P, int Plen, int kmpNext[]); | int KMP_Match(const char *T, int Tlen, const char *P, int Plen) { | int KMP_Match1(const char *T, int Tlen, const char *P, int Plen) { int kmpPI[Plen]; //C99 标准中的变长数组 | int kmpNext[Plen]; //C99 标准中的变长数组 getKmpPrefixFun(P, Plen, kmpPI); //计算前缀函数,存在 kmpPI 中 | getKmpNext(P, Plen, kmpNext); | int Tindex = 0, Pindex = 0; | int Tindex = 0, Pindex = 0; while (Tindex < Tlen && Pindex < Plen) { | while (Tindex < Tlen && Pindex < Plen) { if (T[Tindex] == P[Pindex]) { | if (T[Tindex] == P[Pindex]) { Tindex++; | Tindex++; Pindex++; | Pindex++; } else if (Pindex == 0) { | } else if (Pindex == -1) { /* 不同点 1 */ //在模式串的首位失配,则把文本串后移 1 位 | //在模式串的首位失配(Pindex == -1),则把文本串后移 1 位,模式串从首位重新开始 Tindex++; | Tindex++; /* Pindex = 0 */ | Pindex = 0; | //上行可写为 Pindex++; 从而该分支和上个 if 分支相同,所以可合并上面两个分支 | // 为 if (Pindex == -1 || T[Tindex] == P[Pindex]) {Tindex++; Pindex++;} ... } else { //在模式串其他位置失配 | } else { //在模式串其他位置失配 Pindex = kmpPI[Pindex - 1]; | Pindex = kmpNext[Pindex]; /* 不同点 2 */ } | } } | } if (Pindex >= Plen) { | if (Pindex >= Plen) { return Tindex - Plen; //如果全部匹配成功,返回下标 | return Tindex - Plen; //如果全部匹配成功,返回下标 } else { | } else { return -1; //匹配不成功,返回-1 | return -1; //匹配不成功,返回-1 } | } } | } |
|
求 kmpNext 数组的函数 getKmpNext 的一个实现如下:
//kmpNext数组和前缀函数PI数组有两点不同:kmpNext相对于PI数组整体向右移动一位,且首位设为-1。
void getKmpNext(const char *P, int Plen, int kmpNext[]) {
int i, j;
i = 0;
j = kmpNext[0] = -1;
while (i < Plen) {
if (j == -1 || P[i] == P[j]) {
++i;
++j;
kmpNext[i] = j;
} else {
j = kmpNext[j];
}
}
}
5.4.2. 改进二:减少多余比较
当我们分析到模式串中的第 \(i\) 位与文本串失配时,假设求得应该从模式串的 \(j\) 位重新开始比较,但是如果第 \(j\) 位与第 \(i\) 位字符相同,则第 \(j\) 位一定与文本串也失配。因此,这种情况下模式串的比较位置可以从 \(j\) 位进一步调整为 \(kmpNext[j]\) 位。如图 15 所示。
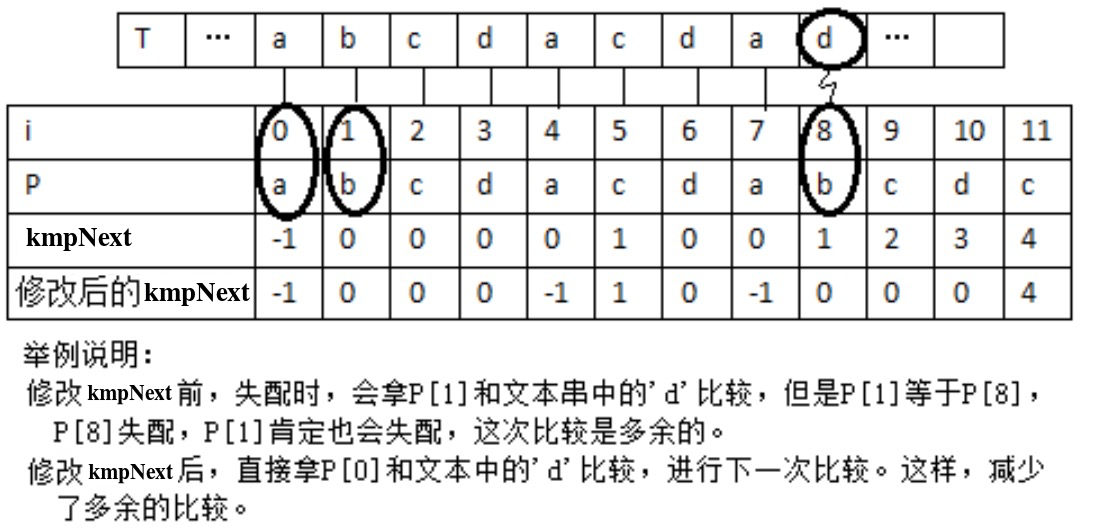
Figure 15: 优化 kmpNext 数组,减少多余比较
下面程序可以求解优化后的 kmpNext 数组:
//求解优化后的kmpNext数组
void getKmpNext1(const char *P, int Plen, int kmpNext[]) {
int i, j;
i = 0;
j = kmpNext[0] = -1;
while (i < Plen) {
if (j == -1 || P[i] == P[j]) {
++i;
++j;
if (P[i] == P[j]) { // 与前面getKmpNext的区别就是多了这个if分支
kmpNext[i] = kmpNext[j];
} else {
kmpNext[i] = j;
}
} else {
j = kmpNext[j];
}
}
}