Bitcoin Mining and Verifying
Table of Contents
1. 比特币简介
一段时间内的交易打成的一个包,称为“区块(Block)”,比特币全网约平均每 10 分钟(这是故意设计的行为)产生一个区块,每一个区块都链接到上一个区块,依次相连形成“区块链(Blockchain)”,如图 1 所示。
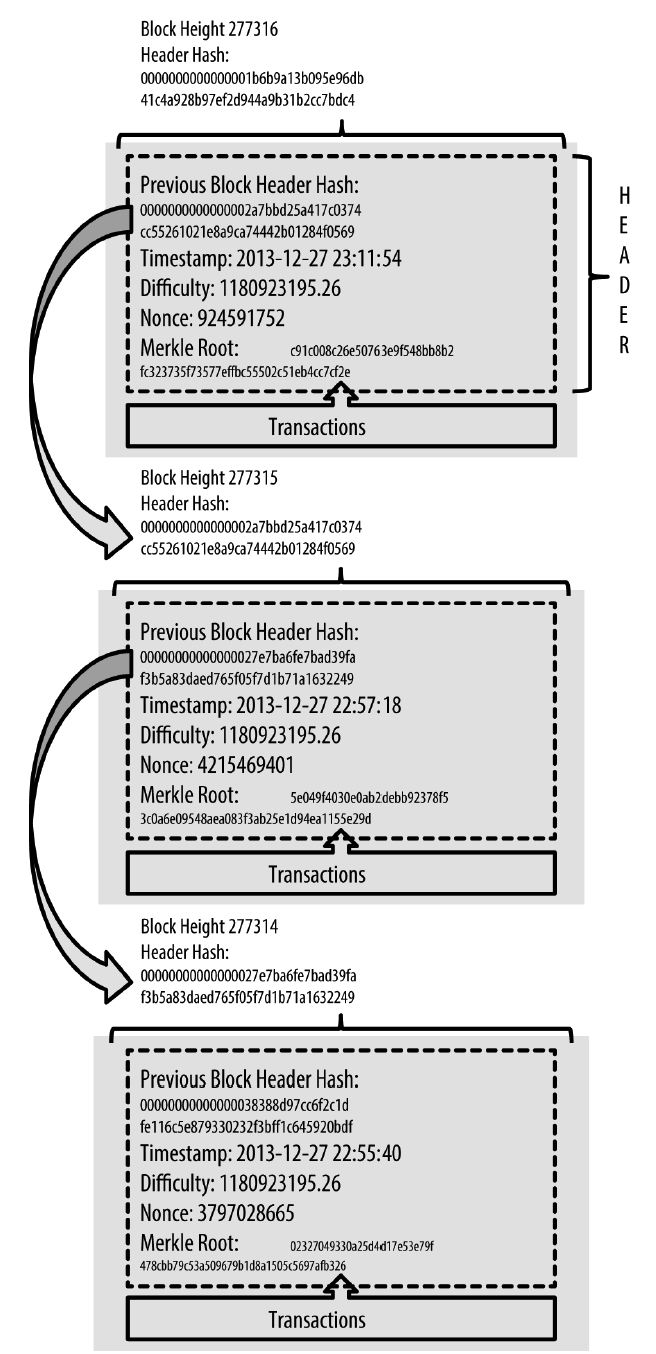
Figure 1: Bitcoin Blockchain
从网站 https://blockchain.info/ 上可以看到所有 Block 的信息。
2. 比特币挖矿
为了确保有节点愿意打包比特币交易,比特币定义了奖励机制:打包交易的节点将获得比特币作为酬劳,具体酬劳可分为两个部分:
第一部分:最开始(2009 年 1 月开始)是每打包一个区块奖励 50 个比特币,之后每经过 21 万个区块(约 4 年时间)奖励将减半一次(2012 年 11 月开始变为奖励 25 个,2016 年 7 月开始变为奖励 12.5 个,依此类推直到 2140 年左右区块奖励不足 1 聪(1比特币等于 1 亿聪)为止,此时区块奖励总和约为 2100 万比特币,这就是比特币 2100 万总量的来源。
第二部分:交易创建者支付的交易手续费(Transaction Fees)。
注:2140 年后的打包奖励将只来源于交易创建者支付的交易手续费(即上面提到的第二部分奖励)。
2.1. 争夺区块打包权
由于有打包奖励的存在,使得有大量节点想打包比特币交易。那到底应该选择哪个节点来打包呢?比特币网络采用的方式是: 出一个数学难题,谁先解出这个难题就要谁打包,它就可以获取相应的打包奖励。
在介绍这个数学难题前,我们先介绍一下 sha256 哈希算法,它可以把任意长度的输入变为 256 bits 的摘要。下面是计算 sha256 哈希的 python 例子:
#!/usr/bin/env python
import hashlib
text = "I am Satoshi Nakamoto"
for nonce in range(20):
# add the nonce to the end of the text
input = text + str(nonce)
# calculate the SHA-256 hash of the input (text+nonce)
hash = hashlib.sha256(input.encode('utf-8')).hexdigest()
# show the input and hash result
print(input + ' ==> ' + hash)
运行上面程序,将得到下面输出:
I am Satoshi Nakamoto0 ==> a80a81401765c8eddee25df36728d732acb6d135bcdee6c2f87a3784279cfaed I am Satoshi Nakamoto1 ==> f7bc9a6304a4647bb41241a677b5345fe3cd30db882c8281cf24fbb7645b6240 I am Satoshi Nakamoto2 ==> ea758a8134b115298a1583ffb80ae62939a2d086273ef5a7b14fbfe7fb8a799e I am Satoshi Nakamoto3 ==> bfa9779618ff072c903d773de30c99bd6e2fd70bb8f2cbb929400e0976a5c6f4 I am Satoshi Nakamoto4 ==> bce8564de9a83c18c31944a66bde992ff1a77513f888e91c185bd08ab9c831d5 I am Satoshi Nakamoto5 ==> eb362c3cf3479be0a97a20163589038e4dbead49f915e96e8f983f99efa3ef0a I am Satoshi Nakamoto6 ==> 4a2fd48e3be420d0d28e202360cfbaba410beddeebb8ec07a669cd8928a8ba0e I am Satoshi Nakamoto7 ==> 790b5a1349a5f2b909bf74d0d166b17a333c7fd80c0f0eeabf29c4564ada8351 I am Satoshi Nakamoto8 ==> 702c45e5b15aa54b625d68dd947f1597b1fa571d00ac6c3dedfa499f425e7369 I am Satoshi Nakamoto9 ==> 7007cf7dd40f5e933cd89fff5b791ff0614d9c6017fbe831d63d392583564f74 I am Satoshi Nakamoto10 ==> c2f38c81992f4614206a21537bd634af717896430ff1de6fc1ee44a949737705 I am Satoshi Nakamoto11 ==> 7045da6ed8a914690f087690e1e8d662cf9e56f76b445d9dc99c68354c83c102 I am Satoshi Nakamoto12 ==> 60f01db30c1a0d4cbce2b4b22e88b9b93f58f10555a8f0f4f5da97c3926981c0 I am Satoshi Nakamoto13 ==> 0ebc56d59a34f5082aaef3d66b37a661696c2b618e62432727216ba9531041a5 I am Satoshi Nakamoto14 ==> 27ead1ca85da66981fd9da01a8c6816f54cfa0d4834e68a3e2a5477e865164c4 I am Satoshi Nakamoto15 ==> 394809fb809c5f83ce97ab554a2812cd901d3b164ae93492d5718e15006b1db2 I am Satoshi Nakamoto16 ==> 8fa4992219df33f50834465d30474298a7d5ec7c7418e642ba6eae6a7b3785b7 I am Satoshi Nakamoto17 ==> dca9b8b4f8d8e1521fa4eaa46f4f0cdf9ae0e6939477e1c6d89442b121b8a58e I am Satoshi Nakamoto18 ==> 9989a401b2a3a318b01e9ca9a22b0f39d82e48bb51e0d324aaa44ecaba836252 I am Satoshi Nakamoto19 ==> cda56022ecb5b67b2bc93a2d764e75fc6ec6e6e79ff6c39e21d03b45aa5b303a
在上面例子中,输入为“I am Satoshi Nakamoto”后接某个数字,这个数字是变化的,我们称为个变化的数字为“nonce”值。
现在我们可以这样定义一个数学难题:请找一个 nonce 值,使得相应的 sha256 哈希值的 16 进制形式“前面是 1 个 0”。
这个“难题”比较简单,从上面输出中可知 nonce=13 符合要求。会有很多节点在很短的时间内就可以找到一个解,还是很难区分谁先解决了一个难题。这时,我们可以增加数学难题的难度,比如:请找一个 nonce 值,使得相应的 sha256 哈希值的 16 进制形式“前面是连续 6 个 0”。显然,求解这个难题要消费更多的计算机资源,通过从 0 开始遍历可以求出 nonce=133148 符合要求。
I am Satoshi Nakamoto133148 ==> 000000ae24f88d4559acb111099879aec1f193507e4dca700adb4fa807697c2e
^^^^^^
我们换一种表述来描述前面提到的两个数学难题。
“sha256 哈希值的 16 进制形式前面是 1 个 0”相当于:
“sha256 哈希值小于 0x1000000000000000000000000000000000000000000000000000000000000000”。
而,“sha256 哈希值的 16 进制形式前面是 6 个 0”相当于:
“sha256 哈希值小于 0x0000010000000000000000000000000000000000000000000000000000000000”。
从而, 难题可更简单地描述为:请找一个 nonce 值,使得 sha256("I am Satoshi Nakamoto" + nonce)小于某个阈值。 这个阈值称为 target。显然当 target 减小时,求解 nonce 的难度会加大。我们可以通过调整 target 值来动态地调整题目的难度。
寻找合适的 nonce,使得 sha256("I am Satoshi Nakamoto" + nonce)小于某个指定的 target,这就是“比特币挖矿的基本原理”。 当然,真正的比特币挖矿并不是计算 sha256("I am Satoshi Nakamoto" + nonce),但原理是一样的。
一旦有某个节点解决了这个数学难题,它就可以完成当前区块的打包,并把打包结果(当然包含有 nonce 值和新哈希值)广播出去,其它节点收到并验证无误后,就会停止抢这一区块的打包权,转而争抢下一个区块的打包权。
2.2. target 的表达形式
前面介绍过,target 越小,区块哈希值的连续前置 0 就越多,挖矿难度越大。
我们一般用“target bits”(或简称为“bits”)来表达 target。
“bits”为 4 字节大小,前 1 字节为 exponent,后 3 字节为 coefficient。target 的计算公式为:
\[\text{target} = \text{coefficient} \times 2^{(8 \times (\text{exponent} – 3))}\]
假设 bits=0x1d00ffff ,则 exponent=0x1d, coefficient=0x00ffff ,从而 target 为:
target = 0x00ffff * 2**(8*(0x1d - 3)) = 0x00000000FFFF0000000000000000000000000000000000000000000000000000
也就是说,如果设定 bits=0x1d00ffff ,你需要找到的哈希值前面必须有 8 个连续 0(这样哈希值才会小于 target)。
2.3. 挖矿过程(寻找合适 nonce 值的过程)
前面通过简化后的例子介绍了“比特币挖矿的基本原理”,也就是寻找合适 nonce 值,使得使用某种方式计算的哈希值小于指定的 target 值。这节介绍真实的挖矿过程。
Block 中有 6 个域参与 Block 哈希值的计算,如表 1 所示。在这 6 个域中,nonce 值是需要经过计算来寻找的,其它 5 个域则可看作是已知的。
| Field | Size | Description |
|---|---|---|
| Version | 4 bytes | A version number to track software/protocol upgrades |
| Previous Block Hash | 32 bytes | Hash A reference to the hash of the previous (parent) block in the chain |
| Merkle Root Hash | 32 bytes | A hash of the root of the merkle tree of this block’s transactions |
| Timestamp | 4 bytes | The approximate creation time of this block (seconds from Unix Epoch) |
| Target (bits) | 4 bytes | The Proof-of-Work algorithm target for this block |
| Nonce | 4 bytes | A counter used for the Proof-of-Work algorithm |
把这 6 个域组合(具体的组合过程在节 2.3.1 中有介绍)在一起,对其进行两次 sha256 哈希计算:
Block Hash = sha256(sha256(Version + Previous Block + Merkle Root + Timestamp + Bits + Nonce))
^ ^ \ /
| | -------------------------------------------------------------
第2次sha256计算 | 组合这6个域,这里+号仅表示组合,并不是数学上的加号
第1次sha256计算
如果哈希值小于 target,则挖矿成功,可以打包当前块,获得相应奖励。
注 1:寻找合适 nonce 值没有取巧的方法,只能从 0 开始遍历寻找。
注 2:Timestamp 仅仅是一个打包 Block(挖矿成功)的近似时间。不用担心在挖矿前设置了 Timestamp,而成功挖矿时 Timestamp 对不上的问题。
2.3.1. 验证 Block 哈希值正确性
如何验证 Block 正确性呢?比如验证 Block #3 的正确性。可分为两个过程:一是验证它的哈希值小于 target,二是它的哈希值确实是组合了 6 个域后,经过两次 sha256 哈希计算现来的。
Block #3 如下所示:
{
"hash": "0000000082b5015589a3fdf2d4baff403e6f0be035a5d9742c1cae6295464449",
"confirmations": 470914,
"height": 3,
"version": 1,
"merkleroot": "999e1c837c76a1b7fbb7e57baf87b309960f5ffefbf2a9b95dd890602272f644",
"time": 1231470173,
"mediantime": 1231469744,
"nonce": 1844305925,
"bits": "1d00ffff",
"difficulty": 1,
"chainwork": "0000000000000000000000000000000000000000000000000000000400040004",
"previousblockhash": "000000006a625f06636b8bb6ac7b960a8d03705d1ace08b1a19da3fdcc99ddbd",
"nextblockhash": "000000004ebadb55ee9096c9a2f8880e09da59c0d68b1c228da88e48844a1485"
}
首先,我们验证它的哈希值小于 target。由于 bits=1d00ffff ,所以 target 为(参见节 2.2 ):
target = 0x00ffff * 2**(8*(0x1d - 3)) = 0x00000000FFFF0000000000000000000000000000000000000000000000000000
显然“0x0000000082b5015589a3fdf2d4baff403e6f0be035a5d9742c1cae6295464449”小于上面 target 值,这步验证通过。
然后,验证哈希值确实是组合了 6 个域后,经过两次 sha256 哈希计算现来的。具体步骤如下所示。
Block #3 的这 6 个域分别如表 2 所示。
| Field | Block #3 |
|---|---|
| Version | 0x00000001 |
| Previous Block | 0x000000006a625f06636b8bb6ac7b960a8d03705d1ace08b1a19da3fdcc99ddbd |
| Merkle Root | 0x999e1c837c76a1b7fbb7e57baf87b309960f5ffefbf2a9b95dd890602272f644 |
| Timestamp | 0x4966be5d |
| Target (bits) | 0x1d00ffff |
| Nonce | 0x6dede005 |
把它们全部转换为 little-endian 的形式,得表 3 。
| Field | Block #3 |
|---|---|
| Version | 0x01000000 |
| Previous Block | 0xbddd99ccfda39da1b108ce1a5d70038d0a967bacb68b6b63065f626a00000000 |
| Merkle Root | 0x44f672226090d85db9a9f2fbfe5f0f9609b387af7be5b7fbb7a1767c831c9e99 |
| Timestamp | 0x5dbe6649 |
| Target (bits) | 0xffff001d |
| Nonce | 0x05e0ed6d |
直接把这 6 个域的 little-endian 形式“concatinate”在一起,得到:
0x01000000bddd99ccfda39da1b108ce1a5d70038d0a967bacb68b6b63065f626a0000000044f672226090d85db9a9f2fbfe5f0f9609b387af7be5b7fbb7a1767c831c9e995dbe6649ffff001d05e0ed6d
把“concatinate”在一起的结果进行两次 sha256 哈希运算:
#!/usr/bin/env python3
from hashlib import sha256
header = bytes.fromhex("01000000bddd99ccfda39da1b108ce1a5d70038d0a967bacb68b6b63065f626a0000000044f672226090d85db9a9f2fbfe5f0f9609b387af7be5b7fbb7a1767c831c9e995dbe6649ffff001d05e0ed6d")
print(sha256(sha256(header).digest()).hexdigest()) # 4944469562ae1c2c74d9a535e00b6f3e40ffbad4f2fda3895501b58200000000
运行上面 python 程序(两次 sha256 哈希后),得到:
4944469562ae1c2c74d9a535e00b6f3e40ffbad4f2fda3895501b58200000000
再转换一下 endian,得到:
0000000082b5015589a3fdf2d4baff403e6f0be035a5d9742c1cae6295464449
这就是 Block #3 的哈希值,验证通过!
参考:https://www.reddit.com/r/Bitcoin/comments/6gl8ol/how_to_manually_verify_a_hash_from_a_block/
2.4. target 的动态调整过程
如果全网成功打包区块的速度小于 10 分钟,则可以减小 target,以增大难度;成功打包区块的速度大于 10 分钟,则可以减大 target,以减小难度。从而维护在平均每 10 分钟打包一个区块。这个调整过程可总结为:
New Target = Old Target * (Actual Time of Last 2016 Blocks / 20160 minutes)
2.4.1. difficulty 值
Block 中有一个域叫 difficulty,target 越小,difficulty 值越大。
关于 difficulty 的计算,可参考:https://en.bitcoin.it/wiki/Difficulty
关于 difficulty 的变化,可参考:https://blockchain.info/charts/difficulty?timespan=all
3. 附录:Merkle Tree
在节 2.3 中,表 1 的第 3 个域是 Merkle Root Hash,它是 Merkle Tree 的根节点,由 Block 中的所有 Transactions 计算而来,如图 2(摘自:https://www.codemag.com/Article/1805061/Understanding-Blockchain-A-Beginners-Guide-to-Ethereum-Smart-Contract-Programming )所示。
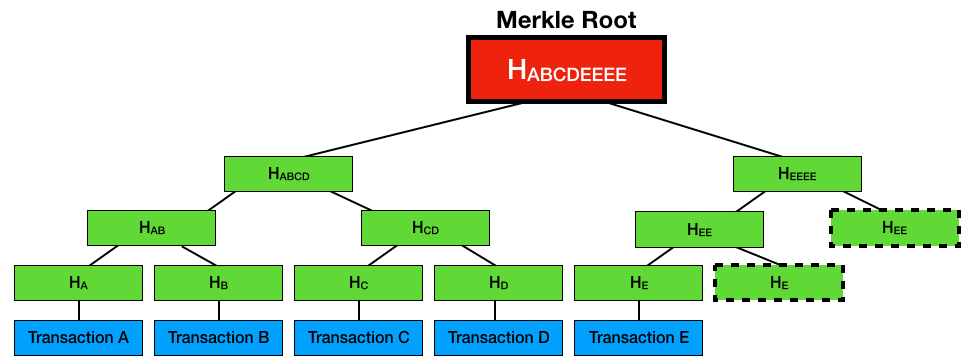
Figure 2: How the Merkle Root is derived from the Merkle Tree
从图 2 中可知, Merkle Tree 中仅仅叶子节点是业务数据(即 Transaction)的直接 hash 值,而非叶节点是其对应子节点串联字符串的 hash 值。
显然,当 Transaction 的个数是奇数时,需要特殊处理。如果 Block 中的 Transaction 个数是 1,则直接使用这个唯一的 Transaction Hash 作为 Merkle Root Hash 即可;如果 Block 中的 Transaction 个数是大于等于 3 的奇数,则最后一个 Transaction Hash 和自己串联进行计算,如图 2 所示。
3.1. Merkle Root 计算实例
下面以 Block 100018 为例(它的 Merkle Root Hash 为 5766798857e436d6243b46b5c1e0af5b6806aa9c2320b3ffd4ecff7b31fd4647),介绍一下 Merkle Root 的具体计算过程。Block 100018 中包含下面 5 个 Transactions:
a335b243f5e343049fccac2cf4d70578ad705831940d3eef48360b0ea3829ed4 d5fd11cb1fabd91c75733f4cf8ff2f91e4c0d7afa4fd132f792eacb3ef56a46c 0441cb66ef0cbf78c9ecb3d5a7d0acf878bfdefae8a77541b3519a54df51e7fd 1a8a27d690889b28d6cb4dacec41e354c62f40d85a7f4b2d7a54ffc736c6ff35 1d543d550676f82bf8bf5b0cc410b16fc6fc353b2a4fd9a0d6a2312ed7338701
下面是具体的计算代码:
#!/usr/bin/env python3 from hashlib import sha256 # Transaction hashs (big endian) in btc block 100018: hashA = "d49e82a30e0b3648ef3e0d94315870ad7805d7f42caccc9f0443e3f543b235a3" hashB = "6ca456efb3ac2e792f13fda4afd7c0e4912ffff84c3f73751cd9ab1fcb11fdd5" hashC = "fde751df549a51b34175a7e8fadebf78f8acd0a7d5b3ecc978bf0cef66cb4104" hashD = "35ffc636c7ff547a2d4b7f5ad8402fc654e341ecac4dcbd6289b8890d6278a1a" hashE = "018733d72e31a2d6a0d94f2a3b35fcc66fb110c40c5bbff82bf87606553d541d" hashAB = sha256(sha256(bytes.fromhex(hashA + hashB)).digest()).hexdigest() hashCD = sha256(sha256(bytes.fromhex(hashC + hashD)).digest()).hexdigest() hashEE = sha256(sha256(bytes.fromhex(hashE + hashE)).digest()).hexdigest() hashABCD = sha256(sha256(bytes.fromhex(hashAB + hashCD)).digest()).hexdigest() hashEEEE = sha256(sha256(bytes.fromhex(hashEE + hashEE)).digest()).hexdigest() merkleRoot = sha256(sha256(bytes.fromhex(hashABCD + hashEEEE)).digest()).hexdigest() # little endian print(merkleRoot) # 4746fd317bffecd4ffb320239caa06685bafe0c1b5463b24d636e45788796657
注意,计算前需要把 hash 转换为 big endian 形式,最后 merkleRoot 的结果是 little endian 形式,转换为 big endian 就是 5766798857e436d6243b46b5c1e0af5b6806aa9c2320b3ffd4ecff7b31fd4647,这和 Block 100018 头中的值是一致的。
3.2. Merkle Tree 优点:可用较小的代价检测 tx 是否存在于 block 中
如果只是校验 Transaction 没有被替换,则使用更简单的 Hash list(如图 3 所示)也能实现目标。
Figure 3: Hash List
之所以使用 Merkle Tree,是因为它有其它优点:可用较小的代价检测某个 Transaction 是否存在于 block 中。
比特币中除了 full node 外,还有一类 light node。对于 light node,它们只下载区块头信息,并不会下载全部的区块数据,这样它们的部署和运行都很快捷。
如图 4(摘自:https://www.codemag.com/Article/1805061/Understanding-Blockchain-A-Beginners-Guide-to-Ethereum-Smart-Contract-Programming )所示,假设 light node 想验证 Transaction C 存在于某个区块中,那么它向 full node 请求红色虚线框住的 3 个哈希值(即 HAB,HD,HEEEE)即可完成验证。
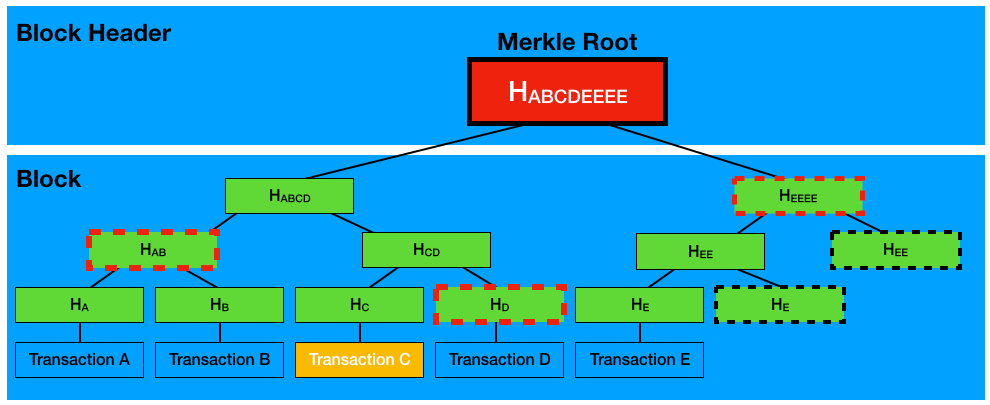
Figure 4: How the Merkle Tree and Merkle Root is used to validate a transaction
3.3. Second Preimage Attack
Merkle Tree 存在 Second Preimage Attack 问题: 用中间某层的 hash 值当原始 data,也能得到相同的 Merkle Root。
Figure 5: Merkle Tree
对于图 5 的例子,如果伪造另一个结构:它只有两个 data 节点,第 1 个 data 内容是“hash0-0 + hash0-1”,而第 2 个 data 内容是“hash1-0 + hash1-1”,这样它的 Merkle Root 显然和 5 是一样的。
一种简单的解决办法是:对原始 data 前面加上 0x00 再计算 hash ;而对中间层的节点前面加上 0x01 后再计算 hash,这样区分了原始 data 和中间的 hash 值,从而避免了 Second Preimage Attack。
4. 参考
Mastering Bitcoin, 2nd Edition

