Bagging and Random Forest
Table of Contents
1. Bagging 和 RF 简介
Bagging 和 Random Forest 都是集成学习(ensemble learning)方法,且 Random Forest 是 Bagging 的扩展变体。
本文主要摘自:《机器学习,周志华,2016》8.3 Bagging 和随机森林
2. Bagging (Bootstrap AGGregatING)
Bagging(Bootstrap AGGregatING)是一种集成学习方法,由 Leo Breiman 于 1994 年提出。
介绍 Bagging 前,先介绍一下 Bootstrap 采样:给定包含 \(N\) 个样本的数据集 \(D\) ,我们对它进行采样得到数据集 \(D'\) :每次随机从 \(D\) 中挑选一个样本,将其拷贝放入 \(D'\) ,然后再将该样本放回初始数据集 \(D\) 中,使得该样本在下次采样时仍有可能被采到;这个过程重复执行 \(N\) 次后,我们就得到包含 \(N\) 个样本的数据集 \(D'\) ,这就是 Bootstrap 采样的结果。 Bootstrap 采样又称为“可重复采样”或者“有放回采样”。
Bagging 方法的基本流程:设训练数据集有 \(N\) 样本,从训练数据集中用 Bootstrap 采样方式采样出 \(T\) 个采样集,然后基于每一个采样集训练出一个基本学习器,再将这些基本学习器进行结合。如何结合呢?Bagging 通常对分类任务使用简单投票法(即获得票数最多的类别作为最终的类别),对回归任务使用简单平均法(即把 \(T\) 个基本学习器结果的平均值作为最终的输出)。
2.1. Bagging 优点
下面介绍 Bagging 的两个优点。
(1) Bagging 方法可以方便地并行化,多个基本学习器可以同时进行训练。 (标准的 AdaBoost 不能并行化,因为它的后一个基本学习器需要前一个基本学习器完成后才能开始训练)。
(2) Bagging 的每个基本学习器使用的训练数据不同,且只包含原始训练数据的部分内容(因为 Bootstrap 采样是“有放回采样”,这样有样本会出现多次,有样本不会出现),这使得, Bagging 不容易出现过拟合现象。
3. Random Forest
随机森林(Random Forest, 简称 RF)是 Bagging 方法的一个扩展变体。
随机森林和 Bagging 的不同有:
(1) 随机森林采用“决策树”为基本学习器;Bagging 是一个通用框架,可以使用任何算法为基本学习器。
(2) 随机森林在决策树的训练过程中引入了“随机属性选择”。
“随机属性选择”描述如下:
传统决策树在选择划分属性时是在当前结点的属性集合(假定在 \(d\) 个属性)中选择一个最优属性;而在随机森林中,对于基决策树的每个结点,先从该结点的属性集合中随机选择一个包含 \(k\) 个属性的子集,然后再从这个子集中选择一个最优属性用于划分。 这里的参数 \(k\) 控制了随机性的引入程度:若令 \(k=d\) ,则基决策树的构建与传统决策树相同;若令 \(k=1\) ,则是随机选择一个属性用于划分;一般情况下,推荐值 \(k=\log_2d\) 。
在 Bagging 方法中,基学习器的“多样性”来自于样本扰动(通过对初始训练集采样);而随机森林中,基学习器的“多样性”不仅来自样本扰动,还来自属性扰动(随机属性选择)。这使得随机森林的泛化能力通常比 Bagging 方法更好。图 1 是在两个 UCI 数据上,随机森林和 Bagging 方法的比较。
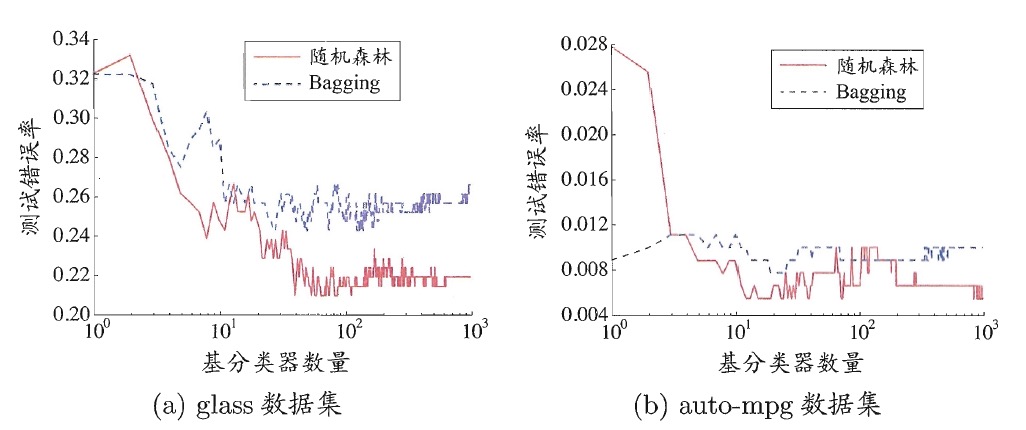
Figure 1: 两个 UCI 数据上,随机森林和 Bagging 方法的比较(随机森林的泛化误差更低)
4. Random Forest vs. Gradient-Boosted Tree
Both Gradient-Boosted Trees (GBTs) and Random Forests are algorithms for learning ensembles of trees, but the training processes are different. There are several practical trade-offs:
(1) GBTs train one tree at a time, so they can take longer to train than random forests. Random Forests can train multiple trees in parallel.
(2) Random Forests can be less prone to overfitting. Training more trees in a Random Forest reduces the likelihood of overfitting, but training more trees with GBTs increases the likelihood of overfitting. (In statistical language, Random Forests reduce variance by using more trees, whereas GBTs reduce bias by using more trees.)
(3) Random Forests can be easier to tune since performance improves monotonically with the number of trees (whereas performance can start to decrease for GBTs if the number of trees grows too large).
In short, both algorithms can be effective, and the choice should be based on the particular dataset.
4.1. Bias vs. Variance
前面提到了:Random Forests reduce variance by using more trees, whereas GBTs reduce bias by using more trees.
这里简单介绍下偏差和方差。偏差和方差可以形象地用图 2(摘自 http://scott.fortmann-roe.com/docs/BiasVariance.html )所示。
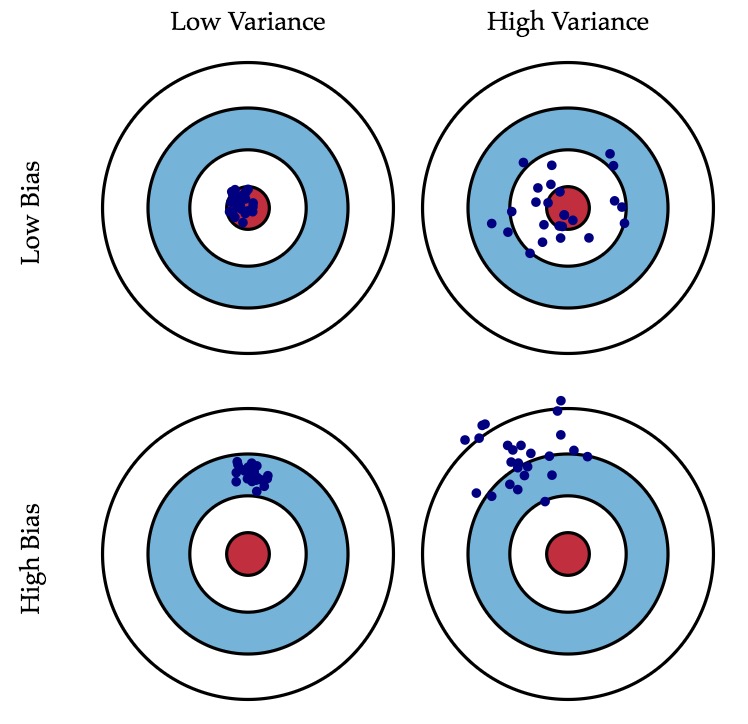
Figure 2: Graphical illustration of bias and variance
可以把泛化误差分解为偏差、方差及噪声之和(其推导过程可参见《机器学习,周志华,2016》2.5 偏差和方差)。
一般来说,“低偏差”和“低方差”不可兼得,这被称为 Bias–variance dilemma , 图 3(摘自 http://scott.fortmann-roe.com/docs/BiasVariance.html )演示了这种情况。
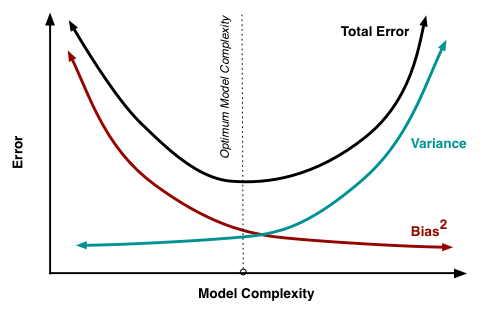
Figure 3: Bias and variance contributing to total error
Random Forest(不容易过拟合)从“减小方差”的角度来提高模型的泛化能力;而 Gradient-Boosted Tree 从“减小偏差”的角度来提高模型的泛化能力。