Fourier Series, Fourier Transform, DFT, FFT

1. 傅里叶级数和变换简介
- 1.1. 数学基础知识回顾——复数
2. 傅里叶级数
3. 傅里叶变换
4. 离散傅里叶变换

1. 傅里叶级数和变换简介

法国数字家傅里叶(Jean-Baptiste Joseph Fourier)被世人铭记的最大贡献记载在他于 1807 年发表的传记中和 1822 年出版“Théorie analytique de la chaleur（热分析理论）”的一书中。傅里叶在这个领域的贡献是，他指出任何“周期函数”都可以表示为不同频率的正弦和（或）余弦之和的形式，每个正弦项和（或）余弦项乘以不同的系数。现在，该和称为傅里叶级数(Fourier series)。这个概念出现后，在当时遭到了怀疑，因为它不直观。

甚至，非周期函数（但该曲线下的面积是有限的）也可以用“正弦和（或）余弦乘以加权函数”的积分来表示。这种情况下的公式就是傅里叶变换(Fourier transform)，其作用在多数理论和应用学科中甚至远大于傅里叶级数。

参考：信号与系统（第二版，郑君里）

1.1. 数学基础知识回顾——复数

后文会用到复数，这里回顾一下关于复数的基本知识。

复数 $C$ 的定义如下： $C = R + j I$ 其中， $R$ 和 $I$ 是实数， $R$ 表示复数的实部， $I$ 表示复数的虚部。 $j$ 是虚数单位，即 $j = \sqrt{- 1}$ （注：数字上常用 $i$ 表示虚数单位，这里用 $j$ 是按照电工学中通常的习惯）。

一个复数 $C$ 的共轭(Complex conjugate)表示为 $C^{*}$ ，其定义为： $C^{*} = R - j I$ 复数从几何的角度可以被看成是平面（称为复平面）上的一个点，其横坐标是实轴（ $R$ 的值），其纵坐标是虚轴（ $I$ 的值）。也就是说，复数 $R + j I$ 是复平面直角坐标系统中的点 $(R, I)$ 。

有时，在极坐标下表示复数很有用： $C = | C | (\cos θ + j \sin θ)$ 其中， $| C | = \sqrt{R^{2} + I^{2}}$ 是复平面的原点到点 $(R, I)$ 的向量的长度， $θ$ 是该向量与实轴的夹角。

利用欧拉公式(Euler’s formula)： $e^{j θ} = \cos θ + j \sin θ$ 极坐标下复数又可以表示（称为指数形式的表示）为： $C = | C | e^{j θ}$

例如，复数 $1 + j 2$ 的极坐标表示是 $\sqrt{5} e^{j θ}$ ，其中 $θ = {64.4}^{\circ}$ 。

前面的公式还可以用于复函数。例如，变量 $u$ 的复函数 $F (u)$ 可表示为 $F (u) = R (u) + j I (u)$ ，其中 $R (u)$ 和 $I (u)$ 分别是实分量函数和虚分量函数。复共轭函数是 $F^{*} (u) = R (u) - j I (u)$ 。

2. 傅里叶级数

2.1. 傅里叶级数基本定义

法国数字家傅里叶发现， 具有周期 $T$ 的连续变量 $t$ 的周期函数 $f (t)$ 可以被描述为乘以适当系数的正弦和余弦和。 这个和就是傅里叶级数，它具有如下形式：

\begin{aligned} f (t) & = a_{0} + a_{1} \cos (\frac{2 π}{T} t) + b_{1} \sin (\frac{2 π}{T} t) + a_{2} \cos (2 \frac{2 π}{T} t) + b_{2} \sin (2 \frac{2 π}{T} t) + \dots + a_{n} \cos (n \frac{2 π}{T} t) + b_{n} \sin (n \frac{2 π}{T} t) \\ (傅里叶级数的三角形式) & = a_{0} + \sum_{n = 1}^{\infty} [a_{n} \cos (n \frac{2 π}{T} t) + b_{n} \sin (n \frac{2 π}{T} t)], (n = 1, 2, \dots) \end{aligned}

其中，各个系数可按以下各式计算。
直流分量：
$a_{0} = \frac{1}{T} \int_{t_{0}}^{t_{0} + T} f (t) d t$
余弦分量的幅度：
$a_{n} = \frac{2}{T} \int_{t_{0}}^{t_{0} + T} f (t) \cos (n \frac{2 π}{T} t) d t, (n = 1, 2, \dots)$
正弦分量的幅度：
$b_{n} = \frac{2}{T} \int_{t_{0}}^{t_{0} + T} f (t) \sin (n \frac{2 π}{T} t) d t, (n = 1, 2, \dots)$
为方便起见，通常积分区间 $t_{0} \sim t_{0} + T$ 取为 $0 \sim T$ 或者 $- \frac{T}{2} \sim \frac{T}{2}$ 。

说明：并非任意周期信号都能进行傅里叶级数展开，需要满足一定的条件才能进行傅里叶级数展开。不过，在实践中，这些条件一般都会满足，这点不介绍这些条件。

2.1.1. 实例：求周期锯齿脉冲信号的傅里叶级数展开

求周期函数 $s (x)$ （如图 1 所示，它是周期锯齿脉冲信号）的傅里叶级数表示。

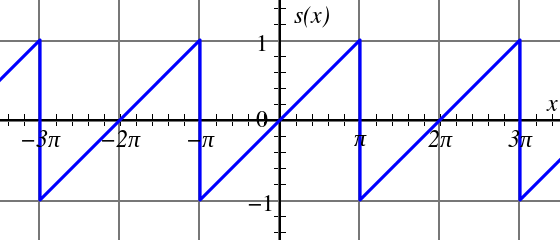
Figure 1: Sawtooth wave, $s (x) = x / π$ on the interval $(- π, π]$

函数 $s (x)$ 的周期为 $T = 2 π$ ，傅里叶级数中直流分量，余弦分量的幅度，正弦分量的幅度分别计算如下。
$\begin{aligned} a_{0} & = \frac{1}{2 π} \int_{- π}^{π} s (x) d x = 0 \\ a_{n} & = \frac{2}{2 π} \int_{- π}^{π} s (x) \cos (n x) d x = 0, (n = 1, 2, \dots) \\ b_{n} & = \frac{2}{2 π} \int_{- π}^{π} s (x) \sin (n x) d x = \frac{2 (- 1)^{n + 1}}{π n}, (n = 1, 2, \dots) \end{aligned}$
把上面系数代入到傅里叶级数展开式中，可得：
$\begin{aligned} s (x) & = a_{0} + \sum_{n = 1}^{\infty} [a_{n} \cos (n \frac{2 π}{T} x) + b_{n} \sin (n \frac{2 π}{T} x)] \\ = \frac{2}{π} \sum_{n = 1}^{\infty} \frac{(- 1)^{n + 1}}{n} \sin (n x) \\ = \frac{2}{π} [\sin (x) - \frac{1}{2} \sin (2 x) + \frac{1}{3} \sin (3 x) - \frac{1}{4} \sin (x) + \dots] \end{aligned}$

由上式知，傅里叶级数展开后，要无限多项才能完全逼近原函数。实际应用中，经常采用有限项级数来代替无限项级数。如，取前 1 到 5 个正弦项，如图 2 所示。

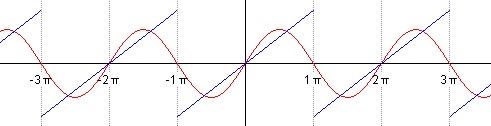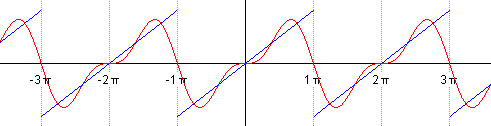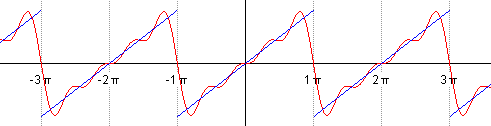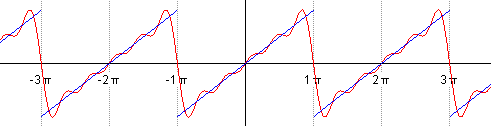
Figure 2: 取前 1 到 5 个正弦项来近似 Sawtooth wave

2.1.1.1. 函数对称性与傅里叶系数的关系

通过前面例子，可知周期锯齿脉冲信号（如图 1 所示，它是奇函数）仅含正弦分量。这不是巧合，利用“正弦函数为奇函数，余弦函数为偶函数”以及奇偶函数的性质，我们容易推导出更一般的结论：
奇函数的傅里叶级数展开后，直流分量和余弦分量为零，只含正弦分量。
偶函数的傅里叶级数展开后，正弦分量为零，只含直流分量和余弦分量。

2.2. 傅里叶级数的另一种常见三角形式（幅度谱，相位谱）

如果将前面介绍的傅里叶级数中“同频率项合并”，傅里叶级数还可以写为另一种形式：

\begin{matrix} (傅里叶级数的另一种常见三角形式) & f (t) = c_{0} + \sum_{n = 1}^{\infty} c_{n} \cos (n \frac{2 π}{T} t + φ_{n}) \end{matrix}

或者写为：
$f (t) = d_{0} + \sum_{n = 1}^{\infty} d_{n} \sin (n \frac{2 π}{T} t + θ_{n})$
各个系数为（ $a_{0}, a_{n}, b_{n}, n = 1, 2, \dots$ 的计算公式前面已经介绍过）：
$\begin{aligned} c_{0} = d_{0} = a_{0} \\ c_{n} = d_{n} = \sqrt{a_{n}^{2} + b_{n}^{2}}, (n = 1, 2, \dots) \\ \tan φ_{n} = - \frac{b_{n}}{a_{n}} \\ \tan θ_{n} = \frac{a_{n}}{b_{n}} \end{aligned}$

通常把频率为 $1 / T$ （此时角频率为 $\frac{2 π}{T}$ ， $n = 1$ ）的分量称为“基波”，把频率为 $2 / T$ （角频率为 $\frac{4 π}{T}$ ）、 $3 / T$ （角频率为 $\frac{6 π}{T}$ ）等的分量称为“二次谐波”，“三次谐波”等。

显然，各分量幅度（ $c_{n}$ 或 $d_{n}$ ）及相位（ $φ_{n}$ 或 $θ_{n}$ ）确定下来后，周期函数的傅里叶级数展开就确定了。

我们把幅度 $c_{n}$ 和角频率 $\frac{2 π n}{T}$ 之间的关系图称为幅度频谱（简称幅度谱），把相位 $φ_{n}$ 和角频率 $\frac{2 π n}{T}$ 之间的关系图称为相位频谱（简称相位谱）。

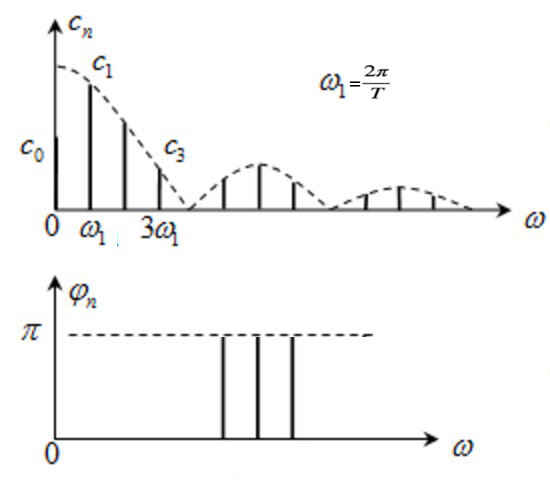
Figure 3: 某周期函数的傅里叶“幅度谱”和“相位谱”

不过，很多时候，相位谱不是很重要，常常直接忽略它。

2.3. 傅里叶级数的指数形式

设周期函数 $f (t)$ 的周期为 $T$ ，记其角频率 $ω_{1} = 2 π / T$ ，下面将从傅里叶级数的基本定义推导出傅里叶级数的指数形式。
由欧拉公式可知 $\cos (n ω_{1} t) = \frac{1}{2} (e^{j n ω_{1} t} + e^{- j n ω_{1} t}), \sin (n ω_{1} t) = \frac{1}{2 j} (e^{j n ω_{1} t} - e^{- j n ω_{1} t})$ ，把这两个式子代入到前面介绍的傅里叶级数基本定义中，有：
$\begin{aligned} f (t) & = a_{0} + \sum_{n = 1}^{\infty} [a_{n} \cos (n ω_{1} t) + b_{n} \sin (n ω_{1} t)] \\ = a_{0} + \sum_{n = 1}^{\infty} (a_{n} \frac{e^{j n ω_{1} t} + e^{- j n ω_{1} t}}{2} + b_{n} \frac{e^{j n ω_{1} t} - e^{- j n ω_{1} t}}{2 j}) \\ = a_{0} + \sum_{n = 1}^{\infty} (\frac{1}{2} (a_{n} - j b_{n}) e^{j n ω_{1} t} + \frac{1}{2} (a_{n} + j b_{n}) e^{- j n ω_{1} t}) \end{aligned}$

令 $F (n ω_{1}) = \frac{1}{2} (a_{n} - j b_{n})$ ，由于 $a_{n}$ 是 $n$ 的偶函数， $b_{n}$ 是 $n$ 的奇函数，可知 $F (- n ω_{1}) = \frac{1}{2} (a_{n} + j b_{n})$ ，从而上式可接着变形为：
$f (t) = a_{0} + \sum_{n = 1}^{\infty} (F (n ω_{1}) e^{j n ω_{1} t} + F (- n ω_{1}) e^{- j n ω_{1} t})$
令 $F (0) = a_{0}$ ，考虑到： $\sum_{n = 1}^{\infty} F (- n ω_{1}) e^{- j n ω_{1} t} = \sum_{n = - 1}^{- \infty} F (n ω_{1}) e^{j n ω_{1} t}$ ，从而上式可接着变形为：
$f (t) = \sum_{n = - \infty}^{\infty} F (n ω_{1}) e^{j ω_{1} t}$
一般我们把 $F (n ω_{1})$ 简写为 $F_{n}$ ，上式即为 周期函数 $f (t)$ （设周期为 $T$ ）的傅里叶级数的指数形式：

\begin{matrix} (傅里叶级数的指数形式) & f (t) = \sum_{n = - \infty}^{\infty} F_{n} e^{j ω_{1} t} \end{matrix}

其中，
$\begin{aligned} ω_{1} & = \frac{2 π}{T} \\ F_{n} & = \frac{1}{T} \int_{t_{0}}^{t_{0} + T} f (t) e^{- j n ω_{1} t} d t, (n = 0, \pm 1, \pm 2, \dots) \end{aligned}$
通常积分区间 $t_{0} \sim t_{0} + T$ 取为 $0 \sim T$ 或者 $- \frac{T}{2} \sim \frac{T}{2}$ 。

显然，如果给出 $F_{n}$ ，则 $f (t)$ 唯一确定。在傅里叶级数的指数形式中傅里叶系数 $F_{n}$ 不再是实数，而是复数，有模有辐角。

注： $F_{n}$ 的推导过程如下： $F_{n} = \frac{1}{2} (a_{n} - j b_{n}) = \frac{1}{T} \int_{t_{0}}^{t_{0} + T} f (t) \cos (n ω_{1} t) d t - j \frac{1}{T} \int_{t_{0}}^{t_{0} + T} f (t) \sin (n ω_{1} t) d t = \frac{1}{T} \int_{t_{0}}^{t_{0} + T} f (t) e^{- j n ω_{1} t} d t, (n = 0, \pm 1, \pm 2, \dots)$

傅里叶级数的指数形式中系数 $F_{n}$ 和傅里叶级数的三角形式中的幅度 $c_{n}$ 和相位 $φ_{n}$ 的关系如下：
$\begin{aligned} F_{0} = c_{0} \\ F_{n} = | F_{n} | e^{j φ_{n}}, (n = 1, 2, \dots) \\ F_{- n} = | F_{- n} | e^{- j φ_{n}}, (n = 1, 2, \dots) \\ | F_{n} | = | F_{- n} | = \frac{1}{2} c_{n}, (n = 1, 2, \dots) \end{aligned}$

2.3.1. 复数频谱（复数幅度谱，复数相位谱）

我们可以画出傅里叶级数指数形式表示的信号频谱。因为 $F_{n}$ 一般是复函数，所有称这种频谱为复数频谱。根据 $F_{n} = | F_{n} | e^{j φ_{n}}$ ，可以画出“复数幅度谱”为“复数相位谱”，如图 4 所示。

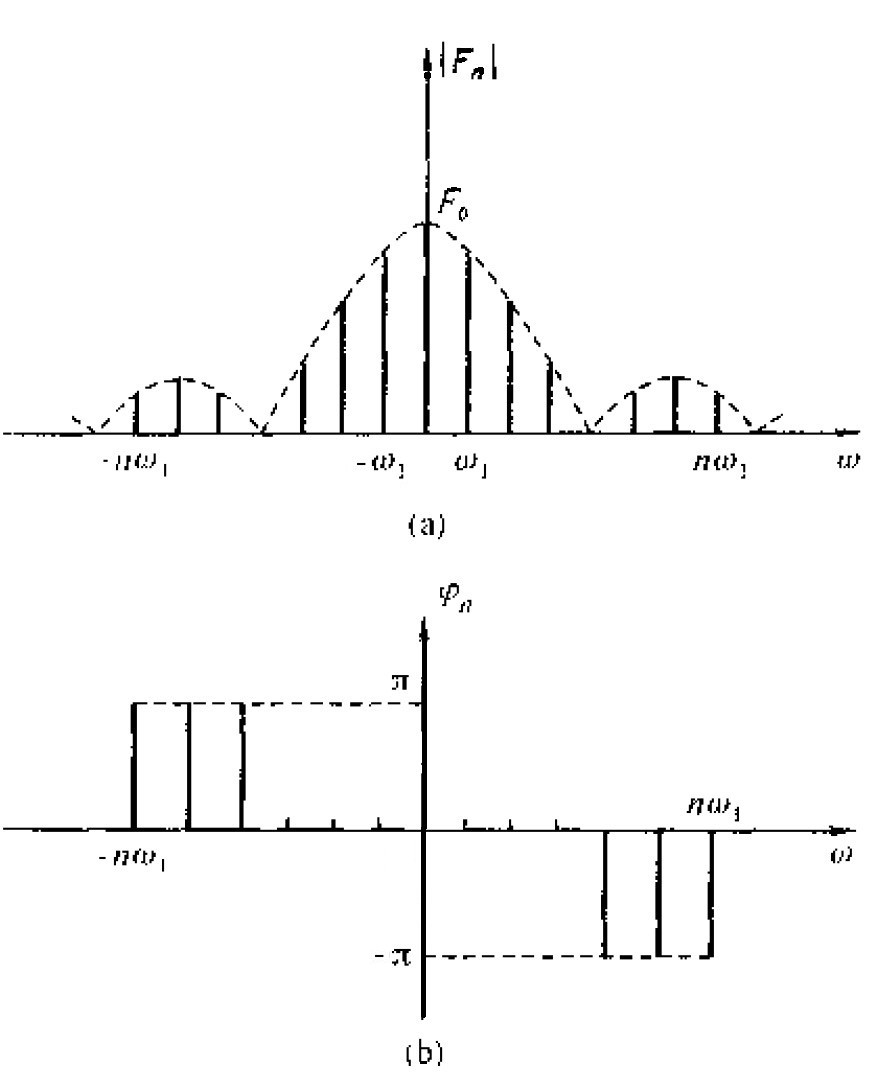
Figure 4: 周期函数的复数频谱示例

由于， $| F_{n} | = | F_{- n} | = \frac{1}{2} c_{n}$ ，所以复数幅度谱是相对纵轴左右对称的。在三角函数的频谱（如图 3 ）中每条谱线代表一个分量的幅度；在指数形式的频谱（如图 4 ）中每个分量的幅度一分为二，在正、负频率相对应的位置上各为一半，所以，只有把正、负频率上对应的这两条谱线加起来才代表一个分量的幅度。

需要说明的是，在复数频谱中出现的负频率是由于将 $\sin (n ω_{1} t)$ 和 $\cos (n ω_{1} t)$ 写成指数形式时，从数字的观点自然分成 $e^{j n ω_{1} t}$ 以及 $e^{- j n ω_{1} t}$ 两项，因而引入了 $- j n ω_{1} t$ 项，所以，负频率的出现完全是数学运算的结果，并没有任何物理意义。

在 $F_{n}$ 为实数的特殊情况下，显然相位不是 0 就是 $π$ ，可以用 $F_{n}$ 的正负分别表示相位 $φ_{n}$ 为 0 和 $π$ ，这时经常把幅度谱和相位谱画在同一张图上（而不是两张图）。后文将介绍这样的例子。

2.4. 实例：求周期矩形脉冲信号的傅里叶频谱

设周期矩形脉冲信号（又称为方波信号） $f (t)$ 的脉冲宽度为 $τ$ ，脉冲幅度为 $E$ ，重复周期为 $T$ （显然角频率 $ω_{1} = 2 π / T$ ），如图 5 所示。求其傅里叶频谱。

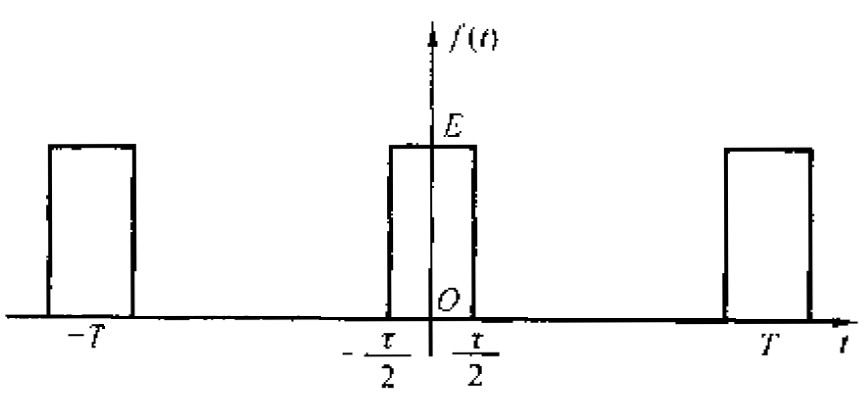
Figure 5: 周期矩形脉冲信号

直流分量 $a_{0}$ ，余弦分量的幅度 $a_{n}$ ，正弦分量的幅度 $b_{n}$ 分别计算如下。
$\begin{aligned} a_{0} & = \frac{1}{T} \int_{- T / 2}^{T / 2} f (t) d t = \frac{1}{T} \int_{- T / 2}^{T / 2} E d t = \frac{E τ}{T} \\ a_{n} & = \frac{2}{T} \int_{- T / 2}^{T / 2} f (t) \cos (n ω_{1} x) d t = \frac{2 E}{n π} \sin (\frac{n π τ}{T}), (n = 1, 2, \dots) \\ b_{n} & = \frac{2}{T} \int_{- T / 2}^{T / 2} f (t) \sin (n ω_{1} x) d t = 0, (n = 1, 2, \dots) \end{aligned}$
从而可求得 $c_{0}, c_{n}, φ_{n} (n = 1, 2, \dots)$ 以及 $F_{n}, (n = 0, \pm 1, \pm 2, \dots)$ 。

其指数形式傅里叶级数幅度和相位如图 6 所示。

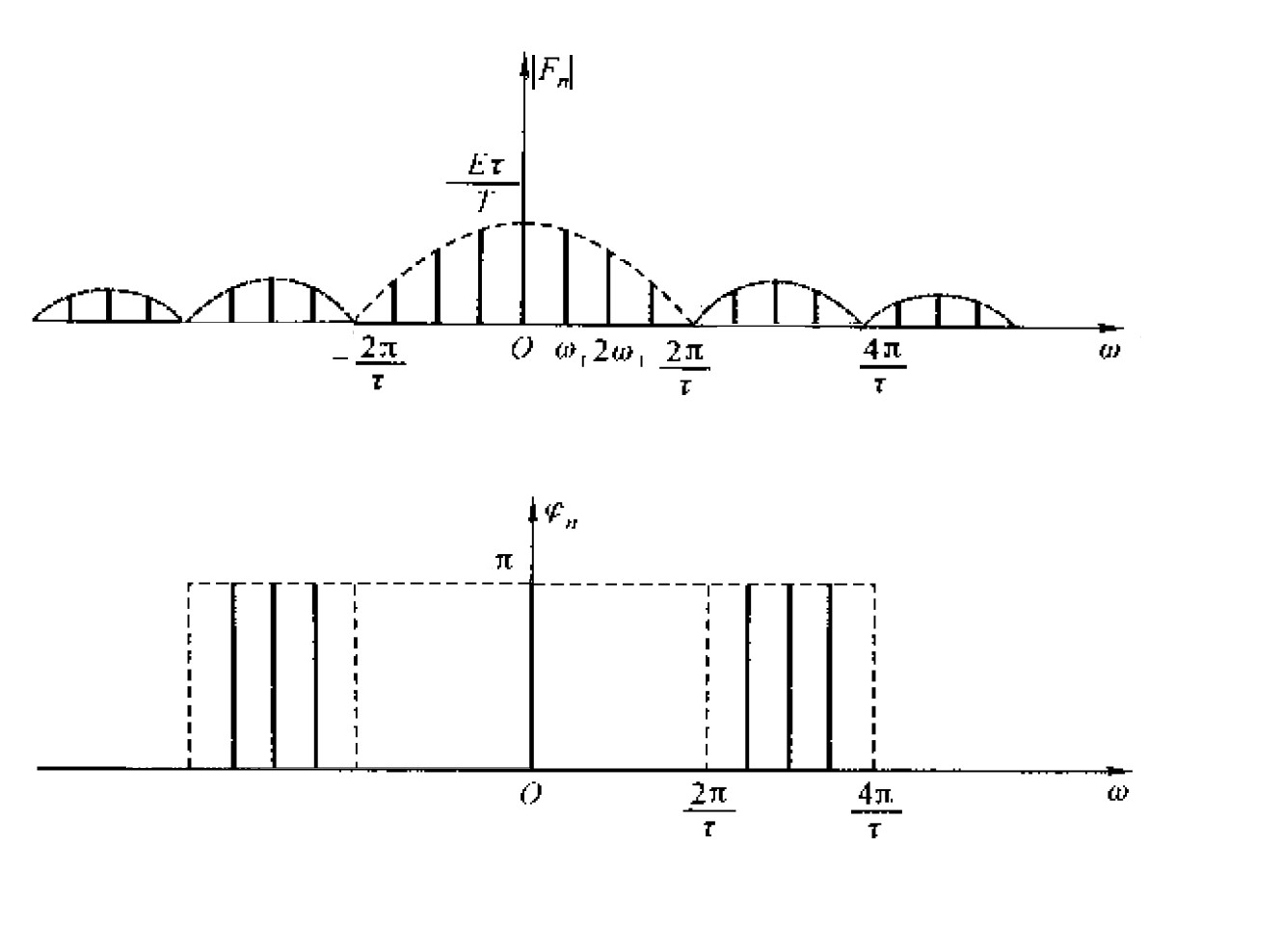
Figure 6: 方波信号指数形式傅里叶级数幅度谱和相位谱

由于， $F_{n}$ 在这个例子中恰为实数（一般情况 $F_{n}$ 为复数），此时相位不是 0 就是 $π$ ，可以用 $F_{n}$ 的正负分别表示相位 $φ_{n}$ 为 0 和 $π$ ，这时我们可以把幅度谱和相位谱画在同一张图上，如图 7 所示。

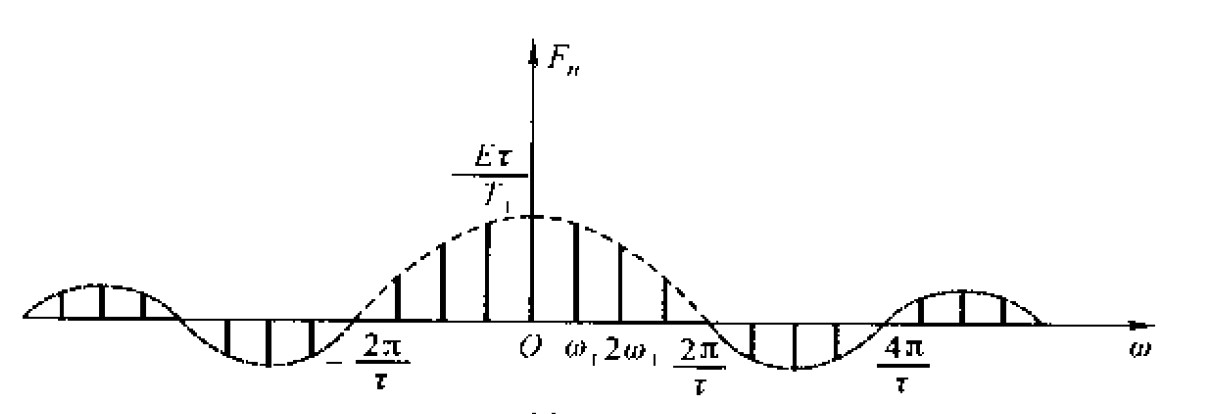
Figure 7: 方波信号指数形式傅里叶级数幅度谱和相位谱（合画图）

3. 傅里叶变换

前面介绍了连续“周期信号”的傅里叶级数，并得到了它的离散频谱。对于连续“非周期信号”，没有傅里叶级数，但可以推导出“傅里叶变换”。

由傅里叶级数的定义可知，对于周期为 $T$ 的周期信号，离散频谱各个分量出现在 $ω_{1}, 2 ω_{1}, 3 ω_{1}, \dots, (ω_{1} = 2 π / T)$ 处。显然， 当周期 $T$ 越大，离散频谱的各个分量会越靠近（因为 $ω_{1}$ 会越小）；当周期 $T \to \infty$ 时（这时就是非周期信号），频谱会变为连续的。 以方波信号为例，其变化趋势如图 8 所示。

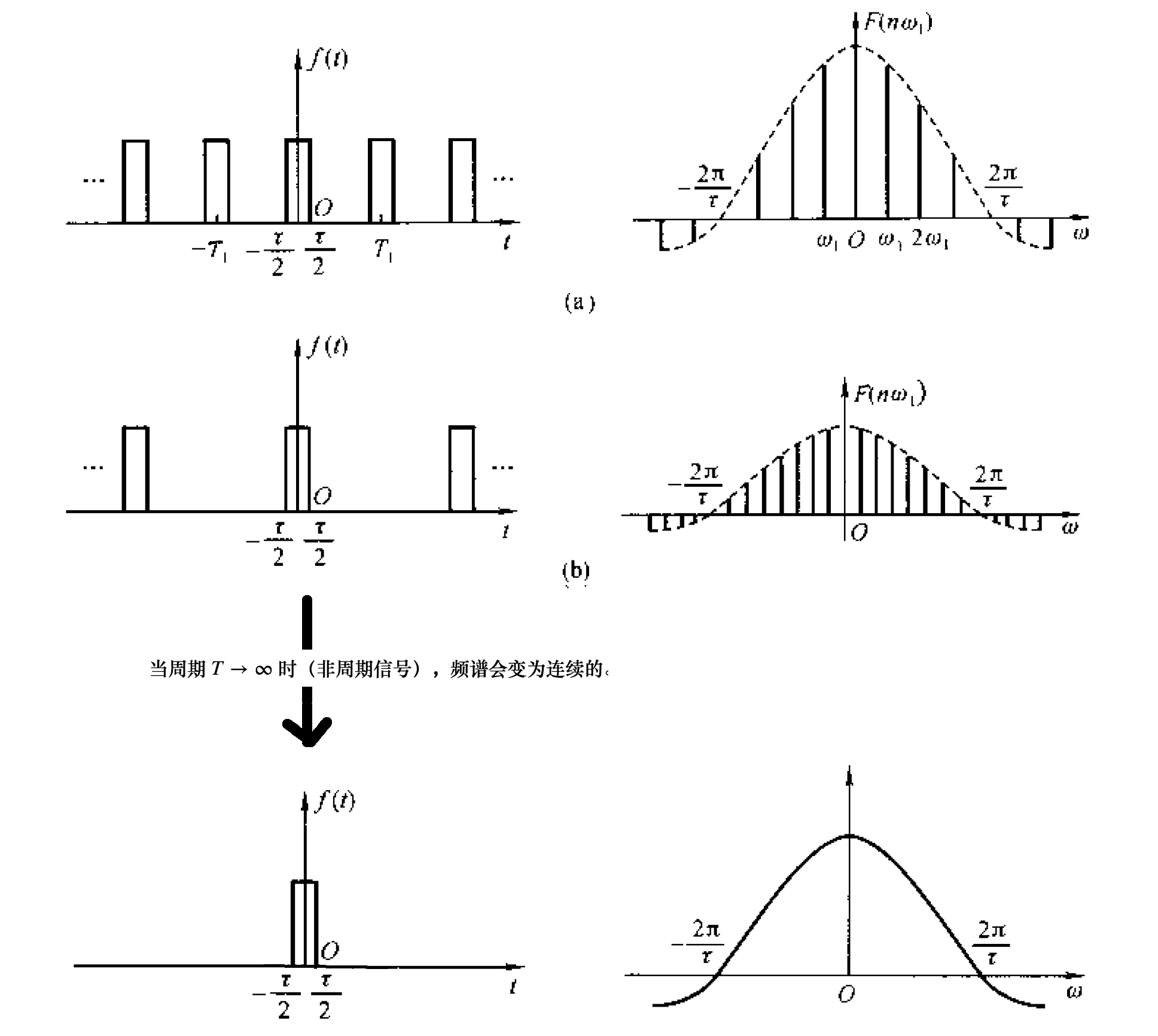
Figure 8: 当周期信号的周期 $T$ 越大时，离散频谱的各个分量会越靠近

3.1. 傅里叶变换定义

由前面的分析知，通过极限的方法，我们可以从周期信号的傅里叶级数导出非周期信号频谱的表示式，这称为傅里叶变换(Fourier transform)。在这里，不严格推导，直接给出非周期信号傅里叶变换的公式。

非周期信号 $f (t)$ 的傅里叶变换为：

\begin{matrix} (傅里叶变换) & F (ω) = F [f (t)] = \int_{- \infty}^{\infty} f (t) e^{- j ω t} d t \end{matrix}

对应的傅里叶逆变换为：

\begin{matrix} (傅里叶逆变换) & f (t) = F^{- 1} [F (ω)] = \frac{1}{2 π} \int_{- \infty}^{\infty} F (ω) e^{- j ω t} d t \end{matrix}

式中， $F (ω)$ 是 $f (t)$ 的频谱函数，它一般是复函数，可以写作：
$F (ω) = | F (ω) | e^{j φ (ω)}$
其中 $| F (ω) |$ 是 $F (ω)$ 的模，它代表信号中各频率分量的相对大小， $φ (ω)$ 是 $F (ω)$ 的相位函数，它表示信号中各频率分量之间的相位关系。类似地， $| F (ω) | \sim ω$ 与 $φ (ω) \sim ω$ 曲线分别称为非周期信号的幅度频谱与相位频谱。

3.2. 实例：求单边指数信号的傅里叶变换

已知，单边指数信号的表示式为：
$f (t) = {\begin{cases} e^{- a t} & (t \geq 0) \\ 0 & (t < 0) \end{cases}$
其中 $a$ 为正实数。

单边指数信号的傅里叶变换推导如下：
$\begin{aligned} F (ω) & = \int_{- \infty}^{\infty} f (t) e^{- j ω t} d t \\ = \int_{0}^{\infty} e^{- a t} e^{- j ω t} d t \\ = \int_{0}^{\infty} e^{(a + j ω) t} d t \\ = \frac{1}{a + j ω} \end{aligned}$
从而：
$\begin{aligned} | F (ω) | = \frac{1}{\sqrt{a^{2} + ω^{2}}} \\ φ (ω) = - \arctan (\frac{ω}{a}) \end{aligned}$
单边指数信号的波形及频谱如图 9 所示。

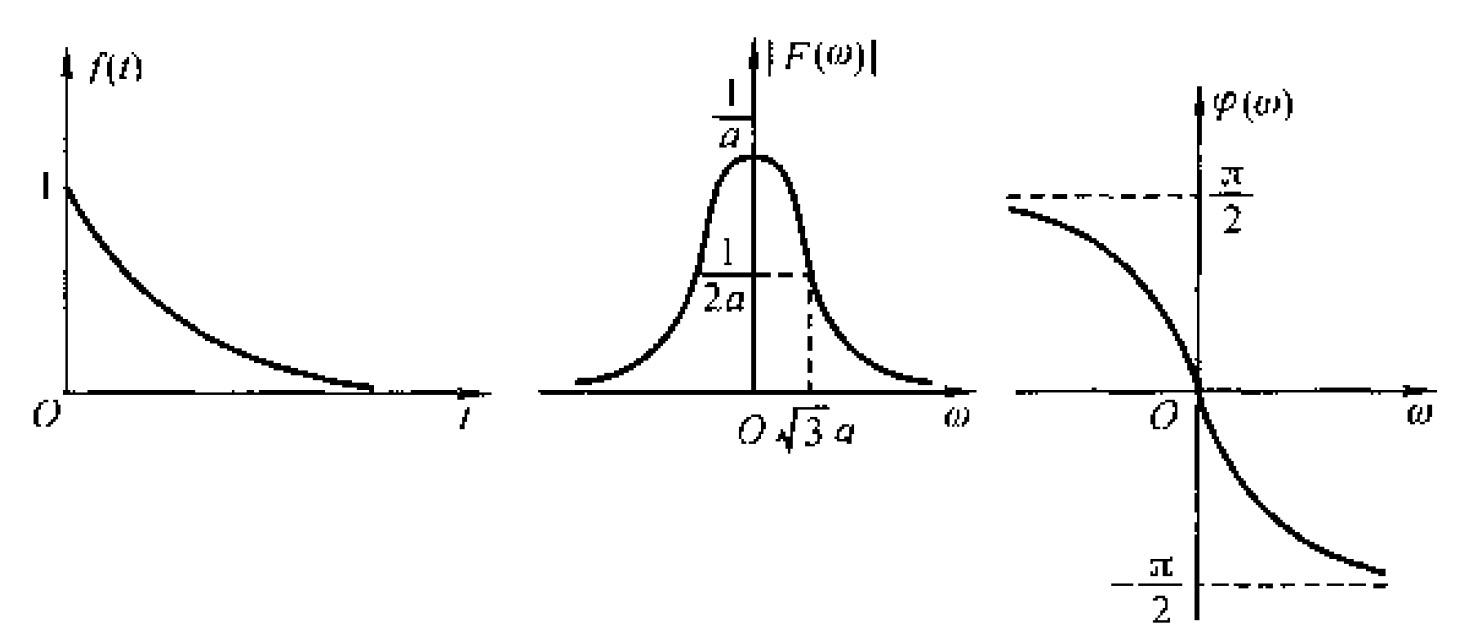
Figure 9: 单边指数信号的波形及频谱

3.3. 卷积定理(Convolution theorem)

对于任意两个信号 $f_{1} (t)$ 和 $f_{2} (t)$ ，两者做卷积运算定义为：
$f_{1} (t) * f_{2} (t) = \int_{- \infty}^{\infty} f_{1} (τ) f_{2} (t - τ) d τ$

时域卷积定理：
设函数 $f_{1} (t)$ 和 $f_{2} (t)$ 的傅里叶变换为 $F_{1} (ω)$ 和 $F_{2} (ω)$ ，则：

\begin{matrix} (时域卷积定理) & F [f_{1} (t) * f_{2} (t)] = F_{1} (ω) \cdot F_{2} (ω) \end{matrix}

证明如下：
$\begin{aligned} F [f_{1} (t) * f_{2} (t)] & = \int_{- \infty}^{\infty} [\int_{- \infty}^{\infty} f_{1} (τ) f_{2} (t - τ) d τ] e^{- j ω t} d t \\ = \int_{- \infty}^{\infty} f_{1} (τ) [\int_{- \infty}^{\infty} f_{2} (t - τ) e^{- j ω t} d t] d τ \\ = \int_{- \infty}^{\infty} f_{1} (τ) F_{2} (ω) e^{- j ω t} d τ \\ = F_{2} (ω) \int_{- \infty}^{\infty} f_{1} (τ) e^{- j ω t} d τ \\ = F_{2} (ω) \cdot F_{1} (ω) \end{aligned}$
它说明： 时域中两信号的卷积等效于在频域中频谱相乘。

频域卷积定理：

\begin{matrix} (频域卷积定理) & F [f_{1} (t) \cdot f_{2} (t)] = \frac{1}{2 π} F_{1} (ω) * F_{2} (ω) \end{matrix}

频域卷积定理的证明过程和时域卷积定理的证明过程类似，这里不再重复。

4. 离散傅里叶变换

设有限长序列 $x (n)$ 长度为 $N$ （在 $0 \leq n \leq N - 1$ 范围内），它的离散傅里叶变换(Discrete Fourier Transform, DFT) $X (k)$ 仍然是一个长度为 $N$ （在 $0 \leq n \leq N - 1$ 范围内）的频域有限长序列。
离散傅里叶变换为：

\begin{matrix} (离散傅里叶变换, DFT) & X (k) = D F T [x (n)] = \sum_{n = 0}^{N - 1} x (n) W^{n k} (0 \leq k \leq N - 1) \end{matrix}

离散傅里叶逆变换为：

\begin{matrix} (离散傅里叶逆变换, IDFT) & x (n) = I D F T [X (k)] = \frac{1}{N} \sum_{k = 0}^{N - 1} X (k) W^{- n k} (0 \leq n \leq N - 1) \end{matrix}

其中， $W_{N} = e^{- j (2 π / N)}$ ，如果所讨论的问题中不涉及 $N$ 的变动，可省略下标，简写为 $W = e^{- j (2 π / N)}$ 。

4.1. 矩阵形式的离散傅里叶变换

前面介绍的离散傅里叶变换及逆变换的公式可以写为矩阵形式。
离散傅里叶变换的矩阵形式：
$[\begin{matrix} X (0) \\ X (1) \\ ⋮ \\ X (N - 1) \end{matrix}] = [\begin{matrix} W^{0} & W^{0} & W^{0} & \dots & W^{0} \\ W^{0} & W^{1 \times 1} & W^{2 \times 1} & \dots & W^{(N - 1) \times 1} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ W^{0} & W^{1 \times (N - 1)} & W^{2 \times (N - 1)} & \dots & W^{(N - 1) \times (N - 1)} \end{matrix}] [\begin{matrix} x (0) \\ x (1) \\ ⋮ \\ x (N - 1) \end{matrix}]$

离散傅里叶逆变换的矩阵形式：
$[\begin{matrix} x (0) \\ x (1) \\ ⋮ \\ x (n - 1) \end{matrix}] = \frac{1}{N} [\begin{matrix} W^{0} & W^{0} & W^{0} & \dots & W^{0} \\ W^{0} & W^{- 1 \times 1} & W^{- 1 \times 2} & \dots & W^{- 1 \times (N - 1)} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ W^{0} & W^{- (N - 1) \times 1} & W^{- (N - 1) \times 2} & \dots & W^{- (N - 1) \times - (N - 1)} \end{matrix}] [\begin{matrix} X (0) \\ X (1) \\ ⋮ \\ X (N - 1) \end{matrix}]$

上面两个公式简写为：

\begin{matrix} (离散傅里叶变换的矩阵形式) & X (k) = W^{n k} x (n) \end{matrix}

和

\begin{matrix} (离散傅里叶逆变换的矩阵形式) & x (n) = \frac{1}{N} W^{- n k} X (k) \end{matrix}

此处， $X (k)$ 与 $x (n)$ 分别为 $N$ 列的列矩阵，而 $W^{n k}$ 与 $W^{- n k}$ 分别为 $N \times N$ 方阵（这两个方阵都是对称矩阵）。

4.2. 实例：求有限序列的离散傅里叶变换

例：求 $x (n) = {1, 1, 1, 1}$ （如图 10 (a)所示）的离散傅里叶变换，再由离散傅里叶逆变换求得 $x (n)$ ，验证结果的正确性。
由 $N = 4$ 得到 $W^{1} = e^{- j (2 π / 4)} = - j$ ，直接应用离散傅里叶变换公式，有：
$\begin{aligned} [\begin{array}{c} X (0) \\ X (1) \\ X (2) \\ X (3) \end{array}] & = [\begin{array}{c} W^{0} & W^{0} & W^{0} & W^{0} \\ W^{0} & W^{1} & W^{2} & W^{3} \\ W^{0} & W^{2} & W^{4} & W^{6} \\ W^{0} & W^{3} & W^{6} & W^{9} \end{array}] [\begin{array}{c} x (0) \\ x (1) \\ x (2) \\ x (3) \end{array}] \\ = [\begin{array}{c} 1 & 1 & 1 & 1 \\ 1 & - j & - 1 & j \\ 1 & - 1 & 1 & - 1 \\ 1 & j & - 1 & - j \end{array}] [\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array}] = [\begin{array}{c} 4 \\ 0 \\ 0 \\ 0 \end{array}] \end{aligned}$

离散傅里叶逆变换为：
$[\begin{matrix} x (0) \\ x (1) \\ x (2) \\ x (3) \end{matrix}] = \frac{1}{4} [\begin{matrix} W^{0} & W^{0} & W^{0} & W^{0} \\ W^{0} & W^{- 1} & W^{- 2} & W^{- 3} \\ W^{0} & W^{- 2} & W^{- 4} & W^{- 6} \\ W^{0} & W^{- 3} & W^{- 6} & W^{- 9} \end{matrix}] [\begin{matrix} 4 \\ 0 \\ 0 \\ 0 \end{matrix}] = [\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix}]$
显然，通过离散傅里叶逆变换可求得原始信号。

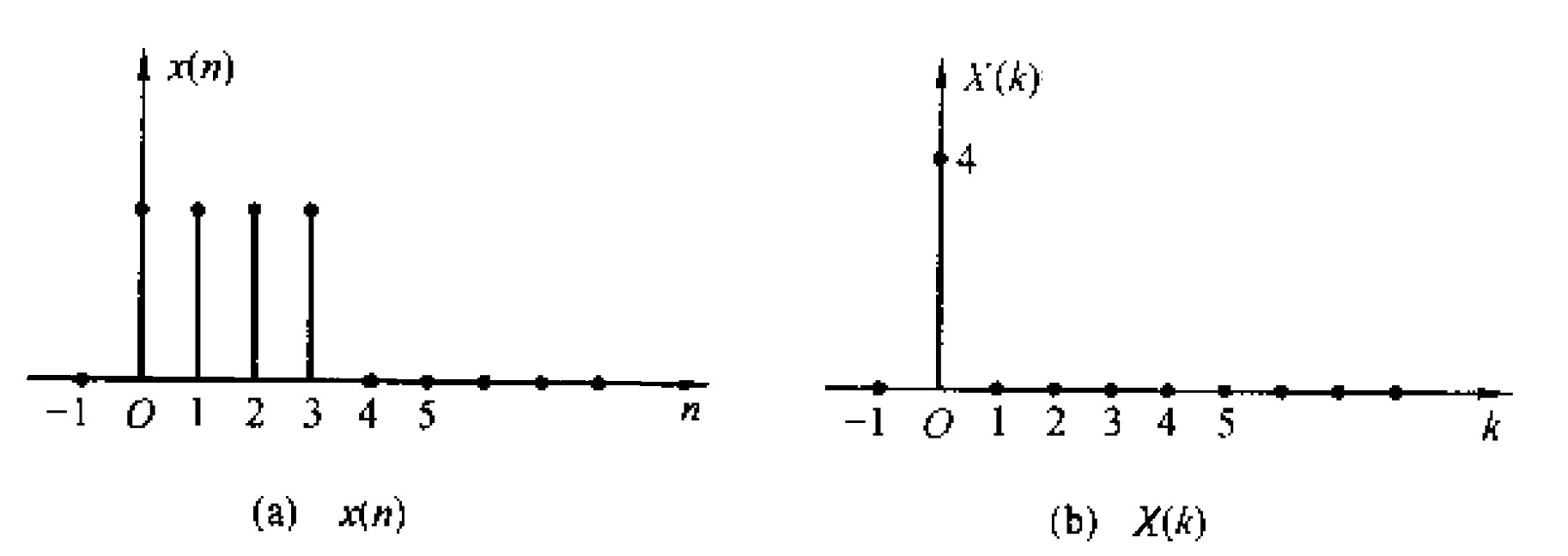
Figure 10: 离散傅里叶变换实例

说明：在这个例子中，离散傅里叶变换得到的序列恰好都为实数。不过，离散傅里叶变换得到的序列一般为复数，比如 $x (n) = {1, 2, 3, 4}$ 的离散傅里叶变换是一个复数序列，计算如下：
$\begin{aligned} [\begin{array}{c} X (0) \\ X (1) \\ X (2) \\ X (3) \end{array}] & = [\begin{array}{c} W^{0} & W^{0} & W^{0} & W^{0} \\ W^{0} & W^{1} & W^{2} & W^{3} \\ W^{0} & W^{2} & W^{4} & W^{6} \\ W^{0} & W^{3} & W^{6} & W^{9} \end{array}] [\begin{array}{c} x (0) \\ x (1) \\ x (2) \\ x (3) \end{array}] \\ = [\begin{array}{c} 1 & 1 & 1 & 1 \\ 1 & - j & - 1 & j \\ 1 & - 1 & 1 & - 1 \\ 1 & j & - 1 & - j \end{array}] [\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array}] = [\begin{array}{c} 10 \\ - 2 + j 2 \\ - 2 \\ - 2 - j 2 \end{array}] \end{aligned}$

4.3. 快速傅里叶变换(FFT)

快速傅里叶变换(Fast Fourier transform, FFT)是一种计算离散傅里叶变换的快速算法。

4.3.1. DFT 的计算量

我们先来了解一下 DFT 的计算量。
由 DFT 定义知，将 $x (n)$ 与 $W^{n k}$ 两两相乘再取和即可得到 $X (k)$ ，即每计算一个 $X (k)$ 值需要进行 $N$ 次复数相乘（一个复数乘法包括 4 个实数乘法和 2 个实数加法），和 $N - 1$ 次复数相加。对于 $N$ 个 $X (k)$ 点，应重复 $N$ 次上述运算。因此， 要完成全部 DFT 运算共需 $N^{2}$ 次复数乘法和 $N (N - 1)$ 次复数加法。
例如，当 $N = 4$ 时，DFT 的矩阵表示式为：
$[\begin{matrix} X (0) \\ X (1) \\ X (2) \\ X (3) \end{matrix}] = [\begin{matrix} W^{0} & W^{0} & W^{0} & W^{0} \\ W^{0} & W^{1} & W^{2} & W^{3} \\ W^{0} & W^{2} & W^{4} & W^{6} \\ W^{0} & W^{3} & W^{6} & W^{9} \end{matrix}] [\begin{matrix} x (0) \\ x (1) \\ x (2) \\ x (3) \end{matrix}]$
显然，求每个 $X (k)$ 值，需要 $N = 4$ 次复数乘法和 $N - 1 = 3$ 次复数加法，要完成全部 DFT 运算共需 $N^{2} = 16$ 次复数乘法和 $N (N - 1)$ 次复数加法。
随着 $N$ 值增大，运算工作量将迅速增长，例如 $N = 10$ 时需要 100 次复数乘法，而当 $N = 1024$ 时，就需要 1048576（一百多万次）次复数乘法运算。所以，当 $N$ 较大时，DFT 的计算量太大，无法对信号进行实时处理。因此，我们需要一种更快的算法来计算 DFT。

4.3.2. Cooley–Tukey FFT algorithm

从 FFT 算法诞生至今，有很多改进和派生的离散傅里叶变换快速算法。最基本的 FFT 是库利-图基 FFT 算法(Cooley–Tukey FFT algorithm)。

库利-图基 FFT 算法描述（这里不证明它的正确性，直接给出结论）如下：
设序列 $x (n)$ 的点数 $N$ 为 2 的整数次幕（即 $N = 2^{L}$ ， $L$ 为整数，如果不满足这个条件，可以人为地加上若干 0 值点，使之达到这一要求）。将 $x (n), (n = 0, 1, \dots, N - 1)$ 先按 $n$ 的偶数子序列和奇数子序列分成以下两组：
$\begin{aligned} x_{1} (r) & = x (2 r), (r = 0, 1, \dots, \frac{N}{2} - 1) \\ x_{2} (r) & = x (2 r + 1), (r = 0, 1, \dots, \frac{N}{2} - 1) \end{aligned}$
记 $X_{1} (k)$ 和 $X_{2} (k)$ 分别是 $x_{1} (r)$ 和 $x_{2} (r)$ 的 $N / 2$ 点 DFT， $W_{N}^{k} = e^{- j (2 π / N) k}$ ，则 $x (n)$ 的离散傅里叶变换的前 $N / 2$ 个值和后 $N / 2$ 个值可分别由下面式子（FFT 核心公式）求得：
$\begin{aligned} X (k) = X_{1} (k) + W_{N}^{k} X_{2} (k), (k = 0, 1, \dots, \frac{N}{2} - 1) \\ X (k + \frac{N}{2}) = X_{1} (k) - W_{N}^{k} X_{2} (k), (k = 0, 1, \dots, \frac{N}{2} - 1) \end{aligned}$
这样，只要求得 0 到 $\frac{N}{2} - 1$ 区间的 $X_{1} (k)$ 和 $X_{2} (k)$ 值，就可以求出 0 到 $N - 1$ 区间内的所有 $X (k)$ 值，显然，这是一种分治策略。对于子序列 $X_{1} (k)$ 和 $X_{2} (k)$ 的求解可以使用同样的思路。图 11 表示了 FFT 算法中利用两个子序列的 DFT 求得整个序列的 DFT 的过程。

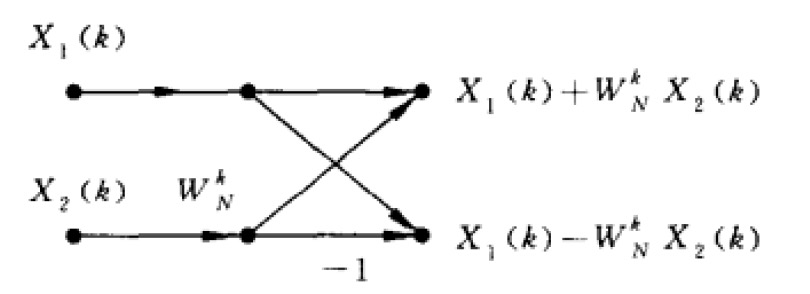
Figure 11: FFT 算法，蝶形信号流图（支路上没有系数时表示该支路传输系数为 1）

参考：
《信号与系统（郑君里，第二版，下册）》9.6 节快速傅里叶变换
《数字信号处理教程（第三版，程佩青）》第四章快速傅里叶变换

4.3.3. 实例：用 FFT 算法计算 DFT

用 FFT 算法求解 $x (n) = {1, 2, 3, 4}$ 的 DFT。

这个例子中 $N = 4$ ，设其偶数子序列 $x_{1} (n) = {1, 3}$ 的 DFT 为 $X_{1} (k)$ ，奇数子序列 $x_{2} (n) = {2, 4}$ 的 DFT 为 $X_{2} (k)$ ，直接利用 FFT 算法公式有：
$\begin{array}{r} X (0) = X_{1} (0) + W_{4}^{0} X_{2} (0) \\ X (1) = X_{1} (1) + W_{4}^{1} X_{2} (1) \\ X (2) = X_{1} (0) - W_{4}^{0} X_{2} (0) \\ X (3) = X_{1} (1) - W_{4}^{1} X_{2} (1) \end{array}$

$X_{1} (k)$ 和 $X_{2} (k)$ 如何求解呢？也可以用 FFT 算法，但序列已经很短了，直接用 DFT 原始定义公式即可：
$\begin{aligned} X_{1} (0) = x (0) + W_{2}^{0} x (2) = 1 + 3 = 4 \\ X_{1} (1) = x (0) - W_{2}^{0} x (2) = 1 - 3 = - 2 \\ X_{2} (0) = x (1) + W_{2}^{0} x (3) = 2 + 4 = 6 \\ X_{2} (1) = x (1) - W_{2}^{0} x (3) = 2 - 4 = - 2 \end{aligned}$

从而， $N = 4$ 时 FFT 算法如图 12 所示。

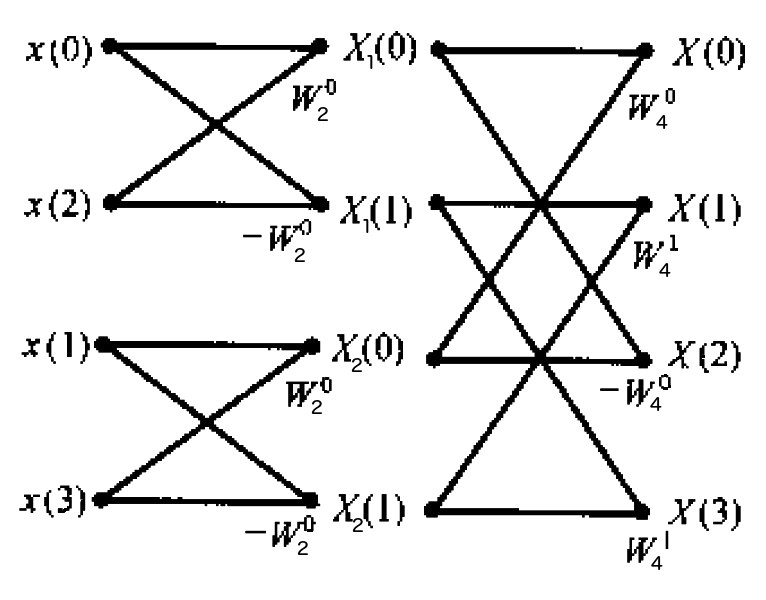
Figure 12: $N = 4$ 时 FFT 算法

容易算得 $W_{4}^{0} = 1, W_{4}^{1} = e^{- j (2 π / 4)} = - j$ ，从而：
$\begin{aligned} X (0) = X_{1} (0) + W_{4}^{0} X_{2} (0) = 4 + 6 = 10 \\ X (1) = X_{1} (1) + W_{4}^{1} X_{2} (1) = - 2 + (- j) (- 2) = - 2 + 2 j \\ X (2) = X_{1} (0) - W_{4}^{0} X_{2} (0) = 4 - 6 = - 2 \\ X (3) = X_{1} (1) - W_{4}^{1} X_{2} (1) = - 2 - (- j) (- 2) = - 2 - 2 j \end{aligned}$

这个结果和不使用 FFT 算法，直接使用 DFT 定义公式得到的结果一样（参见 4.2 ）。

4.3.4. FFT 的计算量

FFT 把一个 $N$ 点的 DFT 分解为两个 $N / 2$ 点 DFT，如果直接计算 $N / 2$ 点 DFT，则由前面分析知一个 $N / 2$ 点 DFT 需要 $(\frac{N}{2})^{2} = \frac{N^{2}}{4}$ 次复数乘法， $\frac{N}{2} (\frac{N}{2} - 1)$ 次复数加法，两个 $N / 2$ 点 DFT，则共需要 $2 \times (\frac{N}{2})^{2} = \frac{N^{2}}{2}$ 将复数乘法和 $N (\frac{N}{2} - 1)$ 次复数加法。此外把两个 $N / 2$ 点 DFT 合成 $N$ 点 DFT 时，还需要 $\frac{N}{2}$ 次复数乘法和 $N$ 次复数加法。所以总共需要 $\frac{N^{2}}{2} + \frac{N}{2} = \frac{N (N + 1)}{2} \approx \frac{N^{2}}{2}$ 次复数乘法和 $N (\frac{N}{2} - 1) + N = \frac{N^{2}}{2}$ 次复数加法。因些，通过把一个 $N$ 点的 DFT 分解为两个 $N / 2$ 点 DFT 后，运算的计算量差不多减少到一半。

显然，对于分解的两个 $N / 2$ 点 DFT，我们不用直接计算，可以再次利用 FFT。从而 $N$ 点 FFT 的运算量会进一步减少。通过更细致的分析可以 FFT 的复数乘法次数是 $\frac{N}{2} \log_{2} N$ ，从而直接计算 DFT 与 FFT 算法的计算量（只考虑了复数乘法）之比为：
$\frac{N^{2}}{\frac{N}{2} \log_{2} N} = \frac{2 N}{\log_{2} N}$
直接计算 DFT 与 FFT 算法的计算量（只考虑了复数乘法）与序列点数 $N$ 的关系曲线如图 13 所示。

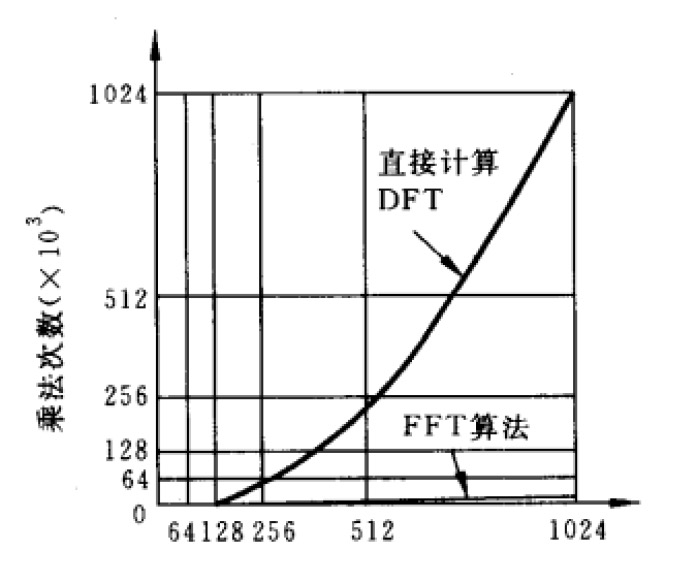
Figure 13: 直接计算 DFT 与 FFT 算法的计算量（只考虑了复数乘法）的比较

4.3.5. FFT 逆变换（快速计算离散傅里叶逆变换）

如何快速地求解离散傅里叶逆变换(IDFT)呢？

我们观察一下离散傅里叶逆变换(IDFT)的公式：
$x (n) = I D F T [X (k)] = \frac{1}{N} \sum_{k = 0}^{N - 1} X (k) W^{- n k} (0 \leq n \leq N - 1)$
与离散傅里叶变换(DFT)公式：
$X (k) = D F T [x (n)] = \sum_{n = 0}^{N - 1} x (n) W^{n k} (0 \leq k \leq N - 1)$
比较两个公式可知，只要把 DFT 运算中的每一个系数 $W^{n k}$ 换成 $W^{- n k}$ ，最后再乘以常数 $1 / N$ ，则 FFT 算法就可以用来运算 IDFT 了。但这需要稍微调整 FFT 程序代码。

下面讨论一种完全不用改变 FFT 的程序就可以快速计算 IDFT 的方法。对 IDFT 公式取共轭：
$x^{*} (n) = \frac{1}{N} \sum_{k = 0}^{N - 1} X^{*} (k) W^{n k}$
从而：
$x (n) = \frac{1}{N} {[\sum_{k = 0}^{N - 1} X^{*} (k) W^{n k}]}^{*} = \frac{1}{N} {[D F T [X^{*} (k)]]}^{*}$

这说明， 只要先将 $X (k)$ 取共轭，就可以直接利用 FFT 程序，最后再将运算结果取一次共轭，并乘以 $1 / N$ ，即得 $x (n)$ 值。 因此，FFT 运算和 IFFT(Inverse Fast Fourier Transform)运算就可以共用一个子程序模块了，这样就很方便了。